Fibroblasts and Alectinib switch the evolutionary games played by non-small cell lung cancer

Abstract

Heterogeneity in strategies for survival and proliferation among the cells which constitute a tumour is a driving force behind the evolution of resistance to cancer therapy. The rules mapping the tumour’s strategy distribution to the fitness of individual strategies can be represented as an evolutionary game. We develop a game assay to measure effective evolutionary games in co-cultures of non-small cell lung cancer cells which are sensitive and resistant to the anaplastic lymphoma kinase inhibitor Alectinib. The games are not only quantitatively different between different environments, but targeted therapy and cancer associated fibroblasts qualitatively switch the type of game being played by the in-vitro population from Leader to Deadlock. This observation provides empirical confirmation of a central theoretical postulate of evolutionary game theory in oncology: we can treat not only the player, but also the game. Although we concentrate on measuring games played by cancer cells, the measurement methodology we develop can be used to advance the study of games in other microscopic systems by providing a quantitative description of non-cell-autonomous effects.

Tumours are heterogeneous, evolving ecosystems [cancerEvoEco, heppner1984tumor], comprised of sub-populations of neoplastic cells that follow distinct strategies for survival and propagation [ibrahim2017defini The success of a strategy employed by any single neoplastic sub-population is dependent on the distribution of other strategies, and on various components of the tumour microenvironment, like cancer associated fibroblasts (CAFs) [SM17]. The EML4-ALK fusion, found in approximately 5% of non-small cell lung cancer (NSCLC) patients, leads to constitutive activation of oncogenic tyrosine kinase activity of ALK, thereby “driving” the disease. Inhibitors of tyrosine kinase activity of ALK (ALK TKI) have proven to be highly clinically efficacious, inducing tumour regression and prolonging patient survival [shaw2013crizotinib, peters2017alectinib]. Unfortunately, virtually all of the tumours that respond to ALK TKIs eventually relapse [shaw2013alk] – an outcome typical of inhibitors of other oncogenic tyrosine kinases [gillies2012evolutionary]. Resistance to ALK TKI, like most targeted therapies, remains a major unresolved clinical challenge. Despite significant advances in deciphering the resultant molecular mechanisms of resistance [katayama2015therapeutic], the evolutionary dynamics of ALK TKI resistance remains poorly understood. The inability of TKI therapies to completely eliminate tumour cells has been shown to be at least partially attributable to protection by aspects of the tumour microenvironment [marusyk2016spatial]. CAFs are one of the main non-malignant components of tumour microenvironment and the interplay between them and tumour cells is a major contributor to microenvironmental resistance, including cytokine mediated protection against ALK inhibitors [YTN+12].

To study the eco-evolutionary dynamics of these various factors, we interrogated the competition between treatment naive cells of ALK mutant NSCLC cell line H3122 – a “workhorse” for studies of ALK+ lung cancer – and a derivative cell line in which we developed resistance to Alectinib – a highly effective clinical ALK TKI [ou2015alectinib] – by selection in progressively increasing concentrations of the drug [DNKAMHS17]. We aimed to come to a quantitative understanding of how these dynamics were affected by clinically relevant concentrations of Alectinib (0.5μM; see [seto2013ch5424802]) in the presence or absence of CAFs isolated from a lung cancer. To achieve this, we developed an assay for quantifying effective games [effectiveGames, spaceConfusion] that is of independent interest to the general study of microscopic systems.

Results

Monotypic vs mixed cultures

To establish baseline characteristics, we performed assays in monotypic cultures of parental (Alectinib-sensitive) and resistant cell lines with and without Alectinib and CAFs. To gather temporally-resolved data for inferring growth rates, we used time lapse microscopy to follow the expansion of therapy resistant and parental cells, differentially labeled with stable expression of selectively neutral GFP and mCherry fluorescent proteins, respectively. From the time series data, we inferred the growth rate with confidence intervals for each one of 6 experimental replicates in four different experimental conditions (total of 24 data points, each with confidence intervals), as seen in Figure 1. As expected, alectinib inhibited growth rates of parental cells (DMSO vs Alectinib: p < .005; DMSO + CAF vs Alectinib + CAF: p < .005), whereas the growth rate of the resistant cells was not affected. And, as previously reported [YTN+12], CAFs partially rescued growth inhibition of parental cells by Alectinib (Alectinib vs Alectinib + CAF: p < .005; Alectinib + CAF vs DMSO: p < .005), without impacting growth rates of resistant cells.

Figure 1:

Monotypic culture exponential growth rates for parental (cyan) and resistant (magenta) cells in indicated experimental conditions. Confidence intervals on each experimental replicate is from confidence on the estimate of growth rate for that single replicate according to the Theil-Sen estimator. Comparisons between experimental conditions (of 6 replicates each) are made using Wilcoxon rank-sum. In addition to conditions linked by lines with reported p-values, conditions labeled by ‘a’ and ‘b’ are pairwise distinguishable with p < .005.

But we did not limit ourselves to monotypic assays. Our experience observing non-cell-autonomous biological interactions [nonCA] and modeling eco-evolutionary interactions [basanta2012investigating, edge, doubleGoods] in cancer led us to suspect that the heterotypic growth rates would differ from monotypic culture. Cell-autonomous fitness effects are ones where the benefits/costs to growth rate are inherent to the cell: the presence of other cells are an irrelevant feature of the micro-environment and the growth rates from monotypic cultures provide all the necessary information. Non-cell-autonomous effects [nonCA] allow fitness to depend on a cell’s micro-environmental context, including the frequency of other cell types: growth rates need to be measured in competitive fitness assays over a range of seeding frequencies. Other microscopic experimental systems in which frequency dependent fitness effects have been considered include, but are not limited to: Escherichia coli [kerr2002local, freqDepEcoli], yeast [yeastPG, gore2009snowdrift], bacterial symbionts of hydra [bacteriaGames], breast cancer [nonCA] and pancreatic cancer [A15]. Hence, we continued our experiments over a range of initial proportions of resistant and parental cells in mixed cultures for each of the four experimental conditions.

Figure 2 shows the resulting growth rates of each cell type in the co-culture experiments for all experimental (color, shape) and initial conditions (opacity is parental cell proportion). In the heterotypic culture – unlike monotypic – CAFs slightly improved the growth rates of the parental cells, even in DMSO. More strikingly, even in the absence of drug, resistant cells tend to have a higher growth rate than parental cells in the same environment (i.e. proportion of parental cells in the co-culture). This is evident from most DMSO points being above the dotted diagonal line (y = x) corresponding to equal growth rate of the two types (this is quantified in Figure 4b and is further discussed in section ‘Leader and Deadlock games in NSCLC’).

Figure 2: Coculture growth rates across four experimental conditions.

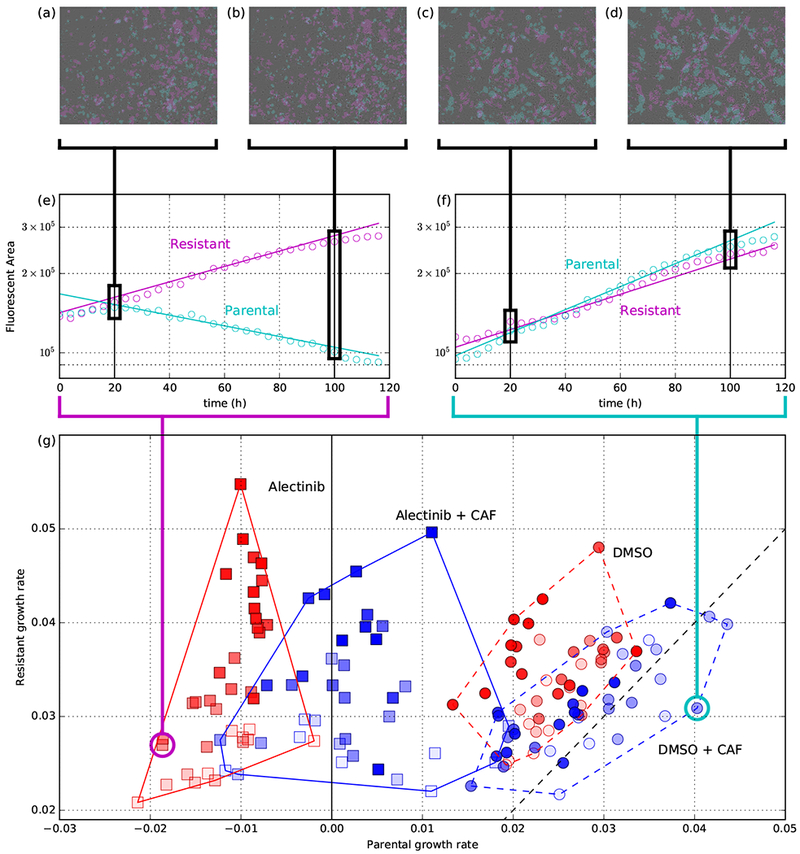
(a-f) serve as a sketch of the analysis procedure to produce the main subfigure (g); for more detailed discussion, see Supplementary Information Section B.4 (a,b,c,d): In each experimental replicate at each time step, we quantify population size by fluorescent area of each cell type (shown: two different time points per well, from two different wells). Together, 30 time-lapse microscopy images (one every 4 hours) from each replicate create (e,f): time-series of parental and resistant population size (shown: two example wells). With x-axis is time, y-axis is log of population size. Exponential growth rates (and confidence intervals; omitted) were estimated for each well using the Theil-Sen estimator. These exponential models are shown as solid lines and their slopes serve as the coordinates in (g). See Figure 3 for growth rate confidence intervals and Supplementary Information Section B.2 for detailed discussion of growth-rate measurement. (g): Each point is a separate replicate of a competitive fitness assay with initial proportion of parental cells represented by opacity and experimental condition represented by shape (DMSO: circle; Alectinib: square) and colour (no CAF: red; + CAF: blue). Each replicate’s x-position corresponds to the measured parental growth rate and y-position for resistant growth rate; the dotted black line corresponds to the line of equal fitness between the two at x = y.

Figure 4: Measured games. (a) Replicator dynamics.

Consider an idealized population of two strategies in a competitive co-culture: parental (P) and resistant (R). When a subpopulation of P interacts with P the subpopulation experiences a fitness effect A; when P interacts with R then P experience fitness effect B and R a fitness effect C; two Rs interact with fitness effects D, summarized in the matrix. This can be interpreted as an idealized exponential growth model for the number of parental (N_P) and resistant (N_R) cells. The dynamics of the proportion of parental cells $p=\frac{N_P}{N_P+N_R}$ over time is described by the replicator equation (bottom). In Supplementary Information Section E we discuss a purely experimental interpretation based on effectiveGames. (b) Mapping of the four measured in vitro games into game space. The x-axis is relative fitness of a resistant focal in a parental monotypic culture: C – A; y-axis is relative fitness of a parental focal in a resistant monotypic culture: B – D. Games measured in our experimental system are given as specific points with error bars based on goodness of fit of linear fitness functions in Figure 3. The games corresponding to our conditions are given as matrices (with entries multiplied by a factor of 100) by their label. See Supplementary Information Section C for more details. The game space is composed of four possible dynamical regimes, one for each quadrant. The typical dynamics of each dynamic regime are represented as qualitative flow diagram between P and R: an upward cyan arrow corresponds to an increase in the parental proportion, and a downward magenta arrow correspond to an increase in the resistant proportion. In the case of the two dynamic regimes observed in our NSCLC system, we also include insets of measured dynamics (c,d): Experimental time-series of proportion of parental cells for DMSO + CAF (c) and Alectinib + CAF (d). Each line corresponds to the time dynamics of a separate well. A line is coloured magenta if proportion of resistant cells increased from start to end; cyan if proportion of parental cells increased; black if statistically indistinguishable proportions at start and end (where start/end are defined as the first/last 5 time-pints (20 hours)). See Supplementary Figure 1 for proportion dynamics of all four games and Supplementary Figure 2 for density dynamics and their correspondence to the exponential growth model from Figure 4a.

Frequency dependence in fitness functions

Although not common in cancer biology, competitive fitness assays are a gold standard for studying bacteria. But they are typically conducted with a single initial ratio of the two competing cell types. However, in Figure 2, if we view the initial proportion of parental to resistant cells as a variable parameter represented by opacity then we can see a hint of frequency dependence in both parental and resistant growth rates. This is shown more clearly as a plot of fitness versus proportion of parental cells in Figure 3. In all four conditions, we see that the growth rate of the resistant and parental cell lines depends on the initial proportion of parental cells. To capture the principle first-order part of this dependence, we consider a line of best fit between initial proportion of parental cells and the growth rates. See equations 1-8 in Supplementary Information Section C (or the matrix entries in Figure 4b) for these lines of best fit. Interpretable versions of these lines of best fit (see Supplementary Information Section D) can be expressed as a regularized fitness function $w_{\mathit{S}}^C$ where S ∈ {P, R} indexes the parental or resistant strategy and C ∈ {DMSO, DMSO + CAF, Alectinib, Alectinib + CAF} indexes the experimental condition. For a description of regularization see Supplementary Information Section D. Finally, for a discussion of higher-order fitness functions, see Supplementary Information Section F.

Figure 3: Fitness functions for competition of parental vs. resistant NSCLC.

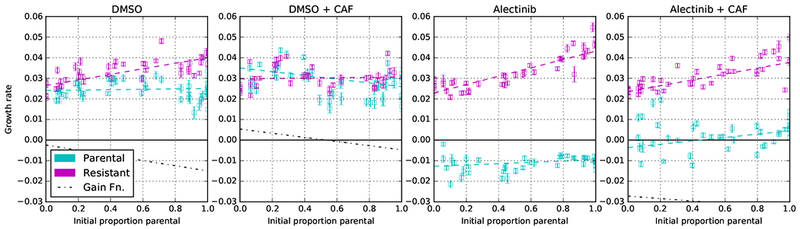
For each plot: growth rate with confidence intervals versus initial proportion of parental cells. This is the same data, measured in the same way, as Figure 2. Cyan data points are growth rates of parental cells, and magenta for resistant cells. Dotted lines represent the linear fitness function of the least-squares best fit; fit error is visualised in Figure 4b. The black dotted line is the gain function for parental (see Figure 4a), it is well below the y = 0 line in the Alectinib conditions (indicating the strong advantage of resistance) and thus cut out of the figure. See Supplementary Information Section C for more discussion and equations for lines of best fit, and Supplementary Information Section F for alternative fits with non-linear fitness functions.

In three of the conditions, resistant cell growth rates increase with increased seeding proportion of parental cells, while parental growth rates remain relatively constant (in the case of no CAFs) or slightly increase (for Alectinib + CAFs). In DMSO, this suggests that parental cells’ fitness is independent of resistant cells: $w_{\mathit{P}}^{\mathrm{DMSO}}$ = 0.025. Parental fitness in DMSO could be well characterized as cell-autonomous. However, resistant cells in monotypic culture have approximately the same fitness as parental cells (Figure 2a), but they benefit from the parental cells in co-culture: $w_{\mathit{R}}^{\mathrm{DMSO}}$ = 0.025 + 0.015p (where p is the proportion of parental cells). Their fitness has a non-cell autonomous component. The positive coefficient in front of p suggests commensalism between resistant and parental cells, i.e. resistant cells benefit from the interaction with the parental cells, without exerting positive or negative impact on them.

The DMSO + CAF case differs from the other three in that we see a constant – although elevated $w_{\mathit{R}}^{\mathrm{DMSO\; +\; CAF}}$ = 0.03 – growth rate in resistant cells; but a linearly decreasing (in p) growth rate of parental cells: $w_{\mathit{P}}^{\mathrm{DMSO\; +\; CAF}}$ = 0.025 + 0.01(1 – p) (or, equivalently: $w_{\mathit{P}}^{\mathrm{DMSO\; +\; CAF}}$ = 0.03 – 0.01($\frac{1}{2}$ – p)). This could be interpreted as CAFs switching the direction of commensalism between parental and resistant cells.

Leader and Deadlock games in NSCLC

The tools of evolutionary game theory (EGT) are well suited for making sense of frequency-dependent fitness [firstEGT, firstOncoEGTl, firstOncoEGT2, basanta2012investigating, A13, edge, A15, doubleGoods]. In EGT, a game is the rule mapping the population’s strategy distribution to the fitness of individual strategies. Previous work has considered games like snowdrift [gore2009snowdrift], stag hunt [bacteriaGames], rock-paper-scissors [kerr2002local], and public goods [yeastPG, A15] alongside experiments. Instead, we experimentally operationalize the effective game (see [effectiveGames, spaceConfusion]) as an assayable hidden variable of a population and its environment. We define the effective game as the game played by an idealized population that shows the same frequency dynamics as the experimental population under consideration. As such, we are not aiming to test EGT as an explanation. Instead, we are defining a game assay to quantitatively describe our system in the language of EGT. In future work, it would be interesting to ask about the best language for describing cancer evolution by testing the game assay against several clearly and well operationalized alternatives to EGT.

To measure the effective game that describes the non-cell-autonomous interactions in NSCLC, we focus on the gain function (see [gainSigns, doubleGoods] for a theoretical perspective): the difference in growth rate between resistant and parental cells as a function of proportion of parental cells. The relatively good fit of a linear dependence of growth rates on parental seeding proportion allows us to describe the interaction as a matrix game – a well-studied class of evolutionary games (see a description in Figure 4a). Note that this linearity is not guaranteed to be a good description for arbitrary experimental systems. For example, the game between the two Betaproteobacteria Curvibacter sp. AEP1.3 and Duganella sp. C1.2 was described by a quadratic gain function [bacteriaGames]. If one views our work from the perspective of model selection then in the main text we proceed from the assumption of linearity. Supplementary Information Section F relaxes this assumption, extends our game assay to non-linear games, and compares linear and non-linear models with information criteria. Our qualitative results are unchanged, although the exact quantitative results for non-linear models differ slightly.

Two strategy matrix games have a convenient representation in a two dimensional game-space (see the model in Figure 4a and Supplementary Information Section C for details). This is the output of our game assay. We plot the inferred games in a game-space spanned by the theoretical fitness advantage a single resistant invader would have if introduced into a parental monotypic culture versus the fitness advantage of a parental invader in a resistant monotypic culture; as shown in Figure 4b. In this representation, there are four qualitatively different types of games corresponding to the four quadrants, each of which we illustrative with a dynamic flow. We can see that the game corresponding to DMSO + CAF – although quantitatively similar to DMSO – is of a qualitatively different type compared to all three of the other combinations.

We can also convert our inferred fitness functions from Figure 3 into a payoff matrix. We do this by having each row correspond to a strategy’s fitness function with the column entries as the p =1 and p = 0 intersects of this line of best fit. These payoff matrix entries are abstract phenomenological quantities that could be implemented by various biological or physical processes [effectiveGames]. If we look at our empirical measurements for DMSO + CAF (upper-right quadrant Figure 4b) we see the Leader game, and Deadlock in the other three cases (we will use DMSO to illustrate the Deadlock game).

The Deadlock game observed in DMSO is in some ways the opposite of the popular Prisoner’s Dilemma (PD) game (in fact, RG05 call it the anti-PD). If we interpret parental as cooperate and resistant as defect then, similar to PD, each player wants to defect regardless of what the other player does (because 4.0 > 2.5 and 2.7 > 2.4; payoff numbers used in these examples are from the matrix entries we measured in Figure 4) but hopes that the other player will cooperate (because 4.0 > 2.7). However, unlike PD, mutual cooperation does not Pareto dominate mutual defection (because 2.5 < 2.7) but is instead strictly dominated by it. Thus, the players are locked into defection. In our system, this corresponds to resistant cells having an advantage over parental in DMSO.

The Leader game observed in DMSO + CAF is one of R67’s four archetypal 2 × 2 games and a social dilemma related to the popular game known as Hawk-Dove, Chicken, or Snowdrift (in fact, RG05 call it Benevolent Chicken). If we interpret parental as ‘lead’ (for Snowdrift: wait) and resistant as ‘work’ (for Snowdrift: shovel) then similar to Snowdrift, mutual work is better than both leading (because 3.0 > 2.6) and thus no work being done (for Snowdrift: both waiting and thus not getting out of the snowdrift) but each player would want to lead while the other works (because 3.5 > 3.0). However, unlike Snowdrift, mutual work is not better than the “sucker’s payoff” of working while the other player leads (because 3.1 > 3.0). R67 sees this as a tension with a player switching from a “natural” point of mutual work to lead and thus benefit both players (3.5 > 3.0,3.1 > 3.0), but if the second player also does the same and becomes a leader then all benefit disappears (because 2.6 is the smallest payoff). In our system, this corresponds to cells in the tumour experiencing selective pressure to lose some but not all of its resistance in DMSO + CAF.

Note that the above intuitive stories are meant as heuristics, and the effective games that we measure are summaries of population level properties [effectiveGames, spaceConfusion]: the population is the player and the two types of cancer cells are the strategies. This means that the matrix entries should not be interpreted as direct interactions between cells, but as general couplings between subpopulations corresponding to different strategies. The coupling term includes not only direct interactions, but also indirect effects due to spatial structure, diffusible goods, contact inhibition, etc.. But this does not mean that an effective game is not interpretable. For example, the Deadlock game captures the phenomenon of the resistant population always being fitter than parental (for example, in DMSO). We noted this effect intuitively in Figure 2 (also see section Cost of resistance) from replicates being above the y = x diagonal. Measuring a Deadlock game for DMSO with confidence intervals that do not extend outside the bottom right quadrant of the game space in figure 4b allows us to show the statistical significance of our prior intuitive understanding. In other words, effective games allow us to quantify frequency-dependent differences in growth rates.

Discussion

Cost of resistance

The classic model of resistance posits that the resistant phenotype receives a benefit in drug (in our case: Alectinib or Alectinib + CAF) but is neutral, or even carries an inherent cost, in the absence of treatment (DMSO or DMSO + CAF). For example, experimentalists frequently regard resistance granting mutations as selectively neutral in the absence of drug, and the modeling community often goes further by considering explicit costs like up-regulating drug efflux pumps, investing in other defensive strategies, or lowering growth rate by switching to sub-optimal growth pathways [anderson2006tumor, ibrahim2017defining]. If we limited ourselves to the monotypic assays of Figure 1, then our observations would be consistent with this classic model of resistance. But in co-culture, we observed that resistant cells have higher fitness than parental cells in the same environment, even in the absence of drug. This is not consistent with the classic model of resistance. This higher fitness of resistant cells might not surprise clinicians as much as the biologists: in clinical experience, tumours that have acquired resistance are often more aggressive than before they were treated, even in the absence of drug. See Supplementary Information Section A.3 for a contrast of the biologist and clinician’s view of resistance in this context.

Treating the game

Measuring a linear gain function has enabled us to develop an assay that represents the inter-dependence between parental and resistant cells as a matrix game. Experimentally cataloging these games allows us to support existing theoretical work in mathematical oncology that considers treatment (or other environmental differences) as changes between qualitatively different game regimes [A13, basanta2012investigating, edge, doubleGoods]. In this framework, treatment has the goal not to directly target cells in the tumour, but instead to perturb the parameters of the game they are playing to allow evolution to steer the tumour towards a more desirable result (for examples, see [A13, basanta2012investigating, edge, doubleGoods, steer, vascTheory]). Empirically, this principle has inspired or built support for interventions like buffer therapy [buffer], vascular renormalization therapy [vascEmp], and adaptive therapy [zhang2017integrating] that target the micro-environment and interactions instead of just attacking the cancer cell population. The success of the zhang2017integrating trial suggests that therapeutic strategies based on modulating competition dynamics are feasible. This highlights the need for a formal experimental method like our game assay that directly measures the games that cancer plays and tracks if and how they change due to treatment.

In our system, we can view an untreated tumour as similar to DMSO + CAF and thus following the Leader game. Treating with Alectinib (move to Alectinib + CAF) or eliminating CAFs through a stromal directed therapy (move to DMSO), moves the game into the lower-right quadrant of Figure 4b, and the game becomes a Deadlock game. Not only are these games quantitatively different among the four environmental conditions – see Figure 4b – but they are also of two qualitatively different types. To our knowledge, neither of the Leader and Deadlock games are considered in the prior EGT literature in oncology. Given that the Deadlock of drug-resistant over drug-sensitive cells is a challenge for classic models of resistance we would be particularly interested in theoretical models of resistance that produce the Deadlock game. In addition to challenging theorists by adding two new entries to the catalogue of games that cancers play, this switch allows us to show that the theoretical construct of EGT – that treatment can qualitatively change the type of game – has a direct experimental implementation. Unfortunately, neither of our in vitro games would lead to a therapeutically desirable outcome if they occurred in a patient.

Heterogeneity and latent resistance

A particularly important difference between Leader and Deadlock dynamics is the existence of an internal fixed point in Leader but not in Deadlock. Fixed points are a property of equilibrium dynamics: in the most general case, even on very long timescales these fixed points might not be realized due to the evolutionary constraints of population size [slowRepDyn] or computation [hardESS, compConstEvo]. Thus, it is important to check to what extent this qualitative difference can translate to a quantitative difference in finite time horizons. In our system, we can see a quantitative difference in the convergence towards the fixed point in the DMSO + CAF condition of Figure 4c, and no such convergence in the other three cases (Figure 4d for Alectinib + CAF; Supplementary Figure 1). Since the strength of selection (magnitude of the gain function) is small near a fixed point, the change in p also slows in the DMSO + CAF condition. We provide a more robust analysis of this in Supplementary Information Sections C and F. It would be of interest for future work to study the long-term experimental stability of these fixed points.

Since the DMSO + CAF condition is our closest to an untreated patient, it might have important consequences for latent resistance. Many classical models of resistance assume a rare preexistent mutant taking over the population after the introduction of drug. In our experimental system, however, if the resistant strategy is preexistent then negative frequency dependent selection will push the population towards a stable polyclonal tumour of resistant and sensitive cells before the introduction of drug. This allows for much higher levels of preexisting heterogeneity in resistance than predicted by the classical picture. As such, we urge theorists to reconsider the assumption of the rare pre-existing resistant clone.

Of course, our results are for a single in vitro system. But if similar games occur in vivo and/or for other cancers, then such preexisting heterogeneity could be a possible evolutionary mechanism behind the speed and robustness of treatment resistance to targeted therapies in patients. This could help explain the ubiquity and speed of resistance that undermines our abilities to cure patients or control their disease in the long term. We will not know this unless we set out to quantify the non-cell autonomous processes in cancer. Building a catalogue of the games cancers play – by adopting our game assay in other cancers, and other experimental contexts – can help resolve this and other questions.

Methods

Cell lines

H3122 cell line was obtained from Dr. E. Haura (Moffitt Cancer Center). Cell line identity was validated by the Moffitt Cancer Center Molecular Genetics core facility using short tandem repeats (STR) analysis. Primary lung cancer associated fibroblasts were obtained from Dr. S. Antonia lab (Moffitt Cancer Center), following the protocols approved by the USF Institutional Review Board. CAFs were isolated as previously described in PMID26935219 and expanded for 3-10 passages prior to the experiments. The Alectinib resistant derivative cell line was obtained through escalating inhibitor concentration protocol, as described in DNKAMHS17. Alectinib sensitive parental H3122 cells were cultured in DMSO for the same length of time, as the alectinib resistant derivate.

Stable GFP and mCherry expressing derivative cell H3122 cell lines were obtained through lentiviral transduction with pLVX-AcGFP (Clontech) and mCherry (obtained from K. Mitsiades, DFCI) vectors, respectively. We cultured both H3122 cells and CAFs in RPMI media (Gibco brand from Thermo Scientific), supplemented with 10% FBS (purchased from Serum Source, Charlotte, NC). Regular tests for mycoplasma contamination were performed with MycoScope PCR based kit from GenLantis, San Diego, CA.

Experimental set-up

The cells were harvested upon reaching 70% confluence and counted using Countess II automatic cell counter (Invitrogen). CAFs were counted manually to avoid segmentation artifacts. Mixtures of parental and resistant H3122 cells were prepared at 8 different ratios: all-resistant, 9:1 resistant to parental, 4:1, 3:2, 2:3, 1:4, 1:9, and all-parental. For the determination of competitive growth rates, 2,000 H3122 cells from the 8 mixtures were seeded with or without 500 CAF cells in 50 μL RPMI media per well into 384 well plates (Corning, catalogue #7200655), with different ratios of differentially labelled parental and alectinib resistant variants: with 6 wells used for each resistant:parental ratio in each of the 4 conditions. 20 hours after seeding, Alectinib – purchased from ChemieTek (Indianapolis, IN) – or DMSO vehicle control, diluted in 20 μL RPMI was added to each well, to achieve final Alectinib concentration of 500 nM/L [seto2013ch5424802]. Time lapse microscopy measurements were performed every 4 hours in phase-contrast white light, as well as green and red fluorescent channels using Incucyte Zoom system from Essen Bioscience.

Game assay

We use the exponential growth rate in the fluorescent area of the two fluorescent channels as our measure of fitness. In order to minimise the impact of growth inhibition by confluency, we analyzed the competitive dynamics during the first 5 days of culture, when the cell population was expanding exponentially. We learned growth rate along with a confidence interval from the time-series of population size in each well using the Theil-Sen estimator. More detail on and justification of this measure of fitness is available in Supplementary Information Section B.2.

Since raw population sizes have different units (GFP Fluorescent Area (GFA) vs mCherry Fluorescent Area (RFA)), we converted them to common cell-number-units (CNU) by learning the linear transform that scales GFA and RFA into CNU. We defined proportions based on this common CNU as p = N_P/(N_p + N_R) where N_{P,R} is the CNU size of parental and resistant populations. The transform of GFA to RFA into CNU is associated with an error that is propagated to measures of p as σ_ρ.

To measure the fitness functions we plotted fitness of each cell-type in each well vs seeding proportion (p) of parental cells in Figure 3. The x-axis proportion of parental cells (p) was computed from the first time-point. We estimated the line of best-fit and error on parameters for this data using least-squares weighted by the inverse of the error on each data point. For the exact lines of best-fit, see Supplementary Information Section C.3.

The p = 0 and p = 1 intercepts of the lines of best fit serve as the entries of the game matrices. Note that in Figure 4b, we multiplied the entries by 100 for easier presentation. The game point are calculated from the matrices as x := C – A and y := B – D, and the error is propagated from the error estimates on lines of best-fit’s parameters.