Skip to main content
. 2019 Apr 9;8:e41046. doi: 10.7554/eLife.41046

Figure 2. Changes in metabolite concentrations and physiological parameters during cellular aging.

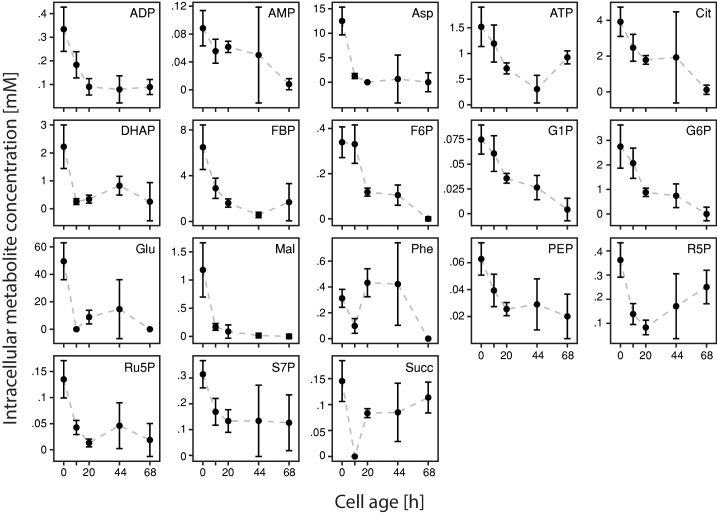
(a) The intracellular metabolite concentrations of 18 metabolites at various cell ages were inferred from LC-MS/MS measurements, cell volume measurements and the fractional abundances of each cell population using non-linear least square regression. Grey dashed lines depict the change of intracellular metabolite concentrations relative to concentrations determined from streptavidin-labeled cells (i.e. young cells at an age of 0 hr). The change in ATP concentration is highlighted in red, and FBP (fructose-1,6-bisphosphate) in blue. Figure 2—figure supplement 4 shows the data for each metabolite in absolute units. Figure 2—source data 1 contains the data. (b) The growth (µ), metabolite uptake and production rates at various cell ages were obtained by measuring the evolution of cell count and extracellular metabolites (including produced carbon dioxide and consumed oxygen) and fitting the acquired data to an ordinary differential equation model. A positive value indicates metabolite production and a negative uptake. To assess the validity of the inference approach physiological rates were independently determined from unlabeled and streptavidin-labeled cell cultures (time point 0 hr), consisting of predominantly young cells. The shading reflects the inverse of the relative uncertainty of the estimation (i.e. values which are depicted with a higher transparency are more uncertain). Figure 2—source data 2 contains the data.

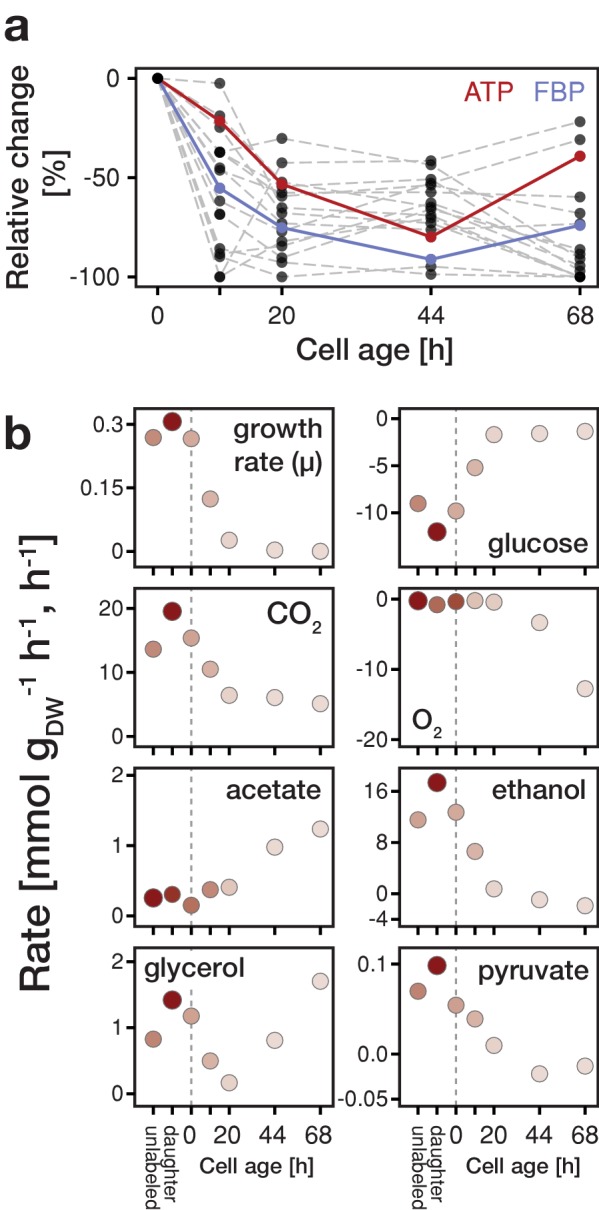
Figure 2—source data 1. Intracellular metabolite concentrations inferred for daughter and aging mother cells.
elife-41046-fig2-data1.xlsx (10.8KB, xlsx)
DOI: 10.7554/eLife.41046.016
Figure 2—source data 2. Growth rates and yields inferred for daughter and aging mother cells.
elife-41046-fig2-data2.xlsx (12.4KB, xlsx)
DOI: 10.7554/eLife.41046.017

Figure 2.

Figure 2—figure supplement 1. The cellular volume gradually increases with cellular age.

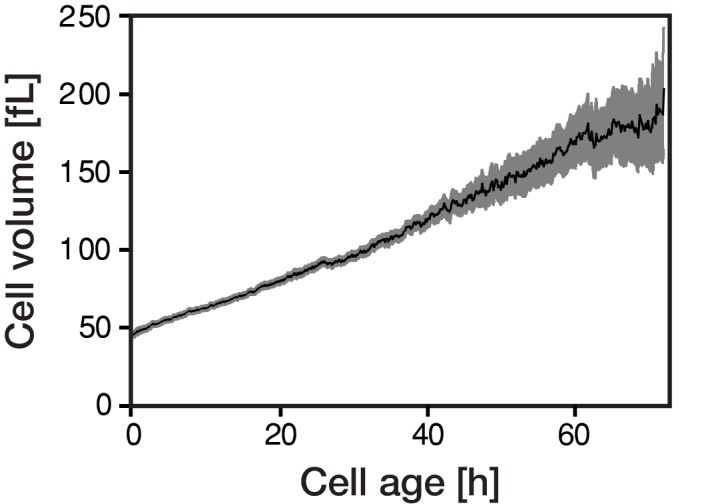
Figure 2—figure supplement 1.

Individual cells of Saccharomyces cerevisiae were tracked in a microfluidics device (Huberts et al., 2013; Lee et al., 2012) and bright field images were recorded throughout their whole lifespan. The cellular volume was subsequently determined from the acquired microscopic data using the ImageJ plugin BudJ.
Figure 2—figure supplement 2. Inference of intracellular metabolite concentrations.

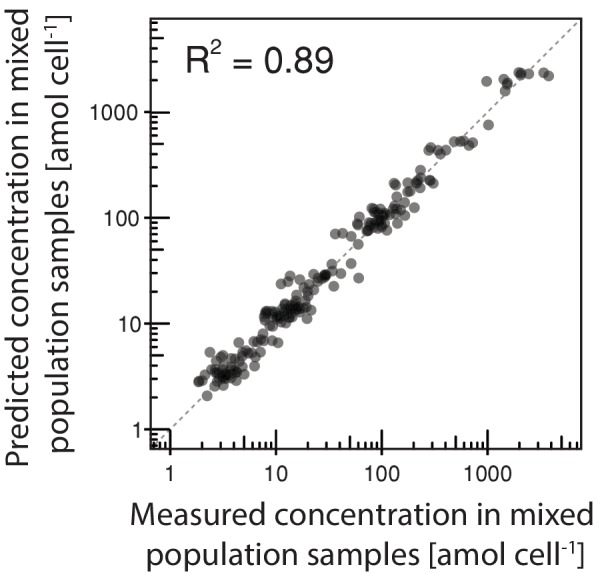
Figure 2—figure supplement 2.

The intracellular concentration of 18 metabolites in daughter and aging mother cells was inferred from data obtained in various mixed population samples using non-negative least square regression where we obtained an excellent fit.
Figure 2—figure supplement 3. Comparison of inferred intracellular metabolite concentrations with independently determined concentrations of young cells.

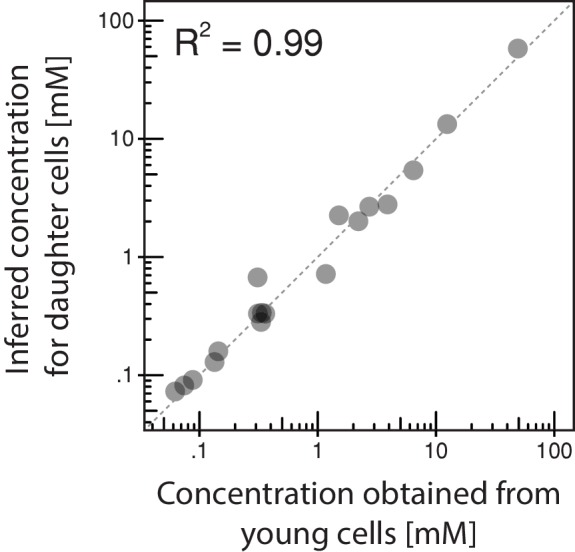
Figure 2—figure supplement 3.

To confirm the validity of inference method for intracellular metabolite concentrations, we determined the metabolite concentration of young streptavidin-labeled cells and compared them to the inferred metabolite concentrations of daughter cells, which, by definition, should have the same phenotype. Here, we found a good consensus, confirming our approach.
Figure 2—figure supplement 4. Inference of intracellular concentrations of 18 metabolites with cell age.

Figure 2—figure supplement 4.

We found a drastic decrease of metabolite concentrations with cell age (starting from young daughter cells (da)) of all 18 metabolites: adenosindiphosphat (ADP), adenosinmonophosphat (AMP), aspartic acid (Asp), adenosintriphosphat (ATP), citric acid (Cit), dihyroxy acetone phosphate (DHAP), fructose 1,6-bisphosphate (FBP), fructose-6-phosphate (F6P), glucose-1-phosphate (G1P), glucose-6-phosphate (G6P), glutamic acid (Glu), malic acid (Mal), phenylalanine (Phe), phosphoenolpyruvic acid (PEP), ribose-5-phosphate (R5P), ribulose-5-phosphate (Ru5P), sedoheptulose-7-phosphate (S7P) and succinic acid (Succ). The standard errors were determined by leave-one-out cross-validation, where we one-by-one removed data points from the set and repeated the estimation procedure.
Figure 2—figure supplement 5. The energy charge remains constant with cell age.

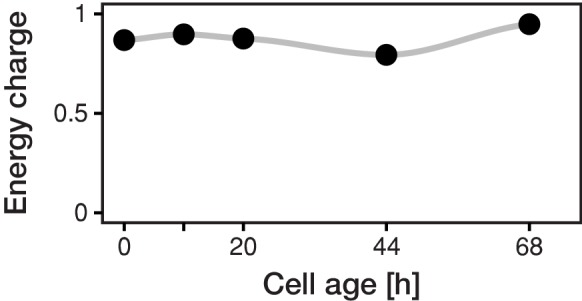
Figure 2—figure supplement 5.

Despite the vast decrease of the inferred concentrations of all three adenosin nucleotides with cell age, the energy charge was maintained between 0.8 and 0.95, which corresponds to values of exponentially growing cultures (Ditzelmüller et al., 1983).
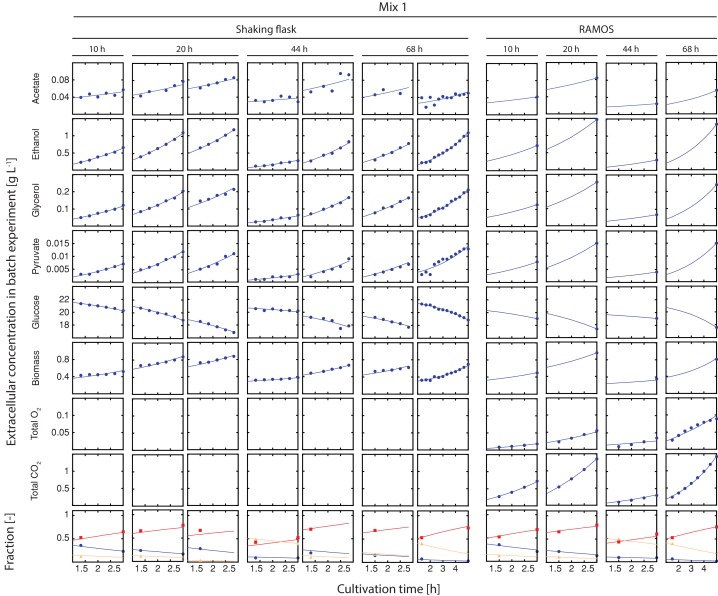
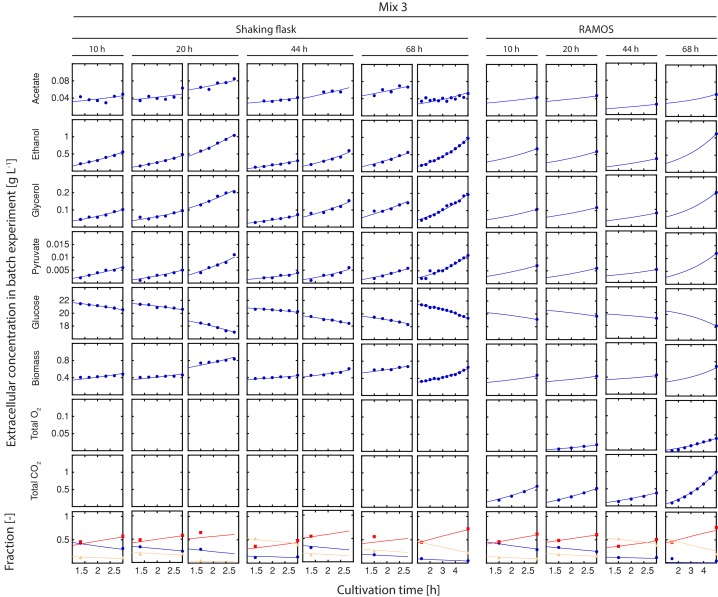
Figure 2—figure supplement 6. Inference of physiological parameters from dynamic changes in extracellular metabolites.

Figure 2—figure supplement 6.

At each time point (after 10, 20, 44 and 68 hr), we measured the evolution of cell count (which was converted to dry weight (i.e. biomass)) and extracellular concentrations of acetate, ethanol, glycerol, pyruvate and glucose over a period of three hours in the harvested sample mix 1. The dry mass specific fractional abundance of each cell population was determined before and after that period. We used a second set of aliquots to measure the evolution of produced carbon dioxide and consumed oxygen using a Respiration Activity Monitoring System (RAMOS) (Hansen et al., 2012). To infer the population-specific physiological rates from the mixed-population samples, we fitted the acquired dynamic data to an ordinary differential equation model, describing the changes of the biomass and extracellular metabolite concentrations in the samples, due to mother and daughter cell growth and their respective metabolism.
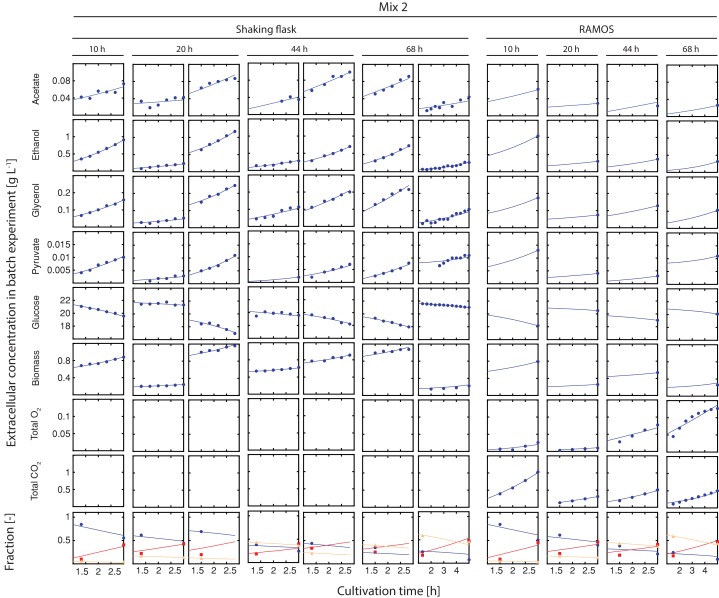
Figure 2—figure supplement 7. Inference of physiological parameters from dynamic changes in extracellular metabolites.

Figure 2—figure supplement 7.

At each time point (after 10, 20, 44 and 68 hr), we measured the evolution of cell count (which was converted to dry weight (i.e. biomass)) and extracellular concentrations of acetate, ethanol, glycerol, pyruvate and glucose over a period of three hours in the harvested sample mix 2. The dry mass specific fractional abundance of each cell population was determined before and after that period. We used a second set of aliquots to measure the evolution of produced carbon dioxide and consumed oxygen using a Respiration Activity Monitoring System (RAMOS) (Hansen et al., 2012). To infer the population-specific physiological rates from the mixed-population samples, we fitted the acquired dynamic data to an ordinary differential equation model, describing the changes of the biomass and extracellular metabolite concentrations in the samples, due to mother and daughter cell growth and their respective metabolism.
Figure 2—figure supplement 8. Inference of physiological parameters from dynamic changes in extracellular metabolites.

Figure 2—figure supplement 8.

At each time point (after 10, 20, 44 and 68 hr), we measured the evolution of cell count (which was converted to dry weight (i.e. biomass)) and extracellular concentrations of acetate, ethanol, glycerol, pyruvate and glucose over a period of three hours in the harvested sample mix 3. The dry mass specific fractional abundance of each cell population was determined before and after that period. We used a second set of aliquots to measure the evolution of produced carbon dioxide and consumed oxygen using a Respiration Activity Monitoring System (RAMOS) (Hansen et al., 2012). To infer the population-specific physiological rates from the mixed-population samples, we fitted the acquired dynamic data to an ordinary differential equation model, describing the changes of the biomass and extracellular metabolite concentrations in the samples, due to mother and daughter cell growth and their respective metabolism.
Figure 2—figure supplement 9. FBP (fructose-1,6-bisphosphate) concentration as function of sugar uptake rate.

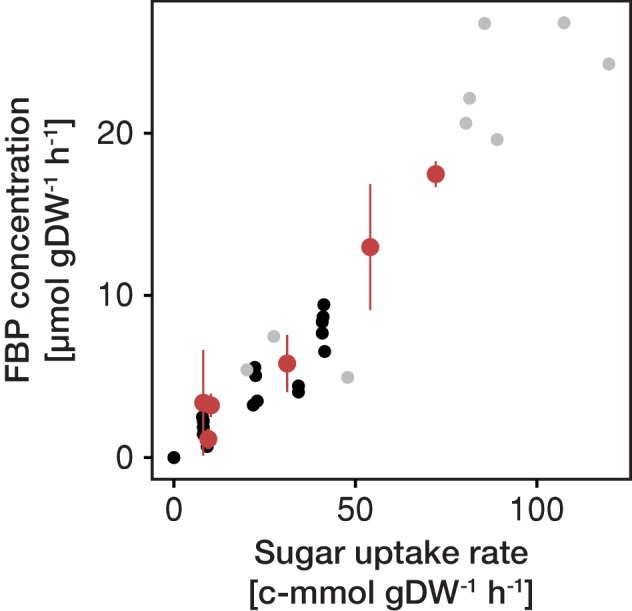
Figure 2—figure supplement 9.

Fructose-1,6-bisphosphate is a glycolytic flux-signaling metabolite and its concentration strictly correlates with the carbon flow through the glycolysis or the sugar uptake rate (Huberts et al., 2012). The independently inferred rate of glycolysis and FBP concentration in aging cells follows this correlation, providing evidence for the validity of the two independently generated data sets, that is physiological rates and metabolite levels. Black dots (Christen and Sauer, 2011), grey dots (de Assis Souza, 2016) and red dots inferred for aging cells.
Figure 2—figure supplement 10. The decreasing growth rate was confirmed using single cell analysis.

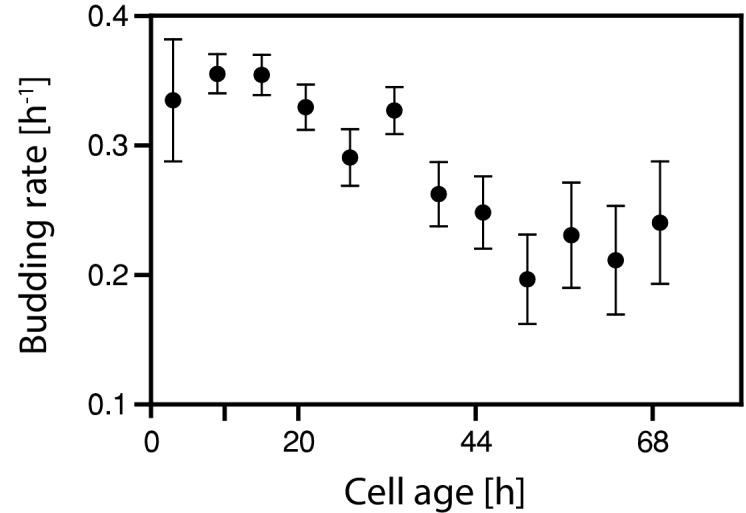
Figure 2—figure supplement 10.

The decreasing growth rate inferred with cell age was confirmed using microfluidics and microscopy. Cells from an exponentially growing batch culture were loaded onto a microfluidics device and monitored for >70 hr. The doubling time (time from bud emergence to next bud emergence) was measured for each cell in bright-field images, and the budding rate for each doubling event (ln(2) td−1) was calculated. Budding rates within 6 hr windows were averaged. Note, that the growth rate in Figure 2b was inferred from the increase of biomass in the culture while here the growth rate is determined from the budding rate of individual cells. Because of the prolonged G1 phase of newborn cells and the asymmetric division, both values are not identical, however, show both a decreasing trend.
Figure 2—figure supplement 11. The yeast proteome progressively transforms form a fermentation- to a respiration-associated state during aging.

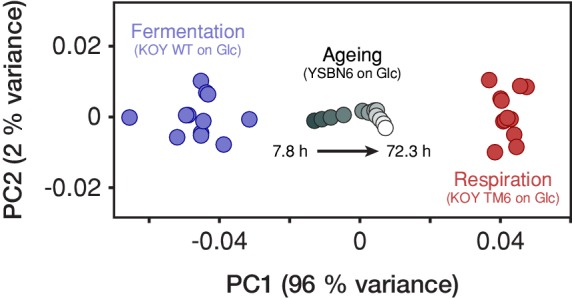
Figure 2—figure supplement 11.

Proteomes of yeast (YSBN6 strain on 2% glucose) obtained at 12 consecutive replicative ages (gradient gray circles) were compared to proteomes of fermenting (KOY WT on 1% glucose) and respiring (KOY TM6 on 1% glucose; Elbing et al., 2004) cells derived from 12 and 13 replicate batch cultures, respectively (blue and red circles). We focused on 396 metabolic proteins present in all proteome data sets and, within each proteome, normalized their abundances by the total one. Next, we centered the 25 proteomes of fermenting and respiring cells together on the origin and performed a principal component analysis (PCA) using the module Sklearn (v0.19.1) in Python (v3.4.3). Next, we centered the proteomes of ageing cells and projected them on two principal components PC1 and PC2 that explain most of the variance among the proteomes of fermenting and respiring cells. PC1 can be interpreted as the fermentation-respiration dimension, that is, the dimension summarizing almost all the differences between the fermentation- and respiration-associated states of the yeast metabolic proteome. Here, we found that the yeast proteome during aging progressively transforms form a fermentation- to a respiration-associated state, similarly as inferred from our physiological analysis (Figures 2b and 3).
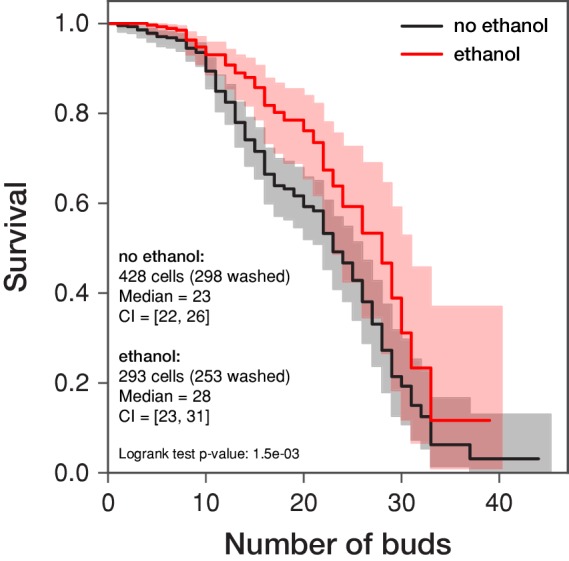
Figure 2—figure supplement 12. Replicative lifespan is increased in the presence of ethanol.

Figure 2—figure supplement 12.

The replicative lifespan of S. cerevisiae is assessed in a microfluidic dissection platform in 0.5% glucose with and without 0.1% ethanol. The curves represent the survival estimates obtained by the Kaplan-Meier procedure considering the numbers of buds produced by the indicated amount of cells (including the cells that were washed out by the medium flow prior death, that is right censoring of the data; these cells are denoted as “washed”). The shaded area demarks the 95 % confidence intervals. The survival estimates were summarized using the median values and their 95 % confidence intervals (CI). Note that the mean survival with its standard error are 22.32 ± 0.76 in the absence of ethanol and 26.44 ± 1.67 in the presence of ethanol. However, as the right censoring of the data biases the calculation of the mean survival, the median is more robust. The survival curves are compared in the log-rank test whose p-value is given.