Abstract
The theory of receptor-ligand binding equilibria has long been well-established in biochemistry, and was primarily constructed to describe dilute aqueous solutions. Accordingly, few computational approaches have been developed for making quantitative predictions of binding probabilities in environments other than dilute isotropic solution. Existing techniques, ranging from simple automated docking procedures to sophisticated thermodynamics-based methods, have been developed with soluble proteins in mind. Biologically and pharmacologically relevant protein-ligand interactions often occur in complex environments, including lamellar phases like membranes and crowded, non-dilute solutions. Here we revisit the theoretical bases of ligand binding equilibria, avoiding overly specific assumptions that are nearly always made when describing receptor-ligand binding. Building on this formalism, we extend the asymptotically exact Alchemical Free Energy Perturbation technique to quantifying occupancies of sites on proteins in a complex bulk, including phase-separated, anisotropic, or non-dilute solutions, using a thermodynamically consistent and easily generalized approach that resolves several ambiguities of current frameworks. To incorporate the complex bulk without overcomplicating the overall thermodynamic cycle, we simplify the common approach for ligand restraints by using a single distance-from-bound-configuration (DBC) ligand restraint during AFEP decoupling from protein. DBC restraints should be generalizable to binding modes of most small molecules, even those with strong orientational dependence. We apply this approach to compute the likelihood that membrane cholesterol binds to known crystallographic sites on 3 GPCRs (beta2-adrenergic, 5HT-2B, and mu-opioid) at a range of concentrations. Non-ideality of cholesterol in a binary cholesterol:phosphatidylcholine (POPC) bilayer is characterized and consistently incorporated into the interpretation. We find that the three sites exhibit very different affinities for cholesterol: the site on the adrenergic receptor is predicted to be high affinity, with 50% occupancy for 1:109 CHOL:POPC mixtures. The site on the 5HT-2B and mu-opioid receptor are predicted to be lower affinity, with 50% occupancy for 1 ∶ 103 CHOL:POPC and 1 ∶ 102 CHOL:POPC respectively. These results could not have been predicted from the crystal structures alone.
Graphical Abstract
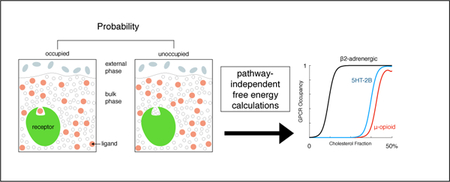
Introduction
Over the past two decades numerous advancements have improved the accuracy and precision of methods for calculating binding free energies. Force field parameters for ligands are now developed consistent with the parent force field using largely automated tools.1–7 Many studies have reported successful use of free energy calculation methods to reproduce or predict experimental binding affinities.8–13 Typical applications involve predicting dissociation constants for ligands binding in dilute-isotropic solution. One of the most common such approaches is double decoupling using Alchemical Free Energy Perturbation (AFEP). Although the method is theoretically exact and pathway independent, it is technically challenging to achieve convergence. Several groups have also laid the groundwork for employing restraints to tremendously improve the convergence of free energsy calculations,14–16 but even in the simple case of a ligand binding to a protein in aqueous solution, designing, implementing, and correcting for such restraints is a delicate process.
The theory associated with current approaches for calculating binding affinities targets an isotropic dilute solution, treated as an ideal mixture quantified on a volume concentration scale. Many affinity prediction problems originate from pharmacology and involve high-affinity binding of dilute ligands, but the increasingly used fragment-based drug design approach implies high concentrations of small, relatively low-affinity ligands.17 In these contexts, non-ideality becomes a potential source of error, which is not currently addressed in the biomedical and pharmacological literature. Binding from even an isotropic non-ideal bulk has not, to our knowledge, been previously addressed using molecular simulation methods for measuring affinities and predicting titration.
Furthermore, many non-ideal biologically relevant situations involve a bulk solution that is a complex or phase-separated fluid, with a high effective ligand concentration (within the preferred phase) even if the overall ligand concentration is low. This scenario is not well-suited to the traditional underlying formalism for treatments of ligand binding. As an example, calculating the binding free energy of a lipid for a site on a membrane protein presents several additional challenges compared to solution calculations. Physiological membranes are frequently non-ideal mixtures composed of multiple species with significant abundances, and consequently cannot be treated as a dilute solution. Even if a dilute solution approximation is made, however, interpretation of calculated binding affinities is also complicated due to ambiguities in the concentration scale and appropriate standard state, since the typical solution standard state (1 M or 1 molecule per 1660 Å3) is not directly trans-ferable to quasi-two-dimensional lipid bilayer systems. (Some authors18 have approximated the volume of the membrane by the volume of the hydrophobic region of the membrane, thus permitting the use of the volume-based solution standard state definition, but this approach is not wholly satisfying since it precludes straightforward comparison between affinity measurements in membranes of different thicknesses.) Quantifying experimental conditions on the water concentration scale would require achieving measurable concentrations of ligand in the water phase, which may not be possible with the most hydrophobic ligands.
In a computational context, free energy calculations with respect to a non-isotropic bulk often introduce additional technical challenges already encountered for large or flexible ligands. Frequently ligand molecules in non-isotropic bulk may have a high aspect ratio and a strong orientation dependence in binding: simple center-of-mass restraints are too simplistic to sufficiently enhance convergence because they leave orientational and conformational degrees of freedom to be extensively sampled during the alchemical simulations. Conversely, more complete restraining schemes require a number of simulations to calculate the free energies of adding successive layers of restraints to the necessary degrees of freedom.13 In the example of a lamellar membrane environment, the distribution of a given lipophilic ligand is non-uniform across the membrane thickness, and superficial binding sites for lipids are not easily described using current restraint schemes.
In this study, we present a general methodological framework for using AFEP calculations to calculate binding free energies for ligands in a complex bulk, including quasi-2D lamellar systems as well as 3D solutions, and accounting for non-ideal and non-dilute mixtures. To make this tractable, we propose several adjustments to current practice:
Extending the formalism for interpreting non-dilute and/or non-3D mixtures for comparison of simulation and empirical results, emphasizing physical observables rather than variables of arbitrary dimension.
Estimation of a concentration-response curve including non-ideality of the bulk bymultiple bulk decoupling calculations at a range of concentrations.
Substantial simplification of the restraint scheme for a bound ligand.
As an example application, we calculate the probability of binding of cholesterol from a POPC bilayer with 0–50% cholesterol to crystallographic sites on three different G-protein coupled receptors (GPCRs) : β2-adrenergic, µ-opioid, and 5-HT2 (serotonin) receptors. Function and organization of GPCRs is highly sensitive to cholesterol,19–21 multiple crystal structures show cholesterol in various binding modes for several classes of GPCR (reviewed recently in ref. 22) and interactions of cholesterol with GPCRs have received considerable interest from computational studies.23–27 To our knowledge, all computational estimates of the occupation probability have been determined based on residence-times from equilibrium molecular dynamics simulations (either atomistic or coarse-grained), which are limited by residence times and lipid diffusion times that are similar to or longer than accessible simulation timescales. In that approach, estimating concentration dependence requires separate simulations of the protein for every concentration. Using our approach, we present probabilities of occupation for a range of cholesterol concentrations (trace to 50%).
Our method also quantifies and explicitly incorporates non-ideality of cholesterol:POPC membranes; we find that they are well-described as quadratic binary mixtures over the range of compositions with stable lamellar phases, with an unfavorable enthalpy of mixing.
This manuscript presents an underlying theory followed by a specific application. Theory is structured as follows: A generalized macroscopic treatment presented in Macroscopic Framework is followed by a consistent Microscopic Framework for use in the interpretation of simulations. The microscopic treatment is then decomposed into intermediate states that are practical for a double decoupling approach, but that also clarify interpretation of concentrations in non-isotropic bulk phases, in Decomposition into Intermediate States. Next we specify how to interpret results of the method in Predicting Ligand Titration, inspired by a double decoupling framework and including a regular solution theory for non-ideality. Finally, in Generic flat-well restraints, we present an approach for simulations with minimal geometric ligand restraints that satisfy assumptions previously made in the formalism.
An application of the method to predict occupancy of cholesterol binding to three different GPCRs is also presented. Details of the implementation for this specific system are provided in Methods. Results demonstrates non-ideality of cholesterol in phospholipid bilayers, which is considered with a fit to regular solution theory, independent of binding to any protein. The final outcome is a prediction of cholesterol titration curves for the three GPCRs.
Theory
There are two equivalent ways to describe the state in which a ligand non-covalently binds to a receptor: 1) a macroscopic framework, in which a new chemical species (the receptor-ligand complex) is created and two separate entities (the free ligand and the receptor) are annihilated or 2) a microscopic framework, in which the bound state refers to a certain spatial localization of the ligand molecule (within the receptor binding site). While the former makes use of the existing familiar framework established for reaction equilibrium, the latter is more directly relatable to the calculations used in explicit computational methods. Although these two conventions are equivalent, consistency within a given treatment is essential. We begin within the macroscopic framework for empirical relevance, then switch to the microscopic framework to rigorously relate experimental observables to quantities accessible from simulations.
Macroscopic Framework
In this framework commonly used by experimental scientists, for consistency with the usual treatment of covalent reactions, the receptor-ligand complex is treated as a new chemical species, whose formation requires the annihilation of a free ligand and an unliganded macromolecule:
| (1) |
For a closed system with NL total ligand molecules, NR total receptor molecules, and a one to one binding stoichiometry, the system composition is specified by the concentration of each supramolecular species, [L], [R], and [RL], at equilibrium, and the probabilities of a ligand being bound or free or a protein site being occupied or unoccupied are pbound, pfree, pocc and punocc respectively. The following definitions and identities also hold, where Table 1 elaborates on the meaning of each symbol.
| (2) |
| (3) |
| (4) |
| (5) |
In a binding assay, [R]tot would typically be fixed, [L]tot would be varied, and pocc would be measured:
| (6) |
Three different issues make the natural independent variable [L]tot only indirectly related to the typical theory that is used to interpret the results (and thus to computational methods). We consider these complicating factors in turn.
Table 1:
Symbols and notation repeated within the theory.
| Molecular Species | |
|---|---|
| S | solvent |
| L | ligand |
| R | receptor (macromolecule) |
| RL | receptor-ligand complex |
| Absolute System Composition | |
| NL | total number of ligand molecules |
| NR | total number of protein molecules |
| nL | total number of ligand molecules (unitary system); nL = NL/NR |
| nS | total number of solvent molecules (unitary system) |
| v | volume of the unitary system |
| generalized reference “volume”; usually v for isotropic solutions | |
| bulk ligand generalized “concentration” ; | |
| [L]tot | total ligand volume concentration; nL/v |
| Equilibrium System Composition | |
| pocc | fraction of binding sites that are occupied (≡ 1 − punocc) |
| pbound | fraction of ligand that is bound (≡ 1 − pfree) |
| [L] | free ligand volume concentration; nLpfree/v |
| {L} | ligand activity |
| Ligand environment | |
| b | ligand coupled to bulk phase |
| g | ligand in gas phase (decoupled) |
| r | ligand coupled to protein |
| Tagged ligand state and restraints | |
| ◾ | unrestrained, in binding site |
| ◽ | unrestrained, all ligands outside binding site |
| − | tagged ligand removed (number of ligand molecules reduced by 1) |
| = | under anisotropic restraint consistent with bulk phase |
| ○ | under isotropic restraint enclosing volume V ○ |
| ▵ | under DBC (distance-from-bound-configuration) restraint |
| α | fraction of bulk phase enclosed by = restraints |
| Probabilities and Statistics | |
| configurational partition function for a system with ligand coupled to phase i under restraints j with composition further specified in Table 2. | |
| generalized binding constant: | |
| bulk/gas partition coefficient of ligand at bulk concentration | |
| h0 | mean-field enthalpy of mixing, vanishes in ideal mixture |
| P0 | bulk/gas partition coefficient in ideal mixture |
Complication 1: Free vs Total
By definition of KA, in the infinitely-dilute limit,
| (7) |
where the latter equality uses Eq. 3. It is common to carry out experiments under conditions of high excess ligand, corresponding to , and then assume that . This assumption, however, is needlessly restrictive, and our general formalism does not depend on it.
Complication 2: Non-ideality; Concentration vs Activity
In the general case, regardless of dilution, the activities of the three species obey:
| (8) |
Here we assume either no interactions between receptors; or that interactions between receptors are not significantly affected by ligand binding, so that non-ideal contributions of occupied and unoccupied receptors cancel out:
| (9) |
| (10) |
In the laboratory, plotting would provide an indication of whether the quantity KAγLpfree was constant, as is frequently assumed. It would not indicate, however, whether non-linearity originated from non-abundant ligand (Complication 1) or non-ideality (Complication 2), but it can be expected that the former case would dominate at low concentrations and the latter case would play a role at higher concentrations. We may write more concisely the dependence of receptor occupancy on total ligand concentration:
| (11) |
where we define an equilibrium coefficient κL with dimensions of inverse concentration :
| (12) |
and that contains all the information related to interactions of the ligand with the protein or in solution.
We are motivated to define this new quantity because our formulation of AFEP yields a value for that can be used to predict experimental observables (pocc) for a given [L]tot. If the relevant experimental conditions are non-ideal with respect to the ligand, affinity predictions can be carried out for those conditions without estimating KA and γL, which would require additional computational work. Thus we avoid the conventional and often artificial reference to infinitely dilute conditions whenever such conditions are not relevant.
Complication 3: Concentration dimensions
Once we release ourselves from a commitment to calculating KA, we are also able to generalize the notion of the relevant concentration. In membranes, for instance, either an area concentration or a mole fraction may provide the most direct relationship with empirical data and physiological mechanisms. In a well-defined but irregular phase (such as a solution of micelles), NL and NR may be the only accessible variables.
Assuming no binding cooperativity among receptors as stated above, a closed system containing NR receptor molecules behaves as NR non-interacting copies of a “unitary” system containing one receptor and possessing the same intensive properties, including the mole fractions of solvent and ligand molecules. Ligand abundance may be measured as the number of ligand molecules in such a unitary system: .
From this point forward, our formalism uses a “generalized total ligand concentration”
| (13) |
| (14) |
where is a generalized volume with dimensions and magnitude for the specific application (note that because it is a unitary volume, it is actually intensive). A convenient choice is (the volume of the unitary system), because then is the volume concentration of the ligand within the phase. In other geometries, it may make sense to set equal to the area of a unitary system (suitable for quasi-2D systems like membranes): or even just set so that , the number of ligand molecules in the unitary system. The equilibrium coefficient is also then generalized to
| (15) |
Then explicitly:
| (16) |
| (17) |
Microscopic Framework
The unitary system connects the macroscopic framework to a microscopic framework that best describes molecular simulations. It is defined as a bulk liquid phase containing a single receptor with a binding site and two types of small molecules, L and S, with composition 1:nL:nS for receptor:L:S, as illustrated in Figure 1. This unitary system is equivalent to a unit cell in a “lattice” binding model.28 Although we refer to the solvent as species S for the sake of simplicity, it may consist of an arbitrary mixture. This liquid (or liquid crystal) phase may coexist with other phases, and we make no assumption about its geometry, so that it may represent membranes, micelles, or other aggregates.
Figure 1: Schematic presentation of the various intermediate states connecting the unoccupied and occupied states of the unitary system.
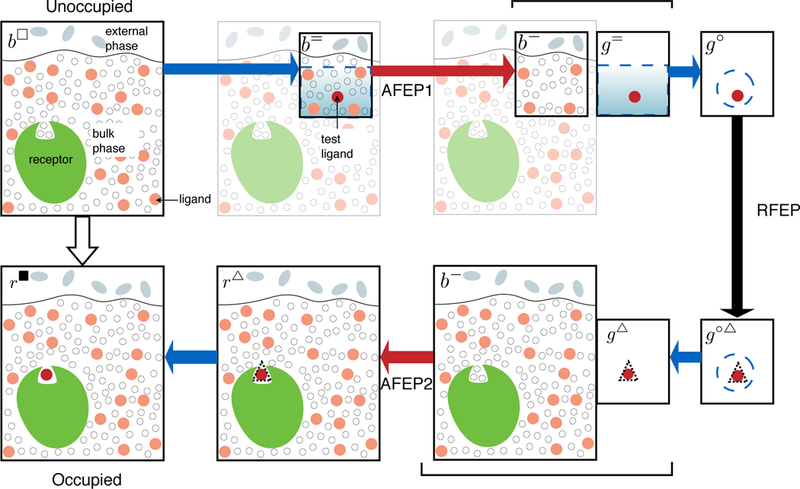
The receptor is green, molecules in the external phase are gray, bulk solvent and ligand molecules are white and pale red circles respectively. The test ligand for decoupling from bulk (AFEP1) and from protein (-AFEP2) is shown as a bright red circle. Blue dashed lines indicate the test ligand is subject to restraints with simple translational geometry, with the shaded gradient indicating possible orientational restraints for highly anisotropic bulk. Black dashed lines indicate the test ligand is under DBC restraints. Systems that are actually simulated are outlined in thicker line, whereas greyed-out components are included in the theory, but omitted from numerical simulations when doing so does not alter the results. Color of arrows represents technique: alchemical free energy perturbation (AFEP, red), restraint free energy perturbation (RFEP, black), analytical (blue). Braces connect pairs of decoupled systems that are sampled simultaneously in alchemical simulations.
In the microscopic perspective, chemical entities are stable, yet a supramolecular receptor-ligand complex may exist when the coordinates of both molecules satisfy certain geometric criteria. Appropriate criteria vary across applications, making a robust and general implementation challenging thus far. We postpone making specific remarks about these geometric criteria, but define them in the abstract as separating the statistical ensemble of our unitary system into two macrostates: either one ligand satisfies the criteria, with probability pocc, or no ligand does, with probability punocc.
To determine the ratio pocc/punocc, we use an approach that generalizes the double decoupling method of Gilson et al.,14 beginning with the overall ratio of partition functions between the state r◾, when one ligand satisfies the structural requirements for occupancy, and the state b◽ in which that ligand is in the bulk environment and no other ligands occupy the binding site,
| (18) |
where and are the configurational partition functions for the b◽ and r◾ states respectively.
A summary of notation and parameter definitions can be found in Table 1, and a relevant thermodynamic cycle is depicted in Figure 1. The AFEP double-decoupling scheme obtains an excess free energy of transfer from two main alchemical simulations, decoupling the ligand from two different locations within this larger system, the binding site and the bulk, and these two calculations can be reasonably carried out in smaller systems modeling the local environment only.
An inherent complication of the AFEP method, which involves gradually decoupling a ligand from its environment over the course of an MD simulation, is that a very weakly or non-coupled ligand will spend significant simulation time exploring configurational states that are highly improbable in the coupled state (for example, unbinding from the site and diffusing freely in the simulation box). Extensive sampling of these states drastically reduces efficiency of the calculation and quality of convergence, since these improbable states make negligible contributions to the binding affinity. Typically, restraints13–16 are applied to the ligand throughout the calculation to restrict sampled configurations to those likely to be found in the coupled state, but the final calculation of the binding affinity must include corrections for any contributions of these restraints, complicating the thermodynamic cycle represented by the overall calculation. Our general approach involves simplification of the usual restraint scheme for bound ligands, and introduces more complex bulk phases which may have their own applied restraints. Although the simplification was motivated by the need to streamline the overall process when including complex bulk phases, it is likely to make calculations in aqueous solution even more straightforward.
Decomposition into Intermediate States
The double decoupling method requires considering states in which a single ligand is interacting with 1) preferred bulk phase (b subscript), 2) ideal gas phase (g subscript), or 3) the environment associated with the protein binding site (r). For convergence purposes it is frequently advisable to impose restraints that confine the ligand to these environments. We describe here a minimum set of such restraints, which confine the ligand to one section of the bulk (= restraints), “coarse” site restraints that confine it in the general region of the binding site (○), and finer Distance-from-Bound-Configuration (DBC or ▵ ) restraints that restrict its RMSD from the bound configuration. For the method to correspond to the binding affinity it is also essential that the site remain unoccupied by identical ligand molecules that may also be in solution, requiring explicit exclusion restraints at high ligand concentrations. As described in Methods, these restraints can be designed so they do no significant work when the ligand is fully coupled to the associated phase.
Relevant combinations of these restraints and coupling schemes for the computational method to calculate the unitary binding probability ratio pocc/punocc are shown in Figure 1, and more details on the composition of various states are given in Table 2. Although these states can be connected in a consistent thermodynamic cycle, we do not explicitly do so to derive the method, due to several terms that cancel.
Instead, to obtain a form for practical for calculation, we multiply and divide by the partition function associated with each state in Figure 1:
| (19) |
In the right hand side, the grouping of terms is inspired by transitions shown in Figure 1, retaining ratios that can be conveniently calculated and omitting some terms that cancel out.
Equation 19 may be simplified by making the following assumptions: (coarse ○ restraints are broader than the DBC ▵ restraints, and hence negligible when superimposed onto them), and (effects of DBC restraints in the bound, coupled state are negligible). Our approach for designing restraints that satisfy these assumptions are in Simulation Methods. This leads to:
| (20) |
All terms in Eq. 20 can be computed either numerically or analytically for a given concentration , and can then be substituted into Eq. 17 to calculate the probability of site occupation at .
Usually, the first and third term can be estimated analytically, as shown in the next section, Predicting Ligand Titration. The first term represents the cost of imposing possible bulk-phase restraints (=); depending on implementation details, this may be unity or a simple ratio of volumes. The third term, yields the cost of switching from the = restraint system to the ○ system; if both are flat wells, it is a ratio of configuration space volumes; if in addition they are purely translational, it is again a ratio of 3-dimensional volumes.
The fourth term, is a correction for the DBC restraints in the gas phase, represented by the RFEP arrow in Figure 1. As with other flat-well potentials, a stiff DBC restraint scales the partition function of the decoupled ligand by a volume ratio. The 3n-dimensional volume enclosed by a DBC restraint is not regular or analytically calculable, but can be estimated numerically, using restraint free energy perturbation (RFEP) simulations coupled with a free energy estimator such as thermodynamic integration (TI) or Overlap Sampling methods.29 In practice, convergence is improved by releasing the DBC restraints in RFEP but maintaining superimposed regular (usually spherical) flat-well center of mass restraints (○ restraints) that enclose the DBC volume to calculate , then correcting for those restraints analytically via .
The second and fifth terms correspond to the AFEP1 and AFEP2 decoupling steps in Figure 1, respectively.
Predicting ligand titration
Experiments frequently involve titrating ligand, and for successful comparison it is desirable to predict the binding probability pocc for a range of ligand concentrations. Such concentration effects (even among non-interacting receptors) have two distinct origins. Increasing the number of ligand molecules nL in a unitary system increases the probability that any ligand will bind; this leads to the “ideal gas” concentration dependence. For solutions with high ligand concentrations, ligand-ligand interactions are non-vanishing and contribute to the cost of solvation within the bulk; this is (to lowest order) a function of the typical number of interacting ligand-ligand pairs, as well as a function of the concentration and the geometry of the bulk. Thus, choosing the most relevant concentration scale for the ligand can be difficult, especially in phase-separated systems.
To our knowledge, most implementations of double decoupling to date have assumed a bulk that is a dilute, isotropic solution. It is possible to calculate pocc directly for any given bulk ligand concentration by simply decoupling from a bulk system at that concentration, but here we summarize a natural approach for incorporating ligand concentration effects into the formalism we have introduced.
Of the five ratios of partition functions in Eq. 20, the first three are directly affected by the bulk ligand concentration and geometry, with distinct expected behavior depending on whether the ligand in bulk is an ideal gas, or in solution that is dilute, non-dilute and/or anisotropic. The expectation for these expressions for each case is given in Table 3. We consider the three deviations in turn.
Table 2:
Properties of systems referenced in Figure 1. This follows the microscopic framework in which only covalent bonds define a molecule. Separate systems are divided by solid lines, while isolated gas-phase systems associated with a unitary system are in an additional, un-separated row lines; column noted Z contains notation for the configurational partition function for the two-system state. Calculating Z◽/Z◾ is the primary goal of the proposed implementation, and the 3 calculations that must be done computationally are noted in the “Technique” column. Other partition function ratios can be calculated analytically or cancel out.
| State | Tagged Ligand Environment | Total Ligand Molecules | Restraints | Restraint Symbol | Z | Technique |
|---|---|---|---|---|---|---|
| b◽ | bulk | nL | none† | Z◽ | ||
| b= | bulk | nL | bulk† | = | AFEP | |
| b− | N/A | nL − 1 | none† | = | ||
| g= | gas-phase | 1 | bulk† | |||
| g○ | gas-phase | 1 | coarse | ○ | RFEP | |
| g○▵ | gas-phase | 1 | coarse and DBC | ○▵ | ||
| g▵ | gas-phase | 1 | DBC | ▵ | AFEP | |
| b− | N/A | nL − 1 | exclusion | |||
| r▵ | receptor | nL | DBC | ▵ | ||
| r◾ | receptor | nL | none | Z◾ |
Exclusion restraints are technically also required, but imposed automatically if simulation does not include protein.
First, if multiple bulk phases are present, and the ligand is strongly localized in one of them (as a lipophilic ligand in a hydrated membrane), is proportional to the volume of the accessible phase (states in which the ligand is outside its preferred phase will not contribute 17 significantly to the partition function). In practice, the volume of a phase with an irregular shape may not be easily characterized, but the bulk restraints (=) can be defined to enclose a regular volume V = and estimating the fraction of the overall bulk phase enclosed in these restraints, as we do here, is more straightforward. We may write:
| (21) |
and estimate the volume ratio α using ligand numbers:
| (22) |
where and are the number of ligand and solvent molecules enclosed by the restraint, respectively. This amounts to estimating the unknown volume v of the bulk phase within the heterogeneous system containing the receptor based on the number density of the more symmetric “pure” bulk system (in the present application, a hydrated binary lipid bilayer). The restraint volume V = is meaningful on the condition that the bulk restraints enclose a region of the bulk that maps to any other region under symmetry operations (such as a given fraction of a homogeneous phase, or one leaflet of a symmetric bilayer).
Second, we have introduced the bulk/gas partition coefficient , which also captures any non-ideality of the bulk. The free energy of solvation for the ligand in a bulk solution with ligand concentration is kBT ln , where
| (23) |
and the system is at standard temperature and pressure.
In a binary mixture of two species A and B, with number fractions x and 1 − x, the simplest deviation from ideal (known as a “simple solution”, “regular solution”, or “quadratic mixture”) yields the following chemical potential for species A:30–32
| (24) |
where µ0 is the chemical potential for species A in an infinitely dilute state, and uAB,uAA,uBB are the mean interaction energies for AB, AA, and BB pairs respectively. If the mean pair interaction energies do not vary with composition, h0 will be a constant.
Here, the natural generalized concentration is mole fraction, so we set . The bulk/gas partition coefficient can be determined by setting the chemical potential in the bulk µb equal to the chemical potential in the gas phase µg:
| (25) |
| (26) |
where xb and xg are the mole fraction of Species A in the A:B mixture in liquid and gas phase, respectively, and is the bulk/gas partition coefficient for species A in an ideal A:B mixture where h0 = 0. Simulations of binary mixtures of coarse-grained lipids have previously shown agreement over a full concentration range.33 We find this model for Px agrees well with simulation results for membranes with less than 50% cholesterol, and use it to predict cholesterol titration in the cholesterol/GPCR application presented below. Instability of the lamellar phase indicates the model must break down for cholesterol fractions greater than 50%.
Finally, for anisotropic phases in which ligand molecules have a strong orientational dependence (as for sterols in a bilayer membrane), bulk (=) restraints may include an orientational component which is not neutral in the gas phase:
| (27) |
where Ω○ and Ω= include the phase-space volume for all non-translational degrees of freedom under the isotropic (○) and bulk (=) restraints, respectively.
Generic flat-well restraints
The implementation assumes restraint schemes that perform no work on the ligand coupled to either the bulk or the binding site. A common scheme for meeting this requirement is a “flatwell” potential. For ligand configurations that are likely in the coupled state, the potential vanishes; for those that are highly unlikely, the potential increases steeply to approximate a hard wall and return the ligand to the “coupled” configuration space. The free energy cost for imposing such a flat-well restraint potential in the decoupled state is due only to the loss of entropy; for a flat-well potential in which the ligand is restrained to a simple geometry, such as a sphere as in refs. 12,34 or a cylinder as in ref. 35, this entropic contribution can be calculated analytically.
Here we use two types of flat-well restraints, depending on the coordinate ξ they are applied to: either the center-of-mass distance of the ligand to the binding site, or DBC coordinates, described in detail in the next section. Our flat-well restraints are half-harmonic wells:
| (28) |
which is parameterized by the threshold distance ξmax and the force constant kξ. ξmax is chosen to make the restraint a flat well, that is, so that the equilibrium distribution of ξ in the coupled state lies almost entirely below ξmax. This ensures that imposing the restraint induces negligible bias on sampling in the coupled state. kξ should be somewhat high to limit the space to be sampled in AFEP simulations; however, it must be low enough to preserve the stability and accuracy of the MD integrator. In a Monte-Carlo simulation where this concern does not apply, a hard wall might be used instead. Imposing this flat-well restraint on a decoupled ligand scales the partition function Z by a volume ratio: , where ZFW and Z are the partition functions with and without the flat-well restraints, respectively, and VFW and V are the configuration volumes accessible to the ligand in the presence and absence of restraints. For a ligand coupled to protein, , while for a ligand coupled to bulk, where α is the fraction of the unitary system bulk enclosed by the restraint.
Distance-to-bound-configuration coordinate
In the past,16,36,37 in order to improve sampling and convergence of the bound ligand in the free energy calculations up to 7 types of restraints (3 translational, 3 orientational and 1 conformational) have been used to restrain the ligand in the bound conformation. By using the DBC restraint, we were able to reduce the number of needed potentials to one.
DBC is the RMSD of ligand coordinates calculated in the frame of reference of the receptor’s binding site. It reflects the deviation of the ligand from its reference position after canceling the deviation of the binding site from its reference position. This formulation allows the receptor-ligand assembly to be unrestrained in the simulation.
Restraint forces applied to DBC are a function of the ligand atoms and the receptor atoms used to define the binding site. However, because the dependency on receptor atoms only occurs through the roto-translational fit, DBC forces correspond to a rigid-body motion, and have no effect on receptor conformation.
Adjusting the width of the DBC restraint allows for adapting to different types of binding: well-defined poses can be narrowly surrounded by a tight flat well, whereas a broad ensemble of loosely bound configurations will require an equally broad restraint. In all cases, the goal is to limit sampling throughout the decoupling process to those configurations that are relevant in the fully coupled state.
We shall now define the DBC coordinate more rigorously. Let XR be a 3n-vector of coordinates of representative atoms of the binding site, and a set of fixed reference coordinates for those atoms. This could encompass an entire macromolecule, or a binding domain, or a smaller region surrounding the site. In the GPCR example of this work, those 22 atoms are a set of alpha carbon atoms located near the superficial binding site; they need not surround it to define the site precisely. We note and the respective centers of mass of those sets of coordinates.
The receptor undergoes a combination of 3 types of motion: a global translation moving its center of mass by , a global rotation R−1 around its center of mass, and internal changes: conformational fluctuations or drift. While we wish to preserve the conformational dynamics of the receptor, its global motion can be removed by applying the inverse rigid-body transformation to each atom i, yielding the roto-translated coordinates :
| (29) |
where the associated with the binding site are as close as possible to their reference locations because R is defined as minimizing the mean square deviation:
| (30) |
If the ligand has diffused in step with the protein complex, without changing its binding mode or conformation, its coordinates will be equal to their reference values.
The distance to bound configuration collective variable d reflects the deviation from that case. It is defined as the RMSD of the roto-translated ligand coordinates with respect to their reference positions :
| (31) |
d can then be used to calculate a restraint potential UDBC(d), such as a flat-well restraint potential as in Eq. 28. The components of the restraint force on the ligand are calculated in the x′ coordinate system (frame of reference of ), before R−1 is used to rotate the force vector back to the original coordinate system (current frame of reference of the simulation). Conversely, a counter-force on receptor atoms arises from the dependence of the optimal translation and rotation on receptor coordinates, but this force acts globally and will not affect internal degrees of freedom.
Calculating the RMSD of coordinates that are roto-translated using a distinct group of atoms for the least-squares fit is a standard part of the Colvars Module toolkit,38 and was applied as is to implement the DBC coordinate. An example script implementing the DBC coordinate and restraint in the NAMD Collective Variables Module is provided in Supplementary Information.
Exclusion restraints
In the AFEP decoupling simulation, ligand molecules other than the one being decoupled will tend to replace the disappearing bound ligand: this is all the more likely when the ligand is concentrated. Formally, the end-point of the AFEP decoupling is a state where no ligand occupies the binding site, which in the present foramlism is defined by the range of DBC coordinate used in the bound ligand restraint. Hence, to sample the unbound state, unperturbed ligands must be excluded from the binding site. In many practical cases, the site forms a well-defined peak in the probability distribution of ligand positions, and thus a simple center-of-mass restraint will prevent binding without otherwise biasing the statistical distribution of unbound ligand molecules.
However, the case of the β2-adrenergic receptor discussed below questions this assumption, as the superficial binding site is frequently lined with a second cholesterol molecule that transitions rapidly to the primary binding site if emptied, without apparent free energy barrier. Preventing specifically this process without adding an arbitrary bias requires a very precise geometric definition of the binding mode, which is provided by the DBC. We achieve this with a flat-well restraint that keeps the DBC above the bound threshold (the local minimum in the equilibrium DBC distribution).
While in theory this could be applied to all unbound ligands, in practice the least-squares fitting involved in the DBC restraint becomes computationally costly when iterated over a large number of molecules. Thus ligands that start farther away from the site than they can diffuse over the timescale of a single simulation run may be left unrestrained. For safety, an intermediate layer of ligands that are near but not immediately around the binding site may be prevented from binding by an inexpensive center-of-mass distance restraint. The lists of ligand molecules affected by these various restraints can be updated periodically, for example between runs at each λ-value in the AFEP simulation. This is the strategy followed by our NAMD implementation, for which a script is provided in SI.
Application: Cholesterol binding to GPCRs
Many crystal structures of G-protein coupled receptors (GPCRs) include resolved cholesterol, but the likelihood of these sites being occupied by cholesterol in a liquid membrane bilayer is unknown. We selected three cholesterol binding sites on three different GCPRs, and applied this approach to predicting the cholesterol concentration required for 50% occupancy when the GPCR is embedded in a POPC bilayer, with a total lipid to protein ratio of 230 lipids (phospholipid or cholesterol) to 1 protein (nS + nL = 230).
Methods
Receptor-bound Cholesterol System Setup
We used the crystal structures of the β2-adrenergic receptor (β2-AR, PDB id 3D4S), serotonin receptor type 2B (5-HT2B, 4NC3), and µ-opioid receptor (5C1M) for setting up receptor-bound cholesterol systems. A phosphatidylcholine (POPC) lipid-bilayer with 0.3 mole fraction of cholesterol was generated using CHARMM-GUI Membrane Builder.39–41 Each protein-cholesterol complex was then embedded in the membrane by aligning the center of the protein and the membrane along the z-direction and removing the overlapping lipids. Residues were protonated according to their standard states at pH 7.4. The systems were solvated using the solvate plugin of VMD with TIP3P water molecules, and Na+/Clions were added to bring the system to a neutral 0.15 M concentration using the autoionize plugin. The final system sizes were about 81×80×102 Å3 and included 162 POPC, 70 cholesterol and ∼ 12,700 water molecules, with a total of ∼70,000 atoms.
Phospholipid-Cholesterol Mixed Bilayer System Setup
For decoupling of a cholesterol molecule from the bulk of a bilayer with a cholesterol mole fraction of xCHOL ranging from 0 to 40% cholesterol, a mixed POPC/cholesterol bilayer was prepared using CHARMM-GUI Membrane Builder, as for the protein-containing system. Na+/Cl- ions were added to the hydrated membrane to provide a neutral 0.15 M concentration. The final systems contained ∼29,000 atoms including about 140 lipids and ∼5,400 water molecules. The bulk restraints (=) enclosed one leaflet, hence half of the 140 lipids . The GPCR-bilayer systems contain about 230 lipids, hence the bulk restraint volume factor is α = 70/230 = 0.3. Three AFEP replicas were run for each cholesterol fraction, and combined via linear averaging.
MD simulations
The prepared systems were subjected to unrestrained molecular dynamics (MD) simulations. MD simulations were performed using the NAMD42 2.12 simulation package updated with Colvars version 2017–09-18,38 CHARMM36 forcefield for the protein43,44 and phospholipids,45 and modified CHARMM36 parameters46 for cholesterol.
All MD simulations were performed using the NPT ensemble with weak coupling to a Langevin thermostat and barostat at 300 K and 1 atm, respectively. Periodic boundary conditions were employed, and the real space electrostatic interactions were truncated at 12 Å, while the long range components were treated using PME method.47 Lennard-Jones interactions were switched off smoothly between 10 and 12 Å. All bonds to hydrogen atoms were constrained using the SHAKE (non-water) or RATTLE (water) algorithms. A multiple-time-step rRESPA method was used, with fast and slow time steps of 2 and 4 fs, respectively.
All systems were first energy minimized for 10,000 steps and then equilibrated. For the cholesterol-protein system, the position of protein Cα atoms and heavy atoms of bound cholesterols were initially restrained using a 5 kcal/mol/Å2 harmonic force constant, which was gradually released over 3 ns. After further unrestrained equilibration, a snapshot at 7 ns was used as the initial structure for the free energy calculations to prevent significant diffusion from the docked position. Unrestrained cholesterol-protein MD simulations were then extended to 40 ns to study the dynamics of the complex. Similar unrestrained MD simulations were performed for cholesterol in the bulk mixed membrane, and the results were used to determine boundaries for the flat-bottom restraints in the free energy calculations.
Details of Restraints
In the application presented here, involving cholesterol decoupled from a bulk that is a membrane bilayer, the membrane associated steps used a flat-well restraint on the distance of the cholesterol center of mass (COM) from the monolayer midplane, as well as a conical restraint on its orientation. The total restraint potential U= for a single cholesterol molecule in the membrane was the sum of the restraint potential Uz on the COM position and Uθ on the orientation,
| (32) |
In the coupled state, only the COM coordinate along the axis that is normal to the membrane is limited; the COM is free to assume any position in the plane of the membrane. The variable used in the COM flat-well potential was the difference between this coordinate and its average value in an unbiased equilibrium simulation, noted as z. The potential for Uz used the form in Eq. 28, where the threshold distance zR is chosen to span the range of z values assumed by a cholesterol molecule in a single leaflet of the bilayer, calculated in an unbiased equilibrium simulation. The restraint volume is .
Cholesterol molecules in the bulk of a lipid bilayer are expected to have a strong preference for orientations parallel to the membrane normal, in which the hydroxyl headgroup is exposed to solvent and the hydrophobic steroid rings and hydrocarbon tail are buried in the core of the bilayer; unbiased equilibrium simulations supported this expectation. The orientational restraint Uθ imposed on the cholesterol in the membrane is therefore a function of the azimuthal angle θ between a vector fit to the cholesterol molecule (pointing toward the hydroxyl) and the normal axis, using the form in Eq. 28, where the threshold value, θR, is half the opening angle of the conical restraint, chosen to encompass the range of θ values assumed by a cholesterol molecule in a single leaflet of the bilayer in an unbiased equilibrium simulation. In the decoupled state, imposing these restraints scales the phase-space volume by .
Coarse protein-associated restraints confine the ligand to the general region of the protein binding site. These restraints also used the form of Eq. 28, with the restraint variable r equal to the difference between the ligand COM and its distance from its bound position, and the threshold distance rR must be chosen to safely encompass all dispersion of the ligand COM in the bound state. The volume of the restraint is ,so Eq. 27 becomes
| (33) |
The DBC restraint involved 11 carbon atoms encompassing the four fused rings of cholesterol. The moving frame of reference of the binding site was based on all alpha carbon atoms located within 15 Å of the crystallographic cholesterol molecules (Supplementary Figure 1). The Collective Variables Module38 was used to define the restraints, with restraint coefficients in Table 4.
Table 3:
Effects of bulk phase and geometry on concentration dependence of each term in Eq. 20, for an ideal gas of ligand, an isotropic solution of ligand, and an anisotropic phase containing both ligand and receptor. Empty cells indicate the ideal gas value should be used. The factor of nL in the first row originates from nL indistinguishable ligands that can be chosen for restraining (and then decoupling). The equilibrium coefficient is obtained by taking the product of the five ratios and dividing by . It is assumed that restraints are designed so and that for the ideal gas and isotropic solution, the generalized reference volume is simply the unitary volume . Although the final expression for for the anisotropic bulk appears considerably more complex, the additional terms can often be estimated analytically.
| Process | Ratio | Ideal Gas | Isotropic Solution | Anisotropic Bulk |
|---|---|---|---|---|
| apply bulk restraints | ||||
| decouple from bulk | 1 | |||
| switch to isotropic restraint | ||||
| add DBC restraint | ||||
| couple to receptor | ||||
| bind from bulk | ||||
Alchemical Free Energy Perturbation Calculations
Decoupling via AFEP was carried using a total of 47 windows were spaced by ∆λ = 0.05 when 0 ≤ λ < 0.5, ∆λ = 0.025 until λ = 0.8, ∆λ = 0.01 until λ = 0.95, and ∆λ = 0.005 until λ = 1. Simulations were performed sequentially (i.e. the initial configuration for λi+1 was the final configuration from the run at λi). Each window was run for 600 ps for equilibration purposes, followed by 2 ns of data collection. Thus the total simulation time for a complete AFEP simulation was 122.2 ns. We tested convergence of the cumulative average for each window by monitoring the progression of ⟨dG⟩ for each λ.
To calculate , RFEP simulations were run using the Colvars Module38 within NAMD, and 21 equally-spaced λ values ranging from 1.0 (full restraints) to 0.0 (zero restraints). Each λ simulation was run for 400 ps, with the first 80ps discarded as equilibration. Restraint free energies were calculated from those simulations using the Simple Overlap Sampling estimator.29
Results
Non-ideality of Cholesterol In POPC Bilayers
was measured for decoupling a single cholesterol molecule from a POPC bilayer at multiple cholesterol concentrations ranging from trace to 40%, via AFEP decoupling, with results shown in Fig. 3A and steps summarized in Table 5. Non-ideality was confirmed, and decreased with increasing cholesterol concentration over most of this range. The data was well-fit by the model in Eq. 26 (P0 = 3 × 1014 and h0 = 1.6 ± 0.6kcal/mol), indicating that pair interactions between cholesterol and POPC were 1.6 kcal/mol less favorable, on average, than interaction between like lipids. We extrapolate the fit to xCHOL = 0.5, which is at the upper limit of cholesterol fractions in stable lipid bilayers. Typical values for the phase boundary between mixed and liquid-ordered phases of binary mixtures of CHOL and POPC lie between 0.3–0.4 at room temperature.48
Figure 3: Dependence of predicted site occupancy on ligand concentration, for cholesterol binding to crystallographic sites on three different GPCRs.
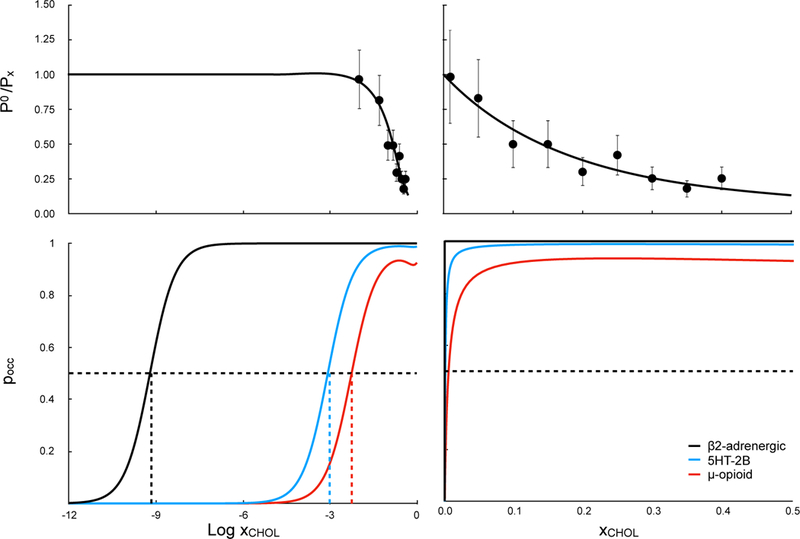
Top: Effect of cholesterol fraction on the normalized gas/bulk partition coefficient P0/Px, as calculated by AFEP decoupling of a single cholesterol molecule from a POPC:CHOL bilayer. Points represent average of three replicas, with standard error bars shown. Curve represents as in Eq. 26, where h0 = 1.6±0.6 kcal/mol and P0 = 3×1014, and both are free fit parameters. Reciprocals are plotted because they are directly used in the double-decoupling scheme. Bottom: Probability pocc of occupied cholesterol-binding sites for three different GPCRs (Figure 2) in POPC:CHOL bilayers according to and the values for κL in Table 6. Left and right columns show the same data plotted vs log xCHOL or xCHOL, respectively. Colored dashed lines indicate the midpoint cholesterol fraction x50 for each receptor.
Table 4: Parameters used for restraint potentials.
Restraints applied to cholesterol molecule while decoupled from bulk or from protein binding site. All restraint potentials used the flat well potential in Eq. 28. COM refers to cholesterol COM.
| Restraint | Variable (ξ) | Force constant (kξ) | Threshold (ξmax) |
|---|---|---|---|
| bulk (=) | COM vertical distance from leaflet midplane | 1000 kcal/mol.Å2 | zR = 11 Å |
| Angle between membrane normal and cholesterol axis | 1000 kcal/mol.deg2 | θR = 0.14π | |
| coarse (○) | COM Distance from crystallographic COM | 100 kcal/mol.Å2 | rR = 5 Å |
| DBC (▵) | RMSD from crystallographic coordinates (Eq. 31) | 100 kcal/mol.Å2 | d = 2 Å |
Cholesterol Affinity for GPCRs
Decoupling of cholesterol from three different GPCRs revealed significant differences in binding probability. Predicted concentration dependence of pocc for cholesterol in crystallographic sites for three different GPCRs is shown in Fig. 3B, with values from AFEP recorded in Table 6.The β2-adrenergic receptor structure 3D4S19 is one of the earliest high-resolution GPCR structures and the first containing resolved cholesterol. The predicted midpoint concentration x50 is 1 cholesterol molecule per 1010 total lipid molecules. Occupation of this binding mode by cholesterol was sufficiently strong that toward the end of a decoupling run in 30% cholesterol, a second cholesterol would reliably fill the site; this prompted the development of the exclusion restraints.
Table 6:
Values for individual ratios of protein-related partition functions in Eq. 20, for cholesterol binding to crystallographic sites on three GPCRs. Predictions as functions of cholesterol fraction are plotted in Fig. 3B. AFEP values reflect the geometric mean of 3 replicas; see SI Table 1 for values from individual replicas and calculation of statistics. See Table 5 for calculation of ..
| Process | Ratio | Method | β2-adrenergic | 5-HT2B | µ-opioid |
|---|---|---|---|---|---|
| add DBC restraint | RFEP | 10−3 | 10−3 | 10−3 | |
| couple to receptor | AFEP | 1025 | 1019 | 1018 | |
| bind from gas phase | Product of previous 2 rows∗ | 1022 | 1016 | 1015 | |
| bind from bulk | κx | ||||
| 109 | 103 | 102 | |||
| half-saturation | x50 | xCHOL for which κxxCHOL = 1 | 10−9 | 10−3 | 10−2 |
restraints are designed so and
Midpoint concentrations for the other two GPCRs tested, the 5-HT2 receptor in structure 4CN3 (x50 = 0.01% cholesterol, or 1 cholesterol molecule per 104 lipid molecules) and the µ-opioid receptor in structure 5C1M (x50 = 0.1% cholesterol or 1 cholesterol per 103 lipid molecules) were significantly higher. Gimpl has recently22 provided a comprehensive discussion of different binding modes of cholesterol for GPCRs; all three binding sites provide favorable hydrogen-bonding interactions for the hydroxyl and hydrophobic contacts for the tetracyclic ring system. Another difference may explain the dramatically higher predicted occupancy of the 3D4S binding site: the presence of a second bound cholesterol molecule, which likely stabilizes the first cholesterol molecule through favorable stacking interactions of the two smooth faces.
It is important to note that these trends may all be dependent upon the “solvent” lipid as well; cholesterol may have higher or lower probability binding to these sites in bilayers composed of phospholipids with different head groups or saturation states.
The fitted activity model based on Equation 24 predicts a non-monotonic variation of cholesterol chemical potential as a function of concentration, with a slight decrease above 12.5%. For high-affinity sites that reach saturation at xCHOL << 12.5%, including the β2adrenergic and 5HT-2B receptor, the binding curve remains sigmoidal. In the real membrane, as the amount of cholesterol is much more than 10%, the bulk becomes significantly more favorable, and the effective affinity of cholesterol for the protein site becomes increasingly weaker. These competing effects result in a plateau for pocc at less than 100% occupancy for the µ-opioid receptor. An even lower affinity site would plateau at pocc < 50%, making the notion of concentration at half-occupation irrelevant for low-affinity binding sites. We note that casting our results for this receptor in the classic form of an affinity constant KA would not allow for accurate binding predictions for the typical range of cholesterol-phospholipid binary mixtures.
Discussion
We have presented an approach for estimating probabilities that a binding site will be occupied by a ligand transferred from a complex, crowded environment such as a mixed lipid membrane. This approach represents an extension of classic AFEP methods for transfer from dilute solution to a protein binding site, and consequently requires no specification or sampling of binding or unbinding pathways. We have provided a generalized derivation that can be applied to transfer of the ligand from non-dilute concentrations in a complex fluid. We have further provided a formalism for interpretation of results that emphasizes connection to laboratory observables in the concentration regime of interest. This approach circumvents questions involving arbitrary standardized concentrations by allowing the receptor concentration (whatever it is) to serve as a natural concentration scale.
There are limited options for experimental assays to predict free energies for cholesterol binding to many transmembrane proteins, including GPCRs. Available methods introduce significant uncertainty in both the independent variable (local cholesterol concentration) and the dependent variable (estimations of binding site occupancy from functional response or structural changes). The infeasibility of an experimental affinity measurement for this process makes a rigorous affinity calculation both particularly relevant and nearly impossible to validate quantitatively.
Nonetheless, there is experimental evidence for high affinity cholesterol binding sites for GPCRs. Milon and colleagues49 measured the unfolding temperature of the β2-adrenergic receptor in the lipidic cubic phase as a function of cholesterol concentration, finding effects on the folding temperature at the minimum concentration they tested, a cholesterol mol fraction of 0.2%. They estimated that this corresponded to a subnanomolar dissociation constant, but volume-based concentration scales for lipids are challenging to interpret, as discussed in the Introduction.
The double-decoupling technique inherent in the application of AFEP, dictates that the free energy of the overall transfer process uses two primary calculations, which quantify the free energy for transfer of the ligand from either the bulk or protein phases to vacuum. The validity of the AFEP approach for each of these two calculations has been previously established (see ref. 50 for a recent review and refs. 13,35,51 for recent applications); a primary novelty in our approach lies in the consideration of more complex bulk phases and, to make this tractable, the use of simplified restraint schemes.
Potential computational sources of error, therefore, are those that need to be considered in any AFEP calculation; namely, poor convergence. In most AFEP calculations of binding affinities, the use of well-designed restraints can significantly improve convergence. We present here a set of restraints that improves convergence while minimizing the complexity of the overall thermodynamic cycle.
The approach relies on the use of distance-to-bound configuration (DBC) restraints, which are effective at narrowly surrounding a well-defined binding pose. This becomes a limitation if several binding poses are relevant to the target binding site and ligand. Then, two alternate avenues may be used:
a broader flat well may be used, so that it encompasses all the relevant poses. This will increase the convergence time of the restrained AFEP simulation, potentially incurring a high cost in additional sampling;
a separate set of simulations could be run for each identified binding pose, each one using narrow DBC restraints. For each pose, three simulations would be required: AFEP decoupling from the binding site under restraints, and free energy calculations of the DBC restraint free energy, for adding the restraint in vacuum and removing it in the binding site.
Compared to other restraint schemes, DBC restraints are able to delineate a superficial binding site as precisely as an internal one, as shown by the present GPCR example. Classic approaches that define the center of the site as the center of a set or receptor atoms are only well-suited to the geometry of an internal binding cavity; they would not apply to such a case of superficial binding.
We suggested that the dramatically higher predicted occupancy of the β2 adrenergic binding site could result from the presence of the second bound cholesterol molecule, which likely stabilizes the first cholesterol molecule through favorable stacking interactions of the two smooth faces. If so, removal of this second cholesterol molecule would reduce the measured receptor-coupling factor , shifting the midpoint concentration for the first site to the right (probably significantly so). This cooperativity provides an interesting example of a concentration regime (below the midpoint concentration of the second cholesterol molecule) in which the approximation that is independent of may not be reliable. It is possible that such favorable interactions may also underly the positive value of h0, but only over concentrations for which cholesterol molecules typically only have one other cholesterol molecule as a nearest-neighbor.
Although the application here involved a membrane, the method should also be suitable for binding to proteins in non-dilute aqueous solution or a range of complex bulk phases, including detergent micelles, polymer melts, nematic or smectic liquid crystals, cubic or hexagonal lipid phases, or lipid domains within monolayers or bilayers. The implementation does assume that receptors do not interact, and cannot be used to predict coupling between ligand concentration and protein organization, including effects of cholesterol concentration on GPCR dimerization. They can still potentially provide insight into such processes; here, the results for the bulk and unitary systems suggest that segregation of cholesterol from phospholipids within protein grooves or behind other cholesterol molecules is highly favorable; dimerization of GPCRs around central cholesterol molecules (as investigated in26) segregates cholesterol molecules quite effectively, indicating a variant of the lipophobic effect52–54 could be a potential driving force for oligomerization.
Supplementary Material
Figure 2: Three crystallographic sites for cholesterol on three different GPCRs.
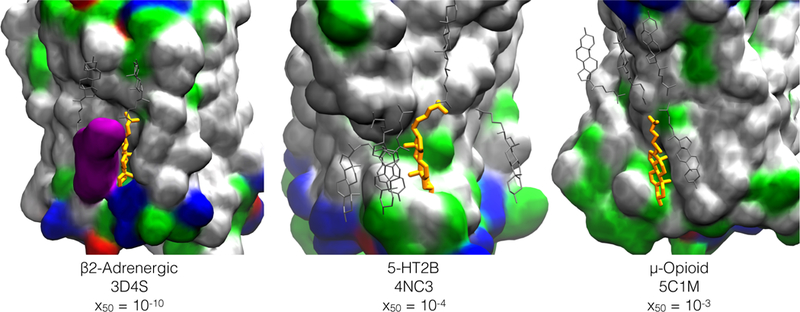
Protein is drawn in space-filling and colored by residue type : hydrophobic (white), polar (green), acidic (red), basic (blue). A second crystallographic cholesterol in the β−2adrenergic structure 3D4S is also shown in space-filling, colored purple. A subset of the additional cholesterol molecules placed by CHARMM-GUI Membrane Builder for a mixture of 7:3 POPC:CHOL are in silver. Crystallographic cholesterol molecule in sites characterized in this work are in orange, and are residue 402,1203, and 404 in structure 3D4S, 4NC3, and 5C1M respectively. The corresponding half-saturation cholesterol fraction x50 is from Table 6; for the µ-opioid receptor, pocc < 50% for the entire cholesterol range.
Table 5:
Values for individual ratios of bulk-associated partition functions in Eq. 20, for cholesterol in a binary CHOL:POPC membrane.
Acknowledgement
GB and RS were supported by research grants NSF MCB1330728 and NIH P01GM5587614A1. TJ was supported by an NIH 5T32GM112596–03. JH acknowledges funding from the French Agence Nationale de la Recherche through LABEX DYNAMO (ANR-11-LABX0011). This project was supported with computational resources from the National Science Foundation XSEDE program through allocation NSF-MCB110149 as well as a local cluster funded by NSF-DBI1126052.
References
- (1).Malde AK; Zuo L; Breeze M; Stroet M; Poger D; Nair PC; Oostenbrink C; Mark AE An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. Journal of chemical theory and computation 2011, 7, 4026–4037. [DOI] [PubMed] [Google Scholar]
- (2).Vanommeslaeghe K; MacKerell AD Automation of the CHARMM General Force Field (CGenFF) I: bond perception and atom typing. Journal of chemical information and modeling 2012, 52, 3144–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Vanommeslaeghe K; Raman EP; MacKerell AD Automation of the CHARMM General Force Field (CGenFF) II: assignment of bonded parameters and partial atomic charges. Journal of chemical information and modeling 2012, 52, 3155–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Mayne CG; Saam J; Schulten K; Tajkhorshid E; Gumbart JC Rapid parameterization of small molecules using the Force Field Toolkit. Journal of computational chemistry 2013, 34, 2757–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Lundborg M; Lindahl E Automatic GROMACS topology generation and comparisons of force fields for solvation free energy calculations. The journal of physical chemistry. B 2015, 119, 810–823. [DOI] [PubMed] [Google Scholar]
- (6).Zheng S; Tang Q; He J; Du S; Xu S; Wang C; Xu Y; Lin F VFFDT: A New Software for Preparing AMBER Force Field Parameters for Metal-Containing Molecular Systems. Journal of chemical information and modeling 2016, 56, 811–818. [DOI] [PubMed] [Google Scholar]
- (7).Dodda LS; Cabeza de Vaca I; Tirado-Rives J; Jorgensen WL LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands. Nucleic acids research 2017, 45, W331–W336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Woo H.-j.; Roux B Calculation of absolute protein-ligand binding free energy from computer simulations. Proceedings of the National Academy of Sciences of the United States of America 2005, 102, 6825–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Gilson MK; Zhou H-X Calculation of Protein-Ligand Binding Affinities. Annual Review of Biophysics and Biomolecular Structure 2007, 36, 21–42. [DOI] [PubMed] [Google Scholar]
- (10).Chipot C Methods in Molecular Biology; Springer Science Business Media, 2008; pp 121–144. [DOI] [PubMed] [Google Scholar]
- (11).Pohorille A; Jarzynski C; Chipot C Good practices in free-energy calculations. The journal of physical chemistry. B 2010, 114, 10235–10253. [DOI] [PubMed] [Google Scholar]
- (12).Hénin J; Brannigan G; Dailey WP; Eckenhoff R; Klein ML An atomistic model for simulations of the general anesthetic isoflurane. The journal of physical chemistry. B 2010, 114, 604–12. [DOI] [PubMed] [Google Scholar]
- (13).Gumbart JC; Roux B; Chipot C Standard binding free energies from computer simulations: What is the best strategy? Journal of chemical theory and computation 2013, 9, 794–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Gilson MK; Given JA; Bush BL; McCammon JA The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophysical journal 1997, 72, 1047–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Boresch S; Tettinger F; Leitgeb M; Karplus M Absolute Binding Free Energies: A Quantitative Approach for Their Calculation. The Journal of Physical Chemistry B 2003, 107, 9535–9551. [Google Scholar]
- (16).Wang J; Deng Y; Roux B Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials. Biophysical journal 2006, 91, 2798–2814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Chen H; Zhou X; Wang A; Zheng Y; Gao Y; Zhou J Evolutions in fragment-based drug design: the deconstruction-reconstruction approach. Drug Discovery Today 2015, 20, 105–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Zhang J; Lazaridis T Calculating the free energy of association of transmembrane helices. Biophysical journal 2006, 91, 1710–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Hanson MA; Cherezov V; Griffith MT; Roth CB; Jaakola VP; Chien EY; Velasquez J; Kuhn P; Stevens RC A Specific Cholesterol Binding Site Is Established by the 2.8 Å Structure of the Human β2-Adrenergic Receptor. Structure 2008, 16, 897–905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Oates J; Watts A Uncovering the intimate relationship between lipids, cholesterol and GPCR activation. Current Opinion in Structural Biology 2011, 21, 802–807. [DOI] [PubMed] [Google Scholar]
- (21).Venkatakrishnan AJ; Deupi X; Lebon G; Tate CG; Schertler GF; Madan Babu M Molecular signatures of G-protein-coupled receptors. Nature 2013, 494, 185–194. [DOI] [PubMed] [Google Scholar]
- (22).Gimpl G Interaction of G protein coupled receptors and cholesterol. Chemistry and Physics of Lipids 2016, 199, 61–73. [DOI] [PubMed] [Google Scholar]
- (23).Grossfield A Recent progress in the study of G protein-coupled receptors with molecular dynamics computer simulations. Biochimica et Biophysica Acta (BBA) - Biomembranes 2011, 1808, 1868–1878. [DOI] [PubMed] [Google Scholar]
- (24).Lee JY; Lyman E Predictions for cholesterol interaction sites on the A2Aadenosine receptor. Journal of the American Chemical Society 2012, 134, 16512–16515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Sengupta D; Chattopadhyay A Identification of Cholesterol Binding Sites in the Serotonin 1A Receptor. The Journal of Physical Chemistry B 2012, 116, 12991–12996. [DOI] [PubMed] [Google Scholar]
- (26).Prasanna X; Chattopadhyay A; Sengupta D Cholesterol modulates the dimer interface of the β2- adrenergic receptor via cholesterol occupancy sites. Biophysical Journal 2014, 106, 1290–1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Sengupta D; Chattopadhyay A Molecular dynamics simulations of GPCRâĂŞcholesterol interaction: An emerging paradigm. BBA - Biomembranes 2015, 1848, 1775–1782. [DOI] [PubMed] [Google Scholar]
- (28).Phillips R; Kondev J; Theriot J; Garcia H Physical Biology of the Cell, 2nd ed.; Garland Sciences, 2012. [Google Scholar]
- (29).Lu N; Singh JK; Kofke DA Appropriate methods to combine forward and reverse free-energy perturbation averages. J. Chem. Phys 2003, 118, 2977–2984. [Google Scholar]
- (30).Rowlinson JS; Swinton FL In Liquids and Liquid Mixtures: Butterworths Monographs in Chemistry; Baldwin JE, Buckingham AD, Danishefsky S, Eds.; Elsevier, 1982. [Google Scholar]
- (31).Silver B The Physical Chemistry of Membranes: An Introduction to the Structure and Dynamics of Biological Membranes; Allen & Unwin, 1985. [Google Scholar]
- (32).Morris JW Notes on the Thermodynamics of Solids (Chapter 18: Solutions); Department of Materials Science and Engineering, University of California-Berkeley, 2008. [Google Scholar]
- (33).Brannigan G; Brown FLH Composition dependence of bilayer elasticity. J. Chem. Phys 2005, 122, 074905. [DOI] [PubMed] [Google Scholar]
- (34).Woll KA; Murlidaran S; Pinch BJ; Hénin J; Wang X; Salari R; Covarrubias M; Dailey WP; Brannigan G; Garcia BA; Eckenhoff RG A Novel Bifunctional Alkylphenol Anesthetic Allows Characterization of GABAA Receptor Subunit Binding Selectivity in Synaptosomes. J Biol Chem 2016, 10.1074/jbc.M116.736975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).LeBard DN; Hénin J; Eckenhoff RG; Klein ML; Brannigan G General anesthetics predicted to block the GLIC pore with micromolar affinity. PLoS computational biology 2012, 8, e1002532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Ge X; Roux B Absolute binding free energy calculations of sparsomycin analogs to the bacterial ribosome. The journal of physical chemistry. B 2010, 114, 9525–39. [DOI] [PubMed] [Google Scholar]
- (37).Mobley DL; Chodera JD; Dill KA On the use of orientational restraints and symmetry corrections in alchemical free energy calculations. The Journal of chemical physics 2006, 125, 084902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Fiorin G; Klein ML; Hénin J Using collective variables to drive molecular dynamics simulations. Molecular Physics 2013, 111, 3345–3362. [Google Scholar]
- (39).Jo S; Kim T; Iyer VG; Im W CHARMM-GUI: A web-based graphical user interface for CHARMM. Journal of Computational Chemistry 2008, 29, 1859–1865. [DOI] [PubMed] [Google Scholar]
- (40).Brooks BR et al. CHARMM: The biomolecular simulation program. Journal of Computational Chemistry 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Jo S; Lim JB; Klauda JB; Im W CHARMM-GUI Membrane Builder for mixed bilayers and its application to yeast membranes. Biophys. J 2009, 97, 50–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kalé L; Schulten K Scalable molecular dynamics with NAMD. Journal of computational chemistry 2005, 26, 1781–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).MacKerell AD et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. The journal of physical chemistry. B 1998, 102, 3586–616. [DOI] [PubMed] [Google Scholar]
- (44).MacKerell AD; Feig M; Brooks CL Improved treatment of the protein backbone in empirical force fields. J. Am. Chem. Soc 2004, 126, 698–699. [DOI] [PubMed] [Google Scholar]
- (45).Klauda JB; Venable RM; Freites JA; O’Connor JW; Tobias DJ; Mondragon-Ramirez C; Vorobyov I; MacKerell AD; Pastor RW Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Lim JB; Rogaski B; Klauda JB Update of the cholesterol force field parameters in CHARMM. J. Phys. Chem. B 2012, 116, 203–210. [DOI] [PubMed] [Google Scholar]
- (47).Essman U; Perela L; Berkowitz ML; Darden T; Pedersen LG A smooth particle mesh {E}wald method. J. Chem. Phys 1995, 103, 8577–8592. [Google Scholar]
- (48).Marsh D Liquid-ordered phases induced by cholesterol: A compendium of binary phase diagrams. Biochimica et Biophysica Acta - Biomembranes 2010, 1798, 688–699. [DOI] [PubMed] [Google Scholar]
- (49).Gater DL; Saurel O; Iordanov I; Liu W; Cherezov V; Milon A Two Classes of Cholesterol Binding Sites for the β2AR Revealed by Thermostability and NMR. Biophysj 2014, 107, 2305–2312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Chodera JD; Mobley DL; Shirts MR; Dixon RW; Branson K; Pande VS Alchemical free energy methods for drug discovery: progress and challenges. Current opinion in structural biology 2011, 21, 150–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Wang L et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- (52).Mokrab Y; Stevens TJ; Mizuguchi K Lipophobicity and the residue environments of the transmembrane alpha-helical bundle. Proteins 2009, 74, 32–49. [DOI] [PubMed] [Google Scholar]
- (53).Duneau J-P; Sturgis JN Lateral organization of biological membranes: role of long-range interactions. European biophysics journal : EBJ 2013, 42, 843–850. [DOI] [PubMed] [Google Scholar]
- (54).Duneau J-P; Khao J; Sturgis JN Lipid perturbation by membrane proteins and the lipophobic effect. Biochimica et biophysica acta 2017, 1859, 126–134. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


