Ion Permeation Through a Phospholipid Membrane: Transition State, Path Splitting, and Calculation of Permeability

Abstract

We investigate the thermodynamics and kinetics of the permeation of a potassium ion through a phospholipid membrane. We illustrate that the conventional reaction coordinate (the position of the ion along the normal to the membrane plane) is insufficient to capture essential elements of the process. It is necessary to add coarse variables that measure membrane distortion. New coarse variables are suggested and a two-dimensional coarse-space is proposed to describe the permeation. We illustrate path splitting and two transition states of comparable barrier heights. The alternative pathways differ by the extent of water solvation of the ion-phosphate pairs. The permeation process cannot be described by a local one-dimensional reaction coordinate and a network formulation is more appropriate. We use Milestoning with Voronoi tessellation in two dimensions to quantify the equilibrium and rate of the permeation of the positively charged ion. The permeation coefficient is computed and compared favorably to experiment.

Graphical Abstract

1. Introduction

Biological membranes separate life processes from mere solutions.¹ They make it possible to retain concentrations and potential gradients across membranes that support non-equilibrium processes essential to life. The separation is, of course, not absolute and numerous materials are transported into and out cells using the cell translocation machinery like channels and pumps. Another important mechanism of transport is of passive permeation, directly through the phospholipid membrane without the investment of energy or the assistance of translocation devices. At a minimum, the passive permeation reduces a desired concentration difference and requires the assistance of pumps in the opposite direction to keep the correct balance.² This “leak” is particularly pronounced for protons.³ Passive permeation is also a typical mechanism in which drugs are translocated into targeted cells.⁴ It is therefore not a surprise that considerable experimental and theoretical work has been devoted to study passive permeation through membranes.

The mechanism in which membranes block most attempts of permeation is by forming a hydrophobic barrier of lipid chains to molecules that are soluble in aqueous solution. The self-energy of a charged molecule in the low dielectric medium of the lipid chains is high compared to aqueous solution, making the permeation across this barrier unlikely.⁵ Here we focus on a permeation process of a positively charged ion, potassium, to illustrate the complexity of the transport mechanism and to study it in details. Considerable modeling work has been done for the permeation of complex charged molecules, such as peptides, through membrane.^6,7 Here we demonstrate however, that the mechanism and quantification of the process of a single ion translocation still pose significant challenges.

Two extreme transport mechanisms were suggested for ion permeation: (i) diffusion solubility model (DSM) and (ii) pore formation.⁸ In DSM the low-dielectric barrier is taken “as is” and ion permeation is computed based on a model of unperturbed membrane. The barrier estimated from DSM for ions is very high and the permeability too low compared to experimental estimates.⁹ The second extreme model is of pore formation in the membrane.¹⁰ The free energy cost is transformed for embedding the ion in low dielectric medium to the cost of membrane perturbation. Such significant disruption is expensive as well, unless the membrane is very thin. Pore formation is also likely to allow the permeation of other molecules making the membrane less selective.

Between the two extreme approaches to modeling permeation, a number of computational studies suggest an intermediate picture.^11,12 The ion generates a local membrane perturbation, dragging a few water molecules and phospholipid head groups as it moves through the membrane. The perturbation that the ion induces does not rise to the level of a pore. The molecules that accompany the ion reduce the electrostatic energy of the ion in the hydrophobic environment at a moderate cost of membrane distortion.

Wilson and Pohorille ¹¹ simulated the permeation of sodium and chloride ions across a glycerol monooleate (GMO) membrane, and numerous studies followed. Tepper and Voth ^3,13 suggested a highly organized mechanism for passive permeation of ions requiring a coupling between ion, solvent, and membrane. The mechanism of ion pairing was investigated in. ¹⁴ Other studies also confirmed that the solubility-diffusion model neglects critical components of the process by assuming that the membrane is intact.¹⁵ DSM and inhomogeneous DSM do not explicitly describe membrane deformation, (e.g. by the use of a slow coarse variable to detect membrane distortion). When the membrane perturbation is significant, like in the translocation of a positively charged ion (potassium) that we study here, the error can be large.^10,12

Ion passage through a membrane is a rare event, or a process with a time scale much longer than molecular vibrations, and short-range diffusion. To model rare events it is useful to differentiate between the set of variables that are necessary to describe the system kinetics and the rest of the degrees of freedom. Separation of time scales assists this classification. The variables that describe the system kinetics change slowly in accord with the overall rate of the reaction. The other variables are “fast” and are in local equilibrium during the progression of the slow variables to the product state. From practical viewpoints we call variables “fast” when their equilibrium distribution can be sampled adequately on time scales accessible to conventional molecular dynamics (MD). The slow variables are called in the literature collective¹⁶ or coarse¹⁷ variables, and are denoted by C. The coarse variables are used to define a free energy landscape, F(C), on which the slow kinetic is conducted. The reduction in the number of degrees of freedom by switching from the full coordinate space R to C is helpful in order to calculate more efficiently kinetic observables, such as the Mean First Passage Time (MFPT) or the permeability coefficient, P, and to obtain qualitative insight into mechanisms.

Identifying the coarse variables is an important task in computational chemistry. However, it is challenging to rigorously determine this set without running first conventional simulations for long times that sample significant motions of the coarse variables themselves. Even with a long trajectory at hand, the analysis and the extraction of the coordinates with methods like diffusion maps¹⁶ can be far from trivial. Moreover, the time scale of the rare event can be so long that obtaining a conventional long time simulations with a significant sampling of coarse space is not an option.

The difficulties in determining C rigorously from MD suggest that our design of computational approaches to compute kinetics should take these challenges into considerations. A precise determination of the coarse variables may not be necessary, and it can also be adjusted to obtain sound approximations. Therefore, it is no surprise that many studies of kinetics use chemical and physical intuition to determine C. Once the rate is computed the quality of the coarse variables can be assessed rigorously, for example by computation of the transmission coefficients¹⁸, the committor^19,20,21, or the overall rate. Here we consider the selection and exploitation of coarse variables in the calculations of the rate of ion permeation across phospholipid membranes. We illustrate the complexity of the selection and note that while the most common choice is not adequate, another simple choice seems to capture the essential features of the process.

Most of simulations of permeation use z as a single coarse variable, where z is the projection of the distance vector from the ion to the membrane center along the normal to the membrane^{7,11-14,22,23}. The choice is intuitive and is working quite well in a number of cases. The assumption made in computing the free energy profile and the kinetics along z, is that there are no other slow variables in the system on the time scale of conventional molecular dynamics. However, it is possible to generate a counter example for ion permeation that suggests the existence of other slow coarse variables.

To check z as a single coarse variable we conducted a steered molecular dynamics simulation (SMD) of a potassium ion passing through a solvated DOPC (1,2-Dioleoyl-SN-glycero-3-phosphocholine) membrane in which the ion is pulled through the membrane along the z direction with a constant velocity of 0.5 Å per nanosecond (see Methods for details of the setup). The SMD trajectory length is ~100ns, which is typical for simulations of this type. If this trajectory was sufficiently long such that all other variables were sampled from an equilibrium distribution for a given z, then when the ion reaches the membrane center symmetrical behavior is expected. Hence, free trajectories of the ion initiated from the center of membrane with random velocities should end with equal probability at each of the membrane leaflets. However, in the above example, all the free trajectories return to the originating side. Only when the ion is pulled further, 8 Å away from the membrane center, transitions to the other membrane leaflet are observed in free trajectories. We therefore conclude that the system is not at equilibrium even if it is conditioned to remain at a specific value of z on a typical MD time scale.

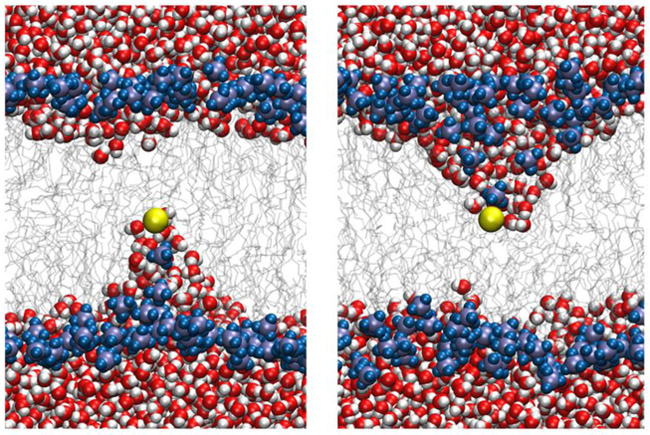
It has been observed by other simulations that the symmetry cannot be captured with only one reaction coordinate (z) except for some thin types of membranes ²⁴. In thicker membranes the system becomes unstable and the ion interacts with phosphates from only one side. Figure 1 illustrates this hysteresis using two MD simulations. In both simulations, the ion is placed in the middle of the membrane and its vertical position is restrained to the vertical position of the center of mass of the membrane. After minimization and equilibration, the ion breaks the symmetry and interacts with phosphates from either the upper or lower leaflet. Water molecules enter the membrane from one side only to keep the ion hydrated. The interaction of the ion with one membrane boundary is so strong that switching from one configuration to the other does not occur in the relevant simulation timescales (hundreds of nanoseconds). This leads to artificially high forces on the ion toward one side and non-symmetric free energy profiles. We were not able to recover a symmetric transition state with a single coarse variable (z).

Fig 1.

Snapshots in time from two simulations of a potassium ion conditioned to be at the center of a DOPC membrane. The ion is shown in yellow and the phosphate groups are shown with blue and violet spheres. The systems are equilibrated for 10ns. Water molecules are in red and white and lipid chains are in gray sticks. The snapshots do not show a symmetrical transition state and in both cases, the ion only interacts with phosphates and water molecules from one leaflet.

The discussion so far suggests that there is at least one more slow or coarse variable besides z for the ion permeation. One way of bypassing the limitation of z as the single reaction coordinate is to conduct better equilibrium simulations for fixed z values using enhanced sampling techniques, overcoming the time scale challenges of conventional MD. Pokhrel and Maibaum ²⁵ showed that umbrella sampling combined with well-tempered metadynamics result in non-symmetric free energy profile for ion permeation but replica exchange umbrella sampling can be helpful to achieve a symmetric free energy profile. However, even if the free energy profile can be symmetrized, computing the kinetics can still be challenging since slow transitions along the hidden coarse variable(s) will not be sampled in kinetic studies, once we turned the enhanced sampling tool off.

To improve the calculations of the free energy two recent studies suggest an extension of the reaction space to include more than a single variable ^6,26. In reference ⁶ multiple independent one-dimensional reaction coordinates were computed assuming that the exchange rate between alternative pathways is slow. In ²⁶ a local cylindrical region is defined around the ion and some atoms of the head groups. They also examined the continuity of the water wire. This new set of coarse variables improves the symmetry of the free energy profile ²⁶. However, the coordinates are rather complex and include undetermined parameters (e.g., the radius of the cylinder). It is desirable to use the simplest and smallest coordinate set that works and leads to efficient calculations of the free energy and the kinetics.

In this paper, we introduce new coarse variables for permeation studies of positively charged permeants and we test them for the calculation of kinetics of potassium permeation through DOPC membrane.

2. Methods:

2.1. Qualitative discussion of the new coarse variables

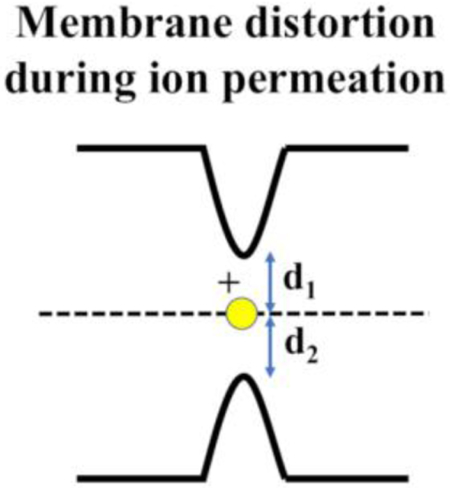
The discussion in the last section suggests that z is insufficient as a single coarse variable for ion permeation through membranes. We propose to use variables that couple ion displacement with membrane perturbation. Membrane perturbation can be either global or local, on a length scale of many or only a few phospholipid molecules, respectively. Global membrane distortions can be described with the tools of continuum mechanics.^27,28 However, significant membrane perturbations observed in conventional MD simulations of permeation⁷ are confined to one or a few phospholipid molecules. While some bending occurs on a length scale of tens of angstrom, the bending is a “fast” variable as we illustrate in Results. Moreover, it is particularly challenging to combine the continuum results with atomic level simulations to obtain time scales, a problem that we are focused on here.

We consider a simple coarse variable at the other extreme; a membrane perturbation dominantly localized on the displacement of one phospholipid molecule from each leaflet. The minimal distances between the ion and phosphate groups on each leaflet are the new coarse variables, which are denoted by d₁ and d₂. The minimal distances are advantageous to the standard vertical position as coarse variables. First, these coarse variables incorporate the membrane deformation to the description of the permeation process. Second, using these coarse variables gives a physically intuitive and a geometrical description of the transition state. The transition state is located at the position in which the ion has the same minimal distance from the phosphate groups of each of the leaflets, measuring the membrane distortion towards the ion.

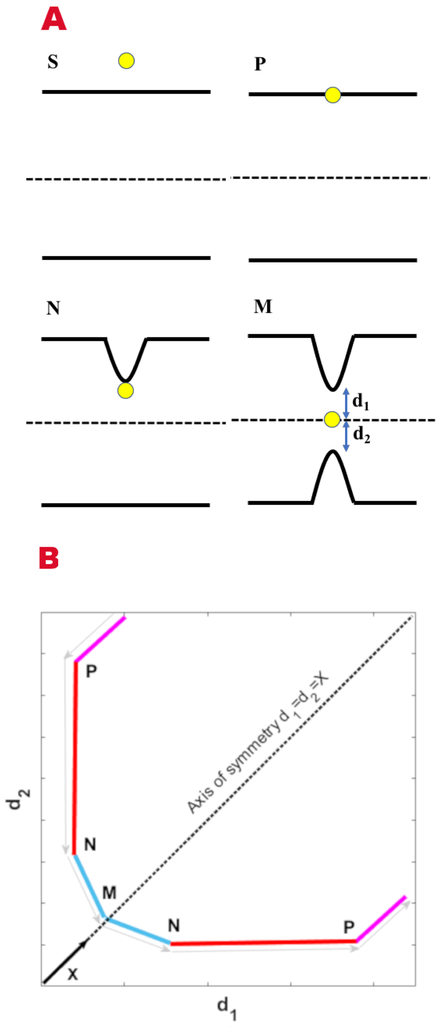
We provide first a qualitative description of how the new coarse variables capture elements of the permeation. Fig. 2 sketches the ion permeation pathway in the space of the two coarse variables d₁ and d₂. When the ion moves toward the membrane from one side (purple line), it is far from the head groups of the other side (~40 Å for a DOPC membrane). Therefore the ion entrance to the upper layer does not impact the membrane structure at the lower layer. Upon entry the ion interacts strongly with at least one of the phospholipid head groups at the upper layer (point P) and drags it along towards the membrane center (red line). During the dragging of the ion and the accompanying phospholipid molecule to the membrane center, the minimal distance d₁ remains roughly constant while d₂ decreases monotonically. At point M the pulling from the upper and lower bilayers becomes symmetric, making the point M the highest energy configuration along the path and a part of the transition state. Passing from point N to M, the ion pulls significantly at least one phospholipid from the lower layer (blue line) while reducing somewhat its interactions with the phospholipid of the entering layer. The rest of the chart from the center to the lower layer is a reverse of the path from the top layer to the membrane center. We note that the symmetric high-energy barrier is not a point but a line in the two-dimensional coarse space such that d₁=d₂ which we parameterize with the variable X.

Fig 2.

A) A schematic representation of ion permeation through a membrane using the new coarse variables. The permeation process starts at point S in solution and continues to point P where the ion, “touching” the membrane, has the shortest distance to a phosphate group. The ion drags the phosphate group into the membrane to reach point N. At point N the ion starts interacting with the lower membrane and pulls a phosphate group from it. At the same time the interaction with the upper phosphate weaken slightly. The last step brings the ion to the transition state M where the ion has the same minimal distance to the phosphate groups at each leaflet and d₁=d₂. B) Schematic representation of the points mentioned in panel A in the space of the two coarse variables d₁ and d₂. The black vector points along X that starts at origin (d₁=d₂=0) and defines the axis of symmetry and transition line.

The free energy landscape as a function of the coarse variables is not sufficient to estimate the rate. Even in the Transition State Theory (TST) we need frequency information or the time scale of crossing the transition state.^29,30 This can be challenging when more than one coarse variable is used. For example, modeling permeation using the Smoluchowski Equation (SE) in a space of more than one curvilinear variable requires a non-trivial coordinate transformation from the Cartesian to the curvilinear space and an estimate of a non-diagonal diffusion tensor.³¹ This is the case for the variables d₁ and d₂. One should also keep in mind that the use of overdamped dynamics is an approximation. Using inertial dynamics (e.g. the Fokker Planck Eq.) makes the above considerations even more complex.

Therefore, once the coarse variables are selected, we use the Milestoning theory and algorithm ³² to compute the free energy and the mean first passage time (MFPT) avoiding the complications mentioned above. In Milestoning only straightforward short trajectories between milestones are required to obtain the overall kinetics and thermodynamics (Section 2.5). Milestoning was used in the past in permeation problems.¹⁷ Depending on need, the calculations can be refined to an exact answer using iterations.³³

2.2. Definition of the coarse variables

The minimal distances between the ion and each of the leaflets are considered coarse variables. The differentiable minimal distance is defined as follows:

$$d_{\text{min}}\approx {\left(\frac{1}{N}\sum _j{(\frac{1}{\Vert r_j\Vert })}^n\right)}^{-1∕n}$$ (1)

The definition in Eq. (1) is programmed in the COLVAR package ³⁴ which we use. N is the total number of atoms of the phosphate groups in each leaflet, r_j is the distance between the ion and atom j of a phosphate group, and the summation is over all the phosphate groups in one leaflet. At the limit of large n, d_min becomes the minimum distance between the ion and any of the phosphate groups. We chose n=100 which in practice indeed selects the minimal distance.

2.3. System preparation:

The DOPC bilayer with 60 lipids on each leaflet was constructed using CHARMM-GUI ³⁵. The bilayer was solvated with TIP3P water molecules and salt concentration of 0.15M potassium chloride (KCl). The system consists of 36779 atoms. Periodic boundary conditions were applied in all directions. All the simulations of this paper have been conducted with the NAMD program ³⁶ and CHARMM36 force field ³⁷. The system was minimized using conjugate gradient algorithm for 10000 steps and then equilibrated in the NPT ensemble using Nose-Hoover Langevin piston pressure control ^38,39 for 5ns at pressure of 1atm and temperature of 303K. The system was then equilibrated in the NVT ensemble at 303K for 10ns using a Langevin thermostat. The water molecules were kept rigid using the SETTLE algorithm ⁴⁰ and all other bond lengths with hydrogen atoms were kept fixed with the SHAKE algorithm ⁴¹. The time step is 1fs in all the simulations. A real space cutoff distance of 12 Å was used and Particle Meshed Ewald (PME)⁴² accounted for long range electrostatic calculations.

2.4. The characterization of the reaction space:

To study kinetics and sample configurations along a pathway from reactants to products a whole path optimization approach was advocated in the past.^43-48 However, for energy landscapes with a single dominating barrier, like the case of the permeating ion, an alternative approach is possible. We locate first the highest free energy hypersurface (transition state) that must be crossed to reach the product from the reactant and then generate the rest of the free energy landscape. We assume that the transition state is when the ion is placed exactly at the membrane center and experiences the most significant dielectric barrier. The last assumption is checked for consistency by estimating the transmission coefficient.¹⁸ A similar approach of probing a dividing surface instead of the path was used in reference. ²⁶ They examined a different set of coarse variables to study ion permeation.

We used restraints to generate configurations conditioned to be on the hyper surface of this symmetrical position. We apply three harmonic restraints on the ion. The first restraint keeps: d₁ ≅ d₂ ≡ d, k(d₁ – d₂)² with a force constant, k, of 100 kcal/mol Ų. Another weaker harmonic restraint with a force constant of 5 kcal/mol Ų was added between the ion and center of mass of the head groups of the membrane, reinforcing the symmetry of the ion interaction with each of the two layers. The final constraint is on the magnitude of the membrane perturbation, setting a fixed numerical value, X, k'(d – X)². The last force constant, k', is 10 kcal/mol Å⁻². Seven values between X=4 Å and X=10 Å separated by 1Å are used to explore the central hyper-surface (Fig. 2) and generate a potential of mean force. At every X window, the system was minimized for 10,000 steps and then equilibrated for 5ns at a constant temperature of 303K with the above restraints. Then another 10ns simulation was conducted to obtain samples of X at every window. The results were analyzed using WHAM algorithm.^49,50 To improve statistics and to accurately overlap distributions, we added a window at X=6.5 Å.

To generate the whole pathway, after obtaining the most probable locations of the transition line along X, we conduct 20 unbiased MD trajectories, releasing the system from the transition line and following the pathway of the ion until it exits the membrane. Combining all the configurations sampled in the trajectories and projecting them onto the coarse space of d₁ and d₂ we obtain the pathways (see also Fig. 7 in Results).

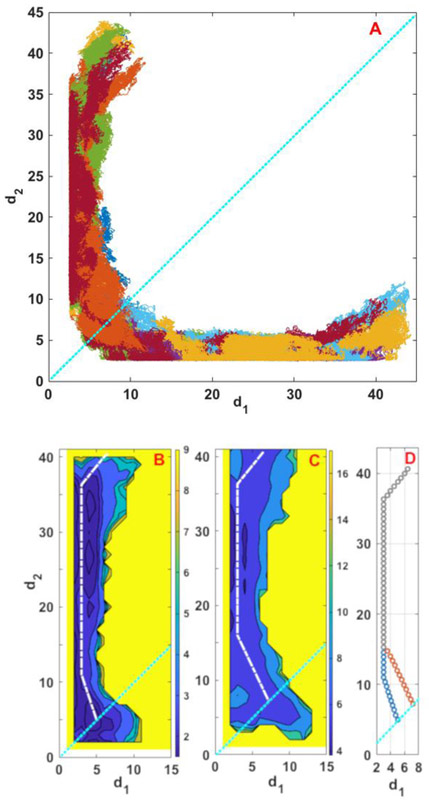
Fig 7.

Finding the permeation pathway by combining 20 unbiased trajectories of the ion from the transition line to the membrane-solvent boundary. (A) Examples of the trajectories initiated at saddle point 2. Each color corresponds to a single trajectory. A few trajectories exit from the upper leaflet and a few from the lower leaflet. Note the significant number of re-crossing of the transition state in a single trajectory indicating that the transition state is diffusive and the direct application of Transition State Theory^29,30 which assumes a single crossing is questionable. (B) and (C) are contour plots of −log[p(d₁, d₂)] where p(d₁, d₂) is the probability density of finding the system at a coarse space point (d₁,d₂) The dashed white lines sketch the permeation pathways as hypothesized in Fig. 2. (D) Path splitting of the permeation process. The two pathways are identical along the grey line but then they split into the blue or red branches arriving at saddle points 1 or 2, respectively. The cyan dashed line in all panels corresponds to the transition line.

2.5. Milestoning

The theory and algorithm of Milestoning were reviewed recently.³² Here we summarize essential elements relevant to the present study. Others have shown how the Milestoning theory can be connected to inhomogeneous DSM.⁵¹ We consider the more general case that may include memory and inertial motion. In Milestoning simulations we follow several steps that we list below:

• (i)Rough sampling of reaction space and determination of anchors and milestones.
• (ii)Sampling short trajectories between milestones (Fig. 3). Based on these trajectories construct a transition matrix, K, and determined the life times, t, of individual milestones.
• (iii)Compute observables such as overall mean first passage time (MFPT), and the free energy profile.

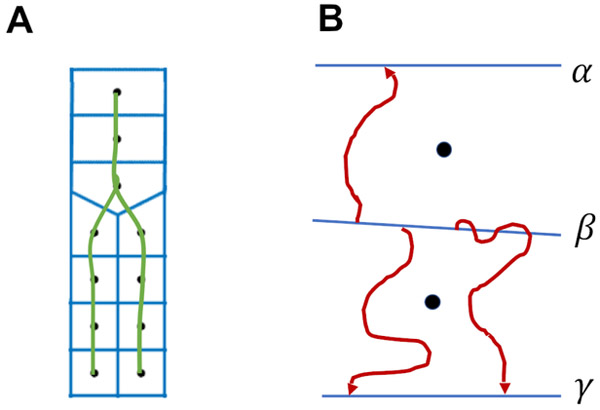
Fig 3.

A) Schematic representation of a branched pathway (green line) defined by a set of points called anchors (black circles). The blue lines that are separating every two neighboring anchors along the path correspond to milestones. B) A schematic representation of three unbiased trajectories initiated at milestone β. Each trajectory is integrated until it crosses for the first time a milestone different from β. The crossing contributes to calculation of the lifetime of milestone β and of the transition probabilities between milestone β and other milestones. In this picture, there are two transitions from milestone β to milestone γ and one transition from milestone β to α. Note that a trajectory is not terminated if it crosses the same milestone it was initiated on. This is illustrated on the right trajectory from milestone β to γ.

The rough sampling mentioned in (i) was conducted from the transition state as explained in the previous section. It is used to partition the coarse space into cells and determine interfaces between cells, which we call milestones (Fig. 3).

We use Voronoi cells to discretize the space as suggested in reference.⁵² Operationally, Voronoi cells are defined by a set of points A_i in the two-dimensional coarse space of (d₁, d₂). We call these points anchors.⁵³ A configuration in coarse space, C is said to be in cell i if it is closest to the anchor of cell i, i.e., ∣C–A_j∣_j≠i > ∣C–A_i∣. Milestones are defined as the interfaces between cells or the set of points with equal distance to two anchors (say i and j) and larger distances to all other anchors. Initial phase space points for the trajectories are sampled at the milestones from the canonical ensemble.

The short trajectories are conducted until each one of them hits another milestone for the first time. The identity of the initial and final milestones, α and β, are recorded and so is the length of the trajectory t_αl, where l is the trajectory index, and α the index of the initiating milestone. Let the number of trajectories initiated at milestone α be n_α and the number of trajectories initiated at α and terminated at milestone β be n_αβ. We estimate the probability of transition between α and β, with the trajectories conditioned to start at α, as K_αβ ≅ n_αβ/n_α. The flux through the milestones, q, is given as the eigenvector with eigenvalue one of the transition matrix: q^tK=q^t.⁵⁴ We also calculate the average lifetimes of the milestones t_α = Σ_l t_αl for all α. The free energy of trajectories that cross milestone α last is given by F_α = −kTlog(q_α t_α). The unnormalized probability that milestone α was last to cross is p_α = q_α t_α and the mean first passage time (MFPT) of the overall reaction is ⟨τ⟩ = p₀(I-K)⁻¹ t where p₀ is the vector of initial conditions, t the vectors of lifetimes, and K the transition matrix with an absorbing boundary condition at the product state (see also section 3.4).

To sample configurations constrained to a milestone between two anchors i and j, a harmonic restraint was applied such that k(d_i-d_j)² where d_i and d_j are the distances of the current configuration from both anchors and k is 500 kcal/mol Å ⁻². Another half harmonic constraint, k·(d_m – d_i)², when d_m < d_i and zero otherwise was applied to prevent the system from getting closer to any other milestone, m.⁵³ The force constants for these half harmonic restraints are also 500 kcal/mol Å⁻². Constrained simulations were conducted at each milestone for 2 ns. From the final 0.5ns, 200 configurations were saved and used to initiate 200 trajectories in the NVE ensemble. A typical trajectory length from initiation until termination at another milestone was 2 picoseconds, significantly shorter than the overall passage time, which is about hours.

Statistical error bars of the observables (the free energy and the MFPT) were estimated according to algorithm described in.⁵⁵ In brief, using the sampling of trajectories we estimate the parameters of the distribution functions from which the transition matrix elements and the lifetimes are sampled. We then sample a significant number of K_αβ and t_α from these distributions and compute the observables, free energy and MFPT, for each sample. The error bars are finally estimated as the variances of the distribution of the observables.

3. Results and discussions

3.1. Transition state

The transition state is assumed when the ion is located at the membrane center and membrane distortion is equal on both leaflets (i.e. d₁=d₂) It is likely to be the position in which the ion has a similar probability to go forward or backward. It is also the set of configurations with maximum dielectric repulsion. The line in coarse space (d₁=d₂) is therefore the transition state which we call the transition line. To determine the weights of configurations along the transition line we compute the potential of mean force (PMF) as a function of X. The PMF is computed by two methods to further assess the reliability of the results: (i) histograms based on long trajectories conditioned to remain at the transition line and (2) umbrella sampling along X. In (i) we run four NVT trajectories, each for 100ns in which the ion is constrained to remain at the transition line. Trajectories are initiated at 4 different positions X=4, 6, 8, and 10 Å to assure that sampling is not affected by the initial conditions. The final 70ns of these trajectories were combined and values of X sampled every one picosecond were used to calculate the PMF. For details on umbrella sampling see Methods section 2.4.

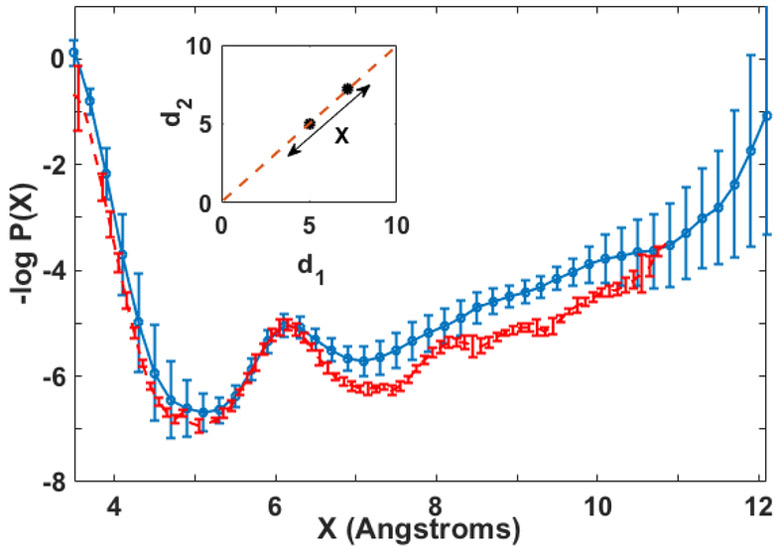
The PMFs are shown in figure 4. Van der Waals repulsion determines the distance of closest approach of the ion to the phosphate (~3.5 Å), which in turn determines the nearest distance in the calculation. The long trajectories and umbrella sampling PMF-s are similar. Both show two minima, one approximately at X=5 Å and the other at X=7.2 Å. The free energy difference between these two saddle points is small (~0.7 kcal/mol) suggesting that they both play important roles in permeation. A small barrier of ~1.2 kcal/mol separates these two saddle points. In Figure 5 we compare the two minima. At X=5 Å the phosphate group interacts with the ion with a smaller number of bridging water molecules compared the saddle point observed at X=7.2 Å. The two discrete saddle points as a function of X correspond roughly to one or two water shells between the ion and the phosphate groups. Since the PMF plots suggest similar free energies for the two saddle points, we considered both of them as possible transition states. Throughout the paper, X=5 Å and X=7.2 Å, are called saddle point 1 and 2. The pathways passing along them from the reactant to the product are called pathway 1 and 2, respectively.

Fig 4.

The free energy change along the transition line d₁=d₂=X obtained from (i) long MD trajectories with system confined to stay along the axis of symmetry (blue) and (ii) umbrella sampling (red). Both plots are similar, which adds confidence in the convergence of the calculation. The two saddle points are located at X=5Å and X=7.2Å.

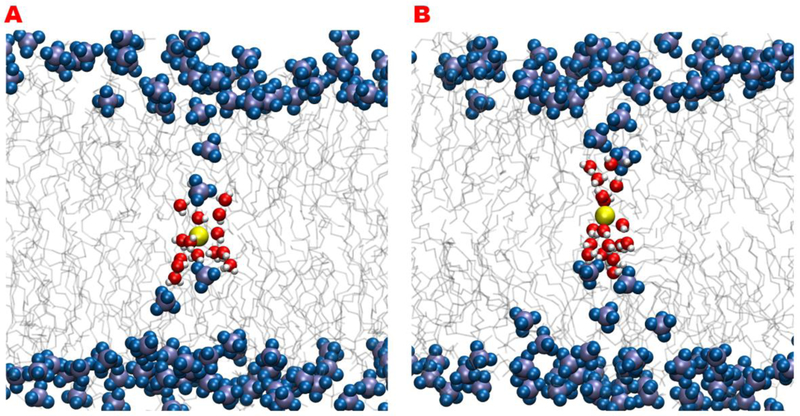
Fig 5.

Sampled configurations with the system at the two saddle points. Panels A and B correspond to saddle point 1 (X=5) and 2 (X=7.2). The yellow spheres are the ions. Water molecules are in red and white and the phosphate heads are in purple and blue. Note the single bridging water molecule between the phosphate and the ion in panel A and the larger number of bridging water molecules in panel B.

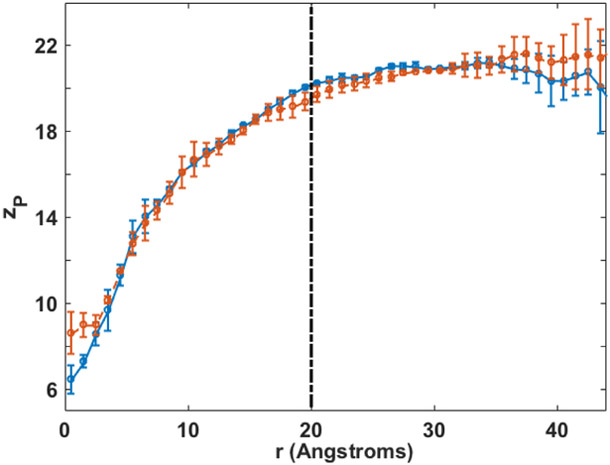
The more extended view of membrane deformation is of interest. We examined the simulations with the ion restrained at either of the saddle points and record the average vertical position of the phosphates (z_P) on both leaflets for different distances r from the ion in the membrane plane. In Fig 6 we show z_P versus r averaged over both leaflets and over 10ns constrained simulations at X=5 Å and X=7.0 Å. The permeation perturbs lipid positions with a radius of 20 Å in the membrane plane. A coarse variable of a membrane cylinder was proposed in reference.²⁶ Our simulations are consistent with the proposed coarse variable. However, the distortion parameters, d₁ and d₂, which we introduced here, are simpler to interpret, analyze, and use. The relative ease in which we converge the statistical averages with the new coarse variables suggests that the global bending is a fast variable.

Fig 6.

Vertical displacement of the phosphorous atom of the DOPC head group from the membrane center versus the distance of the phosphorous atom from the ion the in membrane plane: the transition state 1 (blue) or transition state 2 (red). The ion deforms a region of ~20 Å.

3.2. Ion permeation pathways

To verify a transition line or state it is common to compute the transmission coefficient.¹⁸ Given that the ion starts at the transition line with velocities sampled from the Maxwell distribution we compute the probability that it will continue to the product rather than returning to the reactant. The transition line is ideal if the computed probability (or the transmission coefficient) is half. We selected 20 initial configurations from the simulations at coarse variable X=5 Å (saddle point 1) and X=7.2 Å (saddle point 2) respectively and conducted unbiased simulations. In most cases, the ion leaves the membrane in a few nanoseconds. Twelve trajectories starting from saddle point 1 exit from the upper leaflet and eight trajectories exit from the lower leaflet. For saddle point 2, nine trajectories exit from the upper leaflet and 11 exit from the lower leaflet. The transmission coefficient is estimated as (0.6-0.4) and (0.45-0.55) for saddle points 1 and 2, respectively, suggesting that our transition line is adequate.

Moreover, the unbiased simulations from the transition line to the edges of the membrane make it possible to examine complete pathways of the ion migration through the membrane. The construction of the pathway based on trajectories initiated at the transition state in a membrane was conducted also in reference ²⁶ for a different set of coarse variables. It is a procedure widely used in electronic structure calculations in which a saddle point on the energy landscape is determined first and then the steepest descent path is determined by following the potential gradient downhill.^56,57

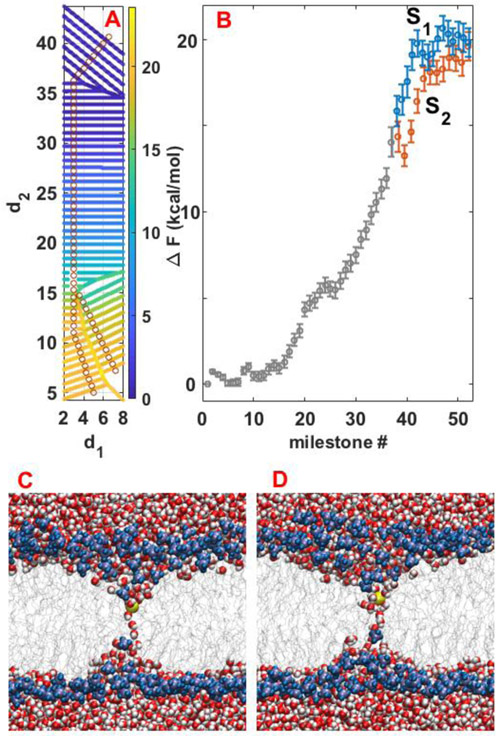
Figure 7A shows the projection of a few of these unbiased trajectories from saddle point 2 in the coarse space of d₁ and d₂. These trajectories follow the sketch of Fig. 2 and our qualitative reasoning about the coarse space. Exploiting the symmetry and overlapping all the trajectories onto one leaflet, we determine an average pathway from the transition line to the membrane’s edge with maximum statistics. Figures 7B and 7C show the results of overlapping all 20 simulations on one leaflet in coarse space for trajectories initiated at saddle points 1 and 2, respectively. We color code −log(p(d₁, d₂)) where p(d₁, d₂) is the probability density of finding the system at coarse position (d₁,d₂) The probability is determined by an average over the 20 trajectories and the bin size was 1Å. The sketched pathways of Fig. 2 are shown with white dashed lines in Fig. 7B and 7C. The main difference is that the two pathways split near d₁ ~ 16 Å. Before d₁~16 Å, the two paths are identical but then they branch, one headed to saddle point 1 and the second branch to saddle point 2. Figure 7D shows how the pathways can be combined to define transition network for the ion permeation. Each point represents one anchor in the Milestoning calculations and the points are located approximately 0.7 Å apart from each other.

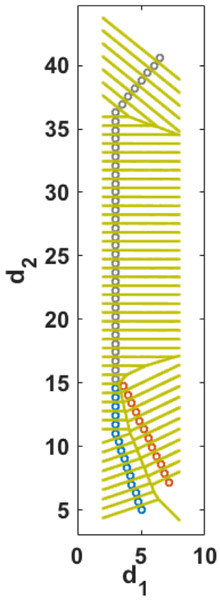
The coarse space of the distances d₁ and d₂ is divided into Voronoi cells. Each of the cells is represented by one coarse space point or an anchor. Fig. 8 illustrates the tessellation of the (d₁, d₂) space.

Fig 8.

A schematic representation of the Voronoi cells and their corresponding milestones (green lines). Each point shows an anchor that determines the center of the Voronoi cell.

3.3. The Free energy landscape and the Committor

The construction of the Voronoi cells and the milestones in our system is discussed in section 2.5 and Fig. 8. With the milestones at hand we sample trajectories between the milestones (see section 2.4) to determine the overall kinetics and thermodynamics. Two hundred short trajectories are computed from each of these milestones and the identity of the initiating and terminating milestones, as well as the times of termination, are stored. Eighty milestones represent the coarse space in two dimensions. In this space some of the milestones are never sampled by terminating trajectories and these milestones are removed from consideration. This removal is possible if the transition network remained efficiently connected between the reactant and products, i.e. that the ion movement from the transition line to the membrane-solvent edge remains accessible through a series of reachable milestones.

The transition matrix and the lifetimes of the milestones are sufficient to compute the free energy landscape. In the calculations of the free energy we use symmetric boundary conditions at the final milestone. The probability for going forward from the final milestones (passing forward the transition line) was set equal to the probability of going backward to the corresponding milestones. Figure 9A shows the free energy landscape by color-coding the milestones and Fig 9B shows one-dimensional free energy pathways from the membrane edges to saddle 1 and saddle 2. For the first 12 milestones, the free energy profile is almost flat and the motion is expected to be diffusive. At this region, the ion can penetrate the membrane and interact with the phosphates groups of an unperturbed membrane. However, the binding is weak that returning to the solution is a probable event. Beyond milestone 12 and with further permeation the ion drags the phosphate groups toward the center of the membrane. This process requires a significant investment of free energy. At the point of path splitting the pathway leading to saddle 2 shows a small but significant reduction in free energy compared to the pathway leading to saddle 1.

Fig 9.

(A) Contour plot of the free energy landscape in each milestone for permeation of potassium ion from DOPC. (B) Free energy profile along the two pathways. The identical part is shown in grey. The blue and red correspond to branches of pathways 1 and 2, respectively. Note that the second pathway is slightly shorter and from the branching point, pathway 2 (red) is stretched to enable comparison of the free energies along the pathways. (C) and (D) show sampled configurations of the system at points S₁ and S₂ shown in panel (B), respectively. In these states water wires connecting both sides of the membrane start to form and this facilitates further permeation of the ion.

The error bars were estimated following the procedure in Methods using a sample of one thousand transition matrices and life times. The barrier heights are estimated at 19.8 ± 0.8 kcal/mol and 19.6 ± 0.8 kcal/mol at transition states 1 and 2, respectively. Interestingly, the transition domain is relatively flat, suggesting a diffusive barrier domain. Water wires (like those shown in Fig. 9C and 9D) make a connection between both bilayers and facilitate the permeation.

Another quantity that can be found directly from the Milestoning calculations is the committor function. Since there are two exit-channels to be considered (saddle 1 and saddle 2), it is more convenient to consider the commitment to not react. The committor of each of the milestone is the probability of going back to the reactant (outside the membrane) before reaching the product (either of the milestones at saddle 1 or saddle 2). We adjust the boundary conditions of the transition matrix as follows ¹⁹:

$$\begin{array}{cc}\hfill & K_{1,1}=1and{K}_{1,j}=0\forall j\ne 1\hfill \\ \hfill & K_{f_1,j}=0\forall j\hfill \\ \hfill & K_{f_2,j}=0\forall j\hfill \end{array}$$ (2)

Where 1 denotes the first milestone outside the membrane and f₁ and f₂ correspond to the milestones at saddle points 1 and 2, respectively. The boundary conditions mean that every trajectory that reaches the saddle points disappears, while the trajectories returning to the reactant accumulate at that milestone. As was shown in ¹⁹ the committor, $\tilde{C}$, can be found by:

$$\tilde{C}={\mathbf{K}}^n{\mathbf{e}}_1$$ (3)

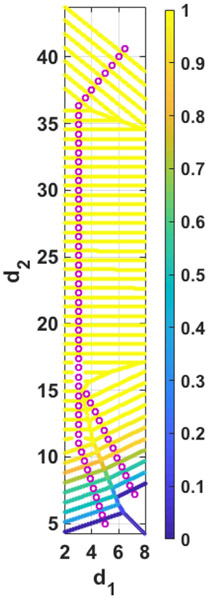
Where e₁ is a vector with all elements equal to zero except e₁₁=1. Fig. 10 shows that the committor is close to one for most of the milestones. Only close enough to the transition line (approximately the final 3Å along each of the pathways) it deviates significantly from unity. This observation is consistent with our suggestion of a single dominant barrier for the ion permeation problem.

Fig 10.

Color-coding the committor function on every milestone. The committor at a milestone is the probability of going first to the reactant (the top layer) than to the product (either of the saddle points).

3.4. Kinetics: MFPT, flux, and permeability

The MFPTs can be obtained directly from Milestoning by adjusting the kinetic matrix to include absorbing boundary conditions at both of the milestones corresponding to the saddle points (see section 2.5). Note that the time for the system to move from the transition line to either side of the membrane-water interface is much smaller than the time to reach the transition line from the membrane boundary.

The computed MFPT is 1.1±1.0 hours for potassium ion to permeate through the DOPC membrane from either of the two pathways.

An interesting question is to compare the contributions of the two pathways that lead to saddle 1 or saddle 2. We compute the number of trajectories that pass these final milestones per unit time (or the flux) under steady state non-equilibrium conditions to the system. The boundary conditions are now:

$$\begin{array}{cc}\hfill & K_{1,2}=1and{K}_{1,j}=0\forall j\ne 2\hfill \\ \hfill & K_{f_1,1}=1and{K}_{f_1,i}=0\forall i\ne 1\hfill \\ \hfill & K_{f_2,1}=1and{K}_{f_2,i}=0\forall i\ne 1\hfill \end{array}$$ (4)

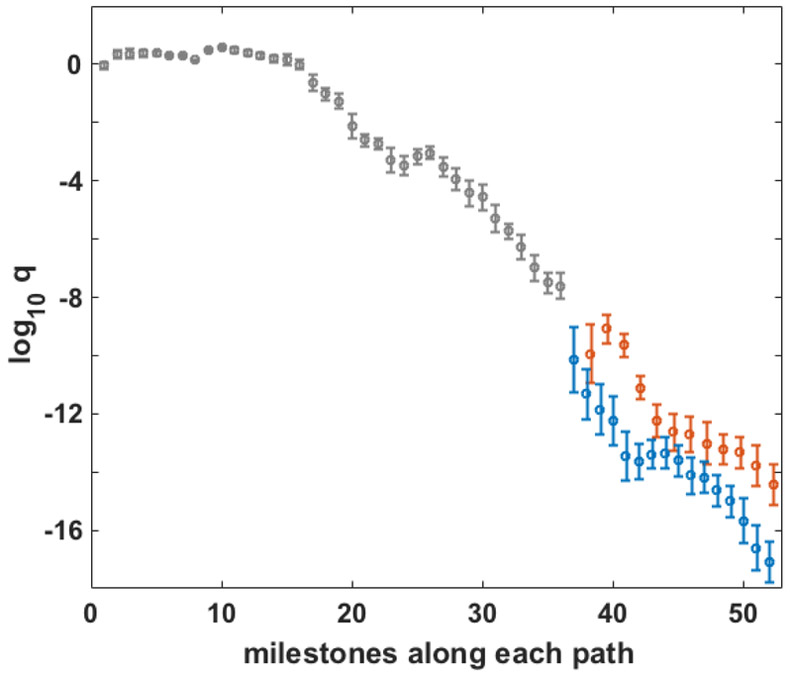
Every trajectory that reaches either of the saddle points returns back to milestone 1. We determine the stationary flux from the linear equation q^tK=q^t. Fig 11 shows the flux through each of the milestones. Significantly larger flux is passing through the second pathway. The flux through saddle point 2 is approximately 500 times larger than the one at saddle point 1. The second pathway is therefore dominant and carries approximately 99.8% of the flux. To verify this, we doubled the number of sampling trajectories of the 3 milestones at the branching region and obtain the same results. Fig 4 shows that the saddle point of the second pathway consists of a larger water bridge between the ion and the phosphate groups compared to the first pathway. The results of the flux emphasize the importance of these bridging water molecules and of the water wires in the ion permeation process.

Fig 11.

Flux passing from each pathway for a steady state condition. The grey part shows the identical part of the paths and blue and red show the branches from pathways 1 and 2, respectively. The q values are normalized to have q=1 at the first milestone.

A relevant quantity measured in experimental studies is the permeability coefficient (P). The coefficient quantifies the capacity of a membrane for permeation as:

$$P=\frac{J}{\mathrm{\Delta }C}$$ (5)

Where J is the current, or the number of permeants passing through the membrane per unit time and per unit area and ΔC is the difference between the concentrations on both sides of the membrane. The experimental studies by Paula et al. ⁹ suggest a permeability of 3.47×10⁻¹² cm/s for passive permeation of potassium ion through a DOPC membrane.

The theory of Milestoning can be used to calculate the permeability directly using steady state flux without any further assumptions (e.g. without assuming overdamped dynamics). The flux vector of Milestoning, q, is determined up to a constant. If q is a solution of q^t=q^tK, αq where α is a positive constant is a solution too. We therefore normalized the flux such that (q)₁ = 1. The absolute value of J can be written as J= J₀ × q_f/q₁ were J₀ is the flux entering the membrane at milestone 1 and q_f = q_f1 + q_f2 is the direct sum over fluxes passing through the two pathways.

The value of J₀ (the flux of ions into the membrane) depends on the ionic concentration and can be estimated from a conventional molecular dynamics simulation. We conducted an unbiased MD on our system for 10ns and count the number of times that any potassium ion hits the first milestone at the membrane-water interface. The hitting events were added for both leaflets to obtain more statistics and divided by two. In 10ns simulations, the potassium ions hit the first milestone 3077 times on each side of the membrane. The membrane surface was estimated from the simulation box to be 4022 Ų and J₀ was estimated to be 1.3 mol/cm²s. From the Milestoning analysis we obtained q_f 8.9 ± 8.2 × 10⁻¹⁵ within a single standard deviation. Setting the salt concentration to 0.15 M in equation (5) leads to 7.3 ± 6.7 ×10⁻¹¹ cm/s for a permeability coefficient, which is close to the experimental value of 3.47 × 10⁻¹².⁹

Note that the calculations of the free energy are done in equilibrium conditions, while the calculations of the MFPT and the flux are conducted using non-equilibrium, but stationary set up. The two types of calculations cannot be compared directly as we observe significant non-equilibrium effects. For example, the depletion of the population, p, near the absorbing boundary causes a higher “effective free energy” estimated as −kTlog(p).

4. Conclusions

We consider the permeation process of a positively charged ion through a phospholipid membrane. We illustrate that the z coordinate, or the ion position along the normal to the membrane, is insufficient to capture all the slow processes in the system that contribute to permeation but are not accessible to conventional molecular dynamics. As a result using a permeation coordinate only the penetration depth of the ion, z, is unlikely to yield converged thermodynamic and kinetic observables. We introduced instead two remarkably simple coarse variables d₁ and d₂. These two variables measure the distance of the ion from the membrane boundaries and capture the distortions of the bilayer. These coarse variables led to efficient and converged calculations of the kinetics and thermodynamics using the theory of Milestoning. Different water solvation during permeation contributed to a splitting of the pathway into two branches and two saddle points in the coarse space. The water solvation is, however, a fast variable that forms and dissociates rapidly on the molecular dynamics time scale. We therefore did not include water-solvation coordinate as a coarse variable. Finally, we also illustrate that our theory in conjunction with current force field reasonable recover the value of the permeation coefficient of potassium through DOPC membrane. We anticipate that similar set of coarse variables can be used to describe the permeation of more complex molecules through biological membranes.