Localized Nanoscale Heating Leads to Ultrafast Hydrogel Volume-Phase Transition

Abstract

The rate of the volume-phase transition for stimuli-responsive hydrogel particles ranging in size from millimeters to nanometers is limited by the rate of water transport, which is proportional to the surface area of the particle. Here, we hypothesized that the rate of volume-phase transition could be accelerated if the stimulus is geometrically controlled from the inside out, thus facilitating outward water ejection. To test this concept, we applied transient absorption spectroscopy, laser temperature-jump spectroscopy, and finite-element analysis modeling to characterize the dynamics of the volume-phase transition of hydrogel particles with a gold nanorod core. Our results demonstrate that the nanoscale heating of the hydrogel particle core led to an ultrafast, 60 ns particle collapse, which is 2–3 orders of magnitude faster than the response generated from conventional heating. This is the fastest recorded response time of a hydrogel material, thus opening potential applications for such stimuli-responsive materials.

Graphical Abstract

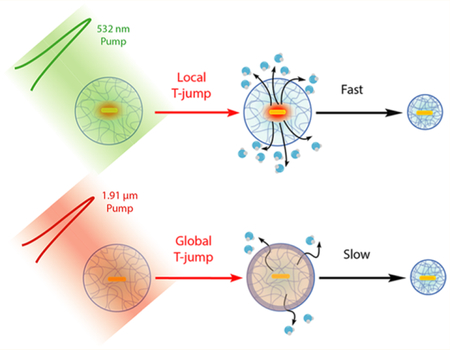
Stimuli-responsive hydrogel materials undergo a volume- phase transition in response to a change in pH, temperature, or ionic strength that enables a wide range of applications, including photonic crystal-based sensors, nanorobots, and adaptive optics.^1,2 Nanoscale and microscale particles composed of these responsive hydrogels are particularly useful because of their ability to interact with light and for their relatively rapid response rates to external stimuli.^3,4 A fundamental question in the application of hydrogel nanomaterials pertains to the speed of the volume- phase transition. Specifically, given the wide interest in using such hydrogels as responsive elements, it is important to de fine the upper limit of the particle response rate. For example, in biomechanics, the dynamics of hydrogel transitions may control the force loading rate (force per unit time), which directly tunes the probability of triggering mechanical signaling events and modulating the likelihood of molecular unfolding.^5–9 In sensing applications, it is important to de fine the time limit for signal propagation. Therefore, the goal of this work is to investigate the speed-limit of nanoparticle hydrogel actuation.

The dynamics of hydrogel nanoparticle volume-phase transition has been previously studied by time-resolved transmittance measurements in combination with a laser- induced temperature-jump.^10,11 For example, bulk water heating by pulsed laser excitation of the water overtone band at 1.9 μm was used to trigger the phase transition and collapse of pNIPAM nanoparticles. By measuring the change of light transmittance, El-Sayed and co-workers showed that polymer collapse occurred on the 0.3–1.5 μs time scale and displayed multiexponential dynamics of the phase transition.¹⁰ Similarly, Asher and co-workers found that pNIPAM nanoparticles colloidal arrays responded to a laser T-jump in a coherent manner with time constants that ranged from ∼900 ns −150 μs and that individual nanoparticles showed a volume-phase transition time scale of ∼100 ns −350 μs.^11,12 Importantly, the nanoscale swelling–deswelling kinetics observed in these experiments are consistent with the Tanaka model, which shows that the lifetime of the volume-phase transition, τ, is proportional to the square of the radius (r²) of the swelled spherical hydrogel.¹³ This model works reasonably well for describing the deswelling-swelling kinetics for hydrogel particles with a radius ranging from 10⁻⁷ m to 10⁻³ m (Figure 1 and Table S1).^11,13–17 Here, we asked whether the Tanaka- de fined speed-limit for hydrogel response kinetics is de fined by the geometry of the heating that drives the volume-phase transition. For example, heating the solvent versus the particle itself may drastically alter the water transport rate and, accordingly, alter the value of τ

Figure 1.

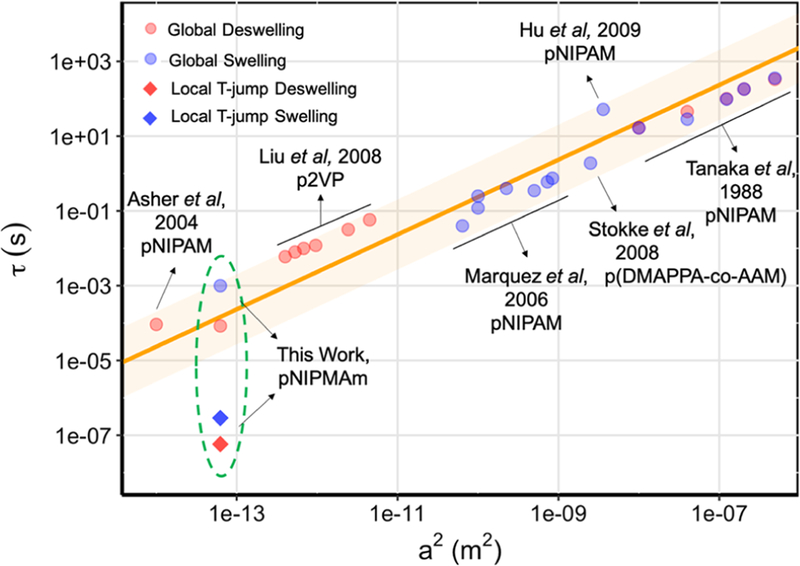
Log−log correlation plot between the characteristic hydrogel particle deswelling−swelling time constant τ and the square of the particle radius, a². Orange line represents the linear relationship described by equation τ = a²/(π²D), where D is the polymer network diffusion coeficient. The shaded orange region represents 3 times the standard deviation of the slope. The red spheres denote the reported values for deswelling process; the blue spheres denote the reported values for swelling process. The two diamonds represent the convoluted time constants measured in local T-jump experiments.

To address this question, we investigated a type of core– shell hydrogel particle, the optomechanical actuator (OMA), composed of a plasmonic gold nanorod (AuNR) core encapsulated with a responsive polymer shell. The OMA nanoparticle harnesses photon energy to generate localized heating that in turn drives the volume-phase transition of the nanogel. OMA nanoparticles have been used for controlling mechano-transduction in living cells, including fibroblasts and T-cells^18,19 and also have been applied as a force clamp for mechanically unfolding biomolecules in a high-throughput fashion.²⁰ De fining the temporal dynamics of the OMA volume-phase transition is particularly important because the mechanical loading rate fundamentally determines the ability of the particle to trigger mechano-transduction events.

In the present study, we triggered the OMA volume transition using two complementary approaches. The first was a “local” T-jump, where the AuNR was directly pumped with a pulsed laser, depositing energy into the AuNR, which is then transported in a radial fashion to the polymer shell. The second approach matched that of the past literature, using a “global” T-jump to drive OMA collapse, in which the laser pump energy was deposited into the bulk solvent. All time- resolved measurements were conducted with nanosecond temporal resolution, revealing the dynamics of the pNIPMAm polymer shell and the local solvent environment surrounding the AuNR. Time-dependent finite element analysis modeling was consistent with experiments, complementing the conclusions of the time-resolved spectroscopy measurements. Importantly, we found that the local T-jump reduced by 2–3 orders of magnitude (Figure 1), thus breaking the r² dependence predicted by the Tanaka model.¹³ In summary, these results demonstrate that nanoscale organization of responsive gels can profoundly influence the dynamics of the material.

RESULTS

Spectroscopic Characterization of Equilibrium Volume-Phase Transition.

The OMA nanoparticle is composed of a gold nanorod (AuNR, 25 nm diameter ×100 nm length) encapsulated by poly(N-isopropylmethylacrylamide) polymer hydrogel (pNIPMAm, ∼ 500 nm diameter, Figure 2a).²¹ The pNIPMAm is a thermoresponsive hydrogel material that undergoes a volume-phase transition, a manifestation of its inherent lower critical solution temperature (LCST).^22–24 This polymer exhibits a temperature-induced cooperative coil– globule transition upon heat absorption.²⁵ As a result, a number of pNIPMAm hydrogel properties are significantly modulated in association with this volume-phase transition, including hydrophobicity,²⁶ size,²⁷ refractive index,¹¹ and porosity.²⁸ We have used the temperature-dependent properties of the hydrogel as a means to trigger the volume-phase transition to measure its response dynamics.

Figure 2.

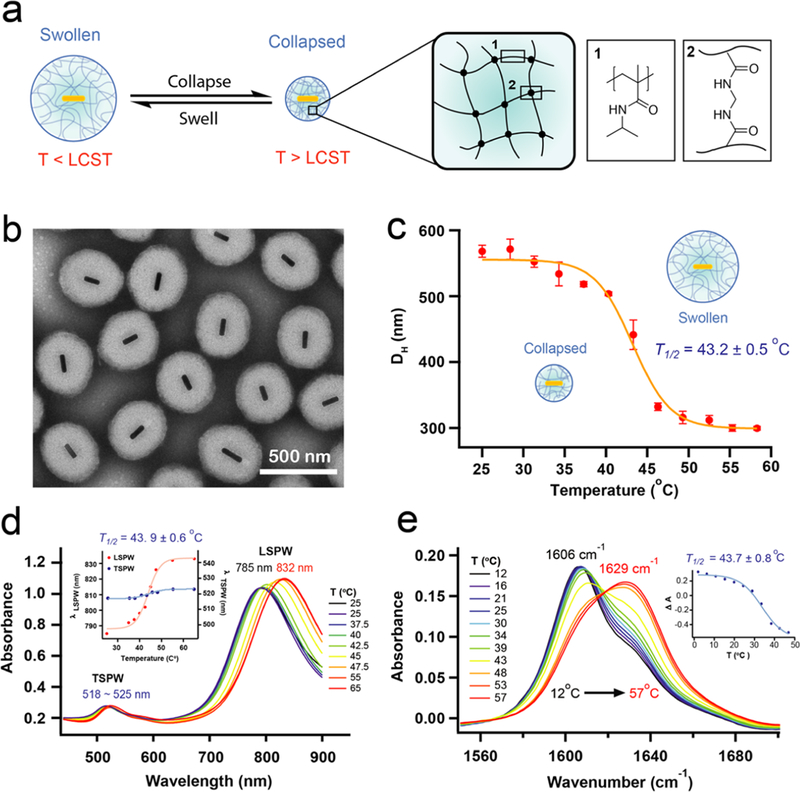
Equilibrium characterization of OMA. (a) The chemical composition of OMA particle polymer shell and its temperature- dependent volume-phase transition. (b) TEM image of OMA particles. (c) Temperature-dependent DLS measurement of OMA particle hydrodynamic diameter. (d) Temperature-dependent UV−vis−near-infrared (NIR) absorbance spectra of OMA. Inset: LSPW and TSPW temperature-dependent wavelength shift. (e) Temperature-dependent steady-state FTIR absorbance spectra. Inset: temperature-dependent OMA deswelling curve monitored at 1606 cm⁻¹.

The chemical composition of the OMA particle polymer shell and its temperature-dependent volume-phase transition are illustrated in Figure 2a. Transmission electron microscopy (TEM) images of the OMA particles con firm a AuNR core (25 nm × 100 nm) encapsulated by a slightly ellipsoidal shaped polymer shell with an average long axis diameter of 400 nm (Figure 2b), which is smaller than that measured in dynamic light scattering (DLS) because the particle is in a dehydrated state in the vacuum conditions employed for TEM imaging. DLS measurements as a function of temperature show a change in hydrodynamic diameter from ∼550 to ∼300 nm as a result of heating the sample above its LCST (Figure 2c). The OMA particle displays the same LCST as that reported for pNIPMAm nanoparticles, which range from 38 to 44 °C,^23,25 thus con firming that the gold core does not significantly alter the LCST. The temperature-dependent hydrodynamic diameter (D_H) curve was fitted to a two-state model that features a sigmoidal function. The OMA phase transition temperature was determined to be T_1/2 = 43.2 ± 0.5 °C with a full width at half-maximum (fwhm) of 8.0 °C for the transition. The transition is slightly broader than what is observed for the bulk pNIPMAm, likely because in the context of the OMA, the cross-linked polymer is less homogeneous and lacks the long- range order of the bulk material necessary to observe a sharp transition.²³

The temperature-dependent UV–vis absorption spectra of the OMA show a shift in the longitudinal surface plasma wavelength (LSPW) associated with the volume phase transition (Figure 2d). The LSPW red-shifts ∼45 nm, whereas the transverse surface plasmon wavelength (TSPW) exhibits a signi ficantly smaller shift when the temperature increases from 25 to 65 °C. The two surface plasmonic bands of AuNR, TSPW and LSPW, allow us to trigger the OMA volume-phase transition by optically pumping the AuNR at its TSPW at 520 nm and monitor its response by the spectral shift of LSPW at 785 nm. The shift of the AuNR LSPW with the volume-phase transition is due to its sensitivity to the local environment at the Au/polymer interface. When the pNIPMAm polymer shell collapses, excluding water near the AuNR surface, the local environment becomes more hydrophobic (lower dielectric constant) thus resulting in a LSPW shift to higher wave- lengths.^21,29 Fitting λ_LSPW versus temperature to a two-state model yields a transition temperature T_1/2 = 43.9 ± 0.6 °C and a fwhm of 9.8 °C, which is in agreement with the DLS measurements.

To probe the chemical structure of the polymer following the volume phase transition, we collected steady-state Fourier- transform infrared (FTIR) spectra of OMA particles as a function of temperature in the D₂O solution (Figures 2e and S1a). The FTIR spectra showed the reversible collapse and swelling processes of the OMA in a temperature-dependent manner, as indicated by the shift of the amide I carbonyl (C=O) stretching band in the region between 1590 and 1640 cm⁻¹ (Figure S1c).^30,31 The D₂O solvent provides a spectral window in the infrared to monitor the shift of amide I band. Below the LCST, the amide I band is strongly shifted to lower frequency due to H-bonds between the amide carbonyl group and nearby D₂O molecules in a similar manner to what is observed for unfolded proteins.^32,33 As the temperature rises above LCST, the pNIPMAm polymer undergoes the volume- phase transition, driven by folding of the polymer coils into a globule state in which the polymer chains self-associate to form H-bonds between backbone amide C=O and N–D groups, squeezing out the D₂O molecules. The temperature-induced volume-phase transition causes a blue shift in the amide I band as shown in Figure 2e. Apparently, the net hydrogen bond strength of the amide hydrogen bonds is weaker than it is for those with solvent D₂O, such that the C=O bond strength increases and the frequency of the amide I C=O stretch increases in the collapsed state. Notably, the pure hydrated or dehydrated states are not observed even when the bulk temperature is much higher or lower than the LCST, as evidenced by the pronounced shoulders that remain at temperature extremes (Figures 2e and S1d). For the collapsed particle, this is probably because the exterior of the particle still interacts with water, and there may also be some trapped water within. For the hydrated particle, it suggests that some of the backbone carbonyls are not well-solvated, perhaps because there are regions of high polymer cross-linking density at the core. The FTIR spectra show a two-state phase transition during both heating and cooling processes, indicated by the isosbestic point observed around 1620 cm⁻¹. The isosbestic point is not perfectly overlapped due to the intrinsic temperature dependence of the amide I band that gives rise to some degree of shifting and broadening.³³ We further analyzed the FTIR spectra over the range between 1550–1700 cm⁻¹ by using principal component analysis to extract the temperature-dependent transition.^34–36 The transition is fitted to a sigmoidal function derived from the two-state transition model. The transition temperatures T_1/2 are estimated to be 43.7 ± 0.8 °C with a fwhm of 19.8 °C (Figure 2e), and 42.1 ± 0.9 °C with a fwhm of 15.9 °C (Figure S1b) for the heating and cooling processes, respectively. These two transition temperatures are the same within experimental error, and the same as measured in DLS and temperature-dependent UV–vis absorption experiments. In summary, the steady-state equilibrium data clearly support a reversible 2-state phase transition for the OMA particles with a transition temperature between 42–44 °C.

Pump–Probe Measurement of Phase-Transition Dynamics.

We probed the dynamics of the OMA volume- phase transition using a temperature-jump (T-jump) to trigger the transition. The T-jump is caused by absorption of a 10 ns laser pulse that either heats the AuNR directly (local heating) or heats the D₂O solvent molecules (global or external heating, Figure 3a). The local T-jump was achieved by pumping the OMA using a 10 ns Q-switched Nd:YAG laser pulse at 532 nm, which is on the shoulder of the TSPW of the AuNR. The local heating triggering event involves several fundamental processes. The plasmonic AuNR functions as a photothermal transducer, absorbing photon energy and rapidly converting it to localized heat, which diffuses into the polymer and raises its temperature above the lower critical solution temperature (LCST, ∼42 °C for pNIPMAm). The time-dependent IR spectral response in the amide I region is shown in Figures 3b and S2b. The principal spectral component extracted from the time-dependent spectral image (Figure 3d inset) resembles the difference spectrum obtained from steady-state FTIR, which indicates the occurrence of the temperature-dependent volume-phase transition in the local T-jump experiment. The transient bleach centered at ∼1605 cm⁻¹ and the transient absorption at ∼1625 cm⁻¹ are consistent with a blue shift of the amide I band in response to the T-jump, characteristic of the volume-phase transition based on the steady-state FTIR data. Principle component analysis of the transient infrared spectral image indicates that the OMA is actuated within ∼100 ns after absorption of the pump laser pulse. Following the initial transition, the transient signals return back to zero as the OMA cools back to the starting temperature and swells back to its hydrated structure (Figure 3b,d). Therefore, the time course of the IR transient was fitted to a triple exponential function in which the first exponential term (τ₁ = 58.2 ± 2.3 ns, A₁ = 60.8%) represents the heating process and the second and third exponential terms (τ₂ = 140 ± 3 ns, A₂ = 36.2% and τ₃ = 2.10 ± 0.07 μs, A₃ = 3.0%, respectively) represent the cooling dynamics (Figure 3d).

Figure 3.

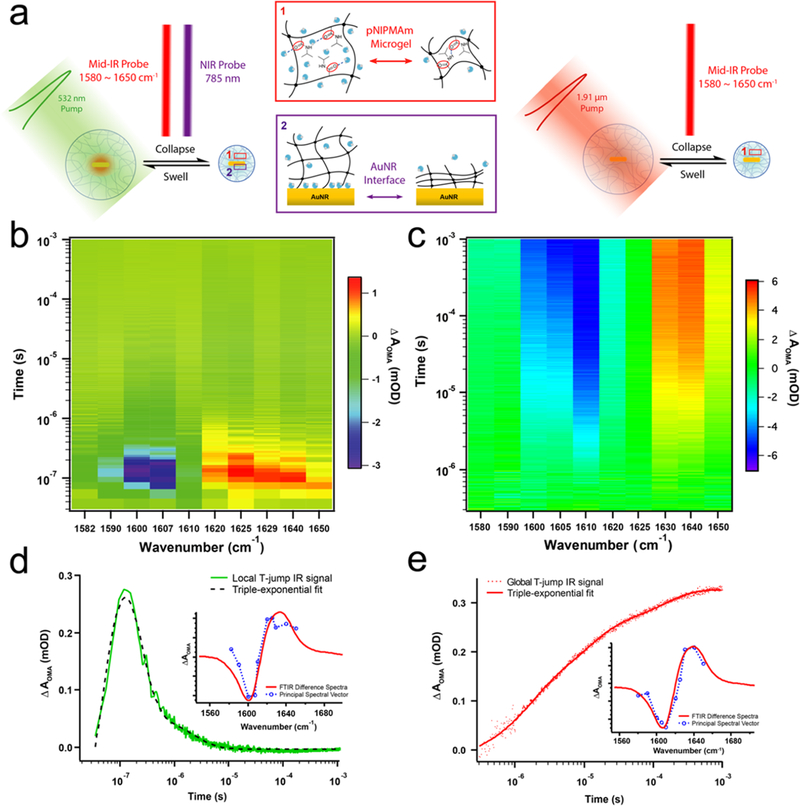
OMA actuation dynamics triggered by local and global T-jump measured by time-resolved IR spectroscopy. (a) Schematic illustration of pump−probe IR measurement of OMA actuation triggered by local and global T-jump. (b) Time-resolved IR spectral image of OMA triggered by local T-jump. (c) Time-resolved IR spectral image of OMA triggered by global T-jump. (d) The kinetic and spectral components of local T-jump IR spectral image. (e) The kinetic and spectral components of global T-jump IR spectral image.

To complement the IR measurement of the polymer, we also simultaneously recorded the transient near-infrared (NIR) absorption of the LSPW at 785 nm that probes the AuNR– polymer interface (Figure S3a). A fast, unresolved bleach is observed for the initial heating response, consistent with steady-state spectra that show a bleach at 785 nm with increasing temperature. The instrument response of the NIR absorption measurement is limited by two factors, the 15 ns time response of the visible detector (Thor Laboratories) and the 10 ns pump pulse width. Apparently, the heating response of the plasmon band at Au–polymer interface is faster than the ∼20 ns instrument response time. Therefore, only the cooling response starting from 50 ns, after the initial dip due to the local heating, is analyzed and fitted. In the transient NIR time course, ΔA_OMA at 785 nm gradually recovers to baseline during the cooling process. The cooling transient is fitted to a triple exponential function, in which τ₁ = 214 ± 4 ns, A₁ = 59.9%; τ₂ = 16.1 ± 0.1 μs, A₂ = 23.1%; and τ₃ = 172 ± 2 μs, A₃ = 17.0%, respectively.

In comparison with local pumping T-jump the AuNR, the global T-jump time-resolved IR spectroscopy provides a feasible tool to study the bulk heating actuation dynamics of OMA (Figures 2a and S5). The 1.9 μm pump radiation was absorbed by weak vibrational combination bands in the D₂O solution, which allowed for nearly uniform heating in the pump–probe overlap region, whereas the OMA particles do not absorb at this wavelength.³⁷ The spectral image in amide I band region in Figure 3b shows the OMA dynamics with a 10 °C global T-jump starting at 35 °C. In comparison, other global T-jump spectral images with different temperature jumps and starting temperatures are shown in Figures S7 and S8. The dynamic response of the OMA shows the same spectral signature as that measured in the local T-jump transient IR absorption (Figure 3e), in which absorption ΔA decreases between 1600–1610 cm⁻¹, and ΔA increases between 1630–1640 cm⁻¹ upon the temperature jump, indicating a blue shift of the amide I band. One of the most important differences in the global T-jump triggered “bulk heating” OMA actuation is that the collapsing kinetics are more than an order of magnitude slower than the “inside-out” mechanism induced by pumping the AuNR in OMA in the local T-jump experiment, as the absorption signal slowly builds on the microsecond time scale. Indeed, after the kinetic component of the spectral image is extracted by principal component analysis, the collapse kinetics was best fitted with a triple-exponential function (Figure S9). Table S2 summarizes the amplitudes and time-constants for T-jumps of 6.5, 10, and 13 °C, and Table S3 summarizes the amplitudes and time- constants for three T-jump experiments with 29, 32, and 35 °C as the starting temperatures. The time-constant for the fastest phase of the collapse ranged from 1.3–1.5 μs, which is about 20-fold slower than that observed in the local T-jump transient IR absorption measurement. The collapse kinetics are also well-modeled using a stretched exponential function, consistent with what has been observed for other temperature- dependent polymer phase-transition kinetics.^38,39

Finite-Element Simulation of Heat-Transfer Dynamics.

To calculate the heat-transfer dynamics and temperature gradient in the OMA nanoparticle during the pulsed laser excitation and subsequent thermal relaxation, we built a three- dimensional geometric model of the OMA nanoparticle (Figure 4a). The particle was modeled as a 500 nm diameter sphere with a AuNR core and solvents filled structure. This approximation is reasonable because more than 90% of the polymer shell volume of the OMA is filled with solvent molecules in the swollen state.^40–42 Given the experimental conditions, the laser power absorbed by each OMA in the sample is estimated to be ∼7.4 × 10⁻⁵ W.⁴³ The detailed calculation is given in the Supporting Information. The initial stage of the simulation consists of a 10 ns heating period corresponding to the pump laser pulse (Figure 4b). Photo- thermal conversion of the absorbed laser pulse in the AuNR represents the only heating source in the OMA during the simulation. The lifetime of the plasmon excited state is at the picosecond time scale and it decays by internal conversion, producing a hot ground state. Therefore, the conversion of the absorbed photon energy to heat occurs within a few picoseconds and can be treated as a delta function on the time scale of the pump–probe experiment. The temperature pro file of the OMA at 20 ns in both the X and Z axes shows that the AuNR reached ∼165 °C at the end of pulsed laser excitation (Figure 4c). The temperature drops exponentially with distance from the AuNR. Although the instantaneous temperature rise at the AuNR–D₂O interface is above the D₂O boiling point (101 °C), the evaporation of D₂O and formation of transient nanobubbles is minimal because this temperature is only maintained for a very short period of time at Au/D₂O surface as the heat quickly dissipates into the surrounding polymer and solvent environment.⁴⁴ Moreover, we observe that a large portion of the 125 nm radius D₂O shell is above pNIPMAm’s LCST (∼42 °C), which allows the volume-phase transition of polymer shell to occur. Subsequently, the heat started to diffuse and the average temperature dropped inside OMA (Figure 4a). The average temperature curves for the 125 nm radius D₂O shell that describe both heating and thermal relaxation processes are fitted with a triple exponential function (Figure 4b). For the average temperature of the 125 nm D₂O shell, the time constant for heating is τ₁ = 6.3 ns, A₁ = 52.9%, and the two time-constants for thermal relaxation (cooling) are τ₂ = 14.1 ns, A₂ = 36.6% and τ₃ = 77 ns, A₃ = 10.5%. These two time constants of cooling process describe the heat diffusion anisotropy due to the cylindrical geometry of the AuNR, particularly in a 125 nm radius D₂O shell. The distance between the longitudinal end of the AuNR to the boundary of the D₂O shell is only 75 nm, whereas the distance between its radial surface to the boundary of the D₂O shell is 112.5 nm. This heat diffusion anisotropy becomes negligible when we treat the 250 nm radius OMA particle as a whole, as the average temperature of the process is well- fitted with a bi- exponential function (Figure S12a,b).

Figure 4.

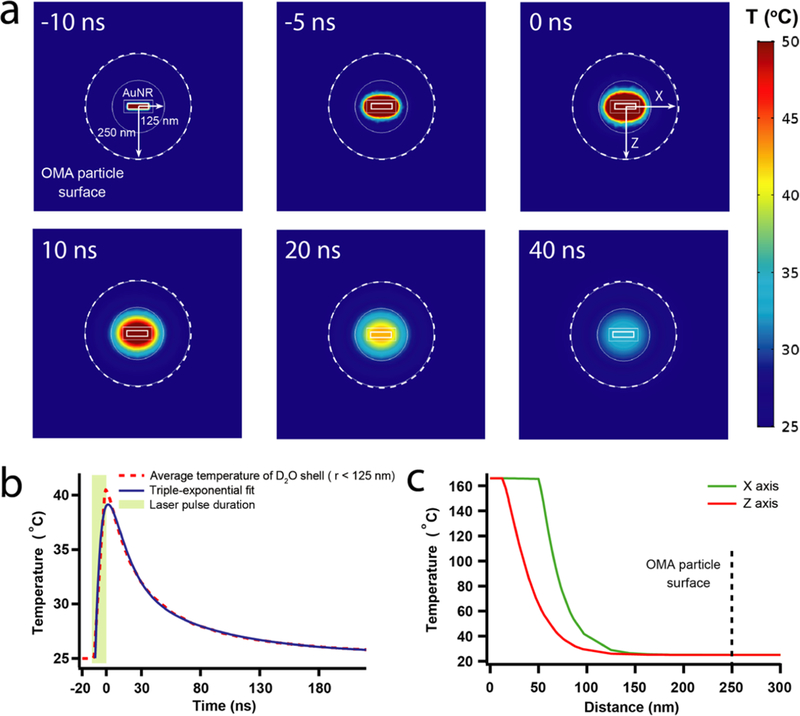
Heat-transfer dynamics of pulse laser stimulated OMA by finite-element analysis using COMSOL Multiphysics. (a) Snapshots of the temperature gradient inside OMA during the laser stimulation and thermal relaxation. (b) The average temperature time course of 125 nm radius D₂O shell during pulse laser stimulation and following thermal relaxation. (c) Temperature pro files of OMA at both the X and Z axes right after 10 ns pulse laser stimulation.

DISCUSSION

The actuation dynamics of OMA by local T-jump and global T-jump are summarized and mapped onto a logarithmic time scale in Figure 5. The response of each physical process during the actuation (heating and cooling) is represented by a color gradient bar that is mapped onto the logarithmic time scale bar. The starting time point of the bar was determined using the value τ_heating × ln2 that corresponds to 50% conversion, whereas the end time point of the bar was determined using τ_cooling × ln(2⁴) that corresponds to 93.75% conversion.

Figure 5.

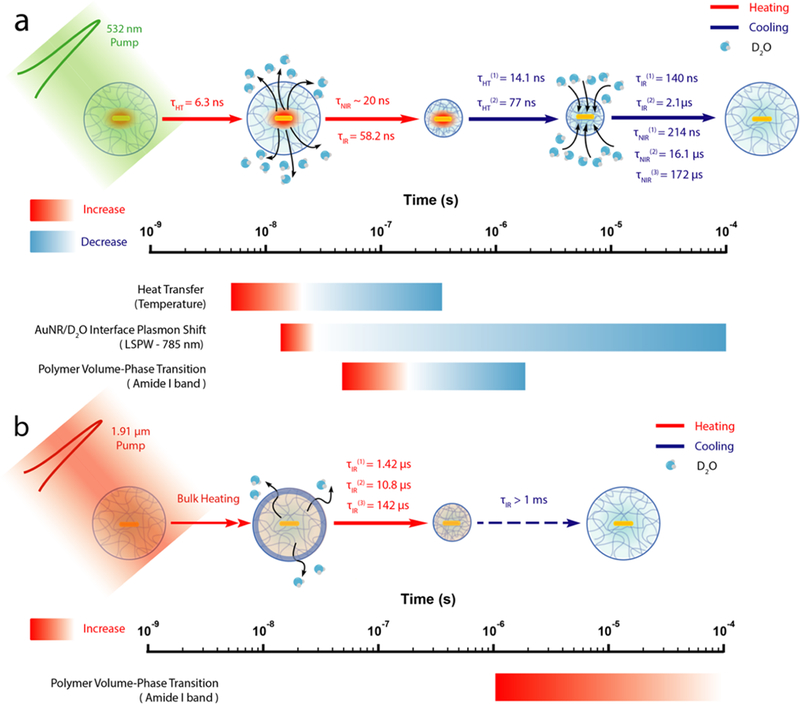
Schematic representation of OMA actuation dynamics and subsequent events on the logarithmic time scale. (a) Local T-jump triggered OMA actuation dynamics and corresponding heating and cooling events shown on the logarithmic time scale. (b) Global T-jump triggered OMA actuation dynamics and corresponding heating and cooling events shown on the logarithmic time scale.

For the local T-jump actuation mechanism, the pump process of the AuNR by the 532 nm laser pulse starts from photon absorption that creates an excited state consisting of a thermalized free electron gas within 2 ps.^45,46 The internal conversion between “hot” electrons and the lattice occurs on longer time scales (∼10 ps) and gives a “hot” ground state, with the energy deposited into phonon modes of the AuNR by inelastic electron–phonon scattering.^47,48 The rate of heat transfer from a gold nanorod through a silica shell to the surrounding solvent was measured to be ∼10¹⁰ s⁻¹ by Alivisatos and co-workers using time-resolved infrared spec- troscopy.⁴⁴ Therefore, the initial heating process is instantaneous on the time scale of our experiment with a 10 ns laser pulse, so the heating of the AuNR will simply follow the duration of the laser pump pulse. The initial heating of the solvent layer around the AuNR will also be very fast as our calculation showed. According to our calculation, the temperature of AuNR reaches up to 160 °C at the end of laser stimulation. Next, the heat is quickly dissipated into surrounding solvent molecules with an average time constant equal to 6.3 ns for the 125 nm radius solvent shell. The solvent layer around the AuNR is rapidly heated up as the pNIPMAm polymer undergoes a volume-phase transition due to a localized high temperature that is above the LCST (42 °C). As a result, D₂O molecules are expelled out due to this polymer coil–globule transition, and the local environment at the AuNR–D₂O interface becomes hydrophobic as detected by declining absorbance at 785 nm because of a red shift of the LSPW. Although the rise of the heating signature at 785 nm is not fully characterized because of the instrument detection limit, the highest temperature is reached within 40 ns. Therefore, the time constant is estimated to less than 20 ns. The heat diffusion is also monitored by transient IR at the amide I band, the carbonyl stretching of the polymer, which exhibits a collapse time constant of 58 ns, about an order of magnitude slower than the heat-transfer time. This means that the OMA collapse dynamics (58 ns) observed by transient IR is fully resolved from the heat-transfer dynamics (6.3 ns) that is obtained from simulation. We ascribe the OMA actuation triggered by a 532 nm laser pulse in the local T-jump experiment to an “inside-out” mechanism. As the heat is generated at the core of OMA by AuNR and dissipates out, the subsequent physical processes are triggered in sequence, from inside to outside. For the “inside-out” mechanism, the deswelling dynamics of OMA is likely limited by the diffusion of D₂O out of the structure.

In comparison, the global T-jump OMA collapse triggered by a 1.9 μm laser pulse shows completely different dynamics (Figure 5b) as we observe pNIPMAm polymer collapse phase extending out to 1 ms and the swelling phase is even slower. We refer to this global T-jump triggered OMA actuation mechanism as the “Uniform Bulk Heating” mechanism as the 1.9 μm laser pulse generated an almost instantaneous T-jump for the bulk D₂O solvent. However, the collapsing kinetics of OMA is about 20-fold slower than that of “inside-out” mechanism, resulted in microsecond actuation dynamics. The swelling time constant is estimated to be around the millisecond time scale using a theoretical model derived from the bulk pNIPAM microgel system.¹³ The slower dynamics triggered by the “uniform bulk heating” mechanism is likely because the initial heating is from the outside, which leads to the formation of a dehydrated polymer “skin” that acts as the barrier for diffusion of D₂O, which hinders hydrogel volume- phase transition. It was shown previously that the amide backbone of the polymer in the coil conformation is surrounded with a cage-like structure of water,^49,50 consistent with the IR results presented here. We speculate that the “inside-out” mechanism will more easily break this hydrogen- bonded network between ordered water molecules and the amide backbone due to the higher initial temperature of the local heating, resulting in an ultrafast coil-to-globule phase transition. Therefore, we expect that a number of factors, including degree of polymer cross-linking, polymer structure, particle size, etc. will also determine the dynamics of OMA actuation.¹⁰

The OMA cooling and swelling dynamics de fine the waiting time for resetting it for the next actuation, which is also a critical parameter for periodic and repetitive OMA actuation applications. For the “inside-out” mechanism, at the beginning of the cooling dynamics, vibrational cooling to the surrounding solvent is fast (∼100–200 ps).^51,52 Next, the heat diffusion during the thermal relaxation is the rate-determining step in the swelling process. The two-phase cooling kinetics with time constants of 14.1 and 77 ns are obtained for the 125 nm radius D₂O solvent shell from the simulation. The presence of two time constants for the cooling process is primarily because of heat diffusion anisotropy due to the cylindrical shape of the AuNR. This heat-transfer anisotropy is particular significant in the 125 nm radius D₂O shell. As the temperature drops below the LCST, the pNIPMAm polymer globule state starts to unfold again during the volume-phase transition and D₂O molecules start to diffuse back into the OMA. The cooling dynamics of OMA monitored by transient IR at C=O stretching band revealed two time constants, 140 ns and 2.1 μs. The cooling transient obtained from monitoring the LSPW absorbance at 785 nm exhibits slower kinetics, with time constants of 214 ns and 16.1 μs. The slower response is a consequence of the longer time it takes for D₂O molecules to diffuse back to the AuNR–polymer interface at the OMA core to cause the shift of LSPW back to 785 nm. In contrast, the IR probe measures the hydration of the C=O groups throughout the polymer shell, which on average is faster than hydration of the AuNR–polymer interface in the center of the OMA. The observation of two cooling and swelling rates indicates that the volume-phase transition of the OMA pNIPMAm polymer shell is not an “all-or-none” process, but rather, it is resolved into two relatively independent transitions that may involve intermediate states during the rehydration.²⁵ For the “Uniform Bulk Heating” mechanism, we observe cooling dynamics for the 6.5 °C T-jump longer than 1 ms (Figure S6). This is not surprising because the large amount of heat deposited in the laser pump region raises the temperature of all the solvent molecules, which must then cool to the surrounding (unheated) solvent. This solvent cooling process is known to occur on the millisecond time scale.⁵³ Therefore, the observed polymer swelling kinetics in this case are likely limited by the cooling rate of the heated probe volume and not by the intrinsic swelling rate.

CONCLUSIONS

In summary, we have demonstrated triggering the OMA particle on the submicrosecond time scale using the pulse laser and conducted a rigorous characterization of OMA’s actuation dynamics by time-resolved spectroscopic measurement and heat-transfer simulation. We have shown that the OMA nanoparticle can be triggered to collapse within 100 ns by a local heating mechanism. Moreover, we can modulate OMA’s actuation dynamics dramatically (2–3 orders of magnitude time scale) by changing the pumping scheme (local T-jump versus global T-jump). These properties of OMAs would be very useful for dynamic force spectroscopy (DFS), a technique that measures the mechanical response of a system by scanning through different force loading rate.^54–58 Conventional approaches of DFS are limited to force loading rates of <10⁶ pN/s.⁵⁵ For the OMA, we can predict a force loading rate about ∼10⁸ pN/s (∼10 pN in 100 ns) from our current and previous measurements, extending the time scale by over 2 orders of magnitude. The significantly higher loading rates that are possible with OMAs would increase the sensitivity of DFS to weaker, shorter lived interactions, which would enable the characterization of the dissociation rate and energy landscape for some extremely nonspontaneous processes according to the theoretical framework established by the Bell–Evans model.^59,60 The broad spectrum of hydrogel phase-transition kinetics might be useful for tailoring drug release rates in hydrogel-based therapeutic delivery applications. The drug- release rate may be finely tuned by either changing the pumping mechanism or modifying the degree of cross-linking of the hydrogel polymer. The ultrafast hydrogel volume-phase transition triggered by localized heating would also make feasible diagnostic applications that require high spatiotemporal response. For example, such core–shell single-particle OMA structures can be used for spatiotemporal thermometry to image transient heat generation in cells with high spatial and temporal resolution.⁶¹

MATERIAL AND METHODS

Synthesis of Optomechanical Actuator Particles.

Preparation of Gold Nanorods.

To synthesize AuNR for OMA preparation, a seed-mediated growth method in a binary surfactant mixture composed of hexadecyltrimethylammonium bromide (CTAB) and sodium oleate (NaOL) developed by Murray and co-workers was applied.⁶² This protocol is also important to control the dimensions of the AuNR, such that its NIR plasmon band was at approximately 800 nm. After completion of the growth of AuNR, the CTAB and NaOL surfactant-coated AuNRs were ligand-exchanged with a thiolated vinyl terminal ligand by adding 20 mg of N,N′-bis(acryloyl)cystamine to 90 mL of AuNR solution along with 10 mL of ethanol while being vigorously stirred at 700 rpm for 12 h. Subsequently, the ligand exchanged AuNR was separated from the solution by centrifugation at 5000 rpm for 60 min. The supernatant was removed and AuNR was dispersed in 15 mL of deionized (DI) water. The final solution was concentrated to 90 mL and characterized using UV–vis–NIR and TEM. This solution was then stored at 4 °C for future usage.

Encapsulation of AuNRs with pNIPMAm Polymerization.

The procedure for encapsulation of the AuNR with pNIPMAm polymerization was adapted from methods noted by Contreras-Caceres et al. and F. Tang et al.^29,63 The polymerization of pNIPMAm on the AuNR surface was carried out as follows: 100 mg of N- isopropylmethacrylamide and 10 mg of the cross-linking agent N,N′-methylenebis(acrylamide) were dissolved in 15 mL of Milli-Q water in a three-neck flask with a water cooling condenser on the top. The mixture was heated to 70 °C under continuous stirring and purged with continuous N₂ flow. Subsequently, 1 mL of previously ligand0exchanged AuNR solution with thiolated vinyl terminal was added to the three-neck flask. After 1 min, pNIPMAm polymerization was initiated by adding 80 μL (0.1 M) of the free radical initiator 2,2′- azobis(2-methylpropionamidine) dihydrochloride (AAPH), and the polymerization was allowed to proceed for 4 h at 70 °C. After the reaction was complete, the reaction mixture was air cooled to the room temperature while being stirred. To remove uncoated AuNR nanoparticles, the reaction mixture was diluted with DI water and centrifuged at 5000 rpm for 10 min, and then the supernatant was removed and the resulting pellet redispersed in DI water. This washing procedure was repeated at least three times, yielding the puri fied OMA nanoparticles.

OMA Particle and AuNR Characterization.

Temperature- dependent DLS was performed on a NanoPlus (Particulate Systems, Norcross, GA). The temperature-dependent UV–vis spectra were collected on Cary 60 UV–vis spectrophotometer (Agilent Technologies). TEM images were acquired on a Hitachi H-7500 transmission electron microscope at an accelerating voltage of 75 kV. A 5–10 μL sample was dropped onto a 200-mesh carbon coated copper grid (Electron Microscopy Sciences) and incubated for 60 s following by wicking away the excess liquid. After 3 rounds of incubation, 5 μL of 1% methylamine tungstate (Ted Pella, Inc.) solution was added on the TEM gird to apply a negative stain on the OMA sample. After 60 s of incubation, the excess liquid was wicked away. For the AuNR sample, no negative staining is required. The sample grids were subsequently dried and stored in a desiccator. The magnification of the OMA particle image is 10k (Figure 2b), and the magnification of the AuNR image is 15 000× (Figure S13).

Temperature-Dependent Steady-State FTIR Measurement.

The OMA sample was freeze-dried using the lyophilizer and then dispersed in D₂O. The final concentration of OMA in the IR window is ∼0.8 nM. The morphology and UV–vis spectra of OMA sample remained the same after the lyophilization. The above steps were repeated at least three times to completely remove H₂O in the sample. A D₂O reference was used for steady-state FTIR. The sample and reference were each injected into one-half of a split infrared transmission cell employing CaF₂ windows sandwiching a dividing Teflon spacer (path length of 130 μm) using a syringe and sealed. FTIR spectra were measured with an MCT equipped Varian Excalibur FTIR spectrometer (Varian Inc., Palo Alto, CA). Samples and references were measured from 12–57 °C. The temperature- dependent spectra were collected with 128 scans at 2 cm⁻¹ resolution and were baseline-corrected using a multipoint spline function.

Local T-Jump Transient IR and Near-IR Absorption Spectroscopy Measurement.

The same sample preparation procedure was followed as for the steady-state FTIR spectroscopy except that an AuNR solution was used as the reference to track the solvent thermal signal. To achieve the solvent exchange from H₂O to D₂O for AuNR solution, 10 kDa MWCO Amicon Ultracentrifugal filter was used. The AuNR solution was concentrated by centrifugation at 3000 rpm for 10 min and redispersed in D₂O. This was repeated five times to achieve as high D₂O solvent percentage as possible. The instrument setup of the simultaneous transient IR and near-IR absorption system that used in our measurement are previously described.⁶⁴ Briefly, a Q- Switch laser (Nd:YAG) was used to generate a 10 ns pulse at 532 nm to pump the sample. The energy of each pulse is ∼820 μJ, and the laser beam was focused to a 1000 μm diameter spot, and the results in the laser field intensity equal those of ∼1.04 × 10⁸ W/cm² during the pulse. The transient IR and NIR spectra were measured simultaneously at room temperature (∼25 °C) using a quantum cascade laser generating IR beam between 1535–1695 cm⁻¹ (Daylight Solutions Inc., Poway, CA) and a NIR diode laser at 785 nm. Samples were rastered between pulses to ensure a unique sample spot was being measured. The amide I band carbonyl stretch and LSPW are simultaneously probed for every pulse, and 50 shots were averaged for every measured wavenumbers. The transient absorption signals ΔA were obtained by calculating the ratio between pumped signal intensity and dark signal intensity. The D₂O solvent thermal signal was subtracted by measuring the solvent response with a AuNR reference solution, yielding ΔA_OMA = ΔA_Total – ΔA_Solvent. The ΔA_OMA corresponds to the OMA signal.

Global T-Jump Time-Resolved IR Measurement.

The OMA sample preparation for global T-Jump IR measurement is the same as that for steady-state FTIR, in which the D₂O was used as the reference for transmission but also as an internal thermometer during the T-jump relaxation (Figure S4). The global T-jump IR apparatus has been described previously.^65–67 Briefly, this is a pump-probe experiment in which a 10 ns 1.91 μm near-IR pump laser pulse (Q- switched Ho:YAG) that absorbed by weak vibrational combination bands of D₂O was used to initiate a rapid T-jump in the sample, thereby perturbing the volume-phase transition of pNIPMAm polymer shell of OMA particles. A quantum cascade laser (Daylight Solutions Inc., Poway, CA) tunable between 1535–1695 cm⁻¹ was used to probe the IR signal change of the amide I band of pNIPMAm polymer in response to the rapid T-jump and following relaxation. The changes in transmission of the IR probe beam were detected by a fast (200 MHz) photovoltaic MCT detector (Kolmar Technologies, Newburyport, MA). The OMA sample signal time courses were extracted by subtracting the change in absorbance of the D₂O reference in response to the T-jump for each wavenumber (Figure S6). The time courses were recorded from the nanosecond to 10 ms time regime. The sample IR window was incubated at 29, 32, and 35 °C by using a water bath circulation system for stabilizing the initial temperature.

Spectral Data Analysis.

The local T-jump transient absorption and global T-jump time-resolved data were first processed by using an in-house Python script with the data analysis library Pandas. The data were then plotted and fitted by using IGOR Pro software (WaveMetrics, Inc.) to a model the multiexponential dynamics of OMA during the volume-phase transition. The principal component analysis was applied for the FTIR, local T-jump transient absorption, and global T-jump time-resolved data sets by conducting singular- value decomposition (SVD) for the data matrix. The eigenvectors that corresponding to spectral components and kinetic components (temperature-dependent component) were then extracted and fitted into corresponding models. More details about SVD and modeling can be found in the Supporting Information.

Finite Element Analysis and Heat-Transfer Simulations of OMA Particles.

The heat-transfer dynamics of OMA is simulated by finite element analysis using the COMSOL Multiphysics 5.2. A 1 μm³ solvent cubic was built to model the single unit solvent environment (D₂O) for each OMA. The geometric model of OMA contains a 250 nm radius sphere that were also filled with D₂O and an AuNR (25 nm diameter ×100 nm length) at the center (Figure S10). Inside the 250 nm radius sphere, there is a 125 nm radius spherical domain and an 85 nm diameter ×160 nm length cylindrical domain that encapsulate the AuNR. This multilayer structure was used to calculate the time series of average temperature in each domain. The approximation that polymer shell of OMA has the same thermal diffusivity as the D₂O solvent shell is reasonable because ∼90% volume of OMA’s polymer shell is filled with solvent in the swollen state.^40–42 The laser power absorbed by AuNR is calculated according to the formula given in the Supporting Information, and herein, we assume 100% photothermal conversion so that AuNR heating power is equivalent to the laser power absorbed by AuNR. A 240 ns time-dependent simulation with 10 ns pump laser duration was run and convergence of the calculation was achieved. All of the parameters, conditions, and underlying heat- transfer equations are described in detail in the Supporting Information.