Abstract
It is essential to study RNA under molecular crowding conditions to better predict secondary structures of RNAs in vivo. No systematic study has been completed to determine the effects of molecular crowding on RNA duplexes of varying lengths and sequence composition. Here, optical melting, circular dichroism, and osmometry data were collected for RNA duplexes in a 20% polyethylene glycol (with an average molecular weight of 200 g/mol) solution (PEG 200), and nearest neighbor parameters were derived using this data. RNA duplexes are destabilized, on average, 1.02 kcal/mol in the presence of 20% PEG 200. The ΔG°37 values predicted by the nearest neighbor parameters for RNA duplexes in 20% PEG 200 were ∼0.65 kcal/mol closer to experimental ΔG°37 values than those predicted by the standard nearest neighbor model. For one DNA sequence in solution with small crowders, the ΔG°37 values predicted by the 20% PEG 200 RNA nearest neighbor parameters were closer to the experimental values than ΔG°37 values predicted by either the RNA or DNA standard nearest neighbor models. This indicates that the nearest neighbor parameters for RNA duplexes in 20% PEG 200 may be generalizable to RNA and DNA duplexes in solutions with small crowding agents.
INTRODUCTION
RNA is a dynamic and versatile biomolecule that is involved in many cellular processes such as protein synthesis (1), catalysis (2,3) and enzyme regulation (4). RNA has three levels of structure: primary, secondary, and tertiary. Primary structure is the RNA sequence, secondary structure occurs when the bases of RNA begin to form base-pairing or other favorable interactions, and tertiary structure is the 3D fold of RNA. While tertiary structure of RNA largely dictates the function of the RNA molecule, tertiary structure is often inferred from the secondary structure. Due to this relationship, it is important to have the ability to predict secondary and tertiary structure to understand the structure and stability of RNA. If the structure of RNA is known, one could better understand its function in the cell and could design pharmaceuticals to target RNA to treat diseases.
As RNA structure has high variability, researchers have worked to develop models to predict RNA secondary structure (5–7). The most widely implemented algorithm is a nearest neighbor model which involves free energy minimization (7). This algorithm utilizes a model based on thermodynamic parameters that were derived from optical melting experiments to predict the RNA secondary structure with the lowest free energy. Software such as RNAStructure (8,9), Mfold (10) and the Vienna software package (11,12) are often used for secondary structure predictions. While successful, the nearest neighbor model has some limitations. One limitation is the experimental conditions under which the thermodynamic parameters were derived. The thermodynamic data used to develop this model were derived from RNA duplexes melted in a standard buffer consisting of 1.0 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na2EDTA. However, the cell contains many other biomolecules in conjunction with RNA, which can result in molecular crowding that may alter the stability of RNA molecules. These biomolecules account for an estimated 20–40% of the cytoplasm (13,14). Current secondary structure prediction algorithms do not take molecular crowding into account when predicting the lowest free energy RNA secondary structure. It is essential to study the effects molecular crowding has on the stability of RNA duplexes to determine how cell-like conditions affect the structure and stability of RNA.
Several recent efforts have studied the effect of molecular crowding on DNA stability. In these studies, synthetic cosolutes of different sizes were used as molecular crowding agents to mimic macromolecular and small molecular crowding. Synthetic cosolutes employed in molecular crowding studies must be water soluble, must not cause precipitation of the nucleic acids, and must not bind nucleic acids more strongly than water (15). One of the most widely implemented synthetic cosolute molecular crowding agents is polyethylene glycol (PEG). PEG is a popular cosolute as it is inert, water soluble, and can be synthesized in a variety of molecular weights for the study of different sized molecular crowding agents. Circular dichroism (CD) studies have shown that the structure of duplexed DNA is not significantly altered when crowded with PEG (16,17). In the presence of small molecular weight PEGs (molecular weight up to 1000 g/mol), the stability of long DNA duplexes (30-mers) was found to increase slightly, while the stability of short DNA duplexes (8- and 17-mers) was found to decrease (16). The introduction of small PEG molecules was also found to decrease the stability of 16- and 18-mer DNA hairpins (18). In addition, small molecular weight PEGs were found to decrease the association rate constant and increase the dissociation rate constant of 10-mer DNA duplexes (19).
Similar to DNA, the stability of RNA molecules was found to decrease when crowded with low molecular weight PEG molecules (molecular weight ≤1000 g/mol) (20,21). Kilburn and co-workers found that the Azoarcus ribozyme was destabilized when crowded with PEG 1000 (22). Likewise, Gu and co-workers discovered that RNA duplexes with terminal tandem adenosine mismatches were destabilized when crowded with PEG 200 (20). Additionally, studies have shown that the stability of RNA molecules increases when crowded with high molecular weight PEG molecules (molecular weight >1000 g/mol) (22–24). Woolley and coworkers studied the duplex stability of a homopolymer RNA duplex, poly(I)•poly(C), and found that duplex stability increased in the presence of large PEG molecules (23). Dupuis and co-workers also found that an RNA tetraloop-receptor complex was stabilized in the presence of PEG 8000 (24). The stabilization observed when nucleic acids are crowded with large molecular weight cosolvents has been attributed to consequences of the excluded volume effect, where the large molecules present result in an increase in the effective nucleic acid concentration, resulting in stabilization (15,22,23). It has also been shown that small molecule crowding induces secondary structure destabilization and tertiary structure stabilization (21).
The destabilization of nucleic acids in the presence of small crowding agents has been attributed to altered solution properties such as dielectric constant, viscosity, and osmotic pressure. Small cosolvents such as ethylene glycol, methanol, and ethanol have been found to decrease the dielectric constant of a solution from ∼80 F/m to between 50–70 F/m (15). This decrease in the dielectric constant may alter the conformation of nucleic acids. For example, RNA and DNA molecules which usually adopt a hairpin conformation in a standard buffer solution were found to dimerize in the presence of neutral cosolvents as a result of the lowered solution dielectric constant (25). Additionally, if the dielectric constant is reduced, an increase in electrostatic interactions between charged species has been observed, including interactions between nucleic acids and metal ions (26). Cosolvents have also been reported to increase the solution viscosity; however, no studies have reported a correlation between duplex stability and solution viscosity (15). When cosolvents alter the osmotic pressure of a solution, this may change the hydration of the duplex which, in turn, may affect the stability of the nucleic acid conformation (18,27). From these studies, it is apparent that standard buffer is not able to effectively mimic crowded conditions.
In addition to altering solution properties, it has been suggested that molecular crowding agents may compete with water to preferentially interact with the exposed bases in single-stranded RNA resulting in stabilization of the single stranded conformation and destabilization of the duplexed structure (20,28). There is a potential for similar preferential interactions between RNA and other cellular molecules to occur within the cell, and these interactions are not accounted for in current structure prediction models.
The studies mentioned above demonstrate that crowding agents do have an effect on RNA stability. However, those experiments were conducted either on large RNA molecules which provide little insight on sequence effects or on a limited dataset of short RNA duplexes which does not allow for model derivation. The focus of this work is to systematically investigate 6- and 8-mer RNA duplexes with different sequence compositions by optical melting, CD, and osmometry experiments in the presence of 20% (v/v) PEG 200 to determine how the global structure and stability are affected by molecular crowding. PEG is a common crowding agent as it is inert and should not directly interact with nucleic acids (26,29). In particular, PEG 200 is often employed to act as a small crowding agent in order to alter solution properties to more closely mimic the crowded cellular environment (15). Since biomolecules account for an estimated 20–40% of the cytoplasm, 20% PEG 200 (v/v) was chosen for this study (13,14). This systematic study with short oligonucleotides provides insight into sequence specificity and provides a large dataset to allow for model derivation. The results of this study show that RNA duplexes are destabilized when crowded by 20% PEG 200, yet the global structure of the duplex is not significantly altered. The thermodynamic data from this study along with thermodynamic data from the literature (20) were used to derive nearest neighbor parameters for RNA duplexes in a 20% PEG 200 solution which can be implemented into structure prediction software to better understand the structure of RNA duplexes in vivo.
MATERIALS AND METHODS
Oligonucleotide synthesis and purification
RNA sequences were chosen based on length and composition. Two different oligonucleotide lengths, 6- and 8-mer duplexes, were studied to determine if oligonucleotides of different lengths were affected differently by molecular crowding conditions. Duplexes with different fractions of G-C base pairs (FGC) were chosen to determine if sequences with different compositions were affected differently by molecular crowding conditions. All 6-mer duplexes had FGC values of 0.33, 0.50, 0.67, or 1.00. All 8-mer duplexes had FGC values of 0.00, 0.25, 0.50, or 0.75. Additionally, a variety of self-complementary and non-self-complementary duplexes were selected. The oligonucleotides were ordered from Integrated DNA Technologies, Inc. (Coralville, IA, USA) and were purified using Waters Sep-Pak C18 cartridges and preparative thin layer chromatography as described previously (30–32).
Duplex formation and optical melting experiments
High temperature absorbance readings at either 260 or 280 nm were measured to determine the single-strand concentrations of RNA using the Beer-Lambert Law and extinction coefficients for each strand, which were determined using the application RNACalc (33). To form each duplex, equal moles of each single strand were combined, and the total duplex concentration was determined via high temperature absorbance readings at either 260 or 280 nm using the average extinction coefficient of both single strands. An appropriate volume of each duplex was reconstituted in a 20% (v/v) PEG 200 melt buffer containing 1.0 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na2EDTA, pH 7.0 to give a maximum absorbance value of ∼2 in a 0.1 cm cuvette. Each duplex was melted nine times using a concentration gradient to obtain a >50-fold concentration range. A Beckman-Coulter DU800 spectrophotometer with a temperature controller was used to perform the optical melting experiments. The duplexes were heated at a rate of 1°C/min to obtain absorbance versus temperature melting curves from 0 to 90°C. Absorbances were collected at 280 nm for G–C rich duplexes and at 260 nm for A–U rich duplexes to maximize hyperchromicity (34).
Data analysis
MeltWin software (33) was used to analyze the optical melting curves and to derive thermodynamic parameters by fitting the curves to a two-state model and plotting the inverse of the melting temperature (Tm) versus the log of concentration according to Equation (1):
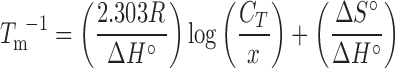 |
(1) |
where x equals 1 or 4 for self-complementary or non-self-complementary duplexes, respectively.
Melting temperatures were calculated at a strand concentration of 1 × 10−4 M (33,34). The change in Gibb's free energy for each duplex was calculated at 37°C using the following equation:
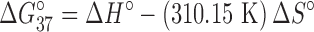 |
(2) |
Each experimental ΔG°37 and Tm value was compared to the ΔG°37 and Tm value predicted for the same sequence using the standard nearest neighbor model (7). Only the values derived from the van’t Hoff plots were used for the derivation of nearest neighbor parameters, as is standard practice (7).
Circular dichroism experiments
A subset of oligonucleotides was studied by CD. Oligonucleotides were prepared as 50 μM duplex concentration samples in a buffer containing 1.0 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na2EDTA, pH 7.0 with and without 20% PEG 200. CD experiments were performed on a Jasco J1500 spectrometer at 25 and 65°C. Each experiment consisted of 20 scans from 320 to 210 nm. The scans were averaged to give one spectrum at each temperature for each duplex.
Vapor-pressure osmometry experiments
Vapor-pressure osmometry experiments were performed on standard and PEG buffers using a Wescor 5100 C vapor pressure osmometer to determine the change in water activity resulting from molecular crowding conditions. The output of the osmometer is milliosmolality (mOsm) which is proportional to molality. Each sample reading was collected five times and averaged to obtain one mOsm value for each sample. The water activity was calculated from the average mOsm using the relationship below (35).
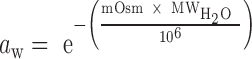 |
(3) |
Derivation of nearest-neighbor parameters for duplexes in 20% PEG 200
Nearest-neighbor parameters were derived from the thermodynamic values for each duplex using linear regression performed by Microsoft Excel’s LINEST function (complete linear least squares curve fitting routine). The LINEST function yielded linearly independent parameters for each combination of nearest neighbors and duplex symmetry, as well as penalties for duplex initiation and terminal A–U pairs.
RESULTS AND DISCUSSION
While PEG 200 is not an exact replica of the cellular environment (36), studies with neutral cosolvents such as PEG can shed light on the stability of RNA duplexes in molecular crowding conditions, conditions more representative of the cellular environment, and can improve RNA structure prediction methods.
Experimental thermodynamic parameters in 20% PEG 200
Thirty-four duplexes were melted in a buffer containing 20% PEG 200. The optical melt curves for each duplex were fit two ways, by averaging the fits of the melt curves and by creating van’t Hoff plots. An example melt curve is shown in Supplementary Figure S1. Table 1 shows the thermodynamic parameters of duplex formation derived from melt curve fits and van’t Hoff plots for 38 duplexes, 34 measured here and four melted previously (20). All van’t Hoff plots derived from the optical melting data showed a linear relationship when the Tm−1 was plotted against the log of the concentration. This suggests that duplex formation, not unimolecular folding, was occurring. A single, sharp transition in the sigmoidal melt curves suggests that there are not competing structures in solution. A two-state transition during melting is assumed when deriving thermodynamic parameters. Because all of the enthalpy parameters derived from the average of the melt curve fits are within 15% of the enthalpy values derived from the van’t Hoff plots, the two-state transition assumption is valid (34).
Table 1.
Thermodynamic parameters for duplex formation.
| T m −1 versus log CT plots | Average curve fits | |||||||
|---|---|---|---|---|---|---|---|---|
| Duplexa | ΔH° (kcal/mol) | ΔS° (eu) | ΔG°37 (kcal/mol) | T m (°C) | ΔH° (kcal/mol) | ΔS° (eu) | ΔG°37 (kcal/mol) | T m (°C) |
| 5′-UCAUGA-3′ | -56.2 ± 5.0 | -171.6 ± 6.9 | -3.00 ± 0.26 | 22.9 | -54.5 ± 4.7 | -165.7 ± 15.5 | -3.08 ± 0.15 | 22.9 |
| 5′-ACUGCG-3′ | -57.4 ± 1.6 | -163.3 ± 5.2 | -6.73 ± 0.02 | 38.1 | -64.4 ± 13.1 | -186.0 ± 42.3 | -6.67 ± 0.15 | 37.7 |
| 5′-AUGGAC-3′ | -48.1 ± 3.5 | -135.8 ± 11.6 | -5.94 ± 0.13 | 33.2 | -59.1 ± 15.6 | -171.8 ± 50.0 | -5.85 ± 0.11 | 33.5 |
| 5′-GCGAUA-3′ | -52.4 ± 3.5 | -151.8 ± 11.8 | -5.32 ± 0.15 | 30.0 | -54.8 ± 3.5 | -159.7 ± 17.3 | -5.24 ± 0.11 | 29.8 |
| 5′-GCUAUG-3′ | -58.8 ± 5.5 | -172.8 ± 18.0 | -5.18 ± 0.23 | 30.0 | -62.2 ± 8.7 | -183.9 ± 28.1 | -5.16 ± 0.21 | 30.3 |
| 5′-ACCGGU-3′ | -53.8 ± 2.9 | -150.5 ± 9.1 | -7.12 ± 0.06 | 45.6 | -54.1 ± 4.0 | -151.5 ± 12.4 | -7.11 ± 0.20 | 45.4 |
| 5′-AGCGCU-3′ | -53.5 ± 2.9 | -150.4 ± 9.4 | -6.80 ± 0.05 | 43.6 | -54.0 ± 1.9 | -152.2 ± 5.9 | -6.79 ± 0.11 | 43.6 |
| 5′-CACGUG-3′ | -53.7 ± 2.8 | -154.4 ± 9.0 | -5.81 ± 0.04 | 37.8 | -59.3 ± 4.0 | -172.2 ± 12.4 | -5.84 ± 0.21 | 37.9 |
| 5′-CAGCUG-3′ | -54.3 ± 0.8 | -156.2 ± 2.7 | -5.85 ± 0.01 | 38.0 | -54.9 ± 1.0 | -158.1 ± 3.2 | -5.86 ± 0.04 | 38.0 |
| 5′-CCAUGG-3′ | -59.8 ± 1.0 | -171.9 ± 3.3 | -6.52 ± 0.01 | 41.4 | -60.4 ± 2.0 | -173.6 ± 6.4 | -6.52 ± 0.05 | 41.4 |
| 5′-CCUAGG-3′ | -54.8 ± 0.8 | -154.3 ± 2.7 | -6.92 ± 0.01 | 44.2 | -59.9 ± 4.1 | -170.6 ± 12.8 | -6.98 ± 0.16 | 43.9 |
| 5′-CUGCAG-3′ | -53.2 ± 2.7 | -151.6 ± 8.7 | -6.19 ± 0.05 | 40.0 | -55.2 ± 2.9 | -157.9 ± 9.0 | -6.18 ± 0.11 | 39.9 |
| 5′-GACGUC-3′ | -54.7 ± 1.4 | -155.0 ± 4.6 | -6.56 ± 0.01 | 42.1 | -59.3 ± 3.3 | -170.0 ± 10.3 | -6.61 ± 0.10 | 42.0 |
| 5′-GAGCUC-3′ | -58.1 ± 3.8 | -165.0 ± 12.0 | -6.90 ± 0.08 | 43.7 | -58.0 ± 4.9 | -164.7 ± 15.4 | -6.94 ± 0.19 | 43.9 |
| 5′-GCAUGC-3′ | -58.7 ± 3.1 | -167.2 ± 9.9 | -6.85 ± 0.05 | 43.3 | -62.1 ± 2.4 | -178.1 ± 7.4 | -6.88 ± 0.16 | 43.1 |
| 5′-CGCGCG-3′ | -52.0 ± 3.8 | -142.6 ± 11.9 | -7.72 ± 0.16 | 49.7 | -55.6 ± 1.3 | -153.9 ± 4.3 | -7.85 ± 0.17 | 49.6 |
| 5′-CGGCCG-3′ | -54.3 ± 1.8 | -147.7 ± 5.4 | -8.49 ± 0.08 | 54.0 | -57.9 ± 5.7 | -159.0 ± 17.9 | -8.62 ± 0.17 | 53.6 |
| 5′-GCCGGC-3′ | -65.6 ± 6.8 | -178.4 ± 20.7 | -10.23 ± 0.46 | 60.1 | -66.3 ± 8.0 | -180.6 ± 24.2 | -10.31 ± 0.58 | 60.3 |
| 5′-GCGCGC-3′ | -61.8 ± 7.0 | -170.0 ± 21.4 | -9.03 ± 0.39 | 54.8 | -62.3 ± 6.2 | -171.4 ± 18.6 | -9.10 ± 0.49 | 55.0 |
| 5′-UAUAUAUA-3′ | -62.5 ± 2.6 | -194.2 ± 9.0 | -2.30 ± 0.17 | 21.1 | -63.1 ± 2.2 | -196.1 ± 7.4 | -2.27 ± 0.09 | 21.1 |
| 5′-UAAUAUUA-3′ | -58.8 ± 4.9 | -183.4 ± 17.0 | -1.88 ± 0.37 | 18.2 | -59.0 ± 1.9 | -184.1 ± 6.2 | -1.88 ± 0.11 | 18.2 |
| 5′-AACUAGUU-3′ | -56.1 ± 1.1 | -161.4 ± 3.6 | -6.02 ± 0.01 | 38.9 | -62.8 ± 4.4 | -183.1 ± 14.1 | -6.01 ± 0.09 | 38.7 |
| 5′-ACUAUAGU-3′ | -62.7 ± 2.1 | -183.2 ± 6.9 | -5.82 ± 0.03 | 37.7 | -66.0 ± 2.4 | -194.0 ± 7.6 | -5.79 ± 0.09 | 37.6 |
| 5′-AGAUAUCU-3′ | -56.5 ± 2.8 | -163.8 ± 9.3 | -5.72 ± 0.06 | 37.2 | -61.2 ± 2.5 | -178.9 ± 8.0 | -5.68 ± 0.07 | 37.0 |
| 5′-GAUAUAUC-3′ | -66.0 ± 2.4 | -195.0 ± 7.9 | -5.48 ± 0.04 | 36.1 | -74.2 ± 4.4 | -221.7 ± 14.2 | -5.41 ± 0.06 | 35.9 |
| 5′-GAAUAUUC-3′ | -66.4 ± 4.7 | -198.7 ± 15.5 | -4.72 ± 0.14 | 32.6 | -68.0 ± 2.1 | -204.1 ± 6.7 | -4.68 ± 0.10 | 32.5 |
| 5′-AACCGGUU-3′ | -63.0 ± 5.7 | -174.2 ± 17.5 | -8.98 ± 0.31 | 54.1 | -61.3 ± 7.1 | -168.8 ± 21.9 | -8.95 ± 0.35 | 54.5 |
| 5′-ACUGCAGU-3′ | -75.7 ± 1.5 | -214.4 ± 4.8 | -9.19 ± 0.06 | 52.1 | -74.7 ± 1.8 | -211.3 ± 5.6 | -9.13 ± 0.09 | 52.1 |
| 5′-GCAAUUGC-3′ | -78.1 ± 1.7 | -225.7 ± 5.3 | -8.09 ± 0.05 | 46.9 | -79.4 ± 3.8 | -229.8 ± 11.9 | -8.15 ± 0.12 | 47.0 |
| 5′-GAACGUUC-3′ | -74.2 ± 2.8 | -214.3 ± 8.8 | -7.76 ± 0.07 | 46.0 | -77.1 ± 3.2 | -223.4 ± 10.4 | -7.82 ± 0.05 | 45.9 |
| 5′-AGCGCGCU-3′ | -82.6 ± 6.0 | -226.1 ± 17.8 | -12.45 ± 0.48 | 64.7 | -82.0 ± 0.8 | -224.5 ± 2.8 | -12.41 ± 0.12 | 64.7 |
| 5′-AGCCGGCU-3′ | -85.8 ± 2.5 | -232.0 ± 7.5 | -13.86 ± 0.23 | 69.7 | -86.3 ± 6.4 | -233.4 ± 18.9 | -13.94 ± 0.57 | 69.8 |
| 5′-GCGAUCGC-3′ | -97.0 ± 6.7 | -272.9 ± 20.2 | -12.38 ± 0.43 | 60.0 | -97.1 ± 3.3 | -273.3 ± 10.3 | -12.38 ± 0.18 | 60.0 |
| 5′-GACCGGUC-3′ | -88.3 ± 2.9 | -242.9 ± 8.5 | -12.93 ± 0.22 | 64.8 | -88.1 ± 3.7 | -242.5 ± 11.4 | -12.92 ± 0.20 | 64.8 |
| 5′-UUAUCGAUAA-3′b | -62.8 ± 2.5 | -180.0 ± 8.0 | -6.94 ± 0.04 | 43.4 | -72.3 ± 9.2 | -220.0 ± 28.5 | -7.02 ± 0.48 | 42.6 |
| 5′-UAUCGAUA-3′b | -64.3 ± 2.3 | -188.6 ± 7.6 | -5.83 ± 0.03 | 37.7 | -63.9 ± 2.6 | -187.0 ± 8.3 | -5.85 ± 0.08 | 37.9 |
| 5′-AGCGCU-3′b | -51.9 ± 5.4 | -154.9 ± 17.3 | -6.60 ± 0.16 | 42.6 | -53.3 ± 3.4 | -150.7 ± 11.5 | -6.57 ± 0.18 | 42.3 |
| 5′-CGCGCG-3′b | -67.1 ± 4.3 | -188.9 ± 13.3 | -8.55 ± 0.16 | 50.9 | -57.6 ± 2.0 | -159.2 ± 6.8 | -8.23 ± 0.17 | 51.4 |
aAll listed strands are paired with their Watson–Crick complement.
bThermodynamic data for these strands are from (20).
Comparison of experimental thermodynamic parameters in 20% PEG 200 to the standard nearest neighbor parameters
In order to determine the effect of 20% PEG 200 on the stability of RNA oligonucleotides, the experimental data collected here was compared to predictions using the standard nearest neighbor parameters (Table 2). On average, the Tm of RNA oligonucleotides in 20% PEG 200 is 6.0°C lower than that predicted in standard buffer, with a range of 11.1°C lower to 1.2°C higher than standard buffer. Similarly, on average, the ΔG°37 values of RNA oligonucleotides in 20% PEG 200 are 1.02 kcal/mol less stable than that predicted in standard buffer, with a range of 0.39 to 2.27 kcal/mol less stable. The changes in both Tm and ΔG°37 values are indicative of destabilization due to the presence of 20% PEG 200.
Table 2.
Comparison between experimental thermodynamic parameters measured in 20% PEG 200 and predicted parameters using either the standard or derived 20% PEG 200 nearest neighbor parameters.
| Duplexa | Length | FGC | Predicted Tm in H2Ob (°C) | T m in PEG (°C) | ΔTmc (°C) | Predicted ΔG°37 in H2Ob (kcal/mol) | ΔG°37 in PEG (kcal/mol) | ΔΔG°37c (kcal/mol) | PEG NN ΔG°37d (kcal/mol) | ΔΔG°37e (kcal/mol) |
|---|---|---|---|---|---|---|---|---|---|---|
| 5′-UCAUGA-3′ | 6 | 0.33 | 25.5 | 22.9 | -2.6 | -4.60 | -3.00 | 1.60 | -3.26 | 0.26 |
| 5′-ACUGCG-3′ | 6 | 0.33 | 44.2 | 38.1 | -6.1 | -7.67 | -6.73 | 0.94 | -6.76 | 0.03 |
| 5′-AUGGAC-3′ | 6 | 0.50 | 36.9 | 33.2 | -3.7 | -6.52 | -5.94 | 0.58 | -5.91 | -0.03 |
| 5′-GCGAUA-3′ | 6 | 0.50 | 33.9 | 30.0 | -3.9 | -6.02 | -5.32 | 0.70 | -5.30 | -0.02 |
| 5′-GCUAUG-3′ | 6 | 0.50 | 31.8 | 30.0 | -1.8 | -5.95 | -5.18 | 0.77 | -5.25 | 0.07 |
| 5′-ACCGGU-3′ | 6 | 0.67 | 53.7 | 45.6 | -8.1 | -7.94 | -7.12 | 0.82 | -7.16 | 0.04 |
| 5′-AGCGCU-3′ | 6 | 0.67 | 53.5 | 43.6 | -9.9 | -7.94 | -6.80 | 1.14 | -6.74 | -0.06 |
| 5′-CACGUG-3′ | 6 | 0.67 | 42.4 | 37.8 | -4.6 | -6.54 | -5.81 | 0.73 | -5.42 | -0.39 |
| 5′-CAGCUG-3′ | 6 | 0.67 | 46.6 | 38.0 | -8.6 | -7.28 | -5.85 | 1.43 | -6.03 | 0.18 |
| 5′-CCAUGG-3′ | 6 | 0.67 | 46.6 | 41.4 | -5.2 | -7.32 | -6.52 | 0.80 | -6.30 | -0.22 |
| 5′-CCUAGG-3′ | 6 | 0.67 | 48.1 | 44.2 | -3.9 | -7.49 | -6.92 | 0.57 | -6.79 | -0.13 |
| 5′-CUGCAG-3′ | 6 | 0.67 | 46.6 | 40.0 | -6.6 | -7.28 | -6.19 | 1.09 | -6.03 | -0.16 |
| 5′-GACGUC-3′ | 6 | 0.67 | 45.1 | 42.1 | -3.0 | -7.02 | -6.56 | 0.46 | -6.32 | -0.24 |
| 5′-GAGCUC-3′ | 6 | 0.67 | 49.0 | 43.7 | -5.3 | -7.76 | -6.90 | 0.86 | -6.93 | 0.03 |
| 5′-GCAUGC-3′ | 6 | 0.67 | 48.3 | 43.3 | -5.0 | -7.64 | -6.85 | 0.79 | -6.52 | -0.33 |
| 5′-CGCGCG-3′ | 6 | 1.0 | 58.5 | 49.7 | -8.8 | -9.40 | -7.72 | 1.68 | -8.14 | 0.42 |
| 5′-CGGCCG-3′ | 6 | 1.0 | 62.2 | 54.0 | -8.2 | -10.14 | -8.49 | 1.65 | -9.17 | 0.68 |
| 5′-GCCGGC-3′ | 6 | 1.0 | 66.6 | 60.1 | -6.5 | -11.20 | -10.23 | 0.97 | -10.42 | 0.19 |
| 5′-GCGCGC-3′ | 6 | 1.0 | 63.1 | 54.8 | -8.3 | -10.46 | -9.03 | 1.43 | -9.39 | 0.36 |
| 5′-UAUAUAUA-3′ | 8 | 0.0 | 25.3 | 21.1 | -4.2 | -3.20 | -2.30 | 0.90 | -2.42 | 0.12 |
| 5′-UAAUAUUA-3′ | 8 | 0.0 | 17.0 | 18.2 | 1.2 | -2.63 | -1.88 | 0.75 | -1.69 | -0.19 |
| 5′-AACUAGUU-3′ | 8 | 0.25 | 43.5 | 38.9 | -4.6 | -6.41 | -6.02 | 0.39 | -5.51 | -0.51 |
| 5′-ACUAUAGU-3′ | 8 | 0.25 | 46.2 | 37.7 | -8.5 | -6.98 | -5.82 | 1.16 | -6.24 | 0.42 |
| 5′-AGAUAUCU-3′ | 8 | 0.25 | 45.6 | 37.2 | -8.4 | -6.97 | -5.72 | 1.25 | -6.01 | 0.29 |
| 5′-GAUAUAUC-3′ | 8 | 0.25 | 39.4 | 36.1 | -3.3 | -6.14 | -5.48 | 0.66 | -5.52 | 0.04 |
| 5′-GAAUAUUC-3′ | 8 | 0.25 | 36.6 | 32.6 | -4.0 | -5.57 | -4.72 | 0.85 | -4.79 | 0.07 |
| 5′-AACCGGUU-3′ | 8 | 0.50 | 59.8 | 54.1 | -5.7 | -9.80 | -8.98 | 0.82 | -8.92 | -0.06 |
| 5′-ACUGCAGU-3′ | 8 | 0.50 | 63.2 | 52.1 | -11.1 | -10.86 | -9.19 | 1.67 | -9.65 | 0.46 |
| 5′-GCAAUUGC-3′ | 8 | 0.50 | 55.0 | 46.9 | -8.1 | -9.50 | -8.09 | 1.41 | -8.28 | 0.19 |
| 5′-GAACGUUC-3′ | 8 | 0.50 | 52.5 | 46.0 | -6.5 | -8.88 | -7.76 | 1.12 | -8.08 | 0.32 |
| 5′-AGCGCGCU-3′ | 8 | 0.75 | 74.2 | 64.7 | -9.5 | -13.72 | -12.45 | 1.27 | -12.37 | -0.08 |
| 5′-AGCCGGCU-3′ | 8 | 0.75 | 77.0 | 69.7 | -7.3 | -14.46 | -13.86 | 0.60 | -13.40 | -0.46 |
| 5′-GCGAUCGC-3′ | 8 | 0.75 | 67.1 | 60.0 | -7.1 | -12.84 | -12.38 | 0.46 | -11.80 | -0.58 |
| 5′-GACCGGUC-3′ | 8 | 0.75 | 70.3 | 64.8 | -5.5 | -13.54 | -12.93 | 0.61 | -12.98 | 0.05 |
| 5′-UUAUCGAUAA-3′f | 10 | 0.20 | 49.0 | 43.4 | -5.6 | -9.21 | -6.94 | 2.27 | -7.24 | 0.30 |
| 5′-UAUCGAUA-3′f | 8 | 0.25 | 41.4 | 37.7 | -3.7 | -7.10 | -5.83 | 1.27 | -5.48 | -0.35 |
| 5′-AGCGCU-3′f | 6 | 0.67 | 51.6 | 42.6 | -9.0 | -7.94 | -6.60 | 1.34 | -6.74 | 0.14 |
| 5′-CGCGCG-3′f | 6 | 1.0 | 58.5 | 50.9 | -7.6 | -9.40 | -8.55 | 0.85 | -8.14 | -0.41 |
| Average | -6.0 | 1.02 | 0.23g |
aAll listed strands are paired with their Watson–Crick complement.
bValues were predicted using the standard nearest neighbor model (7).
cDifference between values predicted using the standard nearest neighbor model and experimental values for duplexes in 20% PEG 200 (7).
dΔG°37 values predicted using the derived parameters for a 20% PEG 200 solution.
eDifference between experimental ΔG°37 values in 20% PEG 200 and values predicted by the derived model for 20% PEG 200.
fThermodynamic data for these strands are from (20).
gAverage of the absolute value of each ΔG°37 value.
To determine if 20% PEG 200 destabilized RNA oligonucleotides differently based on the length of the oligonucleotide, we compared the thermodynamics of the 21 6-mers to the 16 8-mers (the data from the one 10-mer was not included in any comparisons). On average, the ΔTm and ΔΔG°37 values for the 6-mers were –6.0 ± 0.5°C and 1.01 ± 0.08 kcal/mol, respectively. On average, the ΔTm and ΔΔG°37 values for the 8-mers were –6.0 ± 0.7°C and 0.98 ± 0.10 kcal/mol, respectively. Overall, there is no meaningful difference in the destabilization experienced by 6-mers and 8-mers in the presence of 20% PEG 200. It is likely that larger length differences would result in different degrees of destabilization, as was seen in DNA for 8-, 17- and 30-mers (16); however, experimental constraints prevent us from studying significantly shorter or longer duplexes via optical melting.
To determine if 20% PEG 200 destabilized RNA oligonucleotides differently based on FGC, we compared the ΔTm for each FGC value (Supplementary Figure S2, the one value for FGC = 0.20 was not used in this comparison). In general, it appears as if ΔTm increases as FGC increases (R2 = 0.86). Similarly, we compared the ΔΔG°37 for each FGC value (Supplementary Figure S2, the one value for FGC = 0.20 was not used in this comparison). In general, it appears as if ΔΔG°37 is independent of changes in FGC (R2 = 0.17). In both cases, the wide range of values for each FGC value (as illustrated by the error bars in Supplementary Figure S2) prevents us from concluding anything specific. It is likely that factors beyond FGC are affecting the thermodynamics of short RNA oligomers in the presence of 20% PEG 200.
Circular dichroism experiments
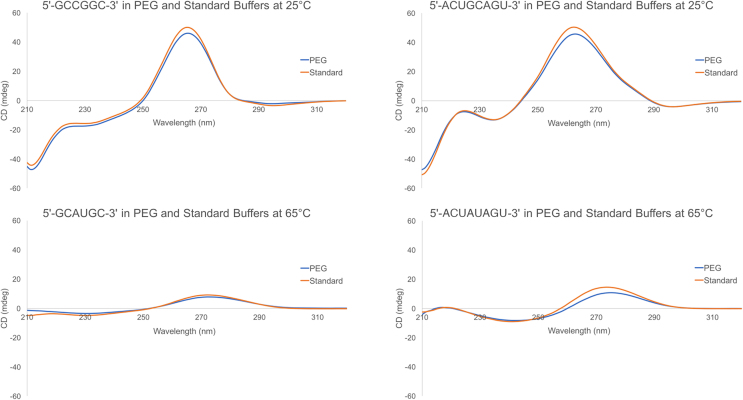
CD experiments were performed on one 6-mer (5′-GCCGGC-3′)2 and one 8-mer (5′-ACUGCAGU-3′)2 duplex in both standard and 20% PEG 200 buffers at 25°C. The CD spectra at 25°C are shown in Figure 1. Both sets of CD spectra at 25°C display a minimum at 210 nm, a maximum at 260 nm, and a small negative region between 300 and 310 nm, consistent with an A-form helical conformation (37). It should be noted that although the right-handed, A-form helical structure is not significantly altered, there is a decrease in the magnitude of CD between the standard buffer and 20% PEG 200 curves at certain wavelength ranges (∼250–280 nm). The magnitude of CD depends largely on the spatial orientation of each base chromophore (38). It is, therefore, plausible that the addition of 20% PEG 200 results in a slight alteration of the spatial orientation of each base chromophore without affecting the global structure of the helix. This shift has the potential to affect the energetics of the helix and have an overall destabilizing effect on the stability of the duplexes (38).
Figure 1.
CD spectra of (5′-GCCGGC-3′)2 (top left) and (5′-ACUGCAGU-3′)2 (top right) in 20% PEG 200 and standard (water) buffers at 25°C and of 5′-GCAUGC-3′ (bottom left) and 5′- ACUAUAGU-3′ (bottom right) in 20% PEG 200 and standard (water) buffers at 65°C.
In addition to room temperature CD, experiments were performed on one 6-mer 5′-GCAUGC-3′ and one 8-mer 5′-ACUAUAGU-3′ at 65°C (above their melting temperatures) to determine if 20% PEG 200 affects the structure of single-stranded oligonucleotides, potentially resulting in the destabilization of the duplexed state. Single-stranded oligonucleotide conformation is sequence and temperature dependent and does not have well-defined CD characteristics compared to the A-form helical structure (39). Even without strict definitions of single-stranded spectra, Figure 1 shows that all four CD spectra of the single-stranded oligonucleotides have similar features: a maximum around 275 nm, a minimum between 230–240 nm, and no CD above 300 nm, indicating that the global conformation of the single-stranded structures are not significantly altered by the presence of 20% PEG 200. Similar to the CD spectra at 25°C, there is a slight decrease in the magnitude of the CD peaks between 20% PEG 200 and standard water buffer, however; as previously mentioned, this is not indicative of a significant conformational change. The spectra from both CD experiments at 25°C and 65°C indicate that the presence of 20% PEG 200 does not result in a significant global conformational change in either the duplexed or single-stranded state.
Water activity measurements in water and PEG 200 buffers
Previous studies have suggested that one cause of duplex destabilization due to molecular crowding is a reduction of solution water activity (15,18,27,29). It has been suggested that G–C rich duplexes may be destabilized more in molecular crowding conditions than A–U rich sequences because G-C pairs are more hydrated than A–U pairs (40). Thus, the lowering of water activity would have a greater effect on G–C rich duplexes in molecular crowding conditions, resulting in a greater degree of destabilization (40). Vapor-pressure osmometry experiments were completed to determine the difference in water activity in standard and 20% PEG 200 buffers. The water activity (aw) of the standard buffer decreased from 0.9646 aw to 0.9365 aw when 20% PEG 200 was introduced to the solution (P value < 0.001). The observed data was consistent with previous studies reporting a lowered water activity in molecular crowding solutions (15,18,27,29,40). Based on observations here and in previous studies with DNA and RNA duplexes in molecular crowding conditions, it is likely that the reduction of the water activity of solution by the addition of 20% PEG 200 is a contributor to the destabilization of duplexes in the presence of 20% PEG 200.
Derivation of nearest neighbor parameters for RNA duplexes in 20% PEG 200 buffer
In addition to studying the relationship between destabilization and sequence length and composition, linearly independent nearest-neighbor parameters were derived for duplexes in 20% PEG 200 (Table 3). Four sequences previously studied in the literature with available thermodynamic parameters in 20% PEG 200 were also included in the derivation of the model so that all available thermodynamic data was utilized (20).
Table 3.
Nearest neighbor parameters for RNA duplexes in 20% PEG 200
| Nearest neighborsa | # Occurrences | ΔH° in PEG (kcal/mol) | ΔS° in PEG (eu) | ΔG°37 in PEG (kcal/mol) |
|---|---|---|---|---|
| AA UU | 14 | -6.3 ± 1.5 | -17.5 ± 4.9 | -0.88 ± 0.09 |
| AU UA | 25 | -6.7 ± 3.1 | -18.2 ± 10.4 | -1.13 ± 0.20 |
| UA AU | 21 | -12.7 ± 3.1 | -36.6 ± 9.8 | -1.36 ± 0.19 |
| CU GA | 25 | -8.8 ± 2.1 | -21.7 ± 6.6 | -2.03 ± 0.12 |
| CA GU | 19 | -13.0 ± 2.5 | -36.0 ± 8.0 | -1.91 ± 0.15 |
| GU CA | 20 | -12.8 ± 1.9 | -33.7 ± 6.1 | -2.36 ± 0.12 |
| GA CU | 25 | -14.5 ± 2.0 | -39.1 ± 6.9 | -2.36 ± 0.13 |
| CG GC | 29 | -9.0 ± 2.5 | -22.0 ± 8.0 | -2.19 ± 0.15 |
| GG CC | 17 | -14.6 ± 2.0 | -36.3 ± 6.4 | -3.32 ± 0.12 |
| GC CG | 30 | -18.9 ± 2.3 | -49.9 ± 7.3 | -3.44 ± 0.14 |
| Terminal AU | 33 | 2.8 ± 1.3 | 7.3 ± 4.2 | 0.55 ± 0.08 |
| Initiation | 38 | 5.3 ± 7.7 | 2.2 ± 24.2 | 4.63 ± 0.46 |
| Symmetric | 34 | 1.0 ± 3.5 | 1.0 ± 10.9 | 0.68 ± 0.21 |
aFor each nearest neighbor, the top sequence is written 5′-3′ and the bottom is written 3′-5′.
The 20% PEG 200 nearest neighbor parameters were used to calculate ΔH°, ΔS° and ΔG°37 values for each duplex (Table 2, Supplementary Tables S1 and S2). The average differences between experimental values and those predicted by the 20% PEG 200 parameters for ΔH°, ΔS°, and ΔG°37 are 4.0 kcal/mol, 11.8 eu, and 0.23 kcal/mol, respectively. The average differences between experimental ΔH°, ΔS° and ΔG°37 values and those predicted using the standard nearest neighbor parameters are 5.4 kcal/mol, 19.4 eu, and 1.02 kcal/mol, respectively. The 20% PEG 200 nearest neighbor parameters result in ΔG°37 values ∼0.8 kcal/mol closer to the experimental values than when using the standard nearest neighbor parameters.
The average deviation between the predicted free energies using the new 20% PEG 200 nearest neighbor parameters and the measured free energies for all duplexes was 0.23 kcal/mol, illustrating the goodness-of-fit for the derived model. To test the predictive nature of the derived nearest neighbor parameters for RNA duplexes in 20% PEG 200, a leave-one-out cross validation was performed. In this validation, one duplex was selected as the test set, and the LINEST function was used on the remaining duplexes to derive nearest neighbor parameters with the test duplex excluded. The resulting nearest neighbor parameters were used to predict the ΔG°37 value of the test duplex. This procedure was repeated for every duplex included in the dataset and resulted in an average difference of 0.35 kcal/mol between the experimental and predicted ΔG°37 values, illustrating the potential predictive power of the derived nearest neighbor parameters for RNA duplexes in 20% PEG 200.
To our knowledge, the effects of molecular crowding by neutral cosolutes on the thermodynamics of short RNA oligomers have only been studied using 20% PEG 200. To test the generality, the 20% PEG 200 RNA model was tested on a DNA oligomer with small molecular crowding agents to predict the experimental ΔG°37 values (16,18). The ΔG°37 values predicted by the 20% PEG 200 RNA nearest neighbor parameters were compared to previously reported experimental ΔG°37 values of DNA duplexes in 20% PEG 200, PEG 1000, and ethylene glycol (EG) (Table 4) (16,18). The average difference between the experimental ΔG°37 values and those predicted by the 20% PEG 200 RNA nearest neighbor parameters is 0.59 kcal/mol. As expected, the difference in the ΔG°37 values for these DNA sequences is slightly higher than the leave-one-out predictive difference of the RNA sequences in 20% PEG 200 (0.35 kcal/mol). However, the ΔG°37 values predicted by the 20% PEG 200 RNA nearest neighbor parameters are closer to the experimental values than ΔG°37 values predicted by either the RNA or DNA standard nearest neighbor models (average differences of 0.90 and 0.65 kcal/mol, respectively) (41). This illustrates that for this particular DNA sequence, the 20% PEG 200 RNA nearest neighbor parameters are better, on average, at predicting ΔG°37 values than either the standard RNA or DNA parameters. More data is needed to determine if these 20% PEG 200 RNA nearest neighbor parameters are generalizable to RNA in the presence of other small, inert molecular crowders (MW < 1000 g/mol) and if these 20% PEG 200 RNA nearest neighbor parameters are better than the standard DNA nearest neighbor parameters at predicting the stability of DNA in the presence of small, inert molecular crowders.
Table 4.
Difference in predicted and experimental ΔG°37 values for d(ATGCGCAT)2 in the presence of small molecular weight crowders
| Crowding Agent | Experimental ΔG°37 (kcal/mol) | 20% PEG 200 RNA NN ΔG°37 (kcal/mol) | PEG ΔΔG°37a (kcal/mol) | Standard RNA NN ΔG°37 (kcal/mol) | RNA ΔΔG°37b (kcal/mol) | Standard DNA NN ΔG°37 (kcal/mol) | DNA ΔΔG°37c (kcal/mol) |
|---|---|---|---|---|---|---|---|
| 20% EG | -9.30 | -8.74 | 0.56 | -10.20 | -0.90 | -8.65 | 0.65 |
| 20% PEG 200 | -8.70 | -8.74 | -0.04 | -10.20 | -1.50 | -8.65 | 0.05 |
| 20% PEG 1000 | -9.90 | -8.74 | 1.16 | -10.20 | -0.30 | -8.65 | 1.25 |
| Averaged | 0.59 | 0.90 | 0.65 |
aDifference between experimental ΔG°37 and ΔG°37 predicted using 20% PEG 200 RNA nearest neighbor parameters.
bDifference between experimental ΔG°37 and ΔG°37 predicted using standard RNA nearest neighbor parameters.
cDifference between experimental ΔG°37 and ΔG°37 predicted using standard DNA nearest neighbor parameters.
dAverage of the absolute value of each ΔG°37 value.
The thermodynamic data from this study shows that molecular crowding by 20% PEG 200 results in the destabilization of short RNA duplexes. The nearest neighbor parameters derived for RNA duplexes in 20% PEG 200 can be used to predict the stability of short RNA oligonucleotides in 20% PEG 200 solutions. This derived model for RNA duplexes in the presence of 20% PEG 200 was more successful at predicting ΔG°37 values of short RNA duplexes in the presence of 20% PEG 200 than the standard RNA nearest neighbor parameters. Additionally, for one DNA duplex in the presence of three inert crowding agents, this model was more successful, on average, than the standard RNA nearest neighbor parameters and the standard DNA nearest neighbor parameters at predicting the stability of the DNA duplex. The continuation of studies of this nature is worthwhile to shed light on the stability of RNA duplexes in the cellular environment. The implementation of the 20% PEG 200 nearest neighbor parameters in structure prediction programs will provide insight on the stability of RNA and DNA duplexes in simulated cell-like conditions.
Supplementary Material
ACKNOWLEDGEMENTS
The authors would like to acknowledge Dr Michael Nichols at the University of Missouri – St. Louis for the use of the Jasco spectrometer for CD studies and Dr Gregory Lanza and Michael Scott from Washington University in St. Louis for the use of the Wescor 5100 C vapor pressure osmometer.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Institutes of Health [2R15GM085699-03]; National Science Foundation Major Research Instrumentation Award [1337638] that funded the acquisition of the Jasco 1500 circular dichroism spectrometer at the University of Missouri-St. Louis. Funding for open access charge: National Institutes of Health.
Conflict of interest statement. None declared.
REFERENCES
- 1. Eddy S.R. Non-coding RNA genes and the modern RNA world. Nat. Rev. Genet. 2001; 2:919–929. [DOI] [PubMed] [Google Scholar]
- 2. Mustoe A.M., Brooks C.L., Al-Hashimi H.M.. Kornberg R.D. Ann. Rev. Biochem. 2014; 83:441–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Breslow R., Xu R.. Recognition and catalysis in nucleic-acid chemistry. Proc. Natl. Acad. Sci. U.S.A. 1993; 90:1201–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Ma Y.L., Yang Y.Z., Wang F., Moyer M.P., Wei Q., Zhang P., Yang Z., Liu W.J., Zhang H.Z., Chen N.W. et al.. Long non-coding RNA CCAL regulates colorectal cancer progression by activating Wnt/beta-catenin signalling pathway via suppression of activator protein 2 alpha. Gut. 2016; 65:1494–1504. [DOI] [PubMed] [Google Scholar]
- 5. Borer P.N., Dengler B., Tinoco I. Jr, Uhlenbeck O.C.. Stability of ribonucleic acid double-stranded helices. J. Mol. Biol. 1974; 86:843–853. [DOI] [PubMed] [Google Scholar]
- 6. Freier S.M., Kierzek R., Jaeger J.A., Sugimoto N., Caruthers M.H., Neilson T., Turner D.H.. Improved free-energy parameters for prediction of RNA duplex stability. Proc. Natl. Acad. Sci. U.S.A. 1986; 83:9373–9377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Xia T.B., SantaLucia J., Burkard M.E., Kierzek R., Schroeder S.J., Jiao X.Q., Cox C., Turner D.H.. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-Crick base pairs. Biochemistry. 1998; 37:14719–14735. [DOI] [PubMed] [Google Scholar]
- 8. Reuter J.S., Mathews D.H.. RNAstructure: Software for RNA secondary structure prediction and analysis. BMC Bioinf. 2010; 11:129–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Bellaousov S., Reuter J.S., Seetin M.G., Mathews D.H.. RNAstructure: web servers for RNA secondary structure prediction and analysis. Nucleic Acids Res. 2013; 41:W471–W474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003; 31:3406–3415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Gruber A.R., Lorenz R., Bernhart S.H., Neuboock R., Hofacker I.L.. The Vienna RNA Websuite. Nucleic Acids Res. 2008; 36:W70–W74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Hofacker I.L. Vienna RNA secondary structure server. Nucleic Acids Res. 2003; 31:3429–3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Zhou H.X., Rivas G.N., Minton A.P.. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Ann. Rev. Biophys. 2008; 37:375–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Strulson C.A., Molden R.C., Keating C.D., Bevilacqua P.C.. RNA catalysis through compartmentalization. Nat. Chem. 2012; 4:941–946. [DOI] [PubMed] [Google Scholar]
- 15. Nakano S., Miyoshi D., Sugimoto N.. Effects of molecular crowding on the structures, interactions, and functions of nucleic acids. Chem. Rev. 2014; 114:2733–2758. [DOI] [PubMed] [Google Scholar]
- 16. Nakano S., Karimata H., Ohmichi T., Kawakami J., Sugimoto N.. The effect of molecular crowding with nucleotide length and cosolute structure on DNA duplex stability. J. Am. Chem. Soc. 2004; 126:14330–14331. [DOI] [PubMed] [Google Scholar]
- 17. Nakano S., Wu L., Oka H., Karimata H.T., Kirihata T., Sato Y., Fujii S., Sakai H., Kuwahara M., Sawai H. et al.. Conformation and the sodium ion condensation on DNA and RNA structures in the presence of a neutral cosolute as a mimic of the intracellular media. Mol. BioSyst. 2008; 4:579–588. [DOI] [PubMed] [Google Scholar]
- 18. Nakano S., Yamaguchi D., Tateishi-Karimata H., Miyoshi D., Sugimoto N.. Hydration changes upon DNA folding studied by osmotic stress experiments. Biophys. J. 2012; 102:2808–2817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Gu X.B., Nakano S., Sugimoto N.. Consecutive GC base pairs determine the energy barrier of DNA duplex formation under molecularly crowded conditions. Chem. Commun. 2007; 26:2750–2752. [DOI] [PubMed] [Google Scholar]
- 20. Gu X.B., Nguyen M.T., Overacre A., Seaton S., Schroeder S.J.. Effects of salt, polyethylene glycol, and locked nucleic acids on thermodynamic stabilities of consecutive terminal adenosine mismatches in RNA duplexes. J. Phys. Chem. B. 2013; 117:3531–3540. [DOI] [PubMed] [Google Scholar]
- 21. Leamy K.A., Yennawar N.H., Bevilacqua P.C.. Cooperative RNA folding under cellular conditions arises from both tertiary structure stabilization and secondary structure destabilization. Biochemistry. 2017; 56:3422–3433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Kilburn D., Roh J.H., Guo L., Briber R.M., Woodson S.A.. Molecular crowding stabilizes folded RNA structure by the excluded volume effect. J. Am. Chem. Soc. 2010; 132:8690–8696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Woolley P., Wills P.R.. Excluded-volume effect of inert macromolecules on the melting of nucleic acids. Biophys. Chem. 1985; 22:89–94. [DOI] [PubMed] [Google Scholar]
- 24. Dupuis N.F., Holmstrom E.D., Nesbitt D.J.. Molecular-crowding effects on single-molecule RNA folding/unfolding thermodynamics and kinetics. Proc. Natl. Acad. Sci. U.S.A. 2014; 111:8464–8469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Nakano S., Hirayama H., Miyoshi D., Sugimoto N.. Dimerization of nucleic acid hairpins in the conditions caused by neutral cosolutes. J. Phys. Chem. B. 2012; 116:7406–7415. [DOI] [PubMed] [Google Scholar]
- 26. Fiorini E., Borner R., Sigel R.K.O.. Mimicking the in vivo environment - The effect of crowding on RNA and biomacromolecular folding and activity. Chimia. 2015; 69:207–212. [DOI] [PubMed] [Google Scholar]
- 27. Spink C.H., Chaires J.B.. Effects of hydration, ion release, and excluded volume on the melting of triplex and duplex DNA. Biochemistry. 1999; 38:496–508. [DOI] [PubMed] [Google Scholar]
- 28. Nakano S.I., Kirihata T., Sugimoto N.. Capture of cationic ligands bound diffusely to base pairs during DNA refolding. Chem. Comm. 2008; 6:700–702. [DOI] [PubMed] [Google Scholar]
- 29. Sugimoto N. Noncanonical structures and their thermodynamics of DNA and RNA under molecular crowding: Beyond the Watson-Crick double helix. Int. Rev. Cell Mol. Biol. 2014; 307:205–273. [DOI] [PubMed] [Google Scholar]
- 30. Wright D.J., Rice J.L., Yanker D.M., Znosko B.M.. Nearest neighbor parameters for Inosine center dot Uridine pairs in RNA duplexes. Biochemistry. 2007; 46:4625–4634. [DOI] [PubMed] [Google Scholar]
- 31. Christiansen M.E., Znosko B.M.. Thermodynamic characterization of tandem mismatches found in naturally occurring RNA. Nucleic Acids Res. 2009; 37:4696–4706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Davis A.R., Znosko B.M.. Thermodynamic characterization of single mismatches found in naturally occurring RNA. Biochemistry. 2007; 46:13425–13436. [DOI] [PubMed] [Google Scholar]
- 33. McDowell J.A., Turner D.H.. Investigation of the structural basis for thermodynamic stabilities of tandem GU mismatches: Solution structure of (rGAGGUCUC)(2) by two-dimensional NMR and simulated annealing. Biochemistry. 1996; 35:14077–14089. [DOI] [PubMed] [Google Scholar]
- 34. Schroeder S.J., Turner D.H.. Optical melting measurements of nucleic acid thermodynamics. Methods Enzymol. 2009; 468:371–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Zhang W., Capp M.W., Bond J.P., Anderson C.F., Record T.R. Jr. Thermodynamic characterization of interactions of native bovine serum albumin with highly excluded (glycine betaine) and moderately accumulated (urea) solutes by a novel application of vapor pressure osmometry. Biochemistry. 1996; 35:10506–10516. [DOI] [PubMed] [Google Scholar]
- 36. Tyrrell J., Weeks K.M., Pielak G.J.. Challenge of mimicking the influences of the cellular environment on RNA structure by PEG-induced macromolecular crowding. Biochemistry. 2015; 54:6447–6453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Bloomfield V.A., Crothers D.M., Tinoco I. Jr. Nucleic acids: Structures, properties, and functions. 2000; Sausalito: University Science Books. [Google Scholar]
- 38. Minetti C.A., Sun J.Y., Jacobs D.P., Kang I., Remeta D.P., Breslauer K.J.. Impact of bistrand abasic sites and proximate orientation on DNA global structure and energetics. Bipolymers. 2018; 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Fasman G.D. Circular Dichroism and the Conformational Analysis of Biomolecules. 1996; NY: Plenum Press. [Google Scholar]
- 40. Rozners E., Moulder J.. Hydration of short DNA, RNA and 2′-OMe oligonucleotides determined by osmotic stressing. Nucleic Acids Res. 2004; 32:248–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. SantaLucia J., Allawi H.T., Seneviratne A.. Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry. 1996; 35:3555–3562. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.