A multi-axial RNA joint with a large range of motion promotes sampling of an active ribozyme conformation

Abstract

Investigating the dynamics of structural elements in functional RNAs is important to better understand their mechanism and for engineering RNAs with novel functions. Previously, we performed rational engineering studies with the Varkud satellite (VS) ribozyme and switched its specificity toward non-natural hairpin substrates through modification of a critical kissing-loop interaction (KLI). We identified functional VS ribozyme variants with surrogate KLIs (ribosomal RNA L88/L22 and human immunodeficiency virus-1 TAR/TAR*), but they displayed ∼100-fold lower cleavage activity. Here, we characterized the dynamics of KLIs to correlate dynamic properties with function and improve the activity of designer ribozymes. Using temperature replica exchange molecular dynamics, we determined that the natural KLI in the VS ribozyme supports conformational sampling of its closed and active state, whereas the surrogate KLIs display more restricted motions. Based on in vitro selection, the cleavage activity of a VS ribozyme variant with the TAR/TAR* KLI could be markedly improved by partly destabilizing the KLI but increasing conformation sampling. We formulated a mechanistic model for substrate binding in which the KLI dynamics contribute to formation of the active site. Our model supports the modular nature of RNA in which subdomain structure and dynamics contribute to define the thermodynamics and kinetics relevant to RNA function.

INTRODUCTION

RNA molecules adopt complex 3D structures to fulfill essential function in diverse cellular processes. RNA architecture is often recognized as being highly modular because RNA molecules contain a diverse but limited set of recurrent structural motifs within their secondary and tertiary structural elements, such as hairpin loops, multi-way junctions and kissing-loop interactions (KLIs) (1). RNA folding typically follows a hierarchical process, where secondary structure elements form first followed by compaction through tertiary contacts (2,3). As part of the RNA secondary structure, paired regions form helical structures and unpaired regions adopt specific structural motifs, which impart orientations to the associated helical domains and contribute to forming tertiary contacts (4). It is becoming clear that local structural elements have inherent flexibility that allows them to explore conformational space. Consequently, each structural element should not simply be viewed as a static structure but rather as a sub-ensemble of structures with specific dynamic properties (4–10). However, despite our growing knowledge of how structural motifs define the 3D structure of RNA and increased appreciation for the importance of RNA dynamics, much remains to be known regarding the dynamics that are inherent to specific structural motifs and how they contribute to RNA structure and function.

The modular and hierarchical organization of RNA structure has been made evident through successful efforts in RNA engineering, an emerging field of research that holds tremendous potential for applications in synthetic biology, nanotechnology and molecular medicine (11,12). Novel RNA function can be created by de novo design of self-assembled nanostructures or incorporation of structural elements into known RNA architectures (11–14). Our laboratory is exploring the latter approach to modify the substrate specificity of the Neurospora Varkud satellite (VS) ribozyme (15,16). The wild-type VS ribozyme specifically recognizes and cleaves its folded hairpin substrate, and we are exploring the potential of this ribozyme to cleave other RNA hairpins, since such structural element regulates a wide variety of cellular and viral RNAs.

The VS ribozyme is a member of the small self-cleaving ribozyme family, which also includes the glmS, hammerhead, hairpin, HDV, hatchet, pistol, twister and twister sister ribozymes (17–19). Like many other self-cleaving ribozymes, it represents a good model system for structure, function and engineering studies because of its relatively small size and its ability to cleave its substrates either in cis or in trans (20,21). The minimal catalytic sequence is comprised of ∼160 nt that form six paired domains. The trans ribozyme (domains II-VI) recognizes its hairpin substrate (stem-loop I or SLI) by way of a KLI, which forms between loop I and loop V (Figure 1A), and this KLI is crucial for efficient cleavage activity (22). The I/V KLI is highly stable and allows formation of the open state of the ribozyme, which is likely the predominant conformation in solution (Figure 1B) (23–26). Subsequently, the G₆₃₈ loop, known as the cleavage site internal loop of the SLI substrate, intimately associate with the A₇₅₆ loop to form the active site within the closed state of the ribozyme (Figure 1A and B) (27) The cleavage mechanism has been thoroughly investigated and involves the N1 atoms of guanine (G₆₃₈) and adenine (A₇₅₆) nucleobases as general base and acid, respectively (18). However, the dynamic processes associated with formation of the active site and involving the transition from the open state to the closed state are yet to be examined.

Figure 1.

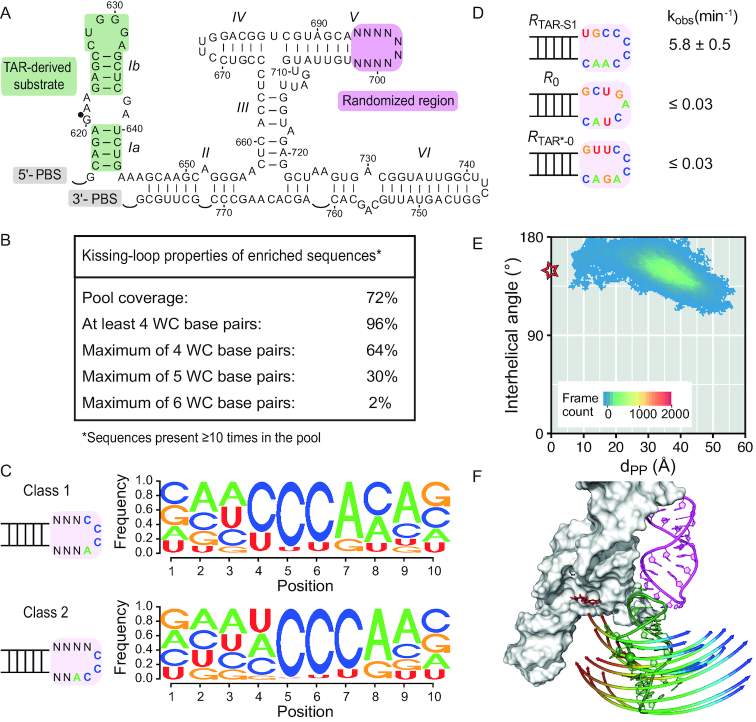
Substitution of the I/V KLI in the Neurospora VS ribozyme. (A) Primary and secondary structures of the parental trans VS ribozyme (R₀) and substrate (S₀). Substrate recognition involves a KLI between loop I and loop V as well as a loop/loop interaction between the G638 loop and the A756 loop, which defines the active site. (B) Representation of the open and closed states of the VS ribozyme. The closed state (right panel) is taken from the crystal structure of the Neurospora VS ribozyme substrate/ribozyme complex with SLI (green) and the SLV (pink) in sticks, helical domains II, III, IV and VI as a white surface, A₇₅₆ in red sticks and the scissile phosphate as a green sphere. A single representative of the many conformations that likely populate the open state (left panel) is similarly illustrated, but with the I/V KLI from the crystal structure replaced by the I/V KLI from the NMR structure of the SLI/SLV complex (24). (C) The I/V KLI of the S₀/R₀ ribozyme complex was previously substituted by the L88/L22 KLI from the rRNA large subunit of Deinococcus radiodurans and by the HIV-1 TAR/TAR* KLI (16). Compared to the VS ribozyme I/V KLI, these other KLIs also display a small number of WC base pairs at their interface (WC bp in KLI), have similar interhelical angles and are thermodynamically stable as judged from their dissociation constant [K_D; (16)]. The k_obs values of the resulting VS ribozyme variants are given for the parental S₀/R₀ pair as well as for the S_L88+1/R_L22-1 and the S_TAR-1/R_TAR*-0 variants (16). Residues at the KLI, either free or involved in KL base pairs, are shown together with the loop closing base pairs.

In recent rational engineering studies (16), we substituted the I/V KLI by two other KLIs with similar thermodynamic and structural properties (Figure 1C): the L88/L22 KLI from the large subunit of the Deinococcus radiodurans ribosomal RNA and the synthetic TAR/TAR* KLI related to the human immunodeficiency virus (HIV-1). The KLI substitutions were successful since the overall structure of the ribozyme remained intact as judged from SHAPE analysis and substantial levels of cleavage activity were obtained for variant substrate/ribozyme (S/R) complexes that incorporate either the L88/L22 KLI (S_L88/R_L22) or TAR/TAR* KLI (S_TAR/R_TAR*). However, the k_obs values for the most active variant S/R complexes (S_L88+1/R_L22-1 and S_TAR-1/R_TAR*-0) were 50- to 160-fold lower than that of the reference S₀/R₀ system, even though the catalytic activities of the variant ribozymes were optimized by fine-tuning the lengths of stems Ib and V (Figure 1C). These kinetic results suggest that the transition from the open state to the closed state is rate-limiting in these KLI variants of the VS ribozyme.

In this work, we investigated the dynamic properties of three kissing-loops (KL) complexes, the I/V, L88/L22 and TAR/TAR* KL complexes, to correlate the dynamics of KLIs with ribozyme function. We ran 50-ns unrestrained Temperature-Replica Exchange Molecular Dynamics (T-REMD), an enhanced atomistic sampling method that has been shown to better explore conformational space than standard molecular dynamics (MD) and that is well suited to investigate ensembles of RNA populations (28). We analyzed the resulting trajectories to characterize the intrinsic dynamics of these KLIs and establish how the dynamics may contribute to the formation of a closed state for substrate cleavage in the VS ribozyme. The T-REMD simulations support the hypothesis that the reduced cleavage activity observed with our KLI variants of the VS ribozyme correlates with restricted motion of their KLI. Furthermore, to improve the cleavage activity of one of the S_TAR/R_TAR* ribozyme variants, we performed in vitro selection and identified an S_TAR/R_TAR* variant with both increased dynamics at the KLI and markedly improved cleavage activity. Based on our results, we formulated a mechanistic model of substrate binding in which the KLI dynamics contributes to the probability of aligning the two key internal loops to form the active site.

MATERIALS AND METHODS

Computational tools and hardware

All system minimization, equilibration and MD simulations were carried out in GROMACS version 2016.3 (29,30) on Compute Canada’s Graham GPU server. For the equilibration and MD simulations, the Amber ff99SB (31) force field was used with the ParmBSC0 nucleic acid parameters (32,33) and chi_ol corrections for glycosidic torsion angle chi (34) using explicit aqueous solvent. The Particle Mesh Ewald method was used to handle electrostatic interactions (35,36). GROMACS tools were employed for processing and analysis of T-REMD trajectories as described in Supplementary Materials and Methods. MC-Sym 3.3.2 (37) and Pymol (The PyMOL Molecular Graphics System, Version 1.9.0 Schrödinger, LLC.) were used for system building and/or structural analysis.

RNA system building and preparation

Three RNA systems were initially built for molecular dynamic studies: the I/V, L88/L22 and TAR/TAR* KL complexes. The starting conformation of the L88/L22 KL complex was obtained from PDB ID: 4IOA [chain A; (38)]. For the other two KL complexes, the starting conformation was obtained by extracting the lowest-energy structure of their representative structural ensembles, namely the second model of PDB ID: 2MI0 (24) and 1KIS (39). The hairpin stems within these three KL complexes were substituted by standard A-form stems generated with MC-Sym 3.3.2 (37) through heavy-atom superposition of the first Watson–Crick base pair following the loop-closing base pair. The resulting hybrid structures (Supplementary Figure S1a) retained the hairpin loop residues and closing base-pair [2MI0: residues 6–16 (I) and 108-114 (V); 1KIS: residues 5–12 (TAR) and 21–28 (TAR*) and 4IOA: residues 423–430 (L22) and 2383–2392 (L88)]. Each RNA complex was solvated with ∼20 000 TIP3P water molecules (40) in a periodic rhombic dodecahedral box and neutralized by addition of K⁺ placed at randomized positions. In addition, K⁺ and Cl⁻ ions equivalent to a concentration of 0.1 M KCl were added to the solvent (41). For simplicity, the addition of Mg²⁺ ions was not considered here. In addition, it was previously shown to have no significant effect on the global dynamics of the I/V KLI (42). For T-REMD of the TAR/TAR-S1 KL complex derived from in vitro selection (Figure 7), the RNA system was built by taking the hybrid structure of the TAR/TAR* KL complex, replacing residues of TAR* such that they match the TAR-S1 sequence (Figure 7D) and modeling the four potential WC base pairs between the TAR and TAR-S1 loops. For RNA system preparation, each RNA system was then copied several times, and each copy was energy minimized and equilibrated at the target temperature and pressure using standard methods (see Supplementary Materials and Methods).

Figure 7.

Improving the cleavage activity of a variant VS ribozyme for its substrate through a more dynamic KLI. (A) In vitro selection library to identify a VS ribozyme sequence that efficiently cleaves a TAR-derived substrate. (B) KL properties of enriched ribozyme sequences (≥10 representatives in the selected pool) from the in vitro selection pool in terms of the number of potential Watson–Crick (WC; G-C, A-U and G-U) base-pairs between loop I and loop V. (C) Sequence preferences of the randomized region for the two classes of enriched ribozyme sequences. (D) SLV loop sequences of a selected ribozyme with high activity (R_TAR-S1), the reference ribozyme (R₀) and a rationally-engineered ribozyme (R_TAR*-0) together with their observed trans cleavage rates (k_obs) of the S_TAR substrate. The k_obs values were determined under the same conditions for results shown here and those in Figure 1C. (E) The 2D heat map of the interhelical angle θ versus d_PP representing all frames of the T-REMD trajectory at 300 K for the selected TAR/TAR-S1 KL complex. The star points to values measured for the I/V KLI within the reference crystal structure (PDB ID: 4R4P; θ = 149° and d_PP = 0). (F) Cartoon representation of the first PC of motion for the TAR/TAR-S1 KL complex represented in the context of the VS ribozyme X-ray structure as in Figure 5.

Production T-REMD simulations

The T-REMD simulations were run in several replicas at evenly distributed temperatures from 300 to 375 K (inclusive bounds), to allow enhanced sampling of the conformational space. The number and temperature of the replicas were automatically generated for each KL complex to ensure an exchange rate of ∼20% between adjacent replicas within the temperature scale (43). This resulted in 58, 60 and 60 replicas for the I/V, L88/L22 and TAR/TAR* KL complexes, respectively. The T-REMD simulations were run for 50 ns with 2-fs time steps, attempting exchange between replicas at each 500 steps and recording a frame for each replica every 200 fs.

Convergence assessment on demultiplexed trajectories

To assess the convergence of the MD simulations (44), the T-REMD trajectories were first demultiplexed to reconstruct continuous trajectories, each one following a single starting structure through the temperature space. An RMSD profile was then built for each demultiplexed trajectory by calculating the pairwise heavy-atom RMSD of each frame with respect to the starting structure.

Computation of Euler angles between the two stems of the KL complexes

Each frame of the T-REMD trajectories at 300 K was analyzed to derive the three Euler angles α, β and γ between the two stems of the KL complexes. The Euler angles were calculated by adapting a method previously developed for RNA interhelical junctions (45). The interhelical angle θ was derived by taking the supplementary angle of the β Euler angle. For comparative analysis, the α, β, γ and θ angles were also calculated for the VS ribozyme crystal structure [PDB ID: 4R4P (27)].

Analysis of the T-REMD trajectories in the context of the crystal structure of the VS ribozyme

To investigate the T-REMD trajectory at 300 K of a given KL complex in the context of the crystal structure of the VS ribozyme, composite models were built that merged the KL interaction of an individual T-REMD frame with a substrate/ribozyme complex, termed S_X/R_X, taken from the crystal structure of the VS ribozyme A₇₅₆G variant [PDB ID: 4R4P (27)], in which S_X is the SLI substrate of one protomer and R_X the helical domains II–VI of the other protomer. First, each frame of the T-REMD trajectories was aligned on the crystal structure by superposing the four core base pairs of stem V (residues 685–688 and 698–701 in the crystal structure; residues 5–8 and 18–21 in the I/V KL complex; residues 5–8 and 19–22 in the L88/L22 KL complex and residues 5–8 and 19–22 in the TAR/TAR* KL complex). Subsequently, the internal loop and stem Ia of SLI from the crystal structure was added to the model, superposing stem Ib from the crystal structure (residues 623–625 and 635–637) on the corresponding residues of the I/V, L88/L22 and TAR/TAR* KL complexes (residues 4–6 and 18–20, 4–6 and 17–19 and 4–6 and 17–19, respectively). From these superpositions, d_PP values were calculated by measuring the distance between phosphorus atoms of the scissile phosphate from the crystal structure and the composite model derived from a given frame of the T-REMD trajectory. Based on the same superpositions, heavy atom RMSD values were calculated between the G₆₃₈ loop and closing base pairs (residues 619–623 and 637–640) of the crystal structure and the frame-derived model.

Principal component analysis of the T-REMD trajectories to characterize the molecular mechanics of KL complexes

A principal component (PC) analysis was performed on the T-REMD trajectories at 300 K to extract the PCs of motions and evaluate their contributions to the overall dynamics of the KL complexes. For each PC, the two extreme projections along the trajectory were reported on the average structure and interpolating frames were calculated to obtain a pseudo-trajectory. The interpolated frames of the pseudo-trajectory were represented in the context of the VS ribozyme crystal structure by building composite models as described above for frames of the T-REMD trajectories.

Root mean square fluctuation analysis of the T-REMD trajectories and identification of the residues responsible for the dynamics of the KL complexes

To capture the dynamics of individual nucleotides with respect to their immediate neighbors in the sequence, the heavy-atom Root-Mean Square Fluctuation (RMSF) was calculated for each pair of consecutive nucleotides. From the two RMSF values calculated for each non-terminal nucleotide, the largest one was retained.

In vitro selection procedure

All DNA sequences (Supplementary Materials and Methods) were obtained from IDT (Integrated DNA Technologies, IA) and gel purified. Double-stranded DNA libraries were generated by polymerase chain reaction (PCR) using 5′- and 3′-primers and the Pfu DNA polymerase, extracted with phenol/chloroform and precipitated with 1/10 volume NaAc 3 M pH 5.3 and 3 volumes ethanol 95%. RNA libraries were prepared by in vitro transcription using T7 RNA polymerase in Transcription buffer (40 mM Tris pH 7.6, 50 mM dithiothreitol, 1 mM spermidine, 0.1% triton, 7.5 mM MgCl₂ and 4 mM of each adenosine triphosphate, cytidine triphosphate, uridine triphosphate and guanosine triphosphate) and incubation for 90 min at 37°C. To improve ribozyme cleavage of the active population, the reaction was incubated for an additional 1–20 min (20, 10, 10, 5, 2 and 1 min for cycles 1, 2, 3, 4, 5 and 6, respectively) after addition of 17.5 mM MgCl₂. The large cleavage product was purified by denaturing gel electrophoresis [10% acrylamide:bisacrylamide (19:1) and 7 M urea]. The RNA product was then reverse transcribed using Superscript III reverse transcriptase with the RT-primer, according to the manufacturer’s protocol (Invitrogen, CA). The next rounds of selection were performed by following the same protocol, starting by regenerating the double-stranded DNA library, as described above.

Next-generation sequencing and sequence analysis of selected ribozymes

PCR products from the sixth round of selection were sequenced by Illumina MiSeq Spike (McGill University and Génome Québec Innovation Centre, Montréal, Canada) and analyzed using tools from the Galaxy Project (46). Briefly, the raw fastq output was first filtered using a Phred quality score of 30, such that 141 511 reads were kept. The dataset was first analyzed to verify that there were no mutations within the ribozyme outside the randomized region, which was found to be the case for all sequences. The ribozyme sequences were then truncated, keeping the eight bases flanking both sides of the randomized region, and the data was processed to obtain each unique sequence and its number of reads. Sequences with 10+ reads were kept and analyzed in terms of their potential for contiguous Watson–Crick (WC) base pairing with loop I. Then, the sequences that could formed at least four base pairs with loop I (96.4% of sequences) were analyzed to identify the positions of loop V residues that could form the four base pairs, and from this analysis two main classes were identified (Figure 7). For each class, position weight matrices were generated by counting the frequency of each base at every position within the randomized region and sequence logo representations were generated using a modified version of SeqLogo (47).

Single-turnover kinetic studies of the S_TAR/R_TAR-S1 complex

The S_TAR/R_TAR-S1 complex is a derivative of the S₀/R₀ complex previously characterized kinetically (15,16), modified in stem Ia and stem-loop Ib to match the HIV-1 TAR RNA sequence (S_TAR: 5′-GCA GAG AAG AGC CUG GGA GCU CGA UCU G-3′) and in stem-loop V to match the selected R_TAR-S1 sequence (Figure 7D). The 5′-end-³²P-labeled S_TAR and unlabeled trans ribozymes (R₀, R_TAR*-0 and R_TAR-S1) were prepared using established procedures (16). Single-turnover kinetic studies with the S_TAR/R_TAR-S1, S_TAR/R₀ and S_TAR/R_TAR*-0 complexes were carried out at 37°C in Kinetic Reaction buffer (50 mM Tris–HCl pH 7.6, 25 mM KCl, 2 mM spermidine and 25 mM MgCl₂) to determine the values of the observed rate constant (k_obs) using a substrate concentration ([S]) of 250 pM and a ribozyme concentration ([R]) of 0.5 μM, as previously described (16).

Isothermal titration calorimetry (ITC)

Isothermal titration calorimetry (ITC) studies, including RNA preparation, data collection and analysis, were performed as previously described (23) with relevant experimental details provided in Supplementary Figure S8.

RESULTS AND DISCUSSION

T-REMD simulations of kissing-loop complexes

We ran 50-ns T-REMD atomistic simulations to characterize the structural dynamics of three KL complexes in explicit solvent (Supplementary Figure S1). The T-REMD approach was used to enhance conformational sampling; MD simulations were run in parallel for ∼60 replicas at evenly-distributed temperatures between 300 and 375 K, with periodic attempts to exchange RNA coordinates between replicas of adjacent temperatures. Thus, the conformational space was sampled for a total MD simulation time of ∼3 μs for each KL complex.

To ensure that the T-REMD protocol allowed for a thorough exploration of the conformational space, the convergence of the demultiplexed trajectories was assessed (44). The demultiplexed trajectories were first obtained by following the continuous trajectory of each starting structure through the temperature space, and for each demultiplexed trajectory an RMSD frequency profile was generated based on heavy atom RMSDs between each frame and the T-REMD starting structure. The resulting RMSD profiles are all very similar with only a few outliers for the I/V KL complex (Supplementary Figure S2a), as well as for the L88/L22 and TAR/TAR* KL complexes (Supplementary Figure S2bc). Moreover, the detection of a single peak in the overlaid profiles indicates that all of the conformations are very similar in terms of RMSD, and that the T-REMD protocol did not induce large structural changes. Thus, the T-REMD trajectories of the I/V, L88/L22 and TAR/TAR* KL complexes converge reasonably well, and this validates the analysis of their structural dynamics.

Basic structural analysis of T-REMD trajectories

For each KL complex, the 250 000 frames of the lowest-temperature T-REMD trajectory (300 K) were structurally characterized using metrics that are either intrinsic to the KL complex or evaluated in the context of the VS ribozyme crystal structure (Figure 2). First, the distribution of Euler angles (α, β and γ) between the two helical stems of the KL complexes were calculated (45), which helped derive the more intuitive interhelical angle θ (Figure 2A). Then, composite models were built starting from the KL complex of each simulated frame and then attaching the internal loop and stem Ia of SLI to one stem (I, L88 or TAR) and the trans VS ribozyme to the other stem (V, L22 or TAR*) via superposition of common helical elements. These composite models allowed for the analysis of individual frames in the context of the VS ribozyme crystal structure. From heavy atom superposition of central base pairs of stem V within the composite model and the crystal structure, we measured the distance between the phosphorus atoms at the scissile phosphate of the two SLI internal loops (d_PP; Figure 2B) as well as the heavy-atom RMSD between these two loops.

Figure 2.

Schematic representation of the parameters used to analyze the T-REMD trajectories. (A) The Euler angles (α, β and γ) were defined from the KL complexes as shown and the interhelical angle θ is calculated as 180° −|β|. (B) Each T-REMD frame of the trajectories (SLV in pink sticks and SLI in green sticks) was analyzed in the context of the VS ribozyme crystal structure (PDB ID: 4R4P; trans ribozyme in white surface with A₇₅₆ in red stick and SLI in gray sticks), superposing the composite model of the frame on stem V as described in ‘Materials and Methods’ section. In this context, the P-P distance (d_PP) corresponds to the distance between the phosphorus atom of the scissile phosphates within the crystal structure (gray sphere) and the selected frame model (green sphere).

The 2D heat maps showing distributions of Euler angles demonstrate that the I/V KL complex explores a wider region of the Euler angle space compared to the L88/L22 and TAR/TAR* KL complexes (Figure 3). The I/V KL complex access interhelical angles that the surrogate KL complexes never adopt during the simulation, notably the set of Euler angles measured for the I/V KL complex within the crystal structure (marked by a star in Figure 3). Thus, the analysis of interhelical Euler angles indicate that the intrinsic global dynamics of the I/V KL complex are less constrained than those of the TAR/TAR* and L88/L22 KL complexes. The restricted global mobility of the surrogate KL complexes is particularly important for the TAR/TAR* KL complex, which is confined to a much narrower range of α, β and γ angles.

Figure 3.

Difference in conformational space between the I/V KL complex and surrogate KL complexes from Euler angle analysis. The 2D heat maps of Euler angle combinations representing all frames of the T-REMD trajectories at 300 K are shown for the (A) I/V, (B) L88/L22 and (C) TAR/TAR* KL complexes. In the 2D maps, the star points to the Euler angle values measured for the I/V KLI within the reference crystal structure (PDB ID: 4R4P; α = −69°; β = −31°; and γ = 71°).

This disparity in conformational space between the I/V KL complex and the surrogate KL complexes was also examined from the 2D heat maps showing the distribution of interhelical angle θ as a function of d_PP (Figure 4). For the I/V KL complex, several frames of the T-REMD trajectory adopt d_PP values approaching 0 Å, and small d_PP values are observed for a wide range of interhelical angles (d_PP < 2 Å for θ = 136°–178°), matching the range observed in the ensemble of 20 lowest-energy NMR structures of the I/V KL complex [θ = 127°–175°; (24)]. This analysis clearly indicates that the trajectory of the I/V KL complex brings the internal loop of the substrate close to its position in the crystal structure (marked by a star in Figure 4), which is compatible with formation of the active site. In contrast, for the L88/L22 and TAR/TAR* KL complexes, d_PP values were all greater than 6 and 11.5 Å, respectively, and these d_PP values directly correlate with the interhelical angle θ. Similar observations were made by examining the 2D heat maps showing the distribution of interhelical angle θ as a function of RMSD (Supplementary Figure S3), where the smallest RMSD value attained by the I/V KLI (2.6 Å), is much smaller than those for both the L88/L22 KL complex (8.7 Å) and the TAR/TAR* KL complexes (14.9 Å). Thus, the I/V KLI allows for a more complex range of motion and enables a large subpopulation of structures to approach the closed state in which the active site is formed.

Figure 4.

Correlation between the interhelical angle θ and the d_PP value for the I/V KL complex and surrogate KL complexes. The 2D heat maps of the interhelical angle θ versus d_PP representing all frames of the T-REMD trajectories at 300 K are shown for the (A) I/V, (B) L88/L22 and (C) TAR/TAR* KL complexes. In the 2D maps, the star points to values measured for the I/V KLI within the reference crystal structure (PDB ID: 4R4P; θ = 149° and d_PP = 0).

Principal component analysis of T-REMD trajectories

To better understand the dynamics associated with the three different KL complexes, a PC analysis was performed on the atomic coordinates of each T-REMD trajectory. This analysis extracts non-overlapping concerted atomic movements, or PCs, from the seemingly random vibrations of atomic positions observed in the T-REMD trajectories. For the three KL complexes, the first five PCs together represent more than 70% of the cumulative percentage of variance (Supplementary Figure S4 and Table 1). Thus, they provide the main contributions of the global motion. Pseudo-trajectories for each of these first five PCs were produced, in which atomic movements are projected along a single PC. Although these pseudo-trajectories can give rise to some partially unrealistic local structures, they are very useful in illustrating the direction and relative amplitude of concerted motions. They are displayed here in the context of the VS ribozyme crystal structure (Figure 5 and Supplementary Movies S1-S15) to provide insights into how specific motions may contribute to active-site formation.

Table 1.

Characteristics of the first five PCs of motion for the I/V, L88/L22 and TAR/TAR* KL complexes

	Principal components
	1	2	3	4	5
I/V
% of variance	34.4	16.3	9.5	7.0	5.2
Type of motion	Twist	Side-to-side bend	Twist	Back-to-front bend	Back-to-front bend
Amplitude of motion (Å)a	44	31	13	21	19
L88/L22
% of variance	24.4	20.8	13.5	8.9	5.3
Type of motion	Bendb	Bendb	Twist	Back-to-front bend	Side-to-sidebend
Amplitude of motion (Å)	38	32	6	11	17
TAR/TAR*
% of variance	31.5	21.7	9.6	7.6	5.3
Type of motion	Bendb	Side-to-side bend	Bendb	Twist	Twist
Amplitude of motion (Å)	34	35	19	6	11

^aThe amplitude of motion was calculated as the distance travelled by the scissile phosphate in the pseudo-trajectory.

^bIt contains almost equivalent back-to-front and side-to-side components.

Figure 5.

Cartoon representations of the first five PCs of motion for the I/V KL complex. (A) The large twist of the first PC, (B) the large side-to-side bend of the second PC, (C) the small twist of the third PC and (D and E) the two small back-to-front bends of the fourth and fifth PCs. The PCs of motion were extracted from the T-REMD trajectory at 300 K for the I/V KL complex and are represented in the context of the reference VS ribozyme X-ray structure (PDB ID: 4R4P; in white surface with A₇₅₆ in red stick), by superposing interpolated frames from the pseudo-trajectory (SLV in pink and SLI in green) as described in ‘Materials and Methods’. The movements of the backbone phosphorus atoms from SLI residues 616-623 and 637-643 are materialized as rainbow-colored arrows along with a single interpolated frame taken at the halfway point of the pseudo-trajectory.

For the I/V KL complex, the first five PCs help to bring the scissile phosphate of the SLI substrate in proximity of the A₇₅₆ internal loop within the ribozyme, with the first two PCs having the greatest impact (Figure 5 and Supplementary Movies S1–S5). The first PC, which accounts for 34% of the variance (Table 1) is characterized by a large-amplitude twist motion of the SLI substrate around an axis that is close to its own principal axis (Figure 5A). Interestingly, this twist motion appears to be correlated with an important structural transition in loop I between compact and loose states (Movie S1). The second PC, with 16% of the variance, is also of large amplitude, but is better described as a side-to-side bend motion that swings the substrate perpendicularly to the II-VI plane formed by helical domains II and VI (Figure 5B). The third PC describes a twist motion that is smaller in amplitude than the first PC, and it accounts for 9.5% of the variance. Finally, the fourth and fifth PCs both describe back-to-front bend motions, during which the substrate travels parallel to the II-VI plane (Figure 5D and E). Taken together these PCs of motion indicate that the I/V KLI can be viewed as a multi-axial ‘RNA joint’ that resembles a ball-and-socket shoulder joint, since it allows circular movements in three orthogonal directions.

Analysis of the individual PCs for the surrogate KL complexes indicate that their global dynamics are similarly composed of a mixture of movements, which includes a twist motion of the substrate around its main axis and different bend motions (Supplementary Figures S5 and S6; Supplementary Movies S6-S15). However, the contribution and amplitude of these movements differ between the three KL complexes (Table 1). Only the PCs for the I/V KL complex have sufficient amplitudes to bring the G₆₃₈ loop in proximity of the A₇₅₆ loop, in agreement with the short d_PP values observed for this complex. Moreover, the I/V KL complex is the only one in which the preeminent motion is a twist of the substrate around an axis that is close to its own principal axis. Whereas twist motions are observed for the L88/L22 and TAR/TAR* KL complexes, their contribution and amplitude are far less important.

Dynamics of KL complexes versus cleavage activity of S/R complexes

In order for the VS ribozyme to cleave its substrate, the G₆₃₈ and A₇₅₆ loops must intimately associate so that the reactive atoms are precisely positioned in the active site. However, in solution, the VS ribozyme is best represented by an ensemble of open conformations in which these two loops are most often apart from each other (25,26,48). Our analysis of T-REMD trajectories suggest that the higher activity of the S₀/R₀ complex compared to the S_L88/R_L22 and S_TAR/R_TAR* complexes (Figure 1C) is linked to the dynamics of the I/V KL complex, which is better suited to allow spatial closeness and proper positioning of the G₆₃₈ loop relative to the A₇₅₆ loop. The twist and side-to-side motions of large amplitude described by the first two PCs can bring the two internal loops in proximity, while other twist and bend motions of smaller amplitude can fine tune the relative position of the two internal loops.

Given that the S_L88/R_L22 and S_TAR/R_TAR* variant complexes display cleavage activity (Figure 1C), it is intriguing that the dynamics of the corresponding KL complexes characterized here does not allow the G₆₃₈ and A₇₅₆ loops to come in proximity. This is clearly shown both from the large d_PP values of the T-REMD frames (Figure 4B and C) and visualization of the main PCs of motions (Supplementary Figures S5 and S6; Supplementary Movies S6-S15). The lack of frames with smaller d_PP values may be due to the limited sampling of the T-REMD simulations. MD/T-REMD simulations that extend to longer timescales or explore higher temperatures might capture closed conformations, possibly by exploring less stable KL structures with fewer base pairs. Indeed, we observed surrogate KL complexes with disrupted KL base pairs in frames with the shortest d_PP values. Alternatively, other dynamic hotspots in the VS ribozyme, potentially the stem III bulge and the two-three way junctions (26), could help to bring the G₆₃₈ and A₇₅₆ loops in sufficient proximity to allow substrate cleavage.

Identification of the local hotspots of motion responsible for the KLI dynamics

To identify local hotspots of motion, we calculated the RMSF of every consecutive pair of residues along the stem-loop sequences for each KL complex (Figure 6). Remarkably, the I/V KL complex exhibits several clusters of residues with high RMSF values (>1.5 Å), defining three local hotspots of motion (residues 8–12 of loop I; residues 16–17 of loop I and residue 15 of loop V), in agreement with previous NMR studies (24). In contrast, fewer residues with high RMSF values were identified for the L88/L22 and TAR/TAR* KL complexes (Supplementary Figure S7), in agreement with more restricted motions associated with these surrogate KL complexes. It is not surprising that for all three KL complexes, the most dynamic residues are found at the junction between the hairpin stem and the KL stem. Unlike the surrogate KL complexes, the I/V KL complex contains several unpaired residues (I: A₉, U₁₀ and G₁₆; V: U₁₁ and U₁₅) and unstable base pairs (I: C₈-G₁₅; V: U₁₀-A₁₆) at this junction (Figure 1 and Supplementary Figure S1) (24).

Figure 6.

Identification of mobile and rigid residues in the I/V KL complex. RMSF values were calculated for phosphate atoms (pale gray), ribose ring atoms (dark gray) and base heavy atoms (black) of the T-REMD trajectories at 300 K. The RMSF values are mapped according to the displayed color scheme on the 3D structure of the I/V KL complex (top panel) that was used to initiate the T-REMD simulation.

Through their association with dynamic hotspots, the unpaired residues and unstable base pair in loop I largely contribute to the conformational dynamics of the I/V KL complex. Although there is a diversity of loop I conformations in the T-REMD trajectory, we noted that several structures adopt a compact loop I conformation in which the two base pairs closing the loops are formed (G₇-C₁₇ and C₈-G₁₅), whereas several other structures adopt a loose loop I conformation in which these base pairs are clearly disrupted. The loose and compact conformations of loop I can both populate the open and closed states when placed in the context of the VS ribozyme (Figure 1B). Interestingly, the large-amplitude twist motion defining the first PC in the I/V KL complex involves a structural transition between compact and loose states of loop I that is coupled to helical winding and unwinding (Movie S1). Such structural transition between loose and compact loop I conformations is not evident for the surrogate KL complexes, and this could explain why the preeminent twist motion observed for the I/V KL complex is not observed for these KL complexes.

RNA engineering by increasing the dynamics of an RNA junction

Given the importance of dynamics at the KLI for the high cleavage activity of the VS ribozyme complex (S₀/R₀), we postulated that the cleavage activity of the variant S_TAR/R_TAR* complex could be increased if one could add some dynamics at the TAR/TAR* KLI. In order to test this hypothesis, we first performed an in vitro selection to identify VS ribozyme variants that more efficiently cleave the S_TAR substrate (Figure 7A). For this selection, the S_TAR substrate was covalently bound to the ribozyme; it contains the HIV-1 TAR RNA sequence in stem Ia and stem-loop Ib but preserved the natural G₆₃₈ loop necessary for formation of the active site. In addition, loop V (5 nt) and the adjacent two closing base pairs (4 nt) were replaced by a stretch of 10 randomized nt to form an RNA library with ∼1 million (4¹⁰) different loop sequences. After six rounds of selection and amplification, next-generation sequencing of the selected ribozyme pool was performed, and enriched sequences (present 10 times or more in the pool) were analyzed in terms of the potential number of consecutive WC base pairs that could form with loop I (Figure 7B). Most of the selected sequences (96%) have the potential to form at least 4 WC base pairs, confirming that the in vitro selection procedure allowed us to select variant VS ribozymes for which cleavage in cis depends on the formation of the KLI. Formation of 4 WC base pairs at the KLI appears to be necessary, but also sufficient for cleavage activity since 64% of the sequences could form a maximum of 4 WC base pairs. Since only 2% of the ribozyme pool has the potential to form the maximum 6 WC base pairs, it appears that increasing the thermodynamic stability of the KLI is not beneficial, but instead this may in fact inhibit the activity. We found two main classes of loop V sequences with the preferred CCCA pattern starting either at position +4 or +5 of the randomized sequence (Figure 7C). In both cases, formation of 4–5 WC base pairs at the KLI could leave several residues unpaired in both KLs, which would provide more dynamics for formation of the active site and more efficient substrate cleavage.

Interestingly, when we modified the trans VS ribozyme R₀ to incorporate one of the selected loop V sequence predicted to form 4 consecutive WC base pairs with S_TAR, the resulting ribozyme (R_TAR-S1) cleaved S_TAR with a relatively high single-turnover rate (k_obs = 5.8 min⁻¹; Figure 7D). This rate is much higher than that previously reported for the most active rationally-engineered S_TAR/R_TAR* complex (k_obs = 0.077 min^-1; Figure 1C) and similar to the rate of the parental S₀/R₀ complex [k_obs = 12.2 min^-1; Figure 1C; (16)]. In addition, the R₀ and R_TAR*-0 ribozymes, which can respectively form 3 and 6 WC consecutive base pairs with S_TAR, both cleave this substrate with a much lower rate (≤200-fold; k_obs ≤0.03 min⁻¹; Figure 7D) than R_TAR-S1. To assess the thermodynamic stability of the KLI formed between the S_TAR substrate and the selected R_TAR-S1ribozyme with improved activity, we performed ITC studies using small stem-loops (Supplementary Figure S8). A K_D of 0.7 ± 0.2 μM was measured for this TAR/TAR-S1 KLI, indicating that it is 120-fold less stable than the TAR/TAR* KLI (0.0059 ± 0.0005 μM; Figure 1). Overall, these results demonstrate that the most active VS ribozyme variant is not the one with the most thermodynamically stable KLI.

We performed a T-REMD simulation to investigate the dynamics of the TAR/TAR-S1 KL complex (Figure 7; Supplementary Figures S9 and S10). Although this T-REMD simulation was initiated from a structural model and did not converge quite to the same extent as the other simulations reported here (Supplementary Figure S9a), broad comparisons with the original TAR/TAR* KL complex can still be drawn. We found that the selected TAR/TAR-S1 KL complex explores a much larger region of the Euler angle space (Supplementary Figure S9b) than the original TAR/TAR* KL complex (Figure 3C), and includes the values determined from the crystal structure (marked by a star in Supplementary Figure S9b). Several frames of the T-REMD trajectory adopt d_PP values (down to 5.6 Å; Supplementary Figure S9b) that are much smaller than the smallest values observed for the TAR/TAR* KL complex (11.5 Å; Figure 4C), and this indicates that the dynamics of TAR/TAR-S1 KL complex brings the internal loop of the substrate closer to its position in the crystal structure. Interestingly, PC analysis of the T-REMD trajectory at 300 K for the TAR/TAR-S1 KL complex reveals a dominating twist motion of the substrate around an axis close to its own principal axis (Figure 7F and Supplementary Figure S10; first PC with 38.4% variance and a 58-Å amplitude of motion), as previously observed for the I/V KL complex, but not the surrogate TAR/TAR* KL complex. Furthermore, higher RMSF values were obtained for the TAR/TAR-S1 KL (Supplementary Figure S9e) compared to TAR/TAR* KL complex (Supplementary Figure S7), and in particular for residues at the junction between the hairpin and the KL stems, in agreement with increased motions associated with the selected TAR/TAR-S1 KLI. A structural analysis of the T-REMD trajectory indicates that the TAR/TAR-S1 KLI has the potential to form 6 base pairs: the 4 predicted WC base pairs involving the central residues of the TAR loop, which are found simultaneously in 75% of the frames, and two cis Watson–Crick/Watson–Crick A-C base pairs involving the first C (in 72% of the frames) and last A (in 22% of the frames) of the TAR loop. As a result, the TAR/TAR-S1 KLI forms a maximum of 3, 4, 5 or 6 base pairs in 10, 23, 50 and 15% of the frames, respectively. In comparison, the TAR/TAR* KLI forms 6 WC base pairs in 76% of the frames. Taken together, our thermodynamic, kinetic and molecular dynamic results demonstrate that the cleavage activity of the variant S_TAR/R_TAR* complex can be significantly increased by changing the sequence of loop V to partly destabilize the KLI and thereby increasing the dynamics at the KL junction.

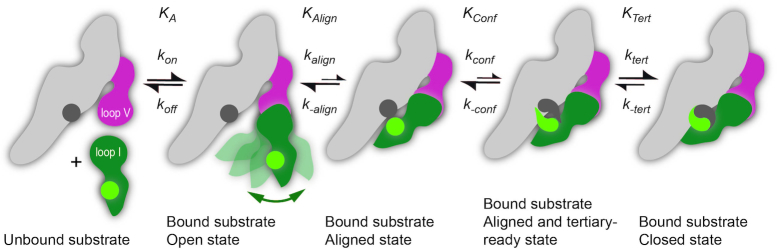
Mechanistic model of substrate binding in the VS ribozyme

Substrate cleavage by the trans VS ribozyme can be considered a two-step kinetic process that involves substrate binding and catalysis. To integrate the knowledge gained from the present studies, we propose a simple mechanistic model that breaks down substrate binding into four substeps (Figure 8). This model describes the binding of pre-shifted substrates as used here but could be expanded to the binding of shiftable substrates as found in the wild-type VS ribozyme by incorporating the helix shift associated with the formation of the KLI (23,24,26,49).

Figure 8.

Simple kinetic model for binding of a pre-shifted substrate to the trans VS ribozyme. Formation of the catalytically-competent state involves at least four steps: binding of the SLI substrate (dark green) to the trans ribozyme via formation of the KLI with stem-loop V (dark pink), alignment of the tertiary contact between the G₆₃₈ loop (light green sphere) and the A₇₅₆ loop (dark gray sphere), adoption of a tertiary-ready state within these two loops and formation of the tertiary interaction.

The first step is the formation of the highly-stable I/V KLI, a process that has been previously described in detail based on structural investigations of free and bound stem-loops (24,26,42,49). Formation of this KLI is the predominant thermodynamic contribution to substrate binding since the SLI substrate binds with similar affinity to an isolated SLV and the full trans ribozyme (23). In addition to substrate binding via the KLI, the G₆₃₈ and A₇₅₆ loops must associate to form the closed state, which depends on three factors: the alignment of the two internal loops (K_Align), the conformational change of the tertiary contact elements (K_Conf) and the actual formation of the tertiary interaction (K_Tert). The alignment of the internal loops is largely governed by the intrinsic dynamics of the KLI, and our T-REMD simulation of the isolated I/V KL complex indicates that only a small portion of the conformational space is compatible with the aligned state. However, additional factors likely contribute to define K_Align, including the electrostatic repulsion associated with bringing helical domains in proximity and the intrinsic dynamics of other subdomains of the VS ribozyme. Conformational changes would be necessary to bring both the G₆₃₈ and A₇₅₆ loops in a tertiary-ready conformation (K_Conf). Based on structural comparisons between the free and bound states of these loops, it was previously shown that only minor conformational changes would allow their less constrained residues to adopt a protruded conformation compatible with the closed state (26). This suggests that the probability of forming the tertiary-ready conformation would depend on the individual probabilities of those protruded conformations within the conformational ensembles of the free G₆₃₈ and A₇₅₆ loops. Once the internal loops adopt an aligned and tertiary-ready state, the free energy of the tertiary interaction (ΔG_Tert related to K_Tert) would likely favor the closed state given the large number of hydrogen bonds and stacking interactions observed in the crystal structure (27,49). In summary, these forward steps, namely formation of the KLI, the aligned state, the tertiary ready state and the tertiary interaction, are all part of the on-rate kinetics for the cleavage reaction, with k_off being defined from the overall thermal stability of the KLI (ΔG_KLI), and thus all these forward steps contribute to determine if the reaction can proceed before the substrate dissociates from the ribozyme.

This mechanistic framework explains why mutations that destabilize the KLI can reduce the activity of the VS ribozyme (22,50) but also specifies that the thermodynamic stability of the KLI is not the sole determinant of substrate binding. As shown here, the more stable TAR/TAR* KLI (K_D = 5.9 nM) yields a less active VS ribozyme variant than the less stable and more dynamic TAR/TAR-SI KLI (K_D = 0.7 μM). Thus, too much stability within the KLI can significantly reduce the cleavage efficiency by not allowing sufficient sampling of the aligned state required for formation of the closed state. This relation between binding events and conformational equilibria of RNA elements is increasingly being recognized as an important hallmark of RNA. In recent pioneering studies, it was formalized and tested in a thermodynamic model of RNA folding (8) and incorporated in high-throughput virtual screening for targeting RNA with small molecules (9).

CONCLUSION

This work was conducted to test the hypothesis that the dynamic properties of the KLI in the VS ribozyme contribute to the rate of substrate cleavage. Our T-REMD simulation of the natural I/V KLI reveals that it functions like a multi-axial RNA joint with a large range of motion, which facilitates formation of the active site through conformational sampling. In contrast, T-REMD simulations showed more restricted motion for two surrogate KLIs that can functionally substitute for the I/V KLI, but produce VS ribozymes with reduced activity, thereby supporting our initial hypothesis. We performed in vitro selection studies to improve the cleavage activity of the S_TAR/R_TAR* ribozyme variant by randomizing the KL of the trans ribozyme. Sequence analysis of the selected ribozyme variants and kinetic studies suggest that the KLI must be appropriately stable yet sufficiently dynamic for efficient substrate cleavage by the VS ribozyme. Moreover, we identified a ribozyme variant that more efficiently cleaves the S_TAR substrate and also forms a more dynamic KLI with the S_TAR substrate than the rationally-engineered R_TAR*. Thus, engineering an RNA junction with a larger range of motion can improve the cleavage activity of a variant ribozyme toward a non-natural substrate by promoting sampling of the active conformation. Based on these results, we propose a mechanistic model of substrate binding in the VS ribozyme that integrates conformational sampling of RNA subdomains. This model also illustrates how the modularity of RNA can be expressed in terms of defining the thermodynamics and kinetics relevant to RNA function. Such integrative view of RNA interaction and conformational dynamics will likely prove important in future applications, such as efforts to engineer RNA with novel functions and to identify specific compounds that target RNA.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Canadian Institutes of Health Research (CIHR) [PJT-148801 to P.L.]; Ph.D. scholarships from the Fonds de Recherche du Québec - Nature et Technologies (FRQ-NT) and the Université de Montréal (to P.D.); Ph.D. scholarships from CIHR and the Université de Montréal (to J.L.-L.). Funding for open access charge: Canadian Institutes of Health Research [PJT-148801 to P.L.].

Conflict of interest statement. None declared.