Patellofemoral cartilage stresses are most sensitive to variations in vastus medialis muscle forces

Abstract

The purpose of this study was to evaluate the effects of variations in quadriceps muscle forces on patellofemoral stress. We created subject-specific finite element models for 21 individuals with chronic patellofemoral pain and 16 pain-free control subjects. We extracted three-dimensional geometries from high resolution magnetic resonance images and registered the geometries to magnetic resonance images from an upright weight bearing squat with the knees flexed at 60°. We estimated quadriceps muscle forces corresponding to 60° knee flexion during a stair climb task from motion analysis and electromyography-driven musculoskeletal modelling. We applied the quadriceps muscle forces to our finite element models and evaluated patellofemoral cartilage stress. We quantified cartilage stress using an energy-based effective stress, a scalar quantity representing the local stress intensity in the tissue. We used probabilistic methods to evaluate the effects of variations in quadriceps muscle forces from five trials of the stair climb task for each subject. Patellofemoral effective stress was most sensitive to variations in forces in the two branches of the vastus medialis muscle. Femur cartilage effective stress was most sensitive to variations in vastus medialis forces in 29/37 (78%) subjects, and patella cartilage effective stress was most sensitive to variations in vastus medialis forces in 21/37 (57%) subjects. Femur cartilage effective stress was more sensitive to variations in vastus medialis longus forces in subjects classified as maltrackers compared to normal tracking subjects (p = 0.006). This study provides new evidence of the importance of the vastus medialis muscle in the treatment of patellofemoral pain.

Introduction

Patellofemoral (PF) pain accounts for roughly one in four knee conditions diagnosed in sports medicine clinics (Devereaux and Lachmann, 1984). A theorized cause for PF pain is elevated stress in the PF joint (Fulkerson and Shea, 1990). Previous studies have reported greater PF stress in subjects with pain compared to pain-free subjects (Farrokhi et al., 2011), and in females compared to males (Besier et al., 2015). Although there are several reasons for elevated stress across the PF joint, lateral patellar maltracking within the trochlear groove is the most commonly cited reason (Grabiner et al., 1994; Fulkerson, 2002; Ward et al., 2007). Lateral patellar maltracking is theorized to decrease PF contact area and increase joint stress, resulting in pain. Lateral patellar maltracking has been attributed to several factors, including patella alta (Pal et al., 2013), large quadriceps angle (Elias et al., 2004), altered mechanical properties of the passive soft-tissue structures around the PF joint (Amis et al., 2003), insufficient joint congruity (Davies et al., 2000), and altered muscle recruitment and kinematics at the hip (Bolgla et al., 2008; Cowan et al., 2009; Souza and Powers, 2009) and ankle (McClay and Manal, 1998; Duffey et al., 2000; Levinger and Gilleard, 2007) joints. Another potential cause of patellar maltracking and elevated PF stress is imbalance in quadriceps muscle activations (Souza and Gross, 1991; Karst and Willett, 1995), and subsequently, imbalance in quadriceps muscle forces (Grabiner et al., 1994; Besier et al., 2009). Direct evidence of quadriceps muscle force imbalance is difficult to obtain (Hug et al., 2015).

We have previously reported relationships between quadriceps muscle activation imbalance and patellar maltracking (Pal et al., 2011; Pal et al., 2012). We used subject-specific quadriceps muscle activations to estimate muscle forces (Besier et al., 2009) and PF stress in pain and pain-free groups (Besier et al., 2015). However, during our gait experiments, we recorded substantial variations in quadriceps muscle activations from individual subjects performing multiple trials of a single activity. Based on our experimental data, we calculated a coefficient of variation of up to 0.27 in quadriceps muscle forces between trials. The ratio of force between vastus lateralis and vastus medialis muscles varied from 1.3 to 4.5 among our subjects. The effects of these substantial variations in quadriceps muscle forces on PF stress remain unclear. Further, variations in force in some quadriceps muscles may influence PF stress more than other quadriceps muscles. These relationships are currently unknown.

The purpose of this study was to evaluate the effects of variations in quadriceps muscle forces on PF stress. We sought to answer three research questions: 1. How much does PF stress change due to variations in quadriceps muscle forces? 2. Is PF stress more sensitive to variations in some quadriceps muscle forces over others? 3. Is PF stress more sensitive to variations in quadriceps muscle forces in subjects with patellar maltracking compared to normal tracking subjects? We hypothesized that variations in quadriceps muscle forces affect PF stress and sought to quantify these relationships.

Materials and Methods

Subject recruitment

We recruited 37 subjects for this study; 21 with chronic PF pain and 16 pain-free controls (Table 1). The PF pain group included 10 males (30.8 ± 4.6 years, 1.78 ± 0.09 m, 73.5 ± 3.9 kg) and 11 females (27.4 ± 4.0 years, 1.65 ± 0.06 m, 58.9 ± 9.2 kg). The pain-free group included 8 males (27.8 ± 2.8 years, 1.79 ± 0.07 m, 73.2 ± 4.2 kg) and 8 females (28.8 ± 4.7 years, 1.66 ± 0.05 m, 58.3 ± 4.6 kg). There were no differences in age, height, or weight between the male PF pain and pain-free subjects, or between the female PF pain and pain-free subjects (two-tailed, unpaired t-tests, p > 0.05 for all cases).

Table 1.

Population characteristics of the patellofemoral pain and pain-free subjects in this study.

	Patellofemoral pain (n = 21)			Pain-free controls (n = 16)
	Mean	SD	Range	Mean	SD	Range
Age (years)	29.0	4.5	19.0 – 36.0	28.3	4.7	22.0 – 35.0
Height (meters)	1.71	0.10	1.57 – 1.90	1.72	0.09	1.58 – 1.91
Weight (kilograms)	64.7	12.2	46.5 – 88.2	65.9	8.9	52.1 – 77.3

We adhered to all policies of our Institutional Review Board during subject recruitment. All subjects were informed on all aspects of the study and provided written consent prior to data collection. The PF pain subjects were recruited from the university’s orthopaedic clinics and sports medicine centers, and were diagnosed by a sports medicine physician (M.F.) with over 25 years of clinical experience. The pain-free subjects were recruited from the local community and screened for previous injuries or knee disorders. The inclusion criteria for the PF pain group included consistent anterior knee pain for three months or longer (ranging from three months to 11 years), and reproducible pain during at least two of the following activities: stair ascent/descent, kneeling, squatting, prolonged sitting, or isometric quadriceps contraction (Brechter and Powers, 2002). For subjects with bilateral pain, the more painful knee at the time of examination was included in this study. The exclusion criteria for PF pain group included demonstrated knee ligament instability, pain in the patellar tendon during clinical exam or signs of degeneration of the patellar tendon observed from MRI, joint line tenderness or knee effusion, previous knee trauma or surgery, patellar dislocation, or signs of osteoarthritis detected from MRI of the knee. We used the Anterior Knee Pain Score (Kujala et al., 1993) to evaluate subjective symptoms and functional limitations in the PF pain subjects. The Anterior Knee Pain Score consists of 13 multiple-choice questions. A score of 100 indicated no pain or disability. The subjects were instructed to complete the questionnaire independently to exclude investigator bias (Kujala et al., 1993). The score for the PF pain subjects averaged 72 (range 55–96).

Subject-specific finite element models

We created finite element (FE) models of all 37 subjects (Fig. 1). The subject-specific FE modelling framework is described in detail elsewhere (Besier et al., 2015). We used high-resolution magnetic resonance (MR) images (1.5T, GE Healthcare, Milwaukee, WI) to create models of surface geometry. The MR scans were fat-suppressed spoiled gradient echo sequences with repetition time 60 milliseconds, echo time 5 milliseconds, flip angle 40°, matrix 256 × 256, field of view 12 × 12 cm, slice thickness 1.5 mm, and scan time 10:25 minutes. We modeled the femur, tibia, and patella bones using rigid three-noded shell elements (edge length ~1 mm) to reduce the complexity of the FE simulations. Subchondral bone is at least two orders of magnitude stiffer than cartilage (Beaupre et al., 2000). This large difference in stiffness between subchondral bone and cartilage ensures that the stresses in the cartilage are minimally affected by the assumption of rigid bones in our FE models (Li et al., 2001; Donahue et al., 2002). We modeled the PF cartilage using eight-noded linear elastic solid elements with an elastic modulus of 12 MPa and a Poisson ratio of 0.47 (Besier et al., 2015). This linear elastic model is a reasonable assumption for dynamic activities such as a stair climb task (Besier et al., 2015). We modeled the patella ligament and quadriceps tendon using one-dimensional tension-only connector elements. The patella ligament was modeled using 10 connector elements distributed evenly across the attachment areas of the tibia and femur, with a total stiffness of 2000 N/mm (Reeves et al., 2003). Individual components of the quadriceps tendon were represented with distinct connector elements: the rectus femoris muscle (RF) with five elements, the vastus lateralis longus (VLL) muscle with three elements, the vastus lateralis oblique (VLO) muscle with two elements, the vastus medialis longus (VML) muscle with three elements, the vastus medialis oblique (VMO) muscle with two elements, and the vastus intermedius (VI) muscle with five elements. Contact between the femur and patella cartilage was modeled using surface-to-surface contact pairs with a friction coefficient of 0.01 (Besier et al., 2015).

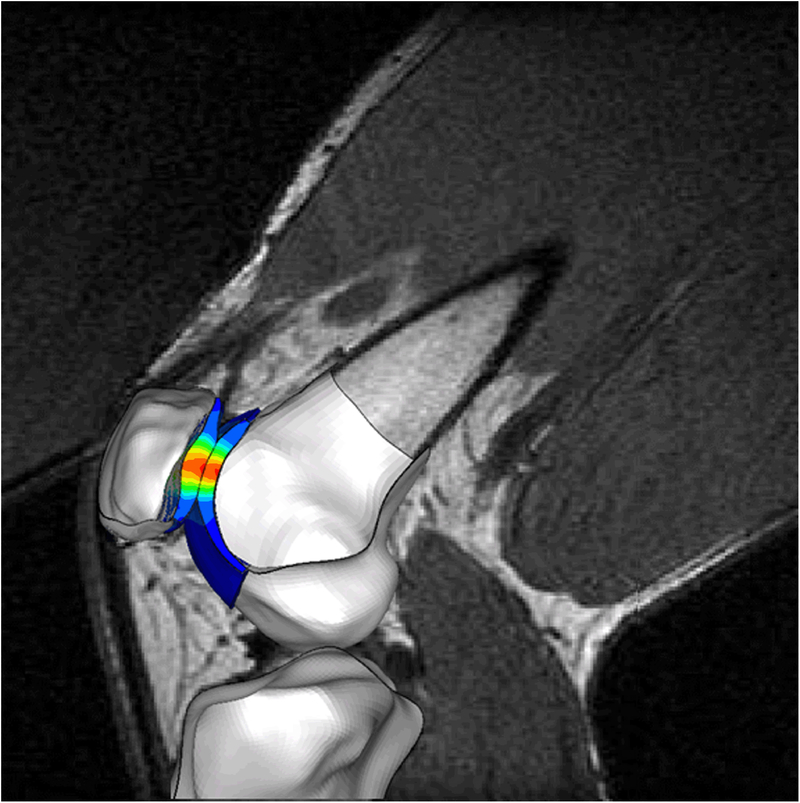
Figure 1.

Subject-specific finite element model simulating weight bearing knee flexion during a stair climb task. Three-dimensional knee geometries were registered to weight bearing magnetic resonance images.

We registered the three-dimensional FE models to images acquired in an open-configuration MR scanner (0.5T SP/i MR, GE Healthcare, Milwaukee, WI) with the knee at 60° flexion during an upright weight bearing squat (Fig. 1) (Pal et al., 2011). We chose to analyze the FE models at 60° knee flexion because this posture corresponds to peak knee extension moments during stair climbing. The subjects were supported in the open-configuration MR scanner by a custom-built low-friction backrest, and a goniometer was used to position the subjects with their knees flexed at 60°. We requested the subjects to load both legs evenly during scanning. A three-dimensional fast spoiled gradient echo sequence was used to obtain contiguous sagittal plane images with repetition time 33 milliseconds, echo time 9 milliseconds, flip angle 45°, matrix 256 × 160 interpolated to 256 × 256, field of view 20 × 20 cm, slice thickness 2 mm, and scan time ~2 minutes. All subjects were able to maintain the upright position for the duration of the scan. We developed custom scripts in Matlab (Mathworks, Natick, MA) to register the three-dimensional FE models created from supine, non-weight bearing MR images to upright weight bearing MR images. We registered the femur, patella, and tibia bones, and aligned the patella ligament and quadriceps tendon connector elements to match the lines of action visible on the upright weight bearing MR images.

We estimated quadriceps muscle forces corresponding to 60° knee flexion during a stair climb task from motion analysis data and electromyography (EMG)-driven musculoskeletal modelling (Lloyd and Besier, 2003). We obtained lower limb kinematics, kinetics, and electromyography (EMG) data from all subjects while performing multiple trials of a stair climb task in a motion analysis laboratory. Retro-reflective markers were placed on lower limb landmarks (Kadaba et al., 1990), and three-dimensional marker trajectories were measured at 60 Hz using a six-camera motion capture system (Motion Analysis Corporation, Santa Rosa, CA). Ground reaction forces were measured at 2,400 Hz from a force plate (Bertec Corporation, Columbus, OH). Marker trajectories were low-pass filtered using a zero-lag fourth-order Butterworth filter with a cut-off frequency of 15 Hz. Standard Newton-Euler inverse dynamics calculations were performed to calculate lower limb joint kinematics and kinetics (Crowninshield and Brand, 1981).

Electromyography signals were recorded using a multi-channel system (Motion Lab Systems, Baton Rouge, LA) with pre-amplified single differential, rectangular silver electrodes with 10 mm inter-electrode distance (DE-2.1, Delsys, Inc, Boston, MA, USA). These surface electrodes were placed on seven lower limb muscles crossing the knee (Besier et al., 2009), including three quadriceps muscles (vastus medialis, vastus lateralis, and rectus femoris). We assumed identical activations for the VMO and VML muscles (vastus medialis electrode), and VLO and VLL muscles (vastus lateralis electrode), since it is difficult to discern these differences using surface EMG techniques. We recorded EMG from the symptomatic or more painful knee for the PF pain subjects, and selected a knee at random for the pain-free subjects. The EMG signals were normalized using maximum voluntary contraction data. Subjects performed five trials of isometric muscle contractions to elicit maximum activation of the quadriceps muscles. A subject sat on a chair with the knee at approximately 80° of flexion and was instructed to extend the knee against the resistance of a tester. Verbal encouragement was given to the subject to try to improve their effort with each trial. The peak EMG value from all five trials was assigned as a muscle’s maximum activation. Resting EMG signals were recorded with a subject seated and relaxed. Raw EMG signals from the stair climb trials were high-pass filtered with a zero-lag fourth-order recursive Butterworth filter (30 Hz) to remove motion artefact, and full-wave rectified and filtered with a Butterworth low-pass filter (6 Hz). The filtered EMG data from the stair climb trials were normalized to the maximum contraction values for each muscle. These normalized EMG data were input to the EMG-driven musculoskeletal model (Lloyd and Besier, 2003). We estimated quadriceps muscle forces from five trials of a stair climb task for each subject using the EMG-driven model.

We applied the quadriceps muscle forces to our FE models to estimate cartilage stresses corresponding to 60° knee flexion during a stair climb task. Quasi-static, finite-sliding analyses were performed using a non-linear FE solver (ABAQUS Explicit, SIMULIA, Providence, RI). The patella was kinematically unconstrained in all six degrees of freedom, while the tibia and femur were constrained in all six degrees of freedom. The individual quadriceps muscle forces were applied to the respective components of the quadriceps tendon connector elements, and the patella was allowed to settle into its lowest energy state in the trochlear groove. We quantified cartilage stress using an energy-based effective stress, a scalar quantity representing the local stress intensity in the tissue (Beaupre et al., 1990; Carter and Beaupre, 2001). Effective stress is given by:

$$EffectiveStress=\sqrt{2*ElasticModulus*StrainEnergyDensity}$$ (1)

We calculated peak strain energy density as the mean of the top 10% of cartilage elements within the layer closest to the bone-cartilage interface, and used this peak strain energy density to calculate effective stress. Effective stress provides one number that reflects the magnitude of the stress tensor (Carter and Beaupre, 2001).

Probabilistic modelling of quadriceps muscle force variation

We quantified the effects of variations in quadriceps muscle forces on PF cartilage stress using probabilistic methods (NESSUS, Southwest Research Institute, San Antonio, TX) (Pal et al., 2007; Pal et al., 2008). The forces in the individual quadriceps muscles were assumed to be normally distributed. The mean quadriceps forces for each subject were obtained by averaging the individual quadriceps forces from the five trials of stair climb. The muscle-specific standard deviations (SD) were represented as percentages of quadriceps forces; for each subject, the SDs of the individual quadriceps forces from the five stair climb trials were represented as percentages of their mean muscle forces. These subject-specific percentages were then averaged over the 37 subjects for each quadriceps muscle. The muscle-specific SDs were: RF 12.5%, VML and VMO each 14.2%, VLL and VLO each 9.9%, and VI 7.5%. We used the Advanced Mean Value (AMV) (Wu et al., 1990; Haldar and Mahadevan, 2000) probabilistic method to evaluate the effects of variations in quadriceps muscle force estimates. For each subject-specific FE model, the AMV method optimized the solution space based on the input distributions and ran an FE trial for each set of optimized muscle forces (Wu et al., 1990; Haldar and Mahadevan, 2000). For monotonic systems, AMV exhibits excellent agreement with the Monte Carlo method, which is based on repeated trials and is computationally more expensive (Pal et al., 2008).

We determined the relative sensitivity of PF cartilage effective stress to individual quadriceps muscle forces using probabilistic importance factors in the AMV method (Haldar and Mahadevan, 2000; Pal et al., 2007). Probabilistic importance factors provide a ranking of the input variables based on changes in output due to perturbations in input variables. The calculation of probabilistic importance factors in the AMV method is complex. An n-dimensional problem is transformed to a standard normal variate space, a most probable point is determined using optimization, and n-dimensional projections of a unit vector to the most probable point represent the probabilistic importance factors (Haldar and Mahadevan, 2000). The sum of the squares of the probabilistic importance factors for all variables is unity.

Classification of subjects into maltracking and normal tracking groups

We classified all subjects into maltracking and normal tracking groups using a previously published method (Pal et al., 2012; Pal et al., 2013). We used two-dimensional patellar tracking measures, patellar tilt and bisect offset, obtained from weight bearing MR images with the knees near full extension (Pal et al., 2012; Pal et al., 2013). The scan parameters for the images with the knees near full extension were the same as the parameters for images with 60° knee flexion described earlier. An oblique-axial plane image was identified from the three-dimensional MR volume; this was done to maintain consistency in methodology with previous studies (Draper et al., 2009; Draper et al., 2011; Pal et al., 2011). The oblique-axial plane was prescribed to intersect the center of the patella and the most posterior points on the femoral condyles. Anatomical landmarks were identified on the oblique-axial plane image; the landmarks included the most lateral and most medial points on the patella, the most posterior points on the femoral condyles, and the deepest point of the trochlear groove. Patellar tilt, a measure of patella internal-external rotation, was defined by the angle between the patella and the posterior femoral condyles (Pal et al., 2011). Bisect offset, a measure of patella medial-lateral translation, was defined as the percentage of the patella lateral to the midline of the femur (Pal et al., 2011). All patellar tilt and bisect offset measurements were performed by the same investigator; the average intraobserver variance between measurements was 2° for patellar tilt and 4% for bisect offset (Pal et al., 2011).

We used gender-specific maltracking thresholds based on patellar tilt and bisect offset measurements to classify subjects into maltracking and normal tracking groups. Gender-specific maltracking thresholds were required because of statistically significant differences in patellar tracking measures between males and females (Pal et al., 2011). A non-Gaussian two-parameter Weibull distribution model best fit the measured patellar tilt and bisect offset data, with r² ≥ 0.84 in all cases. We defined gender-specific patellar tilt and bisect offset values corresponding to the 75^th percentile of the Weibull model as thresholds for maltracking. A subject was classified as a maltracker if his/her patellar tilt or bisect offset value was in the highest quartile of measured population data (Pal et al., 2011). The gender-specific maltracking thresholds were 11.9° (males) and 14.9° (females) for patellar tilt, and 68.9% (males) and 72.0% (females) for bisect offset (Pal et al., 2012).

Data analysis and statistical methods

We quantified the effects of variations in quadriceps muscle forces on peak PF effective stress. The AMV method predicted bounds (5 and 95 percentiles; ±1.65 SD) of peak effective stress at the femur and patella bone-cartilage interfaces. We measured the relative sensitivity of PF effective stress to variations in individual quadriceps muscle forces. We quantified the percentage breakdown of subjects with PF effective stress most sensitive to individual quadriceps muscle forces. We compared the relative sensitivity of PF effective stress to variations in individual quadriceps muscle forces between maltracking and normal tracking subjects using two-tailed, unpaired t-tests (post Bonferroni correction, p < 0.025).

Results

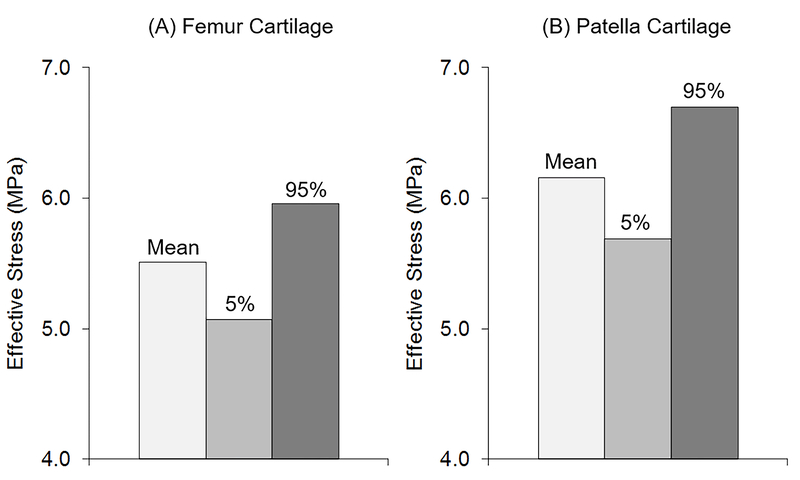
Peak PF effective stress averaged over all subjects (n = 37) changed substantially due to variations in quadriceps muscle forces (Fig. 2). The range of femur cartilage effective stress, given by the difference between the 5% and 95% bounds, represented 16% (0.9 MPa) of mean effective stress (5.5 ± 1.3 MPa, Fig. 2A). Similarly, the range of patella cartilage effective stress represented 17% (1.0 MPa) of mean effective stress (6.2 ± 1.9 MPa, Fig. 2B).

Figure 2.

Mean and 5 and 95 percentile bounds of effective stress in the (A) femur and (B) patella cartilage averaged over all subjects (n = 37).

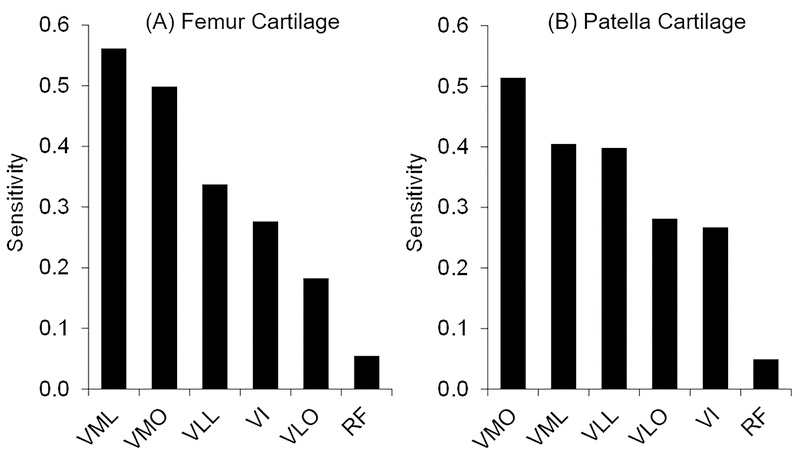
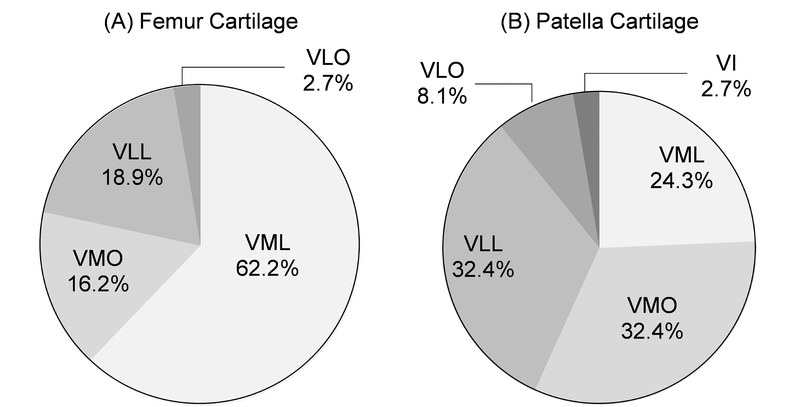
Peak PF effective stress was most sensitive to variations in forces in the two branches of the vastus medialis muscle, VML and VMO, with sensitivity values averaged over all subjects (n = 37, Fig. 3). Femur cartilage effective stress was most sensitive to variations in vastus medialis forces in 29/37 (78%) subjects (Fig. 4A). Patella cartilage effective stress was most sensitive to variations in vastus medialis forces in 21/37 (57%) subjects (Fig. 4B). Patellofemoral effective stress was least sensitive to variations in rectus femoris muscle forces (Figs. 3 and 4).

Figure 3.

Relative sensitivity of effective stress to individual quadriceps muscle forces in the (A) femur and (B) patella cartilage. The sensitivity values represent the projections of a unit vector to a most probable point in a standard normal variate space (Haldar and Mahadevan, 2000). The sensitivity values were averaged over all subjects (n = 37). VML – vastus medialis longus, VMO – vastus medialis oblique, VLL – vastus lateralis longus, VLO – vastus lateralis oblique, VI – vastus intermedius, RF – rectus femoris.

Figure 4.

Percent breakdown of subjects (n = 37) with effective stress most sensitive to individual quadriceps muscle forces in the (A) femur and (B) patella cartilage. There was no subject whose femur cartilage effective stress was most sensitive to variation in rectus femoris or vastus intermedius muscle forces (A), and there was no subject whose patella cartilage effective stress was most sensitive to variation in rectus femoris muscle forces (B).

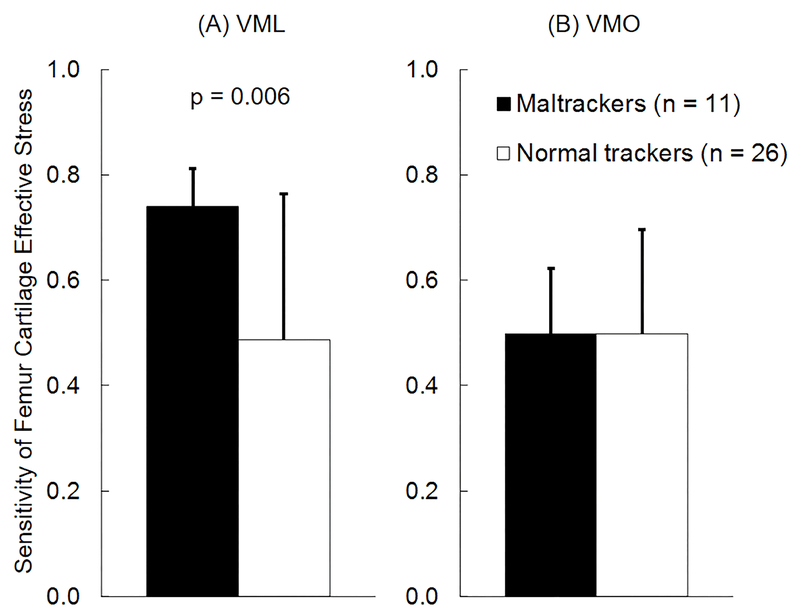
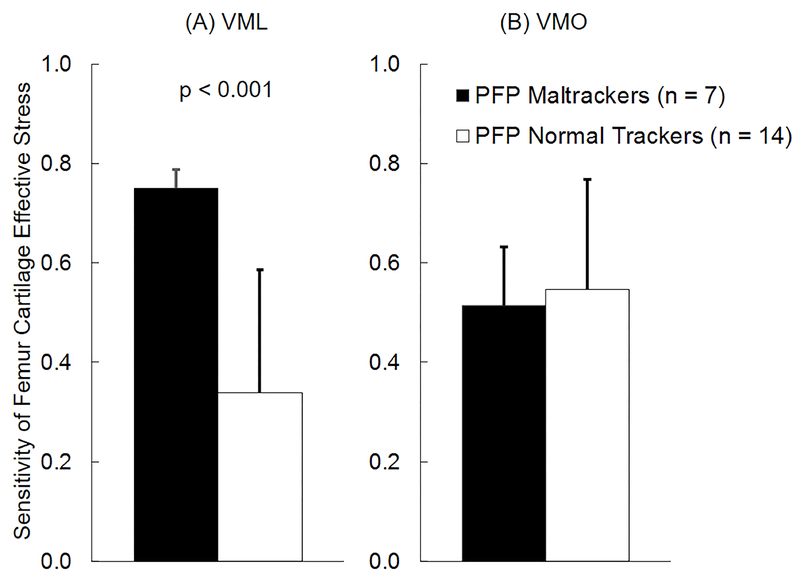
For the combined cohort of PF pain and pain-free subjects, peak femur cartilage effective stress was more sensitive to variations in VML forces in subjects classified as maltrackers (n = 11) compared to normal tracking subjects (n = 26, Fig. 5A). Average sensitivity of femur cartilage effective stress to variations in VML forces for maltracking subjects was 52% greater than normal tracking subjects (p = 0.006, Fig. 5A). This difference was larger in PF pain subjects, where average sensitivity of femur cartilage effective stress to variations in VML forces for maltracking PF pain subjects (n = 7) was 122% greater than normal tracking PF pain subjects (n = 14, p < 0.001, Fig. 6A). There were no differences in sensitivities of femur cartilage effective stress to variations in VML forces in pain-free subjects classified into maltracking and normal tracking groups. There were no differences in sensitivities of femur cartilage effective stress to variations in VMO (Figs. 5B and 6B), VLL, VLO, VI, or RF forces in PF pain and pain-free subjects classified into maltracking and normal tracking groups. There were no differences in sensitivities of patella cartilage effective stress to variations in any of the quadriceps muscle forces in PF pain and pain-free subjects classified into maltracking and normal tracking groups.

Figure 5.

Average (+1 SD) sensitivity of femur cartilage effective stress to variation in (A) vastus medialis longus (VML) and (B) vastus medialis oblique (VMO) muscle forces for all subjects classified into maltracking (n = 11) and normal tracking (n = 26) groups.

Figure 6.

Average (+1 SD) sensitivity of femur cartilage effective stress to variation in (A) vastus medialis longus (VML) and (B) vastus medialis oblique (VMO) muscle forces for patellofemoral pain subjects classified into maltracking (n = 7) and normal tracking (n = 14) groups.

Discussion

The aim of this study was to evaluate the effects of variations in quadriceps muscle forces on PF stress. We sought to answer three research questions. Our first research question was: how much does PF stress change due to variations in quadriceps muscle forces? We found that up to 14% variation in quadriceps muscle forces from multiple trials of a stair climb task resulted in 16–17% change in PF effective stress (Fig. 2). Our second research question was: is PF stress more sensitive to variations in some quadriceps muscle forces over others? Our results showed that PF effective stress was most sensitive to variations in forces in the two branches of the vastus medialis muscle, VML and VMO (Figs. 3 and 4). Our third research question was: is PF stress more sensitive to variations in quadriceps muscle forces in subjects with patellar maltracking compared to normal tracking subjects? We found that femur cartilage effective stress was more sensitive to variations in VML forces in subjects classified as maltrackers compared to normal tracking subjects (Fig. 5A). This difference in sensitivity of femur cartilage effective stress to variations in VML forces between the maltracking and normal tracking groups was greater in PF pain subjects (Fig. 6A), while there were no differences in pain-free subjects. We found no differences in sensitivities of femur cartilage effective stress to variations in VMO (Figs. 5B and 6B), VLL, VLO, VI, or RF forces in PF pain and pain-free subjects classified into maltracking and normal tracking groups.

This study provides evidence that may be important for understanding the role of the vastus medialis muscle in the context of PF pain. The vastus medialis muscle has been studied extensively in the diagnosis and treatment of PF pain (Souza and Gross, 1991; Grabiner et al., 1994; Karst and Willett, 1995; Powers, 2000; Cowan et al., 2001; Cowan et al., 2002; Bennell et al., 2006; Ng et al., 2008; Bennell et al., 2010; Cavazzuti et al., 2010; Pal et al., 2011; Benjafield et al., 2015). Patients with PF pain have been reported to have a weakened or inhibited activation of the vastus medialis muscle, which is theorized to result in an imbalance in quadriceps muscle forces (Karst and Willett, 1995). This imbalance in quadriceps muscle forces is theorized to cause patellar maltracking, leading to elevated PF stress and pain (Fulkerson and Shea, 1990). Although there are several articles addressing the imbalance in quadriceps muscle forces in PF pain patients (Cavazzuti et al., 2010; Chen et al., 2012; Benjafield et al., 2015), the effects of this force imbalance on PF joint stress has remained unclear. Our study shows that out of all the quadriceps muscles, small variations in vastus medialis muscle forces have the greatest effect on PF stress, highlighting the importance of the vastus medialis muscle.

An interesting finding of this study is that femoral cartilage effective stress is more sensitive to variations in VML forces in subjects classified as maltrackers compared to normal tracking subjects (Figs. 5A and 6A). This finding suggests that small changes in VML forces would have a greater effect on PF stresses in maltracking subjects compared to normal tracking subjects. The underlying causes for this phenomenon remains unclear; from our dataset, we are unable to isolate the factors for femoral cartilage effective stress being more sensitive to variations in VML forces in maltracking PF pain subjects compared to normal tracking subjects. We found differences in sensitivities of PF effective stress to variations in only the VML forces; we found no such differences in sensitivities of PF effective stress to variations in other quadriceps muscle forces in PF pain and pain-free subjects classified into maltracking and normal tracking groups.

It is important to point out the limitations of this study. First, we modeled the cartilage as a uniform isotropic linear elastic material. We acknowledge that this assumption does not capture the time-varying properties of cartilage, but a linear elastic material model is fully justified when simulating dynamic activities with loading frequencies greater than 0.01 Hz (Higginson and Snaith, 1979; Li et al., 2001), such as a stair climb task. Second, we used a constant linear elastic material model (elastic modulus of 12 MPa and Poisson ratio of 0.47) for all subjects. Cartilage material property varies between subjects (Keenan et al., 2013), but it is difficult to determine subject-specific cartilage material properties using non-invasive methods. Further, variations in cartilage material properties among subjects would affect the magnitude of cartilage stress. However, the probabilistic analysis and sensitivity results reported in this study are based on the relative change in cartilage stress in a subject, which is independent of the magnitude of cartilage stress. Third, our FE models of the PF joint do not include the medial and lateral PF ligaments. As with cartilage, it is difficult to determine subject-specific material properties for the medial and lateral PF ligaments using non-invasive methods, and their contribution to PF cartilage stress remains unclear.

This computational study provides theoretical evidence in support of clinical interventions targeting the vastus medialis muscle for treatment of PF pain. Clinical evaluation of patients should include accurate measurement of patellar tracking under weight bearing conditions. A patient accurately diagnosed as a maltracker will more likely benefit from clinical interventions targeting weakness or inhibition of the vastus medialis muscles, including muscle retraining (Bennell et al., 2010) or EMG biofeedback (Ng et al., 2008), compared to a patient accurately diagnosed as a normal tracker.