White Matter Hyperintensities in Aging

Abstract

Introduction:

White matter hyperintensities (WMHs) are areas of abnormal signal on magnetic resonance images (MRIs) that characterize various types of histopathological lesions. The load and location of WMHs are important clinical measures that may indicate the presence of small vessel disease in aging and Alzheimer’s disease (AD) patients. Manually segmenting WMHs is time consuming and prone to inter-rater and intra-rater variabilities. Automated tools that can accurately and robustly detect these lesions can be used to measure the vascular burden in individuals with AD or the elderly population in general. Many WMH segmentation techniques use a classifier in combination with a set of intensity and location features to segment WMHs, however, the optimal choice of classifier is unknown.

Methods:

We compare 10 different linear and nonlinear classification techniques to identify WMHs from MRI data. Each classifier is trained and optimized based on a set of features obtained from co-registered MR images containing spatial location and intensity information. We further assessed the performance of the classifiers using different combinations of MRI contrast information. The performances of the different classifiers were compared on three heterogeneous multi-site datasets, including images acquired with different scanners and different scan-parameters. These included data from the ADC study from University of California Davis, the NACC database and the ADNI study. The classifiers (naïve Bayes, logistic regression, decision trees, random forests, support vector machines, k-nearest neighbors, bagging, and boosting) were evaluated using a variety of voxel-wise and volumetric similarity measures such as Dice Kappa similarity index (SI), Intra-Class Correlation (ICC), and sensitivity as well as computational burden and processing times. These investigations enable meaningful comparisons between the performances of different classifiers to determine the most suitable classifiers for segmentation of WMHs. In the spirit of open-source science, we also make available a fully automated tool for segmentation of WMHs with pre-trained classifiers for all these techniques.

Results:

Random Forests yielded the best performance among all classifiers with mean Dice Kappa (SI) of 0.66±0.17 and ICC=0.99 for the ADC dataset (using T1w, T2w, PD, and FLAIR scans), SI=0.72±0.10, ICC=0.93 for the NACC dataset (using T1w and FLAIR scans), SI=0.66±0.23, ICC=0.94 for ADNI1 dataset (using T1w, T2w, and PD scans) and SI=0.72±0.19, ICC=0.96 for ADNI2/GO dataset (using T1w and FLAIR scans). Not using the T2w/PD information did not change the performance of the Random Forest classifier (SI=0.66±0.17, ICC=0.99). However, not using FLAIR information in the ADC dataset significantly decreased the Dice Kappa, but the volumetric correlation did not drastically change (SI=0.47±0.21, ICC=0.95).

Conclusion:

Our investigations showed that with appropriate features, most off-the-shelf classifiers are able to accurately detect WMHs in presence of FLAIR scan information, while Random Forests had the best performance across all datasets. However, we observed that the performances of most linear classifiers and some nonlinear classifiers drastically decline in absence of FLAIR information, with Random Forest still retaining the best performance.

1. Introduction

White matter hyperintensities (WMHs), commonly identified as areas of increased signal in relation with the surrounding white matter regions on T2w, PD and FLAIR MRIs, are one of the non-specific yet typical and constant MRI expressions of cerebral small vessel disease (CSVD), along with lacunar infarcts and microhemorrhages (Conklin et al., 2014; Gouw et al., 2010). They have been shown to be more extensive in patients with Alzheimer’s disease compared to age-matched healthy normal populations (Yoshita et al., 2005). WMHs reflect ischemic injury in the elderly and AD populations and the existence and severity of WMHs can lead to or accelerate decline in cognitive as well as executive functions (Dubois et al., 2014). As a result, the location and load of WMHs are important clinical measures, raising substantial need for their accurate quantifications. WMHs are generally detected using fluid attenuated inversion recovery (FLAIR) or T2w/PD scans. Manually labeling WMHs is challenging due to time constraints as well as inter-rater and intra-rater variabilities (Grimaud et al., 1996). As a result, automated tools that can segment WMHs robustly and with high accuracy are extremely useful, particularly in large scale studies such the Alzheimer’s Disease Neuroimaging Initiative (http://www.loni.ucla.edu/ADNI/), the National Alzheimer’s Coordinating Center (NACC) database (https://www.alz.washington.edu/) and others where it is desired to estimate the contribution of neurovascular disease to cognitive decline.

The heterogeneity in the distribution and patterns of WMHs makes the segmentation task intrinsically complex (Caligiuri et al., 2015). Automated segmentation tools usually integrate information from multiple complementary MRI contrasts including T1w, T2w, PD and FLAIR to reduce uncertainty and improve segmentation accuracy. Most successful fully automated WMH segmentation techniques extract a combination of location and intensity features from these images and use them as inputs to a linear or nonlinear classifier. Here we review the most commonly used linear and nonlinear classifiers in general as well as their application to the task of segmenting lesions in general or WMHs of vascular etiology specifically.

While there have been many studies attempting to segment WMHs using these classification techniques, drawing meaningful comparisons between their performance is not possible since they have been applied to different datasets and results are highly variable across different populations and imaging protocols (García-Lorenzo et al., 2013) (Caligiuri et al., 2015). To our knowledge, no studies have compared the performance of these classification techniques for detecting WMHs against one another on the same datasets, especially for cases where classification is attempted without using the optimal FLAIR information. In this paper, we have extensively compared the performance of these different classification techniques in detecting WMHs with and without FLAIR information using 3 different large publicly available datasets with different scanners and acquisition protocols. This enables us to draw more generalizable conclusions regarding the performance of the classifiers. Our contributions include an extensive comparison of 10 widely used classification techniques in detecting WMHs across 4 different datasets, three of which are from multi-site and multi-scanner studies and across different combinations of imaging modalities. In addition, we make publicly available an implementation of the segmentation tool along with all the pre-trained classifiers (https://www.dropbox.com/sh/zbbqjjo1ilzuun2/AABWN17N2fyzi8p3aSfiA0fEa?dl=0). The proposed tool is generalizable to data from different scanners since it has been trained on data from multiple scanners.

2. Materials and methods

2.1. Subjects

The performances of the different classifiers were assessed based on four datasets of subjects with different ranges of WMH loads. Table 1 shows the demographic information for each dataset.

Table 1 -.

Demographic information for ADC, NACC, ADNI1 and ADNI2/GO datasets.

Dataset	ADC	NACC	ADNI1	ADNI2/GO
N	70	32	53	46
Sex	35 M	15 M	27 M	25 M
Age	78.0±7.3	74.9±8.0	75.7±6.6	74.1±6.5

I). ADC:

This dataset consists of 70 individuals (70–90 years old) with normal cognition, mild cognitive impairment (MCI), and AD dementia from University of California, Davis Alzheimer’s Disease Center (ADC) who were scanned using T1w, double-echo T2w/PD, and FLAIR MRI modalities.

II). NACC:

This dataset consists of a patient sample of 32 MCI and AD subjects obtained from the National Alzheimer’s Coordinating Center (NACC) database which is a database of subjects with a range of cognitive status, i.e. normal cognition, MCI, and demented who received T1w, and FLAIR MRI scans (https://www.alz.washington.edu/). Data consisted of variables from a Uniform Data Set collected from more than 30 Alzheimer’s disease centers (ADC) throughout the United States and cataloged at the NACC. ADCs are National Institute on Aging–funded centers that enroll patients using different participation recruiting practices. A full description of the NACC data set has been previously provided (Beekly et al., 2004; Morris et al., 2006). NACC data used here has been acquired at six different ADCs using eight different scanner models of three different manufacturers. Subjects were selected to have low, medium, and large WMH loads.

ADNI:

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD).

III). ADNI1:

This dataset consists of T1w, T2w, and PD scans of 53 subjects from ADNI1 study. Despite the fact that all subjects had to have Hachinski Ischemic Score of less than or equal to 4 as part of the inclusion criteria (Petersen et al., 2010), we found many subjects that had high WMH loads. Subjects were selected from different sites and scanners and a preliminary assessment was performed to evaluate their WMH load with the goal of acquiring subjects with different scanner information as well as different loads of WMHs. For each scanner model, we selected datasets that had low, medium and high lesion loads. Approximately equal number of male and female subjects were selected. The age of the subjects was also considered for the selection, with the aim of achieving a normal distribution.

IV). ADNI2/GO:

This dataset consists of T1w and FLAIR scans of 46 subjects from ADNI2/GO studies. Subject selection criteria were the same as ADNI1.

2.2. MR imaging

Table 2 summarizes the scanner information as well as the MR imaging parameters for each of the datasets.

Table 2 -.

Scanner information and MRI acquisition parameters for ADC, NACC, ADNI1, and ADNI2/GO datasets.

Modality	Dataset	ADC	NACC	ADNI1	ADNI2/GO
	Scanner Manufacturer	GE MS Philips MS	GE MS	GE MS Philips MS SIEMENS	Philips MS SIEMENS
T1w	Slice	1.5 mm	1.5 mm	1.2 mm	1.2 mm
	No. of slices	128	124	160	196
	Field of view	250×250 cm2	256×256 cm2	192×192 cm2	256×256 cm2
	Scan Matrix	256×256 cm2	256×256 cm2	192×192 cm2	256×256 cm2
	Repetition	9 ms	9 ms	3000 ms	7.2 ms
	Echo time	2.9 ms	1.8 ms	3.55 ms	3.0 ms
	Pulse	FSPGR	FSPGR	MPRAGE	GR
Other	Contrast	FLAIR	FLAIR	T2w/PD	FLAIR
	Slice	3 mm	3 mm	3 mm	5 mm
	No. of slices	48	48	56	42
	Field of view	220×220 cm2	256×256 cm2	256×256 cm2	256×256 cm2
	Scan Matrix	256×192 cm2	256×256 cm2	256×256 cm2	256×256 cm2
	Repetition	11000 ms	11002 ms	3000/3000 ms	11000 ms
	Echo time	144 ms	147 ms	95.2/10.5 ms	150 ms
	Pulse	FSE	Obl	FSE	SE/IR

2.3. Manual segmentation

In ADC, NACC, and ADNI2/GO datasets, the WMHs were manually segmented by experts with FLAIR used as the primary contrast and the other image contrasts used to aid in the decision process to include or exclude a voxel from the lesion mask. For the ADNI1 dataset, T2w was used as the primary contrast. All WMH masks were created fully manually, without using any thresholding technique. ADC, ADNI1 and ADNI2/GO datasets were scored by JM, an MD with training in general radiology, and specialized in MRI imaging methods of quantifying WM pathologies in MS and AD. JM has more than 12 years of experience in reading MRI and developing standardized MRI guidelines to detect WM lesions using different image modalities (Maranzano et al., 2016). The lesions were fully manually traced using the interactive software package Display, part of the MINC Tool Kit (https://github.com/BIC-MNI) developed at the McConnell Brain Imaging Center of the Montreal Neurological Institute. The program allows simultaneous viewing and segmentation in the coronal, sagittal and axial planes, and cycling between each image volume. The image volumes were co-registered so that, when assessing a given voxel or region and switching from one contrast to another (e.g. T1w to FLAIR), the rater can assess the intensity signal of the same region of the brain on each contrast. In the NACC dataset, images were similarly segmented by two raters that had previously received training to segment WMHs, and ascertained by an expert neurologist. The between rater agreement was verified (Dice Kappa=0.70). All the manual raters were also asked to segment 3 scans with low (<5cm³), medium (5–20 cm³), and high (>20 cm³) WMH loads a second time without consulting the initial segmentations. Table 3 shows the intra-rater Dice Kappa obtained from these segmentations as well as WMH volume information for each dataset. Figure 1 shows examples of the available contrasts as well as the manual labels for each dataset.

Table 3 -.

Intra-rater mean Dice Kappa, range of WMHLs, and number (N) of subjects with low (<5cm³), medium (5–20cm³), and high (>20cm³) WMHLs for manual segmentations of WMHs in different datasets. WMHL= White Matter Hyperintensity Load.

Dataset	ADC	NACC	ADNI1	ADNI2/GO
Dice Kappa	0.72	0.78	0.80	0.86
WMHL Range (cm3)	0.2–148.6	0.2–109.0	0.0–119.3	0.2–63.0
NWMHL<5cm3	36	6	14	16
N5cm3<WMHL<20cm3	23	11	10	11
NWMHL<20cm3	11	12	27	18

Fig. 1 -.

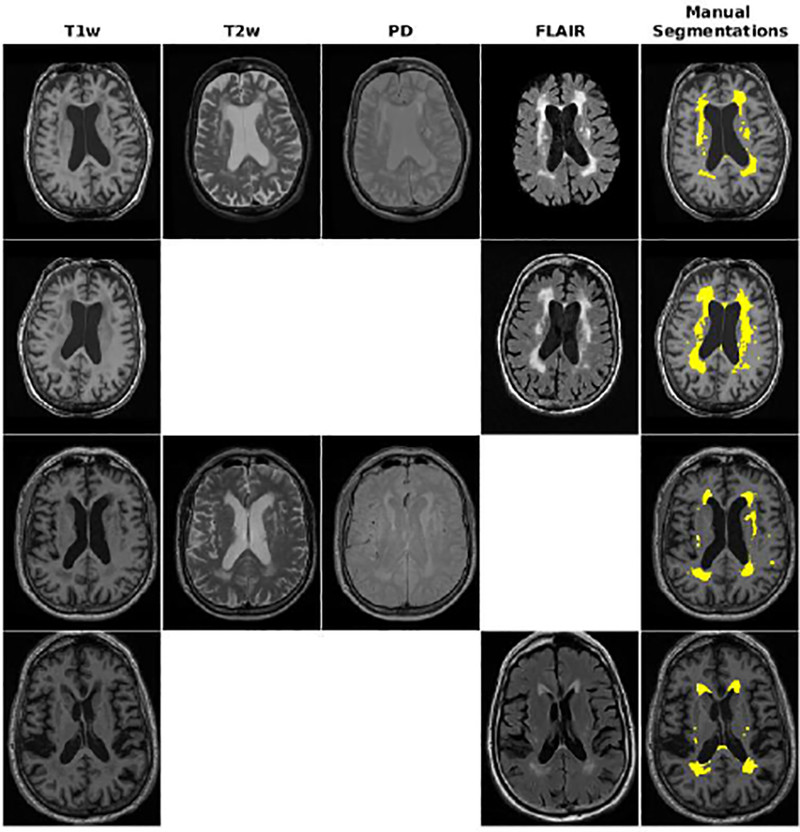
Axial slices comparing manual segmentations and T1w, T2w, PD, and FLAIR information for subjects from ADC, NACC, ADNI1, and ADNI2 datasets. Yellow color indicates regions labeled as WMH in manual segmentations.

2.4. Pre-processing

All the images were preprocessed using our standard pipeline from MINC toolkit, publicly available at https://github.com/BIC-MNI/minc-tools (Aubert-Broche et al., 2013) through three steps: I) Image noise reduction using mincnlm tool (Coupe et al., 2008), II) Correction of image intensity non-uniformity using nu_estimate tool (Sled et al., 1998) and III) Normalization of image intensity into range (0–100) using an intensity histogram matching algorithm (volume_pol tool). The T1w, T2w, PD, and FLAIR images were linearly co-registered using a 6 parameter rigid registration (Collins et al., 1994). The T1w images were linearly and then nonlinearly registered to an average template (Collins and Evans, 1997) created based on data from the ADNI1 study (Fonov et al., 2011a) (Fonov et al., 2011b), enabling the use of anatomical priors in the segmentation process. Brain extraction was performed on the linearly registered T1w images as part of the standard pipeline (Aubert-Broche et al., 2013).

2.5. Features

The classical features that are most commonly used in lesion segmentation tasks are the intensity of the voxel in each MRI contrast (García-Lorenzo et al., 2013). Here, these classical features as well as a variety of intensity and spatial features were used to train the classifiers. These features have been previously validated and verified to be informative in detecting WMHs. The rationale behind the selection of the suggested feature set as well as the contribution of each of the features has been described in more detail in an earlier work (Dadar et al., 2017).

1. Voxel intensity from T1w, T2w, PD, and FLAIR images

2. Average voxel intensity of non-WMH tissue from T1w, T2w, PD, and FLAIR images for the specific voxel location obtained from averaging non-WMH voxels of the training subjects in stereotaxic space. Since datasets were selected to include subjects with very small WMH loads, there were at least several subjects in each training set that had no WMHs in each specific voxel location. The average intensity of non-WMH tissue feature was calculated using data from these subjects.

3. Probability of voxel being a lesion (PWMH) obtained by creating a probability distribution function (PDF) based on the intensity histogram of the WMH labels from manually segmented training data across all WMH voxels

4. Probability of voxel being healthy tissue (PH) obtained by creating a PDF of Non-WMH voxels from manually segmented training data across all non-WMH voxels

5. Ratio of P_H / P_WMH

6. Spatial WMH probability map created by averaging the WMH maps from the training dataset

7. Ratio of T2w/T1w, PD/T1w, FLAIR/T1w

The WMH segmentations were performed in the native space of the primary image contrast, i.e. T2w for ADNI1 and FLAIR for ADC, NACC, and ADNI2/GO datasets to avoid the blurring caused by resampling of the primary image contrast. To achieve this, all images were nonlinearly transformed to the ADNI template space, and all the priors and averages were calculated in this stereotaxic space and then registered back and resampled in the native space using the inverse nonlinear transformations. The final segmentations were performed using the features in the native space of the image with optimal contrast. Therefore, the image with optimal contrast is not resampled, and only a 6-parameter rigid transformation is applied to the other co-registered contrasts (as opposed to other techniques where the nonlinearly registered images are used for segmentation). Figure 2 illustrates a flow-chart of the preprocessing, registration, and feature selection steps of the pipeline.

Fig. 2.

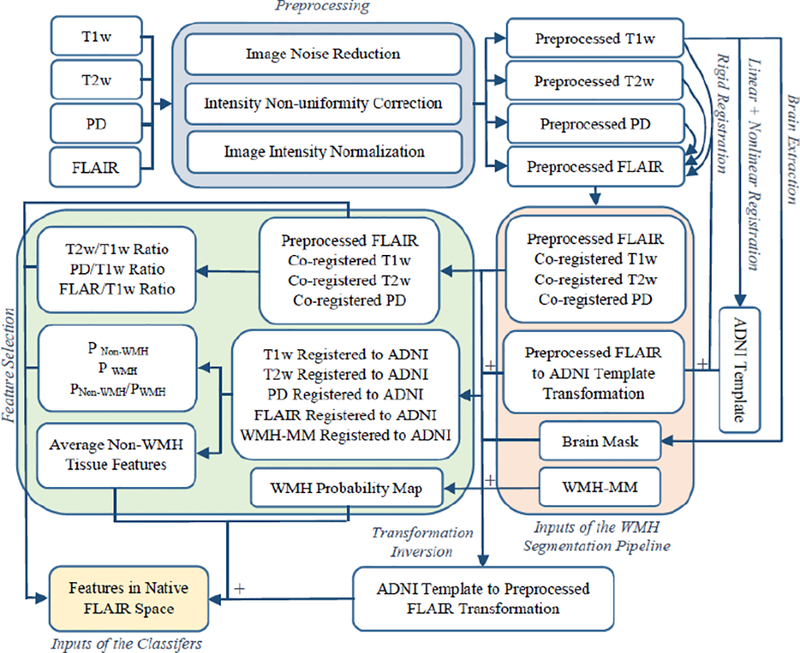
Flow-chart of the preprocessing, registration, and feature selections steps. WMH-MM= White Matter Hyperintensity Manual Mask.

2.6. Classification Methods

In a binary classification setting, a classifier is a function that maps a set of input feature vectors x = (x₁,x₂, …,x_n)^T from feature space X to an output class label set y in Y = {0,1}. Here, we select and compare supervised methods as unsupervised techniques have been shown to be less robust, dependent on initialization, and do not necessarily arrive at meaningful segmentations (Clarke et al., 1995). Specifically for the task of WMH segmentation, supervised methods generally outperform unsupervised techniques (Anbeek et al., 2004; Caligiuri et al., 2015).

2.6.1. Naive Bayes

Naïve Bayes classifiers are a family of probabilistic classifiers that have been used for many simple classification tasks (Lewis, 1998). Naïve Bayes is a probabilistic classifier that returns the label that maximizes the posterior probability p(y|x) as the output, with the underlying assumption that given the class label, all the features are conditionally independent $arg ma{x}_{y}p(y|x)=arg ma{x}_y\frac{p(y){\Pi }_{i=1}^{n}p\left(x_i|y\right)}{p(x)}=arg ma{x}_{y}p(y){\Pi }_{i=1}^{n}p\left(x_i|y\right)$ Naïve Bayes classifiers have previously been used to segment diabetic retinopathy lesions (Köse et al., 2012).

2.6.2. Discriminant Analysis

Linear and Quadratic Discriminant Analysis methods (LDA and QDA) are generalizations of Fisher’s linear discriminant method that can be used for performing classification (Fisher, 1936) (McLachlan, 2004). Using the assumption that the conditional probability density functions of the classes are normally distributed with identical covariance, i.e.

$$p(x|y=k)=\frac{1}{{(2\pi )}^n|\Sigma {|}^{1/2}}exp\left(-1/2{\left(x-{\mu }_k\right)}^t{\Sigma }^{-1}\left(x-{\mu }_k\right)\right)kϵ\{0,1\}$$

LDA predicts input vector x as belonging to a class y based on the log likelihood ratio $ln\frac{p(y=1|x)}{p(y=0|x)}$. QDA is similar to LDA, without the identical covariance assumption.

$$p(x|y=k)=\frac{1}{{(2\pi )}^n{\left|{\Sigma }_k\right|}^{1/2}}exp\left(-1/2{\left(x-{\mu }_k\right)}^t{\Sigma }_k^{-1}\left(x-{\mu }_k\right)\right)kϵ\{0,1\}$$

Amato et al. proposed a non-parametric discriminant analysis technique for segmenting MS lesions (Amato et al., 2003). Akselrod-Ballin et al. have used LDA technique along with Random Forests to segment MS lesions (Akselrod-Ballin et al., 2009).

2.6.3. Logistic Regression

The idea of logistic regression was introduced by Cox with the purpose of estimating a binary response based on a set of independent features (Cox, 1958). The Logistic regression classifier models p(y|x) as a logistic function $h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$ and estimates the error using a cumulative logistic distribution function.

$$E(\theta )=\frac{1}{m}\sum _{i=1}^m\left(-y^i\text{log}\left(h_{\theta }\left(x^i\right)\right)-\left(1-y^i\right)\text{log}\left(1-h_{\theta }\left(x^i\right)\right)\right)$$

Sánchez et al. used a logistic regression classifier for automatic detection of micro-aneurysms in retinal images (Sánchez et al., 2009).

2.6.4. Decision Trees

The idea of performing induction using decision trees was first proposed by Hunt et al. (Hunt et al., 1966) and later developed by Quinlan for classification tasks (Quinlan, 1986). Decision tree classifiers map the feature vector x to conclusions about the target value y using a tree structure in which the leaves represent class labels y and the nodes represent partitionings of feature x that lead to these class labels. The decision tree is generally constructed in 2 phases: 1) A recursive, top-down procedure “grows” a tree to fit the training data. 2) A “pruning” phase to avoid overfitting. Decision tree classifiers have since been used for tissue classification (Chao et al., 2009) and lesion segmentation in Multiple Sclerosis (MS) (Kamber et al., 1992) (Kamber et al., 1995).

2.6.5. Random forests

Initially introduced by Breiman (Breiman, 2001), Random decision forests perform classification and regression by constructing a multitude of independent decision trees and using the mode or mean of their predictions as the final output for classification or regression tasks, respectively. They have since been widely used for lesion segmentation in MS (Geremia et al., 2011) (Maier et al., 2015) (Mitra et al., 2014) (Akselrod-Ballin et al., 2009) as well as for WMH segmentation in aging and AD populations (Ithapu et al., 2014).

2.6.6. K-nearest neighbors

The K-nearest neighbours (KNN) is a non-parametric instance based algorithm developed by Altman for classification and regression (Altman, 1992). The KNN classifier uses majority voting between the labels for the K closest data points in the feature space in the training data to assign a label to the new unseen test data. The distance metric used for determining the closest data points is generally the Euclidian distance for continuous variables or Hamming distance for discrete variables. Due to its simplicity, it has been popular for various applications including segmentation of MS lesions (Wu et al., 2006b) and WMHs (Anbeek et al., 2004).

2.6.7. Support Vector Machines

The idea of performing nonlinear classification using support vector machines (SVMs) was introduced by Boser et al. (Boser et al., 1992). SVMs perform classification by finding a maximum-margin hyperplane that separates the two classes while maximizing the distance between the nearest point from either class. SVMs have been widely used for lesion segmentation tasks in MS populations (Ferrari et al., 2003) (Abdullah et al., 2011) as well as for WMH segmentation in aging and AD populations (Ithapu et al., 2014) (Quddus et al., 2005).

2.6.8. Bagging

Bootstrap aggregating, also called bagging, is a model averaging technique initially introduced by Brieman et al. with the purpose of improving stability and reducing variance (Breiman, 1996). Bagging is an ensemble method that builds multiple classifiers such as decision trees by uniformly sampling the training data with replacement, and voting, to output a consensus prediction. Madabhushi used bagging for detecting prostatic adenocarcinoma from high resolution MR images (Madabhushi et al., 2006).

2.6.9. AdaBoost

Adaptive Boosting or AdaBoost was developed by Freund and Schapire (Freund et al., 1999). AdaBoost performs classification by aggregating the outputs of other learning algorithms (also called weak learners) into a weighted sum that represents the final output of the boosted classifier. The subsequent weak learners are tweaked in favor of the instances that were misclassified by previous classifiers to improve classification accuracy. It has been used for MS lesion segmentation (Wels et al., 2008), interactive lesions segmentation (Li et al., 2007), as well as segmentation of WMHs (Quddus et al., 2005) (Ghafoorian et al., 2016a).

For all classification tasks, the Scikit-learn Python library implementations were used (Pedregosa et al., 2011). For Naïve Bayes, LDA, QDA, SVM, and Decision Tree classifiers, the default settings were used. For KNN, 10 neighbours were used. For Bagging, KNN classifiers were used with the default parameters. For AdaBoost and Random Forests classifiers, 100 estimators were used. Ten-fold cross validation across subjects was used to train and validate the performance of the classifiers; i.e. no voxels from subjects used for validation were used in training and feature selection stages. It is worthwhile noting that the spatial WMH probability maps, average intensities, and PWMH and PH were also calculated through the cross-validation to avoid any overfitting (no data used in testing was used to generate the priors). All the segmentations were performed in the native space for the optimal primary modality to avoid resampling and further blurring of the lesion borders. To achieve this, all the priors and averages were first calculated in the stereotaxic template space and then registered back and recalculated in the native space using the inverse nonlinear transformations.

2.7. Evaluation metrics

There is no single similarity measure that can perfectly reflect the level of agreement between WMH segmentation maps. While Dice Kappa similarity measure (Dice, 1945) is the most commonly used, the Kappa values are highly dependent on the WMH loads and lesion sizes. To address this, the mean Dice Kappa values are generally reported for different ranges of WMH loads, i.e. small (<5 cm³), medium (5–20 cm³), and large (>20 cm³) separately (Admiraal-Behloul et al., 2005; Griffanti et al., 2016; Schmidt et al., 2012; Simões et al., 2013; Steenwijk et al., 2013; Dadar et al., 2017). In this study, while Dice Kappa was used as the primary similarity measure for validation of the classifiers, other similarity measures such as the intra-class correlation coefficient (ICC) for the total WMH loads to measure the volumetric correspondence between the manual and automatic segmentations (Koch, 1982), true positive rate (TPR), positive prediction value (PPV), outline error rate (OER) measuring agreement of the raters in outlining of the same lesion (Wack et al., 2012), and detection error rate (DER) measuring agreement in detecting the same regions (Wack et al., 2012) are reported to facilitate comparison with previously published papers. Table 4 shows the list of these metrics along with their definitions.

Table 4 -.

List of similarity measures and their definitions. The metrics are listed in the table below using the following abbreviations: true positive (TP), true negative (TN), false positive (FP), false negative (FN), true positive rate (TPR), Mean Square Within samples based upon the anova (MSW), Mean Square F Statistic Regression Slope (MSR). CR₁, CR₂, and C₁₂ represent region from only rater 1, region from only rater 2, and the combination of both raters, respectively. |cr| represents area of the connected region, cr ϵ CR₁ or CR₂ represents the set of connected regions that can be labeled either as CR₁ or CR₂. |R₁(cr)|, |R2(cr)| represent the areas of rater 1 and rater 2 regions within cr, respectively (Wack et al., 2012).

Name	Dice Kappa	Intra-class correlation	Sensitivity	Outline Error Rate	Detection Error Rate
Abbreviation	SI	ICC	TPR	OER	DER
Equation	$\frac{2\times TP}{FP+FN+2\times TP}$	$\frac{MSR-MSW}{MSR+MSW}$	$\frac{TP}{TP+FN}$	$\sum _{cr\in C_{12}}|cr|-\left|R_1(cr)\cap R_2(cr)\right|$	$\sum _{cr\in C{R}_{1}orC{R}_2}|cr|$

3. Results

3.1. Segmentation using T1w, T2w, PD, and FLAIR

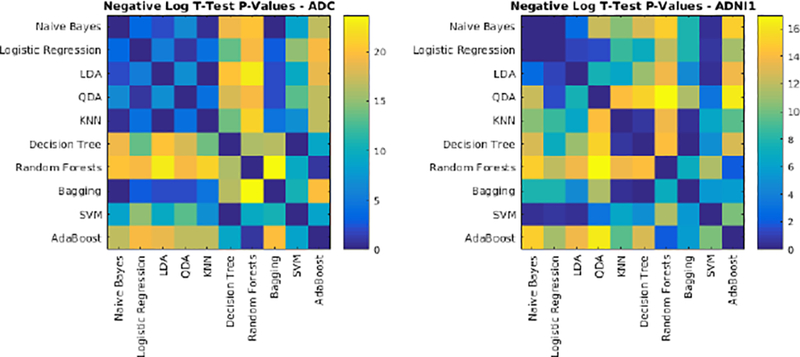
The performance of each classifier was validated through 10-fold cross validation using T1w, T2w, PD, and FLAIR images for the ADC dataset. All voxels within a brain mask that contained the cerebrum, cerebellum and brain stem were classified. Table 5 shows the average Dice Kappa, detection/outline error rates (DER/OER), ICC, TPR, and PPV values for different classifiers. Figure 3 shows boxplot diagrams for the same results separately for subjects with small, medium and large WMH loads. Figure 4 shows the manual and automatic segmentation results of different classifiers on axial slices of one subject. To assess the statistical significance of the results, paired t-tests were performed on the Dice Kappa values of all pairs of classifier comparisons, and p-values were corrected for multiple comparisons using false discovery rate (FDR). Figure 5 shows the negative logarithm of the FDR corrected p-values.

Table 5 -.

Comparison between mean Dice Kappa, detection/outline error rate (DER/OER), intra-class correlation (ICC), true positive rate (TPR), and positive prediction value (PPV) values of different classifiers for segmentation of WMHs using T1w, T2w, PD and FLAIR data in the ADC dataset. Blue color indicates the best performance in terms of SI.

Dataset	SI	DER	OER	ICC	TPR	PPV
Naïve Bayes	0.32±0.27	0.53±0.34	0.82±0.21	0.27	0.23	0.96
Logistic Regression	0.57±0.22	0.32±0.36	0.54±0.14	0.97	0.65	0.57
LDA	0.56±0.23	0.41±0.38	0.46±0.20	0.88	0.48	0.83
QDA	0.36±0.26	0.55±0.36	0.74±0.17	0.44	0.26	0.96
KNN	0.66±0.17	0.18±0.18	0.52±0.18	0.99	0.73	0.65
Decision Trees	0.57±0.18	0.27±0.28	0.58±0.18	0.96	0.58	0.62
Random Forests	0.66±0.17	0.16±0.15	0.53±0.19	0.99	0.73	0.64
Bagging	0.63±0.19	0.21±0.26	0.57±0.03	0.99	0.75	0.58
SVM	0.57±0.24	0.32±0.42	0.54±0.11	0.98	0.66	0.60
AdaBoost	0.63±0.20	0.21±0.24	0.53±0.10	0.98	0.70	0.65

Fig. 3-.

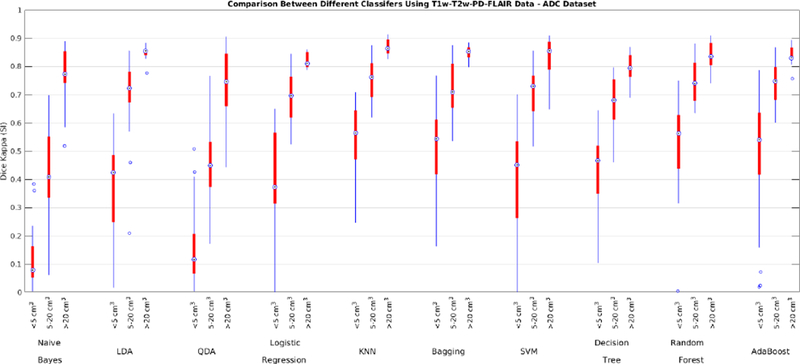
Dice Kappa (SI) for different classification methods for (<5 cm³, left), medium (5–20 cm³, middle), and high (>20 cm³, right) WMH load using T1w, T2w, PD, and FLAIR information for the ADC dataset.

Fig. 4-.

Axial slices comparing manual and automatic segmentations using T1w, T2w, PD, and FLAIR information for a subject from ADC dataset. Yellow color indicates regions labeled as WMH in both manual and automatic segmentations, blue color indicates regions only segmented by the automatic technique, and red color indicates regions only segmented by the manual rater.

Fig. 5-.

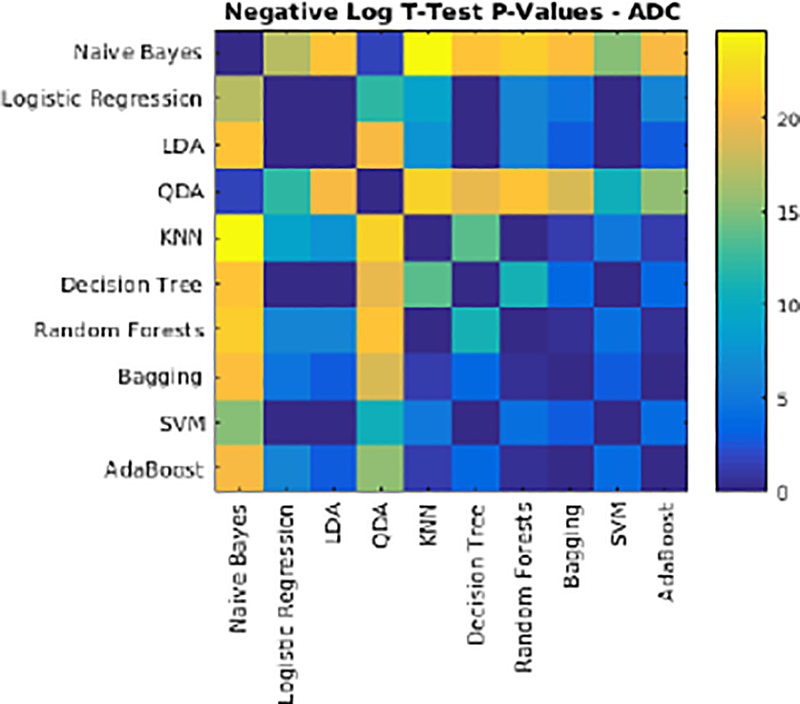
Negative logarithm of FDR corrected p-values of paired t-tests between Dice Kappa values of classifier pairs. Values higher than 1.3 are statistically significant.

3.2. Segmentation using T1w and FLAIR data

The performance of each classifier was validated through 10-fold cross validation using T1w and FLAIR images for the ADC, NACC, and ADNI2/GO datasets (recall that ADNI1 does not have FLAIR data). Table 6 shows the average Dice Kappa and detection/outline error rate (DER/OER) values for different classifiers. Table 7 shows corresponding ICC, TPR, and PPV values. Figure 6 shows boxplot diagrams for the same results separately for subjects with small, medium and large WMH loads. Figure 7 shows the manual and automatic segmentation results of different classifiers on axial slices of one subject. Figure 8 shows the negative logarithm of the FDR corrected p-values of t-tests on Dice Kappa values of different classifier pairs. To assess the contribution of T2+PD features in the performance of different classifiers, paired t-tests were performed between the Dice Kappa values of the segmentations based on T1+T2+PD+FLAIR and T1+FLAIR in the ADC dataset. The “*” in Table 7 indicates the significant differences between the two segmentations, after correction for multiple comparisons using FDR. The performance of Naïve Bayes, QDA, and Bagging has significantly dropped without using FLAIR information.

Table 6 -.

Comparison between mean Dice Kappa and detection/outline error rate (DER/OER) values of different classifiers for segmentation of WMHs using T1w and FLAIR data in the ADC, NACC, and ADNI2/GO datasets. Blue color indicates the best performance in terms of SI.

Dataset	ADC			NACC			ADNI2/GO
Measure	SI	DER	OER	SI	DER	OER	SI	DER	OER
Naïve Bayes	0.42±0.25*	0.34±0.27	0.82±0.30	0.50±0.21	0.43±0.26	0.74±0.34	0.50±0.29	0.43±0.30	0.73±0.39
Logistic	0.56±0.18	0.27±0.24	0.61±0.19	0.65±0.13	0.27±0.39	0.55±0.23	0.64±0.20	0.30±0.40	0.53±0.25
LDA	0.58±0.19	0.35±0.33	0.49±0.17	0.69±0.13	0.21±0.26	0.57±0.36	0.60±0.23	0.21±0.27	0.66±0.41
QDA	0.42±0.23*	0.44±0.32	0.73±0.22	0.54±0.21	0.48±0.32	0.62±0.27	0.51±0.29	0.48±0.34	0.64±0.33
KNN	0.65±0.16	0.18±0.18	0.51±0.18	0.71±0.13	0.15±0.17	0.50±0.23	0.72±0.18	0.17±0.20	0.48±0.24
Decision Trees	0.58±0.16	0.25±0.25	0.58±0.14	0.65±0.12	0.23±0.25	0.55±0.18	0.65±0.22	0.25±0.28	0.54±0.21
Random Forests	0.66±0.14	0.18±0.18	0.50±0.16	0.72±0.10	0.14±0.16	0.48±0.20	0.72±0.19	0.15±0.18	0.47±0.23
Bagging	0.14±0.16*	0.27±0.28	0.63±0.27	0.69±0.13	0.19±0.31	0.53±0.25	0.69±0.17	0.21±0.33	0.51±0.26
SVM	0.56±0.24	0.31±0.37	0.56±0.26	0.67±0.13	0.22±0.37	0.53±0.25	0.68±0.22	0.26±0.40	0.48±0.28
AdaBoost	0.65±0.15	0.18±0.18	0.50±0.17	0.72±0.11	0.16±0.22	0.49±0.23	0.71±0.20	0.18±0.25	0.49±0.27

Table 7 -.

Comparison between intra-class correlation (ICC), true positive rate (TPR), and positive prediction value (PPV) values of different classifiers for segmentation of WMHs in different datasets using T1w and FLAIR data for ADC, NACC, and ADNI2/GO datasets. Blue color indicates the best performance in terms of SI.

Dataset	ADC			NACC			ADNI2/GO
Measure	ICC	TPR	PPV	ICC	TPR	PPV	ICC	TPR	PPV
Naïve Bayes	0.81	0.31	0.93	0.45	0.38	0.89	0.54	0.41	0.91
Logistic Regression	0.98	0.73	0.48	0.85	0.78	0.59	0.86	0.70	0.70
LDA	0.98	0.56	0.65	0.92	0.78	0.63	0.80	0.63	0.71
QDA	0.77	0.30	0.94	0.53	0.42	0.91	0.57	0.41	0.95
KNN	0.99	0.76	0.60	0.94	0.80	0.69	0.96	0.74	0.78
Decision Trees	0.99	0.62	0.58	0.94	0.67	0.69	0.96	0.65	0.76
Random Forests	0.99	0.62	0.58	0.93	0.79	0.71	0.96	0.72	0.80
Bagging	0.16	0.63	0.09	0.89	0.83	0.63	0.91	0.76	0.70
SVM	0.95	0.70	0.56	0.90	0.83	0.60	0.95	0.67	0.79
AdaBoost	0.99	0.73	0.63	0.94	0.78	0.72	0.96	0.71	0.81

Fig. 6-.

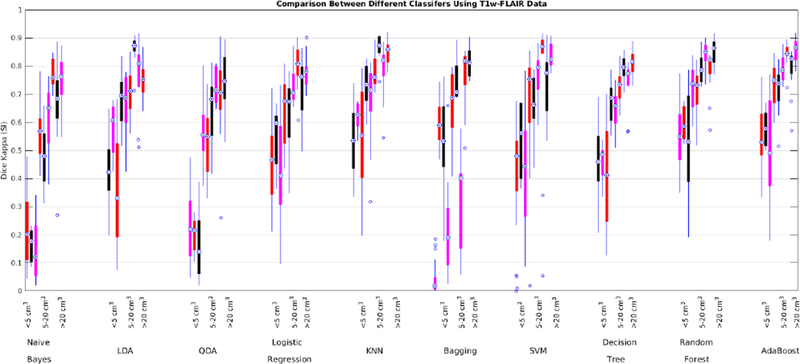
Dice Kappa (SI) for different classification methods for low (<5 cm³, left), medium (5–20 cm³, middle), and high (>20 cm³, right) WMH load using T1w and FLAIR information for ADC (red), NACC (black), and ADNI2/GO (magenta) datasets.

Fig. 7 -.

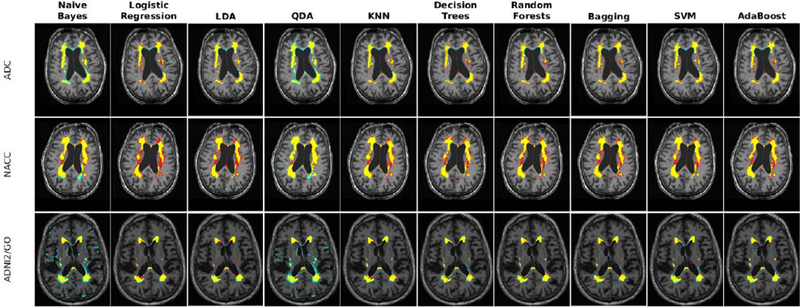
Axial slices comparing manual and automatic segmentations using T1w and FLAIR information in one subject from each of ADC, NACC, and ADNI2/GO datasets. Yellow color indicates regions labeled as WMH in both segmentations, blue color indicates regions only segmented by the automatic technique, and red color indicates regions only segmented by the manual rater.

Fig. 8-.

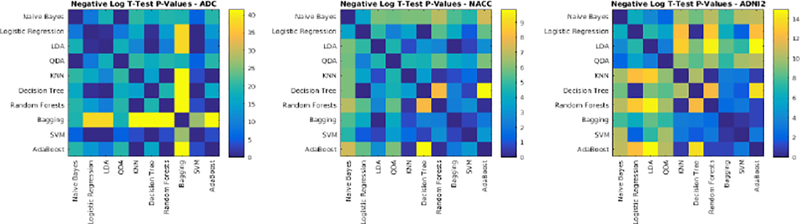
Negative logarithm of FDR corrected p-values of paired t-tests between Dice Kappa values of classifier pairs. Values higher than 1.3 are statistically significant.

3.3. Segmentation using T1w, T2w, and PD data

While FLAIR scans have the optimal contrast for differentiating WMHs from normal appearing white matter (Barkhof and Scheltens, 2002; Alexander et al., 1996; Bakshi et al., 2001), many studies forgo acquisition of FLAIR images in favour of other modalities. In order to take advantage of large studies such as ADNI1 that do not have FLAIR, segmentation methods that can provide accurate segmentation results without using the optimal FLAIR contrast are highly advantageous. A relatively easier task (in comparison to using FLAIR) is to segment WMHs from T1w, T2w, and PD or T1w, and T2w images. While segmenting WMHs solely from T1w images with high accuracy proves to be extremely difficult, being able to obtain an estimate of the WMH load that is significantly correlated with the actual loads can still be useful.

To address the first challenge, we trained and validated the performance of the classifiers using the features obtained from T1w, T2w, and PD images from the ADC and ADNI1 datasets. Table 8 shows the mean Dice Kappa, detection/outline error rates (DER/OER), and the corresponding ICC, TPR, and PPV values for each classifier and dataset, respectively. Figure 9 shows the corresponding boxplot diagrams for these results separately for subjects with small, medium and large WMH loads. Figure 10 shows the segmentation results on the axial slices for different classifiers and datasets. Figure 11 shows the negative logarithm of the FDR corrected p-values of t-tests on Dice Kappa values of different classifier pairs. To assess the contribution of FLAIR features in the performance of different classifiers, paired t-tests were performed between the Dice Kappa values of the segmentations based on T1+T2+PD+FLAIR and T1+T2+PD in the ADC dataset. The “*” symbol in Table 8 indicates the significant differences between the two segmentations, after correction for multiple comparisons using FDR. The performance of all classifiers has significantly dropped without using FLAIR information.

Table 8 -.

Comparison between mean Dice Kappa (SI), detection/outline error rate (DER/OER), intra-class correlation (ICC), true positive rate (TPR), and positive prediction value (PPV) values of different classifiers for segmentation of WMHs using T1w, T2w, and PD data, ADC and ADNI1 datasets. Blue color indicates the best performance in terms of SI.

Dataset	ADC						ADNI1
Measure	SI	DER	OER	ICC	TPR	PPV	SI	DER	OER	ICC	TPR	PPV
Naïve Bayes	0.17±0.17*	0.88±0.39	0.77±0.32	0.10	0.11	0.84	0.34±0.22	0.68±0.33	0.67±0.35	0.09	0.24	0.89
Logistic	0.09±0.14*	1.26±0.73	0.55±0.55	0.46	0.24	0.06	0.44±0.23	0.40±0.48	0.68±0.33	0.68	0.65	0.39
LDA	0.28±0.21*	0.08±0.05	1.35±0.42	0.45	0.24	0.66	0.48±0.28	0.17±0.34	0.82±0.53	0.62	0.46	0.73
QDA	0.13±0.13*	0.63±0.38	1.11±0.37	0.08	0.08	0.90	0.31±0.21	0.63±0.35	0.72±0.29	0.12	0.20	0.93
KNN	0.28±0.24*	0.77±0.68	0.66±0.34	0.69	0.44	0.22	0.59±0.23	0.25±0.33	0.56±0.27	0.74	0.67	0.58
Decision	0.38±0.20*	0.55±0.47	0.69±0.19	0.93	0.38	0.44	0.57±0.25	0.29±0.37	0.57±0.23	0.94	0.57	0.67
Random	0.47±0.21*	0.36±0.34	0.69±0.21	0.95	0.60	0.42	0.66±0.23	0.18±0.29	0.50±0.26	0.94	0.67	0.71
Bagging	0.17±0.18*	0.88±0.70	0.77±0.46	0.37	0.51	0.11	0.54±0.22	0.24±0.38	0.67±0.33	0.59	0.75	0.47
SVM	0.31±0.21*	0.62±0.54	0.76±0.31	0.65	0.48	0.31	0.61±0.24	0.25±0.43	0.56±0.34	0.83	0.62	0.70
AdaBoost	0.44±0.21*	0.43±0.47	0.69±0.21	0.93	0.53	0.42	0.64±0.24	0.20±0.33	0.55±0.32	0.94	0.66	0.73

Fig. 9-.

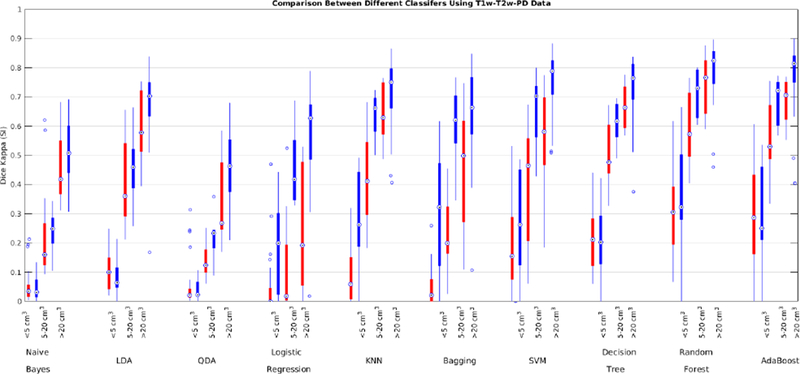
Dice Kappa (SI) for different classification methods for low (<5 cm³, left), medium (5–20 cm³, middle), and high (>20 cm³, right) WMH load using T1w, T2w, and PD information for ADC (red) and ADNI1 (blue) datasets.

Fig. 10 -.

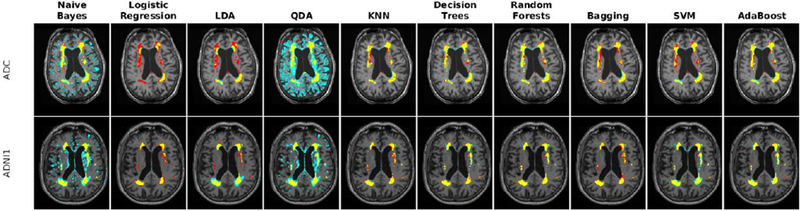
Axial slice comparing manual and automatic segmentations using T1w, T2w, and PD information for a subject from each of ADC and ADNI1 datasets. Yellow color indicates regions labeled as WMH in both segmentations, blue color indicates regions only segmented by the automatic technique, and red color indicates regions only segmented by the manual rater.

Fig. 11-.

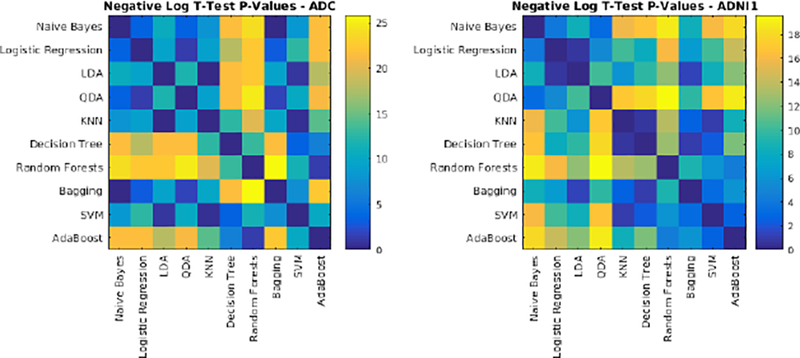
Negative logarithm of FDR corrected p-values of paired t-tests between Dice Kappa values of classifier pairs. Values higher than 1.3 are statistically significant.

3.4. Segmentation using T1w, and T2w data

Many studies forgo acquisition of PD images in favour of acquiring a higher resolution T2w image. Here we assess the performance of the classifiers without using PD images. Table 9 shows the mean Dice Kappa and detection/outline error rates (DER/OER), and the corresponding ICC, TPR, and PPV values for each classifier and dataset, respectively. Figure 12 shows the corresponding boxplot diagrams for these results separately for subjects with small, medium and large WMH loads. Figure 13 shows the segmentation results on the axial slices for different classifiers and datasets. Figure 14 shows the negative logarithm of the FDR corrected p-values of t-tests on Dice Kappa values of different classifier pairs. To assess the contribution of PD feature in the performance of different classifiers, paired t-tests were performed between the Dice Kappa values of the segmentations based on T1+T2+PD and T1+T2 in ADC, and ADNI1 datasets. The “*” symbols in Table 7 indicate the significant differences between the two segmentations, after correction for multiple comparisons using FDR. No classifier has performed significantly worse after removing PD features for either dataset.

Table 9 -.

Comparison between mean Dice Kappa (SI), detection/outline error rate (DER/OER), intra-class correlation (ICC), true positive rate (TPR), and positive prediction value (PPV) values of different classifiers for segmentation of WMHs using T1w, and T2w data – ADC and ADNI1 datasets. Blue color indicates the best performance in terms of SI.

Dataset	ADC						ADNI1
Measure	SI	DER	OER	ICC	TPR	PPV	SI	DER	OER	ICC	TPR	PPV
Naïve Bayes	0.25±0.22	0.59±0.37	0.68±0.41	0.37	0.18	0.79	0.43±0.26	0.52±0.30	0.24±0.21	0.51	0.33	0.87
Logistic	0.16±0.16	0.62±0.70	0.71±0.47	0.43	0.42	0.12	0.42±0.25	0.39±0.50	0.11±0.14	0.79	0.66	0.35
LDA	0.28±0.21	0.08±0.23	1.08±0.55	0.46	0.24	0.66	0.48±0.28	0.17±0.34	0.25±0.20	0.61	0.46	0.72
QDA	0.20±0.18	0.61±0.32	0.80±0.38	0.23	0.13	0.86	0.36±0.23	0.61±0.35	0.20±0.17	0.28	0.25	0.92
KNN	0.27±0.24	0.46±0.59	0.54±0.25	0.83	0.44	0.21	0.58±0.23	0.27±0.37	0.28±0.18	0.90	0.67	0.55
Decision	0.37±0.21	0.38±0.45	0.59±0.22	0.93	0.38	0.43	0.57±0.25	0.29±0.27	0.24±0.18	0.94	0.57	0.66
Random	0.45±0.22	0.25±0.37	0.55±0.27	0.93	0.56	0.41	0.65±0.23	0.19±0.29	0.34±0.19	0.95	0.67	0.70
Bagging	0.24±0.22	0.49±0.65	0.60±0.34	0.68	0.55	0.17	0.57±0.24	0.27±0.42	0.03±0.03	0.86	0.73	0.52
SVM	0.37±0.18	0.47±0.51	0.71±0.35	0.58	0.48	0.48	0.46±0.23	0.38±0.47	0.16±0.11	0.23	0.54	0.62
AdaBoost	0.44±0.21	0.29±0.47	0.57±0.31	0.92	0.53	0.42	0.64±0.25	0.21±0.34	0.26±0.10	0.95	0.66	0.72

Fig. 12 -.

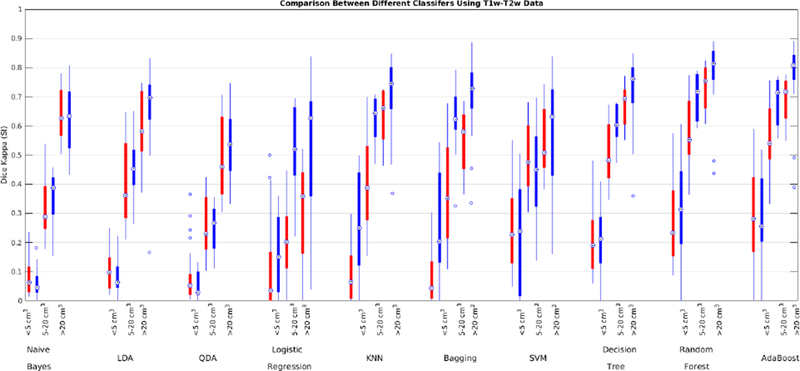
Dice Kappa (SI) for different classification methods for low (<5 cm³, left), medium (5–20 cm³, middle), and high (>20 cm³, right) WMH load using T1w and T2w information for ADC (red) and ADNI1 (blue) datasets.

Fig. 13-.

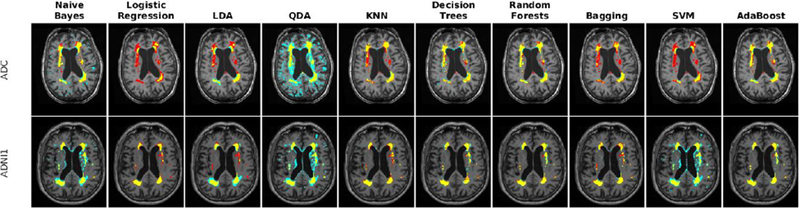
Axial slice comparing manual and automatic segmentations using T1w and T2w information for ADC and ADNI1 datasets. Yellow color indicates regions labeled as WMH in both segmentations, blue color indicates regions only segmented by the automatic technique, and red color indicates regions only segmented by the manual rater.

Figure 14.

Negative logarithm of FDR corrected p-values of paired t-tests between Dice Kappa values of classifier pairs. Values higher than 1.3 are statistically significant.

3.5. Segmentation using only T1w data

To address the second challenge, we trained and validated the performance of the classifiers with features only from T1w images from ADC, NACC, ADNI1, and ADNI2/GO datasets. Table 10 shows the mean Dice Kappa and detection/outline error rates (DER/OER), for each classifier and dataset. Table 11 shows the corresponding ICC, TPR, and PPV values. Figure 15 shows boxplot diagrams for these results separately for subjects with small, medium and large WMH loads. Figure 16 shows the segmentation results on the axial slices for different classifiers from each study. Figure 17 shows the negative logarithm of the FDR corrected p-values of t-tests on Dice Kappa values of different classifier pairs.

Table 10 -.

Comparison between mean Dice Kappa and detection/outline error rate (DER/OER) values of different classifiers for segmentation of WMHs using T1 data for ADC, NACC, ADNI1, and ADNI2/GO datasets. Blue color indicates the best performance in terms of SI.

Dataset	ADC			NACC			ADNI1			ADNI2/GO
Measures	SI	DER	OER	SI	DER	OER	SI	DER	OER	SI	DER	OER
Naïve Bayes	0.24±0.21	0.08±0.03	1.44±0.21	0.32±0.15	0.06±0.03	1.33±0.21	0.42±0.27	0.07±0.23	1.21±0.21	0.38±0.25	0.05±0.04	1.29±0.50
Logistic Regression	0.11±0.14	1.26±0.80	0.52±0.14	0.08±0.13	0.98±0.87	0.72±0.14	0.37±0.19	0.45±0.69	0.95±0.14	0.31±0.15	0.52±0.65	0.99±0.47
LDA	0.25±0.20	0.09±0.05	1.40±0.20	0.34±0.14	0.07±0.04	1.29±0.20	0.44±0.26	0.09±0.23	1.15±0.20	0.41±0.24	0.08±0.05	1.22±0.48
QDA	0.20±0.17	0.28±0.16	1.30±0.17	0.32±0.14	0.15±0.10	1.24±0.17	0.44±0.27	0.11±0.25	1.15±0.17	0.41±0.25	0.10±0.08	1.21±0.49
KNN	0.28±0.18	0.57±0.48	0.86±0.18	0.33±0.13	0.37±0.38	0.94±0.18	0.51±0.22	0.36±0.46	0.75±0.18	0.46±0.19	0.39±0.45	0.81±0.27
Decision Trees	0.24±0.18	0.76±0.49	0.75±0.18	0.30±0.11	0.48±0.38	0.93±0.18	0.41±0.23	0.47±0.46	0.81±0.18	0.39±0.21	0.48±0.41	0.86±0.25
Random Forests	0.34±0.19	0.51±0.44	0.82±0.19	0.40±0.12	0.31±0.30	0.89±0.19	0.51±0.24	0.33±0.42	0.75±0.19	0.48±0.21	0.34±0.37	0.80±0.55
Bagging	0.03±0.03	0.98±0.72	0.86±0.03	0.08±0.12	0.85±0.77	0.92±0.03	0.30±0.21	0.56±0.67	1.01±0.03	0.20±0.17	0.65±0.70	1.02±0.57
SVM	0.16±0.11	0.65±0.41	1.02±0.11	0.28±0.10	0.31±0.34	1.16±0.11	0.36±0.24	0.29±0.42	1.11±0.11	0.39±0.18	0.28±0.35	1.09±0.37
AdaBoost	0.26±0.10	0.48±0.36	0.99±0.10	0.36±0.11	0.26±0.25	1.03±0.10	0.50±0.23	0.26±0.37	0.87±0.10	0.48±0.19	0.27±0.30	0.91±0.28

Table 11 -.

Comparison between intra-class correlation (ICC), true positive rate (TPR), and positive prediction value (PPV) values of different classifiers for segmentation of WMHs in different datasets using T1 data for ADC, NACC, ADNI1, and ADNI2/GO datasets. Blue color indicates the best performance in terms of SI.

Dataset	ADC			NACC			ADNI1			ADNI2/GO
Measure	ICC	TPR	PPV	ICC	TPR	PPV	ICC	TPR	PPV	ICC	TPR	PPV
Naïve Bayes	0.24	0.20	0.67	0.01	0.28	0.56	0.30	0.37	0.74	0.06	0.33	0.74
Logistic Regression	0.08	0.27	0.09	0.00	0.20	0.07	0.22	0.61	0.34	0.17	0.65	0.25
LDA	0.32	0.22	0.64	0.07	0.29	0.54	0.45	0.42	0.68	0.19	0.39	0.68
QDA	0.40	0.15	0.67	0.52	0.25	0.56	0.38	0.40	0.74	0.17	0.37	0.73
KNN	0.36	0.49	0.22	0.14	0.61	0.25	0.55	0.63	0.50	0.54	0.61	0.43
Decision Trees	0.55	0.24	0.37	0.36	0.30	0.38	0.63	0.41	0.54	0.62	0.40	0.51
Random Forests	0.56	0.45	0.31	0.54	0.55	0.36	0.60	0.59	0.56	0.65	0.57	0.50
Bagging	0.01	0.59	0.02	0.23	0.58	0.05	0.23	0.73	0.21	0.16	0.71	0.15
SVM	0.03	0.49	0.13	0.10	0.54	0.22	0.20	0.59	0.41	0.14	0.56	0.43
AdaBoost	0.25	0.49	0.21	0.10	0.61	0.30	0.52	0.60	0.56	0.51	0.59	0.51

Fig. 15 -.

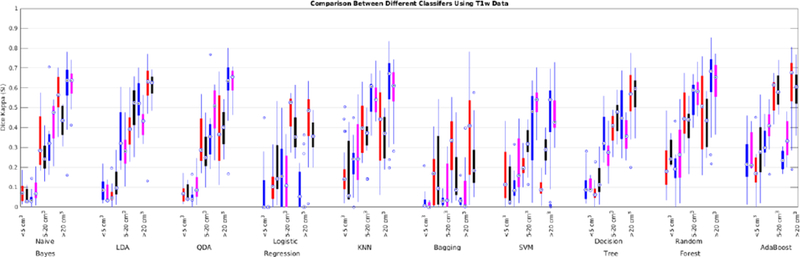
Dice Kappa (SI) for different classification methods for low (<5 cm³), medium (5–20 cm³), and high (>20 cm³) WMH load using only T1w information for ADC (red), NACC (black), ADNI1 (blue), and ADNI2/GO (magenta) datasets.

Fig. 16 -.

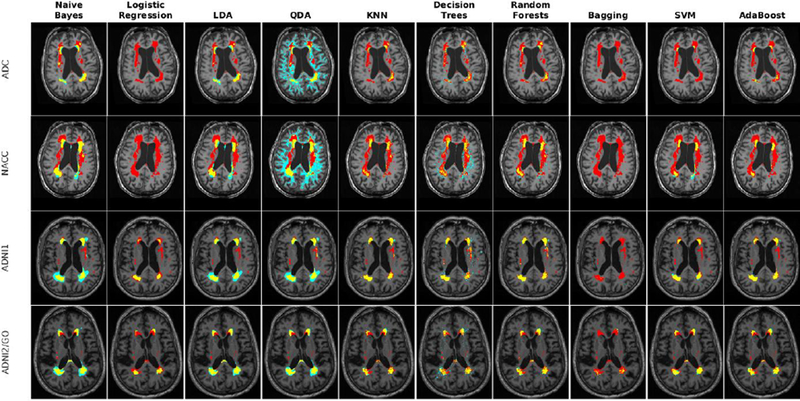
Axial slice comparing manual and automatic segmentations using T1w information for ADC, NACC, ADNI1, and ADNI2/GO datasets. Yellow color indicates regions labeled as WMH in both segmentations, cyan color indicates regions only segmented by the automatic technique, and red color indicates regions only segmented by the manual rater.

Fig. 17 -.

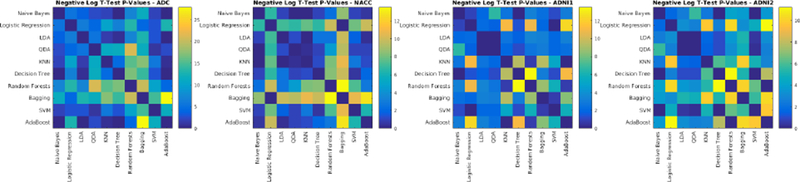
Negative logarithm of FDR corrected p-values of paired t-tests between Dice Kappa values of classifier pairs. Values higher than 1.3 are statistically significant.

3.6. Oversegmentation/Undersegmentation

To provide information regarding oversegmentation/undersegmentation of WMHs, paired t-tests were performed between total WMH loads in small, medium, and large groups on T1+FLAIR (n=147) and T1+T2+PD (n=123) experiments. Table 12 shows the mean and standard deviation of the volumes as well as statistical significance of the differences after correcting for multiple comparisons using FDR correction. From the results, we can see that Naïve Bayes and QDA significantly oversegment WMHs in all three groups. Logistic regression and Bagging significantly undersegment medium and large WMHs. LDA and Decision Trees seem to work well with T1+FLAIR images, but they tend to significantly oversegment when dealing with T1+T2+PD sequences. AdaBoost, KNN, SVM and Random Forest seem to work very well for medium and large WMHs, but slightly oversegment small lesions. However, KNN and SVM seem to show a lot of variability (high standard deviations) for small lesions using T1+T2+PD sequences.

Table 12-.

Mean ± standard deviation of WMH loads in small (<5cm³), medium (5–20cm³), and large (>20cm³) groups. Statistically significant differences from manual segmentations after corrections for multiple comparisons using false discovery rate (FDR) correction are indicated with *

Sequences	T1-FLAIR			T1–T2-PD
Method	Small	Medium	Large	Small	Medium	Large
Manual	1.85±1.39	12.07±4.58	40.02±23.33	1.47±1.14	10.81±4.27	47.62±25.74
Naïve Bayes	18.65±12.52*	33.45±16.79*	68.31±37.88*	91.29±98.89*	89.85±33.56*	148.31±48.49*
Logistic Regression	2.53±2.59*	9.83±4.98*	34.03±25.35*	2.18±5.68	4.44±8.32*	32.80±27.80*
LDA	3.97±3.09*	12.48±5.76	39.49±30.83	22.44±8.16*	28.72±12.14*	53.47±19.22
QDA	17.26±11.21*	32.53±16.05*	73.04±42.40*	121.10±89.30*	129.28±43.98*	205.15±69.82*
KNN	2.42±2.46*	11.00±5.81	41.53±30.49	4.74±21.28	8.74±8.53	45.50±25.54
Decision Trees	3.44±3.24*	12.64±6.35	41.63±25.35	5.10±4.41*	14.03±9.86*	54.30±26.60*
Random Forests	2.62±2.61*	11.47±5.87	40.79±25.37	2.58±3.29	11.51±9.72	51.57±27.38
Bagging	1.46±2.41	7.13±6.23*	28.13±21.69*	3.12±14.95	5.16±7.17*	32.86±20.56*
SVM	2.76±3.23*	11.05±5.90	41.17±30.55	5.49±8.53*	11.98±14.87	49.28±29.49
AdaBoost	2.85±2.78*	11.93±5.97	41.08±25.60	3.42±4.05*	11.94±10.25	52.47±29.93

3.7. Computational burden

In order for a segmentation technique to be applicable to large-scale datasets, reasonable computation time and memory demands are crucial. To assess this, all classifiers were trained on the same dataset consisting of 50 subjects and used to segment 20 subjects on an Intel(R) Core(TM) i7–5600 CPU @ 2.60 GHz machine with 20.0 GBs RAM. Table 13 shows the training as well as segmentation time per subject in seconds for each classifier.

Table 13 -.

Comparison between training and segmentation times (s) between different classifiers

Classifier	Training Time (s)	Segmentation Time (s)
Naïve Bayes	12.45	0.38
Logistic Regression	333.38	0.11
LDA	66.31	0.52
QDA	100.56	0.45
KNN	7718.98	3021.88
Decision Trees	1225.63	0.53
Random Forests	22620.11	7.29
Bagging	8992.54	981.55
SVM	14581.04	0.26
AdaBoost	100766.02	71.16

4. Discussion

In the recent years, there have been many different studies in the literature that address the challenge of automatically segmenting WMHs (Caligiuri et al., 2015; Admiraal-Behloul et al., 2005; Anbeek et al., 2004; Beare et al., 2009; De Boer et al., 2009; Dyrby et al., 2008; Ghafoorian et al., 2016a; Griffanti et al., 2016; Ithapu et al., 2014; Lao et al., 2008; Ong et al., 2012; Schmidt et al., 2012; Simões et al., 2013; Steenwijk et al., 2013; Wu et al., 2006a, 2006b; Yoo et al., 2014; García-Lorenzo et al., 2013; Shiee et al., 2010). However, drawing meaningful comparisons between these segmentation techniques proves to be practically impossible since the results are greatly influenced by the MRI acquisition characteristics and resolution as well as the quality of the manually segmented labels that are used for training and validation. Here we have validated and compared the performance of a variety of different supervised linear and nonlinear classifiers in segmenting WMHs using 4 relatively large datasets. We also provide our fully automated tool for segmentation of WMHs from multiple contrasts of MR images along with the pre-trained classifiers.

Several commonly used linear and nonlinear classifiers with different levels of computational complexity were employed for segmentation of WMHs from multiple contrasts of MR images. In presence of FLAIR information, most methods performed relatively well and can be employed for WMH segmentation. However, the performance of the classifiers declined significantly in absence of the optimal FLAIR modality information, with Random forests and AdaBoost classifiers still retaining the best performance. Using only T1w images, the performance of all classifiers declined drastically with random forest and AdaBoost classifiers still providing the best results. These segmentations tend to detect only the brightest of the WMHs. However, their high volumetric correlation with the gold standard values shows that while not perfectly accurate, they still might be used as surrogate measures to reflect WMH burden if they are also associated with risk factors and clinical measures. This can prove extremely valuable in studies that only have T1w scans and need to take into account the WMH burden.

One of the major issues when using automated techniques for segmenting WMHs is the variability caused by differences in the scanner and acquisition sequences which would in turn lead to differences in contrast and borders of WMHs. As a result, classifiers that are trained on data from a single scanner with a specific acquisition sequence tend to perform poorly on data from different scanners and/or sequences. To increase the generalizability of our tools, we have trained and validated our classifiers using data from different scanners/sites.

It would be worthwhile to note that all of the voxels inside the brain were input to the classifiers and no white matter mask or any mask excluding either ventricles or cerebrospinal fluids were used. This makes the classification task more challenging, but on the other hand, makes the performance of the classifiers more easily comparable with other methods since the results will not be dependent on the quality of the tissue segmentation algorithm or whether specific regions such as brainstem or cerebellum which are generally more challenging to segment are masked out. Another valid concern in using tissue segmentation results is that most tissue classification techniques use only T1w images, on which some of the WMHs appear hypointense. This makes the tissue classification results prone to error since they will be likely to classify WMHs as grey matter while most WMHs occur in the white matter. This misclassification in the initial tissue segmentation will add an extra level of noise to the data that can significantly affect WMH segmentation results. One limitation of our technique is that it has not been validated on patients with stroke; the intensity profile in such subjects is likely very different from the subjects evaluated here.

In detecting WMHs, FLAIR is of the highest importance since it provides the best lesion to WM contrast when compared with T1w, T2w and PD sequences. PD provides the most variable contrast difference between tissue types directly related to the parameters used in its acquisition. The more T2 weighted the PD sequence, the less supplemental contrast information it provides (since the information is already provided by the T2w sequence). Hence, the PD sequence is most meaningful if the parameters allow the CSF to be of the lowest possible signal. The T1w sequence on its own should only be considered in cases where other modalities are not available or their poor image quality prevents their use. The lower information given by T1w images resides in a poorer contrast between the signal of lesions and surrounding WM. Lesion intensity spans from iso-intense to WM to deep hypointense, causing the difficulty in detecting lesions using only T1w images. Another factor that can significantly affect the quality of both manual and automated segmentations is the signal to noise ratio (SNR). A lower SNR will impact the image quality and number of artifacts, which would then translate into poorer performance of either software or manual rater. The ADC, NACC, and ADNI2 FLAIRs had an average SNR value of 17.25±2.37, 20.11±5.52, and 35.11±7.26 as estimated by our denoising tool (Coupe et al., 2008), respectively. This may partially explain the poorer results for ADC data. As a general rule, the highest possible SNR should be attained in each modality employed. In addition to SNR, ringing or ghosting caused by movement and inter-package motion also contribute to the deterioration of image quality.

Manually segmenting WMHs is a challenging task. Lesion edges always exhibit a degree of hyperintense signal that decreases gradually towards the healthy surrounding WM. In other words, no lesion edge goes from one pathologic hyperintense voxel, to a contiguous healthy hypointense WM voxel, and the edges may shift from scoring to scoring by one or two voxels. Additionally, when cases have multiple lesions, the surface to volume ratio of the lesions increases. Even when the rater identifies exactly the same lesions, one extra voxel around the edge of a small lesion may have a large impact on the Dice Kappa value. The small DER values for the manual segmentations further confirm that most of the disagreement between the manual segmentations occurs around the edges (0.03±0.04, 0.05±0.04, 0.03±0.04, and 0.04±0.04 for ADC, NACC, ADNI1, and ADNI2, respectively). Also, the poorer image quality, in terms of SNR, of the ADC dataset, could partially account for the worse intra-rater performance for that dataset.

Segmenting WMHs without the optimal FLAIR modality is a challenging task. Additional errors might arise from comparing segmentations obtained without FLAIR with manual labels that are based on FLAIR images. The extent and borders of WMHs generally do not look the same on the different MRI sequences (Filippi et al., 1996). It has been shown that FLAIR sequence is less sensitive in detecting thalamic lesions in vascular disease populations (Leite et al., 2004). Furthermore, FLAIR may present hyperintense artifacts that can lead to an increase in false positives such as the hyperintensities often observed in insula (Hirai et al., 2000). As a result, a certain degree of disagreement between segmentations obtained with and without FLAIR information is expected. This explains the higher SI values for the ADNI1 dataset where the manual segmentations are based on T2w/PD scans compared with automatic segmentations with the same contrasts in ADC dataset (T1w, T2w, and PD) where FLAIR information was used for the manual segmentations. Additionally, the difference in tissue contrast between the PD sequence of the ADC dataset and ADNI1 may also partially account for the higher SI value for ADNI1. The PD scans in ADNI1 dataset had a higher white-to-grey matter contrast, higher white matter-to-lesion contrast, and better delineation of CSF as a different tissue type, given its low signal. All these characteristics were absent in the ADC dataset, where PD was heavily T2 weighted. These differential characteristics are critical in the WMHs segmentation process either by a rater or an automatic tool, improving the accuracy of the segmentation in the ADNI1 cases.

Using classifiers such as KNN and Bagging with KNN has the additional drawback of longer computation time for segmenting new data. The fact that they do not require rigorous training is generally outweighed by their longer classification times, especially when one needs to segment 100s or 1000s of MRI volumes in larger datasets. In addition, these methods are generally more susceptible to skewedness in class distributions, which is the case in lesion segmentation tasks, since most voxels in the brain are non-WMHs. As a result, the examples of the more frequent non-WMH class tend to dominate the new predictions, simply owing to the fact that they are more common.

Accurate quantification and localization of WMHs is critical since they are important clinical measures in the elderly and AD populations. A Dice Kappa value of 0.7 is considered as a good segmentation in the literature (Caligiuri et al., 2015). Random forest was able to obtain average Dice Kappa values higher than 0.7 for the medium lesion load and 0.8 for large lesion load groups, which is considered as excellent agreement. Their average Dice Kappa for the small lesion group was higher than 0.5, which is still considered as a very good agreement, especially considering the fact that Dice Kappa values are smaller for objects with a high surface to volume ratio, as is the case for subjects with small lesion loads.

The Random Forests technique consistently had the best results across all the experiments when using Dice Kappa (SI) as the primary measure of comparison. Considering the fact that it also had a shorter computational time than the second-best classifier (AdaBoost), Random Forests was the best classifier amongst the nonlinear classification techniques tested. The Linear Discriminant Analysis method was the best linear classifier considering the Dice Kappa results and computation times.

In cases where different classifiers have different strengths and weaknesses, using an ensemble of all the classifiers can improve the overall classification accuracy. Here, performing a voting between the outputs of all 10 classifiers achieved Dice Kappa values of 0.68±0.17, 0.74±0.10, 0.66±0.22, and 0.72±0.19 (versus 0.66±0.17, 0.72±0.10, 0.66±0.23, and 0.72±0.19 for the Random Forest classifier) for ADC, NACC, ADNI1, and ADNI2 datasets, respectively, suggesting a slight improvement for ADC (p=0.001), and NACC (p=0.004), and no difference for ADNI1 and ADNI2 (p>0.05).

As mentioned previously, drawing meaningful comparisons between techniques that have been applied to different datasets, using different brain masks, and with different definitions of WMHs should be done with care. Taking these considerations into account, our Random Forests classifier performs very well in comparison with other methods in the field (Table 14).

Table 14 -.

Comparison of SI (Dice Kappa) for different lesion loads in various studies. (S: small load, M: medium load, L: large load).

Method	Technique	Number (S-M-L%)	Dice (SI)
			S	M	L	Total
Proposed pipeline	Random Forests	70 (36–23–11) 32 (6–11–12) 46 (16–11–18)	0.55 0.57 0.53	0.75 0.73 0.79	0.84 0.84 0.86	0.66 0.72 0.72
Dadar (Dadar et al., 2017)	Linear regression + thresholding	80 (58–31–11) 40 (25–14–1) 10 (2–4–4)	0.49 0.48 0.36	0.74 0.64 0.58	0.87 0.74 0.74	0.62 0.51 0.64
Admiraal (Admiraal–Behloul et al., 2005)	Fuzzy inference	100 (40–35–25)	0.70	0.75	0.82	0.75
Anbeek (Anbeek et al., 2004)	K-nearest neighbors	20 (40–35–25)	0.50	0.75	0.85	0.61
Beare (Beare et al., 2009)	AdaBoost	30		0.50	0.65	0.58
Boer (De Boer et al., 2009)	K-nearest neighbors	20	0.72			0.72
Steenwijk (Steenwijk et al., 2013)	K-nearest neighbors	20 (15–45–40) 18 (40–33–17)	0.78 0.65	0.85 0.72	0.91 0.81	0.84 0.75
Khayati (Khayati et al., 2008)	Adaptive Mixture Model	20 (35–50–15)	0.72	0.75	0.80	0.75
Sajja (Sajja et al., 2006)	Parzen Window	23 (35–65)	0.67		0.84	0.78
Schmidt (Schmidt et al., 2012)	Markov random field	53	0.66	0.79	0.85	0.75
Sheei (Shiee et al., 2010)	Fuzzy segmentation	10	0.63			0.63
Ong (Ong et al., 2012)	Adaptive trimmed mean	38	0.36	0.56	0.71	0.47
Ithapu (Ithapu et al., 2014)	Random Forests Support Vector Machine	38	0.67 0.54			0.67 0.54
Herskovits (Herskovits et al., 2008)	Bayesian classification	42	0.60			0.60
Dyrby (Dyrby et al., 2008)	Neural networks	362	0.45	0.62	0.65	0.56
Erus (Erus et al., 2014)	Abnormality detection + principal component analysis	33 47		0.54 0.66		0.54 0.66
Ghafoorian (Ghafoorian et al., 2016b)	Convolutional neural networks	46	0.79			0.79
Simões (Simões et al., 2013)	Gaussian Mixture Model	28 (14–9–5)	0.51	0.70	0.84	0.62
Yoo (Yoo et al., 2014)	Variable thresholding	32 (7–10–15)	0.59	0.73	0.86	0.76
Griffanti (Griffanti et al., 2016)	K-nearest neighbors	21 109	0.70 0.41	0.69 0.58	0.80 0.68	0.76 0.52

Accurate quantification of WMHs is critical for evaluating the vascular burden contributing to cognitive deficits in the vascular dementia and AD patients as well as the aging population in general. Due to the high variability across different populations, image acquisition parameters and manual segmentation protocols, comparing different techniques in a meaningful way is practically impossible. Here we have extensively compared 10 most widely used off-the-shelf classifiers in segmenting WMHs with and without FLAIR information in terms of accuracy and computational burden. These experiments have enabled us to draw meaningful and generalizable comparisons between different methods and determine which classifiers are best suited to the task of segmenting WMHs.