Abstract
Estimation of allele dosage, using genomic data, in autopolyploids is challenging and current methods often result in the misclassification of genotypes. Some progress has been made when using SNP arrays, but the major challenge is when using next generation sequencing data. Here we compare the use of read depth as continuous parameterization with ploidy parameterizations in the context of genomic selection (GS). Additionally, different sources of information to build relationship matrices were compared. A real breeding population of the autotetraploid species blueberry (Vaccinium corybosum), composed of 1,847 individuals was phenotyped for eight yield and fruit quality traits over two years. Continuous genotypic based models performed as well as the best models. This approach also reduces the computational time and avoids problems associated with misclassification of genotypic classes when assigning dosage in polyploid species. This approach could be very valuable for species with higher ploidy levels or for emerging crops where ploidy is not well understood. To our knowledge, this work constitutes the first study of genomic selection in blueberry. Accuracies are encouraging for application of GS for blueberry breeding. GS could reduce the time for cultivar release by three years, increasing the genetic gain per cycle by 86% on average when compared to phenotypic selection, and 32% when compared with pedigree-based selection. Finally, the genotypic and phenotypic data used in this study are made available for comparative analysis of dosage calling and genomic selection prediction models in the context of autopolyploids.
Keywords: Autopolyploid, Allelic dosage, Genomic Selection, Relationship Matrices, Vaccinium, blueberry, Shared data, Genomic Prediction, GenPred, Shared Data Resources
Polyploidy events are not an exception in plants, as about 70% of Angiosperms and 95% of Pteridophytes underwent at least one polyploidization event (Soltis and Soltis 1999). Polyploids are normally grouped into two categories, autopolyploids and allopolyploids, but intermediate forms are also possible, such as segmental allopolyploids (Spoelhof et al. 2017). Thresholds for polyploid classification have been controversial, but following the general taxonomic definition, autopolyploids arise from within-species whole genome duplication, and allopolyploids arise from whole genome duplication prior to or after an inter-specific hybridization event (Soltis et al. 2007).
Because speciation via ploidy increase can generate new phenotypic variability, this phenomenon is considered a powerful evolutionary source (Hieter and Griffiths 1999; Soltis et al. 2016). Despite the important role of polyploidization in plant evolution, its effects on inheritance of many agronomic traits and population genetics are still poorly understood when compared with diploid species (Dufresne et al. 2014). This especially holds true for autopolyploids. Examples of the complex nature of autopolyploid genetics are the presence of genotypes with higher allele dosage than diploids, larger number of genotypic classes, possibility of multivalent pairing, and poor knowledge of chromosome behavior during meiosis (Slater et al. 2014; Dufresne et al. 2014; Mollinari and Serang 2015).
The advent of high-throughput genotyping methods, associated with the development of genetic and statistical analysis tools, has generated significant genetic gains for diploid species (Desta and Ortiz 2014). However, the application of genomic information to polyploid crops remains a challenge (Comai 2005; Grandke et al. 2016). Although the theory for the computation of average genetic effect assuming arbitrary ploidy have been published by Kempthorne (1957), most of the methods for analysis and interpretation of genetic data in polyploids have only recently been described (see review in Bourke et al. 2018; Kerr et al. 2012; Endelman et al. 2018), and most of them have not yet been fully investigated for different species, especially for new breeding approaches, such as genomic selection.
Genomic selection (GS) is a method to increase the efficiency and accelerate the selection process in breeding programs. GS is used to capture the simultaneous effects of molecular markers distributed across the genome, based in the premise that the linkage disequilibrium between causal polymorphisms and markers allow phenotype prediction based on genotypic values (Meuwissen et al. 2001; Zhang et al. 2011; Daetwyler et al. 2013; de los Campos et al. 2013). Promising results have been reported in GS studies addressing polyploids (e.g., Gouy et al. 2013; Annicchiarico et al. 2015; Ashraf et al. 2016), however simplified assumptions were mostly considered, in other words diploid genetic models were used to circumvent the complexity involved in accurately defining allelic dosage (i.e., the number of copies of each allele at a given polymorphic locus). Besides the existence of methods that allow accounting for ploidy effects (Kerr et al. 2012; Endelman et al. 2018), only a few studies have inserted this factor in the analyses (e.g., Slater et al. 2016; Sverrisdóttir et al. 2017; Nyine et al. 2018). In addition, these methodologies were not yet extensively compared, a point that is addressed in this article.
Polyploidy can affect phenotypes through allelic dosage (additive effect of multiple copies of the same alleles), or by creating more complex interactions between loci or alleles, such as dominance or epistasis (Osborn et al. 2003). Thus, the inclusion of allelic dosage information may improve GS results (e.g., increase of accuracy) by creating a more realistic representation of the effects of each genotypic class. Although the evidence of dosage effects in the expression of important economic traits exists (Guo et al. 1996; Birchler et al. 2001; Adams et al. 2003; Osborn et al. 2003), few studies linking dosage effects to phenotype prediction have been reported in autopolyploid species (e.g.; Slater et al. 2016; Sverrisdóttir et al. 2017; Nyine et al. 2018; Endelman et al. 2018). Genotype classification is one of the major challenges for polyploids. Studies about genotyping calling evaluation for autopolyploids with next generation sequencing (NGS) data showed that none of the existing methods performs properly (Grandke et al. 2016), unless high sequencing coverage (60-80x) is used (Uitdewilligen et al. 2013).
Here we compare a novel approach to GS in the context of autopolyploid, using Vaccinium corymbosum (southern highbush blueberry, SHB) as a model. The cultivated SHB is an autotetraploid, presenting 2n = 4X = 48 chromosomes (Lyrene 2002). Inbreeding depression is strong in SHB and population improvements have been achieved by long-term recurrent phenotypic selection alongside with long testing phase and slow genetic gain per generation (Lyrene 2008). Our goal was to investigate and compare the influence of different sources of information and ploidy parameterizations used to build relationship matrices on phenotype prediction, and thus the potential of GS in blueberry breeding.
Material and Methods
Population and phenotyping
The population used in this study encompasses one cycle of the University of Florida blueberry breeding program’s recurrent selection, comprising 1,847 SHB unique individuals. This population was originated from 124 biparental controlled crosses, from 146 parents that presented superior phenotypic performance (cultivars and advanced stage of breeding). Phenotypic data of eight yield and fruit quality-related traits were collected during two production seasons (2014 and 2015), when the plants were 2.5 and 3.5 years of age at the University of Florida Plant Science Research and Education Unit in Citra (29°24’42.01” N -82°06’36.00” W, Florida, USA). Yield (rated using a 1-5 scale), weight (g), firmness (g mm-1 of compression force), scar diameter (mm), fruit diameter (mm), flower bud density (reported as buds per 20 cm of shoot), soluble solids content (oBrix), and pH were evaluated. The last three traits were phenotyped only in one year – soluble solids content and pH were phenotyped in 2014 and flower buds in 2015.
Five berries (fully mature and presenting picking quality) were randomly sampled to compose the measurement of fruit traits for each individual. Fruit weight was measured using an analytical scale (CP2202S, Sartorious Corp., Bohemia, NY). The FirmTech II firmness tester (BioWorks Inc., Wamego, KS) was used to measure fruit diameter and firmness. The scar diameter was obtained by image analysis of the fruits using FIJI software (Schindelin et al. 2012). The number of flower buds was counted in the main cane upright shoot, in the top 20 cm. A digital pocket refractometer (Atago, U.S.A., Inc., Bellevue, WA) was used to obtain soluble solids measures from 300μl of berry juice. The pH was measured using a glass pH electrode (Mettler-Toldeo, Inc., Schwerzenbach, Switzerland). More details are provided by Amadeu et al. (2016), Cellon et al. (2018), and Ferrão et al. (2018).
Genotyping
Genomic DNA was extracted and genotyped using sequence capture by Rapid Genomics (Gainesville, FL). Polymorphisms were genotyped in genomic regions captured by 31,063 120-mer biotinylated probes, designed based on the 2013 blueberry draft genome sequence (Bian et al. 2014; Gupta et al. 2015). Sequencing was performed in the Illumina HiSeq2000 platform using 100 cycle paired-end sequencing. After trimming (quality score of 20), demultiplexing, and removing barcodes, reads were aligned to the draft genome using Mosaik v.2.2.3 (Lee et al. 2014). Genotypes were called using FreeBayes v.1.0.1 (Garrison and Marth 2012) considering the diploid and tetraploid options. Single-nucleotide polymorphisms (SNPs) were filtered considering i) minimum sequencing depth of 40 (average depth for the population); ii) minimum SNP phred quality score (QUAL) of 10; iii) only biallelic markers; iv) maximum population missing data of 0.5; and v) minor population allele frequency of 0.05. After filtering a total of 85,973 SNP were used in the GS analysis (the average sequencing-depth per sample was 73X). Further information regarding population composition and genotyping approach were described in Ferrão et al. (2018). The genotypes for the diploid calling were coded as 0 (AA), 1 (AB), or 2 (BB). For the tetraploid parameterization they were coded as 0 (AAAA), 1 (AAAB), 2 (AABB), 3 (ABBB), and 4 (BBBB). A third parameterization (assumption-free method) was used, which considered allele ratio , where is the allele count (sequencing depth) of the alternative allele and is the allele count of the reference allele. No dosage calling was performed in this model (File S1); these data varied continuously between 0 and 1.
Population genetics analysis
In order to compare the information captured by each genomic-based relationship matrix, we performed linkage disequilibrium (LD), and principal components (PC) analyses. Pearson correlation tests (r2) were performed for pairwise LD estimation among SNPs within scaffolds, considering draft reference genomes (Bian et al. 2014; Gupta et al., 2015). One SNP was randomly sampled per probe interval, and a total of 22,914 SNPs were used in the analysis. LD was obtained for all marker-based scenarios: i) diploid (G2); ii) tetraploid (G4) and iii) ratio (i.e., continuous genotypes; Gr). The LD decay over physical distance was determined as the mean distance at the LD threshold of r2 = 0.2. To compare the LD among scenarios, the mean distances (Kb) and their interval confidences at r2 = 0.2 were compared. The diversity captured from each relationship matrix was obtained by PC using the R package adegenet v. 1.3-1 (Jombart and Ahmed 2011).
We also evaluated the observed heterozygosity in the population. For this, we obtained the ratio between the number of heterozygote genotypes and the total number of individuals. To estimate the heterozygosity for the continuous genotypes, empirical limits were established based on the mean and standard deviations presented for homozygotes classes of the tetraploid parameterization.
Models
One-step single-trait Bayesian linear mixed models were used to predict breeding values for each individual in the population, as follows:
| (1) |
Where is a vector of the phenotypic values of the trait being analyzed, is the population’s overall mean, b is the fixed effect of year, c is the random effect of ith column position in the field ∼ N (0, ), r is the random effect of the ith row position in the field ∼ N (0, ), a is the random effect of genotype ∼ N (0,), where was replaced by the different additive relationship matrices as described in the next section. The bxa is the random effect of the year by genotype interaction ∼ N (0, ), and e is the random residual effect ∼ N (0, ). Row and column effects were considered nested within year only for the traits evaluated in two years. For traits measured in a single year, the same equation (1) was used without the year and the year by genotype interactions. The variance components for each random variable were: additive (), column (), row (), year-by-genotype interaction (), and residual (). and were incidence matrices for year, column, row, genotype, and year by genotype interaction, respectively. The narrow-sense heritabilities were estimated considering the ratio between the additive variance component and the total phenotypic variance (sum of all variance components).
Relationship matrices
To quantify the effect of the genetic information used to build the relationship matrices on the predictive ability (PA), we performed analyses considering different approaches to modeling the genotypic values in autotetraploid species (Table 1, File S1). The factors tested were: i) the source of information used to build the relationship matrix (pedigree, genomic, or no relationship information); and ii) ploidy information (diploid, tetraploid, and assumption-free method).
Table 1. Methods and assumptions used to compare the influence of relationship matrices, ploidy and continuous genotypes in the prediction of breeding values for blueberry.
| Relationship matrix | Model | Ploidy assumption | Methodology |
|---|---|---|---|
| Identity | I | none | none |
| Pedigree-based | A2 | 2 | Henderson (1976) |
| A4 | 4 | Kerr et al. (2012) | |
| Marker-based | G2 | 2 | VanRaden (2008) |
| G4 | 4 | ||
| Gr | none |
The methods chosen to obtain the relationship matrices are shown in the Table 1. The R package AGHmatrix v. 0.0.3003 (Amadeu et al. 2016) was used to obtain all relationship matrices (description of matrices File S1). The pedigree-based relationship matrices (A) were built considering a diploid model (Henderson 1976) and autotetraploid model without double-reduction (Kerr et al. 2012). The marker-based relationship matrices (G) were based on the incidence matrices of markers effects (X) according to VanRaden (2008) and adapted by Ashraf et al. (2016). Different assumptions can be made regarding the marker allele dosage in autotetraploids (Table 2). We built the X matrices under three assumptions regarding the additive marker allele dosage effect: i) a pseudo-diploid model, where all the heterozygous genotypes were assumed as one class, corresponding to a unique effect (data coded as 0, 1, and 2); ii) an additive autotetraploid model, where each genotype had a specific value, and cumulative additive effect was assumed (data coded as 0, 1, 2, 3, and 4); and iii) an assumption-free method based on the ratio of reads count for the alternative and reference alleles (continuous parameterization, assuming values between 0 and 1), where also a cumulative additive effect was assumed. For the construction of the relationship matrices based on marker data, the missing genotypes were substituted by the mean.
Table 2. Theoretical genotype codes for marker-allele dosage effects considering pseudo-diploid, autotetraploid and continuous parameterizations. Adapted from Slater et al. (2016).
| Genotype | Pseudo-Diploid | Autotetraploid | Continuous valuesa |
|---|---|---|---|
| AAAA | 0 | 0 | 0 - 1 |
| AAAB | 1 | 1 | |
| AABB | 1 | 2 | |
| ABBB | 1 | 3 | |
| BBBB | 2 | 4 |
Continuous value with a ploidy assumption-free parameterization.
Model implementation
The six models described above (Table 1) were fitted using the R package (R Core Team 2018) BGLR v. 1.0.5 (de los Campos and Pérez-Rodríguez 2016). Predictions were based on 30,000 iterations of the Gibbs sampler, in which 5,000 were taken as burn-in, and a thinning of five. The number of iterations, burn-in, and thinning interval parameters were evaluated to define the final values used in the analysis (Figure S1). A single step regression approach was applied to perform all phenotypic BLUP (I matrix), pedigree-BLUP (P-BLUP), and genomic-BLUP (G-BLUP). Default hyper-parameters were used, as previously described (Pérez and de los Campos 2014).
Validation and model comparison
For each trait, models were compared based on their PA, stability (mean square errors), goodness-of-fit, and expected genetic gain. A 10-fold cross validation scheme was applied to compute model PA, for this the genotypes were assigned to ten groups, on each cross-validation step the phenotypic information for one of the groups was omitted (validation set) and predicted considering the model obtained from the remaining nine groups (training set). Because each validation group might have a different mean (Resende et al. 2012b), the phenotypic PA were obtained as the Pearson correlation coefficient between the empirical best linear unbiased estimation values (eBLUEs) obtained by considering all the variables in the equations 1 as fixed (i.e., Least Square means estimations; LSMeans) and the cross-validated breeding values (BV) predicted by the models for each validation fold. The goodness-of-fit for the different models was evaluated with measures of DIC (Spiegelhalter et al. 2002) obtained from the full data set, extracted from the object returned by BGLR. The model with the lowest value for this parameter defined the best fit for the data. For the expected genetic gain estimation we used the following formula: ΔG = ()/L, where PA is the phenotypic predictive ability, is the square root of additive genetic variance in the population, i is the selection intensity, and L is the breeding cycle length. To make it comparable between methods the selection intensity (i) was considered constant for all methods and equal to 1.
Average phenotypic and raw genotypic data used during the current study will become available to promote further studies on the effect of dosage calling in the context of GS modeling.
Data availability
Phenotypic datasets (eBLUES) are available from the Dyrad Digital Repository (accession number doi: 10.5061/dryad.kd4jq6h). Genotypic data and supplemental material are available at Figshare. Files include diploid, tetraploid and continuous genotypes, supplemental information 1 to 5, which includes: 1) description of the matrices used in the study; 2) model convergence figure; 3) LD distribution per parameterization; 4) principal components plots for each parameterization; 5) table of the predictive abilities, MSE, goodness-of-fit and beta for each parameterization. The authors ratify that all data necessary for confirming the conclusions of the article are present within the article, figures, and tables. Supplemental material available at Figshare: https://doi.org/10.25387/g3.7728365.
Results
Population genetics analyses
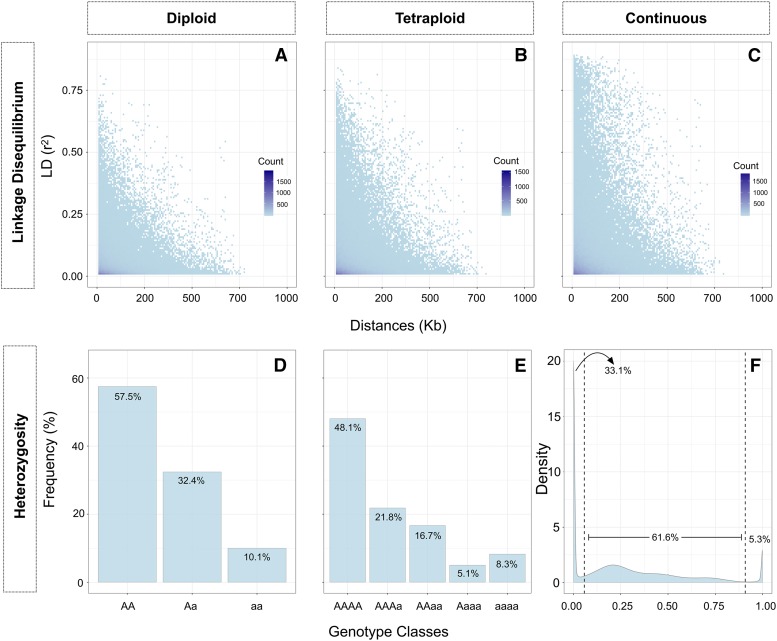
Linkage disequilibrium decayed below r2 = 0.2 at distances of 88.3 Kb, 92.6 Kb, and 98.2 Kb for the diploid, tetraploid and continuous models, respectively (Figure 1A-C). No significant difference was observed considering the confidence interval for the mean distance (Kb) at r2 = 0.2 among different ploidies and continuous genotyping scenarios (Figure S2).
Figure 1.
Linkage disequilibrium decay and heterozygosity for blueberry. Linkage disequilibrium decay estimation using one marker per probe, within scaffolds for (A) diploid, (B) tetraploid and (C) continuous genotype parameterizations. Heterozygosity observed in (D) diploid, (E) tetraploid, and (F) heterozygosity empirically established for the continuous genotypes’ scenario, assuming the limits of 0.058 ≤ X ≤ 0.908.
Similarly, no major differences were found between parameterizations within methodology (i.e., pedigree-based or marker-based methods) in the PC analysis (Figure S3). The first two PC components of the marker-based (G) matrices were consistent across all matrices, explaining approximately 20% of the variation, G2 matrix captured 20.60% of the variation, while G4 captured 21.71%, and Gr captured 23.36% (Figure S3 A-C). The PC analysis results were consistent between pedigree methodologies as well. Approximately 38% of the variation was explained (i.e., 37.74% of the variability was explained for the A2 matrix and 37.86% was explained for the A4 matrix, Figure S3 D-E). The results obtained in the PC analysis did not justify a stratified sampling of cross-validation populations, since no evidence of sub-population structure was detected for any of the relationship matrices.
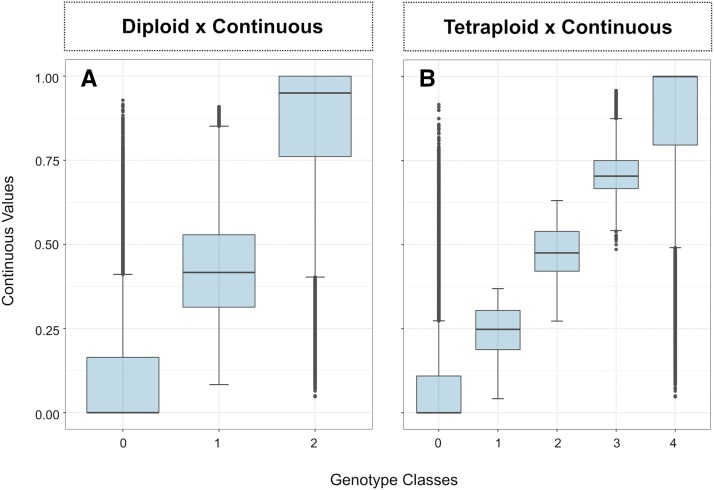
Considering the heterozygosity observed in each scenario, genotypes assumed as homozygotes in the diploid parameterization were classified as one of the possible heterozygote classes in the tetraploid and in the assumption-free parameterizations (Figure 1D-F). As a result of this process, the tetraploid parameterization presented 37.50% more heterozygotes than the diploid parameterization. Considering the empirical thresholds established to compare the proportion of “heterozygotes” in the continuous genotypes with the ploidy parameterizations, values equal to or below 0.058 and equal to or above 0.908 were considered as “homozygotes” classes (dashed lines, Figure 1F). With this, 61.59% of the genotypes were considered “heterozygotes”, thus the continuous method would have presented 89.92% and 41.23% more heterozygotes than the diploid and the tetraploid parameterization, respectively. Nevertheless, some misclassification of data into classes in the diploid and tetraploid parameterization might have occurred (Figure 2A-B).
Figure 2.
Relationship between continuous values and the classes assumed in the (A) diploid and (B) tetraploid parameterizations.
Variance estimates
The posterior means of the genetic parameters are summarized in Table 3. All the traits presented additive genetic variance significantly higher than zero. A wide range of variance was observed within a given parameter for the different methodologies, and most of the values were significantly different from each other (considering Tukey test results; Table 3, Table S1). Marker-based methodologies generated significantly smaller estimations for variance components when compared with pedigree-based estimations. Within marker-based methodologies, the assumption-free parameterization generated significantly smaller estimations. The effects of the difference in the estimation of variance components are reflected in the estimated heritabilities – smaller values were estimated for marker-based methodologies. The lowest heritability was obtained for soluble solids, flower buds, and pH. Considering all methods, narrow-sense heritability values varied between 0.152 and 0.574, for flower buds and fruit weight, respectively.
Table 3. Genetic parameters estimated for eight yield and fruit-related traits analyzed with six linear mixed models, considering the use of ploidy information and continuous genotypes. Source of information, and dosage parameterizations for the relationship matrices indicated by the letters (I, A, or G), and index 2, 4, and r respectively*.
| Trait | Relationship matrix | Additive Variance | Residual Variance | Heritability | EGG 20141 | EGG 20151 |
|---|---|---|---|---|---|---|
| Soluble Solid (°Brix) | I | 0.806 b | 1.794 d | 0.257 a | 0.018 b | — |
| A2 | 0.777 c | 2.129 b | 0.239 b | 0.021 ab | — | |
| A4 | 0.764 c | 2.125 b | 0.236 b | 0.021 ab | — | |
| G2 | 0.848 a | 2.026 c | 0.262 a | 0.028 a | — | |
| G4 | 0.673 d | 2.109 b | 0.215 c | 0.026 a | — | |
| Gr | 0.546 e | 2.241 a | 0.174 d | 0.022 ab | — | |
| Flower Buds | I | 2.133 a | 4.752 d | 0.270 a | — | 0.018 a |
| A2 | 1.247 cd | 6.080 a | 0.153 de | — | 0.019 a | |
| A4 | 1.232 d | 6.070 a | 0.152 e | — | 0.018 a | |
| G2 | 2.106 a | 5.562 c | 0.251 b | — | 0.030 a | |
| G4 | 1.526 b | 5.881 b | 0.188 c | — | 0.025 a | |
| Gr | 1.315 c | 6.115 a | 0.161 d | — | 0.023 a | |
| Fruit Diameter | I | 2.236 f | 6.804 b | 0.162 f | 0.047 b | 0.041 c |
| A2 | 3.647 a | 6.854 b | 0.250 a | 0.063 b | 0.054 bc | |
| A4 | 3.581 b | 6.825 b | 0.247 b | 0.061 b | 0.054 bc | |
| G2 | 3.428 c | 6.799 b | 0.242 c | 0.088 a | 0.079 a | |
| G4 | 2.992 d | 6.954 ab | 0.216 d | 0.083 a | 0.072 ab | |
| Gr | 2.910 e | 7.219 a | 0.207 e | 0.082 a | 0.071 ab | |
| Fruit Firmness | I | 509.180 f | 737.735 b | 0.275 f | 0.567 c | 0.798 c |
| A2 | 806.908 a | 741.089 b | 0.401 a | 0.881 b | 1.16 b | |
| A4 | 786.601 b | 742.547 b | 0.395 b | 0.877 b | 1.135 b | |
| G2 | 725.192 c | 734.332 b | 0.376 c | 1.243 a | 1.511 a | |
| G4 | 659.584 e | 749.865 b | 0.351 e | 1.217 a | 1.446 a | |
| Gr | 687.685 d | 783.729 a | 0.354 d | 1.257 a | 1.490 a | |
| pH | I | 0.053 a | 0.118 d | 0.253 a | 0.005 a | — |
| A2 | 0.052 a | 0.140 c | 0.241 b | 0.006 a | — | |
| A4 | 0.052 a | 0.140 c | 0.238 b | 0.005 a | — | |
| G2 | 0.052 a | 0.141 c | 0.241 b | 0.007 a | — | |
| G4 | 0.040 b | 0.147 b | 0.191 c | 0.006 a | — | |
| Gr | 0.035 c | 0.153 a | 0.165 d | 0.006 a | — | |
| Fruit Scar | I | 0.086 f | 0.073 d | 0.381 f | 0.008 c | 0.009 c |
| A2 | 0.139 a | 0.075 c | 0.528 a | 0.013 b | 0.014 b | |
| A4 | 0.135 b | 0.075 bc | 0.522 b | 0.013 b | 0.014 b | |
| G2 | 0.123 d | 0.075 cd | 0.500 c | 0.018 a | 0.018 a | |
| G4 | 0.115 e | 0.077 b | 0.479 e | 0.018 a | 0.017 a | |
| Gr | 0.126 c | 0.081 a | 0.494 d | 0.019 a | 0.018 a | |
| Fruit Weight | I | 0.217 f | 0.214 b | 0.374 f | 0.013 c | 0.014 c |
| A2 | 0.403 a | 0.207 c | 0.574 a | 0.021 b | 0.021 b | |
| A4 | 0.393 b | 0.205 c | 0.568 b | 0.021 b | 0.021 b | |
| G2 | 0.344 d | 0.206 c | 0.535 c | 0.030 a | 0.029 a | |
| G4 | 0.323 e | 0.215 b | 0.513 e | 0.029 a | 0.027 a | |
| Gr | 0.352 c | 0.231 a | 0.522 d | 0.030 a | 0.028 a | |
| Yield | I | 0.326 f | 0.444 bc | 0.310 f | 0.012 b | 0.015 c |
| A2 | 0.549 a | 0.442 bc | 0.447 a | 0.019 a | 0.022 b | |
| A4 | 0.536 b | 0.442 bc | 0.441 b | 0.020 a | 0.021 b | |
| G2 | 0.470 c | 0.441 c | 0.407 c | 0.026 a | 0.030 a | |
| G4 | 0.421 d | 0.458 b | 0.374 d | 0.024 a | 0.028 a | |
| Gr | 0.411 e | 0.493 a | 0.356 e | 0.023 a | 0.027 a |
Letters based on Tukey test performed considering estimations obtained from 10 independent runs of the full models with BGLR (equation 1).
Expected Genetic Gain on trait scale.
Effect of the genetic information to build the relationship matrices
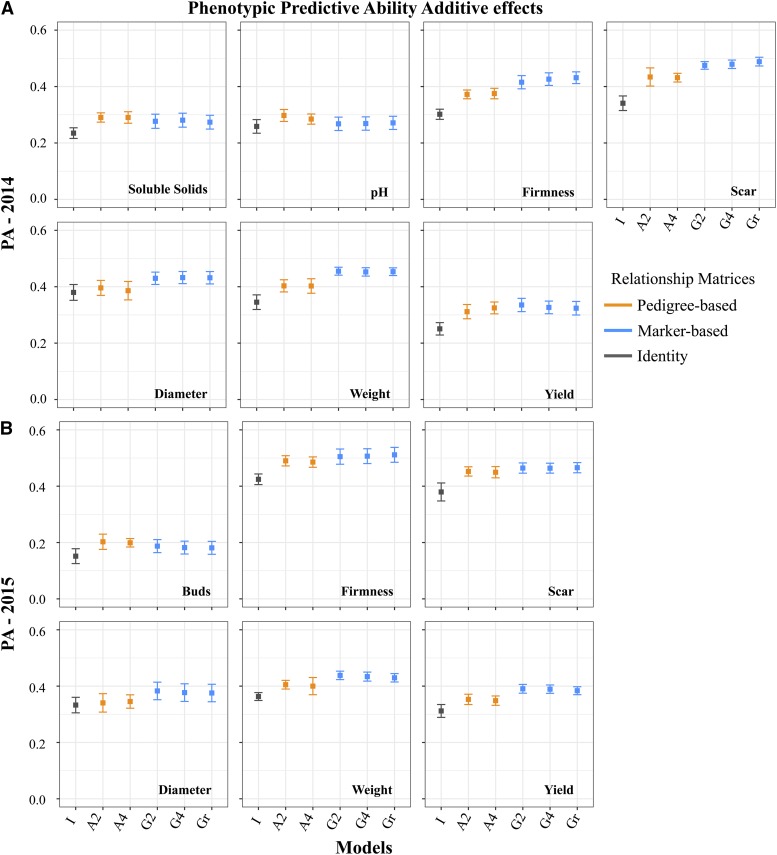
The incorporation of relationship information in the analysis generated better PA results than the phenotypic-BLUP model without it. Overall, we observed that higher values for the phenotypic PA were obtained when marker-based relationship matrices were used, when compared with phenotypic and pedigree BLUP (I and A matrices, respectively). However, the marker-based and pedigree-based results were not always significantly different from each other (Figure 3, Table S1). The use of molecular data yielded phenotypic PA values ranging from 0.27 (pH) to 0.49 (fruit scar) in 2014, and from 0.15 (flower buds) to 0.51 (fruit firmness) in 2015. Lower PA values were obtained for traits with lower heritability and better results were observed for the second year of evaluation. The biggest increase in the PA values can be seen for fruit firmness – when we compared marker and pedigree results, we observed an average increase of 13.37% in 2014. Also, an increase in the PA values of 11% was observed for fruit diameter and yield in 2015 when markers were used instead of pedigree data.
Figure 3.
Phenotypic predictive abilities. Predictive abilities obtained for (A) seven traits in 2014, and (B) for six traits in 2015 considering different dosage parameterizations (indicated by the numbers 2 or 4, and r for ratio values), and different relationship matrices (indicated by the letters I, A, and G) in the prediction of breeding values of 1,847 blueberry genotypes.
The use of pedigree-based relationship matrices generated higher phenotypic PA values for all the traits, when compared with the assumption of unrelated individuals (i.e., identity matrix). Unlike the identity matrix, the use of pedigree-based matrix assumes that there is relationship (expected values) among individuals. The phenotypic PA obtained for the pedigree methods in 2014 yielded values from 0.20 (flower bud) to 0.49 (fruit firmness). As with marker-based methods, smaller values were observed for traits with lower heritability (i.e., pH, brix, and flower bud). For 2015, the PA results for the phenotypic-BLUP were 0.36, 0.38, and 0.42, for fruit weight, fruit scar, and fruit firmness, respectively. The PA values obtained for the same traits with pedigree-BLUP were 0.40, 0.45, and 0.49, respectively. No significant differences between the models’ stability were observed (Table S1).
Use of dosage information and continuous genotypes
Our results indicate that the importance of dosage in GS will vary depending on the trait being analyzed. For example, in 2014 the PA for fruit firmness, fruit scar, and fruit diameter showed modestly better phenotypic PA when the tetraploid and continuous parameterizations were applied, as opposed to the diploid parameterization (Figure 3, Table S1). The addition of more classes for the representation of the genotypic classes added complexity to the models (Table S1), in other words bigger values of DIC were observed for G4 and Gr models. Although no significant difference was observed between marker-based models, the use of relationship matrices derived from continuous genotype data (ploidy-free parameterization) performed equally well as the best models (Figure 3, Table S1).
Expected genetic gain in a perennial fruit tree, blueberry
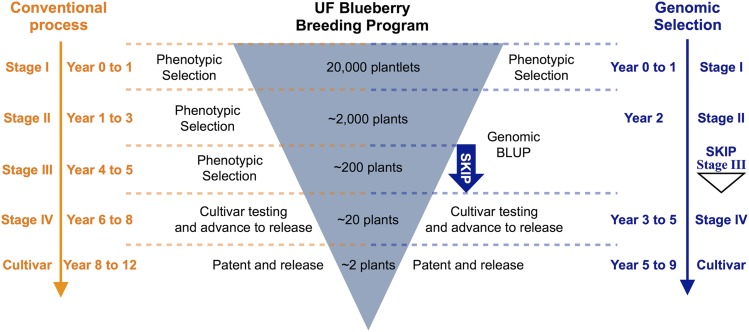
The results obtained for the expected genetic gain (EGG) are summarized in Table 3. GS offers the possibility to accelerate genetic improvement by decreasing the breeding cycle and selecting superior individuals earlier in the breeding program. Considering a breeding cycle (L) of 12 years (Cellon et al. 2018) we propose that routine genomic selection could be implemented in the second stage of the blueberry breeding program, which would allow the omission of a whole stage (stage III), and a three-year reduction for cultivar release (Figure 4).
Figure 4.
Proposal of GS implementation in the University of Florida blueberry breeding program. UF blueberry breeding program stages and times of selection considering the conventional process (left) compared with the proposed process implementing genomic selection (right).
Higher EGG was obtained for all traits when marker-based matrices (i.e., genomic selection) were applied (Table 3), which was mainly related to the reduction in cycle time. The implementation of GS in the second stage population would lead to an increase in the EGG varying from 27% (pH) to 119% (scar) when compared with the application of phenotypic BLUP. Considering the comparison of marker-based and pedigree-based models, an increase of 15% (pH) to 41% (fruit weight, fruit scar, and flower buds) in the EGG was observed (Table 3). In addition, the use of continuous data generated EGG values that were not significantly different of the best models for all traits (Table 3).
Discussion
In this study, six approaches were applied to predict breeding values for eight yield and fruit-quality traits measured in a real blueberry breeding population. Analyses were based on phenotypic, pedigree, and high-density marker data from 1,847 individuals. We compared the expected genetic gain, the stability, and the PA of models considering different sources to build the relationship matrices (only phenotype = BLUP, phenotypes + pedigree = P-BLUP, phenotypes + genomic = G-BLUP). Our results also explored models accounting for ploidy information and compared the use of genotypic data that is independent of assumptions regarding ploidy levels (continuous) to perform GS, avoiding the need for a priori parameterization for a given ploidy level.
Continuous data
Our research showed empirical evidences that the use of continuous genotypic data from NGS can be effectively applied in GS models for autotetraploid species. This method was tested and compared with marker calling methodologies at the individual level in genome wide association studies (Grandke et al. 2016). It was also tested in family pool data for GS (Ashraf et al. 2014; Cericola et al. 2018; Guo et al. 2018), as well as used at the individual level in tetraploid potato for GS by Sverrisdóttir et al. (2017). However, to our knowledge the comparison of continuous genotypes with ploidy parameterizations for genomic selection has not yet been reported. Here we empirically compare diploid, tetraploid, and continuous data at the individual level for the application of genomic selection in an autotetraploid species.
In polyploids, the assignment of genotypic classes based on NGS data has been a major challenge, with high risk of misclassification (Grandke et al. 2016, Bourke et al. 2018). The problem is further exacerbated as the ploidy increases – for a given level of ploidy, n, the expected number of genotypic classes is 2n+1. As a consequence, the signal distribution derived from each genotypic class increasingly approximates a continuous distribution, where no clear separation is observed (Grandke et al. 2016). Despite extensive research to address these challenges (Serang et al. 2012), advances have been mostly limited to SNP arrays in tetraploid data (Schmitz Carley et al. 2017). Studies that evaluated genotype calling with NGS data obtained from polyploids show that no method works properly, and that misclassification of genotypes can significantly interfere in the results of genetic studies (Grandke et al. 2016). This misclassification can be observed in our results when are diploid, or tetraploid parameterization were used in the genomic data (Figure 2A-B), even with our high sequencing depth and with standard parameters of filtering. The use of the continuous genotyping approach provides a relevant alternative to overcome this issue that is independent of assumptions regarding ploidy level. Models that used continuous genotypic data performed as well as the best models and resulted in modestly better predictive abilities for some of the traits (i.e., fruit firmness, fruit scar, and fruit diameter; Table 3), which could indicate better prediction of future populations. The use of continuous genotypes also simplifies the analysis complexity and time, by eliminating the genotype calling and parameterization for a give ploidy, because instead, the ratio of reads assigned to each allele are used. The benefits of continuous genotyping could easily be extended to more complex polyploids (higher ploidies), where the genotype attribution is even more difficult, however higher sequencing depth would be required. Meanwhile, for more complex models, such as those that consider dominance effects, dosage calling is still necessary.
Relationship matrices
Our results also showed that including information based on the genetic merit of the individuals yielded better results when compared with the phenotypic-BLUP analysis (based on the identity matrix; Table 3), corroborating previous studies in the literature (e.g., Muir 2007; Resende et al. 2012a; Muñoz et al. 2014a). In addition, the use of marker-based methodologies generated better predictions than pedigree for most of the traits. Marker-based methods allow the capture of Mendelian segregation (Daetwyler et al. 2013;). This is especially important in our population, since it was composed of 117 full-sib families. In this context, pedigree-based methods have no power to distinguish variance within families. Another advantage is that marker-based methods allows the computation of genetic similarity among unidentified individuals in the pedigree, and corrections of errors in the pedigree, which can affect parameter estimation causing reduction in the genetic gain (Muñoz et al. 2014b).
In our results, some non-significant differences between pedigree and marker-based methods were identified, which could be an effect of the extensive pedigree data used, as well as bias in pedigree-based estimations. Pedigree-based methods can overestimate the reliability of selection and consequently, the accuracy (Bulmer 1971; Gorjanc et al. 2015). Furthermore, it also presents low efficiency to capture and estimate genetic relationships among individuals (Resende et al. 2017).
It is interesting to notice that we used extensive pedigree information that dates back to 1907 for our predictions, which may not be common in other autopolyploid breeding. This extensive information can have significant implications on the estimation of relationship coefficients (Amadeu et al. 2016) and consequently, in breeding value predictions. Therefore, for breeding programs with smaller pedigree depth information, the comparison between accuracies of prediction from marker and pedigree-based methodologies could be even bigger than what was found in our study.
Allele dosage
The results obtained for both models that assumed more than three genotypic classes (G4 and Gr) demonstrate the importance of considering dosage in the prediction of breeding values. However, this will depend on the trait analyzed, as previously reported by Nyine et al. (2018) and Endelman et al. (2018). For example, modest improvement was verified in the PA for fruit firmness, fruit scar, and fruit diameter when this factor was considered in the models. The addition of classes for the representation of ploidy increased the complexity of the models (Figure 3, Table 3, Table S1) however, these assumptions also show a more realistic representation of the nature of the species. The inclusion of nonadditive effects into the models could also improve model accuracy. Endelman et al. (2018) demonstrated that the inclusion of digenic effects, as well as accounting for ploidy information, presented a higher accuracy over diploid models when using a SNP array.
Genomic selection for perennial autopolyploids
We also demonstrate the value of applying GS in a perennial fruit tree, blueberry. One cycle of blueberry breeding takes from 12 to 15 years until the release of a new cultivar (Lyrene 2008; Cellon et al. 2018). By applying selection based on high-density markers at early stages of the program, the time to cultivar release could decrease by three years (Figure 4), significantly improving the expected genetic gain per unit of time. More specifically, the use of GS would lead to an average increase of 86% in the EGG when compared with phenotypic BLUP, and an average increase of 32% over the application of pedigree-based models (Table 3). Implementing GS as we propose here could eliminate one stage in the breeding and selection process toward cultivar development, which will reduce costs associated with field trials and phenotyping. The implementation of GS would require extra financial outlay when genotyping and accurately phenotyping the training population. However, the savings on phenotyping and field trials of future generations (selection populations) could result in a break-even financial exercise, and as a result could be a cost-effective application of GS. However, this financial analysis needs to be performed for each crop in a case-by-case basis. To promote further studies on the effect of dosage calling using NGS, as methods and software improve, we are providing genotypic and phenotypic data to use as comparison of methods in the context of GS.
Funding
This project was funded by the Agriculture and Food Research Initiative Grant no. 2014-67013-22418 to Patricio R. Munoz, James W. Olmstead and Jeffrey B. Endelman from the USDA National Institute of Food and Agriculture. Ivone de Bem Oliveira was funded by the CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior), Grant no: 88881.131685/2016-01.
Conflict of Interest
The authors declare that they have no conflict of interest.
Acknowledgments
The authors thank the University of Florida blueberry breeding program technical support, especially Dr. Paul M. Lyrene, David Norden, and Werner Collante. Special thanks to James Olmstead and Catherine Cellon, who coordinate the phenotyping and genotyping of the population as part of Catherine Cellon’s MS degree.
Footnotes
Supplemental material available at Figshare: https://doi.org/10.25387/g3.7728365.
Communicating editor: D. J. de Koning
Literature Cited
- Adams K. L., Cronn R., Percifield R., Wendel J. F., 2003. Genes duplicated by polyploidy show unequal contributions to the transcriptome and organ-specific reciprocal silencing. Proc. Natl. Acad. Sci. USA 100: 4649–4654. 10.1073/pnas.0630618100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amadeu R. R., Cellon C., Olmstead J. W., Garcia A. A., Resende M. F., et al. , 2016. AGHmatrix: R Package to construct relationship matrices for autotetraploid and diploid species: a blueberry example. Plant Genome 9 10.3835/plantgenome2016.01.0009 [DOI] [PubMed] [Google Scholar]
- Annicchiarico P., Nazzicari N., Li X., Wei Y., Pecetti L., et al. , 2015. Accuracy of genomic selection for alfalfa biomass yield in different reference populations. BMC Genomics 16: 1020 10.1186/s12864-015-2212-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashraf B. H., Jensen J., Asp T., Janss L. L., 2014. Association studies using family pools of outcrossing crops based on allele-frequency estimates from DNA sequencing. Theor. Appl. Genet. 127: 1331–1341. 10.1007/s00122-014-2300-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashraf B. H., Byrne S., Fé D., Czaban A., Asp T., et al. , 2016. Estimating genomic heritabilities at the level of family-pool samples of perennial ryegrass using genotyping-by-sequencing. Theor. Appl. Genet. 129: 45–52. 10.1007/s00122-015-2607-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian Y., Ballington J., Raja A., Brouwer C., Reid R., et al. , 2014. Patterns of simple sequence repeats in cultivated blueberries (Vaccinium section Cyanococcus spp.) and their use in revealing genetic diversity and population structure. Mol. Breed. 34: 675–689. 10.1007/s11032-014-0066-7 [DOI] [Google Scholar]
- Birchler J. A., Bhadra U., Bhadra M. P., Auger D. L., 2001. Dosage-dependent gene regulation in multicellular eukaryotes: implications for dosage compensation, aneuploid syndromes, and quantitative traits. Dev. Biol. 234: 275–288. 10.1006/dbio.2001.0262 [DOI] [PubMed] [Google Scholar]
- Bourke P. M., Voorrips R. E., Visser R. G., Maliepaard C., 2018. Tools for genetic studies in experimental populations of polyploids. Front. Plant Sci. 9: 513 10.3389/fpls.2018.00513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulmer M., 1971. The effect of selection on genetic variability. Am. Nat. 105: 201–211. 10.1086/282718 [DOI] [Google Scholar]
- Cellon C., Amadeu R. R., Olmstead J. W., Mattia M. R., Ferrão L. F. V., et al. , 2018. Estimation of genetic parameters and prediction of breeding values in an autotetraploid blueberry breeding population with extensive pedigree data. Euphytica 214: 87 10.1007/s10681-018-2165-8 [DOI] [Google Scholar]
- Cericola F., Lenk I., Fè D., Byrne S., Jensen C. S., et al. , 2018. Optimized Use of Low-Depth Genotyping-by-Sequencing for Genomic Prediction Among Multi-Parental Family Pools and Single Plants in Perennial Ryegrass (Lolium perenne L.). Front. Plant Sci. 9: 369 10.3389/fpls.2018.00369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comai L., 2005. The advantages and disadvantages of being polyploid. Nat. Rev. Genet. 6: 836–846. 10.1038/nrg1711 [DOI] [PubMed] [Google Scholar]
- Daetwyler H. D., Calus M. P. L., Pong-Wong R., de los Campos G., Hickey J. M., 2013. Genomic Prediction in Animals and Plants: Simulation of Data, Validation, Reporting, and Benchmarking. Genetics 193: 347–365. 10.1534/genetics.112.147983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos, G., and P. Pérez-Rodríguez, 2016 BGLR: Bayesian Generalized Linear Regression. R package version 1.0.5. https://cran.r-project.org/package=BGLR.
- de los Campos G., Hickey J. M., Pong-Wong R., Daetwyler H. D., Calus M. P., 2013. Whole-genome regression and prediction methods Applied to plant and animal breeding. Genetics 193: 327–345. 10.1534/genetics.112.143313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desta Z. A., Ortiz R., 2014. Genomic selection: genome-wide prediction in plant improvement. Trends Plant Sci. 19: 592–601. 10.1016/j.tplants.2014.05.006 [DOI] [PubMed] [Google Scholar]
- Dufresne F., Stift M., Vergilino R., Mable B. K., 2014. Recent progress and challenges in population genetics of polyploid organisms: an overview of current state‐of‐the‐art molecular and statistical tools. Mol. Ecol. 23: 40–69. 10.1111/mec.12581 [DOI] [PubMed] [Google Scholar]
- Endelman J. B., Carley C. A. S., Bethke P. C., Coombs J. J., Clough M. E., et al. , 2018. Genetic variance partitioning and genome-wide prediction with allele dosage information in autotetraploid potato. Genetics 209: 77–87. 10.1534/genetics.118.300685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrão L. F. V., Benevenuto J., de Bem Oliveira I., Cellon C., Olmstead J., et al. , 2018. Insights into the genetic basis of blueberry fruit-related traits using diploid and polyploid models in a GWAS context. Front. Ecol. Evol. 6: 107 10.3389/fevo.2018.00107 [DOI] [Google Scholar]
- Garrison, E., G. and Marth, 2012 Haplotype-based variant detection from short-read sequencing. arXiv preprint arXiv:1207.3907.
- Gorjanc G., Bijma P., Hickey J. M., 2015. Reliability of pedigree-based and genomic evaluations in selected populations. Genet. Sel. Evol. 47: 65 10.1186/s12711-015-0145-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouy M., Rousselle Y., Bastianelli D., Lecomte P., Bonnal L., et al. , 2013. Experimental assessment of the accuracy of genomic selection in sugarcane. Theor. Appl. Genet. 126: 2575–2586. 10.1007/s00122-013-2156-z [DOI] [PubMed] [Google Scholar]
- Grandke F., Singh P., Heuven H. C., De Haan J. R., Metzler D., 2016. Advantages of continuous genotype values over genotype classes for GWAS in higher polyploids: a comparative study in hexaploid chrysanthemum. BMC Genomics 17: 672 10.1186/s12864-016-2926-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo M., Davis D., Birchler J. A., 1996. Dosage effects on gene expression in a maize ploidy series. Genetics 142: 1349–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X., Cericola F., Fè D., Pedersen M. G., Lenk I., et al. , 2018. Genomic Prediction in Tetraploid Ryegrass Using Allele Frequencies Based on Genotyping by Sequencing. Front. Plant Sci. 9: 1165 10.3389/fpls.2018.01165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta V., Estrada A. D., Blakley I., Reid R., Patel K., et al. , 2015. RNA-Seq analysis and annotation of a draft blueberry genome assembly identifies candidate genes involved in fruit ripening, biosynthesis of bioactive compounds, and stage-specific alternative splicing. Gigascience 4: 5 10.1186/s13742-015-0046-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson C. R., 1976. A simple method for computing the inverse of a numerator relationship matrix used in prediction of breeding values. Biometrics 32: 69–83. 10.2307/2529339 [DOI] [Google Scholar]
- Hieter P., Griffiths T., 1999. Polyploidy–more is more or less. Science 285: 210–211. 10.1126/science.285.5425.210 [DOI] [PubMed] [Google Scholar]
- Jombart T., Ahmed I., 2011. adegenet 1.3–1: new tools for the analysis of genome-wide SNP data. Bioinformatics 27: 3070–3071. 10.1093/bioinformatics/btr521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kempthorne O., 1957. An introduction to genetic statistics, John Wiley And Sons, Inc., New York. [Google Scholar]
- Kerr R. J., Li L., Tier B., Dutkowski G. W., McRae T. A., 2012. Use of the numerator relationship matrix in genetic analysis of autopolyploid species. Theor. Appl. Genet. 124: 1271–1282. 10.1007/s00122-012-1785-y [DOI] [PubMed] [Google Scholar]
- Lee W. P., Stromberg M. P., Ward A., Stewart C., Garrison E. P., et al. , 2014. MOSAIK: a hash-based algorithm for accurate next-generation sequencing short-read mapping. PLoS One 9: e90581 10.1371/journal.pone.0090581 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyrene P., 2002. Development of highbush blueberry cultivars adapted to Florida. J. Am. Pomol. Soc. 56: 79. [Google Scholar]
- Lyrene P., 2008. Breeding southern highbush blueberries. Plant Breed. Rev. 30: 353–414. 10.1002/9780470380130.ch8 [DOI] [Google Scholar]
- Meuwissen T. H. E., Hayes B. J., Goddard M. E., 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollinari M., Serang O., 2015. Quantitative SNP genotyping of polyploids with MassARRAY and other platforms, pp. 215–241 in Plant Genotyping edited by Humana Press, New York, NY. [DOI] [PubMed] [Google Scholar]
- Muir W. M., 2007. Comparison of genomic and traditional BLUP‐estimated breeding value accuracy and selection response under alternative trait and genomic parameters. J. Anim. Breed. Genet. 124: 342–355. 10.1111/j.1439-0388.2007.00700.x [DOI] [PubMed] [Google Scholar]
- Muñoz P. R., Resende M. F., Huber D. A., Quesada T., Resende M. D., et al. , 2014a Genomic relationship matrix for correcting pedigree errors in breeding populations: impact on genetic parameters and genomic selection accuracy. Crop Sci. 54: 1115–1123. 10.2135/cropsci2012.12.0673 [DOI] [Google Scholar]
- Muñoz P. R., Resende M. F., Jr., Gezan S. A., Resende M. D. V., de Los Campos G., et al. , 2014b Unraveling additive from nonadditive effects using genomic relationship matrices. Genetics 198: 1759–1768. 10.1534/genetics.114.171322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyine M., Uwimana B., Blavet N., Hřibovà E., Vanrespaille H., et al. , 2018. Genomic prediction in a multiploid crop: genotype by environment interaction and allele dosage effects on predictive ability in banana. Plant Genome 11 10.3835/plantgenome2017.10.0090 [DOI] [PubMed] [Google Scholar]
- Osborn T. C., Pires J. C., Birchler J. A., Auger D. L., Chen Z. J., et al. , 2003. Understanding mechanisms of novel gene expression in polyploids. Trends Genet. 19: 141–147. 10.1016/S0168-9525(03)00015-5 [DOI] [PubMed] [Google Scholar]
- Pérez P., de los Campos G., 2014. Genome-wide regression and prediction with the BGLR statistical package. Genetics 198: 483–495. 10.1534/genetics.114.164442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team, 2018 R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna. Austria. ISBN 3–900051–07–0. URL http://www.R-project.org/.
- Resende M. F. R., Muñoz P., Acosta J. J., Peter G. F., Davis J. M., et al. , 2012a Accelerating the domestication of trees using genomic selection: accuracy of prediction models across ages and environments. New Phytol. 193: 617–624 (erratum: New Phytol. 193: 1099). 10.1111/j.1469-8137.2011.03895.x [DOI] [PubMed] [Google Scholar]
- Resende R. T., Resende M. D. V., Silva F. F., Azevedo C. F., Takahashi E. K., et al. , 2017. Assessing the expected response to genomic selection of individuals and families in Eucalyptus breeding with an additive-dominant model. Heredity 119: 245–255. 10.1038/hdy.2017.37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Resende M. F. R., Muñoz P., Resende M. D., Garrick D. J., Fernando L. R., et al. , 2012b Accuracy of genomic selection methods in a standard data set of loblolly pine (Pinus taeda L.). Genetics 190: 1503–1510. 10.1534/genetics.111.137026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindelin J., Arganda-Carreras I., Frise V., Kaynig E., Longair M., et al. , 2012. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9: 676–682. 10.1038/nmeth.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitz Carley C. A., Coombs J. J., Douches D. S., Bethke P. C., Palta J. P.et al. , 2017. Automated tetraploid genotype calling by hierarchical clustering. Theor. Appl. Genet. 130: 717–726. 10.1007/s00122-016-2845-5 [DOI] [PubMed] [Google Scholar]
- Serang O., Mollinari M., Garcia A. A. F., 2012. Efficient exact maximum a posteriori computation for bayesian SNP genotyping in polyploids. PLoS One 7: e30906 10.1371/journal.pone.0030906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slater A. T., Wilson G. M., Cogan N. O., Forster J. W., Hayes B. J., 2014. Improving the analysis of low heritability complex traits for enhanced genetic gain in potato. Theor. Appl. Genet. 127: 809–820. 10.1007/s00122-013-2258-7 [DOI] [PubMed] [Google Scholar]
- Slater A. T., Cogan N. O., Forster J. W., Hayes B. J., Daetwyler H. D., 2016. Improving genetic gain with genomic selection in autotetraploid potato. Plant Genome 9 10.3835/plantgenome2016.02.0021 [DOI] [PubMed] [Google Scholar]
- Soltis D. E., Visger C. J., Marchant D. B., Soltis P. S., 2016. Polyploidy: pitfalls and paths to a paradigm. Am. J. Bot. 103: 1146–1166. 10.3732/ajb.1500501 [DOI] [PubMed] [Google Scholar]
- Soltis D. E., Soltis P. S., Schemske D. W., Hancock J. F., Thompson J. N., et al. , 2007. Autopolyploidy in angiosperms: have we grossly underestimated the number of species? Taxon 56: 13–30. [Google Scholar]
- Soltis D. E., Soltis P. S., 1999. Polyploidy: recurrent formation and genome evolution. Trends Ecol. Evol. 14: 348–352. 10.1016/S0169-5347(99)01638-9 [DOI] [PubMed] [Google Scholar]
- Spiegelhalter D. J., Best N. G., Carlin B. P., Van Der Linde A., 2002. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Series B Stat. Methodol. 64: 583–639. 10.1111/1467-9868.00353 [DOI] [Google Scholar]
- Spoelhof J. P., Soltis P. S., Soltis D. E., 2017. Pure polyploidy: closing the gaps in autopolyploid research. J. Syst. Evol. 55: 340–352. 10.1111/jse.12253 [DOI] [Google Scholar]
- Sverrisdóttir E., Byrne S., Sundmark E. H. R., Johnsen H. O., Kirk H. G., et al. , 2017. Genomic prediction of starch content and chipping quality in tetraploid potato using genotyping-by-sequencing. Theor. Appl. Genet. 130: 2091–2108. 10.1007/s00122-017-2944-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uitdewilligen J. G., Wolters A. M. A., Bjorn B., Borm T. J., Visser R. G., et al. , 2013. A next-generation sequencing method for genotyping-by-sequencing of highly heterozygous autotetraploid potato. PLoS One 8: e62355 (erratum: PLoS One 10: e0141940). 10.1371/journal.pone.0062355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanRaden P. M., 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91: 4414–4423. 10.3168/jds.2007-0980 [DOI] [PubMed] [Google Scholar]
- Zhang Z., Ding X., Liu J., de Koning D. J., Zhang Q., 2011. Genomic selection for QTL-MAS data using a trait-specific relationship matrix. BMC Proc. 5: S15 10.1186/1753-6561-5-S3-S15 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Phenotypic datasets (eBLUES) are available from the Dyrad Digital Repository (accession number doi: 10.5061/dryad.kd4jq6h). Genotypic data and supplemental material are available at Figshare. Files include diploid, tetraploid and continuous genotypes, supplemental information 1 to 5, which includes: 1) description of the matrices used in the study; 2) model convergence figure; 3) LD distribution per parameterization; 4) principal components plots for each parameterization; 5) table of the predictive abilities, MSE, goodness-of-fit and beta for each parameterization. The authors ratify that all data necessary for confirming the conclusions of the article are present within the article, figures, and tables. Supplemental material available at Figshare: https://doi.org/10.25387/g3.7728365.