Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Apr 17.
Published in final edited form as: Biosens Bioelectron. 2007 Feb 20;22(12):3132–3138. doi: 10.1016/j.bios.2007.02.005

In situ, in-liquid, all-electrical detection of Salmonella typhimurium using lead titanate zirconate/gold-coated glass cantilevers at any dipping depth

Qing Zhu a, Wan Y Shih b,*, Wei-Heng Shih a
PMCID: PMC6469510  NIHMSID: NIHMS29050  PMID: 17387007

Abstract

Most biosensing techniques are indirect, slow, and require labeling. Even though silicon-based microcantilever sensors are sensitive and labelfree, they are not suitable for in-liquid detection. More recently lead zirconate titanate (PZT) thin-film-based microcantilevers are shown to be sensitive and in situ. However, they require microfabrication and must be electrically insulated. In this study, we show that highly sensitive, in situ, Salmonella typhimurium detection can be achieved at 90% relative humidity using a lead zirconate titanate (PZT)/gold-coated glass cantilever 0.7mm long with a non-piezoelectric 2.7mm long gold-coated glass tip by partially dipping the gold-coated glass tip in the suspension at any depth without electrically insulating the PZT. In particular, we showed that at 90% relative humidity and with a dipping depth larger than 0.8mm the PZT/gold-coated glass cantilever showed virtually no background resonance frequency up-shift due to water evaporation and exhibited a mass detection sensitivity of Δm/Δf =−5×10−11 g/Hz. The concentration sensitivities of this PZT/gold-coated glass cantilever were 1×103 and 500 cells/ml in 2 ml of liquid with a 1 and 1.5mm dipping depth, respectively, both more than two orders of magnitude lower than the infectious dose and more than one order of magnitude lower than the detection limit of a commercial Raptor sensor.

Keywords: Piezoelectric cantilever, Cell detection, Mass sensitivity, Dipping depth

1. Introduction

Current methods for pathogen detection in water include filtration culture methods (EPA, on-line publication), fluorescence-based methods (Nie and Zare, 1997; Chuang et al., 2001; Call et al., 2001), fluorescence probes (Chuang et al., 2001), deoxyribonucleic acid (DNA) microarray methods (Call et al., 2001), and others. These approaches do not allow in situ measurements. Another development is microcantilever-based sensors that can be direct and do not require labeling. Antibody receptors are coated on the microcantilever surface to bind the target DNA, protein molecules, or bacteria (Fritz et al., 2000; Schemmel and Gaub, 1999; Baselt et al., 1996; Lee et al., 1996; Han et al., 1996; Thundat et al., 1995; Ilic et al., 2000). Binding of target antigens to the receptors on the microcantilever surface is detected by monitoring the bending displacement of microcantilever’s tip (Fritz et al., 2000; Schemmel and Gaub, 1999; Baselt et al., 1996; Lee et al., 1996; Han et al., 1996), or its resonance frequency shift (Thundat et al., 1995; Ilic et al., 2000). The majority of the microcantilever sensors are based on silicon microcantilevers that require an external actuator and an external optical detector, which cannot withstand damping by water and exhibit low Q factors (the ratio of the resonance peak frequency to the resonance peak width at half peak height) in-liquid (Oden et al., 1996) and render them ineffective for in-water detection. Piezoelectric cantilevers, on the other hand, can self-excite and self-detect the mechanical resonance electrically. In particular, piezoelectric lead zirconate titanate (PZT) cantilevers with a non-piezoelectric tip such as stainless steel or glass at the free end were shown to exhibit good Q values (Shih et al., 2001; Yi et al., 2003; Shih and Shih, 2006) and were demonstrated for all-electrical in situ cell detection with the non-piezoelectric tip serving as the detection pad alleviating the need to insulate the electrodes of the PZT layer (Yi et al., 2003; Shih and Shih, 2006). However, with the detection sensitivity improved with a reduced cantilever size (Shih and Shih, 2006; Yi et al., 2002; Shen et al., 2006a,b), the effect of the water-level change due to evaporation could give rise to a background up-shift in the cantilever resonance frequency (Campbell and Mutharasan, 2005a). Therefore, a predetermined background frequency shift needs to be subtracted from the detection result (Campbell and Mutharasan, 2005b). However, it is known that the background resonance frequency shift depends on the humidity level and the dipping depth (Zhu et al., 2007). Therefore, this predetermined background correction is prone to errors associated with dipping depth variation and humidity level changes from day to day. Often the background correction became an adjustable parameter in the data analysis.

To remove the effect of the background resonance frequency up-shift and to further improve the detection sensitivity of a piezoelectric cantilever without electrical insulation of the PZT layer, in this study we explored all-electrical in situ cell detection using a PZT/gold-coated glass cantilever with a non-piezoelectric gold-coated glass tip at high (90%) relative humidity. The 90% relative humidity was chosen because it was high enough to minimize the background up-shift but not too high to cause condensation which could potentially down-shift the resonance frequency and exaggerate the detection result. Although 90% relative humidity does not readily occur in most air-conditioned interior environment, it can be easily implemented in a semi-closed chamber as we will show below. Furthermore, we will show that the background resonance frequency up-shift diminished at 90% relative humidity at any dipping depth, eliminating the need for adjustable corrections and making the detections more reliable.

2. Experimental procedure

The PZT/gold-coated glass cantilever was constructed by bonding a 127 μm thick PZT layer (T105-H4E-602, Piezo System Inc., Cambridge, MA) 0.7 mm long, 2.3 mm wide to a 150 μm thick glass layer (Fisher Scientific, Pittsburgh, PA) coated with gold using a non-conductive epoxy (Loctite, Rocky Hill, CT). The 150 nm thick gold layer was coated with 10 nm thick chromium as the bonding layer between the glass substrate and the gold layer. Both chromium and gold were deposited by e-beam evaporation (E-gun: 3 kW, vacuum 2×10−6torr) at the Microfabrication Laboratory of University of Pennsylvania. The gold-coated glass layer was extended at the free end to form a 2.7mm long tip which was subsequently immobilized with antibodies for cells detection. An optical micrograph of a PZT/gold-coated glass cantilever is shown in Fig. 1(a). The chemicals used were glycine (Fisher Scientific, Fair Lawn, NJ), N-(3-dimethylaminopropyl)-N′-ethylcarbodiimide hydrochloride (EDC) (Sigma, St. Louis, MO), N-hydroxysuccinimide (NHS) (Aldrich, Milwaukee, WI), HCl (Fisher Scientific, Pittsburg, PA), and 3-mercaptopropionic acid (MPA) (Aldrich, Milwaukee, WI). The heat-killed Salmonella typhimurium cells and the affinity purified antibody to salmonella common structural antigens were purchased from Kirkegaard & Perry Laboratories Inc., Gaithersburg, MD. After each detection, the cantilever was dipped in a mixed solution of glycine and HCl at pH 2.2 for 30 min to release the cells. After the release in the glycine/HCl solution, the antibody-immobilized cantilever sensor was reused for detection. With this glycine/HCl release procedure, the cantilever sensor was reused for more than 40 times. The scanning electron microscopy (SEM) micrographs of the cells captured at the gold-coated cantilever tip were obtained using FEI/Phillips XL30 (FEI Company, Hillsboro, OR). The detection was carried out by monitoring the resonance frequency of the cantilever with an impedance analyzer (Agilent 4294A, Agilent, Palo Alto, CA). The mass detection sensitivity of the gold-coated glass cantilever sensors was calibrated with a 5 MHz AT-cut quartz crystal microbalance (QCM) (QCM100, Stanford Research Systems Inc., Sunnyvale, CA). The resonance frequency of the QCM was also monitored by the Agilent 4294A impedance analyzer.

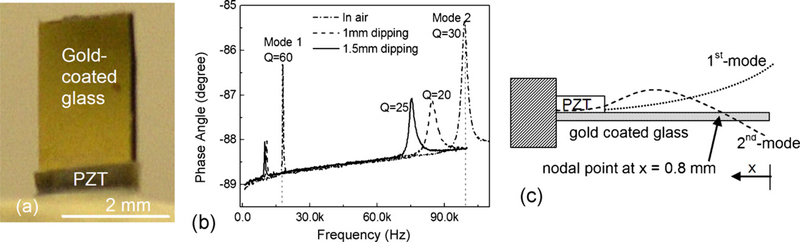
Fig. 1.

Fig. 1.

Open in a new tab

(a) An optical micrograph of the top-side view of the PZT/gold-coated glass cantilever, (b) phase angle vs. frequency resonance spectra in air (dashed-dotted line) and in PBS with a 1 mm (dashed line) and 1.5 mm (solid line) dipping depth, and (c) a schematic side view of the PZT/gold-coated glass cantilever, and the theoretical first- and second-mode flexural vibration waveforms of the PZT/gold-coated glass cantilever.

3. Results and discussion

The optical micrograph of the cantilever is shown in Fig. 1(a) and the in-air phase-angle-versus-frequency resonance spectrum of a PZT/gold-coated glass cantilever is shown in Fig. 1(b) as the dashed-dotted line. Off resonance, the cantilever behaved as a capacitor exhibiting a phase angle close to −90°. At resonance, the flexural motion gave rise to a peak in the real part of the electrical impedance, and hence a peak in the phase angle. The spectrum shows that below 100 kHz, the cantilever exhibited two resonance peaks, the first peak at 18 kHz and the second peak at 99 kHz, with quality factors, Q= 60 and 30 for the 1st and 2nd peaks, respectively. Also shown in Fig. 1(b) as vertical dashed lines are the calculated first- and second-mode flexural resonance frequencies obtained using the method described in Shen et al. (2006a). Both experimental peaks lined up with the vertical dashed lines, indicating that they were the first- and second-mode flexural resonance peaks. The second-mode waveform exhibited a nodal point near the free end. The theoretical first- and second-mode resonance waveforms calculated using the theory of Shen et al. (2006a) are shown along with the schematic side view of the cantilever in Fig. 1(c). Note that the theoretical waveforms were not shown to scale. They only meant to illustrate the spatial variations of the waveforms. As can be seen from Fig. 1(c), the theoretical nodal point of the second-mode waveform was at x = 0.8 mm where x was measured from the free end of the tip. The detections were carried out by monitoring the second-mode resonance frequency at a dipping depth of 1 mm as well as 1.5 mm. The resonance spectra of the cantilever at a dipping depth of 1 and 1.5mm are shown in Fig. 1(b) as the dashed and solid lines, respectively. As can be seen, the resonance frequencies of the cantilever decreased with an increasing dipping depth. The decrease in the cantilever’s resonance frequency in phosphate buffered saline solution (PBS) (the medium of all detections) was mainly due to the mass of the surrounding liquid that moved in phase with the cantilever, which increased the effective mass of the cantilever (Shih et al., 2001). However, the in-PBS resonance frequency peaks still retained the high Q values with Q = 20 and 25 for the second-mode resonance peak at a 1 and a 1.5mm dipping depth, respectively.

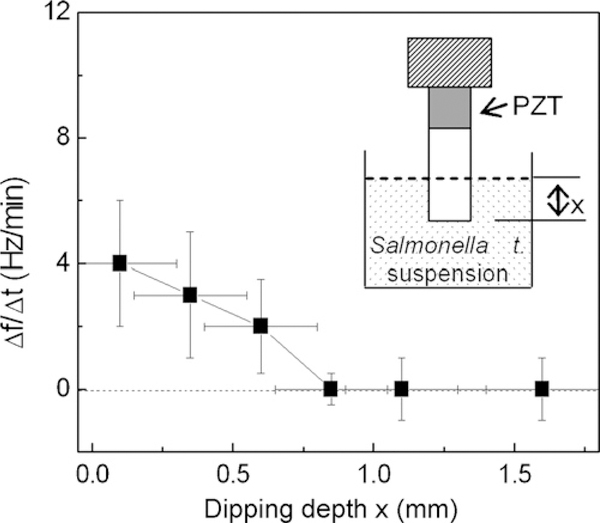
Ninety percent relative humidity was achieved and maintained by blowing water vapor with a humidifier (model 701, Sunbeam Product Inc., Boca Raton, FL) into an open 1261 glove box (model H500280000, Bel-Art Products, Pequannock, NJ). The humidity and temperature were monitored using a humidity and temperature sensor (model 35519–050, VWR International, West Chester, PA). The temperature of the chamber was 21±0.2 °C. The uncertainty of the relative humidity was about±10% at 90% relative humidity as the humidity sensor could only measure the humidity accurately below 90% relative humidity. To determine the rate of water level change, we filled a small container of less than 2 ml capacity with the PBS and placed it at 90% relative humidity for 24 h. At the end of the 24 h, there was no measurable water level change partly due to the high humidity level and partly due to the uncertainty in humidity control from the limitation of the humidity sensor as mentioned above. To measure the cantilever’s background resonance frequency shift at 90% relative humidity, we dipped the cantilever in the PBS at different dipping depths, x and monitored the cantilever’s second-mode resonance frequency for 30 min at each dipping level. A schematic of the dipping configuration is shown in the insert of Fig. 2. The rate of resonance frequency up-shift, Δf/Δt versus dipping depth x at 90% relative humidity is shown in Fig. 2 with Δt = 30 min and Δf denoting the corresponding frequency shift. As can be seen, at 90% relative humidity, Δf/Δt decreased with an increasing dipping depth and became negligible for all x ≥ 0.8 mm. The above results indicated that with a controlled 90% relative humidity, there was virtually no background resonance frequency up-shift at x ≥ 0.8 mm and the background resonance frequency was stable with fluctuations no larger than 10 Hz.

Fig. 2.

Fig. 2.

Open in a new tab

Rate of resonance frequency shift, Δf/Δt vs. dipping depth, x, at 90% relative humidity. The insert is a schematic of the PZT/gold-coated glass cantilever partially immersed in PBS with a dipping depth, x. Note that for x larger than 0.8 mm, Δf/Δt was essentially negligible and the background resonance frequency was stable with a fluctuation no more than 10 Hz.

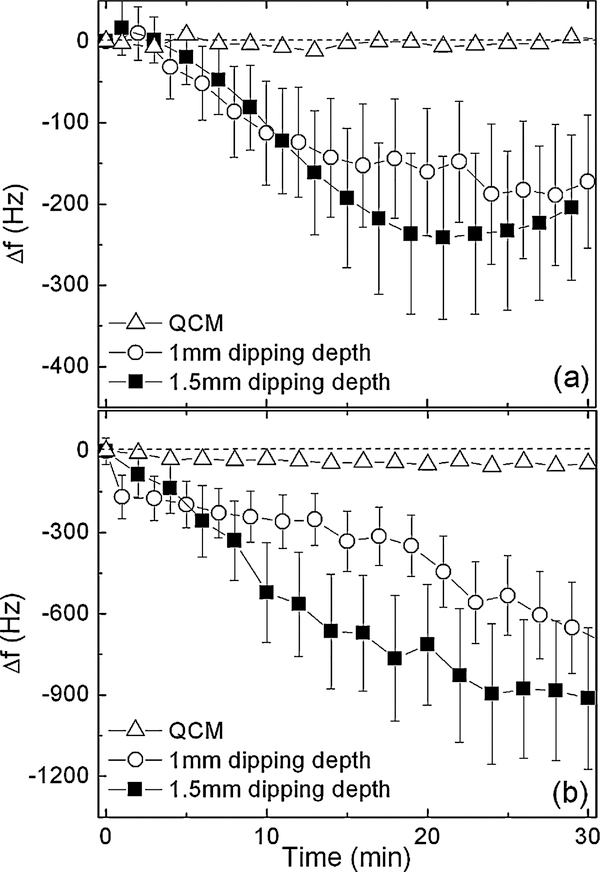
The gold-coated glass tip was first cleaned with a mixture of one part H2O2 and two parts 98% H2SO4 for 5 min and rinsed with distilled water. The cleaned gold-coated tip was then dipped in a 2 mM MPA solution for 3 h to form a self-assembled monolayer. The MPA-coated tip was then soaked in a solution containing 5 mg/ml of EDC and 5 mg/ml of NHS for 30 min to activate the carboxyl group to form an amide. After rinsing with distilled water, the tip was dipped in a 400 nM antibody solution for 30 min to immobilize the antibody on the cantilever tip by the reaction of the amide with a primary amine of the antibody to result in a peptide bond. The above immobilization procedure was taken from references (Hermanson, 1996; Fung and Wong, 2001). In Fig. 3(a) and (b), we plot the resonance frequency shift versus time for the first 30 min of NHS modification and antibody immobilization, respectively. The open circles and the full squares denote a 1 and a 1.5 mm dipping depth, respectively. To estimate the sensitivity of the cantilever, the same procedures were also carried out on a gold electrode of a 5 MHz QCM to measure the mass increase due to the binding of the adsorbed mass. The resonance frequency of the QCM was also measured using the Agilent 4294A impedance analyzer. The resultant resonance frequency shifts versus time from the QCM were also plotted in Fig. 3(a) and (b) (open triangles). Fig. 3(a) shows that 30 min of NHS modification resulted in a down-shift of 170 and 240 Hz in the cantilever’s second-mode resonance frequency at a 1 and a 1.5 mm dipping depth, respectively while 30 min of the same procedure did not yield a discernable resonance frequency shift in the QCM. Fig. 3(b) shows that 30 min of antibody immobilization at the cantilever tip resulted in a 680 and a 900 Hz down-shift at a 1 and a 1.5 mm dipping depth, respectively, while 30 min of the same procedure yielded a frequency down-shift of 45 Hz in the QCM.

Fig. 3.

Fig. 3.

Open in a new tab

Resonance frequency shift vs. time during (a) EDC/NHS modification and (b) antibody immobilization. The open circles (full squares) denote the results of cantilever at a 1 mm (1.5 mm) dipping depth. The open triangles denote results of the 5 MHz QCM. Note the large fluctuation in the resonance frequency during the detection was a signature of the binding events that took place during the detection, which was different from the stable background resonance frequency shown in Fig. 2 with a fluctuation no larger than 10 Hz.

For signal/noise ratio comparison, the present antibody immobilization procedure yielded a resonance frequency shift (signal) of 45 Hz with the QCM relative to a noise level of around 15 Hz. The signal/noise ratio of a 5 MHz QCM was therefore about 3. For the same antibody immobilization procedure yielded resonance frequency shifts of 680 and 900 Hz at 1 and 1.5 mm dipping depths of the PZT/gold-coated cantilever, respectively, relative to a noise level of 30 Hz. The signal noise ratios of the PZT/gold-coated glass cantilever were 23 and 30 at 1 and 1.5 mm dipping depths, respectively, which, as can be seen, were significantly higher than that of a 5 MHz QCM.

From the QCM measurement, the mass change per unit area Γ at the gold-coated electrode due to the antibodies immobilization could be deduced by the Sauerbrey equation (Ward and Buttry, 1990; Lin et al., 1993; Buttry and Ward, 1992):

ΔfQ=−2fQ2GρΓ (1)

where ΔfQ is the resonance frequency shift of QCM, G and ρ the shear modulus and the density of quartz, respectively, fQ the resonance frequency of the QCM. With fQ =5×106 Hz, G=2.947×1010 Pa, ρ = 2648kg/m3 and ΔfQ =−45Hz, Eq. (1) gave Γ = 7.9×10−7g/cm2. The mass detection sensitivity of the PZT/gold-coated glass cantilever, (Δm/Δf) is:

ΔmΔf=ΓAΔf (2)

where Δf and A are the resonance frequency shift and the area of detection of the PZT/gold-coated glass cantilever. The detection area, A = 2wx ≅ 5 ± 1 and 7±1 mm2 for a 1 and a 1.5 mm dipping depth, respectively, where w was the cantilever width, x the dipping depth, and the numerical factor 2 took into account the fact that the cantilever tip was gold-coated on both sides. In deducing Δm/Δf using Eq. (2), the main source of error was the uncertainty in the dipping depth, which was about 0.2 mm. With Δf =−680 and −900 Hz at a 1 and a 1.5 mm dipping depth, respectively, we obtained Δm/Δf≅−5±1×10−11 g/Hz for both the 1 and 1.5 mm dipping depths. Note that even though the adsorbed mass density deduced from the QCM measurement could contain the contribution of water “associated” with the antigen, it would not affect the study since the same “associated” water occurred in the detection by the PZT/glass cantilever as well.

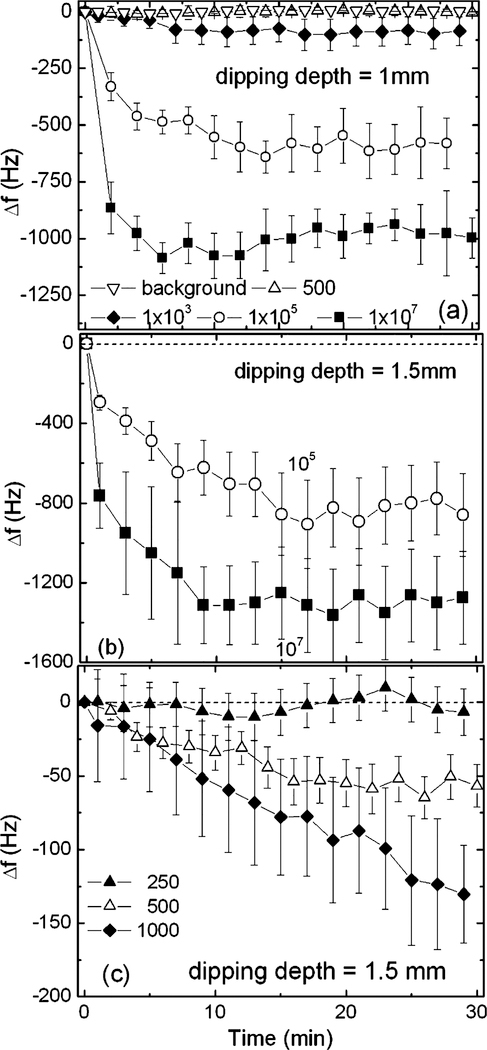
The antibody-coated cantilever was then used to detect S. typhimurium at various concentrations with a volume of 2 ml for up to 30 min. In Fig. 4(a)–(c), we plot the resultant Δf versus time from the PZT/gold-coated cantilever at various S. typhimurium concentrations with a 1 and a 1.5 mm dipping depth, respectively. Full squares, open circles, full diamonds, open up triangles, full up triangles, and open down triangles denote 1×107, 1×105, 1×103, 500, 250, and 0 cells/ml (background), respectively. The detections were repeatable as each curve was the average of 3–4 independent measurements. As shown in Fig. 4(a)–(c), with a 1 mm dipping depth, Δf was −1000±180, −600±100, and −90±30 Hz at 1×107, 1×105, and 1×103 cells/ml, respectively. With a 1.5 mm dipping depth, Δf was −1400±200, −900±100, −130±40 and −50±30Hz at 1×107, 1×105, 1×103 and 500 cells/ml, respectively. Clearly, at a 1 mm dipping depth, the lowest detectable concentration was 1000 cells/ml with a Δf =−90±30 Hz at t = 30 min. At a 1.5 mm dipping depth, the lowest detectable concentration was further lowered to 500 cells/ml with a Δf =−50±30 Hz at t = 30 min. Note that the values of the Δf obtained under these conditions, −90±30 Hz at a 1 mm dipping depth and −50±30 Hz at a 1.5 mm dipping depth, were well above the standard deviations at these concentrations. In addition, they were also well above the 20 Hz standard deviations at 500 cells/ml at a 1 mm dipping depth and at 250 cells/ml at a 1.5 mm dipping depth where there was no discernable resonance frequency shift (see Fig. 4(a)–(c)). These results put the detection limit of the current PZT/gold-coated glass cantilever at 1×103 and 500 cells/ml for a 1 and a 1.5 mm dipping depth, respectively.

Fig. 4.

Fig. 4.

Open in a new tab

Resonance frequency shift vs. time of Salmonella typhimurium detection with (a) 1 mm, (b) and (c) 1.5 mm dipping depth. The full squares, open circles, full diamonds, open up triangles, full up triangles, and open down triangles denote 1×107, 1×105, 1×103, 500, 250 cells/ml, and the background, respectively. Note as similar to Fig. 3(a) and (b) the large fluctuations in the resonance frequency shift at higher concentrations were signatures of the binding events that took place during the detection, which was different from the decreased fluctuations in the resonance frequency shift at low concentrations and the stable background resonance frequency shown in Fig. 2 with a fluctuation no larger than 10 Hz.

To validate the results shown in Fig. 4(a)–(c) and in Table 1, the PZT/gold-coated glass cantilever surface was examined by scanning electron microscopy (SEM) after 30 min of detection. Fig. 5(a)–(c) shows the SEM micrographs of the captured S. typhimurium cells on the PZT/gold-coated glass cantilever surface at t =30 min from 1×107, 1×105, and 1×103 cells/ml suspensions, respectively. Note that Fig. 5(c) does not represent the typical coverage in a 1×103 cells/ml suspension. Because of the low concentration, the coverage on the sensor surface was not uniform. Fig. 5(c) merely served to show that there was cell binding at this concentration. Counting the cells present in the small area represented by Fig. 5(c) alone would greatly exaggerate the coverage at that concentration.

Table 1.

Resonance frequency shift at 30min obtained by PZT/gold-coated glass cantilever at different dipping depths

Concentration (cells/ml) Δf(Hz)
1 mm dipping depth 1.5mm dipping depth
1 × 107 −1000±180 −1400±200
1 × 105 −600±100 −900±100
1 × 103 −100±30 −130±40
500 Not measurable −60±30
250 Not measurable Not measurable
Open in a new tab

Fig. 5.

Fig. 5.

Open in a new tab

SEM micrographs the PZT/gold-coated cantilever surface after 30 min detection in (a) 1×107 cells/ml, (b) 1×105 cells/ml, and (c) 1×103 cells/ml S. typhimurium suspension.

The cell counting methods were reliable for detection at higher concentrations such as 107 and 105 cells/ml as more cells were present on a given surface area and within a micrograph the distributions of the cells were also more uniform. Therefore, we only did the cell counting on the micrographs obtained at 107 and 105 cells/ml such as those shown in Fig. 5(a) and (b) for coverage determination. Moreover, the result of the cell counting at each concentration was the average over 3–5 micrographs (not all shown). A single S. typhimurium cell was about 1.5 μm long and 1 μm wide with a mass of about 1×10−12 g (see the scanning electron microscopy (SEM) micrographs of S. typhimurium shown in Fig. 5(a)–(c)). By counting the number of cells on the SEM micrographs as described above, we obtained Δm/Δf= −6±5×10−11 g/Hz for both the 1 and 1.5 mm dipping depths and for both the 1×107, and 1×105 cells/ml concentrations, consistent with the mass detection sensitivity obtained from the antibody immobilization results. In addition, the same mass detection sensitivity was obtained by the cell counting method over four different sets of micrographs (obtained at two different concentrations, each at two different dipping depths), indicating the validity of the mass detection sensitivity estimated by the cell counting method. Comparing to the Δm/Δf of −5±1×10−11 as determined from the antibody immobilization experiment described above, the Δm/Δf determined by the cell counting method had a significantly larger error bar. This was due to the fact that in addition to the uncertainty of the dipping depth, the cell counting method also had the uncertainty of the cell mass (not every cell had the same size) and the uncertainty of the number of cells captured per SEM frame. The fact that both the antibody immobilization experiment and the cell counting experiments at four different detection conditions gave essentially the same Δm/Δf indicated the validity of the deduced Δm/Δf.

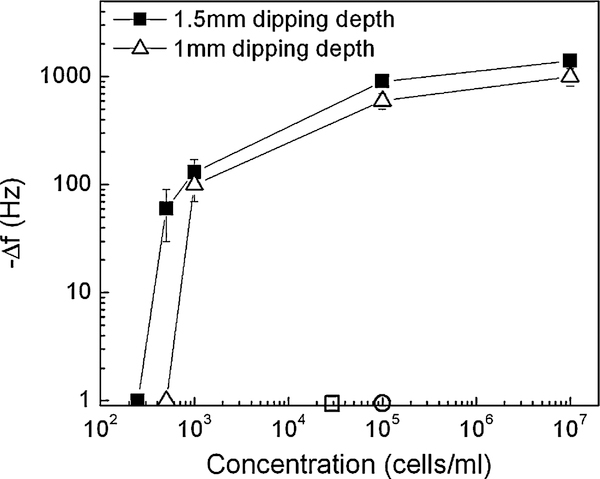
In summary, we plot the Δf at 30 min versus S. typhimurium concentration as obtained by the PZT/gold-coated glass cantilever in Fig. 6 with full squares and open triangles denoting a 1.5 and 1mm dipping depth, respectively. Also shown in Fig. 6 were the infectious dose (open circle) and the detection limit of a commercial Raptor (open square). The current detection limits of 1×103 cells/ml at a 1 mm dipping depth and 500 cells/ml at a 1.5 mm dipping depth were well below the infectious dose, 1×105 cells/ml (Pathirana et al., 2000). It was also lower than the 2×104 cells/ml detection limit of the commercial Raptor sensor (Raptor Portable, Multianalyte Bioassay Detection System).

Fig. 6.

Fig. 6.

Open in a new tab

−Δf vs. concentration at 90% relative humidity of the PZT/gold-coated glass cantilever where open triangles and full squares denote a 1 and 1.5 mm dipping depth, respectively, where Δf denotes the resonance frequency shift after 30 min. The infectious dose and the detection limit of a commercial Raptor are denoted by the open circle and open square, respectively.

It is interesting to note that the experimental mass sensitivity deduced from the detection experiments was more than two orders of magnitude better than those obtained using the theory described in Shen et al. (2006a). Considering a cantilever as an effective simple harmonic oscillator, its resonance frequency can be shifted by either a change in mass or a change in effective spring constant. The theoretical calculation considered only the change in mass (Shen et al., 2006a). The more-than-two- orders-of-magnitude enhancement of the Δm/Δf over the mass loading effect alone indicated that change in the effective spring constant was the dominant factor for the present resonance frequency shifts. Similar two-orders-of-magnitude mass sensitivity enhancements over the mass loading effect were also observed in other PZT microcantilever sensors, and the change in effective spring was attributed to the induced stress by the antibody and antigen attachment to the sensor surface (Lee et al., 2004a,b, 2005). Note that the spring constant change of the cantilever sensor is not similar to changes in viscosity measurement in QCM devices. The binding stress enhanced sensitivity was also present in in-air detection (Chen et al., 1995; Lee et al., 2004a,b, 2005; McFarland et al., 2005; Shen et al., 2006b) which changed the effective spring constant while QCM’s frequency shift due to viscosity change was mainly due to the viscous damping effect. In addition, in the cantilever case, a decrease in resonance frequency in the liquid environment implies a compressive stress in the adsorbed layer and hence a tensile stress in the cantilever (Fritz et al., 2000; Cherian and Thundat, 2002; McFarland et al., 2005). When removed from the liquid environment the same adsorbed layer could cause the cantilever’s resonance frequency to increase (McFarland et al., 2005) implying a compressive stress in the cantilever by the drying of the adsorbed layer. So far we have not seen similar binding stress effect in the QCM.

Exactly how the induced stress affects a cantilever’s resonance frequency is not within the scope of this paper. A closer examination of the induced stress effect on a cantilever’s mass sensitivity will be provided in a future publication.

4. Conclusion

We have examined non-insulated PZT/gold-coated glass cantilevers for in situ detection of S. typhimurium at 90% relative humidity by partially dipping the gold-coated glass tip in the suspension. The PZT/gold-coated glass cantilever is consisted of a 0.127 mm thick PZT layer about 0.7 mm long, 2.3 mm wide bonded to a 0.15 mm thick gold-coated glass layer with a 2.7 mm long gold-coated glass tip for detection. We showed that at 90% relative humidity at any dipping depth larger than 0.8 mm the resonance frequency was stable with no background resonance frequency up-shift. This allowed the PZT/gold-coated glass cantilevers for in situ bio-detection without the need to insulate the PZT. The mass detection sensitivity of the gold-coated glass cantilever was consistently determined as Δm/Δf =−5 to 6×10−11 g/Hz from (1) the antibody immobilization detection result using the mass change per unit area obtained from the QCM and (2) from the S. typhimurium detection result by counting the number of cells captured on the cantilever surface. The PZT/gold-coated glass cantilever exhibited a detection limit of 1×103 and 500 cells/ml with a 1 and 1.5 mm dipping depth, respectively, both of which were more than two orders of magnitude lower than the infectious dose and more than one order of magnitude lower than the detection limit of a commercial Raptor sensor.

Acknowledgements

This work was supported in part by the National Institute of Health (NIH) under the grant number, R01 EB00720 and the Environmental Protection Agency (EPA) under grant number, R829604.

References

  1. Baselt DR, Lee GU, Colton RJ, 1996. J. Vac. Sci. Technol. B 14 (2), 789–793. [Google Scholar]
  2. Brenner PK, Ranking CC, Roybal RY, Stelma NG Jr., Scarpino VP, Dufour PA, 1993. Appl. Environ. Microbiol 59 (11), 3534–3544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Buttry DA, Ward MD, 1992. Chem. Rev 92, 1355–1379. [Google Scholar]
  4. Call DR, Brockman FJ, Chandler DP, 2001. Int. J. Food Microbiol 67 (1–2), 71–80. [DOI] [PubMed] [Google Scholar]
  5. Campbell GA, Mutharasan R, 2005a. Sens. Actuators A: Phys. 122 (2), 326–334. [Google Scholar]
  6. Campbell GA, Mutharasan R, 2005b. Biosens. Bioelectron 21, 462–473. [DOI] [PubMed] [Google Scholar]
  7. Chen GY, Thundat T, Wachter EA, Warmack RJ, 1995. J. Appl. Phys 77 (8), 3618–3622. [Google Scholar]
  8. Cherian S, Thundat T, 2002. Appl. Phys. Lett 80 (12), 2219–2221. [Google Scholar]
  9. Chuang H, Macuch P, Tabacco MB, 2001. Anal. Chem 73 (1), 462–466. [DOI] [PubMed] [Google Scholar]
  10. EPA, 2002. On-line publication, URL: http://www.epa.gov/nerlcwww/online.htm.
  11. Fritz J, Baller MK, Lang HP, Rothuizen H, Vettiger P, Meyer E, Guntherodt H-J, Gerber C, Gimzewski JK, 2000. Science 288 (5464), 316–318. [DOI] [PubMed] [Google Scholar]
  12. Fung YS, Wong YY, 2001. Anal. Chem 73, 5302–5309. [DOI] [PubMed] [Google Scholar]
  13. Han W, Lindsay SM, Jing T, 1996. Appl. Phys. Lett 69 (26), 4111–4113. [Google Scholar]
  14. Hermanson GT, 1996. Bioconjugate Techniques. Academic Press. [Google Scholar]
  15. Ilic B, Czaplewsli D, Craighead HG, Neuzil P, Campagnolo C, Batt C, 2000. Appl. Phys. Lett 77 (3), 450–452. [Google Scholar]
  16. Lee GU, Kidwell DA, Colton RJ, 1996. US Patent 8,505,547.
  17. Lee JH, Hwang KS, Park J, Yoon KH, Yoon DS, Kim TS, 2005. Biosens. Bioelectron 20, 2157–2162. [DOI] [PubMed] [Google Scholar]
  18. Lee JH, Kim TS, Yoon KH, 2004a. Appl. Phys. Lett 84 (16), 3187–3189. [Google Scholar]
  19. Lee JH, Yoon KH, Hwang KS, Park J, Ahn S, Kim TS, 2004b. Biosens. Bioelectron 20, 269–275. [DOI] [PubMed] [Google Scholar]
  20. Lin Z, Yip CM, Joseph IS, Ward MD, 1993. Anal. Chem 65 (11), 1546–1551. [Google Scholar]
  21. McFarland AW, Poggi MA, Doyle MJ, Bottomley LA, Colton JS, 2005. Appl. Phys. Lett 87, 053505. [Google Scholar]
  22. Nie S, Zare NR, 1997. Annu. Rev. Biophys. Biomol. Struct 26, 567–596. [DOI] [PubMed] [Google Scholar]
  23. Oden PI, Chen GY, Steele RA, Warmack RJ, Thundat T, 1996. Appl. Phys. Lett 68 (26), 3814–3816. [Google Scholar]
  24. Pathirana ST, Barbaree J, Chin BA, Hartell MG, Neely WC, Vodyanoy V, 2000. Biosens. Bioelectron 15, 135–141. [DOI] [PubMed] [Google Scholar]
  25. Raptor Portable, Multianalyte Bioassay Detection System, 2006. URL: http://www.resrchintl.com/raptor-detection-system.html.
  26. Schemmel A, Gaub HE, 1999. Rev. Sci. Instrum 70 (2), 1313–1317. [Google Scholar]
  27. Shen Z, Shih WY, Shih W-H, 2006a. Rev. Sci. Instrum 77 (6), 065101. [Google Scholar]
  28. Shen Z, Shih WY, Shih W-H, 2006b. Appl. Phys. Lett 89, 023506. [Google Scholar]
  29. Shih WY, Li X, Gu H, Shih W-H, Aksay IA, 2001. J. Appl. Phys. 89 (2), 1497–1505. [Google Scholar]
  30. Shih WY, Shih W-H, 2006. In: Kumar C (Ed.), Series on Nanotechnology for Life Sciences, vol. 5: Impact of Nanomaterials on Environment. Wiley-VCH, Hoboken. [Google Scholar]
  31. Thundat T, Wachter EA, Sharp SL, Warmack RJ, 1995. Appl. Phys. Lett. 66 (13), 1695–1697. [Google Scholar]
  32. Ward MD, Buttry DA, 1990. Science 249 (4972), 1000–1007. [DOI] [PubMed] [Google Scholar]
  33. Yi JW, Shih WY, Mutharasan R, Shih W-H, 2003. J. Appl. Phys. 93 (1), 619–625. [Google Scholar]
  34. Yi JW, Shih WY, Shih W-H, 2002. J Appl. Phys. 91 (3), 1680–1686. [Google Scholar]
  35. Zhu Q, Shih WY, Shih W-H, 2007. Sens. Actuators B, doi: 10.1016/j.snb.2007.02.030. [DOI] [Google Scholar]

RESOURCES