Local field potentials encode place cell ensemble activation during hippocampal sharp wave-ripples

SUMMARY

Whether the activation of spiking cell ensembles can be encoded in the local field potential (LFP) remains unclear. We address this question by fcombining in vivo electrophysiological recordings in the rat hippocampus with realistic biophysical modeling, and explore the LFP of place cell sequence spiking (‘replays’) during sharp wave-ripples. We show that multi-site perisomatic LFP-amplitudes, in the ~150–200 Hz frequency band, reliably reflect spatial constellations of spiking cells, embedded within non-spiking populations, and encode activation of local place cell ensembles during in vivo replays. We find spatiotemporal patterns in the LFP, which remain consistent between sequence replays, in conjunction with the ordered activation of place cell ensembles. Clustering such patterns provides an efficient segregation of replay events from non-replay-associated ripples. This work demonstrates how spatiotemporal ensemble spiking is encoded extracellularly, providing a window for efficient, LFP-based detection and monitoring of structured population activity in vivo.

INTRODUCTION

The exact neuronal mechanisms giving rise to the local field potential (LFP) - i.e. lowpass filtered (< 500 Hz) extracellular voltage recording – remain elusive. Although postsynaptic and other transmembrane currents, summed over local neuronal populations, are considered key contributors to the LFP signal (Logothetis 2003; Buzsáki et al., 2012; Einevoll et al., 2013), active membrane currents and population spiking have been shown to affect LFP at frequencies above ~80 Hz (Zanos et al., 2011; Buzsáki et al., 2012). Correlations between firing rates and high-frequency (>90 Hz) LFP power have been observed (Ray et al., 2008; Ray and Maunsell, 2011; Belluscio et al., 2012; Scheffer -Texeira et al., 2013; Anastassiou et al, 2015) and computational modeling showed that >100 Hz oscillatory LFP is significantly shaped by synchronous extracellular action potentials (EAP) from local pyramidal populations (Schomburg et al., 2012; Anastassiou et al, 2013; Reimann et al, 2013). Even though these studies indicate a link between high-frequency LFP and population spiking, our understanding of how specific neural spike patterns could be encoded by the LFP remains limited.

Sharp wave-ripple complexes (SWR) are typical examples of fast oscillatory LFP events, observed in the hippocampus during deep sleep and wakeful immobility. They consist of an extensive depolarization in the CA1 dendritic layer (sharp wave), arising from population bursts in CA3, accompanied by a ~150–200 Hz oscillation in the pyramidal layer (ripple; Buzsáki et al. 1992) shaped by synchronized inhibition (Ylinen et al, 1995; Taxidis et al., 2012-2013). During SWR, firing patterns of sequentially activated place cells, observed during wakeful exploration, are replayed at a fast temporal-scale, either in forward or reverse order (Lee and Wilson, 2002; Diba and Buzsáki, 2007; Karlsson and Frank, 2009). These place cell sequence ‘replays’, along with correlated prefrontal cortical activity (Peyrache et al., 2009) and memory impairment caused by on-line ripple disruption (Girardeau et al., 2009; Jadhav et al., 2012), indicate that SWR play an important role in memory consolidation (Buzsáki, 2010).

Importantly, replays can also serve as templates for studying how the activation of specific spiking ensembles can be encoded in the LFP. To this end, we employ biophysical modeling in combination with analyses of in vivo extracellular recordings of LFP and unit activity from areas CA3 and CA1 in rat hippocampus (Diba and Buzsáki, 2007). We find that spiking cell ensembles are encoded in the amplitude of the ripple-frequency LFP and replays of place cell sequences yield consistent spatiotemporal patterns in the LFP, which provide a novel LFP-based tool for the monitoring of circuit activity.

RESULTS

The amplitude of simulated ripples reflects spatial distributions of active cells

During SWR, extracellular action potentials (EAP) from cells within a radius of ~100–200 μm around an electrode contribute to the high-frequency ripple (~100–200 Hz; Schomburg et al., 2012). To address how different spatial constellations of spiking cells shape the ripple LFP, we developed a multi-compartmental biophysical model of CA1 neuronal populations simulating LFP during SWR (Figure 1A; see Methods). We employed the spike input received by CA1 pyramidal cells in a CA3-CA1 network model simulating SWR (Taxidis et al., 2012, 2013), to drive a multi-compartmental, biophysically realistic CA1 pyramidal neuron model that accurately emulates experimentally recorded EAP waveforms (Gold et al., 2006). Each instantiation of the multi-compartmental neuron received a different number of Schaffer-collateral excitatory synapses (Figure S1), leading to cells experiencing strong or weak excitatory drive from CA3. Only ‘strongly-driven’ cells overcame ripple-modulated inhibition during SWR and produced action potentials, whereas ‘weakly-driven’ ones remained mostly subthreshold (Figure 1A). LFP signals were simulated by adding all transmembrane and postsynaptic currents from each compartment of each cell, weighted by the distance to the virtual electrodes.

Figure 1:

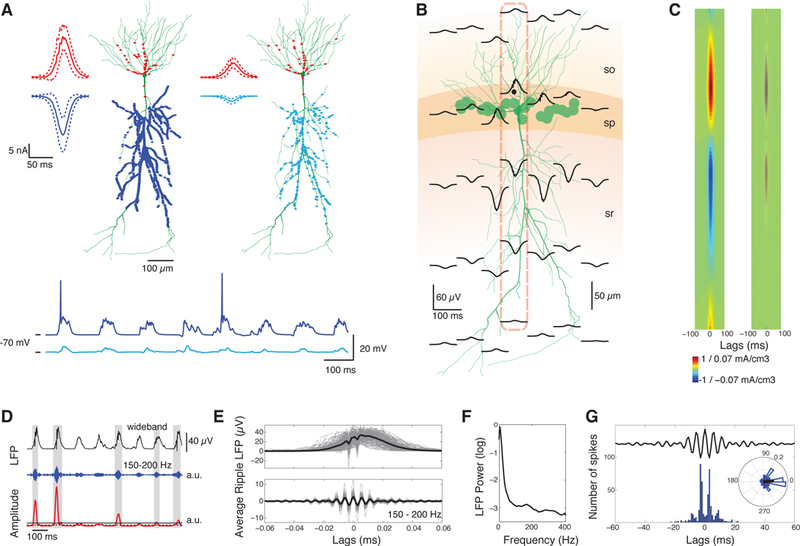
SWR LFP in a pyramidal population model. A. Top: Distribution of excitatory (blue) and inhibitory (red) synapses in apical dendrites and perisomatic regions, respectively, in two example pyramidal cells; one strongly-driven by numerous Schaffer-collateral excitatory synapses (blue dots) and one weakly-driven by fewer synapses (cyan dots). Traces depict average SWR IPSCs (mean ± SD, red) and EPSCs (blue and cyan), summed over all corresponding synapses. Inhibitory inputs are high-frequency (ripple) modulated. Stronger excitation leads to higher depolarization and larger IPSCs. Bottom: Somatic membrane potential of the two neurons during a series of SWR. B. Average wideband LFP during SWR (n = 165) in a population of 25 cells (green disks indicate somatic locations) consisting of negative deflections at the dendritic layer (sharp waves) and high-frequency perisomatic oscillations (ripples). Each trace represents the average LFP at the respective location. Layers, corresponding to stratum oriens (so), pyramidale (sp) and radiatum (sr), are in different colors. C. Average wideband (left) and 150–200 Hz filtered CSD (right) along the dashed axis in B. D. Wideband (black), 150–200 Hz filtered LFP segment (blue) and its amplitude (red) from the dotted location in B. Solid and dashed lines mark ripple-detection and ripple-edge thresholds, respectively. Detected ripple segments are highlighted in grey. Time segment is the same as in A. E. Aligned ripples (grey) and average wideband (top) and filtered ripple (bottom, black lines). F. Normalized power spectrum of the LFP from the dotted location in B. Ripples produce a peak at ~150–200 Hz. G. Spike histogram of all neurons, correlated with the average ripple, and spike phase distribution vector (right). Spikes are strongly correlated with ripple troughs (0^o; p < 0.001 circular V-test).

Our simulated extracellular signals (Figures 1B-G) capture the main components of experimentally recorded SWR LFP (Ylinen et al. 1995; Csicsvari et al., 1999) including: (i) negative deflections in stratum radiatum (sharp waves) combined with 150–200 Hz oscillations in the pyramidal-layer (ripples), (ii) dendritic sinks and somatic sources in current source densities (CSD), mirroring excitatory and inhibitory synaptic inputs respectively, (iii) ~150–200 Hz ripple-modulated perisomatic transmembrane currents, observed through filtered CSD and power spectral analysis, (iv) EAP-waveforms visible in individual ripples and (v) spiking peaks phase-locked to ripple troughs (p < 0.001, circular V-test).

To examine how different spatial distributions of cells spiking during SWR shape the LFP, we simulated a population of three strongly-driven cells surrounded by six weakly-driven ones. Average SWR LFP and corresponding ‘ripple-amplitudes’ (binned sum of squared values of 150–200 Hz filtered LFP) were computed along three virtual electrode probes spanning the entire dendritic extent (Figure 2A). The position of spiking cells determined the ripple-amplitude distribution at the pyramidal layer, with large amplitudes at the middle perisomatic electrode closest to EAP, and weaker amplitudes at the outer electrodes in symmetric distance from EAP sources. Repeating the simulation after placing the spiking cells at one end of the population, produced monotonically decreasing perisomatic ripple-amplitudes with increasing distance from EAP sources (Figure 2B), reflecting the new spiking location. Unlike perisomatic LFP, dendritic-layer ripple-amplitude distributions did not reflect the spiking cell distributions, due to the extensive dendritic arborization of each neuron, that shaped dendritic-layer LFP at distant locations.

Figure 2:

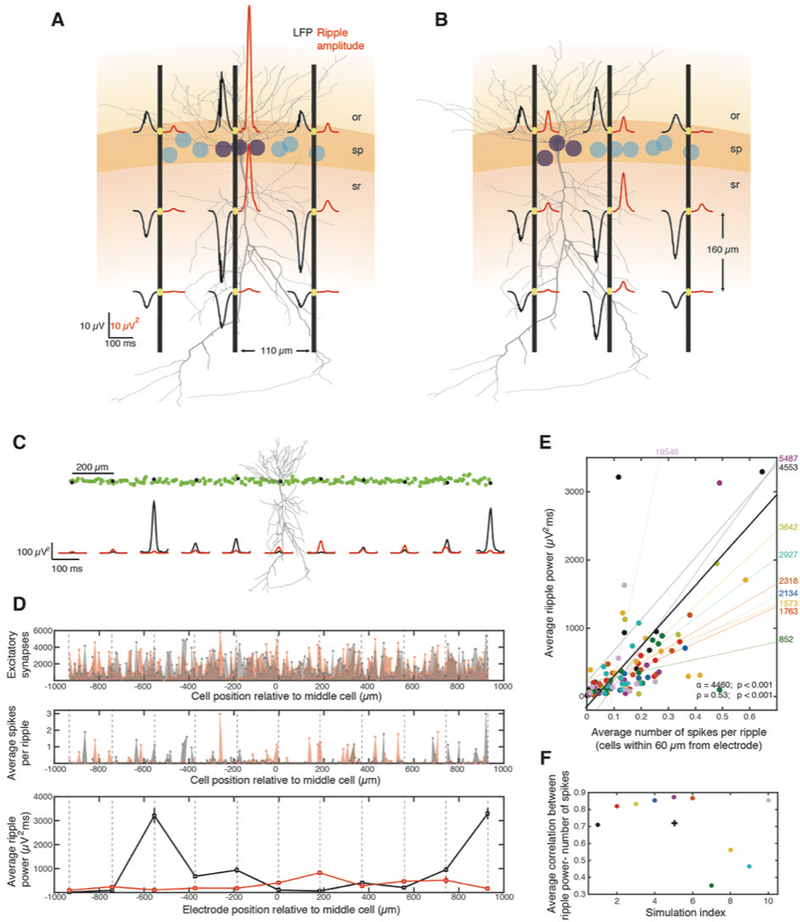
Multi-site ripple-amplitudes reflect spatial distributions of spiking cells. A. Average wideband LFP (black traces) and corresponding ripple-amplitudes (red traces) of simulated SWR (n = 168) along three virtual electrode probes (black vertical lines). Strongly-driven, spiking cells (purple) were surrounded by weakly-driven subthreshold ones (cyan). Full morphology of one example cell is shown. Same layer colors and notation as in Figure 1B. B. Same as A, but with spiking neurons grouped at one side. Ripple-amplitudes at pyramidal layer reflect distance from spiking. C. Top: Spatial arrangement of a pyramidal population. Green circles indicate somatic locations (n = 201 cells) and one example cell is shown. LFP was simulated at pyramidal layer sites (‘electrodes’, black dots) and the middle one was used for ripple detection. Bottom: Ripple-amplitudes at the electrodes before (black) and after shuffling the cell order and repeating the simulation (red). D. Number of excitatory synapses on each cell of the population (top), average number of emitted spikes during SWR (middle) and average ripple-power (mean ± se, bottom) versus position along the pyramidal layer (central cell is at 0 μm). Dashed lines mark virtual electrodes. Black and red traces: same simulations as in C. Ripple-power was significantly different between the simulations at all electrodes (p < 0.01, Wilcoxon test, FDR-corrected [WT-FDR]) reflecting differences in number of spikes around each site. E. Average ripple-power at each electrode versus average number of spikes from cells <60 μm from the electrode. Each simulation (n = 10), with random shuffling of cell order, is shown in different color (black and red are simulations in C-D; one outlier point was omitted for plotting clarity). Thin lines represent the least-squares linear fit for each simulation (slopes are shown on right). Average ripple-power and number of spikes are significantly correlated (thick line: Least squares linear fit; α: slope, p < 0.001, F-test; ρ: Pearson correlation, p < 0.001, Student’s t-test). F. Average Pearson correlation for distributions of each simulation (same colors), over all electrodes, and average correlation over all simulations (cross; <ρ > = 0.72; p < 0.001, tailed sign test).

Next, we simulated a neural population (n = 201 cells) spanning ~2 mm, where spiking and non-spiking cells were intermingled. LFP was simulated along the pyramidal layer of the population in 11 sites, 200 ± 10 μm apart (mean ± SD, Methods) and the average ripple-amplitude was computed at each site (Figure 2C). We repeated this simulation 10 times, each time randomly reshuffling the spatial cell order so that the neighborhood around each LFP site consisted of a different set of cells. To compare ripple-amplitudes throughout the SWR duration, we used the integral of each amplitude trace (‘ripple-power’). Once more, differences between simulations in ripple-power at each electrode, reflected differences in the number of spikes produced near the electrode (Figure 2D). Ripple-power at each electrode in each simulation was highly correlated with the average number of spikes produced around the electrode (Figure 2E). This held both when pooling all simulations (Pearson correlation: ρ = 0.53; p < 0.001, Student’s t-test) and for the average simulation (average Pearson correlation per-session: <ρ > = 0.72; p < 0.001, tailed sign test; Figure 2F).

The correlation between ripple-power and number of nearby spikes depended on the distance of spiking cells from the recording electrode. When accounting for spikes from cells increasingly farther away, correlations dropped monotonically, since EAP from cells closer to the electrode have greater influence on ripple-amplitude (Figure S1). When accounting only for cells within a range of distances around the electrode, correlations dropped more rapidly, reaching zero for cells positioned >60 μm away from an electrode, while the number of cells within each range remained relatively constant (Figure S1).

Our simulations demonstrate that spiking of local cell ensembles around each electrode is encoded by the electrode’s ripple-amplitude, so that distributions of ripple-amplitudes reflect spatial constellations of spiking cells. We applied our modeling-based insights to in vivo recorded SWR LFP concomitant with place cell spiking patterns.

In vivo ripples containing sequence replays are dominated by variable spiking patters of active place cells

In previously described experiments (Diba and Buzsáki, 2007), LFP and unit activity were recorded from hippocampal CA3 and CA1 regions of rats, while crossing a linear track for water reward at each end. CA1 pyramidal-layer LFP was characterized by ~6–10 Hz theta oscillations during running and by transient (45.2 ± 30.3 ms; mean ± SD) ~120–200 Hz ripple oscillations during immobility on the reward platforms. During track crossings, CA3 and CA1 place cells were activated in sequence, usually at one direction of motion (27.17% ± 11.57% place cells per-session had bidirectional fields). We split pyramidal units from each session into three subsets: cells with place field in leftward crossings (‘L-sequence’), cells with place field in rightward crossings (‘R-sequence’, Figure 3A) and cells that had no detectable place fields (‘non-place cells’). Bidirectional cells were assigned to both sequences.

Figure 3:

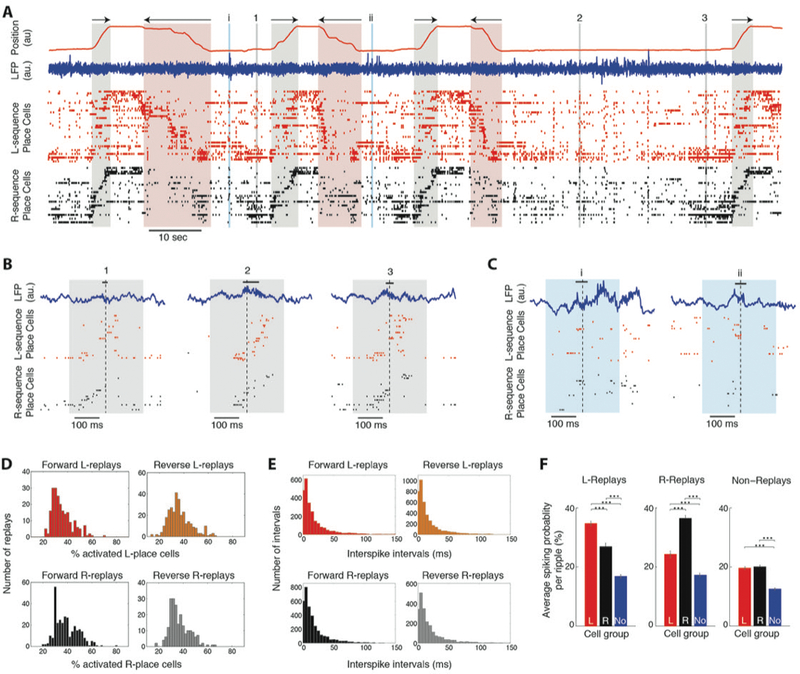
In vivo sequence replays are dominated by variable spiking patterns of active place cells. A. Position along the linear track (red trace) and direction of motion (arrows) during leftward and rightward crossings (highlighted in red and black respectively). Blue trace: LFP recorded from the CA1 pyramidal layer. Ticks: unit discharges of two pyramidal place cell populations (CA3 and CA1 combined), one encoding leftward crossings (red, ‘L-sequence’; n = 38 cells) and the other rightward crossings (black, ‘R-sequence’; n = 30). Place cells of each sequence are stacked (from top to bottom) according to the location of their place fields on the track (from left to right). Bidirectional place cells were included in both sequences. Colored boxes: LFP ripples detected during immobility at the track platforms. B. Expanded numbered segments (1, 2, 3) in A, displaying examples of forward ‘R-replays’. Black bars: detected ripple segments. Dashed lines: peak power of the LFP ripple (0 ms). C. Expanded latin-numbered (i,ii) segments in A, displaying examples of ‘non-replays’ with uncorrelated or sparse place cell discharges. D. Histograms of percentage of activated place cells (producing at least one spike) during replays of their sequence (all sessions pooled). E. Histograms of time intervals between the first spikes of consecutively activated place cells during replays of their sequence. F. Average spiking probability (% ripples where a cell produced at least one spike) of each cell group during each ripple type (mean ± sem; ‘L’: L-sequence, ‘R’: R-sequence, ‘No’: Non-place cells). Asterisks: p < 0.001, WT-FDR.

Spike discharges during ripples ‘replayed’ these place-cell sequences in forward or reverse order. Four different types of replays were observed: forward and reverse ‘L-replays’ and forward and reverse ‘R-replays’ (Figure 3B). 18.6% of all detected ripples (n = 5701) qualified as significant replays. Of those, 20.6% represented forward and 29.3% reverse L-replays. 30% represented forward and 20.1% reverse R-replays. The remaining 81.4% of ripples, referred to as ‘non-replays’, contained sparse or uncorrelated place cell spiking (Figure 3C). On average, place cells spiked in sequence during replays, yet the spiking profiles of individual replays were highly variable (Figure 3B). The number of place cells activated during replays of a sequence varied between ~20–60% and intervals between the first spikes of sequentially activated place cells ranged from 0 to ~100 ms (Figures 3D-E). Moreover, cells belonging to the opposite sequence were also occasionally active, often in a partially reversed order (Figure 3B), adding to the variability of the overall spiking content of each replay event.

Our simulated ripple LFP was shaped by distinct groups of active cells, embedded within subthreshold populations. To assess whether such active ensembles dominated in vivo ripples, we computed each cell’s spiking probability during each ripple type. Sessions with at least 5 L-replays and 5 R-replays were considered (n = 16 sessions, 1219 units). We found that during replays of a sequence (L or R), cells not associated to the sequence (R or L, respectively, and non-place cells) had significantly lower spiking probability (p < 0.001, Wilcoxon test [WT]; Figure 3F), indicating that sequences are generally replayed with relatively low non-sequence-associated (noise) spiking. Moreover, although most cells discharged during few non-replays, place cells had higher spiking probability than non-place cells during the average non-replay (p < 0.001, WT; Figure 3F). This increased participation of place cells in non-replays implies a number of potentially undetected replay-like events that did not meet our detection criteria (Methods).

In sum, similarly to our model, place cells of a given sequence form an active group of pyramidal neurons during replays of the sequence, while non-associated neurons remain relatively silent.

In vivo ripple-amplitudes encode spiking activity of local cell ensembles

Spikes from individual cells can dominate LFP at high frequencies spanning >200 Hz (Zanos et al., 2011). To show that collective spiking of pyramidal cell ensembles is reflected in the ripple amplitude better than in other LFP frequency bands, we examined whether the ripple-band best correlates with changes in population spiking during SWR. We calculated correlations between the amplitude of a CA1 pyramidal layer LFP, filtered over various frequency bands, and the collective firing rate from all CA1 pyramidal units during ripples (both measures z-scored). Correlations were computed over a range of lags to allow for short delays between LFP and phase-shifted spiking at distant locations (Patel et al., 2013), and maximum-correlations for different frequency bands were compared (Figure 4A). Average maximum-correlations were significantly higher for the 150–200 Hz frequency band compared to any other frequency band (p < 0.05; tailed two-sample t-test, FDR; Figure 4B). Similarly, average maximum correlations between CA3 pyramidal-layer LFP and collective CA3 firing rates peaked for a wider 150–250 Hz frequency range, and were significantly higher for the 150–200 Hz band compared to <150 Hz frequencies (p < 0.001; tailed two-sample t-test, FDR) but not compared to ≥150 Hz frequency bands (p > 0.05). These findings suggest that changes in collective pyramidal firing rates are best encoded by fluctuations in the amplitude of the ripple-frequency LFP component.

Figure 4:

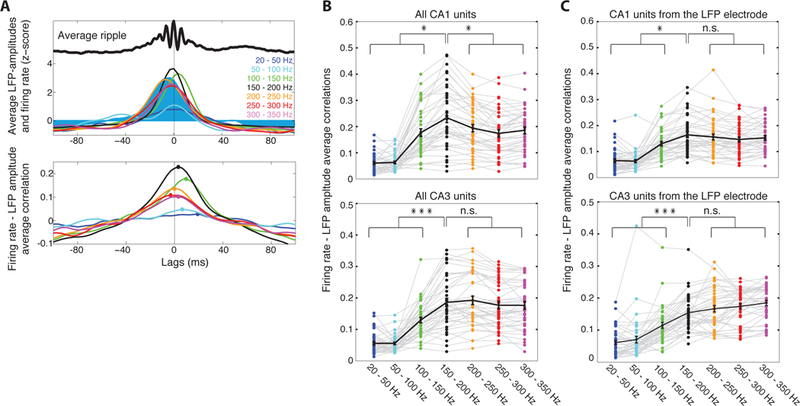
Ripple-amplitudes encode collective pyramidal firing during in vivo SWR. A. Top: Amplitude of CA1 pyramidal layer LFP, filtered at various frequency bands (colored traces), during the average ripple (black trace) in a recording session. Filled trace: average firing rate of all CA1 pyramidal units. All traces are z-score normalized. Bottom: Average correlations between firing rate and LFP amplitudes during ripples in one recording session. Colors correspond to frequency bands in A. Points indicate maximum correlation for each band. B. Top: Average maximum correlations during ripples in each recording session (colored points) and averaged over sessions (black line; mean ± sem). Average 150–200 Hz correlation is significantly higher than any other band. Bottom: Same analysis for CA3 LFP and units. C. Same analysis but for firing rates only from units from the same probe as the LFP. Asterisks: one, p < 0.05; three, p < 0.001, n.s., non-significant, p > 0.05; tailed t-test, FDR).

Are in vivo ripple-amplitudes shaped by EAP from a wide population around the electrode, or do they simply reflect the spikes of units detected at the electrode? When repeating the above analysis using firing rates only from units recorded at the corresponding probe, ripple frequency-band correlations were weaker for both CA1 and CA3, and did not exhibit significant differences with correlations of higher frequency bands in CA1 (p > 0.05; tailed two-sample t-test, FDR; Figure 4C). Moreover, even though replays were accompanied by more spikes than non-replays (p < 0.001, WT), differences in average ripple-amplitude or power per-probe were not significant (p > 0.05, WT; Figure S2). Finally, we did not find a correlation between average ripple-power at a probe and average number of spikes recorded by the probe (Figure S2). Collectively, these findings suggest that spikes of detected units influence the LFP at a range of high frequencies, spanning beyond 300 Hz, and are not sufficient to account for the entirety of the recorded ripple-amplitudes.

A lower-frequency after-potential component of large EAP, from few cells very close to an electrode, could directly leak into the recorded LFP, significantly influencing ripple-amplitudes at that location (Anastassiou et al, 2015). The activation of such pyramidal cells with larger EAP would lead to higher ripple-amplitudes, compared to those where these cells did not spike. For each detected unit, we compared average ripple-power at the probe where it was detected, when the cell spiked versus when it did not (cells that spiked during at least 10 ripples and did not spike during at least the same amount were considered; n = 2487). We did not observe a minority of ‘ripple-influencing’ cells, as 52.5% of all cells and 39.6% of cells per-electrode, on average, yielded significantly higher ripple-power when they spiked (p < 0.05; tailed WT-FDR; Figure S2). Plotting the relative increase in average ripple-power when each cell spiked, compared to when it did not, versus its average spike amplitude, also did not reveal a minority of high spike-amplitude cells yielding the largest power increase (Figure S2). In contrast, spiking of multiple cells with low EAP coincided with large ripple-power increase.

These analyses corroborate that ripple-amplitudes of perisomatic LFP during in vivo SWR are not influenced solely by few nearby cells but reflect collective spiking activity of surrounding ensembles of neurons, including cells beyond those detected as discrete units.

Activation of specific cell ensembles yields consistent ripple-amplitudes during replays

Our simulations suggested that ripple-amplitudes recorded by an electrode reflect local spiking. Therefore, when the same cell ensemble around the electrode is activated during ripples, the resulting ripple-amplitude will remain broadly unaltered, compared to when different ensembles of cells are activated over a similar set of ripples.

We first tested this hypothesis with our computational model. Ripples from individual simulations (the 10 simulations shown in Figures 2C-F, each with a different spatial cell order) were compared with ripples from ‘mixed simulations’ (equal sets of ripples created by randomly selecting events from all 10 simulations). Individual simulations yielded ripple-amplitudes with lower variability relative to mixed ones (Figure 5A). This variability was quantified through the coefficient of variation (CV, SD normalized by the mean) of ripple-power at each electrode. The average simulated electrode yielded significantly lower ripple-power CV in individual simulations compared to the corresponding mixed ones (Figure 5B, p < 0.001; tailed WT). The same holds when averaging ripple-power CV per-site over all individual simulations versus mixed ones and over all electrodes (Figures 5C-D, p < 0.001, tailed WT).

Figure 5:

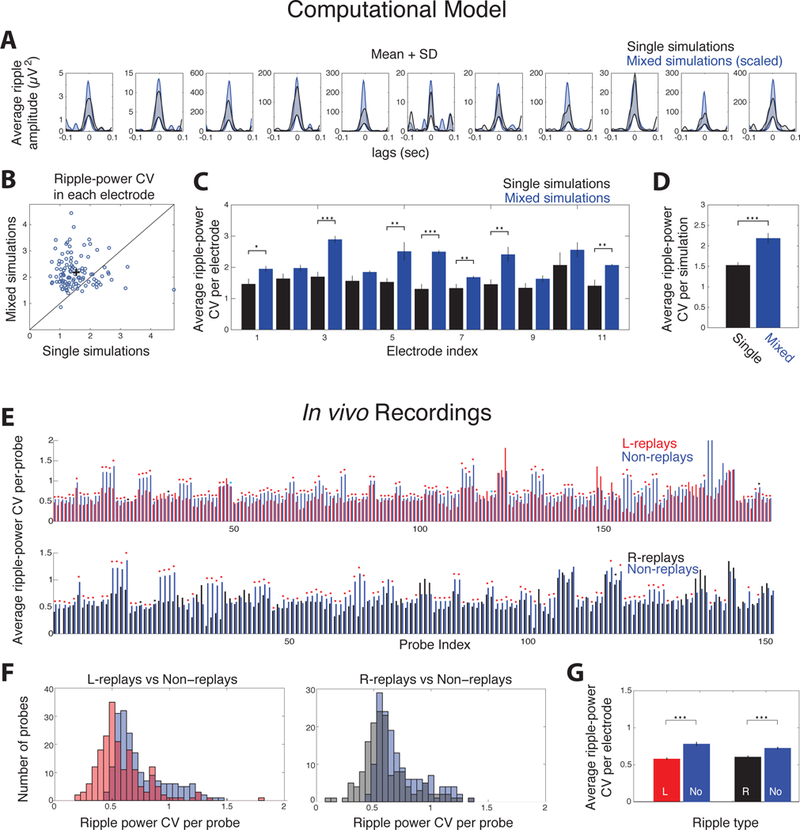
Activation of place cell ensembles in replays yields robust ripple-amplitudes compared to non-replays. A. Mean+SD ripple-amplitude in each LFP-simulation electrode during a single simulation (black) and a ‘mixed’ one (random ripples from all simulations; blue; scaled so both means have same maximum value). Shaded areas designate the area between mean and mean+SD. B. Ripple-power coefficient of variation (CV) at each site in each individual simulation versus the mixed one. Average CV was significantly higher in mixed simulations (cross; CV = 1.53 and 2.18 for single and mixed simulations respectively; p < 0.001; tailed WT). C-D. Average ripple-power CV at each site over all simulations (C) and over all electrodes (D) for individual (black) and mixed simulations (blue). Asterisks: one: p < 0.05; two: p < 0.01; three: p < 0.001; tailed WT-FDR in C and tailed t-test in D). E. Average ripple-power CV in recording probes containing L-sequence (top) or R-sequence place cells (bottom) in each session. Each probe’s average CV (bootstrapping, n = 500) of L-replays (red) or R-replays (black) is next to the corresponding CV of non-replays (blue). Asterisks: blue, p < 0.05; black, p < 0.01; red, p < 0.001, tailed WT-FDR). F. Distribution of average CV per-probe for L-replays (red) and R-replays (black) compared to non-replay CV (blue). G. Mean CV over all probes (mean ± se) was significantly lower for replays of both sequences compared to non-replays (p < 0.001, tailed WT).

Extending this analysis to in vivo replays, ripple-amplitudes should be less variable during forward and reverse replays of a sequence (fixed ensembles of place cells) compared to non-replays (variable sets of spiking cells). Again, we compared the ripple-power CV between replays and non-replays at the same recording site. Sessions containing at least 3 replays of a sequence (n = 24 for L-replays; n = 18 for R-replays) and probes where at least one cell of the corresponding sequence was detected were considered (n = 196 for L-sequence; n = 152 for R-sequence). Distributions of replay and non-replay CV were computed for each CA1 or CA3 probe by bootstrapping (500 bootstraps; see Methods). We compared average L-replay and R-replay CV (forward and reverse replays pooled) at each probe, with the corresponding average non-replay CV at the same probe. Most probes yielded significantly lower ripple-power CV during replays compared to non-replays (80.1% and 72.4% probes had significantly lower CV during L-replays and R-replays respectively; p < 0.01, tailed WT-FDR; Figure 5E). Hence, the average CV per-probe was significantly lower for replays of either sequence compared to non-replays (Figures 5F-G, p < 0.001, tailed WT).

Similarly, after pooling all probes and recording sessions and normalizing ripple-power distribution in each probe by its mean, the average ripple-power SD of replays (computed by bootstrapping; 1000 bootstraps) was significantly lower than that of non-replays (p < 0.001, WT; Figure S3). To ensure outliers within the larger, non-replay set did not bias our results we performed two control tests. First, we removed non-replays with ripple-power beyond the outmost replay values, so that both sets have the same power range. We then removed events from both sets that had ripple-power beyond mean ± 2×SD of the corresponding replay set. In both cases, the corresponding SD of replays was significantly lower than that of non-replays (Figure S3).

Conclusively, both computational modeling and in vivo analyses support that activation of specific place cell ensembles around each electrode yields consistent LFP ripple-power, compared to activations of variable sets of cells during non-replays.

Sequential activation of cell ensembles during replays yields consistent spatiotemporal LFP patterns

Based on our previous findings, the sequential activation of specific cell ensembles during replays could yield spatiotemporal patterns on the combined ripple-amplitudes over multiple recording sites.

To test this hypothesis through our model, we split all 201 cells used in the 10 aforementioned simulations with different cell order, into ‘place cell groups’. Time delays were implemented on the simulated extracellular fields of each group so that neuronal spiking retained the ripple rhythmicity, while cell groups spiked in a temporal sequence mimicking place cell replays (Figure 6A, Methods). We implemented this scheme separately in each simulation and computed the new LFP over the same 11 sites as before. Ripple-amplitudes in each site were z-score normalized over ±100 ms around the ripple peak (0 ms), yielding a two dimensional (site index vs. time) spatiotemporal pattern of the ripple (‘LFP-pattern’). LFP-patterns of ripples in each simulation exhibited similar characteristics, whereas mixed simulations (created as before), yielded more variable LFP-patterns as these originated from variable spiking sequences, mimicking non-replays (Figures 6B-C). ‘Similarity’ between a pair of LFP-patterns was quantified by their temporal correlation at each electrode over a range of time-lags, averaged over all electrodes and over all lags (Methods). Maximum correlation between most pattern pairs was observed for lags close to zero (Figure 6D), indicating the validity of the ripple-peak as a reference point (0 ms). Importantly, the average similarity between pairs of LFP-patterns was significantly higher than the similarity between pattern pairs of the corresponding mixed simulations (Figure 6E). The same holds when averaging over individual versus mixed simulations (p < 0.05) and after pooling all pattern pairs from individual and mixed simulations (p < 0.001; tailed WT; Figure 6F). These results support our hypothesis that specific cell ensembles, spiking in sequence, yield consistent LFP-patterns, compared to spatiotemporal variable patterns stemming from different sets of spiking sequences.

Figure 6:

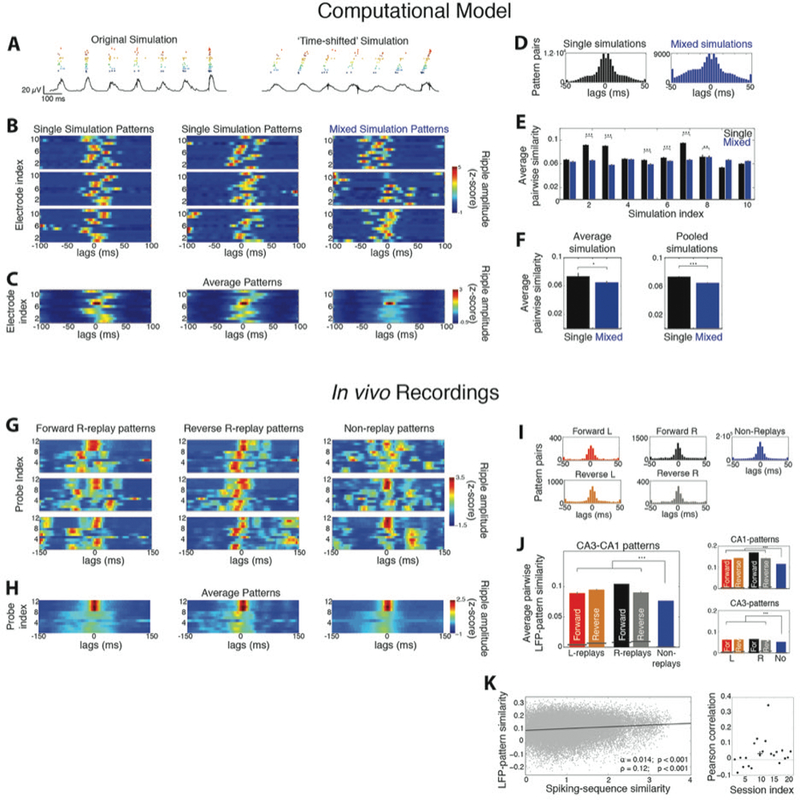
Replays yield consistent spatiotemporal LFP-patterns compared to non-replays. A. Example raster plot of all spiking cells and ripple LFP (black trace) in a simulation, before (left) and after (right) introducing time shifts to the membrane potential of cell groups. Each ‘place cell group’ is indicated by a different color. B. Example LFP-patterns of ripples from individual simulations (left and middle) and from a ‘mixed simulation’ (right; 0 ms: ripple peak). C. Average LFP-patterns from the corresponding simulations. D. Distribution of lags yielding maximum correlation between all pairs of LFP-patterns in single and mixed simulations. E. Average similarity between pairs of LFP-patterns in each single simulation (black) versus the corresponding mixed one (blue; mean ± se). F. Average similarity per-simulation (left) and after pooling all simulations (right). LFP-patterns of individual simulations were significantly more similar to each other than those of mixed ones. G. Examples of LFP-patterns from in vivo recorded forward R-replays (left), reverse R-replays (middle) and non-replays (right) in one session. Probes 1–8 and 9–12 are located in CA3 and CA1, respectively. H. Average patterns of the corresponding ripple types in G. I. Distributions of lags yielding maximum pairwise LFP-pattern correlation for all ripple types. J. Average similarity (mean ± se) between LFP-patterns of all replay types was significantly higher than that between non-replays. Black lines indicate chance-similarity baselines. Right: Same for patterns computed only over the CA1 or CA3 probes. K. LFP-pattern similarity between all pairs of ripples in a recording session versus their spiking profile similarity. The two measures were significantly correlated (line: least squares linear fit; α: slope, p < 0.001, F-test; ρ: Pearson correlation, p < 0.001, Student’s t-test). Right: Distribution of Pearson correlations for each session. The average per-session correlation was statistically significant (cross: <ρ> = 0.04; p < 0.05, tailed sign test). All patterns in this figure were smoothed over time with 5-point moving average for plotting clarity. Asterisks: one, p < 0.05; two, p < 0.01; three, p < 0.001; tailed WT-FDR).

Similarly, in our in vivo recordings, sequential activation of place cell ensembles during replays should yield more consistent LFP-patterns than those of non-replays. Although variability in the LFP-patterns of ripples in each session was higher than in our model, groups of replay LFP-patterns exhibited similar characteristics (Figures 6G-H). Maximum similarity between pattern pairs of any ripple-type was again mainly observed for lags close to zero (Figure 6I) and average similarity between pattern pairs of any ripple-type was statistically significant (Figure 6J; p < 0.001, tailed sign test, Methods). Importantly, average similarity was significantly higher for pattern pairs belonging to any given replay type than for non-replay pairs (p < 0.001; WT-FDR; Figure 6J). This held even when restricting the analysis to LFP-patterns from probes located only in CA3 or only in CA1, indicating that no specific probes or CA area biased our analysis. Thus, LFP-patterns during replays were more consistent than patterns of non-replays, supporting our simulations.

Since spiking profiles varied during replays and given ripple-amplitudes reflect activity beyond detected spikes, we asked whether LFP-patterns during replays were more consistent than spiking-based ones. “Firing rate-patterns” were constructed by replacing the ripple-amplitude of each probe, in the LFP-pattern definition, with the total firing rate recorded by the probe (Figure S4). Indeed, firing-rate patterns were more variable than LFP ones, as indicated by the roughly uniform distributions of time lags yielding maximum pairwise similarity and by the lower pairwise similarity for all ripple types (p < 0.001; WT-FDR, Figure S4). Nevertheless, the LFP- and firing rate-pattern of ripple events partially overlapped, as suggested by their positive mean correlation (p < 0.001, tailed sign test). Consequently, average similarity between firing rate-patterns was, again, higher for all replay types than for non-replays (p < 0.001; WT-FDR).

We next asked whether high similarity between any two ripples could indicate similar spiking profiles, when their replay content is unknown. Similarity of spiking profiles of two ripples was quantified by the total Spearman correlation between their corresponding L-sequence and R-sequence spiking (Methods). Analyzing all ripple pairs in each session yielded a statistically significant correlation between spiking similarity and LFP-pattern similarity between two ripples during the average recording session (<ρ> = 0.04; p < 0.05, tailed sign test; Figure 6K). This suggests that LFP-pattern similarity could be applied to tracing spiking pattern similarity between ripples.

Finally, we tested our analysis by reducing the two-dimensional patterns into one-dimensional sequences. By tracing the probe with the maximum z-scored ripple-amplitude at each time-point of a pattern, we acquired a sequence of probe indexes for each ripple (‘LFP-sequence’). Even though LFP-sequences were more heterogeneous than corresponding patterns, they supported our main findings (Figure S5).

Conclusively, both computational and experimental analyses corroborate that LFP-patterns reflect the sequential activation of local cell ensembles. They are thus consistent between ripples with a specific spiking content (replays) compared to ripples with variable content (non-replays), with the LFP similarity between two ripples being related to their spiking similarity.

Clustering similar LFP-patterns segregates replays from non-replays

Since similar LFP-patterns reflect similar sequential spiking, we asked whether LFP-pattern similarity could discern different types of replays in our dataset. When comparing how similar patterns of a given replay type were with each other, versus with patterns of all other replay types, we only found forward R-replays to be significantly more similar to each other (p < 0.001; tailed WT-FDR; Figure S6). This can be attributed to the small sample size of detected replays in individual sessions and the high variability between sessions, as well as the inherent variability in LFP-patterns. Moreover, unless the spatial topology of the L- and R-sequences in a session is considerably different (different number/distribution of ensemble cells around each electrode), their LFP-patterns may, in principle, be similar.

We next examined whether replays (restricted spiking profile) could be segregated from non-replays (variable spiking) via their LFP-pattern similarity. Could such segregation discern actual non-replays from ‘replay-like’ ones (with partially sequential spiking that did not meet our replay-detection criteria)? We constructed a hierarchical tree of all LFP-patterns in each recording session, based on Euclidean distances of pattern similarity (Methods). Ripples with similar patterns were mainly grouped under one of the two main branches, while the other branch contained patterns of lower similarity, separating all ripples in the session into two clusters (Figures 7A-D). ‘Cluster 2’ was set as the one containing the highest average pairwise similarity (average similarity per cluster over all sessions = 0.04 and 0.12, respectively; p < 0.001, WT). Cluster 2 had larger size on average (mean fraction of ripples per cluster = 37.4% and 62.6%; p < 0.001, t-test) and, even though both clusters were mainly composed of non-replays, it contained many non-replay patterns of high pairwise similarity and a higher ratio of replays (mean ratio of replays per cluster = 31.9%, 68.1%; p < 0.001; WT; only sessions with at least 4 replays included; n = 30). This led to a less noisy average pattern in Cluster 2 than in Cluster 1 (Figure 7E). Also, there was no difference in ripple-power of events in the two clusters (average ripple-power per-probe: Cluster 1 = 0.64 mV²ms; Cluster 2 = 0.76 mV²ms; p > 0.05, WT). To quantify the degree of overall sequential spiking at each cluster, we computed the total median Spearman correlation over the L- and R-sequences for all ripples in the cluster (Figures 7F-G, Methods). This measure was on average significantly higher for Cluster 2 (0.58 versus 0.73 respectively; p < 0.05, WT; Figure 7H), indicating that Cluster 2 contained ripples of higher replay content (more sequential spiking) than Cluster 1; most of which were initially classified as non-replays.

Figure 7.

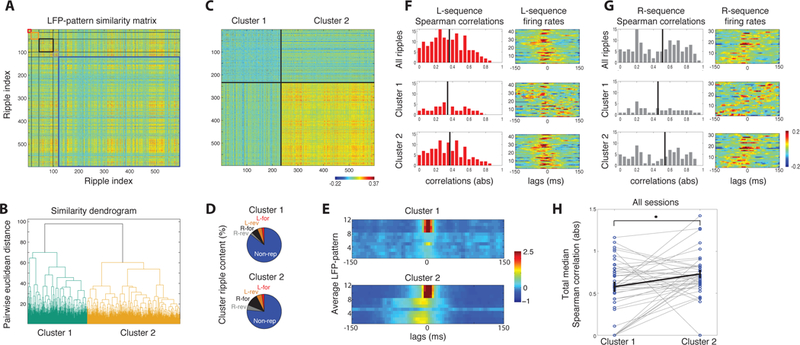
Clustering similar LFP-patterns segregates ripples with replay content from non-replays. A. Similarity matrix between all pairs of ripples from one session. Each entry {i,j} is z-scored correlation between LFP-patterns of ripples i and j. Forward and reverse L-replays (red and orange box), forward and reverse R-replays (black and grey box) and non-replays (blue box) are ordered separately. B. Hierarchical tree of all ripples (based on Euclidean distance metric). All ripples are split into two clusters corresponding to the two main branches. C. Same correlation matrix as in A, reordered after clustering. Cluster 2 contains ripples with higher pairwise similarity than Cluster 1. D. Ripple-type composition of each cluster. Cluster 2 contains higher percentage of replays. E. Average LFP-patterns over the two clusters. F. Left: Histogram of absolute Spearman correlations of the L-sequence over all ripples (top), ripples in Cluster 1 (middle) and Cluster 2 (bottom). Vertical lines: medians. Right: Average z-scored firing rates of L-sequence over the corresponding ripples. Cells stacked according to their place field (as in Figure 3). G. Same for the R-sequence. Cluster 2 contains ripples with higher sequential spiking content. H. Distribution of total median Spearman correlations (Methods) over ripples in the two clusters for all recording sessions (points). Black line depicts average over all sessions (mean ± se). Cluster 2 contains, on average, ripples with significantly more correlated sequential spiking.

Finally to ensure our results were not affected by any confounds of pairwise comparisons or the similarity measure definition, we applied self-organizing mapping (SOM; Reichinnek et al., 2010) on the complete set of LFP-patterns in a session. Processed LFP-patterns were mapped onto a grid of SOM units so that patterns with similar characteristics were mapped onto neighborhoods of units (Kohonen, 1995). K-means clustering segregated these neighborhoods, clustering similar LFP-patterns together (Methods). As before, replay patterns were not efficiently segregated into different replay types with this method (Figure S7), supporting our previous finding. SOM analysis on all LFP-patterns of a session yielded two clusters. Cluster 2 was set as the one with more tightly clustered patterns (Methods), reflecting our previous condition of highest average similarity between patterns. Analyzing all recording sessions yielded that the average Cluster 2 had again higher replay content than Cluster 1 (0.66 versus 0.77 respectively; p < 0.05, two-sample t-test; Figure S7), supporting our pairwise similarity-based clustering.

Therefore, by clustering similar LFP-patterns, ripples with replay content can be efficiently segregated from actual non-replay events, uncovering replays that did not meet place cell-based detection criteria.

DISCUSSION

The biophysical mechanisms contributing to LFP are still under debate (Buzsáki et al., 2012; Logothetis 2003; Einevol et al., 2013). Apart from the prevailing view of passive transmembrane and postsynaptic currents as the main LFP sources, there is increasing evidence of a direct, though complex, relationship between spiking activity and LFP (Ray et al., 2008; Kuokkanen et al., 2010; Reichinnek et al., 2010; Ray and Maunsell, 2011; Belluscio et al., 2012; Scheffer-Teixeira et al., 2013; Schomburg et al., 2014; Anastassiou et al., 2015), supported by computational work that highlights the importance of active conductances and EAP in shaping high-frequency (>100 Hz) oscillatory LFP (Reimann et al., 2013; Schomburg et al., 2012). Moreover, the LFP can encode information about sensory stimuli (Montemurro et al., 2008) or spatial location during navigation (Agarwal et al. 2014). Yet, our understanding of how extracellular signals encode neural circuit activity remains limited.

Here we combined biophysical modeling with in vivo electrophysiological recordings, to study relationships between the ~150–200 Hz ripple-frequency LFP and the spiking activity of spatiotemporally distributed place cell ensembles. In summary we demonstrated that: (i) in simulated SWR, multi-site amplitudes of perisomatic LFP, filtered at ripple bandwidth, reflect spatial constellations of active cells embedded within a subthreshold background. (ii) During in vivo replays, the sequence’s place cells form such active cell ensembles. The sequential activation of these ensembles yields (iii) more consistent ripple-amplitudes and (iv) more similar spatiotemporal LFP-patterns during replays, compared to non replay-associated ripples. (v) Clustering ripples with similar LFP-patterns can separate replays from ripples with uncorrelated spiking, introducing a new approach to detecting such activations based solely on LFP.

Previous studies have yielded valuable insights on how neural spiking can be encoded by the LFP (Reichinnek et al., 2010; Agarwal et al., 2014). However, we still have limited understanding of how LFP-features are linked to specific biophysical mechanisms (e.g. extracellular spike waveforms, active subsets of neurons, after-potentials, etc.) or to spiking or stimulus information. By pairing realistic biophysical modeling with behaviorally relevant in vivo recordings, we explored specific biophysical links between cell ensemble spiking and its extracellular signature in a detailed manner. Such biophysical insight in LFP signals can be readily exploited for a spectrum of applications, and expanded by sophisticated encoding/decoding techniques to obtain even more information from extracellular signals, be it from the LFP, ECoG or EEG (Buzsáki et al. 2012; Khodagholy et al. 2015). Understanding how extracellular signals encode behaviorally relevant neuronal circuits, like the assemblies of hippocampal place cells, is critical, as it provides a window into their organization and functionality. Importantly, efficient interpretation of such signals is crucial for clinically relevant studies where access to neuronal spiking is limited. Brain-machine interface studies in primates and humans (Hwang and Andersen, 2013; Markowitz et al., 2011) and depth recordings from patients implanted with microelectrodes (Kraskov et al., 2007; Rutishauser et al., 2010) are typical examples where LFP has been or can be used as the main interface readout to assess population activity patterns (e.g. during epileptic seizures).

An important question is how spiking activity of local neuronal populations is encoded in the LFP compared to detected spikes. Depending on cell morphology and position relative to the electrode, population architecture and correlation of synaptic inputs (Gold et al., 2006; Łęski et al., 2013; Lindén et al., 2011; Reimann et al., 2013), the LFP can be affected by active currents and EAP of pyramidal cells located up to ~200 μm away from the electrode (Kajikawa and Schroeder, 2011; Schomburg et al., 2012). Ripples are examples of highly synchronous spiking, potentially controlled by rhythmic perisomatic inhibition (Taxidis et al., 2012; 2013), leading to an LFP that is shaped by EAP hundreds of μm from the electrode, far beyond the radius for which spikes can be reliably detected (Buzsáki, 2004). Our results support that the LFP efficiently encodes activity at the level of local ensembles, overcoming the underrepresentation of collective spiking by clustered and multiunit activity.

Finally, our findings provide a window into the spatiotemporal architecture of place cell ensembles forming a spiking sequence (Buzsáki, 2010; Harris et al., 2003). They imply a sufficient number of place cells around an electrode to influence its LFP, suggesting that place cell sequences may be formed by local ensembles throughout CA3 and CA1 rather than by homogeneously-distributed interconnected cells that would lead to synchrony of LFP features over multiple recording sites. Activity propagation between these ensembles, giving rise to the observed LFP-patterns, could be regulated by connectivity (e.g. recurrent excitation in CA3), or by sequential activation of afferent inputs (e.g. Schaffer collaterals in CA1; Dragoi and Buzsáki, 2006). A synfire-like activation of spatially distributed cell ensembles allows for both the sequential activation of topologically dispersed place cells (Dombeck et al., 2010), as well as our observed variability in individual replay patterns, as the exact combination of ensemble cells that spiked in a replay could vary.

EXPERIMENTAL PROCEDURES

Computational model

Cell population

Pyramidal cells were simulated with a multi-compartmental CA1 pyramidal neuron model, based on reconstructed cells from the rat hippocampus, that accurately simulates EAP waveforms of CA1 neurons (Gold et al., 2006; Schomburg et al., 2012). The model incorporated one fast inactivating Na⁺ current and six K⁺ currents distributed along various compartments. Dendritic spines, implemented by altering the passive properties of each compartment, were distributed in both apical and basal dendrites with variable densities (Gold et al., 2006). Synaptic inputs to the cell were adopted from a CA3-CA1 network model of SWR (Taxidis et al., 2012, 2013). Briefly, each CA network is a one-dimensional array of pyramidal cells and perisomatic interneurons, reproducing anatomical and functional properties of the corresponding CA area (Taxidis et al., 2012). The CA3 network produced periodic quasi-synchronized population bursts, driving the CA1 through Schaffer-collateral excitatory connections. Recurrent inhibition in CA1 organized interneuronal responses into ripple-frequency (~150–200 Hz) synchronous oscillatory spiking. Pyramidal cells were entrained by ripple-modulated inhibition combined with CA3-driven depolarization.

Neural populations were instantiated by simulating copies of the single multi-compartmental neuron model. The presynaptic input received by each copy was that of a different pyramidal cell in the CA1 network. Inhibitory synapses were distributed with uniform probability over perisomatic segments (<50 μm from the soma). Excitatory synapses were distributed along apical dendritic segments (between 100 μm and 400 μm from the soma), with distribution probability equal to the normalized spine density in these compartments (Figure S1). Excitatory (AMPA) and inhibitory (GABA_A-mediated) postsynaptic currents were considered (reversal potentials = 0 mV and −75 mV respectively). Synaptic conductance kinetics were alpha-type exponential functions with τ_rise = 1 ms and τ_decay = 2 ms and 7 ms, respectively, and peak conductances of 0.5 nS and 0.6 nS. Each copy of the neuron model received a different number of excitatory synapses, so that some neurons received few (“weakly-driven”) and others received numerous synapses (“strongly-driven” cells).

Neurons were positioned parallel along the x-axis with distances between the centers of their somatic compartments taken from a normal distribution of 10 ± 10 μm (mean ± SD). Each position was also permuted over the y-axis following a normal distribution with SD = 10 μm, creating a simulated pyramidal layer approximately 50 μm wide.

Local Field Potentials

The extracellular potential V_i^e at a given point, stemming from the total transmembrane current I_i of a neuronal compartment i was calculated by approximating the compartment as a line source (Holt and Koch, 1999):

$V_i^e=\frac{I_i}{4\pi \sigma l_i}\left|\log \frac{\sqrt{h^2+r^2}-h}{\sqrt{s^2+r^2}-s}\right|$

where σ = 0.3 S/m is the extracellular medium conductivity, l_i is the compartment’s length, r is the extracellular point’s perpendicular distance from a line through the compartment, h is the longitudinal distance of the point’s projection on the line from one end of the compartment and s is the respective distance from the other end (so that s = l+h). For the total extracellular potential at the point, the extracellular potentials from all transmembrane and postsynaptic currents of all compartments of all cells, recorded every 1 ms, were added linearly. Extracellular potentials were computed either over a rectangular spatial grid with 50 μm spacing (Figures 1 and 2A-B), or along the pyramidal layer, at distances taken from a normal distribution of 200 ± 10 μm (mean ± SD; Figures 2C and 5-6). LFP was acquired by lowpassing (< 450 Hz) these signals with a 20-th order Butterworth filter. Current source densities (CSDs) were computed using the LFP second spatial derivative along the dendritic arborization axis (Nicholson and Freeman, 1975).

Ripple and Spike Detection

SWR were detected through the computed LFP at a given location. The LFP was bandpassed at 150 – 200 Hz with a linear-phase FIR filter. ‘Ripple-amplitude’ is defined as the sum of squared values of the filtered LFP, computed over 50%-overlapping 6 ms-long time bins. Ripples were detected when ripple-amplitudes exceeded 0.3 × SD (over the whole simulation) and ripple boundaries were set where they dropped below 0.1 × SD. Ripples lasting less than 10 ms were discarded and consecutive ripples less than 10 ms apart were concatenated. Mean ripple duration over all simulations was on 39.95 ± 12.33 ms (mean ± SD). Ripples were aligned over the peak of the filtered LFP. Ripple phase was computed from the Hilbert transform of the average ripple-bandpassed LFP.

Spikes were detected when the somatic membrane potential of neurons exceeded −50 mV.

Individual and mixed simulations

We performed 10 simulations of 201 cells each. Each simulation contained the same set of cells arranged in the same positions but with the order of cells randomly shuffled. LFP was simulated at the same locations in all simulations. For each individual simulation i, containing r_i number of ripples, a corresponding “mixed simulation” was created by randomly choosing r_i/10 ripples from each of the 10 simulations and storing their ripple-amplitude and power. The ripple-power coefficient of variation (CV; SD/mean) in each LFP site was computed for both individual and mixed simulations.

To simulate spiking sequences, all cells in each simulation were randomly split into 10 groups of 20 cells each (one group containing 21 cells). Each group was assigned a time delay of 5 ms more than the previous one, so that the time delay of the first group was 0 ms, that of the second was 5 ms (i.e. approximately one ripple cycle), the third 10 ms (2 ripple cycles) and so on. Therefore, neurons spiked at ripple troughs (retaining the ripple rhythmicity) while each cell group represented a ‘place field’, with all groups spiking in temporal sequence, on average. The LFP was computed for each simulation and all ripples were detected as before. Using all LFP-simulating sites, we computed the ‘LFP-pattern’ of each detected ripple following the same algorithm as for the in vivo data (see below). ‘Mixed simulation’ patterns for each individual simulation, were constructed by randomly choosing patterns from all simulations as before.

Numerical Methods

Simulations of the CA3-CA1 network model were performed in the Python-based neural network simulator Brian (Goodman and Brette, 2008), using a second-order Runge-Kutta method with a time step of 0.05 ms. Single CA1 pyramidal cell models were simulated in NEURON, using a second order Crank-Nicholson method with variable time-step ≤ 1 ms. Computation and analysis of modeled extracellular potentials were performed in MATLAB. All results shown here are from simulations generating 30 sec of data.

In vivo recordings

For detailed description of experimental procedures, see Diba and Buzsáki (2007). Briefly, LFP and population activity from hippocampal areas CA3 and CA1 were recorded in three male Sprague-Dawley rats, trained to cross a linear track (79 cm, 125 cm and 170 cm long) for water reward at resting platforms on both ends. Animals were implanted in the left dorsal CA3 and CA1 pyramidal layers with 8 and 4 silicon probes respectively, 200 μm apart, with 8 staggered channels each, 20 μm apart. Spike detection, putative cell clustering and pyramidal cell-interneuron separation were performed with freely available software and previously described methods. In total, 41 sessions from all three animals are included, with 4030 units as pyramidal cells and 482 as interneurons. The latter were excluded from our analysis.

Motion, place field and replay detection

Motion was detected when the animal’s velocity exceeded 3 × mean and immobility was assumed when it dropped below 10 cm/s. For one animal, these thresholds were set to 1.8 × mean velocity and 30 cm/s respectively. Motion segments < 1 sec-long were discarded and consecutive segments closer than 1 sec were concatenated. The direction of track crossing was assessed based on the animal’s location at the beginning, middle and end of each segment. Over a total recording duration of 28,958 sec (706.3 sec per-session on average), 3141 sec corresponded to leftward motion, 3034 sec to rightward motion and 22,783 sec to immobility (76.6, 74 and 555.7 s sec per-session on average, respectively).

The track was split into 5 cm-long spatial bins and the firing rate of each pyramidal unit was calculated as the number of spikes within each bin, normalized by the time spent in the bin. All firing rates were smoothed with 5-point moving average and the average firing rate of each cell was calculated separately for leftward and rightward track crossings. Sparsely spiking cells with average firing rate peak non-significantly above zero (t-test, p > 0.05) were ignored. To ensure constricted Gaussian-like place fields, we discarded cells whose average firing rate trace along the track was above its mean value in more than one third of all bins. Each place field was set as the midpoint of the spatial bin where the place cell’s average rate peaked. From a total of 4030 pyramidal units, we detected 1688 place cells (41.17 ± 19.77 per-session, mean ± SD). On average, 28.43% ± 9.53% units per-session had place cells only in leftward crossings, 27.06% ± 8.83% only in rightward ones and 27.17% ± 11.57% were bidirectional.

Replays were detected during ripples recorded at the CA1 pyramidal layer (see below for ripple detection), through the spiking activity of place cells within ±150 ms around each ripple peak, using a similar method as in Diba and Buzsáki (2007). For each ripple, the Spearman correlation (P_S) was computed between the sequence of activated place cells, ordered by their first spike time during the ripple, and the sequence of their place fields. This was done separately for L- and R-sequence place cells (correlations denoted by P_S(L_i) and P_S(R_i) respectively for ripple i). Only sequences containing spikes from at least 5 cells or 30% of all place cells of the corresponding sequence (whichever is greater) were considered. To detect significant positive or negative correlations, each spiking sequence was randomly shuffled 500 times and the correlation of each permutation with the order of place fields was computed. Sequences were considered significantly correlated (forward replays) or anti-correlated (reverse replays) with the place field order if their correlation was higher or lower, respectively, than 95% of the permutation correlations. Using the median spike or the mean spike time of each place cell to construct the sequences, instead of the first spike times, yielded similar results. Events that had a mixed classification (e.g. both forward replay of the L-sequence and reverse replay of the R-sequence) were classified according to which of the replays yielded the highest absolute correlation with the respective place field order.

LFP processing, firing rate calculations, ripple detection and analysis

From each probe, we only used the LFP from the channel located within the pyramidal layer. This was taken to be the channel that recorded the highest average ripple-amplitude (see below). Bandpass filtering over frequency bands was performed with a fifth-order Butterworth filter. The amplitude of each filtered LFP was estimated as the sum of its squared values calculated over 50%-overlapping 8 ms-long time bins. ‘Ripple-amplitude’ is defined as the amplitude of the 120–200 Hz filtered LFP.

Ripples were detected during immobility, when the ripple-amplitude from the CA1 electrode with the highest amplitudes, exceeded 2 × SD in one animal and 5.5 × SD in two animals. Ripple boundaries were set when the amplitude dropped below 1 × SD. Higher detection thresholds reduced the number of ripples but did not alter our findings. Ripples lasting < 20 ms were discarded and consecutive ones less than 50 ms apart were concatenated. Ripples were aligned over the maximum point of the filtered LFP (0 ms).

‘Ripple-power’ for both modeled and recorded ripples is defined as the integral amplitude (total area below the amplitude trace) within ±40 ms around the ripple peak. We bootstrapped ripple-power distributions by repetitively drawing random samples of size equal to the total distribution size, with replacement. The ripple-power CV was calculated separately for each bootstrap. For the correlation of ripple-power with spike amplitude, the maximum absolute voltage of the average EAP of each pyramidal unit was used. Only cells that participated in at least 10 ripples and remained silent in at least 10 ripples were considered in that analysis (n = 2487). Cells were split intro three groups according to whether their average spike amplitude was below mean (mean = 23.5 μV, ‘low spike amplitude’ group, 69.4% of cells), between mean and mean + SD (mean + SD = 49 μV, ‘medium’ group, 19.6% of cells) or above mean + SD (‘high’ group, 11% of cells). The relative increase in average ripple-power when the unit spiked compared to when it did not, was computed at the electrode where the unit was detected.

Firing rates were computed over the same time bins as LFP amplitudes (see above). Correlations with LFP amplitudes were computed for lags up to ±100 ms around ripple peaks and averaged over all ripples in a session.

LFP-pattern analysis and clustering

‘LFP-patterns’ were constructed using the ripple-amplitude from the pyramidal-layer channel of each probe. Each amplitude trace was z-score normalized over ±100 ms around the peak of each ripple for simulated ripples and over ±150 ms around the ripple peak for recorded ones. ‘Similarity’ between a pair of patterns was quantified as their average correlation over lags within ±50 ms around the ripple peak. For each lag, correlations were calculated over corresponding probes and averaged across probes. Averaging over probes was performed to account for all LFP sites and correlations over multiple lags were computed since an LFP-pattern often needed to be transposed in time to best overlap with another one. This measure yielded low values even when considering the similarity of an LFP-pattern with itself (average self-similarity of LFP-patterns = 0.13 ± 0.02 for simulated patterns and 0.17 ± 0.07 for in vivo ones), mainly due to averaging over all lags. ‘Chance correlation baselines’ were calculated by repeating this analysis after randomly shuffling each pattern’s ripple-amplitudes over time, separately for each probe.

‘Spiking similarity’ S(i,j) between ripples i and j was quantified through their L- and R-sequence Spearman correlations, P_S(L_i) and P_S(R_i) respectively, as:

$$S\left(i,j\right)=\left|P_S\left(Li\right)+P_S\left(Lj\right)\right|+\left|P_S\left(Ri\right)+P_S\left(Rj\right)\right|.$$

Absolute sums were used since two sequences with reverse-replay spiking patterns will both have negative Spearman correlations. Only sessions with at least 10 replays in total were considered in this analysis (n = 21 sessions).

LFP-patterns from all ripples in a session were clustered based on their similarity matrix where each entry is the pattern similarity between the corresponding pair of ripples. Each row of the similarity matrix was z-score normalized and a hierarchical tree was constructed using agglomerative complete-linkage clustering with a Euclidian distance. This clustering approach allowed dissimilar LFP-patterns to be clustered together. All ripples were clustered into the two main branches of the hierarchical tree. Larger number of clusters did not improve results since different replays did not yield different patterns on average. For each cluster, we computed the distribution of absolute Spearman correlations of the L- and R-sequence. Absolute values were used to merge forward and reverse sequences. The medians of the two distributions were added to quantify the total replay content of each cluster. Again, only ripples containing spikes from at least 5 cells or 30% of all place cells (whichever is greater) of the corresponding L- or R-sequence were considered for this analysis and clusters containing no such events for either sequence were set to zero replay content. For Figure 7, the firing rate of each place cell was calculated over each ripple in each cluster, then was z-score normalized and smoothed with 5-point moving average. Cells that never spiked during ripples were removed.

Statistics

Most statistical tests between distribution-averages were done under the Wilcoxon median test as the corresponding distributions were not sufficiently close to normality under the Lillieform normality test (p > 0.05). Using t-tests for mean value comparisons yielded similar results. Circular statistics were performed using the Circstat toolbox (Berens, 2009). F-tests were applied to test significance of goodness of linear fit and Student’s t-test for correlation significance. P-values were FDR-corrected for multiple comparisons. WT-FDR denotes FDR-corrected Wilcoxon test.