Combining Multiple Biomarkers Linearly to Maximize the Partial Area under the ROC Curve

Abstract

It is now common in clinical practice to make clinical decisions based on combinations of multiple biomarkers. In this paper, we propose new approaches for combining multiple biomarkers linearly to maximize the partial area under the receiver operating characteristic curve (pAUC). The parametric and nonparametric methods that have been developed for this purpose have limitations. When the biomarker values for populations with and without a given disease follow a multivariate normal distribution, it is easy to implement our proposed parametric approach, which adopts an alternative analytic expression of the pAUC. When normality assumptions are violated, a kernel-based approach is presented, which handles multiple biomarkers simultaneously. We evaluated the proposed as well as existing methods through simulations and discovered that when the covariance matrices for the disease and non-disease samples are disproportional, traditional methods (such as the logistic regression) are more likely to fail to maximize the pAUC while the proposed methods are more robust. The proposed approaches are illustrated through application to a prostate cancer data set, and a rank-based leave-one-out cross-validation procedure is proposed to obtain a realistic estimate of the pAUC when there is no independent validation set available.

1. Introduction

Prostate cancer is one of the most common and lethal malignancies among men, and accounts for almost 30,000 deaths in the United States each year [1]. Predicting an individual’s outcome from prostate cancer remains a major challenge following a diagnosis of this biologically and clinically heterogeneous disease. A majority of patients who are diagnosed with clinically localized prostate cancer will experience an indolent form of the disease, but it will become metastatic for a subset of these patients. Early treatment of primary prostate cancer is very effective. However, the treatment decision is currently guided mainly by the Gleason score [2], which is insufficient to correctly identify patients with aggressive disease. Thus, researchers are devoted to finding additional biomarkers that can be combined with the Gleason score to predict the aggressiveness of a prostate cancer.

A recent radical prostatectomy (RP) cohort study conducted at the Fred Hutchinson Cancer Research Center [3] has investigated epigenome-wide DNA methylation profiles in primary prostate tumor tissue samples obtained from men undergoing RP.

The goal is to develop a composite test to identify as many patients as possible who are likely to develop aggressive disease, maintaining a high level of true-positive rate (TPR, also known as sensitivity) for aggressive disease, while reducing the false-positive rate (FPR, also known as 1-specificity) for indolent disease to prevent over treatment, which is currently a major problem in prostate cancer management.

A composite test can be obtained by linearly combining multiple biomarkers, and its performance can be evaluated through the receiver operating characteristic (ROC) curve. For detailed reviews of statistical methods on ROC see [4] and [5]. When seeking the optimal linear combination of biomarkers, several useful summary indices for the ROC curve can be considered as the objective function. For example, the total area under the ROC curve (AUC) [6–9], or the Youden’s index [10,11].

Although the composite test that is combined on the basis of the AUC or Youden’s index will have higher overall classification accuracy for the entire FPR (or TPR) range, there may be times when only a restricted range of FPR (or TPR) is relevant to clinical practice. For example, in the aforementioned study of the RP cohort, only the high TPR region is of interest and the biomarkers need to be combined to maximize the overall specificity over that high TPR region, which is equivalent to maximizing the partial area under the ROC curve (pAUC). The pAUC was suggested as a summary index to evaluate a portion of the ROC curve in [12] and [13]. Based on the work of Su and Liu [6], Liu et al. [14] derived alternative linear combinations that have higher sensitivity over a range of high (or low) specificity under the multivariate normal assumption. Pepe and Thompson [7] developed distribution-free and smooth distribution-free approaches to find the linear combination that maximizes the empirical pAUC. Hse and Hsueh [15] derived the first derivative of the pAUC with respect to the linear coefficients under the normality assumption, and proposed an algorithm that adopts multiple initial points to numerically search for the optimal linear combination that maximizes the pAUC.

Our study also concerns linearly combining the results of several biomarkers to yield a composite diagnostic test that maximizes the pAUC over a specific FPR (or TPR) region. In Section 2 we propose a parametric approach under the normality assumption. Hsu and Hsueh [15] determined that the pAUC maximizer may not be unique and that local maximizers do exist. In accordance with these determinations, we suggest an improved algorithm to further alleviate this issue. In Section 3, we present a non-parametric approach based on a kernel smoother, for when normality assumptions cannot be justified. In Section 4, we compare our proposed methods to existing methods through extensive simulation studies. In Section 5, we apply our proposed methods to the data obtained from the aforementioned RP cohort study. We provide a discussion and conclusion in Section 6.

2. The Parametric Approach under a Normal Assumption

2.1. Preliminaries

Let the variable Y denote a collection of continuous biomarker measurements. Let D and $\overline{D}$ denote disease samples and non-disease samples, respectively. Then Y_D = (Y_D1,Y_D2,. . .,Y_Dm)^T and ${\mathit{Y}}_{\overline{D}}={\left({\mathit{Y}}_{\overline{D}1},{\mathit{Y}}_{\overline{D}2},\dots ,{\mathit{Y}}_{\overline{D}m}\right)}^T$ are m continuous biomarker measurements collected from the disease group and the non-disease group, respectively. We also denote n_D and $n_{\overline{D}}$ as the number of samples with and without the disease, respectively. Under the normality assumption, we assume one multivariate normal distribution (MVN) for Y_D and another for ${\mathit{Y}}_{\overline{D}}$, i.e., Y_D ∼ MVN(μ_D, Σ_D) and ${\mathit{Y}}_{\overline{D}}\sim \mathrm{MVN}\left({\mathit{\mu }}_{\overline{D}},{\mathbf{\Sigma }}_{\overline{D}}\right)$, where μ_D and ${\mathit{\mu }}_{\overline{D}}$ are the mean vectors for the disease and non-disease groups, respectively; and Σ_D and ${\mathbf{\Sigma }}_{\overline{D}}$ are the m × m covariance matrices for the disease and non-disease groups, respectively. We denote β = (β₁, β₂, . . . , β_m) as a set of coefficients that defines a linear combination of the m biomarkers. Then, W_D and ${\mathit{W}}_{\overline{D}}$, the combined scores for the respective disease and non-disease groups, follow univariate normal distributions:

$${\mathit{W}}_D={\mathit{\beta }}^T{\mathit{Y}}_D\sim N({\mu }_{{\mathit{W}}_D},{\sigma }_{{\mathit{W}}_D}^2),{\mathit{W}}_{\overline{D}}={\mathit{\beta }}^T{\mathit{Y}}_{\overline{D}}\sim N({\mu }_{{\mathit{W}}_{\overline{D}}},{\sigma }_{{\mathit{W}}_{\overline{D}}}^2),$$

where ${\mu }_{{\mathit{W}}_D}={\mathit{\beta }}^T{\mathit{\mu }}_D$ and ${\mu }_{{\mathit{W}}_{\overline{D}}}={\mathit{\beta }}^T{\mathit{\mu }}_{\overline{D}}$ are the means of the combined scores for the respective disease and non-disease groups; ${\sigma }_{{\mathit{W}}_D}^2={\mathit{\beta }}^T{\mathbf{\Sigma }}_D\mathit{\beta }$ and ${\sigma }_{{\mathit{W}}_{\overline{D}}}^2={\mathit{\beta }}^T{\mathbf{\Sigma }}_{\overline{D}}\mathit{\beta }$ are the variances of the combined scores for the respective disease and non-disease groups.

Then, without loss of generality, we specify a clinically relevant FPR region [0, t₀], and the pAUC of the combined scores is defined as

$$\mathrm{pAUC}\left(\mathit{\beta },t_0\right)={\int }_0^{t_0}\mathrm{ROC}(t)dt={\int }_0^{t_0}\mathrm{\Phi }\left(\frac{{\mu }_{{\mathit{W}}_D}-{\mu }_{{\mathit{W}}_{\overline{D}}}+{\sigma }_{{\mathit{W}}_{\overline{D}}}{\mathrm{\Phi }}^{-1}(t)}{{\sigma }_{{\mathit{W}}_D}}\right)dt,$$ (1)

where Φ is the cumulative distribution function of the standard normal distribution. The goal is to find the optimal linear coefficients β* that maximize the pAUC over the FPR region [0, t₀], i.e.,

$${\mathit{\beta }}^{*}=\arg \underset{\mathit{\beta }}{\max }\mathrm{pAUC}\left(\mathit{\beta },t_0\right).$$ (2)

To distinguish the pAUC in Eq. (1) from another type of pAUC that is to the right of the ROC curve and which is defined with respect to the TPR, some of the literature denotes the former type of pAUC as pAUC_FPR, and the latter as pAUC_TPR. Note that pAUC_TPR can be converted to pAUC_FPR by simply switching the disease status in the original data. This study focuses mainly on pAUC_FPR as it is more conventional and intuitive to represent the area under the ROC curve in such a way; and “pAUC” that appears hereafter refers to pAUC_FPR unless otherwise stated.

2.2. Limitations of existing parametric methods based on the normality assumption

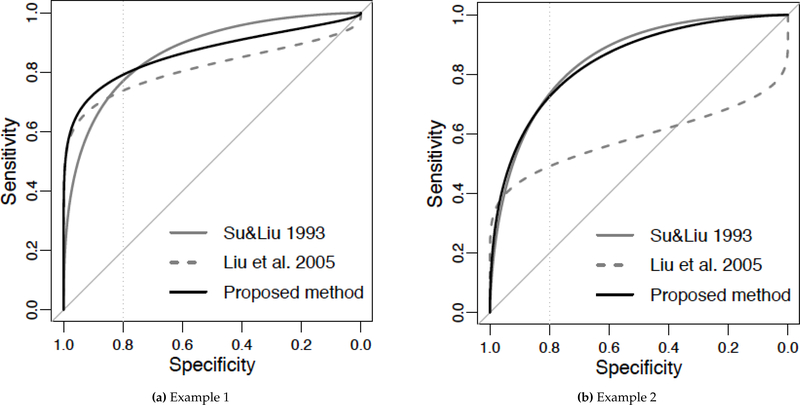
When covariance matrices Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are proportional, Su and Liu [6] proved that Fisher’s discriminant coefficients can lead to an ROC curve that dominates the others on the entire FPR range. However, when covariance matrices Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are NOT proportional, the dominant combination no longer exists. Su and Liu developed the coefficients for maximizing the AUC, but such a combination does not necessarily maximize the pAUC over a predetermined FPR region. Liu et al. [14] developed linear combinations that can favor a high or low specificity region, and their combination dominates any other given combination over a certain FPR region. One limitation of this method is that the dominance region of their combination is neither uniform nor prespecified, but depends on the linear combination to which it is being compared. Therefore, it is not guaranteed to achieve the optimal pAUC over the predetermined clinically relevant FPR region. Figure 1 provides two simple examples of the limitations of these two methods.

Figure 1.

Bi-normal ROC curves when Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are not proportional. Assume that the clinically relevant FPR region is [0, 0.2], indicated by the vertical line drawn at 80% specificity. Two biomarkers are combined linearly to form a composite test. The solid and dashed ROC curves in gray correspond to composite tests combined using Su and Liu’s coefficients and Liu et al.’s coefficients, respectively; the solid ROC curve in black corresponds to the composite tests combined by the proposed parametric method (Section 2). Although Su and Liu’s ROC curve may have the largest AUC and Liu et al’s ROC curve has the largest pAUC over a certain specificity region that is not necessarily the clinically relevant region, the ROC curve corresponding to the proposed method has the largest pAUC over the clinically relevant FPR region. The parameters used: Example 1, μ_D = (3,3), ${\mathit{\mu }}_{\overline{D}}$ = (0,0), σ_D = (3,2), ${\mathit{\sigma }}_{\overline{D}}$ = (1,2), and correlation 0.5; Example 2, μ_D = (1,3), ${\mathit{\mu }}_{\overline{D}}$ = (0,0), σ_D = (3,2), ${\mathit{\sigma }}_{\overline{D}}$ = (1,2), and correlation 0.5. σ_D and ${\mathit{\sigma }}_{\overline{D}}$ are the marginal standard deviations of the disease and non-disease groups, respectively.

In order to directly maximize the pAUC over a predetermined FPR range, Hsu and Hsueh [15] proposed to solve the equation of the first derivative of the pAUC for β. It may be difficult for readers to implement their approach because it requests the gradient of the pAUC function defined in Eq. (1), which is complicated and is not readily available in statistical packages. Furthermore, their algorithm that adopts multiple initial points may help reduce the risk of multiple maxima, but can still be further improved.

2.3. The proposed parametric approach

There are two obstacles to optimize the pAUC under the normality assumption: firstly, although the AUC has a simple analytic expression, such an expression does not exist for the pAUC [4, p.84]; and secondly, multiple local extrema exist, as discovered by [15]. The proposed parametric approach aims to overcome these two obstacles.

2.3.1. An alternative analytic expression for pAUC

An alternative analytic expression for the pAUC was provided by [12,16]. Assuming a single marker with ${\mathit{Y}}_{\overline{D}}\sim N(0,1)$ and Y_D ∼ N(μ, σ²), the alternative pAUC expression is defined as

$$\text{pAUC}\left(t_0\right)=F_{\text{BVN}}\left(\frac{\mu }{\sqrt{1+{\sigma }^2}},{\mathrm{\Phi }}^{-1}\left(t_0\right);\frac{-1}{\sqrt{1+{\sigma }^2}}\right),$$

where F_BVN(z, u; ρ) = P(Z < z, U < u) denotes the distribution function of random variables Z and U that jointly have a standardized bivariate normal distribution with correlation ρ. Rewriting the above equation by adopting our notations to accommodate the linear combination of multiple biomarkers (refer to the Web Appendix for detailed derivation), the pAUC objective function in our proposed approach is given by

$${\mathrm{pAUC}}_N\left(\mathit{\beta },t_0\right)=F_{BVN}\left(\frac{{\mathit{\beta }}^T\left({\mathit{\mu }}_D-{\mathit{\mu }}_{\overline{D}}\right)}{\sqrt{{\mathit{\beta }}^T\left({\mathbf{\Sigma }}_{\overline{D}}+{\mathbf{\Sigma }}_D\right)\mathit{\beta }}},{\mathrm{\Phi }}^{-1}\left(t_0\right);-\frac{\sqrt{{\mathit{\beta }}^T{\mathbf{\Sigma }}_{\overline{D}}\mathit{\beta }}}{\sqrt{{\mathit{\beta }}^T\left({\mathbf{\Sigma }}_{\overline{D}}+{\mathbf{\Sigma }}_D\right)\mathit{\beta }}}\right),$$ (3)

where the subscript “N” indicates the normality assumption. Then, several nonlinear optimization procedures, such as the R package nloptr [17], can be applied to solve the optimization problem stated in Eq. (2), with the pAUC defined in Eq. (3) as the objective function. When the population parameters in Eq. (3) are not available, sample means and covariance matrices can be used instead.

2.3.2. The issue of multiple maximizers

In the pAUC optimization problem, the issue of multiple local maximizers may be two-fold. Firstly, the linear coefficients are not identifiable because in the feasible region there exist different vectors of linear coefficients that are essentially equivalent, in the sense that they result in the exact same ROC curve and hence the same pAUC as well. Multiple maximizers produced by equivalent vectors of linear coefficients are essentially duplicates and can be removed by standardizing, which is discussed hereafter. Secondly, local maximizers that correspond to vectors of linear coefficients may not be equivalent to each other, as pointed out by [15]. To alleviate the risk of the latter kind of multiple local maximizers, one can divide the feasible region into non-overlapping sub-regions, hoping that in each sub-region there exists only one unique local maximizer. Then the optimization procedure can be performed separately on each sub-region and the results can be combined. Next, we discuss how to standardize the linear coefficients and divide the feasible region.

Standardize the linear coefficients:

One important mathematical property of the ROC curve is that it is invariant to monotone transformations of the test scores [4]. Therefore, given a vector of linear coefficients β and a positive scalar a, we consider β and aβ to be equivalent because they lead to the exact same ROC curve and pAUC. The ROC curve and the pAUC are invariant to negative scalar transformations, provided that one flips the signs of the combined scores to ensure that higher scores indicate disease. Based on this property, we can standardize a given vector of linear coefficients β = (β₁, β₂, . . . , β_m) as follows:

$$\tilde{\mathit{\beta }}=\frac{\mathrm{sgn}\left({\beta }^{max}\right)}{\left|{\beta }^{max}\right|}\mathit{\beta },$$ (4)

where $\tilde{\mathit{\beta }}$ is the standardized vector of coefficients, sgn() is the sign function, and β^max is the coefficient with the largest absolute value in β, i.e., |β^max| = max(|β₁|, |β₂|, . . . , |β_m|). A standardized vector of linear coefficients satisfies the following conditions:

1. The largest coefficient(s) is always equal to one. The corresponding biomarker(s) can be considered as anchor marker(s).

2. All coefficients ∈ [−1, 1].

We can further define that two vectors of linear coefficients are equivalent if they have the same standardized form. Note that this definition implies that we allow the signs of the combined scores to flip when the resulting AUC is less than 0.5.

Divide the feasible region:

Under the settings where there are two biomarkers to be combined to maximize the empirical AUC, Pepe and Thompson [7] suggested that the grid search for the optimal ${\mathit{\beta }}^{*}=\left({\beta }_1^{*},{\beta }_2^{*}\right)$ in the 2-D space is equivalent to 1) setting β₁ = 1 and searching within [−1, 1] for β₂ that maximizes the empirical AUC; 2) setting β₂ = 1 and searching within [−1, 1] for β₁ that maximizes the empirical AUC; and 3) combining the results obtained by the two searches and taking the coefficients that result in a larger AUC as the optimal coefficients. We found that this strategy not only divides the feasible region into two non-overlapping subregions, but also guarantees that each sub-region does not contain any equivalent vectors of coefficients.

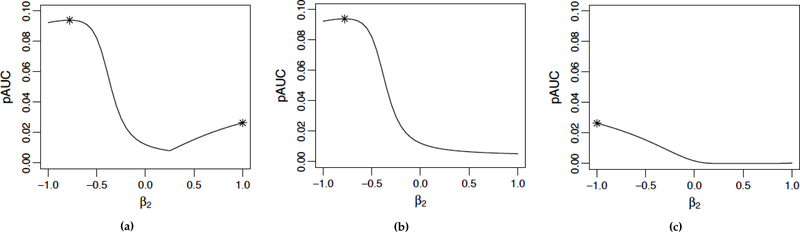
As stated in the introduction of standardized vector of coefficients, Pepe and Thompson’s [7] search pattern implies that we should automatically flip the sign of the combined scores when the AUC is less than 0.5, otherwise the coefficients of the form (−1, β₂) or (β₁, −1) will never be checked. We discovered that allowing the sign to flip during a numerical search may introduce multiple maximizers, as illustrated in Figure 2. This may not affect the performance of a grid search as in [7], but will certainly make the parametric optimization procedure subject to the choice of the initial values and hence should be avoided. Therefore, we suggest forbidding a sign flip, and instead fixing each coefficient to be not only 1, but also −1 as two separate searches.

Figure 2.

Illustration of multiple local maximizers introduced by allowing the sign of the combined score to flip. (a) Set β₁ = 1 and allow the sign of the combined score to flip whenever the AUC is less than 0.5. The two local maximizers are indicated by asterisks. (b) and (c): Set β₁ = 1 and −1, respectively, and forbid a sign flip. Then only a unique maximizer exists for each search.

2.3.3. The proposed algorithm

When the multivariate normality assumption is valid, the proposed algorithm for searching for the optimal linear combination of m biomarkers that maximizes the pAUC over the clinically relevant FPR range [0, t₀] is as follows:

1. Set the first biomarker as the anchor marker by fixing its coefficient β₁ to be 1, and then −1.

2. After fixing β₁, let the remaining m−1 coefficients vary within [−1, 1] and solve the optimization problem stated in Eq. (1) for the optimal m-dimensional coefficient vector β^∗ using the pAUC_N defined in Eq. (3) as the objective function. The maximal pAUCs obtained when β₁ = 1 and β₁ = −1 are denoted as ${\text{pAUC}}_{N,{\beta }_1=1}^{*}$ and ${\mathrm{pAUC}}_{N,{\beta }_1=-1}^{*}$, respectively.

3. Repeat steps 1 and 2 for each biomarker. Then the optimal pAUC is $\max \{{\text{pAUC}}_{N,{\beta }_1=1}^{*},{\text{pAUC}}_{N,{\beta }_2=-1}^{*},{\text{pAUC}}_{N,{\beta }_2=1}^{*},{\text{pAUC}}_{N,{\beta }_2=-1}^{*},\dots ,{\text{pAUC}}_{N,{\beta }_m=1}^{*},{\text{pAUC}}_{N,{\beta }_m=-1}^{*}\}$, and its corresponding coefficient vector is the optimal vector of linear coefficients.

Note that essentially this algorithm divides an n-dimensional optimization problem into 2n smaller optimization problems of dimension (n − 1). Each of the (n − 1)-dimensional optimization problems will be solved by existing optimization procedures such as those provided in the nloptr R package. Alternatively, one can consider the proposed algorithm as a multiple initial-point algorithm which adopts 2n initial points. The proposed algorithm is different from Hsu and Hsueh’s [15] multiple initial-point algorithm as each initial point used by the proposed algorithm defines a n − 1 dimensional sub-region that does not contain any equivalent vectors of coefficients. Therefore, when comparing the proposed algorithm to direct optimization^†, as the number of markers increases, the effect of dimension reduction may weaken, but the effect of multiple initial-points will still enable the proposed algorithm to outperform direct optimization (Web Table 10). This proposed algorithm can help alleviate, but cannot guarantee to eliminate, the issue of multiple maximizers.

To verify our proposed algorithm, we combined 2 to 20 biomarkers in a simulation study. The covariance matrices of the multivariate normal distribution for the disease and non-disease groups were set to be proportional so that the true optimal pAUC and its corresponding linear coefficients could be obtained using Su and Liu’s method. The proposed parametric method (PMuN) and Su and Liu’s method (Su1993) were applied using the true population parameters directly. The optimal pAUC (Web Table 1) and linear coefficients (results not shown) obtained by our proposed approach are highly concordant with the truth. We also compared our approach to Hsu and Hsueh’s multiple initial-point approach by using the examples described in [15]. For the combination of 2 to 4 markers, the results from both approaches are comparable and our approach is only slightly better (results not shown). However, for the “electrical impedance spectroscopy for breast tissue” example [18], in which there are 9 markers available for disease detection, our approach showed rather large improvements in pAUC (Table 1). Note that though we combined up to 20 markers in our simulation, in practice it is generally not recommended to combine 20 or more markers due to the increased risk of overfitting.

Table 1.

Comparison between the proposed PMuN method and Hsu&Hsueh’s method using the electrical impedance spectroscopy data. To compare the two methods on an equal footing, we recalculated Hsu&Hsueh’s pAUC values by plugging their coefficients into Eq. (3).

FPR range	PMuN	Hsu&Hsueh
[0, 0.1]	0.049	0.048
[0, 0.2]	0.131	0.128
[0, 0.3]	0.228	0.186
[0, 0.4]	0.327	0.284
[0, 0.5]	0.428	0.383

3. Nonparametric Methods

When parametric assumptions do not hold, parametric expressions of the pAUC are no longer valid. As an alternative, the empirical pAUC proposed by [7] can be used as the objective function. The empirical pAUC of the combined scores W_D = β^TY_D and ${\mathit{W}}_{\overline{D}}={\mathit{\beta }}^T{\mathit{Y}}_{\overline{D}}$ is defined as

$${\text{pAUC}}_E\left(\mathit{\beta },t_0\right)=P\left[{\mathit{W}}_D>{\mathit{W}}_{\overline{D}}\text{and}{\mathit{W}}_{\overline{D}}>S_{{\mathit{W}}_{\overline{D}}}^{-1}\left(t_0\right)\right],$$ (5)

where the subscript “E” stands for “empirical”. This nonparametric objective function does not rely on any assumptions about the underlying distributions of the biomarker values and therefore is more robust. One limitation is that since the empirical pAUC defined in Eq. (5) is not a smooth function with respect to β, the optimization that uses it as the objective function is usually done through a grid search, which becomes computationally inaccessible for more than three biomarkers. Therefore, when m > 3 biomarkers are involved, instead of searching simultaneously for all m coefficients, some step-wise approaches have been proposed to lower the computational demand. Examples are the step-wise method in [7] and the step-down method in [19].

The step-wise approach in [7] works as follows: Firstly, find the two markers whose optimal linear combination is the best in the sense of having maximal pAUC among all pairs of biomarkers. Without loss of generality denote the derived combined score as W¹(α₂) = Y₁ + α₂Y₂. Secondly, find the next marker that, when combined with W¹(α₂) yields the best pAUC among all remaining biomarkers. Without loss of generality denote the optimized score as W²(α₂, α₃) = Y₁ + α₂Y₂ + α₃Y₃. Finally, one can proceed with this fashion until all m biomarekrs are included in the linear combination.

The step-down procedure introduced in [19] can also be used to combine multiple markers: Firstly, estimate the individual pAUC of each of the m markers using Eq. (5), and sort the m markers based on their estimated pAUC from the largest to the smallest. Secondly, combine the first two markers (with the largest individual pAUCs) using grid search. Thirdly, having derived the combined score obtained in the last step, combine it with the marker with the third largest individual pAUC using grid search. Finally, Proceed in this fashion until all markers are included in the linear combination.

As pointed out in [7], the advantage of step-wise approaches is that each step requires computation for only two markers at a time. The disadvantage is that the coefficients derived in this fashion may not be optimal in the m-dimensional space.

3.1. The proposed kernel-based approach

In order to overcome the limitations of existing nonparametric approaches, here we explore a kernel-based approach which can simultaneously take into account all biomarkers without using a grid search. Given a set of linear coefficients β, we consider normal kernel functions to obtain kernel-based density estimates for the disease and non-disease groups that respectively correspond to the combined scores W_D and ${\mathit{W}}_{\overline{D}}$ [20]. These kernel density estimates are of the following form:

$${\widehat{f}}_{\overline{D}}(w)=\frac{1}{n_{\overline{D}}{h}_{\overline{D}}}\sum _{i=1}^{n_{\overline{D}}}K\left(\frac{w-W_{\overline{D}i}}{h_{\overline{D}}}\right),$$ (6)

where $K(t)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}$, and $h_{\overline{D}}$ is the bandwidth for the non-disease group. We employ a plug-in bandwidth of the form $h_{\overline{D}}=0.9min(sd(W_{\overline{D}i}),IQR(W_{\overline{D}i}))n_{\overline{D}i}^{0.2}$, as introduced in [21]. The notation is similar for the corresponding kernel density estimate of the disease group, ${\widehat{f}}_D(w)$. For an overview of kernel smoothers and the corresponding bandwidths, see also [22]. After obtaining the estimates of the two underlying densities of the combined scores for the disease and non-disease groups, namely ${\widehat{f}}_D(w)$ and ${\widehat{f}}_{\overline{D}}(w)$, respectively, we can obtain the corresponding survivor function of the non-disease group ${\widehat{S}}_{\overline{D}}(w)={\int }_w^{\infty }{\widehat{f}}_{\overline{D}}(t)dt$ and similarly for the disease group, ${\widehat{S}}_D(w)$. The underlying kernel-based ROC estimate is then obtained by

$${\text{ROC}}_{\text{K}}(t)={\widehat{S}}_D({\widehat{S}}_{\overline{D}}^{-1}(t)).$$

Then the kernel-based pAUC estimate can be obtained as

$${\text{pAUC}}_{\text{K}}={\int }_0^{t_0}{\text{ROC}}_{\text{K}}(t)dt.$$ (7)

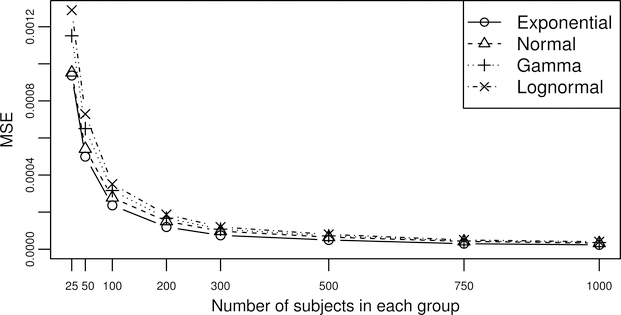
To assess the performance of this kernel-based pAUC estimate where the sample size is finite, we examine four different distributions (exponential, normal, gamma, and lognormal) and 8 different sample sizes from (50, 50) to (1000, 1000). For each distribution, we pre-specify the means and variances for the control group and the case group and then obtain numerically the true pAUC over the FPR range [0, 0.3]. Then for each sample size, after generating 1000 sets of marker values from the pre-specified distribution, we calculate pAUC_K(0.3) for each set of marker value and compare them with the true pAUC to obtained the mean square error (MSE). In Figure 3, the MSEs for all distributions drop dramatically as the sample size increases from (25, 25) to (100, 100); however, after having a sample size of (200, 200), further increase of the sample size only results in minor decrease in the MSE. Therefore, we would recommend a sample size of 100 subjects in each group as the minimal required sample size for the kernel-based pAUC estimate.

Figure 3.

MSEs of the kernel-based pAUC estimate plot against different sample sizes for four different distributions.

A nice feature of the kernel-based pAUC estimate is that it represents a continuous function with respect to the coefficient vector β. As a result, instead of using grid-search or step-wise type of approaches, when pAUC_K is used as the objective function, we can handle all biomarkers simultaneously and use existing optimization procedure (such as nloptr) to look for the optimal solution. However, the issue of multiple maximizers also exists and therefore, a similar algorithm to that of the PMuN approach is recommended. The proposed KS approach is as follows:

1. Set the first biomarker as the anchor marker by fixing its coefficient β₁ to be 1, and then −1.

2. After fixing β₁, let the remaining m−1 coefficients vary within [−1, 1] and solve the optimization problem stated in Eq. (1) for the optimal m-dimensional coefficient vector β^∗ using the pAUC_K defined in Eq. (7) as the objective function. The maximal pAUCs obtained when β₁ = 1 and β₁ = −1 are denoted as ${\text{pAUC}}_{\text{K},{\beta }_1=1}^{*}$ and ${\text{pAUC}}_{\text{K},{\beta }_1=-1}^{*}$, respectively.

3. Repeat steps 1 and 2 for each biomarker. Then the optimal pAUC is $\max \{{\text{pAUC}}_{\text{K},{\beta }_1=1}^{*},{\text{pAUC}}_{\text{K},{\beta }_2=-1}^{*},{\text{pAUC}}_{\text{K},{\beta }_2=1}^{*},{\text{pAUC}}_{\text{K},{\beta }_2=-1}^{*},\dots ,{\text{pAUC}}_{\text{K},{\beta }_m=1}^{*},{\text{pAUC}}_{\text{K},{\beta }_m=-1}^{*}\}$, and its corresponding coefficient vector is the optimal vector of linear coefficients.

Note that this algorithm looks exactly the same as the PMuN algorithm except that pAUC_K, instead of pAUC_N, is used as the objective function. Also note that when maximizing pAUC_K, for a new choice of coefficient vector β, the kernel density estimation of the combined scores needs to be performed again in order to update the corresponding pAUC_k.

4. Simulation Study

In this section, we assess the performance of eight methods: the approaches of Su and Liu [6] (Su1993) and Liu et al. [14] (Liu2005), the proposed PMuN, the step-wise method of Pepe and Thompson [7] (SW-Pepe), the stepdown method of Kang et al. [19] (Stepdown), the proposed kernel smoother method (KS), logistic regression, and a full grid search using the empirical pAUC, Eq. (5), as the objective function (GS, as described in [7]). For logistic regression, although its objective function is the logistic likelihood function rather than the pAUC, we include it in our simulation study because it is the technique most commonly used to linearly combine multiple biomarkers.

When the performance of a combination method is evaluated by a re-substitution method, the estimated performance measure is usually overly optimistic for estimating the diagnostic/prognostic accuracy of future observations and could be misleading, as a procedure that overfits the most may look the “best” [19, 23–25]. Therefore in our simulation study, for each setting we generate one large validation set with a sample size of (100000, 100000). Then for each of the 1000 Monte Carlo repetitions under this setting, we obtain the linear coefficients from the training set, and apply them to the large validation set to calculate the combined scores, based on which the empirical pAUCs of different methods are compared. This provides unbiased comparison of different methods. Some literature would generate an independent validation set of the same size of the training set for each repetition; however, since the sample size of the training sets in our simulation studies could be very small (for example, 25 patients in each group), the use of a large validation set can reduce the variability. Three performance measures are used to compare different methods under each setting:

1. Mean pAUC: this is calculated as the average of the 1000 validated pAUCs, which is defined as the empirical pAUCs calculated in the large validation set.

2. Average rank of pAUC: within each of the 1000 repetition, we obtain the rank of different methods based on their validated pAUCs: the method with the largest validated pAUC receives rank 1, and the method with the second largest validated pAUC receives rank 2, and so on. Then the average rank of each method after 1000 repetitions is obtained and a lower number indicates a better performance.

3. Total MSE of the coefficient estimates: when the true optimal coefficient vector is available, we also assess the accuracy of the coefficient estimates of different methods using total MSE, which is defined as the sum of the MSEs of all elements in the coefficient vector. All coefficient vectors are standardized using Eq. 4 prior to the MSE calculation.

4.1. Multivariate distributions

In the first part of the simulation study, we generate data from known multivariate distributions. Three different distributions are considered, namely, normal, lognormal, and gamma distributions. Multivariate lognormal and gamma data are generated with a normal copula. Three biomarkers are considered so that a full grid search is possible in order to get a performance reference. Detailed parameters and settings used for simulation are summarized in Web Table 2. When data are generated from multivariate normal distributions, the true optimal pAUC and the corresponding coefficients for each scenario are obtained by using a full grid search on Eq. (3) with true population parameters. Simulation results are summarized and the three performance measures are presented in Web Table 3 (n = 50, exchangeable correlations), Web Table 4 (n = 200, exchangeable correlations), and Web Table 5 (n = 200, unstructured correlations).

The results showed that performances of some methods are consistent across all settings, while other methods only work well under certain settings. Methods with consistent performances across different simulation settings are: the proposed PMuN approach, the proposed KS approach, and the two step-wise methods (Stepdown and SW pepe). The PMuN method almost always achieves the best or the second best performance under all settings. When Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are disproportional, the KS approach is slightly worse than the PMuN method and usually has the second best performance; however, when Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are proportional, the Su1993 and logistic regression would very likely outperform the KS approach. The reason why Su1993 and logistic regression perform well under such conditions is discussed below. The two step-wise methods consistently achieve a rank between 4 to 6 out of 8 methods and therefore are not recommended. Note that in our simulation study the PMuN method also performs well when the data are generated from multivariate gamma and lognormal distributions.

The methods that only work well under certain settings are as follows:

• Su and Liu’s method (Su1993) and logistic regression perform well when Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are proportional and can sometimes outperform the PMuN and the KS methods. But both methods perform poorly when Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are disproportional.

  Notice that when Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are proportional and the normality assumption is true, the Su and Liu’s method should be optimal; logistic regression can produce identical mean pAUCs as the Su and Liu’s method but with worse average ranks. This is consistent with what Efron proved in [26]: under such conditions, logistic regression does the same thing as Fisher’s discriminant analysis but less effectively. However, when data are generated from gamma or lognormal distributions, logistic regression performs better than Su and Liu’s method because logistic regression doesn’t rely on the normality assumption.

• Liu et al.’s method (Liu2005) performs poorly when Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are proportional, but may perform well when Σ_D and ${\mathrm{\Sigma }}_{\overline{D}}$ are disproportional.

• The grid-search approach performs poorly when the sample size is only (25, 25); but its performance improves as the sample size increases to (100, 100).

The above mentioned methods can perform well under specific scenarios but may perform poorly under other scenarios. Their performances are unstable and can fluctuate across different settings; therefore these methods are generally not recommended.

4.2. Logistic model

In Section 4.1 we generated data from known distributions without knowing the underlying true relationship between markers. In this section we will generate data based on the pre-determined underlying true combination rule. The data are generated according to the logistic model, that is, logitP[D|Y] = G(Y), where G(Y) is some function of Y (discussed below). The data generating procedure is described as follows:

1. Generate an initial set of biomarker values of N subjects from a single multivariate distribution. Note that in this step, we do not distinguish between the disease and non-disease groups. Choose N accordingly so that in step 5 we have a large enough candidate pool to guarantee the desired sample size.

2. Compute pseudo scores as S = G(Y) and re-center them at 0, denoted as S_c.

3. Convert the centered pseudo scores S_c to risk scores as R = P[D|Y] = logit⁻¹(S_c).

4. For each subject, generate his disease status according to a Bernoulli distribution using his risk score as the success probability, that is, the probability of a subject having the disease is equal to his risk score.

5. Randomly select n_D subjects from the disease group and $n_{\overline{D}}$ subjects from the non-disease group using the disease status defined in step 4.

The advantage of such a data generation technique is that we can control the complexity of the underlying optimal combination of biomarkers rule through the function G() while also maintain the key features of the original distribution used for generating the initial set of biomarker values^‡. The optimal pAUC for each Monte Carlo sample can be calculated from the ROC curve generated using the risk scores; and the true optimal pAUC can be estimated by the average of all 1000 Monte Carlo repetitions.

Firstly, we consider 5 biomarkers and a linear underlying combination rule, that is G(Y) = 1 × Y₁ + 0.6 × Y₂ − 0.3 × Y₃ + 0.4 × Y₄ − 0.5 × Y₅. Three multivariate distributions (normal, gamma and lognormal) are considered when generating the initial set of biomarker values. The empirical pAUCs achieved by different methods in the large test set are summarized in Web Table 6. The logistic regression yields estimates that have the least bias; this is because the data were generated by assuming that the linear logistic model was the true underlying model. The Su1993 method also performs well as such data generating mechanism guarantees the existence of a dominant ROC curve; therefore, methods that maximize AUC (such as the Su1993 method) would also maximize the pAUC under such scenario. Among the three nonparametric methods, the proposed KS method always yields better mean pAUC and higher rank than the two step-wise methods, which is expected as step-wise approaches become more suboptimal as the number of biomarkers increases. As for the coefficient estimates, the proposed KS method can provide robust and accurate coefficient estimates with even smaller MSEs than those produced by logistic regression.

Secondly, we consider 5 biomarkers and a second-order polynomial combination rule obtained from the quadratic polynomial basis, that is, G(Y) = 1 × l(Y)² + 0.5 × l(Y), where l(Y) = 1 × Y₁ + 0.6 × Y₂ − 0.3 × Y₃ + 0.4 × Y₄ − 0.5 × Y₅. Here only normal distribution is used for generating the initial set of biomarker values. The results are also presented in Web Table 6. The logistic regression approach no longer yields the best performance as the true underlying model is not linear; the approaches that achieve better performance in this experiment are the two proposed approaches.

4.3. Scenarios in which logistic regression fails to maximize the pAUC

Logistic regression is commonly used for biomarker selection and panel building because of its robust performance. From the aforementioned simulation studies, the robustness of logistic regression is also observed when the covariance matrices for the disease and non-disease groups are proportional. When the covariance matrices are not proportional, however, the coefficient estimates obtained by logistic regression can be far from the true optimal coefficients (which is indicated by the increased total MSE for coefficient estimates in Web Table 4–6). In this section, we carry out further simulation studies that focus on the scenarios where the covariance matrices are not proportional in order to further investigate situations where logistic regression would fail to yield the optimal linear combination that maximizes the pAUC. For each setting, two biomarkers are considered and the linear coefficients obtained from a training set by logistic regression and the proposed KS method are compared in an independently generated validation set^§. The distribution of the relative difference in pAUC, which is defined as (pAUC_E,proposed − pAUC_E,logistic)/pAUC_E,logistic for each simulation repetition, is examined. For selected examples, we also use a 2-D scatterplot and a ROC plot to illustrate the performance difference between logistic regression and the KS method. Bivariate normal, lognormal and gamma distributions are examined, and the sample size used is (100,100). Without loss of generality, the FPR range of interest is set to be [0, 0.3].

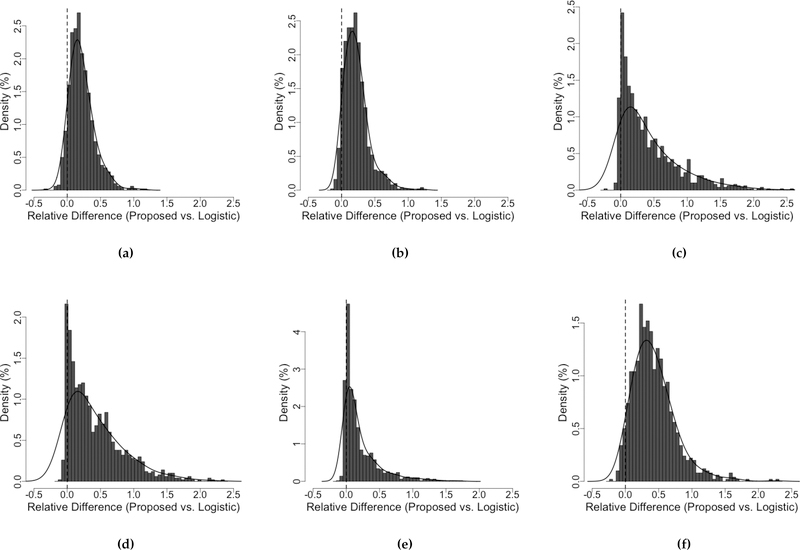
In Figure 4, the distributions of the relative difference in pAUC suggest that the performance of the proposed KS method dominates that of the logistic regression method under every setting. Depends on the scenario, the gain in pAUC by using the proposed KS method can be as large as 200%, with an average of about 50% - 70%; and the logistic regression rarely outperforms the KS method.

Figure 4.

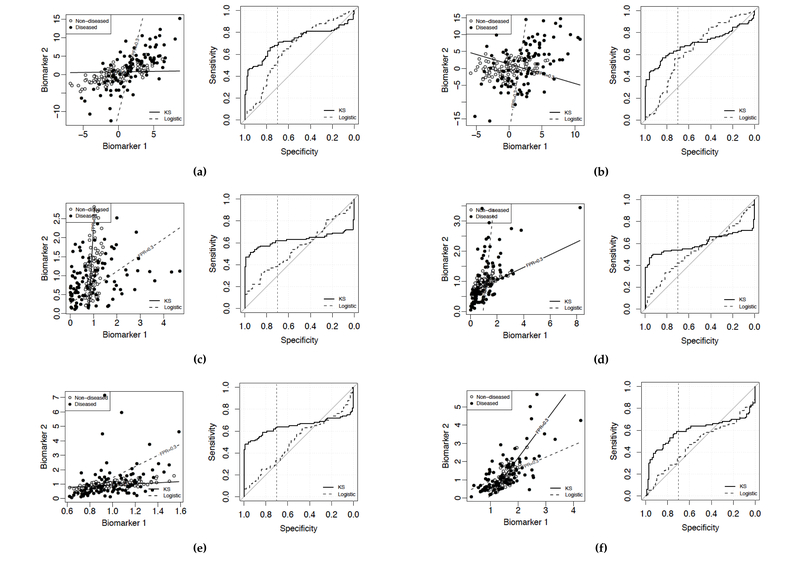
Distributions of the relative difference in pAUC between the proposed KS approach and the logistic regression illustrate that logistic regression is not optimal. The relative difference in pAUC is defined as (pAUC_E,proposed − pAUC_E,logistic)/pAUC_E,logistic for each simulation repetition. The FPR range of interest is [0,0.3]. Population parameters used for data generation are (a) Normal: ${\mathit{\mu }}_{\overline{D}}$ = (0,0), ${\mathit{\sigma }}_{\overline{D}}$ = (2.7,2), μ_D = (2, 2), σ_D = (3, 5), correlation = 0.7. (b) Normal: ${\mathit{\mu }}_{\overline{D}}$ = (0,0), ${\mathit{\sigma }}_{\overline{D}}$ = (3,2), μ_D = (2, 2), σ_D = (3, 6), correlation = 0.3. (c) Gamma: ${\mathit{\mu }}_{\overline{D}}$ = (1,1), ${\mathit{\sigma }}_{\overline{D}}$ = (0.2,0.5), μ_D = (1.1, 1.1), σ_D = (1.2, 0.7), correlation = 0.3. (d) Gamma: ${\mathit{\mu }}_{\overline{D}}$ = (1,1), ${\mathit{\sigma }}_{\overline{D}}$ = (0.6,0.2), μ_D = (1.1, 1.1), σ_D = (1.1, 0.8), correlation = 0.7. (e) Lognormal: ${\mathit{\mu }}_{\overline{D}}$ = (1,1), ${\mathit{\sigma }}_{\overline{D}}$ = (0.2,0.2), μ_D = (1.2, 1,2), σ_D = (0.2, 1.2), correlation = 0.7. (f) Lognormal: ${\mathit{\mu }}_{\overline{D}}$ = (1.5,1), ${\mathit{\sigma }}_{\overline{D}}$ = (0.2,0.5), μ_D = (1.7, 1.2), σ_D = (0.7, 1.2), correlation = 0.7. σ_D and ${\mathit{\sigma }}_{\overline{D}}$ are the marginal standard deviations of the disease and non-disease groups, respectively.

In Figure 5, we visualize some selected examples. Recall that a decision rule based on the linearly combined scores classifies a subject as having the disease if his combined score exceeds a threshold. The lines on the scatterplots are the contour lines that correspond to the threshold at FPR= 0.3. Lines associated with different thresholds should follow the same direction and be parallel to those shown in the figure. Note that these scatterplots and ROC curves do not incorporate sampling variability and are generated from a training sample and a test sample from some underlying truth, with reasonably large sample sizes.

Figure 5.

Scatterplots and ROC plots generated with varying population parameters illustrate that logistic regression is not optimal. Solid lines correspond to the proposed KS method; dashed lines correspond to logistic regression. pAUCs are maximized over the FPR range [0,0.3]. Each straight line in a scatter plot indicates the direction of the classification rule based on the linear combination obtained by the corresponding method, and corresponds to the threshold at FPR = 0.3. The vertical dotted line in the ROC plot indicates 70% specificity. Population parameters used for each scenario are as explained in the description of Figure 4.

A similar pattern emerges from all the scenarios shown in Figure 5. Over the FPR range of interest, [0, 0.3], the ROC curve of the combination rule obtained by logistic regression is only slightly higher than the diagonal line, which corresponds to the ROC curve of a useless test; whereas the ROC curve of the combination rule obtained by the proposed KS method is notably better. Therefore, under such scenarios, the linear coefficients obtained from logistic regression do not maximize the pAUC over the FPR region of interest; whereas the coefficients obtained by approaches that adopt a pAUC measure as the objective function (such as the proposed approaches) yield results that are far superior. Since there is no biological basis that different biomarkers should have similar variance ratios between disease and non-disease group, we consider this as an important limitation for logistic regression and an important advantage for the proposed approaches.

5. Application to the RP Cohort Study

In this section, we apply the existing and proposed methods to the data obtained from the aforementioned RP cohort study. DNA methylation data were generated from the prostate tumor tissue samples obtained from 327 men during surgery to remove the prostate gland. Over a mean follow-up period of 8.2 years, 303 of them had no evidence of disease recurrence (non-disease group) and 24 had metastatic-lethal disease recurrence (disease group). The goal is to develop a biomarker panel that can identify tumors that will recur in a metastatic-lethal form. The data available for this analysis include the Gleason scores and the methylation β-values (which are calculated as β = m/(m + u + 100), where m and u are the signal intensities for methylated and unmethylated CpG sites, respectively) of the top 42 CpG sites that are most predictive of metastatic-lethal prostate cancer selected from the initial 478,998 CpG sites on the basis of three criteria: the AUC, pAUC over the FPR range [0, 0.05], and P-value (Wald test). Among the 42 CpG sites, 8 were successfully validated in an independent cohort from Eastern Virginia Medical School, which included 65 prostate cancer patients (41 with non-recurrent disease and 24 with metastatic-lethal recurrent disease. For details refer to [27]).

Determining how to further select biomarkers from the top 42 CpG sites is beyond the scope of this paper. In order to demonstrate our proposed methods, we consider three subsets of these 42 CpG sites, that is, a) the top 3 CpG sites with the highest pAUCs over the FPR range [0, 0.05]; b) the top 5 CpG sites with the highest pAUCs over the FPR range [0, 0.05]; and c) the 8 CpG sites that were validated in the Eastern Virginia cohort. Biomarkers in each of the three subsets, together with the Gleason scores, are combined linearly using the existing and proposed methods discussed in this paper.

Note that maintaining high sensitivity (≥ 0.95) for the patients with a metastatic-lethal form of disease recurrence while maximizing specificity for patients without disease recurrence in order to reduce over treatment means that, when combining biomarkers, we should maximize the pAUC that corresponds to the high TPR range [0.95, 1], namely, the pAUC_TPR. Therefore, we need to switch the labels of the disease and non-disease groups before applying the nonparametric methods.

Since there is no independent validation set, internal validation estimates will be used to compare different methods. While an unbiased estimate of AUC can be obtained by the leave-one-pair-out (LOPO) cross-validation method proposed by Huang et al. [25], its application to pAUC is difficult because, unlike the calculation of AUC, not all “pairs” but only those in which the observation from the control group is greater than a pre-determined cutoff (determined by the FPR range) will contribute to the pAUC. Therefore, we propose a rank-based leave-one-out (RB-LOO) cross-validation estimate for pAUC. The procedure is as follows:

1. Leave the first observation out, and train the model using the remaining observations to obtain the linear coefficients. Apply the obtained coefficients to all observations (also including the first observation which was left out and was not used for model training) and rank the resulting combined scores from low to high. The observation with the lowest combined score gets rank 1, and the observation with the second lowest combined score gets rank 2, and so on. Record the rank of the first observation as R₁.

2. Repeat Step 1 for the ith observation – that is, leaving the ith observation out to obtain its corresponding rank R_i – until each observation has been left out exactly once.

3. Then the ROC curve constructed using the ranks (R_i’s) is the RB-LOO cross-validated ROC curve; and the pAUC calculated from this ROC curve is the RB-LOO cross-validation estimate for the true pAUC.

In this RB-LOO cross-validation procedure, the ith observation does not contribute to the training of the ith model. which is then used to calculate the rank R_i. Therefore the rank R_i can be considered as a validated score of the ith observation. Here we use ranks rather than the actual combined scores because the ranks are comparable across repetitions but the combined scores may not be. The proposed RB-LOO cross-validation can also be used to validate AUC, and the results are consistent with the LOPO estimates (Web Table 8). Next, we will use the RB-LOO cross-validated pAUC as a realistic estimate to compare different methods.

Table 2 summarizes the RB-LOO cross-validation estimates for each method. The proposed KS method achieves the highest pAUC for all three scenarios and its performance is far superior to that of logistic regression for scenario a). Note that the β-values are bounded by 0 and 1 and are generally not normally distributed. Therefore the PMuN doesn’t perform very well. For exploratory purpose we also build models using the methylation M-values, which are defined as M = log₂(m + 100/u + 100) and are essentially a logit transform of the corresponding β-values. M-values can take values from (−∞, ∞) and are more likely to be normally distributed. We use the Shapiro-Wilk test in R to check the normality assumption and find out that a majority of the markers in the selected subsets pass the test: only 1 marker in Subset (b), or 2 markers in subset (c) fail the test. The RB-LOO cross-validation estimates of the pAUCs based on M-values are summarized in Table 3. We observe that the performance of the PMuN approach becomes better. The two proposed approaches both outperform the logistic regression in all three scenarios. The SW-pepe method achieves good performance in scenario b) but is unstable and performs poorly in scenario c).

Table 2.

Results of the RP cohort application: Rank-based LOO cross-validation estimate of pAUCs for different methods on different subsets of biomarkers based on methylation β values. The training perforamnces are provided within parentheses.

Biomarkers	PMuN	KS	Stepdown	SW-pepe	Logistic
Subset a) + Gleason	0.011(0.024)	0.028(0.037)	0.011(0.029)	0.017(0.034)	0.017(0.022)
Subset b) + Gleason	0.017(0.029)	0.020(0.037)	0.015(0.035)	0.018(0.035)	0.019(0.021)
Subset c) + Gleason	0.026(0.036)	0.027(0.042)	0.012(0.041)	0.002(0.042)	0.027(0.031)

The pAUC for Gleason Score alone: 0.004

Table 3.

Results of the RP cohort application: Rank-based LOO cross-validation estimate of pAUCs for different methods on different subsets of biomarkers based on methylation M values. The training perforamnces are provied within parentheses.

Biomarkers	PMuN	KS	Stepdown	SW-pepe	Logistic
Subset a) + Gleason	0.017(0.025)	0.025(0.037)	0.012(0.030)	0.023(0.035)	0.016(0.020)
Subset b) + Gleason	0.018(0.029)	0.018(0.038)	0.014(0.033)	0.032(0.035)	0.017(0.020)
Subset c) + Gleason	0.031(0.037)	0.035(0.042)	0.016(0.041)	0.003(0.039)	0.028(0.032)

The pAUC for Gleason Score alone: 0.004

The common trend that emerges from both Table 2 and 3 is that all five methods except the logistic regression method experience a noticeable drop from the training pAUC to the RB-LOO cross-validated pAUC. This is because we are estimating the pAUC over the region of sensitivity ≥ 0.95 with only 24 cases; therefore the inclusion or exclusion of one case could have a substantial impact on the trained coefficients. Logistic regression, on the other hand, focuses on the overall separation of the two groups and is less susceptible to the inclusion or exclusion of one subject. Despite the large drop in pAUC from training to validation, the proposed KS method and the PMuN method (under the normality assumption) still outperform logistic regression in terms of the RB-LOO cross-validated pAUC and therefore are recommended.

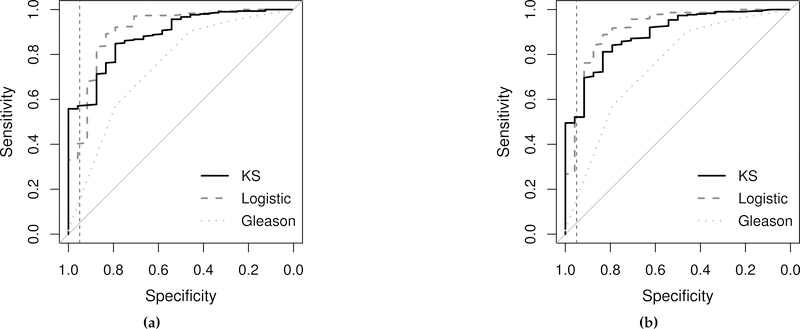
In Figure 6, we visualize the differences in the RB-LOO cross-validated ROC curves between the KS method and logistic regression for subset a). The ROC curve for Gleason score is also provided as a reference. Note that the ROC curves in Figure 6 are plotted with disease labels switched in order to convert pAUC_TPR into pAUC_FPR. Therefore the specificity in those plots is indeed the sensitivity w.r.t. the original labels, and the sensitivity in those plots is indeed the specificity w.r.t. the original labels. Based on the figure, if we pick a threshold that corresponds to a sensitivity (w.r.t. the original labels) > 95% for the combined scores, using the combination rules obtained by the proposed KS method can save about 20% of the patients without a aggressive disease from unnecessary work-up and treatment as compared to the combination rules obtained by logistic regression.

Figure 6.

ROC curves for the RP cohort application plotted with disease status reversed. Black solid lines are the RB-LOO cross-validated ROC curves obtained by the proposed KS method; gray dashed lines are the RB-LOO cross-validated curves obtained by logistic regression; gray dotted lines are the ROC curve for Gleason score. The vertical dashed line in each plot is drawn at 95% specificity. The RB-LOO cross-validated pAUCs are summarized in Table 2. Biomarkers included in each subplot are (a) Subset a) (β-values) + Gleason score; (b) Subset a) (M-values) + Gleason score.

6. Discussion and Conclusion

The main contribution of this article is to propose two new pAUC measures, Eq. (3) and Eq. (7), that can be used as the objective function when searching for the optimal linear combination that maximizes the pAUC, as well as an algorithm that helps alleviate the issue of multiple local maximizers. Both proposed pAUC measures are continuous functions with respect to the linear coefficient vector β; therefore, common optimization procedures can be used in place of a grid search in order to efficiently handle situations in which the number of biomarkers exceeds three. Although our methods would work with a large number of biomarkers, we suggest that biomarker panel building should focus on small to mild number of markers. For problems with a large number of markers the main challenge is how to rank and select individual candidates while controlling for FDR in order to come up with a small subset of markers for panel building, therefore is beyond the scope of this study. For the aforementioned reasons, we would recommend apply our methods on up to 20 markers.

The proposed approaches have been compared to existing approaches through simulation studies. When the pAUC obtained by re-substitution may be overly optimistic, for each simulation settings we generate a single large test set with (100000, 100000) subjects to calculate the validated pAUC. The proposed PMuN approach and the KS approach are robust under different settings and are recommended. The two step-wise approaches (Stepdown and SW-Pepe) achieve moderate performances and their performances start to drop as the number of biomarkers increased, which is expected because such step-wise approaches are computationally less demanding; but they do not examine the whole feasible region and therefore do not necessarily provide optimal results.

In order to assess the impact of different optimization procedures on the performance of proposed optimization algorithm compared to direct optimization, we have tested four different procedures in R: fminbnd() from neldermead, nloptr() from nloptr, optim() from stats, and the generalized simulated annealing procedure GenSA() from GenSA. The number of markers tested varied from 5 to 20. The proposed algorithm always outperforms the direct optimization except when generalized simulated annealing procedure is used, where the difference in performance becomes negligible (Web Table 10). However, the average time-to-complete was almost doubled for direct optimization (Web Table 11). To conclude, for the four commonly used optimization procedures that we have tested, the proposed algorithm is recommended.

The asymptotics of a kernel-based ROC curve are well studied in the literature. The building block was founded by Nadaraya [28] back in 1963 where he proved the consistency of a kernel-based distribution estimate. Lloyd and Yong [29] proved that the kernel-based ROC is better than the empirical one by showing that the empirical estimator is deficient compared to the kernel-based. In our case, given the derived coefficients of combination, the kernel-based ROC as derived by the combined generated score naturally attains all the properties discussed in [29]. However, future work needs to be considered regarding the asymptotic underlying theory that takes into account the variability of the estimated coefficients.

There are several concerns associated with the KS approach: 1) sample size, 2) computational time, and 3) the appropriate bandwidth. Firstly, based on our simulation studies, a sample size of about 100 patients in each group should be the minimal required sample size for the KS approach to generate robust estimates. Secondly, to compare the computational time of the proposed KS method to those of other methods, we list the average running time of each method using sample sizes (100,100) in Web Table 35. The proposed KS method takes considerably longer time than the other methods as the number of biomarkers increases. The proposed PMuN method is significantly faster than the KS method; therefore, we should consider using the PMuN method if the data follow a multivariate normal distribution after some monotonic transformation. Finally, there are different choices of bandwidths available for the kernel-based pAUC estimator. We observed that under certain scenarios, the kernel-based pAUCs underestimate the true pAUCs, which may be fixed by choosing a different bandwidth. Further investigation of this issue is required.

The performance of logistic regression in the context of linearly combining biomarkers to maximize the pAUC has been closely examined. We discovered that the proportionality of the covariance matrices of the disease and non-disease groups can greatly influence the performance of logistic regression in maximizing the pAUC. Through simulation studies, we can conclude that logistic regression performs well when the covariance matrices are proportional; however, its performance is extremely inconsistent when the covariance matrices are not proportional. Disproportional covariance matrices are common in practice as the biomarker values in the disease group tend to have large variance, and the extent of this increased variance very likely differs among the biomarkers and is driven by the underlying biology. Therefore, in practice, approaches that directly optimize the pAUC should be considered first.