MLS: Joint Manifold-Learning and Sparsity-Aware Framework for Highly Accelerated Dynamic Magnetic Resonance Imaging

Abstract

Manifold-based models have been recently exploited for accelerating dynamic magnetic resonance imaging (dMRI). While manifold-based models have shown to be more efficient than conventional low-rank approaches, joint low-rank and sparsity-aware modeling still appears to be very efficient due to the inherent sparsity within dMR images. In this paper, we propose a joint manifold-learning and sparsity-aware framework for dMRI. The proposed method establishes a link between the recently developed manifold models and conventional sparsity-aware models. Dynamic MR images are modeled as points located on or close to a smooth manifold, and a novel data-driven manifold-learning approach, which preserves affine relation among images, is used to learn the low-dimensional embedding of the dynamic images. The temporal basis learnt from such an approach efficiently captures the inherent periodicity of dynamic images and hence sparsity along temporal direction is enforced during reconstruction. The proposed framework is validated by extensive numerical tests on phantom and in-vivo data sets.

I. Introduction

Key challenges in obtaining high spatio-temporal resolution images in dynamic magnetic resonance imaging (dMRI) are long data acquisition time, patient discomfort and inherent physical limitations in data acquisition [1], [2]. Sub-Nyquist sampling techniques, called compressed sensing (CS) [3]–[5] and low-rank (LR) based frameworks [6]–[9] have shown great potential to accelerate data acquisition process in MRI. These methods enforce signal prior information, such as low-rankness and/or sparseness, by using the techniques such as the conventional principal component analysis (PCA), singular value decomposition (SVD) to learn data correlations, and/or Fourier sparse priors.

Recently, manifold-learning models have shown to be superior to conventional PCA-based low-rank models [10], [11]. Few kernel-based frameworks [12], [13] and manifold based frameworks [14]–[17] have been explored in reconstructing dMRI from highly undersampled k-space data. While these methods have shown considerable improvement over conventional low-rank based models, they overlook the sparsity which arises naturally along the dMRI temporal direction. Joint low-rank and sparsity-aware models [4], [7], [8] have already shown significant improvement over schemes that rely only on low-rank or sparsity properties. Motivated by recent developments in manifold learning, this paper advocates a generalized joint manifold-learning and sparsity-cognizant framework for highly accelerated dMRI. The proposed method builds a bridge between manifold-learning methods [16], [17] and models which capitalize on sparsity arguments [7], [8].

The rest of the paper is organized as follows. Section II describes the basic principles behind dMRI with undersampled data, Section III presents the proposed method, and section IV validates the advocated approach using extensive numerical tests on data. Finally, section V concludes the paper.

II. Background

Let, the N × N_fr Casorati matrix $X=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\mathrm{...}{\mathbf{x}}_{N_{\text{fr}}}\right]$ be the dynamic image series, where N = Number of phase encoding lines (N_p) × Number of frequency encoding lines (N_f) and each column x_i of X is the i^th image. The data acquisition process in dMRI can be then formulated as:

$$\mathbf{Y}=\varphi (\mathbf{x})+\mathbf{V},$$ (1)

where ϕ is a measurement operator that incorporates Fourier undersampling along each column of X and V stands for noise. The dynamic image series X is recovered from the acquired undersampled k-space data Y by solving following regularized optimization problem:

$${\text{arg min}}_{\mathbf{x}}{‖\mathbf{Y}-\varphi \left(\mathbf{x}\right)‖}_{\text{F}}^2+\lambda \mathcal{R}\left(\mathbf{x}\right).$$ (2)

Typically, $\mathcal{R}(\cdot )$ is the Fourier sparsity-aware loss along temporal direction ${‖\mathcal{F}(\mathbf{x})‖}_1$ or low-rank priors.

In this paper, we present a novel joint manifold learning and sparse framework, (we termed as MLS) for recovering dMR images from highly undersampled k-space data. The proposed method can be divided into three steps. Although, dynamic images ${\mathbf{x}}_i\in {ℂ}^N,i=1,2,\mathrm{...}{N}_{\text{fr}}$ are high dimensional in the input space, the images live on or close to the smooth otherwise unknown manifold, $\mathcal{M}$ of dimension $M\ll N$. We model dynamic images as points on or close to this manifold $\mathcal{M}$. The first step is to learn such a smooth manifold. In the first step the manifold geometry is learned by describing neighborhood of each image based on affine combination and compute the nonlinear mapping that embeds $\mathcal{M}$ into ${ℂ}^M$. Dynamic MR images naturally exhibit periodicity along time. In the second step, we establish a mechanism to capture such periodicity and enforce sparse representation of dynamic image series in the manifold to formalize the joint manifold and sparse framework. Finally in the third step, desired dynamic image series is reconstructed using regularized inverse problem framework.

III. Proposed Framework

A. Manifold learning and embedding

Given an image ${\mathbf{x}}_i\in {ℂ}^N,i=1,\mathrm{...},N_{\text{fr}}$ from a dynamic image series, we assume there exists a smooth M-dimensional $\left(M\ll N\right)$ manifold $\mathcal{M}\subset {ℂ}^N$ such that x_i’s lie on or close to $\mathcal{M}$ as shown in the Fig. 1. Similar to majority of manifold based methods, the most important part in manifold learning is to define the neighborhoods of each signal (image) that defines the manifold geometry. While, the Euclidean-distance is used in most of the works to define neighborhood relations, e.g., [10], here we capitalize on the properties of the tangent spaces of a smooth manifold to define neighborhoods. Each image x_i can be approximated by the affine combination of its neighbors [17], [18]: ${\mathbf{x}}_i\approx {\sum }_{n=1}^{N_{\text{fr}}}{\omega }_i^n{\mathbf{x}}_n$, where ω_i is a sparse weight vector that defines the manifold geometry. Such weight vectors can be computed by solving the following ℓ₁-constrained least-squares problem:

$${\mathbf{\omega }}_i=\underset{{\mathbf{\omega }}_i^H{1}_{N_{\text{fr}}}=1,{\omega }_i^i=0}{\text{argmin}}{‖{\mathbf{x}}_i-{\sum }_{n=1}^{N_{\text{fr}}}{\omega }_i^n{\mathbf{x}}_n‖}^2+\beta {‖{\mathbf{\omega }}_i‖}_1,$$ (3)

where $1_{N_{\text{fr}}}$ is the all-one vector. The constraint ${\mathbf{\omega }}_i^H{1}_{N_{\text{fr}}}=1$, where (·)^H denotes Hermitian transposition, ensures affine neighboring relations, ${\omega }_i^i=0$ excludes x_i from being a neighbor of itself, and β ≥ 0 is the parameter to control the number of neighbors. Hence, the manifold geometry of dynamic image series is described by an N_fr × N_fr weight matrix W whose entries are ${\omega }_i^n$.

Fig. 1.

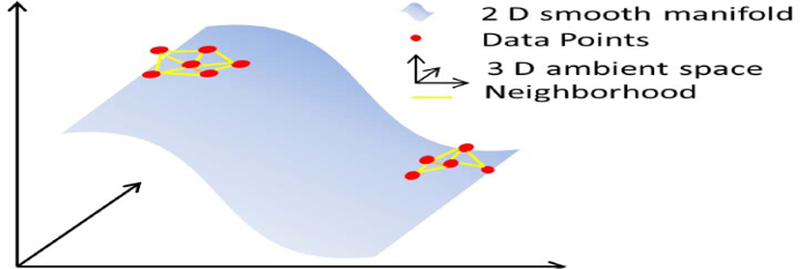
Illustration of a smooth manifold. Three-dimensional data points lying close to the 2-dimensional smooth manifold surface.

Often times, in machine learning applications and dimensionality reduction problems, the objective of manifold learning is to find a M dimensional basis Ψ that preserves the manifold geometry such that:

$$\underset{\begin{array}{c}\mathbf{\Psi }\in {ℂ}^{M\times N_{\text{fr}}},\mathbf{\Psi }{\mathbf{\Psi }}^H={\mathbf{I}}_M,\\ \mathbf{\Psi }{1}_M=0_M\end{array}}{\text{argmin}}{\sum }_{i=\mathbf{1}}^{N_{\text{fr}}}{‖{\psi }_i-{\sum }_{n=1}^{N_{\text{fr}}}{\omega }_i^n{\mathbf{\psi }}_n‖}^2,$$ (4)

where $\mathbf{\Psi }=\left[{\psi }_1{\psi }_2\mathrm{...}{\psi }_{N_{\text{fr}}}\right]$. Constraint ΨΨ^H = I_M, where I_M is an M × M identity matrix, excludes the trivial all-zero solution, and Ψ1_M = 0 centers the columns of Ψ around 0. The desired Ψ is given by the eigen-decomposition of the N_fr × N_fr matrix $\mathcal{K}:=\left(I-W\right){\left(I-W\right)}^H$ such that rows ${\psi }^m$, m = 1, 2,…M of Ψ are the eigenvectors $\mathcal{K}$ that correspond to the M least significant eigenvalues. [10], [18].

Unfortunately, unlike in many machine learning applications such as clustering and classification, lack of training data is a big challenge in learning based MRI reconstruction frameworks. Full images x_i are not available in dMRI reconstruction applications, rather, they are the desired unknowns. In dMRI, pseudo random sampling pattern that fully samples few low frequency central k-space lines and randomly undersamples outer k-space lines is prevailed as shown in Fig.2. Such low frequency signals that are sampled in all temporal frames, called “navigators,”. Because of the linearity of Fourier transform, the neighborhood relation W in (3) holds for the k-space as well and hence the navigators are used to estimate the weight matrix W. It is important to note here that unlike in many dimension reduction problems, where the objective is to learn manifold from massive sets of training data and find a M low dimensional embedding for a test signal, such massive training data is not available in accelerated dMR reconstruction problem. Instead, our objective here is to reconstruct the dMR images from highly undersampled k-space data. For such purpose, we generalize partial separable model for dMRI [6], [7] and explicitly use Ψ as temporal basis of the dynamic image series. Representing the image series Casorati matrix as X = UΨ, regularized solution of (2) takes the form:

$$\text{arg}{\text{min}}_{\mathbf{U}}{‖\mathbf{Y}-\varphi \left(\mathbf{U}\mathbf{\Psi }\right)‖}_{\text{F}}^2+\lambda \mathcal{R}\left(\mathbf{U}\mathbf{\Psi }\right).$$ (5)

Fig. 2.

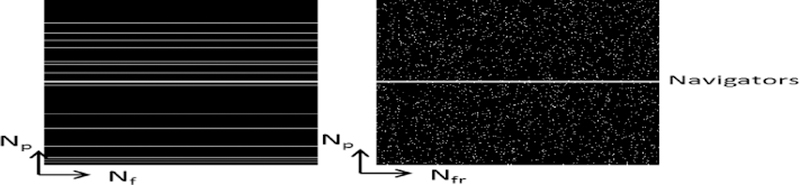
1-D Cartesian undersampling pattern with navigator lines. Left: phase encoding and frequency encoding direction. Right: phase encoding and temporal frame direction.

B. Sparsity enforcement

After finding the temporal basis Ψ, the next step is to enforce sparsity in the reconstruction framework. Many works [4], [5], [7] have shown that, Fourier basis provides efficient sparse representation along temporal direction for dMRI. In [17] we have shown that the temporal basis computed using manifold based framework efficiently captures the inherent low order harmonics in dMRI. Motivated by the fact that Fourier basis is suitable for sparse representation of periodic signals and the temporal basis learned from manifold efficiently captures periodicity, the sparsity-enforcing regularizer $\mathcal{R}\left(\cdot \right)$ in (2) is defined as

$$\mathcal{R}\left(\mathbf{U}\mathbf{\Psi }\right)={‖\mathbf{U}{\mathbf{\Psi }}_f‖}_1,$$ (6)

where ${\mathbf{\Psi }}_f=\mathcal{F}\left(\mathbf{\Psi }\right)$, $\mathcal{F}$ is the Fourier transform operator along temporal direction.

Substituting (6) in (5) we get the sparsity-aware manifold framework for dMRI reconstruction as

$$\text{arg}{\text{min}}_{\mathbf{U}}{‖Y-\varphi \left(\mathbf{U}\mathbf{\Psi }\right)‖}_{\text{F}}^2+\lambda {‖\mathbf{U}{\mathbf{\Psi }}_f‖}_1.$$ (7)

The problem formulation in (7) is similar to the conventional partial separable and sparse (PS-sparse) [7] model and low rank and sparse model (SLR) [8]. While these conventional frameworks use SVD for low rank temporal basis estimation, we learn the temporal basis from the affine relation of images in dMR series.

C. Image reconstruction

The ℓ₁-regularized image reconstruction framework, similar to (7), has been widely used in many image reconstruction applications [4], [5], [7]. The regularizer term in (7) is non-differentiable, hence the problem in (7) is difficult to solve. In [19] such a regularizer is approximated by the Huber function $\mathcal{H}\left(r\right):ℂ\to ℂ$:

$$\mathcal{H}\left(r\right)=\left\{\begin{array}{cc}\frac{{\left|r\right|}^2}{2\delta },\hfill & \text{if}\hspace{0.17em}\left|r\right|\le \delta \\ \left|r\right|-\frac{\delta }{2},\hfill & \text{if}\hspace{0.17em}\left|r\right|\ge \delta .\end{array}\right.$$ (8)

and the problem in (7) can be rewritten as

$$\text{arg}{\text{min}}_{\mathbf{U}}{‖\mathbf{Y}-\varphi (\mathbf{U}\mathbf{\Psi })‖}_{\text{F}}^2+\lambda {\sum }_{j=1}^N{\sum }_{k=1}^{N_{\text{fr}}}\mathcal{H}({(\mathbf{U}{\mathbf{\Psi }}_f)}_{j,k})$$ (9)

For simplicity and fairness in comparison, the problem in (9) is solved using half quadratic minimization problem [19] which is also used in [7]. Introducing an auxiliary variable, Z = UΨ_f , (9) can be rewritten as

$$\text{arg}{\text{min}}_{\mathbf{U},\mathbf{Z}}{‖\mathbf{Y}-\varphi (\mathbf{U}\mathbf{\Psi })‖}_{\text{F}}^2+\frac{\lambda }{2\delta }{‖\mathbf{U}{\mathbf{\Psi }}_f-\mathbf{Z}‖}_{\text{F}}^2+\lambda {‖\rho (\mathbf{Z})‖}_1,$$ (10)

where $\rho \left(\cdot \right):{ℂ}^{P\times Q}\to {ℂ}^{D\times 1},D=P\times Q$ is a vectorizing operator. Finally, (10) can be solved iteratively alternating over U and Z until convergence. Specifically, at (t)^th iteration,

$${\mathbf{Z}}^{\left(t\right)}=\text{arg}{\text{min}}_{\mathbf{Z}}\frac{1}{2\delta }{‖{\mathbf{U}}^{\left(t-1\right)}{\mathbf{\Psi }}_f-\mathbf{Z}‖}_{\text{F}}^2+{‖\rho (\mathbf{Z})‖}_1,$$ (11)

$${\mathbf{U}}^{\left(t\right)}=\text{arg}{\text{min}}_{\mathbf{U}}{‖\mathbf{Y}-\mathbf{U}\mathbf{\Psi }‖}_{\text{F}}^2+\frac{\lambda }{2\delta }{‖\mathbf{U}{\mathbf{\Psi }}_f-{\mathbf{Z}}^t‖}_{\text{F}}^2.$$ (12)

Once an optimal U* is obtained at convergence, the desired dynamic image series is computed as X = U*Ψ

IV. Results and Discussion

The proposed method is verified by extensive testing on phantom and in-vivo data sets. All experiments are performed in quad core workstation Intel(R) 3.6 GHz with windows 7, 32 GB RAM running MATLAB 2014. The performance of the proposed methods is compared with the state-of-the-art PS-sparse method [7]. For fairness of comparison both methods were solved through same optimization pipeline. The performance is quantified using the Reconstruction Error (RE) as in (13). Parameters in all methods were tuned heuristically and the results with the least RE are presented.

$$\text{RE}=\frac{{‖{\mathbf{X}}_{\text{REF}}-{\mathbf{X}}_{\text{REC}}‖}_{\text{F}}}{{‖{\mathbf{X}}_{\text{REF}}‖}_{\text{F}}}.$$ (13)

A. Cardiac Cine Phantom

An MRXCAT [20] phantom based on extended cardiac torso (XCAT) was used to generate breath-hold cardiac cine data of matrix size (N_p × N_f × N_fr) 408 × 408 × 360. It included around 15 cardiac cycles and 24 cardiac phases. Undersampling was mimicked using retrospective undersampling with Cartesian sampling as shown in Fig. 2. Each frame has about 12 acquired phase encoding lines out of which 4 are navigator lines, with net reduction factor of about 32.

At first, we studied how well the proposed affine relation based on the manifold-learning approach captures the inherent periodicity of the dMR image series. Furthermore, it is important that few navigator lines should accurately approximate such a relation. We compared the temporal basis calculated using using full data (reference) and using 4 navigator lines. Fig. 3 shows that the proposed method efficiently captures the periodicity in cardiac cycle and cardiac phases.

Fig. 3.

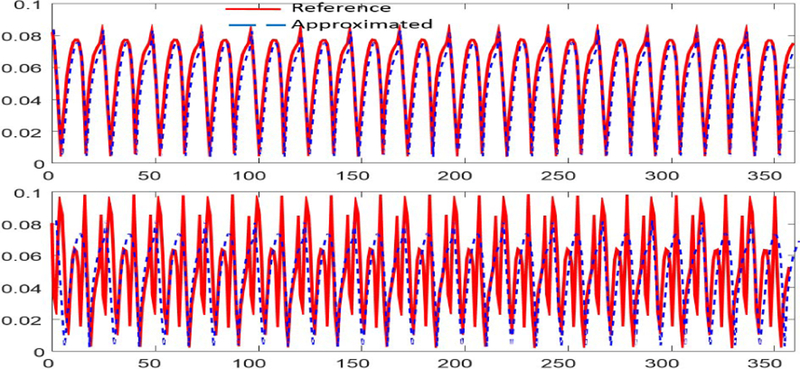
Comparison of representative temporal basis.Top to Bottom: 2nd and 3rd temporal basis capturing periodicity in cardiac cycle and phases.

Two spatial frames representing cardiac region of interest(ROI) from systole and diastole cardiac stages are shown in Fig.4. From Fig.4 we can see that PS-sparse tends to demonstrate noise-like artifacts and ring like artifact in the myocardial region. Fig.5 shows the x-t cross section along dotted line in the reference image. It shows that the PS-sparse method have ripple like aliasing artifacts. RE for each method are presented in parenthesis in Fig.4. Computational times for PS-sparse and proposed method are 46 and 52 mins, respectively.

Fig. 4.

Spatial results for numeric cine phantom. Representative diastole and systole phase. Left to Right: Reference, PS-sparse (0.0652), proposed MLS (0.0431). Top to Bottom: diastole phase, error maps (x10), systole phase, error Maps (x10).

Fig. 5.

Temporal x-t cross section results for numeric cine phantom. Top to bottom: Reference, PS-sparse, proposed MLS.

B. In-vivo cardiac cine data

For in-vivo experiment, we used cardiac MRI (CMR) from a patient with systolic dysfunction. The acquisition parameters used were TR/TE = 5.4/4ms, FOV 360 × 340 mm, spatial resolution about 1.8 mm. The scanned data was single cardiac cycle and thin plate spline spatio temporal deformation [21] was used to generate 5 cycles to mimicking quasi-periodicity. The data matrix was of size 192 × 156 × 130. Retrospective Cartesian undersampling, with 12 acquired lines per frame was used, out which 4 are navigators. From Fig.6 we can see that the proposed method gives cleaner and sharper images whereas in the PS-sparse method the myocardial region looks to be blurred. The temporal result in Fig.7 shows that the PS sparse method smooths out the details. Moreover, the RE values also indicate the proposed method outperforms the PS-sparse method. Computational times for PS-sparse and proposed method are 16 and 21 mins, respectively.

Fig. 6.

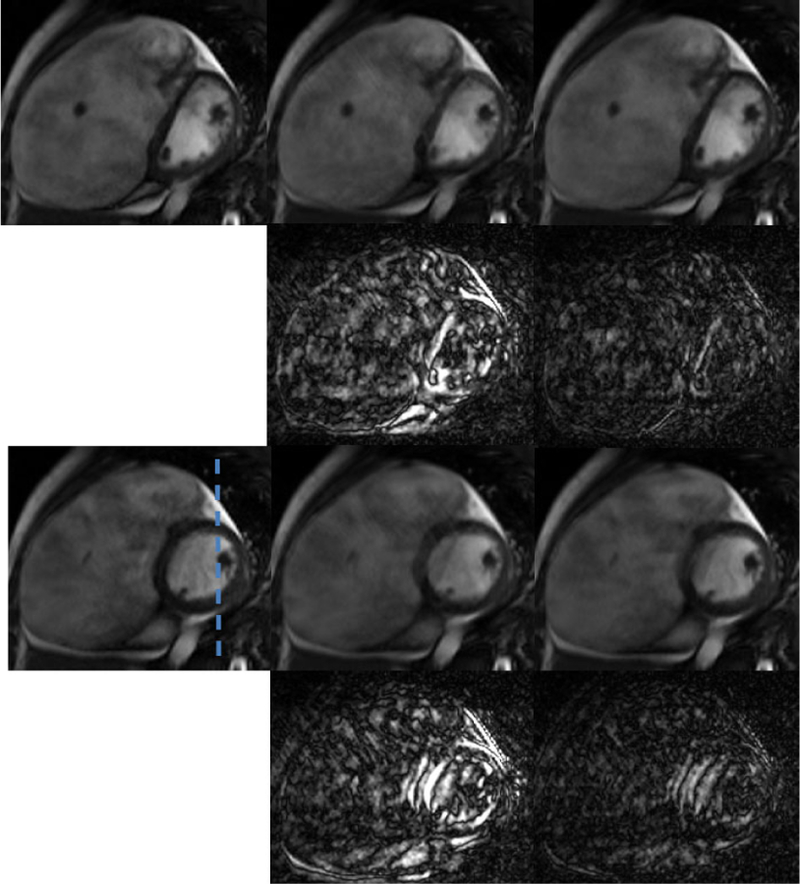
Spatial results from in-vivo cardiac MR to study atrial and ventricular dilation. Representative diastole and systole phase. Left to Right: Reference, PS-sparse (0.0587), proposed MLS (0.0460). Top to Bottom: diastole phase, error maps (×10), systole phase, error maps (×10.)

Fig. 7.

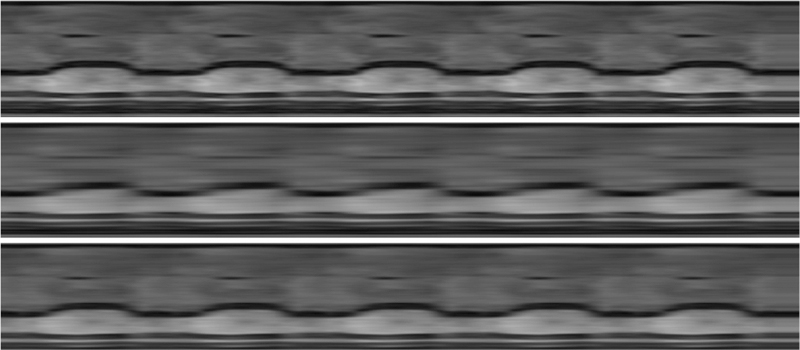
Temporal x-t cross section results for cardiac in-vivo MR study. Top to bottom: Reference, PS-sparse, proposed MLS.

V. Conclusion

In this paper, we presented a novel framework that builds the bridge between the manifold-learning and sparsity-cognizant model for accelerating dMRI. We proposed a novel data-driven technique to learn the manifold and hence build the temporal basis for dMR images. Within the proposed manifold model, the inherent periodicity of dMR images is exploited to enforce sparsity during reconstruction. The proposed joint manifold and sparsity model have shown to be superior than conventional low-rank and sparsity-aware model. Extensive study of the proposed method on more data sets and applications is desired. Although the proposed method presents specific manifold learning approach and uses Fourier transform as sparsifying transform it can be easily extended to many other state of the art manifold learning and learning based sparse encoding techniques.