Statistical Methods for Standard Membrane-Feeding Assays to Measure Transmission Blocking or Reducing Activity in Malaria

Abstract

Transmission blocking vaccines for malaria are not designed to directly protect vaccinated people from malaria disease, but to reduce the probability of infecting other people by interfering with the growth of the malaria parasite in mosquitoes. Standard membrane-feeding assays compare the growth of parasites in mosquitoes from a test sample (using antibodies from a vaccinated person) compared to a control sample. There is debate about whether to estimate the transmission reducing activity (TRA) which compares the mean number of parasites between test and control samples, or transmission blocking activity (TBA) which compares the proportion of infected mosquitoes. TBA appears biologically more important since each mosquito with any parasites is potentially infective; however, TBA is less reproducible and may be an overly strict criterion for screening vaccine candidates. Through a statistical model, we show that the TBA estimand depends on μ_c, the mean number of parasites in the control mosquitoes, a parameter not easily experimentally controlled. We develop a standardized TBA estimator based on the model and a given target value for μ_c which has better mean squared error than alternative methods. We discuss types of statistical inference needed for using these assays for vaccine development¹.

1. Introduction

The World Health Organization estimated 214 million cases and 0.4 million deaths from malaria in 2015, with most deaths in children under 5 (WHO, 2015). Malaria is caused by infection with a Plasmodium parasite, and deaths are mainly due to Plasmodium falciparum (WHO, 2015). No highly effective malaria vaccine has been developed, although the RTS,S/AS01 malaria vaccine given to infants and young children has shown vaccine efficacy for clinical malaria during the 20 months after vaccination of 45% (95% confidence interval (CI): 41% to 49%) (RTS,S Clinical Trials Partnership, 2014). However, in 5–17 month old children, using a bi-phasic exponential model, the vaccine efficacy to prevent new infections is estimated to begin at 74%, but reduces to 28% at 1 year after vaccination (White et al., 2015). Since there is no highly effective traditional malaria vaccine, other tools are needed such as transmission blocking vaccines (TBVs). TBVs are not designed to confer direct and immediate protection of vaccinees from malaria disease, but are designed to produce human antibodies that interfere with malaria parasite development inside the mosquito, thus reducing the probability of infecting other people (WHO, 2015). Several TBVs are being developed and an efficacious TBV may be important for controlling malaria epidemics and eradicating malaria (malERA Consultative Group on Vaccines et al., 2011; Nunes et al., 2014).

TBV development moves from animal studies to clinical trials (phase I, II, and III). Early on, it is useful to measure the transmission blocking efficacy for each vaccinated individual animal or human. For a final Phase III trial of the efficacy of TBVs, a cluster randomized trial would probably be ideal (Delrieu et al., 2015), but other approaches for licensure using individual transmission blocking efficacy measures have been discussed (Nunes et al., 2014). Additionally, estimates for the probability that a mosquito becomes infected after a single feed on a vaccinated or an unvaccinated individual are useful for models of malaria transmission (Smith et al., 2011).

There are many types of assays to measure mosquito transmission of Plasmodium parasites (Sinden et al., 2012). The direct skin-feeding assay (DSFA, mosquitoes fed on the skin of malaria infected subjects) and direct membrane-feeding assay (DMFA, mosquitoes fed through a feeding apparatus a mixture of control/test antibodies and malaria infected blood collected from humans) need to be conducted in a field site where malaria is endemic (transporting gametocytes – parasites in the transmissible stage – destroys their viability). Unfortunately these procedures have high failure rates in producing infective mosquitoes, even when used with non-vaccinated individuals (Bousema et al., 2012). The standard membrane-feeding assay (SMFA) avoids this problem. In the SMFA, the antibodies from a test sample are mixed with blood and large amounts of lab-raised gametocytes and fed to mosquitoes through a membrane. A similar procedure is done using control antibodies (e.g., antibodies from individuals that have not been exposed to malaria or the vaccine). Then for both the test and control procedures the number of parasites (in the oocyst stage) growing in each mosquito are counted. The large numbers of gametocytes ensure that (in the control group at least) there is a high probability of infective mosquitoes and hence a successful assay. Bousema et al. (2013) argue that “the SMFA is rightfully the current gold standard for ranking TRI [transmission-reducing intervention] candidates and prioritizing the most promising TRI candidates for further development”.

Despite being the gold standard assay, the SMFA has no preferred readout. Two common SMFA results are the transmission reducing activity (TRA, also called the percent inhibition of mean oocyst intensity) and the transmission blocking activity (TBA, also called the percent inhibition of prevalence). A common TRA estimator for a single test sample is

$$r=100\left(1-\frac{{\widehat{\mu }}_t}{{\widehat{\mu }}_c}\right),$$ (1)

and a common estimator of TBA is

$$b=100\left(1-\frac{{\widehat{p}}_t}{{\widehat{p}}_c}\right)$$ (2)

where ${\widehat{\mu }}_t$ and ${\widehat{\mu }}_c$ are the mean number of oocysts per mosquito from the test sample and from the control sample, respectively, and ${\widehat{p}}_t$ and ${\widehat{p}}_c$ are the proportion of infected mosquitoes (that is, the proportion of mosquitoes with at least 1 oocyst) from the two samples (Figure 1). Some argue that TBA is biologically the more important measure because in the field if a mosquito has a single oocyst, it has the potential to become infective. The lack of consensus on whether to use TRA or TBA to analyze SMFA data is a crucial issue in the field of TBV research (Wu et al., 2015).

Figure 1:

SMFA and the two readouts, estimating TRA and TBA. From left to right: Several containers of mosquitoes (COMs) are fed on the same feed-day and are maintained for a week. Then each mosquito is dissected and oocysts in the midgut counted. Mosquitoes with 0 oocysts are uninfected, those with 1 or greater are infected. Within each test and control COM, 20 mosquitoes are summarized by their oocyst counts mean $\left(\widehat{\mu }\right)$ and prevalence $\left(\widehat{p}\right)$ (e.g., proportion infected), which are used in estimating TRA and TBA.

One important difference between TBA and TRA is in the stability of the two assay results from replicates of a single homogeneous test sample. Replicates of TBA estimates using b systematically depend on the associated ${\widehat{\mu }}_c$ values from each replicate, while replicates of TRA estimates using r do not appear to have such a dependence. We show this using previously unpublished 4B7 monoclonal antibody data, creating many ostensibly identical test sample replicates at a concentration of 94 μg/ml. We run SMFAs on many replicates and select the 20 replicates with the lowest values of ${\widehat{\mu }}_c$ (between 0.1 to 6.0 oocysts) and the 20 replicates with the highest values of ${\widehat{\mu }}_c$ (between 30.0 and 81.0 oocysts). The mean of the 20 TRA estimates of the low control mean group was 92.5 compared to the 95.2 average of the 20 TRA estimates of the high control mean group (using Welch’s t-test: p-value= 0.25, 95% CI on difference of mean TRAs: (−7.24, 2.00)). The mean of the 20 TBA estimates of the low control mean group was 79.7 compared to the 42.9 average of the 20 TBA estimates of the high control mean group (Welch’s t-test p-value < 0.001, 95% CI on difference of mean TBAs: (24.84, 48.75)).

This strong relationship between ${\widehat{\mu }}_c$ and TBA estimates, and lack of a similar relationship with ${\widehat{\mu }}_c$ and TRA estimates has been previously recognized (e.g., see Figure 4 in Churcher et al., 2012). The former relationship is important for the interpretation of TBA, since typically ${\widehat{\mu }}_c$ is larger in SMFAs than in the field. For two replicates of the same test sample with quite different ${\widehat{\mu }}_c$ values, the replicate with the associated ${\widehat{\mu }}_c$ value closer to mean oocyst values seen in the field would have the TBA result closer to the biologically meaningful one. Thus, we need to reduce the TBA estimates’ dependence on ${\widehat{\mu }}_c$ and to be able to bridge the readout from these lab-based SMFAs to expected results from field-based assays such as the DSFA or DMFA (Nunes et al., 2014).

Figure 4:

The COM-wise standard deviation vs. the COM-wise mean on the log scale for polyclonal controls and the mean-variance equality line (dashed) represents the Poisson model.

In this paper, we tackle statistical issues related to SMFAs. In Section 3 we model the number of oocysts in each mosquito in the SMFA as a zero inflated, negative binomial model with random effects specified for each container of mosquitoes and each feed-day that the assay is performed. Others have used this or similar models (Churcher et al., 2012; Miura et al., 2013), and have discussed the relationship between TRA and TBA estimates and ${\widehat{\mu }}_c$. Unlike previous work, our work focuses on not just recognizing the problem of the dependence of the TBA estimator on ${\widehat{\mu }}_c$, but on offering a solution. The solution begins by formally defining the estimands related to the TRA and TBA (Sections 4 and 5, respectively) within the context of the model. Previously the TRA and TBA have been defined only in terms of the two common estimators r and b, and hence there has been no study of the properties of those estimators with respect to their associated estimands nor of alternative estimators. The TBA estimand depends on the control mean, µ_c, while the TRA estimand does not. Under our model, the true μ_c values (not just their estimates) vary for different implementations of the assay on different feed days, meaning that the TBA estimand itself varies. Our solution is to use a targeted TBA estimand, where we set μ_c to ${\mu }_c^{\ast }$ a preset target for μ_c, to standardize instead of relying on a ${\widehat{\mu }}_c$ estimate from that assay (Section 5.2). The TBA estimand is named “targeted” because of the target ${\mu }_c^{\ast }$ value and has no affiliation with targeted maximum likelihood estimation. We develop standardized TBA estimators that use ${\mu }_c^{\ast }$ to estimate specific targeted TBA estimands, and hence allow more rational comparisons of TBA results from samples assayed on different feed days (or in different labs) than the unstandardized estimates. Further, by appropriately choosing ${\mu }_c^{\ast }$, the targeted TBA estimand gives us a bridge to interpret TBA results closer to their likely values in a malaria endemic field.

With a formal statistical model, we explore statistical inferences for individual SMFA estimators for both the TRA (Section 4.3) and targeted TBA estimands (Section 5.3). Previous work has focused on the model building and demonstrating the relationship between TRA and TBA estimates, not on inferences from single test samples (Churcher et al., 2012; Miura et al., 2013). Currently in the scientific literature, statistical tests on single (possibly pooled) test samples that ignore the hierarchical structure and clustering of mosquitoes in SMFA are state of the art (Jones et al., 2015; Kumar et al., 2015; Patra et al., 2015; Roeffen et al., 2015; Armistead et al., 2014). In Section 4.3 we propose simulation-based single test sample TRA confidence intervals that properly account for the correlation structure of the data. Our proposed confidence intervals have much better simulated coverage than the simpler ones that treat the mosquitoes’ oocyst counts as independent. Using the relationship between TRA and TBA estimands from our model allows inferences on individual TRA estimates to be translated to inferences on individual TBA estimates (Section 5.3).

An alternative to using our proposed standardized TBA estimator to estimate the targeted TBA estimand interpretable in a malaria endemic field is to restructure the SMFA so that the ${\widehat{\mu }}_c$ values are close to those observed in the field (Sauerwein and Bousema, 2015). One way to do this is with a “restricted” TBA estimator, where we repeatedly run an assay using the simple TBA estimator b until we get an assay with ${\widehat{\mu }}_c$ reasonably close the target, ${\mu }_c^{\ast }$. In Section 5.5, we compare the restricted and the standardized TBA estimators through simulation and show that the latter approach is much more efficient. Finally, we study statistical inferences for two sample TBV trials in Section 6 and end the paper with a Discussion (Section 7).

2. Background

2.1. Plasmodium falciparum Life Cycle

The Plasmodium falciparum life cycle occurs partly within humans and partly within mosquitoes. First, a mosquito takes a blood meal that includes red blood cells that contain the sexual stage of the parasite (the gametocytes). The parasites mature in the mosquito and develop into oocyst stage parasites in approximately 1 week. Each oocyst internally creates and eventually releases many sporozoites, which travel to the mosquito’s salivary gland. If the mosquito bites a human after that, the sporozoites invade the human’s liver cells. Within the liver cell the sporozoites change and multiply into many merozoites, which are released when the liver cell ruptures and invade red blood cells. In this blood-stage of the parasite, there can be many cycles within the infected human where the red blood cells are invaded, the parasites multiply, and the red blood cells rupture to release more merozoites to repeat the cycle. This blood-stage parasite is responsible for all malaria symptoms: fevers, headaches, nausea, vomiting, fatigue, and other severe outcomes – including death. Some blood-stage parasites differentiate into gametocytes and may be taken up by a mosquito and complete the life cycle.

2.2. Standard Membrane-Feeding Assay

There are no globally accepted standard reagents or protocols for the SMFA; we give only a brief review of the SMFA protocol for the data in this paper. To start, the NF54 strain of Plasmodium falciparum is maintained in the lab for 14–16 days to induce mature, infectious, gametocytes. For each day the feeding assay is done, the cultures are mixed with normal human serum (the liquid part of blood without blood cells or clotting factors) and normal human red blood cells in predefined proportions (0.15–0.2% gametocytes and 50% red blood cells by volume). The two types of samples are created by combining that gametocyte mixture with test antibodies or control antibodies in concentrations determined by the test sample. There are two types of antibodies in the test samples: polyclonal or monoclonal. Polyclonal antibodies are produced in vivo from either animals or humans, while monoclonal antibodies are produced from a hybrid of an antibody producing white blood cell (a B cell) that produces the antibody of interest and a cancerous white blood cell (myeloma). Then either the test or control sample is put in a feeding apparatus covered with a membrane that is exposed to about 50 (Anopheles stephensi) mosquitoes, each about 3 to 7 days old. After the mosquitoes feed on a blood meal (a mixture of gametocyte culture and test (or control) antibody) through the membrane, the mosquitoes are maintained for 8 days. We call a group of mosquitoes that feed on the same blood meal a container of mosquitoes (COM). A subset of those mosquitoes that have taken blood meals (typically n = 20 per sample) are dissected manually to count the number of oocysts in each mosquito (see Figure 1).

There remains considerable variability in the assay despite its detailed protocol. Although the gametocytes and mosquitoes are both raised in a temperature-controlled environment, with highly regimented protocols, some biological variability cannot be easily eliminated. Moreover, this assay is very labor intensive and takes about 3 weeks to complete. Repeating the assay on two different aliquots from the same sample would almost double the already large labor burden of the assay, and in some cases there is not enough antibody to repeat the assay anyway. Since the within-sample variability cannot be reduced to a negligible part of the between sample variability, it is important to have a good model of assay variability.

3. Fitting a Model to Data

3.1. Description of Model-Building Data

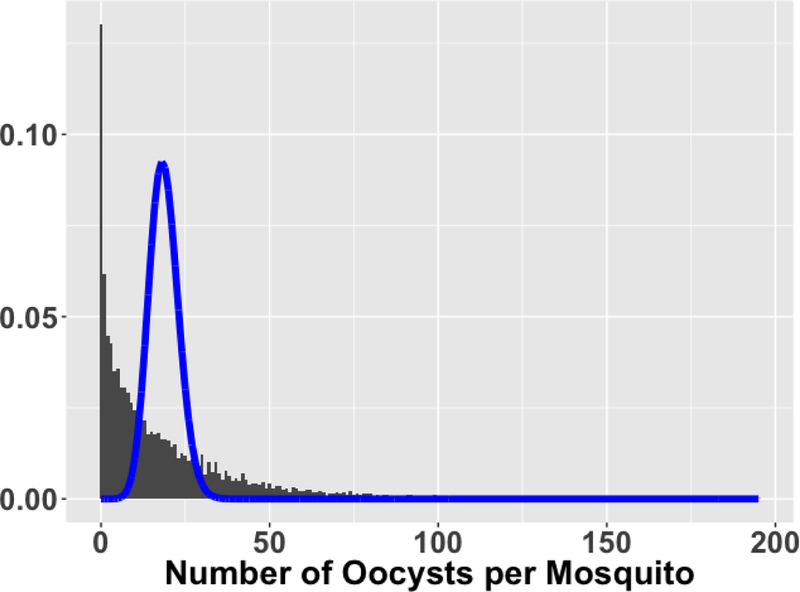
The model-building data uses only containers of mosquitoes (COMs) fed using polyclonal control antibodies. The data have a hierarchical structure: each mosquito has its own oocyst count, mosquitoes are clustered into COMs, and COMs are clustered into feed-days. The model-building data have 9804 mosquitoes in 492 COMs on 105 feed-days, translating to about 20 mosquitoes per COM and about 5 COMs per feed-day. The mean number of oocysts per mosquito is 18.66 with a variance of 522.3, which is 28 times larger than the mean and is clearly overdispersed compared to a Poisson model (Figure 2).

Figure 2:

Histogram of 9804 oocyst counts from polyclonal control COMs with Poisson(mean=18.66) density overlay. Note the excessive proportion of zeroes and skewing to the right, both extremes contributing to overdispersion.

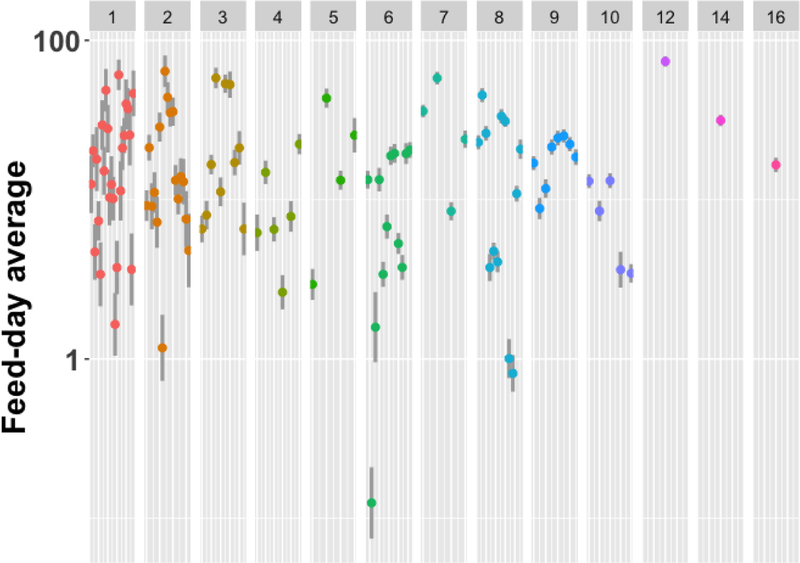
The hierarchical structure could explain some of that overdispersion. To visualize variation across feed-days, we plot mean oocyst count maximum likelihood estimates for each feed-day (ignoring COM grouping) from a Poisson model with linear overdispersion (McCullagh and Nelder, 1989) (Figure 3). The feed-day effect is substantial for these data.

Figure 3:

Each feed-day average oocysts maximum likelihood estimate (dot) is presented with 95% confidence intervals (vertical line) from a Poisson family generalized linear model accounting for overdispersion (McCullagh and Nelder, 1989), displayed on a log scale with separate panels for each number of COMs. 25 feed-days had 1 COM (left-most dots), 1 feed-day had 16 COMs (right-most dot). The highest feed-day average of about 75 had 12 COMs (240 mosquitoes). The lowest feed-day average of 0.125 had 6 COMs (120 mosquitoes).

The relation between the sample COM-wise means and standard deviations (or variances) help inform model choice. We plot the within-COM standard deviation versus the within-COM mean (both on the log scale) against the equality line for the variance and mean (Figure 4).

3.2. A Representative Count Model

The ultimate goal is to develop methodology and inference for the TRA and TBA, but to do so we first need a reasonable model of the data-generating process. We use a zero-inflated negative binomial random effects model, denoted as ZINB2-RE. We call the specific fit (i.e., the estimated parameter values) on the model building data the representative count model (RCM). Later (in Figure 5), we will show that the RCM fits the test COMs reasonably well, even though the parameters are estimated from only the control COMs.

Figure 5:

Standard deviation of oocyst counts by mean oocyst counts, both plotted on a log scale. For each panel, the solid line is the predicted standard deviation from the ZINB2-RE RCM as a function of the mean. The dashed line is the relation for a Poisson distributed oocyst count, where mean=variance. The points $\left(\overline{y},s\right)$, vary across panels, and are the sample mean and standard deviation of the oocyst counts from ∼20 mosquitoes in a COM. R² values measuring the fit of those points to the ZINB2-RE RCM are (0.91, 0.94, 0.92, 0.98) from left to right. R² values on the untransformed scale are (0.74, 0.87, 0.80, 0.91). Poly-Ctrl are the polyclonal controls upon which the RCM is built. The remaining three panels are the test COMs of monoclonal 4B7 antibodies; test COMs of monoclonal 1B3, 3E12, or IIC5B10 antibodies; and test COMs of polyclonal antibodies (Poly-Test).

Let Y_ijk be the oocyst count of the kth mosquito in the jth COM of the ith feed-day experiment. Each mosquito’s likelihood contribution given the random effect for the ith feed-day, f_i, and the random effect for the jth COM of the ith feed-day, c_ij, is:

$$L_{ijk}\left(Y_{ijk}=y_{ijk}|\pi ,\theta ,\gamma ,f_i,c_{ij}\right)=\{\begin{array}{l}\pi +\left(1-\pi \right){\left(1+\frac{{\lambda }_{ij}}{\theta }\right)}^{-\theta },\\ \left(1-\pi \right)\frac{\Gamma \left(y_{ijk}+\theta \right)}{\Gamma \left(y_{ijk}+1\right)\Gamma \left(\theta \right)}\frac{{\left(\frac{{\lambda }_{ij}}{\theta }\right)}^{y_{ijk}}}{{\left(1+\frac{{\lambda }_{ij}}{\theta }\right)}^{y_{ijk}+\theta }},\begin{array}{c}{y}_{ijk}=0\\ \hspace{1em}\hspace{1em}{y}_{ijk}=1,2,\mathrm{...}\end{array}\end{array}$$

where π is the zero inflation parameter, θ is the negative binomial dispersion parameter, λ_ij is the random mean effect from the negative binomial portion of the model, and log(λ_ij) = γ + f_i + c_ij. We assume the feed-day and COM random effects are independently and normally distributed $f_i\sim N\left(0,{\sigma }_f^2\right)$ and $c_{ij}\sim N\left(0,{\sigma }_c^2\right)$, respectively. Assigning ψ = [γ, π, σ_c, σ_f , θ], the fit on the model-building data estimates the RCM: ${\widehat{\psi }}^{RCM}=\left[\widehat{\gamma }=2.57,\widehat{\pi }=0.056,{\widehat{\sigma }}_c=0.2306,{\widehat{\sigma }}_f=1.042,\widehat{\theta }=1.93\right]$. Software implementation in SAS and R are discussed in Section S1 and the vignette of the Supplementary Materials. The necessity of zero-inflation, negative binomial (as opposed to Poisson), or random-effects can be tested via likelihood ratio tests (LRTs), since the ZINB2-RE nests simpler models. Each of the null hypotheses for the LRTs involve parameters on the boundary of their domain (for zero-inflation, π = 0; for negative binomial, θ = ∞; and for random-effects, σ_f = σ_c = 0). These nonstandard likelihood ratio tests have test statistics that follow a mixture of chi-square distributions (Self and Liang, 1987). The choice of ZINB2-RE over the simpler models is resoundingly supported by the data (see Section S2 of the Supplementary Materials).

3.3. Validating the Representative Count Model

We check how the mean-variance relationship of the RCM holds for the test COMs of different antibodies. We group these test COMs into three distinct datasets based on being polyclonal or monoclonal, the intended specific antigens, and sample size: COMs of monoclonal 4B7 antibodies; COMs of monoclonal 1B3, 3E12, or IIC5B10 antibodies; and test COMs of polyclonal antibodies. Test COMs of monoclonal 4B7 antibodies consist of 4295 mosquitoes among 215 COMs across 104 feed-days tested at various doses. Test COMs of monoclonal 1B3, 3E12, or IIC5B10 antibodies consist of 1240 mosquitoes among 62 COMs across 18 feed-days tested at various doses. Test COMs of polyclonal antibodies consist of 5255 mosquitoes among 264 COMs across 33 feed-days.

Figure 5 (with R² values listed in caption) gives a visual check of the fits. We calculate the R² values on both the log transformed standard deviations (to match the scale of the plot) and the untransformed values. Here are the details of the former. Let μ_ij = (1 − π)λ_ij and

$$V\left({\mu }_{ij};\psi \right)={\mu }_{ij}+\left(\frac{\pi }{1-\pi }+\frac{1}{\theta }\frac{1}{\left(1-\pi \right)}\right){\mu }_{ij}^2.$$

be the mean and the variance of Y_ijk, given the random effects. The RCM estimator of the standard error of Y_ijk is ${\widehat{\sigma }}_{ij}^{RCM}=\sqrt{V\left({\overline{y}}_{ij};{\widehat{\psi }}^{RCM}\right)}$, where ${\overline{y}}_{ij}={\sum }_{k=1}^{K_{ij}}{y}_{ijk}/K_{ij}$ is the observed COM-wise mean that incorporates random effects. Comparing ${\widehat{\sigma }}_{ij}^{RCM}$ to the observed COM-wise standard deviation $s_{ij}={\sum }_{k=1}^{K_{ij}}{\left(Y_{ijk}-{\overline{Y}}_{ij}\right)}^2/\left(K_{ij}-1\right)$ on the log scale gives

$$R^2=1-\frac{{\sum }_{i,j}{\left(\log s_{ij}-\log {\widehat{\sigma }}_{ij}^{RCM}\right)}^2}{{\sum }_{i,j}{\left(\log s_{ij}-\frac{1}{T}{\sum }_{i,j}\log s_{ij}\right)}^2},$$

where T is the total number of COMs in the dataset. The ZINB2-RE was not fit for each of the test datasets, instead the parameters ${\widehat{\psi }}^{RCM}$ generate the same mean-variance line to which each test dataset’s COM standard deviation and mean are evaluated. The high R² and the mean-variance line centered on each cloud of data indicates a feasible representation of the mean-variance relation and the data generating process, for both control and test data of different antibody types.

3.4. The RCM on a Test Sample

Each test sample has an associated control sample measured on the same feed-day. We expand the notation for λ_ij to accommodate both test and control samples. Let log(λ_ij) = γ + β_hI(X_ij = 1) + f_i + c_ij, where β_h is the effect of the hth test sample (which is measured on the jth COM of the ith feed-day, which we call the ijth feed-COM), X_ij = 1 if the ijth feed-COM is the hth test sample and X_ij = 0 if the ijth feed-COM is a control sample. The model for the hth test sample and associated control sample is defined by ψ^X = [γ, π, σ_c, σ_f , θ, β_h] and the likelihood contribution given random effects, L_ijk (Y_ijk = y_ijk|X_ij, ψ^X, f_i, c_ij, now depends on X_ij.

We assume any and all variation follows that of the controls as estimated by the RCM and that all of the information of the test sample enters the model through β_h via the λ_ij parameter (this assumption seems reasonable given the generalizability of the mean-variance relationship of the RCM to the test COMs in Section 3.3). For example, we assume that the test sample does not affect the zero inflation parameter, π, so that the zero inflation represents some process independent of the vaccine effects that somehow stops all oocyst development for both test and control samples. (This assumption, a topic of future work, could be tested by, for example, parameterizing the zero inflation parameter to depend linearly on λ_ij and testing if the coefficient was zero.)

4. TRA

4.1. Defining the TRA Estimand

For all of Section 4, we consider only one test sample so we omit the h subscript in β_h. We consider three options for defining the TRA estimand from the ZINB-RE2 model that are all equivalent. All three options are functions of ratios of expectations, but differ on how the random effects are handled. First, we consider integrating out the random effects. In this case, the ratio of expectations is simple since we can factor out the test effect from the numerator expectation, and the two double integrations with respect to the random effects cancel. This gives Ω_R, the TRA estimand:

$${\Omega }_R=100\left(1-\frac{E\left(Y_{ijk}|X_{ij}=1,{\psi }^X\right)}{E\left(Y_{i{j}^{\prime }{k}^{\prime }}|X_{i{j}^{\prime }}=0,{\psi }^X\right)}\right)=100\left(1-\rho \right),$$

where ρ = exp(β). Next, a feed-day-specific TRA estimand gives the same result by conditioning on the feed-day random effect and integrating over only the COM random effect c_ij and simplifying:

$$100\left(1-\frac{E\left(Y_{ijk}|X_{ij}=1,{\psi }^X,f_i=f\right)}{E\left(Y_{i{j}^{\prime }{k}^{\prime }}|X_{i{j}^{\prime }}=0,{\psi }^X,f_i=f\right)}\right)=100\left(1-\rho \right)={\Omega }_R.$$

The equivalences of these two estimands allows TRA to be estimated across feed-days or within feed-days, depending on the application. Finally, Ω_R can be defined as representing an ideal assay where the random effects are eliminated (i.e., σ_f = σ_c = 0).

4.2. Estimating TRA

By definition Ω_R is a function of ρ only, and a simple estimator uses $\widehat{\rho }={\widehat{\mu }}_t/{\widehat{\mu }}_c$ giving ${\widehat{\Omega }}_R=r$ (recall equation (1)). This simple estimate uses no data from other samples, ensuring the independence of the TRA estimator between different samples. In the case of sample replicates, the mean of the ratios or the ratios of the means can be used (see Section S3 in the supplementary materials).

4.3. Confidence Intervals on a Single Test Sample TRA Estimand

In practice, we want the TRA estimator of a test sample to depend only on the output from its test COM and its associated control COM; we do not want the TRA estimator to vary depending on what other test samples or other control samples are measured with it. But if we use only a test COM and its control COM results, we cannot estimate the standard deviation of the random effects for feed-day, σ_f, since there is only one feed-day observed. Further, we cannot estimate the standard deviation of the COMs, σ_c, since there are only two COMs used, and they have different samples (a test and a control). That is why we need the RCM which estimated those random effects using many nearly identical control samples.

We consider 7 methods for calculating ad hoc confidence intervals on the TRA (details in Section S4 of the supplementary materials). The first 5 methods (t-Welch, WMW-HL, Delta, and ZINB-Wald and ZINB-LRT) assume that there is no variability in the COMs (implying that σ_c = 0). The sixth and seventh methods (ZINBRE-Sim1 and ZINBRE-Sim2) are like percentile parametric bootstrap methods on the ZINB2-RE model, except we use the observed data to only estimate the fixed effects in the negative binomial part of the model. For the other parameters, we use values from ${\widehat{\psi }}^{RMC}$ for π, σ_f, and θ, and for ZINBRE-Sim1 we use σ_c = 0.2306 also from the RCM, while for ZINBRE-Sim2 the σ_c is randomly sampled from a lognormal distribution with mean 0.2306 for each bootstrap replication.

We evaluate the 7 methods by 1000 replications of two COMs (test and control) using 20 mosquitoes per COM with the ZINB2-RE model under each of 12 scenarios: 4 levels of TRA (0, 20, 50, 80) by 3 levels of COM variability (σ_c from the RCM, and the lower and upper 95% percentile bootstrap CI bounds for σ_c using the 9804 control mosquitoes and 2000 bootstrap samples), and other parameters from the RCM. Table 1 gives the percent of the 95% CI that covered the true TRA. Although assuming ${\widehat{\sigma }}_c$ is known and fixed is a crude approximation (ZINBRE-Sim1), Table 1 shows that both simulation approaches perform better in terms of simulated coverage than implicitly assuming σ_c = 0 as is done for the first 5 methods. Allowing variability on ${\widehat{\sigma }}_c$ (ZINBRE-Sim2) gives slightly higher coverage than ${\widehat{\sigma }}_c$ fixed. Although the coverage of ZINBRE-Sim1 and ZINBRE-Sim2 can be less (or greater) than nominal if the true σ_c is greater (or less) than σ_c from the RCM, the coverage is much improved over all the alternative methods. We recommend using ZINBRE-Sim1 or ZINBRE-Sim2.

Table 1:

Simulated percent coverage of single test sample 95% confidence intervals using 7 methods (t-Welch=Welch’s t-test; WMW-HL=Hodges-Lehmann CIs based on Wilcoxon-Mann-Whitney test; Delta=delta method; ZINB-Wald= Wald CIs from the ZINB model; ZINB-LRT= CIs from the ZINB model based on the Likelihood Ratio Test; ZINB-RE Sim1 and Sim2=simulation based methods, Sim1 uses σ_c = 0.2306 always and Sim2 simulates values of σ_c with mean 0.2306). We simulated 1000 data sets from each of twelve scenarios: 4 levels of true TRA (0,20,50, and 80) and each done at 3 levels of true σ_c (σ_c = 0.2306, as estimated in the RCM, as well as at the bounds of a 2000-iteration bootstrap 95% percentile confidence interval (0.1587, 0.3006)).

					ZINB		ZINB-RE
TRA	σc	t-Welch	WMW-HL	Delta	Wald	LRT	Sim1	Sim2
0	0.2306	86.3	83.4	80.1	75.6	78.1	94.7	95.9
20	0.2306	86.9	84.3	80.8	74.5	78.9	95.9	96.7
50	0.2306	85.0	82.5	81.3	78.6	77.2	94.5	95.6
80	0.2306	74.4	76.1	81.3	81.3	81.3	94.7	96.3
0	0.1587	91.0	89.0	88.6	84.9	86.0	98.7	99.2
20	0.1587	90.7	87.2	88.1	84.8	87.4	98.0	98.7
50	0.1587	88.9	87.8	88.7	84.7	87.4	98.5	98.7
80	0.1587	78.7	81.1	87.6	87.0	86.8	98.3	98.2
0	0.3006	79.3	75.3	71.8	69.2	71.4	90.4	91.8
20	0.3006	82.0	77.4	74.3	69.1	71.9	92.2	93.2
50	0.3006	78.8	74.9	73.3	68.5	72.2	90.8	92.4
80	0.3006	73.2	73.4	75.6	72.7	72.5	91.2	91.9

5. TBA

5.1. Defining the TBA Estimand

For the TRA estimand, the ratio of expectations simplifies to a straightforward function of β, regardless of how the random effects are handled. For TBA, the way we handle the random effects changes the TBA estimand.

Consider first using the ratio of unconditional expectations on the indicator that the counts are greater than 0, to get the “overall TBA” estimand. Using the fact that if Z is a zero-inflated negative binomial random variable,

$$E\left(I\left(Z>0\right)|\mu ,\theta ,\pi \right)=\left(1-\pi \right)\left\{1-{\left(\frac{\theta }{\mu +\theta }\right)}^{\theta }\right\},$$

and π does not depend on X_ij, the overall TBA estimand derived from the model is:

$$\begin{gathered} {\Omega }_B^{overall}=100\left(1-\frac{E\left(I\left(Y_{ijk}>0\right)|X_{ij}=1,{\psi }^X\right)}{E\left(I\left(Y_{i^{\prime }{j}^{\prime }{k}^{\prime }}>0\right)|X_{i^{\prime }{j}^{\prime }}=0,{\psi }^X\right)}\right) \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=100\left(1-\frac{{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\left\{1-{\left(\frac{\theta }{\exp \left(\gamma +\beta +s+t\right)+\theta }\right)}^{\theta }\right\}\frac{1}{{\sigma }_c}\varphi \left(\frac{t}{{\sigma }_c}\right)\frac{1}{{\sigma }_f}\varphi \left(\frac{s}{{\sigma }_f}\right)ds\hspace{0.17em}dt}{{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\left\{1-{\left(\frac{\theta }{\exp \left(\gamma +s+t\right)+\theta }\right)}^{\theta }\right\}\frac{1}{{\sigma }_c}\varphi \left(\frac{t}{{\sigma }_c}\right)\frac{1}{{\sigma }_f}\varphi \left(\frac{s}{{\sigma }_f}\right)ds\hspace{0.17em}dt}\right), \end{gathered}$$

where φ(·) is the standard normal density. Aside from being mathematically intractable, the result depends on the random effects distributions for COM and feed-day. Those random effects distributions are needed to properly adjust for the unavoidable variability in the assay, but are not directly related to the biological construct we are trying to measure. If we could control that variability in the assay, the ideal TBA estimand would be equivalent to setting σ_f = σ_c = 0, to give

$${\Omega }_B^{ideal}=100\left(1-\frac{\left\{1-{\left(\frac{\theta }{\exp \left(\gamma +\beta \right)+\theta }\right)}^{\theta }\right\}}{\left\{1-{\left(\frac{\theta }{\exp \left(\gamma \right)+\theta }\right)}^{\theta }\right\}}\right).$$

This ideal TBA estimand depends on γ, which is related to the mean control effect over many assays on different feed-days. Thus, γ is also related to the assay design, not to the biological construct of interest. Further, any one test and control sample pair is measured on one specific feed-day, and the individual feed-day random effect will affect the expected value of b. This is seen in the example of TBA values stratified by control mean in the Introduction.

Consider a feed-day-specific TBA estimand,

$$\begin{gathered} {\Omega }_B^f=100\left(1-\frac{E\left(I\left(Y_{ijk}>0\right)|X_{ij}=1,{\psi }^X,f_i=f\right)}{E\left(I\left(Y_{i{j}^{\prime }{k}^{\prime }}>0\right)|X_{i{j}^{\prime }}=0,{\psi }^X,f_i=f\right)}\right) \\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}=100\left(1-\frac{{\int }_{-\infty }^{\infty }\left\{1-{\left(\frac{\theta }{\rho {\mu }_{ci}\exp \left(t\right)+\theta }\right)}^{\theta }\right\}\frac{1}{{\sigma }_c}\varphi \left(\frac{t}{{\sigma }_c}\right)dt}{{\int }_{-\infty }^{\infty }\left\{1-{\left(\frac{\theta }{{\mu }_{ci}\exp \left(t\right)+\theta }\right)}^{\theta }\right\}\frac{1}{{\sigma }_c}\varphi \left(\frac{t}{{\sigma }_c}\right)dt}\right) \\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}=:{\Omega }_B^f\left({\mu }_{ci},\rho ,\theta ,{\sigma }_c\right), \end{gathered}$$

where μ_ci = exp(γ + f ). A partially ideal version of this estimand eliminates the COM random effects by taking the limit as σ_c goes to zero, giving

$${\Omega }_B^f\left({\mu }_{ci},\rho ,\theta ,0\right)\equiv \underset{{\sigma }_c\to 0}{\lim }{\Omega }_B^f\left({\mu }_{ci},\rho ,\theta ,{\sigma }_c\right)=100\left(1-\frac{1-{\left(\frac{\theta }{\rho {\mu }_{ci}+\theta }\right)}^{\theta }}{1-{\left(\frac{\theta }{{\mu }_{ci}+\theta }\right)}^{\theta }}\right).$$

There is little practical interest in a TBA estimand for a particular feed-day. For a general TBA estimand, µ_ci could be set to some target value, say ${\mu }_c^{\ast }$, to give the targeted TBA estimand:

$${\Omega }_B\left({\mu }_c^{\ast },\rho ,\theta \right)\hspace{1em}:=\hspace{1em}{\Omega }_B^f\left({\mu }_{ci}={\mu }_c^{\ast },\rho ,\theta ,0\right),$$

which is our estimand of interest for TBA. By fixing ${\mu }_c^{\ast }$, the estimand does not change with μ_ci from different feed-days, so that estimators of the targeted TBA estimand will be comparable across feed days. Choosing ${\mu }_c^{\ast }$ close to the control mean seen in the field is useful for bridging to biologically meaningful constructs. For comparing TBA results between different labs, we recommend that each laboratory use their own lab-specific θ estimate for defining the targeted TBA estimand and associated estimators.

5.2. Two estimators of the Targeted TBA estimand

We propose two estimators of ${\Omega }_B\left({\mu }_c^{\ast },\rho ,\theta \right)$. Both estimators use only data from a single test sample from one feed, so we exclude the test sample and feed subscripts here and in Section 5.3.

Restricted TBA estimator

Let ${\widehat{\mu }}_c$ and ${\widehat{p}}_c$ be the mean oocyst count and the sample proportion for the control COM, and similarly define ${\widehat{\mu }}_t$ and ${\widehat{p}}_t$ for the test COM. For a target control mean ${\mu }_c^{\ast }$, define two restriction bounds ${\tau }_L<{\mu }_c^{\ast }$ and ${\tau }_U<{\mu }_c^{\ast }$ and calculate TBA only if ${\widehat{\mu }}_c\in \left({\tau }_L,{\tau }_U\right)$, otherwise discard data from the feed-day. The restricted TBA estimator is then ${\widehat{\Omega }}_{B1}=100\left(1-\frac{{\widehat{p}}_t}{{\widehat{p}}_c}\right)$, provided ${\widehat{\mu }}_c\in \left({\tau }_L,{\tau }_U\right)$.

Standardized TBA estimator

Another estimator of the targeted TBA estimand, ${\Omega }_B\left({\mu }_c^{\ast },\rho ,\theta \right)$ is the standardized TBA estimator:

$${\widehat{\Omega }}_{B2}={\Omega }_B\left({\mu }_c^{\ast },\widehat{\rho },\widehat{\theta }\right)=100\left(1-\frac{1-{\left(\frac{\widehat{\theta }}{\widehat{\rho }{\mu }_c^{\ast }+\widehat{\theta }}\right)}^{\widehat{\theta }}}{1-{\left(\frac{\widehat{\theta }}{{\mu }_c^{\ast }+\widehat{\theta }}\right)}^{\widehat{\theta }}}\right).$$

where $\widehat{\rho }={\widehat{\mu }}_t/{\widehat{\mu }}_c$ and $\widehat{\theta }=1.93$ is estimated from the RCM. Note, ${\widehat{\Omega }}_{B2}$ is calculated regardless of the value of ${\widehat{\mu }}_c$ and discards no data, unlike ${\widehat{\Omega }}_{B1}$.

5.3. Confidence Intervals for a Single Test Sample Targeted TBA Estimand

In this section, we give confidence intervals for the targeted TBA estimand for each of the two estimators of it.

Restricted Estimator

If the true unknown μ_c is equal to ${\mu }_c^{\ast }$ and σ_c is set equal to 0, then

$${\Omega }_B\left({\mu }_c^{\ast },\rho ,\theta \right)=100\left(1-\frac{E\left({\widehat{p}}_t\right)}{E\left({\widehat{p}}_c\right)}\right).$$

Treating $\frac{{\widehat{p}}_t}{{\widehat{p}}_c}$ as a ratio of proportions from two independent binomials, we use the melded binomial confidence intervals on the ratio of binomial parameters, say (R_L, R_U ) (Fay et al., 2015), to get a confidence interval for ${\Omega }_B\left({\mu }_c^{\ast },\rho ,\theta \right):\left(100\left(1-R_U\right),100\left(1-R_L\right)\right)$. This confidence interval is approximate because the restriction requiring ${\widehat{\mu }}_c\in \left({\tau }_L,{\tau }_U\right)$ does not ensure that ${\mu }_c={\mu }_c^{\ast }$, but only makes it more likely that μ_c will be somewhat close to ${\mu }_c^{\ast }$.

Standardized Estimator

If (TRA_L, TRA_U ) is the 95% CI for the TRA estimand, then a 95% CI for the targeted TBA estimand, ${\Omega }_B\left({\mu }_c^{\ast },\rho ,\theta \right)$, based on the standardized TBA is:

$$\left(100\left(1-\frac{1-{\left(\frac{\widehat{\theta }}{{\rho }_L{\mu }_c^{\ast }+\widehat{\theta }}\right)}^{\widehat{\theta }}}{1-{\left(\frac{\widehat{\theta }}{{\mu }_c^{\ast }+\widehat{\theta }}\right)}^{\widehat{\theta }}}\right),100\left(1-\frac{1-{\left(\frac{\widehat{\theta }}{{\rho }_U{\mu }_c^{\ast }+\widehat{\theta }}\right)}^{\widehat{\theta }}}{1-{\left(\frac{\widehat{\theta }}{{\mu }_c^{\ast }+\widehat{\theta }}\right)}^{\widehat{\theta }}}\right)\right)$$

where ρ_K = 1 − TRA_K/100, K = L, U . Since these are monotonic increasing functions for ρ given a fixed ${\mu }_c^{\ast }$, the coverage probabilities for the standardized TBA estimator would match those of the corresponding to the (TRA_L, TRA_U ) for the TRA estimator as reported in the Section 4.3. Additionally, any assay that showed the TRA estimand significantly greater than 0 would infer the targeted TBA estimand as significantly greater than 0, regardless of the target control mean. For example, if a TRA estimate was 85 (95% CI (82, 88)), the standardized TBA associated with the lab (e.g., with a target of ${\mu }_c^{\ast }=15$) to be 21 (95% CI (17, 27)) whereas the standardized TBA associated with the field $\left({\mu }_c^{\ast }=2\right)$ it would be 67 (95% CI (62, 73)).

5.4. Demonstration of the Need for TBA Standardization or Restriction

In Figure 6 we plot many TBA estimates from nearly identical samples to show that the unstandardized TBA estimates generally decrease as a function of mean control count, while the standardized ones do not. Here are the details. We take 100 ostensively identical test samples of 4B7 monoclonal antibody each prepared at a concentration of 94 μg/ml, create a test COM for each sample, and feed these 100 test COMs on 98 different feed days. We randomly assign each test COM to a unique control COM from the same feed-day to create 100 pairs. For the ith pair of test and control COMs (i = 1, 2, … 100) we calculate the control mean, ${\widehat{\mu }}_{ci}$, and an unstandardized TBA estimate, $b_i=100\left(i=1-{\widehat{p}}_{it}/{\widehat{p}}_{ic}\right)$, where ${\widehat{p}}_{it}$, and ${\widehat{p}}_{ic}$ are the proportion of infected mosquitoes from the test and control COM, respectively. The left three panels of Figure 6 plot b_i vs. ${\widehat{\mu }}_{ci}$ for different strata of ${\widehat{\mu }}_{ci}$: ‘low’ $\left({\widehat{\mu }}_{ic}\in \left(0,6\right]\right)$, ‘med’ $\left({\widehat{\mu }}_{ic}\in \left(6,30\right]\right)$, and ‘high’ $\left({\widehat{\mu }}_{ic}\in \left(30,81\right]\right)$. Each b_i is plotted with its 95% confidence interval for TBA using the melded confidence interval on the ratio. Within each panel, two summary measures are depicted by a square and triangle (their displayed x-values are meaningless). The squares and their associated 95% confidence intervals are calculated from the means and t-test confidence intervals on the mean of the transformed b_i values (using the log(1 − b_i/100) transformation to be closer to normality), which are back transformed to the original TBA scale. (The meta-regression estimates [triangles] are an alternate way of summarizing the data and are discussed in Section 6 and Supplementary Section S5). Those TBA summaries within strata (the squares) reflect the trend seen on the groups of TBA estimates across strata: the higher the control mean, the lower the unstandardized TBA estimate.

Figure 6:

Comparing Unstandardized and Standardized TBA estimators with a 4B7 monoclonal antibody 94 μg/ml dose, , stratified by control mean groups (low, med, high), with summary measures (Meta-regression and t-test) for each panel. Lines are 95% confidence intervals. For a target mean of 2, the Unstandardized-low panel corresponds to empirical restricted TBA estimates where $\left({\tau }_L=0,{\tau }_U=6\right)$, while the Unstandardized-med and Unstandardized-high estimates would be discarded. The 3 right panels show the Standardized TBA estimator. The meta-regression and t-test meta-estimates are very similar due to almost all the sample sizes being equal for every TBA estimate.

The correction for this trend is displayed in similar fashion in the right three panels. Standardized TBA estimates, using ${\widehat{\Omega }}_{B2,i}\left({\mu }_c^{\ast }=2,{\widehat{\rho }}_i,\widehat{\theta }\right)$ with ${\widehat{\rho }}_i={\widehat{\mu }}_{it}/{\widehat{\mu }}_{ic}$ and $\widehat{\theta }=1.93$, are plotted by their ${\widehat{\mu }}_{ci}$ (with 95% confidence intervals as in Section 5.3). The square (and triangle) symbols in the right panels are analogous to those in the left ones. Actual μ values in the malaria endemic fields can be very low and also vary depending on many factors, such as endemicity, season, and mosquito species. We chose ${\mu }_c^{\ast }=2$ as a reasonable, representative value in the field.

In Figure 6 we see from the square symbols that the unstandardized TBA estimates decrease as the control mean increases, while the standardized TBA estimates do not. The standardization tends to shift up the estimates of the medium and high control mean groups to a similar level of the low control mean group, which is expected because the target mean of 2 is in the range of the low group. We can think of the unstandardized TBA estimates in the leftmost panel as restricted TBA estimates, restricted to ${\widehat{\mu }}_{ic}\in \left(0,6\right]$ and discarding the other two strata’s data. The unstandardized TBA estimates in the med and high panels are poor estimators of Ω_B(2), because their control means are far from the target of ${\mu }_c^{\ast }=2$. The right two panels of Figure 6 show that we can estimate ${\Omega }_B\left({\mu }_c^{\ast }\right)$ by standardized TBA fairly well, and thus we can use all of the data.

5.5. Comparing the Two estimators of ${\Omega }_B\left({\mu }_c^{\ast }\right)$

We now compare the restricted and standardized TBA estimators by simulation. Using ${\widehat{\psi }}^{RCM}$ (Section 3.2), we simulated 10,000 data sets of two COMs (test and control) using the ZINB2-RE with the RCM for each of 80 simulation scenarios (10 TRAs × 4 levels of mosquitoes in a COM × 2 target control mean oocysts).

Let I₊ be the number of data sets where ${\widehat{\mu }}_{ic}\in \left({\mu }_c^{\ast }-2,{\mu }_c^{\ast }+2\right)$, the simulated mean squared error (sMSE) of ${\widehat{\Omega }}_{B1}$ is calculated as $\frac{1}{I_{+}}{\sum \left({\widehat{\Omega }}_{B1,i}-{\Omega }_B\left({\mu }_c^{\ast },\rho ,\widehat{\theta }\right)\right)}^2$ where the summation is only over the I₊ iterations that are not discarded. To give equal footing, we calculate the sMSE for the standardized TBA by using an average of standardized TBA values, ${\widehat{\Omega }}_{B2avg,i}=\frac{1}{g_i}{\sum }_{j=i}^k{\widehat{\Omega }}_{B2,j}$

where the (k+1)st iteration is the next iteration that was not discarded for the restricted TBA, and g_i = k − I + 1. The associated sMSE is $\frac{1}{I_{+}}{\sum \left({\widehat{\Omega }}_{B2avg,i}-{\Omega }_B\left({\mu }_c^{\ast },\rho ,\widehat{\theta }\right)\right)}^2$. All these simulated mean squared errors are displayed in Figure 7.

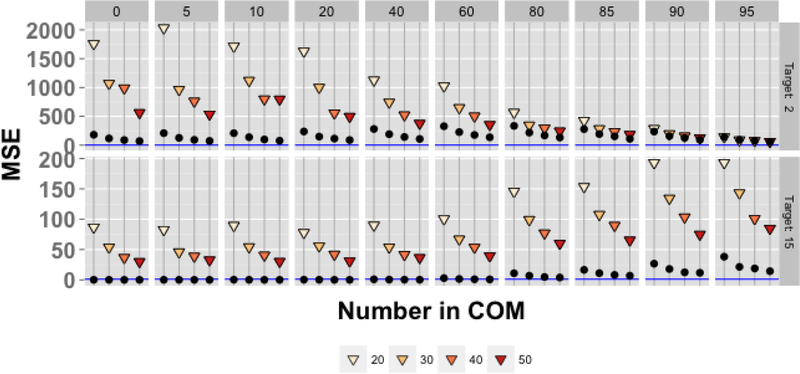
Figure 7:

Simulated MSEs of the restricted TBA (shaded triangles) and standardized TBA (black dots) approaches for targets of ${\mu }_c^{*}=2$ and ${\mu }_c^{*}=15$ for different number of mosquitoes in each COM (M ∈ {20, 30, 40, 50}) and different True TRA values Ω_R ∈ {0, 5, 10, 20, 40, 60, 80, 85, 90, 95}.

The standardized TBA estimator is more precise across all levels except for the highest TRA of control mean 2. For a given target control mean and TRA, increasing the number of mosquitoes in each COM will lower the MSE.

6. Two Sample Study Using SMFA Responses

Consider a two sample study where the primary efficacy outcome for each individual is measured by SMFA. For example, a human phase II trial where each subject is randomized to receive either a transmission blocking vaccine or a placebo vaccine and then is measured by SMFA at a pre-specified time post-vaccination. We suggest using TRA instead of TBA for the endpoint and show in this section an interpretation of difference in means of the sample TRA values.

Consider first the estimand for measuring the effect of the vaccine in the study. Let ${\mu }_{ij}^{kt}$ and ${\mu }_{i{j}^{\prime }}^{kt}$ be the mean oocyst counts for the kth subject’s test COM and associated control COM, respectively. Write the TRA effect for the kth subject including the random effects for COM and feed-day as $TR{A}_{k\left(ij\right)}=100\left(1-\frac{{\mu }_{ij}^{kt}}{{\mu }_{i{j}^{\prime }}^{kt}}\right)$, and write the analogous log of the ratio effect as log(ρ_k(ij)) =log(1 − TRA_k(ij)/100). Then taking expectations over the random effects, we get

$$\begin{gathered} E\left(\log \left({\rho }_{k\left(ij\right)}\right)\right)=E\left\{\log \left({\mu }_{ij}^{kt}\right)-\log \left({\mu }_{i{j}^{\prime }}^{kc}\right)\right\} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.5em}\hspace{1em}=E\left(\gamma +{\beta }_k+f_i+c_{ij}-\gamma -f_i-c_{i{j}^{\prime }}\right)={\beta }_k+E\left(c_{ij}-c_{i{j}^{\prime }}\right)={\beta }_k. \end{gathered}$$ (3)

Assume that if subject k got the experimental vaccine (or placebo), then β_k comes from a distribution with mean B_v (or B_p). Then the expected difference in means of the β_k values would be B_v − B_p. We interpret 100(1 − exp(B_v − B_p)) ≡ TRA_vp as the estimand of the vaccine’s TRA effect compared to placebo, and call this the transmission reducing vaccine activity (TRVA). In terms of the model, letting k index a random individual that got vaccine (measured on the ijth and ij′th feed-COMs) and letting k′ index a random individual that got placebo (abth and ab′th feed-COMs), we get,

$$\begin{gathered} E\left(\log \left({\rho }_{k\left(ij\right)}^v\right)-\log \left({\rho }_{k^{\prime }\left(ab\right)}^p\right)\right)=E\left\{\log \left({\mu }_{ij}^{kt}\right)-\log \left({\mu }_{i{j}^{\prime }}^{kc}\right)-\left[\log \left({\mu }_{ab}^{k^{\prime }t}\right)-\log \left({\mu }_{a{b}^{\prime }}^{k^{\prime }c}\right)\right]\right\} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E\left\{\log \left({\mu }_{ij}^{kt}\right)-\log \left({\mu }_{ab}^{k^{\prime }t}\right)\right\}+E\left\{\log \left({\mu }_{a{b}^{\prime }}^{k^{\prime }c}\right)-\log \left({\mu }_{i{j}^{\prime }}^{kc}\right)\right\} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E\left\{\log \left({\mu }_{ij}^{kt}\right)-\log \left({\mu }_{ab}^{k^{\prime }t}\right)\right\}=B_v-B_p, \end{gathered}$$ (4)

where the second term in the middle line is 0 because E(f_af_i) + E(c_abc_ij) = 0. The placebo test sample in the TRVA effect is acting like the control sample in the single test TRA, since the mean of the placebo test sample $\left({\mu }_{ab}^{kt}\right)$ in equation (4) replaces the mean control sample $\left({\mu }_{ij}^{kc}\right)$ in equation (3). For the TBA effects, there is no such simple vaccine effect, since the TBA effect for the kth subject depends on the target control mean and the overdispersion parameter. Thus, for simplicity of reporting, we recommend presenting inferences in terms of TRVA for two sample situations, rather than defining an analogous estimand for TBA. Alternatively, we can simply estimate the expected value of individual standardized TBA values within group using the t-test (see Section 5.4).

Let ${\tilde{\beta }}_k=\log \left({\tilde{\mu }}_{ij}^{kt}/{\tilde{\mu }}_{i{j}^{\prime }}^{kc}\right)$ be our estimate of β_k, where ${\tilde{\mu }}_{il}^{ka}$, for a = t, c is the mean number of oocysts per mosquito in the ℓth COM of the ith feed-day, except we replace zero means with 1/(2n_iℓ) with n_iℓ being the number of dissected mosquitoes in that COM. This practical ad hoc adjustment avoids log(0) values and introduces some bias, but since the bias is the same in both groups, this will not affect the validity of the resulting two sample tests. Let $\tilde{\Delta }$ be the mean ${\tilde{\beta }}_k$ values from subjects in the vaccine group minus the analogous mean for the placebo group. Then our estimator of TRVA is $100\left(1-\exp \left(\tilde{\Delta }\right)\right)$. One choice of tests is Welch’s t-test on the ${\tilde{\beta }}_k$ values, which automatically gives matching confidence intervals on the difference in means in the two groups, say (∆_L, ∆_U ), leading to a confidence interval on the TRVA of (100(1 − exp(∆_U )), 100(1 − exp(∆_L)). Some have used meta-analysis regression to combine information across many assays (Da et al., 2013), but upon closer examination, there is little practical advantage of using meta-analysis regression over t-tests in the SMFA setting (see Supplement Section S5).

An alternative analysis could use the Wilcoxon-Mann-Whitney (WMW) on the ${\tilde{\beta }}_k$ values, and the associated Hodges-Lehmann confidence intervals. The two-sided WMW p-value has the advantage of being invariant to monotonic transformations, so it is the same as if the test were performed on the TRA estimates, ${\tilde{r}}_k=100\left(1-\exp \left(\tilde{\beta }\right)\right)$, or the standardized TBA estimates, ${\Omega }_B\left({\mu }_c^{\ast },\exp \left({\tilde{\beta }}_k\right),\widehat{\theta }\right)$, regardless of the standard ${\mu }_c^{\ast }$. However, the Hodges-Lehmann confidence intervals must be done on the ${\tilde{\beta }}_k$ values themselves (not the transformations) since the range of possible values of β_k is (−∞, ∞) which allows the necessary location shift assumption.

7. Discussion

This paper has studied a statistical model for SMFAs, shown that the model fits the data from one lab reasonably well, and defined estimands for TRA and TBA under that model. Because the TRA estimand does not depend on the mean of the control oocyst counts while the TBA estimand does, the TRA estimand is recommended. If a TBA estimand must be used, a targeted TBA estimand based on a “target” mean control oocyst count is necessary to allow comparison of values over different feed-days. This targeted TBA estimand may be estimated with either our new standardized TBA estimator or a restricted TBA estimator. Simulations have shown that the standardized TBA estimator is much more efficient. We developed confidence intervals for the individual TRA estimand and individual targeted TBA estimand.

A potential drawback of our standardized TBA estimator is its dependency on one specific model and on the specific value, $\widehat{\theta }$. A concern is that the model may not fit SMFA data well from other laboratories or on slightly modified assays. We have partially addressed this question by showing that the model developed and fit using control polyclonal antibody data fits test polyclonal and monoclonal antibody data quite well (with R² values greater than 0.90). If the method is applied to data from another lab, we recommend refitting the parameter estimates of our model using data from that lab (or at least checking that the parameter estimates presented here fit reasonably well to that lab). Churcher et al. (2012) used a similar but more complicated model for SMFA data, which allows the zero inflation and the overdispersion parameters to depend on the mean oocyst counts through non-linear functions. Although they have not used their model for standardizing TBA estimates, their model does relate the TBA, control mean, and the TRA (see Churcher et al., 2012, Figure 2B), and it provides a similar relationship as our simpler model (see Miura et al., 2013, Figure 8). Using the more complicated Churcher et al. (2012) model for TBA standardization requires further work, especially since available software does not easily allow zero inflation parameters to depend on the mean of the negative binomial part, while simultaneously allowing the needed random effects for feed-day and COM. Further, although Churcher et al. (2012) show that the added complexity of their model is better for their data, it is not clear how their model will perform on data from other laboratories. As with any model building, we need to balance the closeness of the fit to the model-building data (which can be improved with more complex models) and expected closeness of fit to other data sets from slightly modified assay designs (which may be diminished with overly complex models).

Despite this potential drawback, one advantage of the proposed standardized TBA estimator, which bases the targeted TBA estimand confidence intervals on the associated confidence intervals for the TRA estimand, is that the targeted TBA estimand and TRA estimand inferences will match in the sense that test samples that yield inference for the TRA estimand as statistically significantly different from 0 will also have a statistically significant targeted TBA estimand different from 0 and vice versa. This matching property does not depend on the target control mean, the goodness-of-fit of our model, or its generalizability. The fit of the model is more important when a TBA estimate is needed to use in some other prediction model (see e.g., Smith et al., 2011).

We have developed a useful estimand for two group studies with SMFA as an endpoint, and shown that simple tests such as the Wilcoxon-Mann-Whitney or Welch’s t-test can be used where the response for the kth subjects is a transformation of a TRA estimate, ${\tilde{\beta }}_k$. Analogous tests can be used for different designs. For example, for a three group study a Kruskal-Wallis test or analysis of variance test could be used on the ${\tilde{\beta }}_k$ values. Further discussion on designing multiple assays for a study is relegated to Section S6 in the Supplementary materials.

Fundamentally, we have proposed a model for malaria researchers to use to address the statistical issues with SMFAs, showing that the TRA estimator typically provides a good reproducible measure. Importantly, if TBA is a desired readout we have demonstrated that the common, unadjusted estimator b is deficient and that some kind of adjustment (either restriction or standardization) must be used if TBA as an outcome measure is to be compared between SMFAs done at different times or in different labs.