In pursuit of the mechanics that shape cell surfaces

Abstract

Robust and responsive, the surface of a cell is as important as its interior when it comes to mechanically regulating form and function. New techniques are shedding light on this role, and a common language to describe its properties is now needed.

Cells are now broadly appreciated to be mechanical as well as biochemical systems. They generate, transmit and respond to forces through an intricate network of mechanical components, resulting in cell movement and shape change, as well as altered signalling, modulated expression and even genomic damage. Contributions to cell mechanics from molecular motors, cytoskeletal filaments and mechanosensitive proteins have received significant attention, and the cell surface — comprising the plasma membrane and underlying cortical cytoskeleton — has emerged as a unique mechanical system capable of exerting both local and global control of cell form and function. The physical properties of the cell surface can be rapidly modulated, enabling cells to generate or accommodate changes in shape. This Perspective examines the role that cell surface mechanics plays across multiple length scales and in multiple cell types and surveys the experimental techniques that are providing new physical insight into the powerful mechanical border of cells.

Cell surface mechanics during crawling motility

The importance of cell surface mechanics is clear from the coordinated shape changes involved in crawling motility. Through extensive biochemical and genetic studies, we know many of the key cytoskeletal players in cell movement^1,2. In the simplest description, assembly of actin monomers into filaments at the leading edge generates sufficient local force to displace the cell’s plasma membrane at the leading edge^3–5 and motor-based contractility retracts the trailing edge at the back of the cell to generate forward motion⁶.

Since the plasma membrane is a deformable barrier, growth of actin filaments oriented towards the membrane during cell spreading⁴ and cell polarization⁷ can cause an increase in plasma membrane tension as the force of polymerization unfolds wrinkles in the membrane. During cell polarization this increase in plasma membrane tension acts to constrain the spread of the existing leading edge and prevents the formation of secondary fronts in chemotactic cells such as neutrophils⁷, providing a possible mechanism for constraining the overall size of protrusions. One way that changes in tension could regulate actin assembly at the leading edge size is purely mechanical. In support of this, a model consisting entirely of mechanical interactions between the actin cytoskeleton, myosin and the plasma membrane was found to be sufficient to predict the polarized morphologies of keratocytes⁸, as well as the relation between cell shape and speed⁵.

How else could increasing plasma membrane tension limit the expansion of the existing leading edge and prevent formation of secondary fronts? And specifically, could biochemical signalling mediated by cell surface mechanics contribute to leading edge size regulation? This question motivated a collaboration between biologists and physicists that brought together cell biology, mechanical measurements and modelling to better understand regulation of neutrophil motility. We imaged actin filament nucleation in the leading edge of cells and directly quantified plasma membrane tension with an atomic force microscope. Using a series of knock down, chemical and mechanical perturbations, we found that elevated membrane tension limits actin polymerization through phospholipase D2 (PLD2) and the mammalian target of rapamycin complex 2 (mTORC2) by an as yet uncharacterized mechanism. In the absence of this pathway, neutrophils exhibit larger leading edges, higher membrane tension and profoundly defective chemotaxis. Moreover, mathematical modelling indicated that this feedback circuit is a favourable topology to enable competition between protrusions during neutrophil polarization⁹. Our work, together with other recent findings^10,11, highlight how biochemical signals, membrane tension and the actin cytoskeleton can collaborate to generate large-scale cellular organization.

In this Perspective, we give an overview of cell surface mechanics and its role in cellular form and function. We first discuss the composition and dynamics of the cell membrane and its underlying cortex and how these determine cell surface mechanics. We then summarize current methods to measure cell surface physical properties and clarify the terminology surrounding cell surface mechanics. Finally, we discuss future directions for research on cell surface mechanics, including how physical models could contribute to our understanding of cellular mechanics.

Molecular characterization of the cell surface

The field of mechanobiology has advanced dramatically since the early twentieth century, when D’Arcy Thompson published On Growth and Form and described how physical forces contribute to determining the size and shape of living organisms (reviewed in ref. ¹²). As Thompson appreciated a century ago, cell shape is the result not only of internal forces driving growth and movement but also of finely tuned cell surface mechanics. Living organisms mould the form and function of their cells and tissues by regulating the deformability and displacement of cell surfaces, achieving control of shape at multiple length scales.

The cell surface comprises the plasma membrane, the underlying cortical cytoskeleton and the ‘glue’ that binds them together — the membrane-to-cortex attachment or membrane-to-cortex adhesion energy (MCA). Their molecular origin is diverse: the plasma membrane is composed of a milieu of lipids and glycolipids with peripheral and embedded transmembrane proteins and glycoproteins. In most eukaryotic cells lacking a cell wall, including animal cells and amoebae, the cortex is composed of a thin actin network crosslinked by myosin motors and actin binding proteins, as well as networks of other filaments including septins. MCA is mediated by a layer of specialized proteins (like the ezrin, radixin, moesin (ERM) family), but also involves nonspecific frictional forces between the cortex and the plasma membrane (by, for example, electrostatic or van der Waals forces). MCA proteins generally have an F-actin binding domain and a domain that binds either directly to lipids or to proteins embedded in the membrane.

Variations in membrane, MCA or cortex composition are observed sub-cellularly, between cell types and over time. For example, cells regulate their lipid composition during the cell cycle, with consequences for both signalling and cell structure¹³. Moreover, MCA has been shown to differ between different cell regions¹⁴, tissue types¹⁵ and germ layers¹⁶. Such variation in MCA can be accomplished by differences in the expression level or by altering the binding activity of the MCA protein domains by cellular signalling¹⁶. The composition of the cell cortex also varies during the cell cycle and particularly between cell types. Classic examples are the surface of red blood cells and neurons, where an actin–spectrin cytoskeletal network provides mechanical resilience during capillary flow¹⁷ and touch sensation¹⁸, respectively. Mutations that interfere with the formation of this network cause severe anaemia¹⁹ and motor and cognitive disorders²⁰, highlighting how molecular differences lead to mechanical differences.

The role of specific membrane proteins in the regulation of membrane mechanics, and vice versa, has been the focus of recent studies. BAR (Bin/amphiphysin/Rvs) protein scaffolding on membrane deformations creates a frictional barrier for lipid diffusion that is critical for processes like endocytosis. The generated deformation can be elongated by motor activity, resulting in a local increase in membrane tension that ultimately generates membrane scission²¹. Other membrane proteins respond to membrane tension, such as mechanosensitive channels like Piezo1, critical for responsiveness to touch in metazoans²².

Quantification of cell surface mechanics

Quantification of cell surface mechanics typically involves combining direct mechanical measurements with mathematical models to delineate the individual contributions of the plasma membrane (in-plane tension and bending rigidity), MCA (adhesion energy) and cortex (stiffness and cortical tension).

Membrane tension is a measure of the energetic cost of stretching a membrane (measured in J m^–2 = N m^–1). In a pure lipid bilayer/water system, it is the energy required to expand the surface area in the plane of the lipid bilayer (T_m). The molecular origin of tension is the tight packing of hydrophobic lipid molecules to avoid contact with water molecules. In cells, plasma membrane tension can appear greater than in pure lipid vesicles due to MCA and peripheral proteins that provide additional resistance to membrane deformation. MCA is defined as the free energy that is released when a unit area of membrane detaches from the cell cortex. Overall plasma membrane tension in cells is therefore approximated as the sum of T_m and MCA. It can be measured, for example, by pulling a membrane nanotube (or tether) and holding it with a constant length until it breaks by using an atomic force microscope (AFM) cantilever or an optical or magnetic tweezer^23–25 (Table 1; Fig. 1). Its magnitude covers a wide range, from 3×10^–6 N m^–1 on apical membranes of epithelial cells to 276×10^–6 N m^–1 in keratocytes (reviewed in ref. ²⁶) . To separate T_m from MCA, one can measure the tether force on cells whose membrane is detached from the cortex by actin depolymerizing agents^27–29. Since cortex perturbations dramatically change overall cell morphology and thus might also affect T_m, the contribution of MCA can be more natively estimated by dynamically pulling membrane tethers at different speeds until they break, where the T_m is constant but MCA scales with the speed of tether pulling. To interpret such measurements, a classical model by Hochmuth and Sheetz²⁴ or a more recent by Brochard-Wyart et al.³⁰ have been used.

Table 1 |.

Methods to characterize the cell surface

	Technique	Examples	Measured quantity	Schematic
Membrane tension	Tether pulling using AFM	40× 10–12 N for HL60 cells9	Tether rupture force	Fig. 1a
	Interferometric particle detection using optical tweezers	65× 10–6 N m−1 for erythrocytes44	Power spectral density of the quadrant photodiode voltage	Fig. 1b
	Tether pulling using optical or magnetic tweezers	29× 10–12 N for MEF cells45	Tether rupture force	Fig. 1c
	Tether pulling using shear fluid	86–172× 10–12 N for shear rates of 100–250 s–1 for neutrophils46	Approach velocity, shear rate, tether length and cell size	Fig. 1d
Cortical tension	AFM compression (with a flat cantilever or a bead)	1.6× 10–3 N m–1 for HeLa cells during metaphase47	Compressive force, contact angles of cellular deformation for a flat cantilever or deflection of the cantilever with a bead	Fig. 1e,i
	Dual plate compression	1.75 dyn cm–1 (or 175× 10–5 N m–1) for sea urchin eggs 40 minutes after fertilization48	Compressive force, contact angles of cellular deformation	Fig. 1f
	Laser ablation	9.15 μm min–1 orthogonal outward velocity in the anterior cortex of the one-cell C. elegans embryo49	Response of cortex to laser ablation	Fig. 1g
	Micropipette aspiration	0.035 dyn cm–1 (or 3.5× 10–5 N m–1) for passive blood granulocytes38	Aspiration pressure and cellular deformation	Fig. 1h
Surface elasticity and viscoelasticity	AFM indentation	855 Pa for HL60 cells50	Deflection of the cantilever	Fig. 1i
	Brillouin microscopy	5.41–8.06 GPa for plants ECM51 and 2.78 GPa for the nuclear envelope52	Brillouin peak shift and width	Fig. 1j
	Magnetic twisting cytometry	10–11–10–8 Pa m–1 for a broad range of cancer cells lines53	Bead displacement to a twisting magnetic field with different frequencies	Fig. 1k
Cortical thickness	Electron microscopy	Tens of nm (ref. 54)	Thickness of the cortical layer	Fig. 1l
	Fluorescence microscopy	186 nm for the cortex of mitotic HeLa cells55	Fluorescence peak distance	Fig. 1m
Bending rigidity	Interferometric particle detection using optical tweezers	2.8× 10–19 N m (or 67.6kBT) for erythrocytes44	Power spectral density of the quadrant photodiode voltage or standard deviation of the distribution of fluctuation amplitudes	Fig. 1b
	Micropipette aspiration	10–19 N m for red blood cells or lipid bilayers23 and 1–2× 10–18 N m for cell types with a simple cortex56	In the low tension regime, the slope of the area dilation versus the logarithm of the tension	Fig. 1h
	Flicker spectroscopy	5× 10–13 erg (or 0.5× 10–19 N m) for erythrocytes57	Shape fluctuations of vesicles from time series of optical microscopy snapshots	Fig. 1n
	Micropipette aspiration combined with optical tweezers	2.7× 10–19 N m for neutrophils24	The slope of the equilibrium tube force with the square root of the tension	Fig. 1c,h
Membrane viscosity	Molecular rotors and flippers combined with FLIM	270 cP (or 0.27 Pa s) in SKOV cells at 23 °C (ref. 58)	Fluorescence	Fig. 1o
	Interferometric particle detection using optical tweezers	81× 10–3 Pa s for erythrocytes44	Power spectral density of the quadrant photodiode voltage	Fig. 1b

Fig. 1 |. Schematics of methods to characterize the cell surface.

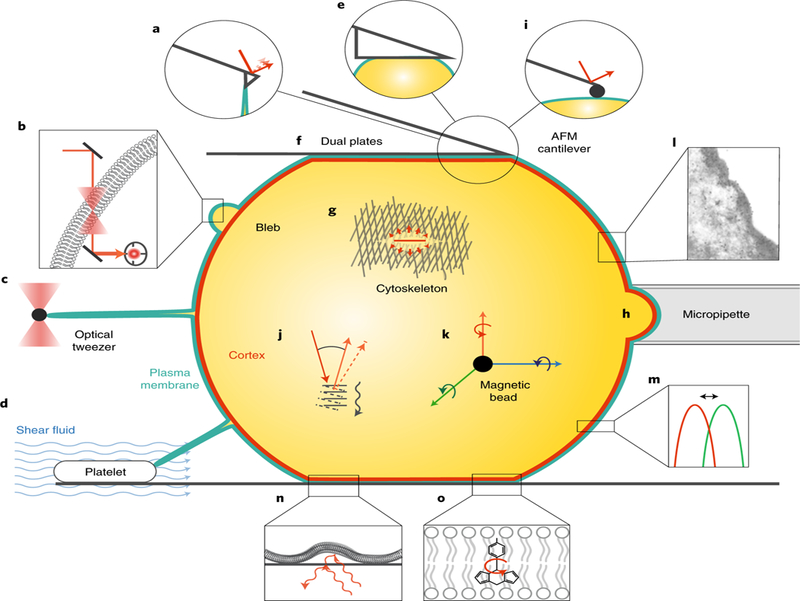
Understanding how cell shape is controlled at the molecular level requires a combination of quantitative experiments and physical modelling to relate the microscopic organization and dynamics of cortical and membrane components to global mechanical properties. See Table 1 for an overview of current techniques for quantifying cell surface mechanical properties of single cells, corresponding to the schematics pictured here. For techniques relevant to tissue mechanics and active force generation, we refer the reader to excellent recent reviews^59–62. a, Tether pulling using AFM. b, Interferometric particle detection using optical tweezers. c, Tether pulling using optical or magnetic tweezers. d, Tether pulling using shear fluid. e, AFM compression with a flat cantilever. f, Dual plate compression. g, Laser ablation. h, Micropipette aspiration. i, AFM indentation. j, Brillouin microscopy. k, Magnetic twisting cytometry. l, Electron microscopy. m, Fluorescence microscopy. n, Flicker spectroscopy. o, Molecular rotors and flippers combined with FLIM. Panel l reproduced from ref. ⁵⁴, EMBO.

Lipid bilayer membranes resist both extension, shear and bending. Thus, three moduli characterize membranes: the area stretch modulus (also known as the area compressibility modulus or area expansion modulus), the shear modulus and the bending rigidity. The area stretch modulus is a measure of the stiffness of the membrane under tension (measured in N m^–1). At high tension values, and once most thermal fluctuations are smoothed out, its value is 0.1–1 N m^–1 for various types of lipid bilayers and about 0.45 N m^–1 (450 dyn cm^–1) for red blood cells³¹. Cell membranes are thus quite resistant to extension and often treated as inextensible. When subjected to shear stresses in the plane of the membrane, a pure lipid bilayer behaves essentially as a liquid, thus the shear modulus is very small for membranes, on the order of 10^–6 N m^–1. The bending rigidity is a measure of the energy associated with its bending (measured in k_BT or N m). In general, membranes made from lipids with unsaturated acyl chains have a lower bending modulus than membranes made from lipids with saturated acyl chains. Moreover, cholesterol increases the bending rigidity. Several methods have been developed to measure bending rigidity (Table 1; Fig. 1; reviewed in ref. ³²).

The cell cortex tightly interacts with the plasma membrane. Cortical tension is the force per unit length exerted on a piece of the cortex by the cortical network around it (measured in J m^–2 = N m^–1). Tension gradients result in local contractions and drive cell deformations. Molecularly, cortical tension is governed by actomyosin contractility (reviewed in ref. ³³) and cortical actin architecture³⁴. The cell cortex undergoes rapid turnover, making it both mechanically rigid and highly plastic. Providing further complexity, the cell cortex is composed of actin filaments polymerized by both Arp2/3-complex activators as well as formins³⁵. The resulting filaments might have different lengths and have different effective turnover rates and this underlies differential mechanical properties^36,37. A wide range of experimental techniques have been used to measure cortical tension (Table 1; Fig. 1). Its magnitude varies considerably between cell types, ranging from approximately 10^–5 N m^–1 in blood granulocytes³⁸ to 10^–3 N m^–1 in D. discoideum cells^39,40.

The dynamic plasticity of the cell surface is essential for cells to rapidly change shape, move and exert forces. Interestingly, cell surface mechanics often have opposing effects on cell shape: cytoskeletal assembly and disassembly is intimately linked with membrane shape changes of the plasma membrane and organelles^27,41, but the ability of the cytoskeleton to influence membrane shape changes is physically limited by in-plane membrane tension and MCA³. Signalling feedback loops have been identified between membrane tension and actin polymerization^9,10. On the other hand, specifically perturbing membrane or cortical mechanics does not necessarily affect the other⁴². This highlights how we are only beginning to understand the logic of how cell surface mechanics affect signalling, cell shape and movement, and how that logic might be context dependent. This is due, at least in part, to limited information on the mechanical properties of the cell surface. Multidisciplinary approaches and specific experimental tools to measure and control cellular forces over multiple time, length and force scales are needed to understand how cellular morphogenesis, which drives complex cell behaviour such as cell motility and division, arises from membrane and cortical mechanics.

Future research on cell surface mechanics

The complexity, variability and importance of cell surface mechanics remain to be uncovered in many cellular processes. Three trends will help to account for its continued importance. First, a growing range of experimental techniques and mathematical models are being developed to allow measurement of cell surface mechanical properties (Table 1; Fig. 1). While many still require specialized skills and instruments, they are becoming more widely available. Second, a common language to describe cell surface mechanics is emerging. While errors in terminology and even units persist, the inclusion of mechanics in methods and discussions will move the field to a more careful quantification of cell surface properties. Third, understanding cell behaviour is often incomplete without consideration of cell surface mechanics. In this manner, efforts to explain biology will continue to demand investigation of cell mechanics, both internal and at the surface, to explain cell form and function.

Of course, many challenges remain: identifying molecular determinants of cell surface mechanics continues to be a challenge. Compounding this, recent studies highlight the importance of not only the composition but also the specific architecture of actin networks for their mechanical properties^34,43. Moreover, bending modulus and MCA may also vary locally due to spatial variations in lipid composition and MCA proteins. This complicates efforts to obtain cell surface properties from measurements at one location on the cell. Some of those challenges can be addressed with the help of physical models and numerical simulations. Studies such as Chugh et al.³⁴ exemplify how computational models can be used to identify the physical mechanisms responsible for the emergence of a given regime of cell surface mechanics.

If regulation of cell surface mechanics is important for proper cell function, then disruption of cell surface mechanics could be responsible for some pathologies. This raises the intriguing question of whether mechanical investigations of the cell membrane and cortex will reveal new molecular targets and offer new opportunities for intervention. Our challenge going forward is to understand mechanistically how, when and why cell surface mechanics choices are made.