Imaging localized neuronal activity at fast time scales through biomechanics

Noninvasive measurement of fast neuronal activity, based on tissue stiffness maps from MRI elastography, is presented.

Abstract

Mapping neuronal activity noninvasively is a key requirement for in vivo human neuroscience. Traditional functional magnetic resonance (MR) imaging, with a temporal response of seconds, cannot measure high-level cognitive processes evolving in tens of milliseconds. To advance neuroscience, imaging of fast neuronal processes is required. Here, we show in vivo imaging of fast neuronal processes at 100-ms time scales by quantifying brain biomechanics noninvasively with MR elastography. We show brain stiffness changes of ~10% in response to repetitive electric stimulation of a mouse hind paw over two orders of frequency from 0.1 to 10 Hz. We demonstrate in mice that regional patterns of stiffness modulation are synchronous with stimulus switching and evolve with frequency. For very fast stimuli (100 ms), mechanical changes are mainly located in the thalamus, the relay location for afferent cortical input. Our results demonstrate a new methodology for noninvasively tracking brain functional activity at high speed.

INTRODUCTION

Blood oxygenation level–dependent (BOLD) functional magnetic resonance imaging (fMRI) (1, 2) has transformed the field of neuroscience by measuring neuronal activity via a neurovascular coupling (3). The BOLD neurovascular coupling, however, is a slow process limiting the sensitivity of BOLD fMRI to time scales of the order of several seconds, with a cutoff frequency of ~0.1 Hz. Many high-level cognitive processes, meanwhile, evolve over time scales of 10 to 100 ms (4). Gaining access to conscious and nonconscious processing at these fast time scales, which is important for an understanding of the neuronal architecture, requires the development of a noninvasive imaging method that combines the speed of electroencephalography or optical methods with the spatial resolution of MRI.

Using the technique of lock-in amplification, where a cyclic ON/OFF stimulus is applied and the phase-synchronous response is averaged over many cycles, some fMRI studies have been able to measure BOLD responses for frequencies of up to 0.75 Hz (5). Because of its slow temporal response, however, the signal amplitude of the differential response between ON/OFF stimulus states decreases to 0.04%, which is two orders of magnitude smaller compared with that of classical BOLD experiments operating at time scales of ~0.1 Hz. This renders the clinical translation of approaches that use neurovascular coupling as a source for tracking fast neuronal signals extremely difficult.

Functional Doppler-based ultrasound has recently demonstrated sensitivity to neurovascular-induced changes in smaller blood vessels (6). Thus, while plane-wave illumination–based ultrasound provides very high temporal resolution, the mechanism responsible for its contrast is not fast. Furthermore, the application of ultrasound to the adult brain is challenging due to strong aberration and attenuation of sound within the skull.

In contrast to the slow neurovascular responses to neuronal activity, mechanical changes at the cellular level can be fast (7, 8). Swelling of nerve fibers during the action potential was observed at a time scale of ~5 ms (8). Images of an axon of a cultured neuron demonstrated physical displacement and swelling when electrically stimulated (9), caused either by transmembrane flux of ions and water or by cytoskeleton shape change, with the axon returning to the baseline after cessation of action potential firing. Action potentials evoke transient contractions of dendritic spines likely to be mediated by Ca²⁺ influx through voltage-gated Ca²⁺ channels (10). The magnitude of contraction was around 5 to 10% at a spine size of ~1 μm, with a transient twitch at time scales of hundreds of milliseconds to 2 s. So far, these prior investigations have been limited to in vitro work and mostly invasive detection approaches.

Here, we demonstrate a new strategy to image functionally mediated mechanical changes in vivo noninvasively, at short time scales (100 ms) and high spatial resolution (300 μm in-plane and 900 μm through-plane), via MR elastography (MRE) (11). We present a novel concept enabling the fast measurement of mechanical changes induced by neuronal activity via an interleaved MRE acquisition in conjunction with a new finite element–based reconstruction approach for quantifying tissue viscoelasticity (12). Applied to sedated mice exposed to oscillatory electrical shock stimulation, we demonstrate the ability to image fast localized mechanical changes in vivo. This approach confirms that neuronal activity is tightly coupled to mechanical changes, that those stiffness changes are of the order of 10% and robust over two orders of magnitude in switching time (100 ms to 10 s), and that, for the shortest time scale, mechanical changes occur predominantly in the thalamus. We show that responsive brain regions are generally stiffer during the stimulus OFF state than the ON state, thereby raising important questions about the mechanism, particularly recovery and inhibitory processes.

RESULTS

Interleaved data acquisition provides sensitivity to time scales as short as 100 ms

MRE is an established MRI technique for in vivo quantification of tissue biomechanical properties via imaging of externally induced propagating mechanical (sound) waves (11). Both the stiffness and dissipation of tissue are measured, as schematically shown in Fig. 1 (A and B), where the wavelength and attenuation of a mechanical shear wave are the corresponding physical attributes. Synchronous alternation of a magnetic field gradient at the mechanical vibration frequency produces a net phase shift in the MRI signal proportional to the waves’ displacement, with submicrometer motion sensitivity. This enables the measurement of the three-dimensional (3D) displacement field necessary to solve the Navier equation for calculating the complex-valued shear modulus, i.e., G* = G′ + iG″, with G′ being the elasticity and G″ the viscosity, respectively, and i = √−1 (13). We use a novel head rocking system that generates mechanical vibrations propagating through the entire mouse brain by rotating the head through a pivot point located near the neck (Fig. 1C) (14).

Fig. 1. MRE basics, experimental setup, and MRE data.

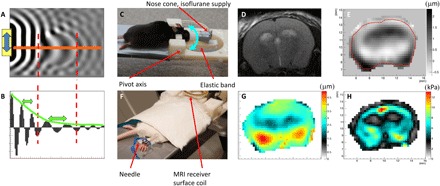
(A) 2D numerical simulation example of shear wave displacement field. (B) Plot of displacement along the orange line in (A) shows an increase in wavelength in the stiff ellipsoidal inclusion and attenuation of the wave due to frictional forces in the medium. (C) Head rocking MRE system adapted to the mouse. The cyan double-arrow indicates the pivoting direction of the movable front part. (D) T2-weighted anatomical image, (E) measured displacement field in through-slice direction at one time point (μm), (F) placement of electrical stimulation needles in the hind limb, (G) total induced displacement amplitude (μm), and (H) resulting real part of the complex shear modulus after the reconstruction process. The photographs used in Fig. 1 (C and F) are provided courtesy of N. Nazari, Boston University, and S. Patz, Brigham and Women’s Hospital, respectively.

Our previous work in mice showed maps of viscoelasticity at the identical resolution used here with scan times of about 23 min to generate a single dataset (15). To enable measurement of fast mechanical changes during time periods as short as 100 ms, we developed a new MRE sequence protocol that acquires data in an interleaved manner, switching in synchrony with the state of an applied electrical stimulus that oscillates between ON and OFF. Depending on the duration of the stimulus state, different amounts of data can be acquired. In general, MRE requires the measurement of the displacement field in both space (“slices”) and time (“wave phases”). Classical BOLD fMRI protocols switch between stimulus states at typical time scales of ~10 s. For our MRE acquisition, such a time is sufficient to acquire one line of the imaging matrix (k-space line) for all slices and all wave phases during one stimulus state (Fig. 2A, SLOW sequence). To explore temporal changes at time scales of 1 s, one stimulus state is only long enough to loop over all slices for a given wave phase (Fig. 2B, FAST sequence). Pushing the limits to 100 ms allows for the acquisition of only one combination of slice/wave phase during a stimulus state (Fig. 2C, Ultra-FAST paradigm). Consequently, each acquisition protocol has a different sensitivity to the temporal evolution of any mechanical changes that accompany neuronal activity during a stimulus state.

Fig. 2. Data collection schemes and LFP.

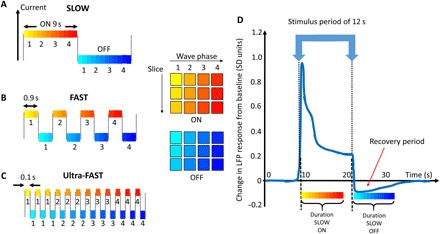
(A to C) Different colors schematically represent the elapsed time from a stimulus transient at which a slice/wave phase combination is acquired (here, three slices and four wave phases are shown, representatively). The SLOW (A), FAST (B), and Ultra-FAST(C) stimulus times (9 s, 0.9 s, and 100 ms) allow for acquisition of MRE data from all slice/wave phase combinations, all slices for a single wave phase, and a single slice/single wave phase combination, respectively. (D) Schematic representation of one section of the temporal local field potential (LFP) deviation from baseline for a 12-s block design visual stimulus [adapted from Fig. 5C from (16)]. The LFP shows a high transient response immediately after the stimulus is either switched ON or OFF. The Ultra-FAST acquisition is most sensitive to any transient response, whereas the SLOW acquisition is sensitive to the average response over its longer stimulus time.

On the basis of the work by Logothetis et al. (16), who took intracortical recordings from the visual cortex of macaque monkeys exposed to visual stimuli, we expect that the local field potential (LFP) has a transient behavior with a very fast initial component, a plateau, and a drop below baseline immediately after the stimulus is turned off (Fig. 2D). Assuming that changes in the LFP go along with changes in biomechanics, we therefore expect to observe changes in stiffness maps depending on stimulus switching frequency. To enhance our sensitivity to subtle changes in biomechanics, we furthermore developed a novel approach to reconstruct viscoelasticity from the wave data (12). The solution of the Navier equation is now based on first-order spatial derivatives due to a finite element–based approach. This provides elevated sensitivity to small stiffness changes due to reduced noise compared with previous techniques that use second- or third-order spatial derivatives (13, 17).

To directly visualize and quantify a neuromechanical coupling, we performed experiments on sedated mice exposed to a hind limb electrical shock stimulus (18). Two 30-gauge hypodermic needles were inserted into a hind limb to deliver the electrical stimulation pulses (Fig. 1F). The electrical current (1.5 to 2 mA, 250-μs duration) was adjusted until a small twitch in one of the hind limb digits was observed. The hind limb was used rather than the fore limb to make sure the electrical leads were as far as possible from the head to avoid potential interferences with the MRI data acquisition. All experiments were conducted in accordance with the local Institutional Animal Care and Use Committee (IACUC).

Visualization of stiffness changes induced by neuronal activity

Figure 3A shows the corresponding elasticity images (G′) for a SLOW experiment from an individual animal, where electrical stimulation pulses were applied at 3 Hz during the ON state. A clear and pronounced increase in stiffness in the cingulate/retrosplenial region is visible in the OFF state compared with the ON state (pink arrow). The cingulate/retrosplenial region is known as a “saliency” area that responds to noxious stimuli (19). The motor cortex and the hind limb primary somatosensory cortex are immediately adjacent to the cingulate/retrosplenial cortex and are likely to be activated by a shock stimulus. In a separate control scan, the two stimulus states were both set to OFF. As expected, the resulting two elasticity maps are identical except for noise contributions. The general appearance of the control maps agrees qualitatively with prior studies (15). These observations persist when results from seven animals are averaged together after each individual case is first coregistered to an anatomic atlas (Fig. 3B) (20). This suggests a common mechanical brain response to neuronal activity.

Fig. 3. fMRE results.

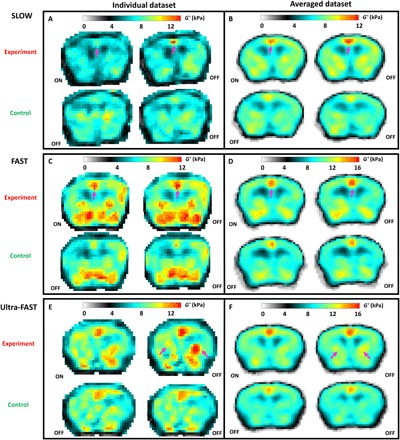
(A, C, and E) Examples of elasticity (G′) maps from single animals studied with the SLOW, FAST, and Ultra-FAST protocol for experiment and control scans. ON/OFF refer to the stimulus state. Pink arrows indicate regions where the difference between the ON and OFF stimulus states of the experiment scan is readily observable. (B, D, and F) Averaged G′ results from experiment and control scans for the SLOW, FAST, and Ultra-FAST protocols, respectively, after registration to a common anatomical reference (20). Note that the dynamic range of the G′ scale is adjusted to highlight the differences.

Significant stiffness changes are seen at a 100-ms time scale

We obtain similar results for the FAST experiment where the ON/OFF states are switched at 1.1 Hz (Fig. 3, C and D). Here, the electrical stimulation was pulsed at 10 Hz to ensure a minimum of 10 pulses per ON state. Again, the averaged stiffness maps (number of mice = 5) demonstrate a localized elevated stiffness increase in the region of the cingulate/retrosplenial gyrus for the experiment OFF state compared with the ON state.

At the highest stimulus switching frequency of 10 Hz (Ultra-FAST experiment in six mice, electrical stimuli delivered at 100 Hz), a stiffness increase during the OFF state is mainly localized in the thalamus region (Fig. 3, E and F, pink arrows) and less in the cingulate/retrosplenial region. This demonstrates that localized stiffness changes accompanying neuronal activity persist at time scales as short at 100 ms and that the location of mechanically active regions changes rapidly with time and, hence, frequency. Although both G′ and G″ were reconstructed, significant differences were only observed for G′ for all experiments. Potential mechanisms that are responsible for the observed neuromechanical coupling must hence affect mainly the stiffness and less so the dissipative processes.

The purpose of changing the rate of modulation of the stimulus from ON to OFF, i.e., the SLOW, FAST, and Ultra-FAST protocols, was to demonstrate that there is a robust stiffness difference between the two stimulus states for different stimulus modulation frequencies. To have a minimum of 10 stimulation pulses during each ON period, the frequency at which electric shock pulses were applied during the ON period is different for each modulation frequency. Since an electric shock necessarily excites a wide variety of different neuronal fibers and there is a known difference in both the frequency response and the latency of different types of afferent neurons, it is only appropriate to make qualitative and not quantitative comparisons between SLOW, FAST, and Ultra-FAST results.

The expected high similarity between the elasticity maps for the control experiments is used to calculate the noise level in our data and to define a z score as a threshold for significance. While the mean difference between voxel pairs of the two OFF state elasticity maps was always close to zero, the SD (σ) for G′ ranged from 0.52 to 0.72 kPa and for G″ from 0.55 to 0.81 kPa.

Regional development of stiffness changes with switching frequency: The thalamus as the gate keeper

In the following, we consider G′ difference maps between the OFF and ON states (normalized to the ON state) where only pixels are shown with a z score larger than unity, i.e., $|\mathit{z}|=\frac{|\mathrm{\Delta }\mathit{G}\prime |}{\mathrm{\sigma }}>1$. Activated brain tissue during the OFF state is generally stiffer than that during the ON state (displayed here as a positive percentage). In particular, a significant mechanical activation of the cingulate/retrosplenial region ranging from 5 to 15% is now visible for all three switching frequencies (Fig. 4A). Neuronal traffic to the central cingulate/retrosplenial area includes signal from C and Aδ fibers. Because of their relatively low levels of axonal myelination, they have a lower propagation speed compared with tactile fibers. Their frequency response also decreases above ~3 Hz due to their relatively long refractory periods compared with somatosensory-only neurons (21). Hence, one expects a monotonically decreasing nociceptive response in the cingulate/retrosplenial region with increasing electrical pulse frequency, which is 3, 10, and 100 Hz for the SLOW, FAST, and Ultra-FAST experiments, respectively. The size of the activated region in the cingulate/retrosplenial region and the magnitude of change decreases with increasing electrical pulse frequency (SLOW: 14 pixels and average percent change of 8.4%, FAST: 14 pixels and 5.7%, and Ultra-FAST: 3 pixels and 5%).

Fig. 4. Differences in stiffness between stimulus states.

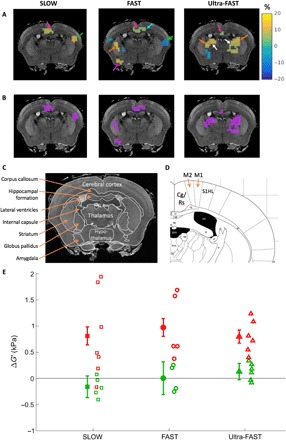
(A) Percentage differences between the OFF and ON states of the experiment scans (relative to the ON states) are shown overlaid on an anatomically matching T1-weighted atlas image (24) and where only pixels with |z| > 1 are shown. Activated regions include the cingulate/retrosplenial (Cg/Rs) cortex (pink arrow) and the immediate surrounding region of primary contralateral hind limb somatosensory cortex (S1HL) and primary (M1) and secondary (M2) motor cortex (cyan arrow). Also activated are regions in the thalamus (white), striatum (orange), and amygdala (purple). (B) Mean G′ differences (kPa) from regions in (A) with z > 1 (i.e., showing a positive difference) are shown as purple regions superimposed on anatomical images. Labeled anatomical images from Waxholm (C) and Paxinos (D) atlas references (24, 25) corresponding to the MRE slice location. (E) The mean of the purple regions of interest (ROIs) is shown for each animal individually (open symbols) and as an average for each value of stimulus frequeny studied (closed symbols). The error bars are the SEM from the ROI averaged over all animals. The application of a repetitive ON/OFF noxious stimulus leads to significant stiffness variations on both an individual and ensemble level (red), whereas no statistically significant stiffness changes are observed for OFF/OFF control scans (green).

The contralateral primary and secondary somatosensory cortices are areas known to be implicated in pain-related neuronal activity (19). We observe the primary somatosensory cortex activated in the FAST experiment and the secondary somatosensory cortex activated both in the SLOW and FAST experiments, however with opposite stiffness responses during the ON versus the OFF state. The opposite responses during the FAST protocol may arise from a communication time delay between the primary and the secondary somatosensory cortex (22).

An exciting observation is that the thalamus only shows activation for the Ultra-FAST experiment. The thalamus is the relay location for afferent neuronal traffic to the cortex, and the Ultra-FAST acquisition protocol is most sensitive to mechanical changes immediately after the signal transient (Fig. 2D). Furthermore, the level of adaptation to repetitive stimuli is greatly reduced in the thalamus compared with other cortical regions. For instance, patch clamp measurements in a rodent whisker barrel cortex from a whisker stimulus at 20 Hz have shown strong adaptation during the stimulation period, resulting in a depression of the neuronal response (23). Accordingly, one would predict minimal mechanical activation response in the cortex and maximal activation in the thalamus for the Ultra-FAST acquisition, and this is indeed what is observed.

To aid in identifying the activated regions, Fig. 4 (C and D) shows labeled anatomical images from the Waxholm (24) and Paxinos (25) mouse atlas databases that best match the MRE slice location shown. The Paxinos image is a magnified portion of the original atlas image and shows in detail the region immediately adjacent to the cingulate/retrosplenial (Cg/Rs) region that includes the primary (M1) and secondary (M2) motor cortex and hind limb primary somatosensory cortex (S1HL).

Robust mechanical change of 10% over two orders of magnitude in time

To demonstrate the evolution of stiffness changes with stimulus switching frequency, we show in Fig. 4E the stiffness differences of brain regions with a z > +1 for the SLOW, FAST, and Ultra-FAST cases. These regions are shown in purple in Fig. 4B. The data show that over a range of stimulus switching frequencies covering two orders of magnitude, there is a clear difference between OFF and ON stimulus states, both for individual animal studies and on an ensemble level. The mean stiffness difference of about 1 kPa is largely independent of stimulus switching frequency. This result is in contrast to the differential signal measured in BOLD experiments, where an increase in switching frequency from 0.1 to 1 Hz leads to severe signal loss. As expected, control scans show no stiffness changes (Fig. 4E), indicating the reproducibility and stability of the scans.

DISCUSSION

Imaging fast neuronal activity noninvasively at high spatial resolution is one of the most challenging goals in neuroimaging. In this study, we present the first spatial visualization of fast localized stiffness changes induced by neuronal activity with a noninvasive method. Our new approach combines novel hardware to induce shear waves in the rodent brain with a segmented interleaved functional MRE acquisition protocol (fig. S1) that is sensitive to mechanical changes at time scales as short as 100 ms. We developed a novel finite element–based approach for calculating maps of the complex shear modulus from 3D wave data using first-order spatial derivatives that provides improved signal-to-noise ratio (SNR) over previously established second- or third-order–based methods. This technology enables us to characterize the spatiotemporal evolution of brain stiffness changes in mice exposed to repetitive ON/OFF periods of electrical stimuli that cover two orders of magnitude of time scales down to 100 ms. While we discuss in this work the exclusively obtained data in mice, the translation of this technology to humans is straightforward, and preliminary data have already been obtained (26).

Previously, other functional imaging modalities have shown the cingulate gyrus, primary and secondary somatosensory cortex, thalamus, striatum, and amygdala as regions implicated in nociception (19). Our results demonstrate that those regions are also mechanically activated in response to neuronal shock stimuli, with significant changes in stiffness while dissipation remains unchanged. This is consistent with rheology studies in cells that, regardless of cell type and stimulus, generally show a transition from a more fluid-like to a more solid-like behavior when they become stiffer (27). The observed lack of concomitantly activated regions for G′ and G″ rules out poroelasticity as a potential source for the observed effect, as that would affect both shear elasticity and viscosity (28). We observe a robust ~10% mechanical change in the cingulate/retrosplenial gyrus region over two orders of magnitude of stimulus switching frequency. Consequently, the mechanism responsible for the observed stiffness changes must be fast and apparently quasi lossless. The physical concept of entropic elasticity is a potential candidate to explain these fast mechanical transitions (29).

Our data show that the location, the phase, and the intensity of the observed elasticity changes are functions of stimulus switching frequency. Adaptation and, hence, attenuation of the neuronal response during sustained repetitive ON/OFF sensory stimulation, and incomplete recovery before the next stimulation pulse, have been widely studied (23). The thalamus, as the relay for afferent neuronal traffic, is however far less affected by adaptation. For the fastest switching protocol, i.e., at 10 Hz, changes in the primary and secondary somatosensory cortex are largely suppressed in our data, with only a small region remaining within the cingulate/retrosplenial gyrus (Fig. 4A). At that time scale, mechanical changes occur almost exclusively in the thalamus region, emphasizing our sensitivity to fast neuronal processes.

An important aspect of our observation is that significant stiffness changes persist to frequencies where hemodynamics cannot follow (Fig. 5). This indicates that the observed mechanical changes are more tightly coupled to primary neuronal activity and represent a fundamental advantage over traditional BOLD fMRI based on slow neurovascular coupling. It also precludes a direct comparison between functional MRE and classical fMRI experiments at those time scales.

Fig. 5. Modeling the hemodynamic response as a function of stimulus switching frequency f_s.

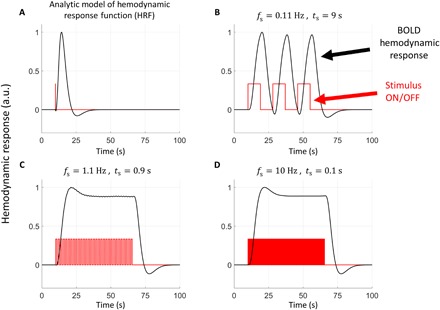
(A) Analytical model of cortical hemodynamic response function (HRF) based on measurements by Tian et al. (3). a.u., arbitrary units. (B to D) Convolution of the HRF analytical expression with stimulus switching at different values of f_s. The code used to calculate these graphs was obtained from www.fil.ion.ucl.ac.uk/spm/software/spm12/. The change in the hemodynamic response between the stimulus ON and OFF states is significant for (B) and negligible for (C) and (D).

Currently, the reason for an elevated stiffness during the experiment OFF state compared with the ON state is unknown. Data obtained by Logothetis et al. (16), who conducted a series of experiments to understand the source of traditional BOLD fMRI, demonstrated that during the OFF period of a block design (visual) stimulus, the LFP falls below the baseline potential for several seconds (Fig. 2D). Moreover, the time before the below-baseline LFP returned back to baseline depended on the duration of the stimulus. Using the Logothetis et al. data as a guide, since LFP decreases below baseline immediately after the stimulus is turned OFF, it seems plausible that ionic shifts during the recovery process may contribute to the observed elevated stiffness that we measure during the OFF state period. The complex interplay of simultaneous mechanosensitive processes (30), however, makes it challenging to isolate the underlying mechanism. Detailed future work will be necessary to determine the exact mechanism(s) behind our observations.

Potential neuromechanical coupling mechanisms that are fast enough to explain our results include hydrostatic pressure changes (31) and neural activity–related potassium influx from extracellular spaces that results in water influx into astrocyte-glial cells both by osmotic pressure gradients (32) and pH regulatory transport mechanisms (33). Water influx into astrocyte-glial cells can result in a stiffness decrease due to reduced molecular crowding (34). Other neuromechanical coupling mechanisms are increased cytoskeletal prestress due to actin polymerization and/or actomyosin contractile activation following synaptic activity and calcium ion influx (35) and, possibly, a previously unappreciated very fast microvascular response. Hence, one cannot easily point to a single mechanism that explains our results. Thus, the magnitude of the LFP may not be a complete indicator of the strength or sign of the elasticity response.

The BOLD response, governed by the mouse hemodynamic response function (HRF) that reaches a peak in ~3 s and relaxes back to equilibrium in a time period >10 s (Fig. 5A), is a relatively slow response that cannot respond to the stimulus switching rate for either the FAST or Ultra-FAST case. Rather, for these cases (Fig. 5, C and D), the BOLD response reaches a steady state that is constant for both ON and OFF stimulus states. The stiffness change associated with this steady-state vascularization acts as a bias for both stimulus states. Assuming that enhanced blood flow results in increased vascular pressure to the capillary bed, Gennisson et al. (36) demonstrated that this results in a stiffness increase. For the SLOW experiments, the BOLD response is not saturated; rather, its response is shifted due to its latency toward the OFF state with its maximum just at the transient (Fig. 5B). This produces an out-of-phase stiffening for the SLOW case. The BOLD response is, hence, either adding to our observations (for SLOW) or represents a constant background stiffening.

An increase in astrocyte-glial cell volume with a corresponding decrease in molecular crowding and stiffness (34) secondary to potassium ion influx into the astrocyte during neuronal activity could explain our observations of a softer stiffness for stimulus ON compared with stimulus OFF. We note that the response of astrocyte-glial cells to hyper- or hypotonicity involves multiple mechanisms with different time constants (32). One study, however, showed that the presence of aquaporin-4 channels in a membrane allowed water influx into a vesicle with a time constant of 8.3 ms (37). This time constant is sufficiently fast to allow water transport into and out of astrocyte-glial cells at the stimulus switching frequencies we studied. Experiments at extremely low switching frequencies should allow to disentangle the effects from BOLD and molecular crowding, i.e., when the BOLD response peaks during ON for instance.

The current acquisition time required to perform a single functional MRE (fMRE) experiment is 46 min. We believe this time can be substantially shortened by using a number of advanced MRI techniques. For example, multielement radio frequency receiver coils will both improve the SNR and allow for parallel imaging. Improving the SNR will likely allow one to reduce the number of wave phases by a factor of 2, whereas parallel imaging will likely reduce imaging time by an additional factor of 2. Further improvements in gradient encoding, such as the use of Hadamard encoding (38), are expected to allow a further factor of 2 reduction in imaging time. Together, these improvements would lead to a 5-min fMRE experiment, which would be much more efficient and greatly increase its adoption and use.

Note that the imaging strategy described here, i.e., a repetitive ON/OFF stimulus, can be broadened to allow one to observe the propagation of neuronal activity. For this, we propose a single ON period followed by multiple OFF periods. As an example, consider the repetitive pattern: ON/OFF/OFF/OFF/OFF. If each section time is, for instance, 10 ms, which is achievable on clinical systems (26), then one will be able to acquire five elasticity maps showing the propagation of neural activity in 10-ms time steps over an overall period of 50 ms.

CONCLUSIONS AND FUTURE DIRECTIONS

The fMRE methodology as described here is capable of providing maps that show what regions of the brain respond to a fast-changing stimulus. We anticipate that mapping neuronal activity by the measurement of tissue stiffness will provide a new methodology for studying brain function at high temporal and spatial resolution with specific application to tracking neural circuitry at high speed. We look forward to future studies of neuronal propagation with different stimuli at different stimulus switching frequencies, which will allow for the elucidation of the different neuromechanical coupling mechanisms with their different amplitudes and time constants. The translation of our approach to humans is imminent, and we have already obtained preliminary data in the human visual cortex (26). Thus, fMRE has great potential to facilitate and deepen the understanding of the pathway of neuronal signals propagating in the in vivo brain, including the elucidation of impaired neural circuitry associated with pathologic subcomponents of neuronal physiology.

MATERIALS AND METHODS

MRE pulse sequence

A spin-echo MRE sequence with 300-μm isotropic image resolution (14) was modified for functional imaging (fMRE). The alterations were allowed for interleaved acquisition of two different conditions of electrical stimulation. The modifications were different for each of the three stimulus switching frequencies investigated. In an MRE sequence, one acquires data at different phases of the mechanical shear wave induced in the sample. We refer to these as “mechanical shear wave phases” or simply wave phases. Different wave phases were acquired by temporally shifting the entire acquisition and thereby the location of the motion encoding gradients (MEGs) relative to the mechanical vibration. We collected eight wave phases. Since the mechanical vibration frequency was 1 kHz, this corresponds to temporal shifts of one-eighth of 1 ms between wave phases. The Fourier transform of the wave phase data at a particular position in space gives the amplitude and phase of the mechanical shear wave. Sequence details are as follows: repetition time (TR) per slice = 100 ms, no. of slices = 9, actual TR = 900 ms, spin echo time (TE) = 29 ms, and number of averages = 1. The mechanical vibrations were applied at 1-kHz frequency. The shear wave amplitude magnitude was <5 μm and typically varied between 1 and 3 μm for each of the three orthogonal directions. The MEG time and amplitude were 20 ms and 650 mT/m, respectively. Data were acquired on a 64 by 64 by 9 matrix with a readout bandwidth of 20 kHz. Additional details of the looping structure for each stimulus switching frequency are provided in the Supplementary Materials.

Rationale for choice of stimulation

Different types of stimulation were considered, including whisker barrel stimulation, both hind limb and fore limb electrical stimulation, and audio stimulation. Whisker barrel stimulation was ruled out because of the possibility that the mechanical vibration of the head used for elastography might cause a background steady-state stimulation of the whisker barrel, thereby making it difficult to differentiate between different stimulus states. Audio stimulation was not chosen because of the large noises from gradient switching that could easily confound any audio stimulus. Note that to minimize any brain activation from the large gradient noise, even though it was relatively constant for both stimulus states, both ears were filled with gel.

We settled on electrical stimulation of the hind limb rather than the fore limb because the hind limb was farther from the brain, and we wanted to have a large distance from the electrodes inserted in the hind limb and the brain to ensure the magnetic field created by the electrode current produced a negligible phase shift in the MRI signal. The hind limb was gently stretched toward the tail such that when the electrodes were inserted into the hind limb, the closest distance of the electrodes to the brain was typically >7 cm. The electrical leads were twisted tightly to avoid producing a stray magnetic field when current pulses were applied. Since the magnetic field due to the electrical stimulation current goes as the inverse squared power of the distance to the measuring point, the magnetic field created by the current in the electrodes could not possibly create a localized field similar to the activation regions observed. Furthermore, we did a sham experiment on a phantom, with the closest position of the electrodes being 7 cm from the center of the phantom. An electrical current of several milliamps was alternated in the electrodes as for the ON and OFF stimulus states. No observable changes in the two interleaved acquisitions were observed. If any stray magnetic field had been generated, it would have affected the entire brain rather than a localized region. We conclude that the leads themselves could not have created what is reported here.

Modeling the BOLD response

As traditional BOLD fMRI is a well-established technique to measure brain function, it is natural to ask whether the increase in both cerebral blood flow and volume that are part of the BOLD response could induce mechanical changes in the tissue that would be reflected in our elastography results. To address this question, consider Fig. 5 that shows an analytical model of the HRF and its convolution with a stimulus for different stimulus switching speeds. Notice that at the slowest switching frequency, the BOLD response can follow the stimulus, and hence, there is a large alternating vascular effect. At higher stimulus switching frequencies, however, while there is a vascular response due to the temporal asymmetry of the HRF, the difference in the hemodynamic response between stimuli becomes negligible as the stimulus switching frequency reaches 10 Hz. Thus, although the viscoelastic results for any scan may be affected by the BOLD response, at the higher stimulus switching frequencies, the difference in viscoelastic properties between the two interleaved stimuli was negligible if biomechanics were solely affected by the neurovascular effect. Thus, we conclude that, at the highest stimulus switching frequency, differences between the two experiment scans, i.e., stimulus ON and OFF, do not depend on the neurovascular coupling responsible for BOLD and must be due to a mechanism that can respond to stimulus switching at a much faster rate. The measured stiffness and viscosity values are the result of all physiological mechanisms that influence the shear modulus. In particular, the response to the SLOW stimulus switching frequency may include mechanical effects, if any, from the neurovascular coupling.

MRE shear modulus reconstruction

The general methodology behind MRE is to oscillate the magnetic field gradients synchronously with the applied mechanical vibrations applied to the tissue. From this, a phase shift in the MRI data was produced that is proportional to the shear wave displacement. The shear modulus G was calculated via MRE reconstruction, which inverts the linear elasticity equations using the acquired wave displacement data as input.

The reconstruction method used here computes G at each voxel independently using data in a local neighborhood over which G is assumed to be constant. The finite element method (FEM) was used with divergence-free basis functions to isolate the shear component of the wave data. Additional factors, including low-order approximations, small mesh size, removal of data that lead to negative moduli, and weighted averaging of G based on residual error, work to improve accuracy and robustness of the result (12). The resulting images of G, also called elastograms, have the same resolution as the raw MRE phase images. In practice, however, because spatial derivatives are used in the elastography reconstruction, there is a small smoothing of neighboring voxels in the reconstructed shear modulus maps.

Registration

Before averaging elastograms from different experiments, they are first coregistered onto a common anatomical atlas map chosen from the Waxholm database (20) to best match identically positioned slices from a T2-weighted set of images. The resolution of the Waxholm image was reduced to that of the MRE images, and a 2D registration was performed (translation, rotation, and scaling of the 2D plane) to define a spatial mapping between each MRE magnitude image and the reference Waxholm image. As the registration algorithm was most sensitive to brain boundaries and because there may have been up to a one voxel shift in the slice location between each study, a manual ±1 voxel adjustment was sometimes made to best align the ventricles, which were the most prominent internal brain structure. This manual adjustment was performed on one of the elastograms from each experiment and applied to the remainder from the same experiment.

Threshold of difference elasticity maps for statistically significant values

For each protocol, the experiment (ON|OFF) and control (OFF|OFF) elastograms were averaged over different studies after transformation to the Waxholm anatomical atlas space. The resulting averages of experiment stimulus ON elastograms were subtracted from the corresponding averaged experiment stimulus OFF elastograms to find shear modulus difference maps shown in Fig. 4. Differences between the two averaged control elastograms were used to assess scan reproducibility. Thus, the distribution of voxel-by-voxel differences over the entire brain between the two averaged control maps was evaluated by fitting the distribution to a Gaussian. The SD of the Gaussian fit was then used to define a threshold where only shear modulus changes above the threshold are considered significant as shown in Fig. 4A. The SD values (σ) thus obtained for ΔG′ for the SLOW, FAST, and Ultra-FAST cases are 0.55, 0.72, and 0.52 kPa, respectively. Similarly, the values obtained for ΔG″ are 0.60, 0.81, and 0.56 kPa.

In addition, since a 2-cm-diameter surface coil was used to receive the nuclear magnetic resonance signal, the SNR at a particular location in the brain is dependent on its distance to the surface coil. The SNR was seen to decay by a factor of approximately 1.75 from the top to the bottom of the mouse brain. An analysis of variation in reconstructed shear modulus shows that this change in SNR leads to a 1.6× increase in the variability of G. To account for this, the threshold values were varied linearly by this factor, from top to bottom, with the value at the level of the ventricles set to the calculated SD. There may be slow drifts in the overall stiffness of the brain due to changes in the physiology over time. However, because each line of k-space for the two stimulus states is acquired within seconds of each other, the difference between the two elastography maps for a particular scan is immune to long-term drifts (see Data Integrity section below).

Animal experimental results

For the three stimulus switching frequencies—SLOW, FAST, and Ultra-FAST—a total of seven, five, and four animals were studied, respectively. The animals studied in the Ultra-FAST protocol were studied twice, with a minimum of 6 weeks separating each study. A small number of the scans were rejected because of severe artifacts, low SNR, and/or inability to unwrap phase. Those artifacts originated from hardware failures, like mechanical fractures in the 3D-printed plastic parts of the head rocker. Further details are provided in the Supplementary Materials. After registration to the Waxholm anatomical database, the elasticity maps from different animal studies were averaged together. The purple region of interest (ROI) regions shown in Fig. 4B are those voxels from the averaged studies where (i) the experiment OFF stiffness is greater than the ON stiffness ( ΔG′ > 0), (ii) where the z score is >1, and (iii) that are part of a voxel cluster size >2. The mean and SD values of these purple ROI regions, shown as closed symbols in Fig. 4E, are given in table S2. The purple ROI regions are then applied to the anatomically registered elasticity maps for each individual animal, and the mean and SD values for the purple ROI regions for each individual animal (open symbols in Fig. 4E) are given in table S3.

Data integrity

As a measure of data integrity, we computed the whole-brain stiffness for each individual scan and the group average for each modulation frequency of the stimulus. The stability of these measurements is presented in Fig. 6. There are no statistically significant differences between any two interleaved acquisitions, demonstrating the validity of our approach to compare stiffness maps obtained from a single scan. Also, while there is a trend, there is no statistically significant difference between experiment and control scans. The trend is most likely a result of prolonged anesthesia and, hence, changes in hemodynamics, as total study duration was about 2.5 hours with the control scan always done at the end (39). As a result, the only quantitative comparisons made in the data reported here are between interleaved maps acquired in a single scan. Because of edge effects and smoothing in the reconstruction, the central slices have the highest quality. As we always averaged three slices of the elasticity maps to improve SNR, the three slices that were averaged are the three central slices of the nine slices acquired. Data reported in Fig. 6 therefore only use the three central slices.

Fig. 6. Quality Assurance (QA) measures of fMRE data.

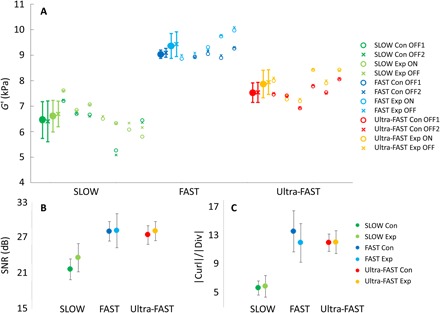
(A) Average G′ from the entire brain shown for each individual animal study (open symbols) and for the average over all animals (closed symbols). “Con” and “Exp” stand for control and experiment, respectively. (B) SNR in decibel averaged over all animals for each stimulus switching frequency. (C) Average value of the magnitude of curl/divergence over the entire brain subsequently averaged over all animals in each stimulus switching speed. Note that nine slices were measured; however, the analysis here uses only the three central slices. Derivative calculations and necessary smoothing processes for the reconstruction reduce the data quality of the edge slices, and therefore, only the three central slices were used for all results reported here as they have the highest quality.

We do however observe global changes between the SLOW, FAST, and Ultra-FAST acquisition, which can be traced back to subtle differences in SNR (Fig. 6B) and, consequently, quality (Fig. 6C). Here, quality was quantified by the ratio of the magnitude of the curl over the magnitude of the divergence of the displacement field. Since tissue is incompressible, the divergence should be close to zero, while the curl carries the shear signal that we exploit to calculate the complex shear modulus. Apparently, the SLOW acquisition exhibits the lowest SNR and quality, while the FAST data have the best quality. This difference in quality is directly reflected in changes in overall stiffness as the reconstruction of the complex shear modulus is sensitive to noise. Consequently, at this point, we do not compare absolute stiffnesses from different switching frequencies.

Statistical significance

In addition to the P values determined using parametric statistics and quoted in the main manuscript, we also evaluated the statistics with nonparametric methods. This is because our sample size was too small to evaluate whether the data were normally distributed. Using an unpaired nonparametric Wilcoxon rank sum test, P values for the experiment scan SLOW, FAST, and Ultra-FAST data shown as open symbols in Fig. 4E are 0.012, 0.014, and 0.004, respectively. The reason an unpaired test was used is because we did not have complete datasets for all animals and the unpaired statistics allows one to use all the data.

Animal preparation

Healthy adult C57BL/6 mice were used for the experiments. Animals were housed in a climate-controlled room with a 12-hour light/12-hour dark cycle and offered food and water ad libitum. All experiments were conducted in accordance with the local IACUC. For imaging, anesthesia was induced using 2% isoflurane in a 100% oxygen mixture, after which the animal was transferred to a custom apparatus, previously described (14) to provide mechanical oscillation at 1000 Hz to the head. The animals’ eyes were lubricated immediately after induction of anesthesia, and gel was placed in both ears to reduce possible stimulation of the auditory cortex from MRI scanner noise. Note that even if auditory stimulation is present and produces viscoelastic changes, it would be a constant shift in stiffness that is present in all scans, both experiment and control. A brief description of the custom MRE apparatus is as follows. The animal was placed prone with its neck placed between two posts that are part of a cradle holding the head. The head was pushed firmly against the posts by a nose cone that is not only free to slide axially but also tensioned with an elastic band to squeeze the snout toward the posts. The entire cradle is held on pivot points and allowed to rotate from a linear mechanical oscillation provided by a plastic rod connected to an external vibration source. The amplitude of the mechanical shear waves induced in the mouse is typically less than 3 μm. A 2-cm-diameter surface coil, used for reception of the MRI signal, was held in place a few millimeters above the mouse head by a stationary frame. The animal can breathe spontaneously. The respiratory rate was constantly monitored, and the isoflurane level was maintained at ~1.5% with adjustments to keep the respiration rate between 40 and 70 breaths per minute.

Two 30-gauge hypodermic needles were inserted into the hind limb foot pad to deliver the electrical current stimulation pulses. In most cases, the right hind limb was used. Occasionally, however, a digit twitch was not observed, and the needles were then placed in the left limb. For these cases, the right/left orientation was switched so that all images appear as if the stimulation was on the right. The images were displayed in radiological coordinates such that the contralateral or left side is always displayed on the right side of the MRE maps.

Code availability

Standard routines were used to perform phase unwrapping of the MRI complex data and to compute the complex Fourier component at the mechanical excitation frequency, which is the complex valued displacement vector. The elastography reconstructions were performed as described in Fovargue et al. (12).

Data availability

Data are available at https://force.isd.kcl.ac.uk/index.php/s/oeMHlJo58frfgSd using the password “FMREdata.” A README file describing the files is provided. Briefly, the data provided were the real and imaginary reconstructed MRI data in Bruker “2dseq” format for all eight wave phases, the phase unwrapped data used as input for the elastography reconstruction, and the complex G′ and G″ reconstructions.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/4/eaav3816/DC1

MRE pulse sequence

Animal experimental results

The cingulate gyrus region does not include major blood vessels

Fig. S1. Schematic of the fMRE pulse sequence.

Fig. S2. Location of blood vessels compared to location of stiffness increase in the cingulate/retrosplenial gyrus region.

Table S1. Each animal study included both an experiment and a control scan.

Table S2. Averaged ROI differences.

Table S3. Individual animal ROI differences.

Movie S1. Video of Hind Limb Electrical Stimulation.