Predicting the variable ocean carbon sink

The oceanic uptake of CO₂ varies substantially in time; here, we show that we can predict this uptake 2 years into the future.

Abstract

Strong decadal variations in the oceanic uptake of carbon dioxide (CO₂) observed over the past three decades challenge our ability to predict the strength of the ocean carbon sink. By assimilating atmospheric and oceanic observational data products into an Earth system model–based decadal prediction system, we can reproduce the observed variations of the ocean carbon uptake globally. We find that variations of the ocean CO₂ uptake are predictable up to 2 years in advance globally, albeit there is evidence for a higher predictive skill up to 5 years regionally. We further suggest that while temperature variations largely determine shorter-term (<3 years) predictability, nonthermal drivers are responsible for longer-term (>3 years) predictability, especially at high latitudes.

INTRODUCTION

The strength of ocean carbon uptake together with the land carbon uptake determines the fraction of anthropogenic emissions remaining in the atmosphere and hence modulates present and future warming (1, 2). To meet the terms of the Paris Agreement, the undersigning parties have adopted the mitigation goal of limiting surface warming below 2.0°C and even pursuing a limit of 1.5°C relative to the preindustrial level and the use of quinquennial global stocktakes to track the long-term mitigation efforts (3). One essential challenge in the context of meeting the agreed climate targets of the Paris Agreement is to understand and predict near-term variations of the ocean carbon uptake under a changing climate, as well as to constrain uncertainties of the projected carbon uptake (4, 5). While predictive skill for key physical climate variables has been well established over the past decade (6–9), predictions of the near-term evolution of the ocean carbon sink (10, 11) and the related ocean biogeochemistry (12, 13) are only starting to emerge. Consequently, there is a gap in our understanding of the drivers and the time scales of the predictability of the ocean carbon sink variations. Previous studies on ocean CO₂ uptake using Earth system model (ESM)–based decadal predictions systems (10, 11) revealed a potential predictability (i.e., predictive skill was verified against the respective model simulations instead of observations) of up to 7 years. These studies, however, were limited to the internally consistent model environments and did not confront the attained predictive skill against observational products. In this study, we move a step further to compare our model predictions with observation-based estimates of the ocean carbon uptake and further investigate the mechanisms maintaining predictive skill.

Recent observational studies have suggested that large decadal variations in the ocean CO₂ uptake (14–16) are insufficiently represented in state-of-the-art ESM simulations, thereby challenging the validity of such an internally consistent skill assessment performed in previous studies (10, 11). ESM-based large ensemble simulations have been identified as potential tools for assessing the observed variability of the ocean carbon sink (17), underlining the importance of initial states. Yet, as of now, we still lack understanding of (i) whether the observed variations in the ocean CO₂ uptake can be reproduced by ESMs starting from initial states that are close to observations; (ii) to what extent the observed variations are predictable; and (iii) what the drivers of predictability are.

We address the knowledge gaps outlined by the above questions by assimilating observational/reanalysis data products into a higher-resolution configuration of the Max Planck Institute (MPI)–ESM (MPI-ESM-HR) (18) and show that observed decadal variations of the ocean CO₂ uptake are reproduced in the model. These variations are predictable up to 2 years in advance globally, owing to improvements of the initialization mean state and phase of the climate system. We find even higher predictive skill regionally, of up to 5 years with significantly improved skill in major CO₂ sink regions such as the North Pacific and the Southern Ocean.

RESULTS

We analyze three sets of simulations from the MPI-ESM-HR decadal prediction system to quantify predictive skill for the ocean CO₂ uptake: (i) an assimilation simulation in which the three-dimensional (3D) atmospheric and oceanic physical states are restored toward observational/reanalysis products (19–22); (ii) an ensemble of five initialized retrospective predictions, i.e., 10-year-long prediction simulations starting from the assimilation run; and (iii) an ensemble of five uninitialized simulations, i.e., continuous historical simulations, used as a reference to quantify the improvement of predictive skill of ocean carbon sink in the initialized simulations due to initialization. Note that there is no assimilation of any observational data of carbon cycle variables. Therefore, the observed variations are introduced to the ocean carbon cycle only through the perturbations of the ocean physics due to assimilation. Details of the simulations are summarized in Materials and Methods and table S1. Previous decadal prediction systems based on a lower-resolution configuration of the MPI-ESM have succeeded in predicting different features of the Earth system, such as the temperature and the meridional overturning circulation (6). The MPI-ESM-HR shows improvement of atmospheric dynamics in the extra-tropics and ocean dynamics in the tropics relative to the low-resolution model, which makes it more suitable for making predictions (18).

Our analysis is designed as follows. As an observation-based benchmark of predictive skill, we use the SOM-FFN (self-organizing map–feed-forward network) estimates of the global air-sea CO₂ flux for the period of 1982–2015 (15). The SOM-FFN estimate is based on the largest available collection of surface ocean CO₂ observations (23) and well represents the variations in the ocean carbon cycle due to internal and forced variations of the climate system and anthropogenic emissions (24). In addition, this observational product has been extensively evaluated (15) and widely used in recent studies (14, 16, 25) to address questions related to the ocean CO₂ uptake variability. The initial shock and model drift is often an issue of decadal predictions (26); the carbon cycle also shows an initial shock in the initialized simulations when the model starts from initial states of the assimilation and runs freely (see fig. S1). As suggested by the Decadal Climate Prediction Project (DCPP) for the sixth Climate Model Intercomparison Project (CMIP6) (26), the anomalies relative to their respective climatological means, which correct the different mean states, should be considered for comparing model predictions with observations. Therefore, we remove the climatological means and consider the time series of the anomalies for the respective statistics in this study. We show mainly ensemble mean results, and predictive skill is quantified on the basis of the anomaly correlation coefficient. We use a nonparametric bootstrap approach (27) to assess the significance of predictive skill (see Materials and Methods for details). The spatial maps of predictive skill were calculated for the time period 1982–2013 with the MurCSS tool (28).

Our assimilation simulation reproduces the decadal variations of the global ocean CO₂ uptake suggested by the SOM-FFN product, illustrating a steady CO₂ flux in the 1980s and 1990s, followed by a strong intensification of the uptake in the subsequent decade (Fig. 1). This prominent decadal variation of the strength of the ocean CO₂ uptake (i.e., weakening uptake in the 1990s and strengthening uptake in the 2000s) simultaneously occurs in all major sink regions, such as the North Pacific, the North Atlantic, and the Southern Ocean (fig. S2). While the uninitialized historical simulation can adequately simulate the forced trend of the ocean CO₂ uptake, the observed decadal variations are suppressed (Fig. 1 and fig. S3 showing detrended time series). The predictability of the ocean carbon uptake from ensembles of predictions, i.e., the initialized simulations, starting from the assimilation states, which are close to observations, shows that the model still retains the memory of decadal variations for 2 years globally, highlighting a 2-year predictability horizon compared to the observation-based estimates (Fig. 1B). The potential predictive skill, i.e., when the prediction is verified against the assimilation simulation, is in general higher (Fig. 1C), which is consistent with our previous results (10, 11). Analysis of the detrended time series also shows similar results (fig. S3); the correlation between the second lead year predictions and the data-based estimates is increased from 0.71 to 0.81. The initialized run produced a stronger trend (0.04 Pg C year⁻²) than the observation-based estimates (0.02 Pg C year⁻²). This trend difference and the increasing dominance of trend relative to multiyear variations in the initialized run lead to a lower correlation of the original time series between the initialized run and the observation-based estimates. This suggests that the initialized runs, in addition to tracking the atmospheric CO₂ growth, are capable of maintaining the observed multiyear variations of ocean carbon sink strength for some years. The detrended correlations between the initialized simulation and the assimilation (fig. S3C) are smaller than the detrended correlations between the initialized simulations and the SOM-FFN data–based estimates (fig. S3B). This is because the initialized simulation and the assimilation share a similar long-term trend (see Fig. 1A, black and red dotted curves) induced by the anthropogenic forcing that is removed by the detrending. The detrended correlations between the initialized simulations and the assimilation are still significantly larger than the correlations between the uninitialized simulations and the assimilation until a lead time of 3 years (fig. S3C). This further confirms that the multiyear predictability of the carbon cycle originates predominantly from the multiyear to decadal variations in the ocean carbon uptake, not from the near-linear trend due to the increasing CO₂ uptake following the increasing anthropogenic CO₂.

Fig. 1. Temporal evolution and predictive skill of the global CO₂ flux into the ocean.

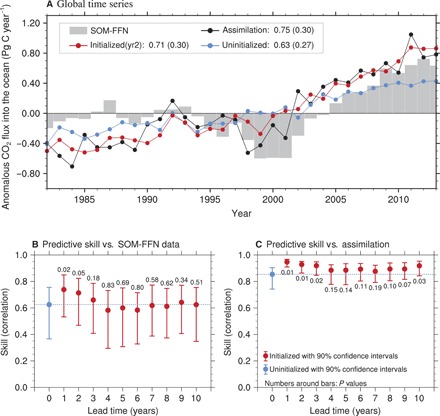
(A) Time series of anomalous CO₂ flux into the ocean from SOM-FFN data–based estimates (15) and MPI-ESM simulations with respect to the climatological mean. Gray bars show SOM-FFN data. Assimilation, initialized simulation at a lead time of 2 years, and uninitialized simulations are shown in black, red, and blue, respectively. Here, the anomalies refer to conditions in which the respective climatological means are removed, and the positive values indicate anomalous uptake of CO₂ by the ocean. The numbers show the correlation coefficients and root mean square error (in parentheses) against SOM-FFN data. (B) Correlation skill of the global CO₂ flux into the ocean against SOM-FFN data–based estimates. The blue dot and red dots show the uninitialized correlation and initialized correlation at different lead years, respectively. The blue dashed line extends the uninitialized correlation for easy comparison. The vertical bars provide 90% confidence intervals, and the numbers above the bars show the P values based on a bootstrap approach (27). (C) The same as (B), but for correlation skill against assimilation.

The dynamics of the CO₂ flux between the atmosphere and the ocean is mainly driven by the air-sea difference of pCO₂, i.e., ΔpCO₂ = pCO₂^sea − pCO₂^atm, with pCO₂^sea being the main driver for the variability in the carbon fluxes (14, 29). Here, the predictive skill of ΔpCO₂ at a lead time of 2 years (Fig. 2) is similar to that of the air-sea CO₂ flux (fig. S4). The coherent regional predictive skill of the ocean CO₂ uptake is indicated by the high correlations of both the assimilation and the SOM-FFN data–based estimates with the initialized simulations (Fig. 2, A and B). The correlations with the uninitialized simulations are lower (Fig. 2, C and D), indicating an improvement due to initialization. This improved predictability within the model framework is also visible spatially with improved predictive skill at a lead time of 2 years (Fig. 2F) being present in the most ocean areas. While the globally integrated variations of the air-sea CO₂ fluxes are notably improved (Fig. 1) due to initialization, the spatial patterns are rather inhomogeneous when the same predictive skill tests are applied and compared to the observation-based SOM-FFN estimate (Fig. 2E). Significant improvement due to initialization is found in the Southern Ocean and the North Pacific, but not in the North Atlantic, where the variations are already captured quite well in the uninitialized simulation (Fig. 2C).

Fig. 2. Predictive skill of the ΔpCO₂ (pCO₂^sea − pCO₂^atm) at a lead time of 2 years.

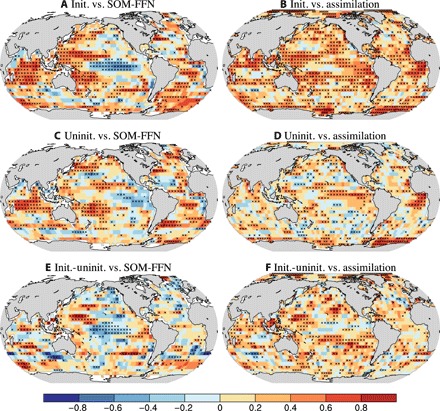
We show skill against SOM-FFN data–based estimates (left panels: A, C, and E) and against assimilation (right panels: B, D, and F). First row: Correlations with initialized simulations. Second row: Correlations with uninitialized simulations. Third row: Difference of the correlations between initialized and uninitialized simulations. The values are computed over the years from 1982 to 2013 with the MurCSS tool for central evaluation of predictive skill (28). Crosses denote significant skill at the 95% confidence level based on a bootstrap approach (27).

The regionally varying predictive skill suggests that there is a contribution of different underlying mechanisms in different regions. Therefore, it is plausible that the observed reduced spatial skill when compared to the SOM-FFN product results from a misrepresentation of the individual drivers contributing to the CO₂ flux. We attribute the drivers of the ocean CO₂ uptake into thermal and nonthermal components [analogous to (14, 30)], where pCO₂^sea is mainly affected by CO₂ solubility (thermal), ocean circulation, and biology (nonthermal). These components are 6 months out of phase for most of the global ocean (30). This is also reproduced in the monthly time series of the ΔpCO₂ and its thermal and nonthermal components from the SOM-FFN product, shown in fig. S5. To separate the terms, we use the temperature sensitivity of 0.0423°C⁻¹ (31) and the modeled temperature variations to isolate the thermal and nonthermal components (see Materials and Methods). Note that the two components are scaled according to their respective effects; therefore, they are not additive. The decadal trend patterns within the individual components of the assimilation run resemble those of the SOM-FFN data–based estimates (figs. S6 and S7). The MPI-ESM decadal prediction system reveals higher predictive skill, of the same order of magnitude as found for the ΔpCO₂, of the individual thermal and nonthermal components (Fig. 3). The spatial pattern of the thermal and nonthermal correlations is, in general, similar with high correlations almost everywhere. This suggests that lower spatial predictive skill in the total flux can be attributed to a mismatch in the relative dominance of the individual components, while the representation of the ocean carbon cycle drivers is very well captured. The correlations of the thermal component with the SOM-FFN estimates (Fig. 3, left column) and the assimilation (fig. S8, left column) are very similar. This reflects the imprint of the predictive skill of sea surface temperature.

Fig. 3. Predictive skill of ocean surface pCO₂ thermal and nonthermal components at a lead time of 2 years.

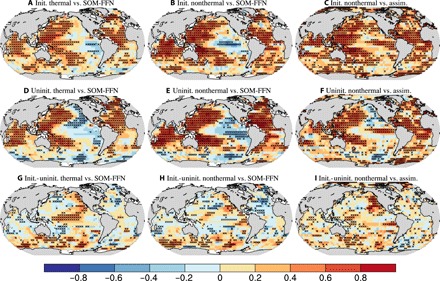
Columns 1 (A, D, and G) and 2 (B, E, and H) show the correlations between the initialized simulations and SOM-FFN data–based estimates for the thermal and nonthermal components, respectively. Column 3 (C, F, and I) shows the nonthermal part correlation between the initialized simulations and the assimilation. First row (A–C): Correlations with initialized simulations. Second row (D–F): Correlations with uninitialized simulations. Third row (G–I): Difference of the correlations between the initialized and uninitialized simulations. The values are computed over the years from 1982 to 2013 with the MurCSS tool for central evaluation of predictive skill (28). Crosses denote significant skill at the 95% confidence level based on a bootstrap approach (27). The thermal component correlation is based on pCO₂^sea, and the nonthermal component correlation is based on ΔpCO₂ (pCO₂^sea − pCO₂^atm) (14).

The results presented above are based on a lead time of 2 years, while regionally, the predictability horizon of ocean CO₂ uptake and the relative contribution of its separate regulation drivers is higher. The ΔpCO₂ (Fig. 4, A and B) shows unique patterns of lead years with a dominance of the nonthermal component (Fig. 4, E and F), especially for the skill against the assimilation run and in the high latitudes, where the nonthermal component dominates the pCO₂ variability [see (30)]. In the North Pacific and the Southeastern Pacific, the improved skill is retained for up to 5 years (Fig. 4, A and B), while the thermal component shows relatively long lead times of predictability, mainly in the mid-high latitude of the Southern Ocean (Fig. 4, C and D). The zonal mean predictability horizon, i.e., lead years with improved predictive skill, shows longer predictive skill of the nonthermal component than the thermal component, particularly for the potential predictive skill against assimilation and for the regions at high latitudes (Fig. 4, G and H). This suggests the importance of the nonthermal component of the ocean CO₂ uptake in potentially maintaining predictability longer than 3 years, while the temperature-driven component only maintains predictability that is shorter than 3 years in the middle to low latitudes.

Fig. 4. Lead years with improved skill.

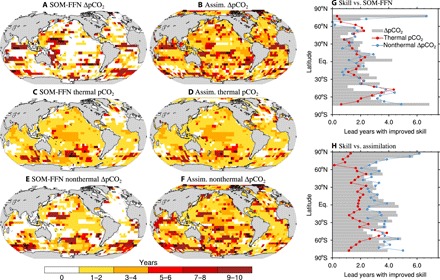
Left maps: The spatial pattern of the lead years with improved skill for ΔpCO₂ (A and B) and its thermal (C and D) and nonthermal (E and F) components, i.e., when correlations of the initialized simulations are larger than 0 and are larger than the uninitialized simulations, against SOM-FFN data–based estimates (left) and the assimilation (right). Crosses indicate that the improved skill is statistically significant at the 95% confidence level for the first 5 lead years. Right bar charts: Zonal mean of lead years with improved predictive skill of ΔpCO₂ (gray bars) and its thermal and nonthermal components (red and blue dotted lines, respectively) against SOM-FFN estimates (G) and assimilation (H).

This first assessment of the predictability of the globally integrated ocean CO₂ uptake based on the MPI-ESM decadal prediction system reveals a predictive skill of 2 years against SOM-FFN observational data–based estimates. We showed for the first time that assimilating 3D ocean and atmosphere physics into an ESM not only improves the predictive skill relative to control simulations but also reproduces the observed decadal variations in the ocean CO₂ uptake. We further illustrate that delineating thermal and nonthermal variabilities in the CO₂ uptake—and thereby removing a potential misrepresentation of the strength of the individual components—further improves our prediction with respect to the observational estimate, highlighting the high potential of our CO₂ prediction system. While the thermal regulation shows predictive skill for time scales shorter than 3 years, the nonthermal regulation of the air-sea CO₂ flux is responsible for maintaining a predictive skill longer than 3 years.

DISCUSSION

Our decadal prediction system provides a powerful tool for monitoring and predicting the future evolution of one of the most important carbon sinks, and hence, our predictions have an implication for understanding the future global carbon cycle and how it might change because of climate change. Decadal prediction studies of the ocean carbon uptake and corresponding processes are still in their early stages, facing a number of challenges arising from limited observations and the substantial uncertainty in observational air-sea CO₂ flux estimates, arising in part from the paucity in the observational coverage and assimilation techniques; yet, their importance is unequivocal to support the stocktaking process and the mitigation efforts of the United Nations Framework Convention on Climate Change (UNFCCC) Paris Agreement. However, to fulfill the protocol of the Paris Agreement aiming at monitoring, verifying, and further revising the nationally determined contributions in every 5 years, further efforts in improving the skill of predicting the carbon cycle in the whole globe and different regions are required. A synthesis of different initialization methods, high-resolution models, and implementation of more comprehensive processes into ESM-based prediction systems (e.g., the interactive carbon cycle and the feedback of ocean biogeochemistry on climate), should contribute toward improving predictability of the global carbon cycle.

MATERIALS AND METHODS

Assimilation and preassimilation for ocean biogeochemistry

The assimilation is through nudging observations into the ESM. The following observational products/reanalysis data are used for the assimilation: for the atmosphere, 3D full-field temperature, divergence, vorticity, and surface pressure from the European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis ERA40 (19) and ERA-Interim (20); and for the ocean, 3D anomalous temperature and salinity from the ECMWF Ocean Reanalysis System 4 (21) and sea-ice area fraction from the National Snow and Ice Data Center (NSIDC) satellite observations (22). Comparison of anomaly initialization versus full-field initialization of the ocean component suggested that the anomaly initialization outperforms the full-field initialization with regard to the ocean heat budget in the North Atlantic subpolar gyre region (32).

As ocean carbon cycle observations are not assimilated, the ocean biogeochemistry tracers only adjust to the variations of ocean physics due to assimilation. The ocean biogeochemical processes need a longer time of around 20 years for the surface variables to adjust to the new assimilated physical climate state. To eliminate the spurious trend due to the adjustment of the ocean biogeochemistry at the beginning of the assimilation run, we performed an additional preassimilation run for ocean biogeochemistry of around 50 years. In this preassimilation, we fixed the CO₂ forcing for ocean biogeochemistry to the value at the beginning of the assimilation run (year 1958). The atmospheric and ocean dynamics are nudging toward the ECMWF reanalysis data and NSIDC observations as in the assimilation. The restart files of ocean biogeochemistry in the preassimilation were used to start the assimilation. We reduced the silicate and dissolved inorganic carbon concentration globally according to observations so that the magnitude of the global ocean carbon sink is close to observations. This only alters the climatology, not the multiyear variations of the ocean biogeochemistry. The tuning of ocean biogeochemistry during assimilation is transferred to the initialized simulations via initialization from the assimilation. It is unnecessary to tune the uninitialized simulations in which the model was run freely.

Predictive skill quantification

The predictive skill of ocean CO₂ uptake is represented by the anomaly correlation coefficient of model retrospective predictions against the SOM-FFN data. The anomalies were calculated by removing the climatological mean of the ensemble mean for the uninitialized simulations. For the initialized simulations, the anomalies were calculated with respect to the climatological mean of the ensemble members and the lead time. In addition, we estimated the potential predictive skill shown as correlations of the model predictions against the assimilation run to represent the potential upper limit of the predictability and to interpret the possible inconsistencies between the modeled and observed variabilities of CO₂ uptake. Furthermore, we also estimated an improved predictive skill due to initialization, which is expressed as the difference of correlations between the initialized and uninitialized simulations.

We used a nonparametric bootstrap approach, which was introduced by Goddard et al. (27) and is widely used in the decadal prediction studies, to assess the significance of predictive skill. In general, the bootstrap approach resamples the occurrence of the existing ensembles of simulations and obtains a probabilistic distribution of the correlations.

To generate the probability distribution of predictive skill, we resampled the model simulations and the observations regarding the ensembles (five members) and time steps (32 years from 1982 to 2013); the sample size was up to 160 (i.e., five members times 32 years). We used U_mt, I_mt, and O_t to represent the mth member and tth time step of the uninitialized simulation, the initialized simulation, and the observation/assimilation, respectively. The m is from 1 to 5, and the t is from 1 to 32. For each resampling, a new ensemble is generated by random selection from the five ensemble members and the 32-year time series with replacement. To ensure a fair comparison, the initialized simulations and the uninitialized simulations are resampled in pairs using the same resample indices. The correlations are calculated with the resampled ensemble mean. We repeated this process 1000 times to generate a large sample covering the probability of the predictive skill.

Significance tests, i.e., P values, were calculated according to the null hypothesis, i.e., the difference of correlations (C_d) between the initialized and uninitialized simulations is smaller or equal to zero. We combined the five initialized and the five uninitialized simulations together, resampled the ensemble members, and then divided the 10 ensemble members back into two ensembles each with five members. On the basis of the two new ensembles, we did the resampling by random selection from the 32-year time steps with replacement, calculated the correlation difference between the two new ensembles, and compared it with the C_d. This process was also repeated 1000 times to check whether there was a possibility to generate correlation difference as large as that in the initialized and uninitialized simulations based on random resamples.

The spatial maps of predictive skill were produced with the MurCSS tool (28). This is a central evaluation tool developed according to the framework for decadal prediction skill assessment suggested by Goddard et al. (27).

Thermal and nonthermal components of ocean surface pCO₂

We separate the ocean surface pCO₂ to thermal and nonthermal components following (30)

$${\text{pCO}}_2,\text{therm} =\overline{{\text{pCO}}_2}\cdot {\mathit{e}}^{[0.0423\cdot (\mathit{T}-\overline{\mathit{T}}\left)\right]}$$ (1)

$${\text{pCO}}_2,\text{nontherm} ={\text{pCO}}_2\cdot {\mathit{e}}^{[0.0423\cdot (\overline{\mathit{T}}-\mathit{T}\left)\right]}$$ (2)

Here, T is the sea surface temperature. The constant is according to the ratio between ocean surface pCO₂ and temperature $\frac{\partial \text{ln} {\text{pCO}}_2}{\partial \mathit{T}}=0.0423°{\mathrm{C}}^{-1}$. $\overline{{\text{pCO}}_2}$ and $\overline{\mathit{T}}$ refer to climatological mean pCO₂ and T. For the thermal component, the effects of temperature changes on pCO₂ are expressed by perturbing the climatology mean pCO₂ with observed temperature anomalies. For the nonthermal component, these temperature anomaly effects are removed by normalizing the evolution of pCO₂ to the climatology temperature. Therefore, the thermal component represents the pCO₂ variations affected by temperature, and the nonthermal component represents the pCO₂ variations, which are affected by circulation and biology changes via modifying the surface concentration of dissolved inorganic carbon, alkalinity, and nutrient. The National Oceanic and Atmospheric Administration (NOAA) Optimum Interpolation Sea Surface Temperature V2 (33) was used for the thermal and nonthermal component separation of the SOM-FFN data–based estimates of ocean surface pCO₂. The ΔpCO₂ of the SOM-FFN data–based estimates was calculated relative to the atmospheric pCO₂ based on the zonal mean dry air mixing ratio from the NOAA marine boundary layer reference (34).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/4/eaav6471/DC1

Fig. S1. Time series of the CO₂ flux into the ocean from MPI-ESM-HR simulations.

Fig. S2. Decadal trends of CO₂ flux into the ocean.

Fig. S3. The same as Fig. 1, but for detrended global CO₂ uptake by the ocean.

Fig. S4. Predictive skill of the air-sea CO₂ flux at a lead time of 2 years.

Fig. S5. Monthly ocean surface pCO₂ (gray bars) and its thermal (red) and nonthermal (blue) components.

Fig. S6. Decadal trends of ΔpCO₂ (pCO₂^sea − pCO₂^atm) and its thermal and nonthermal components from 1992 to 2001.

Fig. S7. The same as fig. S6, but for 2002–2011.

Fig. S8. Predictive skill of pCO₂ thermal and nonthermal components at a lead time of 2 years against assimilation.

Table S1. Summary of the simulations used in this study based on the MPI-ESM-HR decadal prediction system.