Abstract
The rate of complete resection of glioma has improved with the introduction of 5-aminolevulinic acid-induced protoporphyrin IX (ALA-PpIX) fluorescence image guidance. Surgical outcomes are further enhanced when the fluorescence signal is decoupled from the intrinsic tissue optical absorption and scattering obtained from diffuse reflectance measurements, yielding the absolute PpIX concentration, [PpIX]. Spatial frequency domain imaging (SFDI) was used previously to measure [PpIX] in near-surface tumors under blue fluorescence excitation. Here, we extend this to subsurface [PpIX] fluorescence under red-light excitation. The decay rate of the modulation amplitude of the fluorescence signal was used to calculate the PpIX depth, which was then applied in a forward diffusion model to estimate [PpIX] at depth. For brain-like optical properties in phantoms with PpIX fluorescent inclusions, the depth can be recovered up to depths of 9.5 mm ± 0.4 mm, with [PpIX] ranging from 5 to 15 μg/ml within an average deviation of 15% from the true [PpIX] value.
Keywords: spatial frequency domain, quantitative fluorescence, depth-resolved fluorescence imaging, protoporphyrin IX, glioma
Introduction
The survival and quality of life of glioma patients depend critically on the extent of surgical resection [1], with significant benefit only if >90% and >70% of the MRI-enhancing tumor is removed in high- and low- grade gliomas, respectively [1]. Fluorescence-guided surgery (FGS), incorporating fluorescence into the neurosurgical microscope, yields higher complete-resection rates without interrupting the surgical workflow [2], using the endogenous fluorophore protoporphyrin IX (PpIX) following oral dose of 5-aminolevelunic acid (ALA). The violet/blue light at 405 ± 5 nm that is used to excite the red PpIX fluorescence limits detection to ~1 mm below the resection surface [3]. New near-infrared fluorophores are under investigation for surgical guidance in a variety of tumor types [3] that would address this limitation. Nevertheless, the high tumor specificity and metabolic targeting of ALA-PpIX are of value, motivating the use of red-light excitation FGS, as we recently reported in patients with various intracranial tumors [4]. That study demonstrated enhanced tumor resection by enabling detection of sub-surface PpIX fluorescence up to ~5 mm depth [4].
Visual assessment of red-excitation PpIX fluorescence has limited sensitivity, since the PpIX absorption is 1–2 orders-of-magnitude lower than at 405 nm. The detected fluorescence intensity depends strongly also on the depth, so that strong fluorescence at depth cannot easily be distinguished from weak fluorescence at or just below the surface. Hence, the objective here is to enhance red-excitation PpIX-mediated FGS by converting the raw fluorescence images to quantitative topographic images, whereby the subsurface tumor depth is determined as well as the absolute fluorophore concentration at that depth that correlates with the degree of malignancy [5]. This method is termed quantitative depth fluorescence imaging, qDFI. Previous clinical studies using a point-spectroscopic approach to quantify the PpIX concentration at the surface of the resection bed have shown significant improvements in sensitivity and specificity of detecting residual tumor, both for high-grade [6] and low-grade glioma [7]. The detection of subsurface tumor may also be generally applicable, both in neurosurgery (e.g. to detect tumor extending below the resection bed) and in other organs (e.g. head & neck) where sensitive and accurate location of subsurface tumor is of value even prior to the start of resection. qDFI is enabled by exploiting the quantitative and depth-resolving properties of spatial frequency domain imaging (SFDI) [8], a form of diffuse optical imaging in which white-light that is spatially modulated at predetermined spatial frequencies is projected onto the tissue surface. The spatially-resolved diffuse reflectance images as a function of spatial frequency are used in a light transport model to extract the tissue absorption (μa) and reduced scattering coefficient () in the form of 2D maps [8]. We have previously shown that quantitative fluorescence imaging (qFI) under blue-light excitation and enabled by SFDI can recover 2D surface (<1 mm depth) images of [PpIX] in an intracranial rat tumor model with 90% accuracy and with a minimum detectable [PpIX] of 13 ng/ml [9]. The depth-encoding capability of SFDI arises from tissue acting as a low-pass filter, the modulated light at high spatial frequencies being attenuated faster than at low frequency [8]. Hence, varying the frequency effectively samples the tissue at different depths. To encode the fluorophore depth, SFDI can be implemented in fluorescence mode, i.e. the excitation light is spatially modulated, and the spatially-resolved fluorescence images are collected at multiple spatial frequencies.
The first demonstration of SFDI-enabled depth-resolved fluorescence imaging was by Konecky et al [10] using red-light SFDI to excite PpIX in sub-surface intracranial tumors in mice and used to recover the PpIX concentration [11]. However, the tumor depth had to be known a priori. Here, we measure the fluorescence modulation amplitude as a function of spatial frequency to determine the tumor depth. With this information, and after recovering the tissue optical properties from white-light SFDI, a diffusion-based forward model is applied to the raw fluorescence images to decouple the PpIX depth and concentration.
2. Methods
2.1. Instrumentation
The hyperspectral fluorescence imaging system combined with SFDI has been described in detail elsewhere [12,13]. Briefly, 6 LED sources (390, 440, 475, 512, 586 and 632 nm with 20 nm bandwidth) are used to simulate white-light SFDI to map the tissue optical properties [8]. In fluorescence mode, only the 632 nm LED is activated. The light is reflected by a spatial light modulator onto the sample. For detection, a visible-range liquid crystal tunable filter is coupled to a 14-bit CCD detector array, rendering a field-of-view of 5 cm by 5 cm with 2 cm depth of view at the focal plane. A 650 nm long-pass filter is used to block the incoming red excitation light during fluorescence imaging, which requires 100 to 1000 ms, depending on the fluorophore depth. Diffuse reflectance images are acquired in 50 ms per spatial frequency per wavelength. Six patterns are projected sequentially at spatial frequencies of 0, 0.05, 0.1, 0.2, 0.27 and 0.38 mm−1 and spectrally-resolved images are collected for each.
2.2. Tissue-simulating phantoms and ex vivo tissue model
Tissue-simulating liquid phantoms with PpIX inclusions (3.2 mm inner, 4.8 mm outer diameter glass capillaries) were used to determine the accuracy in recovering the PpIX depth and concentration (Supplementary information and Table S1). The sub-surface depth was varied by removing or adding liquid, keeping a fixed distance between the instrument and the inclusion. Each phantom was prepared and imaged in triplicate. Minced bovine muscle was then used to test the performance under more realistic biological conditions. The tissue was pressed into a similar container and a thin cylindrical inclusion (1.6 mm inner, 3.2 mm outer diameter) containing a fixed PpIX concentration (5 μg/ml) was placed on top. Additional tissue covered the inclusion to 3 different depths (2.5, 4.5, 9 mm) and triplicate images were collected at each depth.
2.3. Modeling of fluorescence imaging in the spatial frequency domain.
Sub-surface imaging was modeled as a point fluorescent source in a semi-infinite diffusive medium with an air-tissue boundary, for which the detected signal is [13]:
| (1) |
, where each term is defined in Table 1. The factor is removed by measuring the fluorescence with a known fluorophore concentration under the same imaging conditions. Knowing μax,m and at, λx and λm, The steady-state diffusion equation with an extended light source normally incident on a semi-infinite homogenous medium is used to solve for φx for a known source depth, zs [13]. Σm (ρ, z = zs) is then determined for all radial distances, in turn solving for fm (ρ) [13].
Table 1.
Parameter definitions
| Parameter | Description |
|---|---|
| ρ (cm) | radial distance from source |
| Ω (sr) | camera acceptance angle |
| irradiance at the excitation wavelength λx | |
| zs (cm) | Distance between the phantom surface and the top of the fluorescent inclusion. Subscript s indicates one unknown depth |
| excitation fluence rate at zs | |
| S (cm−1) | product of the fluorophore absorption coefficient and fluorescence quantum yield |
| Σm | fluorescence emission escaping at the surface at a radial distance ρ from the point source at zs |
| fluorophore concentration | |
| λx and λm (nm) | excitation and emission wavelengths |
| fx (mm−1) | spatial frequency |
| Mf (x,y,fx)z | fluorescence modulation amplitude at fx and for a given depth z |
| source intensity | |
| MTFsystem (x,y,fx)z | system total modulation transfer function at fx and z |
| Fm (x,y,fx)z | predicted spatially-resolved diffuse fluorescence in the spatial frequency domain for a source at depth z |
2.4. Red SFDI for fluorophore depth.
In fluorescence mode, 632 nm sinusoidal patterns were projected on the sample surface at each spatial frequency and spatial phase (Supplementary information). Planar and SFD fluorescence images were acquired for each depth, integrating over 660–720 nm in steps of 10 nm. A 10 by 20 pixel (~2.4 mm by 4.8 mm) region-of-interest at the center of the inclusion was selected, within which to determine the fluorescence modulation amplitude, Mf (fx), which was then recovered using a demodulation scheme as per Equation S2. Mf depends on both the fluorophore and the imaging system:
| (2) |
At each unknown depth, was calculated, thereby normalizing to the DC modulation amplitude (fx = 0) and rendering this ratio independent of the fluorophore concentration or quantum yield. Using the optical properties from white-light SFDI, Fm (x,y,fx)z can be predicted by diffusion theory. MTFsystem (fx)z was determined experimentally by measuring Mfnorm (fx) from a calibration liquid phantom of known optical properties and fluorophore concentration in the inclusion and predicting Fm (x,y,fx)z. Since MTFsystem (fx)z is predetermined by imaging a reference phantom placed at fixed distances to the detector, the actual MTFsystem (fx)z in the operating room would be recalculated based on the distance between the surgical field and the microscope using a robust registration technique, based for example on optical flow motion tracking applied to the intraoperative stereo images [14].
For an unknown depth zs, Mfnorm (fx) is obtained experimentally. With the pre-determined MTFsystem (x,y,fx)z and Fm (x,y,fx)z, the predicted modulated fluorescence, Mfpredicted (x,y,fx)z, can be obtained from all depths. Mfnorm_predicted (x,y,fx)z is then obtained by dividing the product on the right side of Equation 2 by its value for fx = 0, i.e.
| (3) |
The factor is removed by this normalization step. The result is a look-up table of Fm (fx) values expected from a fluorophore originating from depth z = 0 to 30 mm for each pair of optical properties as determined by white-light SFDI. Least-squares fits were used to find the minimum difference between the measured and the predicted Mfnorm_predicted (x,y,fx)z, yielding zs. Once zs is known, the only unknown in Equation 1 is C, i.e. [PpIX].
3. Results and Discussion
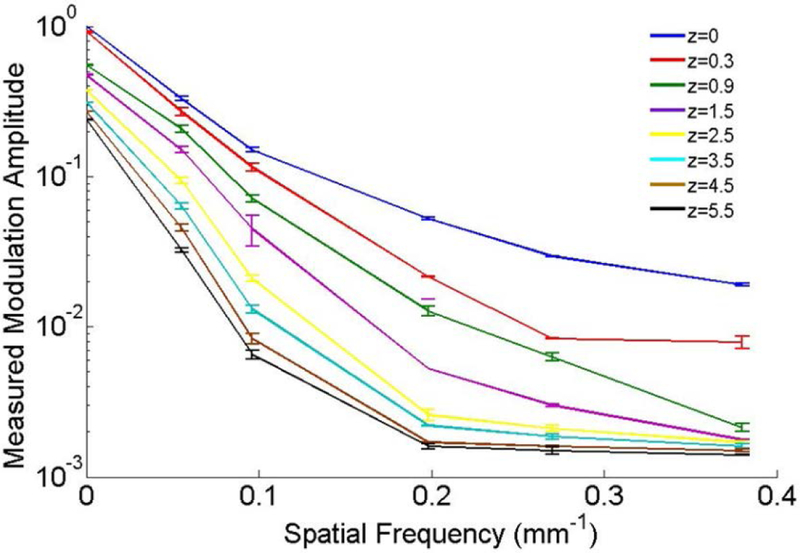
The fluorescence modulation amplitude, Mf (fx), measured in the same phantom with the PpIX inclusion located at different depths is plotted as a function of fx in Figure 1. For clarity, each amplitude is normalized to the modulation at z=0 and fx = 0: however, for qDFI analysis, Mf (fx) is normalized to Mf (0) at the same inclusion depth. As shown below, Mf vs. fx decays faster with increasing inclusion depth because the modulation amplitude becomes less sensitive to high spatial-frequency patterns than at more superficial depths, which is sensitive to both low and high-spatial frequency patterns and so has a slower decay rate. This difference is exploited to recover the subsurface depth.
Figure 1.
The measured normalized fluorescence modulation amplitude vs. spatial frequency for different inclusion depths, z. The inclusion contained 10 μg/ml of PpIX mixed with blood and Intralipid to simulate μa,m= 0.001 mm−1 and μ’s,m= 1 mm−1 at 705 nm. Error bars are the standard deviation across three replicates.
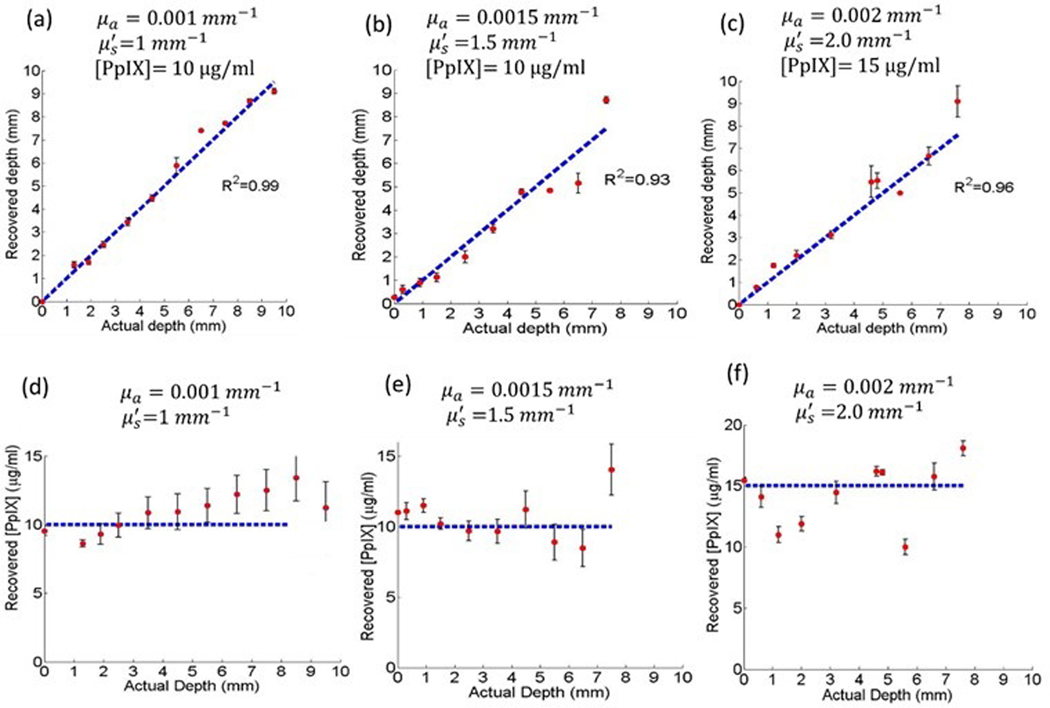
The calculated fluorescent inclusion depths are plotted in Figures 2 (a-c) against the known depths. Interestingly, the agreement was equally good at small depths, likely because the algorithm compares the modulation decay rate over several frequencies rather than the amplitude at only one spatial frequency. The maximum depth that could be determined with high accuracy depended inversely on the tissue turbidity and directly on the fluorophore concentration. The [PpIX] values recovered at each inclusion depth are shown in Figures 2 (d-f) The larger the discrepancy in depth estimation, the larger the discrepancy in recovering the fluorophore concentration.
Figure 2.
(a-c) Recovered depths for phantoms with different optical properties and PpIX concentrations. The best fit to the line of equality is indicated. Error bars are the standard deviation from 3 replicates. (d-f) Recovered [PpIX] for three phantoms with different optical properties and [PpIX] values as indicated by the horizontal dashed lines. Error bars are the standard deviation from 3 replicates.
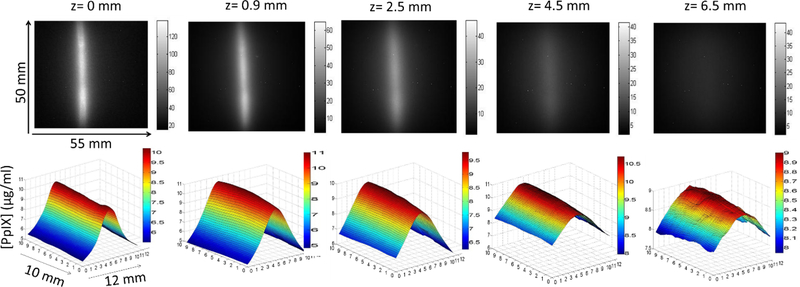
For a minimum signal-to-background ratio of 2 in the fluorescence images, the depth could be recovered to within ± 0.45 mm and [PpIX] values within ±10% of the actual values at 95% confidence level up to a depth of 5–9 mm, depending on the tissue turbidity. The first row in Figure 3 presents an example of the raw fluorescence images for different inclusion depths. The intensity falls to half its original intensity at a depth of 0.9 mm and at 6.5 mm the inclusion is not discernable from the background fluorescence. The quantitative [PpIX] topographic plots (second row in Figure 3) were obtained after applying the qDFI algorithm, where the inclusion boundaries were delineated using the demodulated fluorescence images at higher frequencies that had superior contrast to the diffuse planar images. [PpIX] is accurately reconstructed to within 10% of its nominal value of 10 μg/ml, even at the larger inclusion depths. These plots show also that the lateral resolution deteriorates with depth, as would be expected.
Figure 3.
Top: raw fluorescent images from different depths in the liquid phantom with μa,m= 0.0015, μ’s,m= 1.5 mm−1 and [PpIX]= 10 μg/ml: grayscale bar indicates signal intensity across the 55 mm by 50 mm FOV. Bottom: the reconstructed topographic maps of the [PpIX] within an ROI encompassing the cylindrical inclusion and surrounding medium.
The results for the ex vivo tissue model are summarized in Table 2. The measured tissue optical properties are in the approximate range of brain tissue [15]. The average recovered depths from three ROIs were within 10% of the nominal depths, except at 9 mm where the demodulated images had limited spatial resolution and contrast (signal-to-background = 1.8). The derived PpIX concentrations were within 15% of the actual values for the first two depths, increasing to 40% at the largest depth, at which both the recovered [PpIX] and depth were statistically different from their known values (p <0.05), based on a two-sided t-test.
Table 2.
Estimated depths and [PpIX] in ex vivo tissue with [PpIX] of the inclusion = 5 μg/ml. The measured tissue optical properties were: μax = 0.012 ± 0.0007 mm−1, μ’s,x = 2.74 ± 0.14 mm−1, μa,m= 0.0046 ± 0.00014 mm−1 and μ’s,m= 2.24 ± 0.085 mm−1, * indicates p < 0.05
| nominal depth (mm) | 2.5 | 4.5 | 9 |
|---|---|---|---|
| estimated depth (mm) | 2.30 ± 0.02 | 5.00 ± 0.07 | 6.48 ± 0.03* |
| estimated [PpIX] (μg/ml) | 4.88 ± 0.32 | 6.4 ± 0.85 | 7.04 ± 0.78* |
Table S2 shows the sensitivity of the depth and [PpIX] estimated by qDFI to uncertainties in the measured optical properties, as analyzed using forward-model calculations. The relative uncertainties in the depth are somewhat less than those in μa and μs’, probably because the calculated depth depends on the rate of change in fluence rate as a function of spatial frequency, rather than directly on the optical properties. This is a major advantage of the technique, as small changes in tissue optical properties within the imaged volume will not greatly affect the accuracy in recovering the tumor depth. The depth error then propagates to the [PpIX] estimate. There is, however, an upper concentration beyond which the fluorophore absorption itself may contribute significantly to the total absorption at the excitation wavelength; this was around 18 μg/ml for μa,m =0.002 mm−1 and μs,m’=2.0 mm−1. Not accounting for this added absorption results in overestimating the excitation fluence rate, thereby underestimating the fluorophore concentration.
This work and others [16] demonstrate that modeling the fluorophore as a point-like source rather than as its true cylindrical shape does not undermine the diffuse-fluorescence model. The modulation patterns were projected parallel to the inclusion, so that the demodulated images fully reconstructed it without boundary-induced artefacts. For irregularly-shaped tumors with undefined boundaries there may be an optimum SFDI illumination approach and this is under investigation. Although 1-D SFDI already improves the lateral resolution for imaging sub-surface inhomogeneities (Figure 3) [17], projecting 2-D patterns or an oblique illumination pattern should further enhance the lateral resolution for tumors of complex shape, and so be beneficial to delineate multiple closely-spaced sub-surface tumors, as well as for more accurately estimating the fluorophore concentration at larger depths. For example, with the current setup, we can detect two adjacent cylindrical inclusions with a 2 mm separation distance for μa,m =0.0015 mm−1 and μs,m’=1.5mm−1, but the minimum detectable separation as a function of the optical properties and inclusion depth has not yet been investigated.
The measurements in ex vivo tissue demonstrated that the fluorophore depth and concentration can be recovered with similar accuracy as in the tissue-simulating phantoms. The ex vivo tissue used here showed no detectable autofluorescence in the 700–715 nm range. However, this contribution becomes significant in vivo, including in patients, particularly with low levels of PpIX in the tumor, such as in low-grade glioma [7]. Hence, spectral subtraction will be required, and it will also be necessary to characterize and subtract the signal from any PpIX photoproducts.
In our previous work with qFI (i.e. quantitative imaging of surface PpIX-rich tumors) in an in vivo rat model, the marked specular reflection from the dura was a confounding factor, even with cross polarizers, while removing the dura caused serious bleeding artefacts [9]. To resolve this, a higher resolution imaging system with a smaller field of view is recommended so that only the exposed brain is imaged. Hence, it is planned to translate this qDFI technique directly into first human clinical studies to avoid this problem. Finally, intraoperative navigation should be used to measure the distance between the resection cavity and the neurosurgical microscope [14] so that MTFsystem (x,y,fx)z can be recalculated from stereo images at arbitrary camera settings using a single calibration at fixed (reference) zoom and focus settings.
Conclusions
We have demonstrated the feasibility of qDFI for determining both the (topographic) depth and fluorophore concentration of subsurface fluorescent inclusions in tissue and tissue-like media and have established the accuracy of these measurements, at least under conditions where the tissue is optically homogeneous. The results are encouraging in the context of translating to clinical use, including in glioma resection. A further application of imaging the absolute fluorophore concentration in tissue would be in photodynamic therapy as part of accurate dosimetry [18].
Supplementary Material
Acknowledgements
This work was supported by the National Institute of Health (US) grant # R01 NS052274.
Footnotes
Disclosures
DWR, KDP and BCW are co-founders of Insight Surgical Technologies LLC that is commercializing quantitative fluorescence spectroscopy and imaging.
References
- [1].Almeida JP, Chaichana KL, Rincon-Torroella J, and Rincon-Torroella A, Quinones-Hinojosa A, Curr Neurol Neurosci Rep, 2015, 15, 517. [DOI] [PubMed] [Google Scholar]
- [2].Leroy H, Vermandel M, Lejeune J, Mordon S, and Reyns N, Lasers Surg. Med, 2015, 47, 441. [DOI] [PubMed] [Google Scholar]
- [3].Hong G, Antaris AL, and Dai H, Nat Biomed Eng, 2017, 1,0010. [Google Scholar]
- [4].Roberts DW, Olsen JD, Evans LT, Kolste K, Fan X, Bravo JJ, Wilson BC, Leblond F, Marios M, and Paulsen KD, J Neurosurg, 2017, 4,1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Valdés PA, Kim A, Brantsch M, Niu C, Moses ZB ZB, Tosteson TD, Wilson BC, Paulsen KD, Roberts DW, and Harris B, Neuro Oncol, 2011, 13, 846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Valdés PA, Leblond F, Kim A, Harris BT, Wilson BC, Fan X, Tosteson TD, Hartov A, Ji S, Paulsen KD and Roberts DW, J Neurosurg, 2011, 115, 11–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Valdés PA,Jacobs V, Harris BT, Wilson BC, Leblond F, Paulsen KD and Paulsen DW, J Neurosurg, 2015, 123, 771–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Cuccia DJ, Bevilacqua F, Durkin AJ, Ayers FR, and Tromberg BJ, J Biomed Opt, 2009,14, 024012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Sibai M, Fisher C, Veilleux I, Ellitott JT, Leblond F, and Wilson BC, J Biomed Opt, 2017, 22, 076007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Konecky SD, Mazhar A, Cuccia D, Durkin AJ, Schotland JC, and Tromberg BJ, Opt Express, 2009, 17,14780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Konecky SD, Owen CM, Rice T, Valdes PA, Kolste K, Wilson BC, Leblond F, Roberts DW, Paulsen KD, and Tromberg BJ, J Biomed Opt, 2012, 17, 0560081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Sibai M, Veilleux I, Elliott JT, Leblond F, and Wilson BC, Biomed Opt Expr, 2015, 6, 4923 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Sibai M, PhD thesis, University of Toronto; (Canada: ), 2018 [Google Scholar]
- [14].Ji S, Fan X, Roberts DW, and Paulsen KD, Med Image Comput Comput Assist Inter, 2014, 17, 440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Valdés PA, Kim A, Leblond F, Onde OM, Harris BT, Paulsen KD, Wilson BC, and Roberts DW, J Biomed Opt, 2011, 16, 116007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Comsa DC, Farrell TJ, and Patterson MS, Phys Med Biol, 2008, 53, 5797–5802. [DOI] [PubMed] [Google Scholar]
- [17].Mazhar A, Cuccia DJ, Gioux S, Durkin AJ, Frangioni JV, and Tromberg BJ, J Biomed Opt 2010, 15, 010506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Wilson BC and Patterson MS, Phys Med Biol, 2008, 53, R61–R109. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.