Ferritin Exhibits Michaelis-Menten Behavior with Oxygen but not with Iron During Iron Oxidation and Core Mineralization

Abstract

The excessively high and inconsistent literature values for K_{m, Fe} and K_{m, O2} prompted us to examine the iron oxidation kinetics in ferritin, the major iron storage protein in mammals, and to determine whether a traditional Michaelis-Menten enzymatic behavior is obeyed. The kinetics of Fe(II) oxidation and mineralization catalyzed by three different types of ferritins (recombinant human homopolymer 24H, HuHF, human heteropolymer ~ 21H:3L, HL, and horse spleen heteropolymer ~ 3.3H:20.7L, HosF) were therefore studied under physiologically relevant O₂ concentrations, but also in the presence of excess Fe(II) and O₂ concentrations. The observed iron oxidation kinetics exhibited two distinct phases (Phase I and Phase II), neither of which obeyed Michaelis-Menten kinetics. While Phase I was very rapid and corresponded to the oxidation of approximately 2 Fe(II) ions per H-subunit, Phase II was much slower and varied linearly with the concentration of iron(II) cations in solution, independent of the size of the iron core. Under low oxygen concentration close to physiological, the iron uptake kinetics revealed a Michaelis-Menten behavior with K_m,O2 values in the low μM range (i.e. ~ 1 – 2 μM range). Our experimental K_m,O2 values are significantly lower than typical cellular oxygen, indicating that iron oxidation and mineralization in ferritin should not be affected by the oxygenation levels of cells, and should proceed even under hypoxic events. A kinetic model is proposed in which the inhibition of the protein’s activity is caused by bound iron(III) cations at the ferroxidase center, with the rate limiting step corresponding to an exchange or a displacement reaction between incoming iron(II) cations and bound Fe(III) cations.

Graphical Abstract

Iron uptake into mammalian ferritins reveals oxygen (but not iron) saturation kinetics and physiologically relevant Km,O₂ values.

Introduction

Iron is an essential nutrient for virtually most forms of life and an important component of many cellular processes including oxygen transport, electron transfer reactions, energy metabolism, DNA synthesis and gene regulation¹. To mitigate problems associated with iron-initiated radical chemistry, and the insolubility of Fe(III) ions at neutral pHs, cells synthesize ferritin, a ubiquitous and well-characterized iron storage and detoxification protein, capable of sequestering thousands of iron atoms in the form of a biologically available ferric oxy/hydroxide mineral core^2–7. For most organisms, ferritin is a polypeptide of 24-subunits that can vary, selectively, in amino acid sequence and subunit type, and can be either enzymatically active (due to di-iron ferroxidase centers present on H-subunits or H-like subunits having a MW of ~ 21,000 kDa) or enzymatically inactive (no ferroxidase centers on L-subunits having a MW of ~ 19,000 kDa). In mammals, the H- and L-subunits co-assemble in various H:L ratios with a tissue specific distribution to form a shell-like structure with 4/3/2 octahedral symmetry^{2, 5–8}. Examples of isoferritins from different human tissues include placenta (~ 20% H, 80% L), spleen (~ 10% H, 90% L), liver (~ 50% H, 50% L), and heart (~ 90% H, 10% L). The active H-subunit has a ferroxidase center that rapidly catalyzes the oxidation of Fe(II) to Fe(III), and ultimately its hydrolysis to form the iron inorganic core inside the protein shell, whereas the L-subunit does not. A recent study from our laboratory demonstrated a dual role for the L-subunit in facilitating iron turnover at the ferroxidase centers of H-subunits, and in mineralization of the iron core⁸.

While the majority of iron present in living systems is predominantly associated with enzymes and proteins, a minor fraction is chelatable and loosely bound to a heterogeneous population of ligands, including polypeptides and metal complexing groups such as carboxylates, phosphates, amides, thiolates, and hydroxylates^{9, 10}. This exchangeable pool of iron is referred to as cellular labile iron pool (LIP), is redox-active with an estimated concentration within mammalian cells in the low μM range (i.e. less than 5 % of the estimated total cell iron pool of 20 to 100 μM). In extracellular fluids, iron is tightly chelated by transferrin (i.e. affinity constant ~ 10²² M⁻¹), and is safely carried to the interior of cells, via receptor-mediated endocytosis. This process involves the transferrin receptor which has nM affinity to the iron-loaded protein¹¹. The interaction of the iron-loaded transferrin with the transferrin receptor is a key cellular process that occurs during the normal course of iron metabolism. However, although iron bound to transferrin is redox-inactive, and virtually non-exchangeable, transferrin is only about 30% saturated with iron in normal human serum. The approximately 25–50 μM transferrin present in the serum is unequally distributed between fully saturated diferric-protein complex (~ 27%), half saturated monoferric-protein complexes (~ 11–23%) and iron-free protein (~ 40%)¹².

Over the past several decades, numerous in-vitro studies have aimed at understanding the mechanism of iron uptake, oxidation, and core formation in ferritins. In most ferritins, two widely accepted models have been proposed, the protein catalysis model, and the crystal growth model, or a combination thereof^2–8, although key structural differences and disagreements on suggested steps of the proposed models remain unresolved^{13, 14, 15}. Nonetheless, the overall and generally accepted multistep mechanism involves the binding of ferrous ions at the protein catalytic sites, followed by oxidation and movement of the resulting protein-ferric intermediate species (μ−1,2-peroxo-diFe(III) and μ-oxo(hydroxo)-bridged diiron(III)) into the protein cavity, where a stable nucleus of crystalline mineral (ferrihydrite) starts to form. The growing mineral core then provides additional nucleation sites onto which incoming Fe(II) can be further deposited and oxidized. While a large majority of these studies has been performed with recombinant homopolymeric ferritin of H- or L-type subunits, the widespread occurrence of heteropolymeric ferritins in mammals, necessitated a detailed mechanistic understanding of the complementary roles of H- and L-subunits in the biological processing and management of iron by these proteins. A recent study from our lab examined the kinetics of iron oxidation and mineralization reactions in recombinant heteropolymeric human ferritin, using ferritin samples with different H to L compositions (i.e. H-rich or ~20H:4L and L-rich or ~22L:2H). The data demonstrated a critical role of L-subunits in enhancing the activity of H-subunits, and increasing the capacity of the protein to take up iron, in support of the different distributions of isoferritins of different subunits composition in tissues of different organs⁸. However, while heteropolymeric H-rich ferritin sample outperformed the homopolymeric H-subunits ferritin in terms of iron oxidation and core formation kinetics, important enzymatic parameters including K_M, V_max, k_cat, and catalytic efficiency k_cat/K_M were missing. Previously published values were either compromised by the experimental conditions employed, including uncontrolled and high oxygen concentration, the chelating ability of the buffer used^{16, 17}, or were excessively high (i.e. in the mM range)^{18, 19}, and physiologically irrelevant, considering the low μM [O₂] and cellular labile iron pool concentrations. Here, we explore and compare the enzymatic activity, and kinetic parameters of three different ferritin samples, including an H-rich heteropolymer ferritin (~20–21H:4–3L), an exclusively homopolymer H-chain ferritin (100% H), and a naturally occurring heteropolymer ferritin from horse spleen (~21–22L:3–2H).

Materials and Methods

Ferritin samples and chemicals.

The H-rich human heteropolymer (HL) and homopolymer H-chain (HuHF) ferritin samples were produced and purified as described elsewhere^{8, 25}. All of the proteins employed in this study are iron-free (apo-protein), although we do not discount the presence of minute amounts of iron inside the protein’s cavity. Protein concentrations were determined spectrophotometrically at 280 nm using a molar absorptivity of 24,000 M⁻¹cm⁻¹ per subunit for HL, 21,000 M⁻¹cm⁻¹ per subunit for HuHF⁸, and 19,500 M⁻¹cm⁻¹ per subunit for HosF²⁶. The subunit composition of recombinant heteropolymer ferritin was quantified by SDS−CGE and SDS−PAGE⁸ and was found to contain ~ 15% L-subunits and ~ 85% H-subunits (i.e. ~ 20–21 H and 3–4 L). All chemicals employed in this study were reagent grade and used without further purification. MOPS (3-(N-morpholino)propanesulfonic acid) buffer was purchased from Research Organics (Cleveland, OH), ferrous sulfate heptahydrate from J. T. Baker (Phillipsburg, NJ), sodium dithionite, 2,2’-bipyridyl and iron-free horse spleen (HosF) ferritin from Sigma-Aldrich (St. Louis, MO). Fe(II) stock solutions were freshly prepared immediately before each experiment in a dilute HCl solution at pH 2.0.

Kinetic measurements.

Conventional UV−vis spectroscopy was performed on a Varian Cary 50 Bio spectrophotometer from Agilent Technologies. All experiments were conducted at 25 °C, in 100 mM MOPS buffer and 100 mM NaCl, pH 7.4, and reagents concentrations for each experiments are given in the figure captions. All kinetic experiments were repeated two to four times using independent protein preparations to ensure reproducibility. The kinetic traces shown in the figures represent one of multiple individual runs.

Iron oxidation kinetics in the presence of excess O₂.

The kinetics of iron oxidation in ferritin were followed at 305 nm where the Fe(III) oxo(hydroxo) species absorbs. The concentrations of HuHF, HL and HosF ferritin samples employed in this study were 0.5, 0.5, and 5 μM, respectively, and the Fe(II) concentrations added to these samples varied between 20 and 250 μM for HuHF and HL, and 30 to 215 μM for HosF. The use of 10-fold higher concentration of HosF was necessary to compensate for the low H-subunit content of the protein, and the overall lower oxidation rates. Under these conditions, the Fe(II)/ferritin ratios varied between a minimum of ~ 2 Fe/H-subunit to a maximum of ~ 500 Fe/protein. The instrument was zeroed using the ferritin solution, prepared in buffer as the blank. Typically two or three μL of a ferrous sulfate solution prepared in deionized H₂O (pH 2) were injected into a 1.0 mL protein solution, with rapid spin bar stirring under the conditions stated in the figure captions. Time-dependent absorbance kinetic traces were collected at 25 °C and the data analyzed with Excel or OriginLab version 8.0 (OriginLab Corp.).

Iron oxidation kinetics in the presence of excess Fe(II) and low O₂ concentrations.

Additional kinetic experiments were performed in the presence of reduced O₂ concentrations (11 to 30 μM) and a large excess of Fe(II) (at least ten-fold excess over O₂). Solutions of ferritin in 100 MOPS, and 100 mM NaCl, pH 7.4, iron(II) sulfate in pH 5.0 water, and distilled water were deoxygenated by repeated vacuuming under constant stirring and purging with pure nitrogen or argon gas [21]. The degassed solutions were transferred via gas-tight Hamilton syringes into a tightly septum-sealed and nitrogen-filled (or argon-filled) quartz UV-vis cuvette at 25 °C, while avoiding the formation of pockets of gas above the solution. The final experimental conditions after mixing all reagents were as follow: 0.2–1 μM of ferritin in 50 mM MOPS, 50 mM NaCl, pH 7.4, 11–30 μM dissolved oxygen, and 140 to 500 μM of Fe²⁺. The method used to calculate the iron oxidation rates and the concentrations of remaining Fe(II) and O₂ in solution are described below in detail.

In brief, the initial concentration of dissolved oxygen is calculated based on the final [Fe³⁺] cations produced during the oxidation reaction, assuming either 4:1 or 2:1 Fe^II:O₂ stoichiometry. The concentration of remaining oxygen in solution at any point during the kinetic is calculated based on the difference between the initial calculated concentration of oxygen and one of the two Fe^II:O₂ presumed oxidation ratios (i.e. 4 [Fe³⁺] for the 4:1 Fe^II:O₂ ratio and 2 [Fe³⁺] for the 2:1 Fe^II:O₂ ratio)”. We note that a direct measurement of [O₂] in solution is not a practical approach given the low sensitivity, inaccuracy, and responsiveness of commercially available oxygen electrodes, particularly in the most interesting area of our kinetic studies (i.e. under low O₂ concentration). To overcome this limitation, we adopted a new approach based on the known Fe^II:O₂ oxidation stoichiometry, as discussed above.

Results

We believe that maintaining about 1 μM concentration of labile iron pool must involve a dynamic equilibrium process, and a constant overall rate of exchange between iron uptake and iron release. While iron release is a complex process that involves the proteolytic degradation of ferritin in lysosome,^{20, 21} and possibly alternative processes of iron mobilization, either by reduction^{22, 23} or direct chelation,²⁴ the mechanism of iron uptake, oxidation, and mineralization inside ferritin is relatively well understood. In cell-free conditions, iron oxidation kinetics can be easily monitored by light absorption of the oxidized iron(III)-protein complex at 305 nm⁸. However, due to the low molar absorptivity of the iron-protein complex, this assay becomes insensitive to the typical 1 μM cytosolic concentration of labile Fe²⁺ cations. One solution is to extrapolate and deduce the iron oxidation rates from kinetics conducted at much higher iron concentrations. Assuming the iron oxidation reactions obey Michaelis-Menten kinetics, the values of K_m and V_max for Fe²⁺ and O₂ can be easily determined.

Km for iron

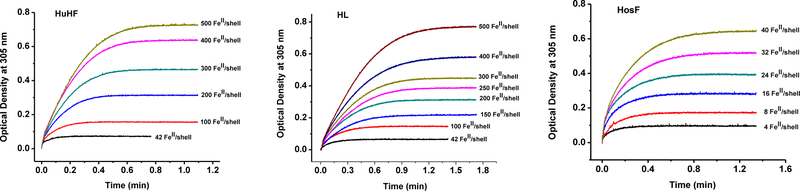
In our measurements of the Km value for iron in ferritin, the working protein solutions were exposed to atmospheric oxygen for a prolonged period. Under these conditions, the concentrations of dissolved oxygen is around 250 μM at 25 °C, a value much higher than the reported Km for O₂^{16, 17, 19, 25}. Furthermore, considering either 2:1 or 4:1 Fe^II:O₂ ratios, the [O₂] is in large excess even at the highest Fe(II) concentration (i.e. 250 μM) used in our experiments. Figure 1 shows the kinetic traces of the optical densities at 305 nm, where the Fe^III-oxo(hydroxo)-protein complex absorbs, as a function of reaction time.

Figure 1.

Kinetic curves for the catalytic oxidation of Fe(II) by recombinant human homopolymer apo-HuHF (left), recombinant human heteropolymer apo-HL (middle), and apo-HosF (right). The experimental conditions are: HuHF (0.5 μM), HL (0.5 μM), HosF (5 μM), in 100 mM MOPS buffer and 100 mM NaCl, pH 7.4 and 25 °C. The ratio of Fe(II)/protein is shown on each panel and is color coded.

In these experiments, and at all levels of iron additions, the reaction proceeded quickly in all three ferritin samples with > 90% of Fe(II) mineralized within less than one minute, even at the largest concentration of Fe(II) employed (i.e. 250 μM). The 10-fold higher concentration of HosF translates into approximately one order of magnitude slower rates of iron mineralization, compared to HuHF and HL, and is consistent with the approximately ten times higher number of H-subunits present in these proteins.

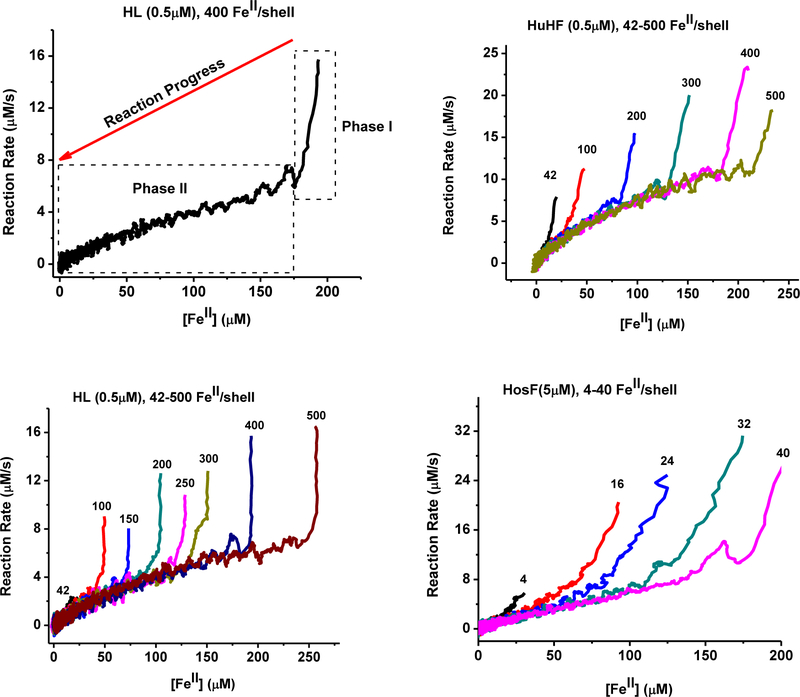
As previously observed⁸, iron oxidation in ferritin proceeds with an initial maximal rate, and slows down as the concentration of iron(II) cations is depleted from the medium, in favor of the formation of the mineralized iron(III) hydroxide core. A common approach for calculating the rate constants of these enzymatic reactions, and ultimately K_m and V_max parameters, involves fitting the kinetic traces using polynomial or exponential fits provided in various software packages, or simply by choosing the Michaelis–Menten kinetic equation in data analysis software like OriginLab. The problem with such approach is that the reaction kinetic is implicitly assumed to follow Michaelis–Menten behavior. To properly analyze the kinetics of iron(II) oxidation in ferritin, and to determine the applicability of Michaelis–Menten equation, we calculated the reaction rates by numerical differentiation of the kinetic curves. This calculation is accomplished by analyzing the changes in the concentration of oxidized iron (calculated by dividing the absorbance value at 305 nm by 3000 M⁻¹cm⁻¹, which is the average molar absorptivity constant of the Fe(III)-ferritin complex) observed over a period of 1.00 sec. Initially, the concentration of iron(II) cations added to each ferritin sample is known; however, we determined the exact concentration of oxidized iron inside ferritin, at the end of the kinetic run, using Beer Lambert’s law, and a molar absorptivity of 3000 M⁻¹cm^{−1 8}. This allowed us to calculate the concentration of remaining iron(II) cations in solution during the progress of the oxidation reaction. Clearly, this numerical differentiation approach leads to a strong amplification of the noise in the original data. To minimize this effect, we averaged the initial and the final concentrations of oxidized iron, by subsequently analyzing 10 successive absorption measurements, separated by 0.25 sec time interval. This method of calculation of reaction rates, allows their measurement at any point during the kinetic run as a function of the remaining Fe(II) concentrations in solution. The results of the three ferritin samples (HuHF, HL and HosF) tested in this study are shown in Figure 2, and reveal a completely different behavior than the presumed Michaelis-Menten kinetics. An initial short and very rapid reaction phase is observed immediately after the addition of Fe(II) to an oxygenated ferritin solution in buffer, followed by a second much slower phase that continues until all Fe(II) ions present in solution are fully depleted.

Figure 2.

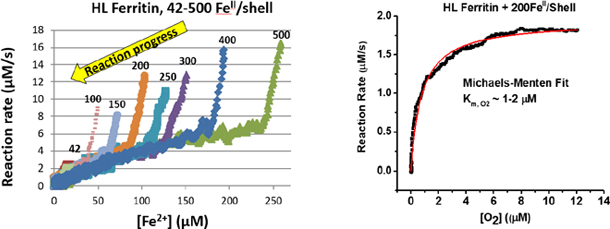
Plots of the reaction rates vs. the concentration of remaining Fe(II) cations in solution. Top left: typical plot for HL ferritin with 400 Fe^II/shell; Top right and Bottom: overlay of several reaction rate plots at different ratios of Fe^II/shell for HuHF, Hl, and HosF, as indicated next to each curve. The experimental conditions are those of Figure 1.

Table 1 shows that at the transition point between Phase I and Phase II, the iron loading of the three proteins is estimated at 41–71 Fe^III/shell for HuHF, 41–56 Fe^III/shell for HL, and 8–11 Fe^III/shell for HosF, corresponding to 2.6 ± 0.4, 2.2 ± 0.3, and 3.2 ± 0.6 Fe^III/H-subunit for the three proteins, respectively.

Table 1.

Analysis of the iron oxidation kinetics in HuHF, HL, and HosF shown in Figures 1 and 2. The experimental conditions are provided in the caption of Figure 1.

HuHF					(Assuming 24 H)
FeII/shell added	Experimentally calculated [FeII]	Remaining [FeII] in solution	[FeIII] at the transition point (between Phase I and Phase II)	FeIII/shell at transition	FeIII/H-chain at transition
500	249 ± 13	214 ± 11	36 ± 2	71 ± 5	2.9 ± 0.2
400	211 ± 2	172 ± 3	39 ± 1	79 ± 2	3.3 ± 0.1
300	155 ± 2	122 ± 4	33 ± 2	66 ± 4	2.7 ± 0.1
200	101 ± 3	77 ± 1	24 ± 3	48 ± 5	2.0 ± 0.1
100	50 ± 2	30 ± 1	20 ± 1	41 ± 1	2.5 ± 0.1
	--			Average	2.6 ± 0.4
HL	--				(Assuming 21 H)
500	284 ± 37	256 ± 35	28 ± 2	56 ± 3	2.6 ± 0.1
400	195 ± 3	171 ± 2	24 ± 2	48 ± 3	2.2 ± 0.1
300	148 ± 5	120 ± 1	27 ± 5	55 ± 10	2.5 ± 0.4
250	122 ± 10	99 ± 3	23 ± 6	47 ± 13	2.1 ± 0.5
200	105 ± 1	83 ± 1	22 ± 1	43 ± 3	2.0 ± 0.2
150	73 ± 1	52 ± 3	21 ± 3	41 ± 6	1.9 ± 0.3
	--			Average	2.2 ± 0.3
HosF	--				(Assuming 3.3 H)
40	212 ± 6	157 ± 6	55 ± 1	11 ± 1	3.3 ± 0.03
32	172 ± 4	115 ± 1	57 ± 3	11 ± 1	3.3± 0.18
24	126 ± 2	77 ± 1	49 ± 1	10 ± 1	3.0 ± 0.003
16	94 ± 1	55 ± 4	38 ± 3	8 ± 1	2.4 ± 0.21
				Average	3.0 ± 0.5

The gradual decrease in reaction rates observed in Phase II of Figure 2 is proportional to the concentration of remaining Fe(II) cations in solution. As more Fe(II) ions are oxidized by the protein, and the inorganic mineral core continues to grow, the second phase of the kinetic traces had little effect on the reaction rates, irrespective of the amount of added iron (Fig. 2), or the size of the inorganic iron core (Fig. 3). For instance, in HL ferritin (Fig. 2), the reaction rates at 30 μM of remaining Fe(II) are in the range 1.6 ± 0.3 μM/s at iron loadings of 250, 200, 150, 125, and 75 μM. In HuHF and HosF, at 30 μM remaining Fe(II), these rates were 3.5 ± 0.3 μM/s and 2.9 ± 0.5 μM/s, respectively. The lack of a second phase (Phase II) under low Fe(II) concentrations (i.e. stoichiometric amounts of ~ 2 Fe(II)/di-iron center or 42 Fe(II)/shell for HuHF and HL, and 4 Fe(II)/shell for HosF, Fig. 2), suggest the absence of a displacement reaction of bound Fe(III) cations by incoming Fe(II) cations.

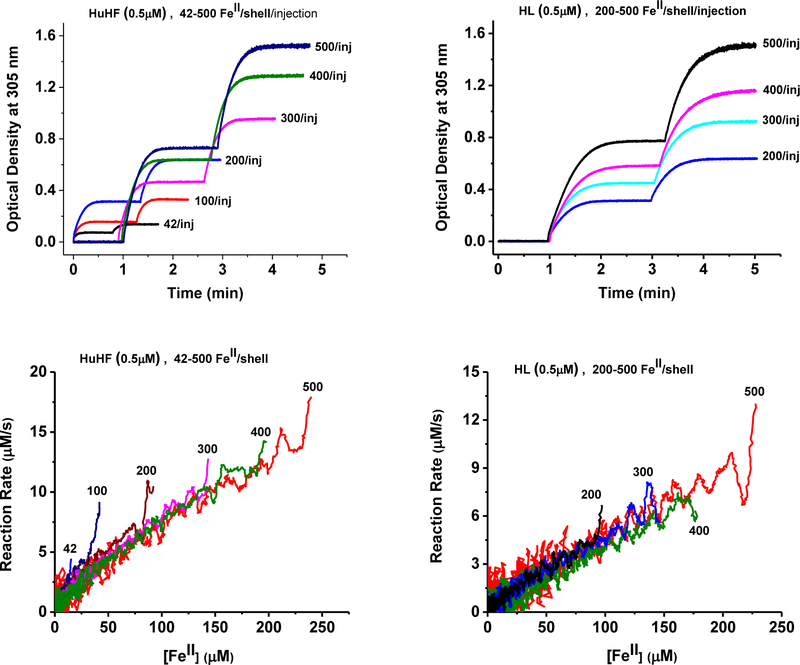
Figure 3.

Top: Representative kinetic curves for two successive injections of the same amount of Fe^II/shell, as indicated on each plot, in the presence of HuHF (left) or HL ferritin (right). Bottom: Plots of the reaction rates vs. the concentration of remaining iron(II) cations in solution following the second addition of Fe(II) to the same protein sample (as shown on each panel), HuHF (left), and HL (right). The experimental conditions are the same as in Figure 1.

To obtain more insights into the origin of the transition between Phases I and II, and to examine the effect of an existing iron core within the ferritin cavity, two back-to-back injections of Fe(II) solutions were made to the same HuHF and HL ferritin samples (Fig.3). The results showed a dramatically shortened (in the case of HuHF) or almost inexistent first phase (in the case of HL), suggesting that a different iron oxidation mechanism had taken, in the presence of an existing iron core. Here again, the reaction rates exhibit a linear dependency on the amount of Fe(II) present in solution.

Fe(II) oxidation under low concentration of O₂ - Km for oxygen

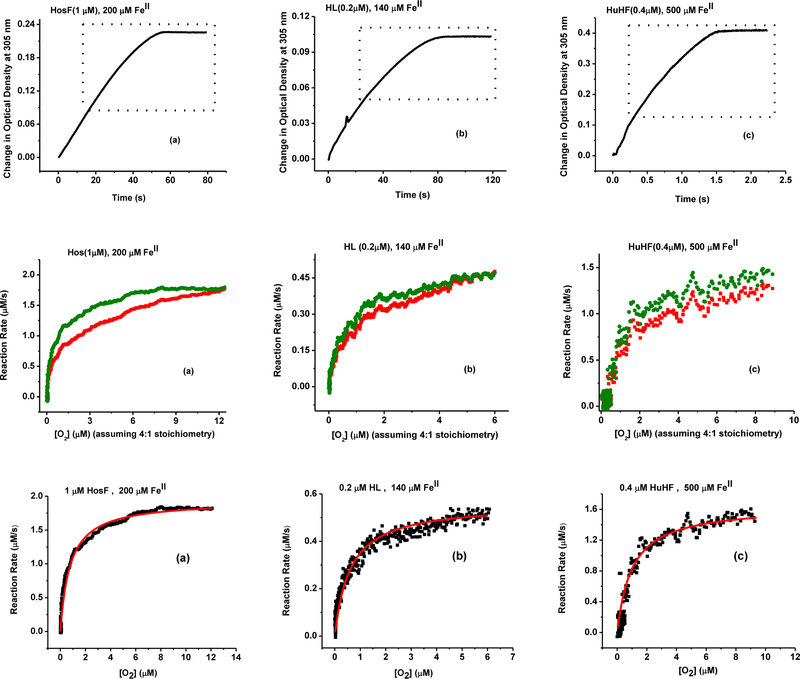
The iron oxidation kinetics described above are based on the assumption that the reaction rate does not depend on the concentration of oxygen in solution. However, because of the large discrepancy in the literature values of Km for O₂ (i.e. 6 – 140 μM)^{18, 25}, we sought to investigate the effect of O₂ on the reaction rates. One of the reasons for this wide range of Km values stems from the difficulty in maintaining and accurately monitoring the concentration of soluble oxygen in solution. In an earlier study, we used a sensitive oxygen microelectrode to measure and monitor in real time the concentration of oxygen²³ in solution, and its effect on the rates of the reductive release of iron from ferritin. Unfortunately, this method becomes unreliable when monitoring very low concentrations of oxygen, particularly if these concentrations are rapidly changing. Nonetheless, to overcome this problem, we conducted kinetic experiments in a tightly sealed UV-vis cuvette, using partially deoxygenated ferritin solutions containing [O₂] ranging between 20 and 40 μM. With this set up, the possibility of oxygen exchange with air is minimized²³, particularly considering the short reaction time (< 2 min), and the large excess of [Fe(II)] employed. The reaction kinetics in the homogeneous solution progressed until all dissolved oxygen is depleted, and large excess of Fe(II) remained in solution. Under these conditions, the ratio of Fe(II) to O₂ is shown to occur at 4 Fe(II) per 1 O₂, and therefore it is possible to calculate both the concentration of oxygen at any time of the reaction as a one-fourth of the total concentration of Fe(II) in solution. A typical absorbance vs. time kinetic trace for these types of reactions are shown in Figure 4a–c, top.

Figure 4.

(Top row) Iron oxidation kinetics at 305 nm under low oxygen concentration using (a) HosF (1.0 μM), Fe(II) (200 μM), and approximately 19 μM O₂; (b) HL (0.2 μM), Fe(II) (140 μM), and approximately 11 μM of O₂; (c) HuHF (0.4 μM),Fe(II) (500 μM), and approximately 30 μM O₂. (Middle row): Dependence of the reaction rates on the concentration of remaining O₂, calculated assuming 4:1 Fe^II:O₂ stoichiometry. Red and green curves are kinetics before and after correction (more details in the text). (Lower row) Michaelis-Menten fit to the corrected kinetic curves for the calculation of K_m and V_max parameters.

Calculation of K_m,O2 and V_max parameters for HuHF, HL, and HosF

Following the same methodology described above, the kinetic curves under low oxygen concentration (Fig. 4) were numerically differentiated for our three proteins (HuHF, HL, and HosF), to determine how the reaction rates change as a function of remaining [O₂] in solution. To minimize the reaction noise, the reaction rates were calculated using changes in Fe(III) concentrations (calculated from optical densities as an average of four measurements within 1 s time interval) over 2.5 s time period, and then converted into μM/s. Once oxygen is fully depleted from the solution, the concentration of oxidized iron (i.e. 75.5 μM in the case of HosF) was calculated from the absorbance value of 0.226 at 60 seconds (Fig. 4a, top). Assuming a 4:1 Fe^II:O₂ ratio, the initial solution concentration of oxygen (i.e. 75.5/4=18.9 μM) is used to experimentally determine the concentration of dissolved oxygen at any time during the oxidation reaction. The reaction rates are then plotted as a function of remaining [O₂] in solution, and are shown in Figure 4 (middle and bottom panels). However, because of the presence of 2 phases (Fig. 2), only the second slow phase of the reaction (dotted box of Fig. 4, top) is further analyzed. To make sure that only Phase II of the reaction is selected, the kinetic data were analyzed at a concentration of Fe(III) that is twice or more than that observed at the end of Phase I (i.e. ≥ 2 × 11 Fe^III/shell for HosF, Table 1). This corresponds to an [Fe³⁺] spanning between 22 and 75.5 μM, and an [O₂] concentration of 13 – 0 μM, respectively (assuming 4:1 Fe^II:O₂ stoichiometry). During that time frame (i.e. 13 – 60 s, Fig. 4a), the concentration of [Fe(II)]_remaining in solution ranges between 177 μM and 124.7 μM, and can be accounted for by multiplying the calculated reaction rates (Fig. 4, middle, red uncorrected curve) by the ratio of [Fe(II)]_{initial (177 μM)}/[Fe(II)]_current. This adjustment is possible because during Phase II, the reaction rates depend linearly on [Fe(II)]. The adjusted kinetic traces (Fig. 4, middle panels, green corrected curves) are remarkably similar to classical Michaelis-Menten kinetics, the fit of which yielded the following parameters: V_max = 1.94 ± 0.01 μM/s and K_m,O2 = 0.77 ± 0.03 μM.

Although the total concentration of available [Fe(II)] in solution is in large excess compared to the concentration of HosF (i.e. 22–75 Fe^III/shell), and although the stoichiometry of Fe^II:O₂ reported in the literature is close to 4:1, it behooved us to repeat the above analysis assuming an oxidation ratio of 2Fe^II:1O₂. Indeed, the Fe^II:O₂ ratio may depend on the overall experimental conditions including total iron concentration present in solution, pH, iron chelators, buffer and protein type^27–30. Because the concentration of oxygen in solution is calculated based on the Fe^II:O₂ stoichiometry, the value of K_mO2 will also depend on that stoichiometry. The most reliable and straightforward way to address the uncertainty in the value of K_mO2 is to assume that the actual stoichiometry of the reaction is anywhere between 4:1 and 2:1. A re-analysis of the kinetics assuming a 2Fe^II:1O₂ oxidation stoichiometry showed an analogous Michaelis-Menten behavior; however, the value of K_mO2 was twice as large (i.e. K_mO2 = 1.54 ± 0.06 μM). Based on these calculations, it can be concluded that the average K_mO2 for the iron oxidation reaction in HosF is 1.15 ± 0.54 μM for 2 < Fe^II:O₂ < 4.

A similar analysis was performed with recombinant heteropolymer HL ferritin (Fig. 4) under deficient [O₂], [HL] = 0.2 μM, and an initial total [Fe(II)] = 140 μM. The concentration of oxidized iron at the end of the experiment in Fig. 4 was calculated to be 45.5 μM, corresponding to an initial O₂ concentration of 11.3 μM, assuming a 4:1 Fe^II:O₂ ratio. In the case of HL ferritin (Fig. 2), Phase II of the reaction occurs around 48 Fe^III/shell, which when adjusted for the 0.2 μM concentration of HL and the 2Fe^II: 1O₂, corresponds to a mineralized iron(III) concentration of about 20 μM. The remaining [Fe(II)] (i.e. 120 μM) correlates with a reaction time of about 35 seconds (Fig. 4b, top). The plot of the reaction rates as a function of [O₂] in the solution was calculated as previously described, and is shown in Fig. 4b, middle. Here again, a fit using the Michaelis-Menten equation yielded a V_max value of 0.52 ± 0.03 μM/s and a K_mO2 of 0.46 ± 0.02 μM, with an average K_mO2 value for HL of 0.69 ± 0.32 μM for 2 < Fe^II:O₂ < 4. Analogous fitting of the HuHF experiments yielded a Vmax value of 1.61 ± 0.03 μM/s and a K_mO2 of 1.30 ± 0.08 μM assuming a 4Fe^II: 1O₂, and an average K_mO2 value for HuHF of 1.95 ± 0.92 μM for 2 < Fe^II:O₂ < 4.

Discussion

Under our experimental conditions, our data show that the rates of iron oxidation as a function of Fe(II) concentration, in the three types of ferritin, HuHF, HL, and HosF examined here, do not follow Michaelis-Menten kinetics. The reaction rates were substantially higher at high Fe(II) concentrations, suggesting pseudo-first order kinetics. However, the existence of two distinct iron oxidation phases indicates that the reaction mechanism is much more complex. The rapid decrease of reaction rates during Phase I could not be attributed to a decrease in the concentration of Fe(II), since it does not dramatically change during that phase, particularly under high Fe(II) concentrations (i.e. 400 or 500 Fe^II/shell additions in HuHF or HL ferritin, and 40 Fe^II/shell in HosF). Instead, we believe that the rapid decrease of reaction rates during Phase I is caused by the inhibition of the catalytic activity of the ferroxidase centers when the oxidized Fe(III) cations remain bound to these centers. Table 1 shows that the Fe^III/H-subunit inhibition stoichiometry is between 2 and 2.5 for HuHF and HL, and around 3.5 for HosF. The oxidized Fe(III) cations at the ferroxidase centers of the H-subunit must either dissociate (i.e. detach from the center), or the ferroxidase centers act as a cofactor for the oxidation of incoming Fe(II) ions (^{4, 13–15}. In either case, more Fe(II) ions would get oxidized and ultimately join the growing inorganic ferrihydrite core inside the ferritin cavity, in analogy to what has been previously proposed for bacterioferritins⁴. The dissociation of Fe(III) cations represents the rate-limiting step of the reaction that can be accelerated by other metal cations such as Fe(II), or by chelate ligands capable of binding Fe(III) ions. This suggested reaction mechanism is compatible with several observations including, (1) the pseudo-first order kinetics during Phase II, (2) the absence (or significantly depressed) Phase I following the second addition of Fe(II) cations, (3) the previously reported enhanced effect of phosphate, a known Fe(III) chelate ligand³¹ on the rate of Fe(II) oxidation³².

An earlier study using an E.coli ferritin (i.e. bacterioferritin) found that the oxidized di-Fe(III)-protein complex that forms at the ferroxidase center of the protein is stable, and acts as a catalytic site for O₂ reduction, but that in P. aeruginosa bacterioferritin, the di-iron complex is a transit site for the transfer of Fe(III) ions into the central cavity. In E.coli, and with the assistance of a tyrosyl radical, two additional Fe(II) sites provide the necessary electrons to reduce the di-Fe(III)-protein complex to a di-Fe(II)-complex. The hydrolysis of the oxidized iron at the two additional iron sites contributes to the formation of the ferritin mineral core. The reduced di-Fe(II)-protein complex further reacts with O₂ or H₂O₂, and the cycle is repeated until all of the Fe(II) ions are oxidized⁴.

The notion that the rate limiting step during iron oxidation in ferritin might involve an exchange reaction between Fe(III) ions at the ferroxidase centers (or at nearby oxidation sites) by incoming Fe(II), is at variance with the previously proposed surface catalytic activity of the inorganic iron core¹⁷. To the best of our knowledge, ferroxidase activity has never been observed on isolated iron(III) cores. Furthermore, comparison of Fe(II) oxidation rates catalyzed by HL ferritin, using initial concentrations of 150 to 500 Fe^II/shell, shows very similar reaction rates (i.e. ~ 2.5 μM/s) at 50 μM [Fe(II)] remaining in solution (Fig. 2 left, Fig. 3, right), suggesting that the protein ferroxidase activity is independent on the size of the iron(III) hydroxide core. Similar results were observed with HuHF and HosF (Figs. 2, 3).

The results of Figures 1 and 2 show that the Fe(III) turnover numbers for HuHF, HL, and HosF are 40 s⁻¹, 24 s⁻¹, and 7 s⁻¹, corresponding to 1.7 s⁻¹, 1.2 s⁻¹ and 2.1 s⁻¹ per H-subunit, assuming 24, 21, and 3.3 H subunits for HuHF, HL, and HosF, respectively. More specifically, the concentration of Fe(II) at the beginning of Phase I is approximately 200 μM for the three experiments involving 0.5 μM HuHF or HL (400 Fe^II/shell), and 5 μM HosF (40 Fe^II/shell). These conditions correspond to about 12 Fe^II/H-subunit with initial rates of the iron oxidation reactions of approximately 20 μM/s, 12 μM/s, and 35 μM/s, for HuHF, HL, and HosF, respectively (Fig. 2). When a second injection of Fe(II) is made to the same protein sample (i.e. another 400 Fe^II/shell, for HuHF or HL) immediately after the 1^st Fe(II) oxidation reaction is completed, turnover numbers of 1.0 s⁻¹ for HuHF, and 0.8 s⁻¹ for HL are observed (Fig. 3).

In contrast to Phase I, the reaction rates during Phase II slow down dramatically, presumably because most of the protein’s ferroxidase centers are already occupied by Fe(III) cations, and are thus “inactive”, until Fe(III) ions are displaced (or exchanged) by new incoming Fe(II) ions. Under oxygen deficient conditions (i.e. low μM range), direct measurements of the concentration of dissolved oxygen in solution using commercial oxygen microelectrodes is challenging, due to their relatively slow response and poor precision. However, the reaction rates as a function of [O₂] can be easily calculated, although indirectly, by monitoring the concentration of oxidized iron inside ferritin at 305 nm. Figure 4 shows that the reaction rates show a Michaelis-Menten type kinetics at [O₂] less than 10 μM, with the sharpest change occurring at less than 2 μM [O₂]. Because the Fe^II:O₂ stoichiometry can vary between 2:1 and 4:1 (depending on the experimental conditions and the ratio of the Fe^II/shell added), the calculated [O₂] concentration will consequently vary, resulting in as much as doubling of the experimentally calculated K_m,O2 values. Assuming 4Fe^II:1O₂ stoichiometry, the experimentally calculated K_m,O2 values for HuHF, HL, and HosF are 1.95±0.92 μM, 0.69±0.32 μM, and 1.15±0.54 μM, respectively. These values are much lower than the lowest reported K_m,O2 values in the literature (i.e. 6±2 μM for HuHF, 60±12 μM for HL, and 140±30 μM for HosF)¹⁸. Considering the similarity in the structure-function relationships of the three types of ferritin tested here, we believe that these relatively similar K_m,O2 values are much more reasonable than the reported literature values.

Clearly, our experimental K_m,O2 values have important physiological implications. For instance, the concentration of oxygen in living cells is in the range of 1.3–2.5 kPa³³ (i.e. ~ 18–34 μM), but much lower (i.e. ~ 7 μM) inside mitochondria. Our measured K_m,O2 values are much lower than these cellular O₂ concentrations, suggesting that neither iron mineralization inside ferritin, nor the iron oxidation rates, should be affected by variations in cellular oxygenation level, including under conditions of severe hypoxia.

Conclusions

The kinetics of iron(II) oxidation catalyzed by three different types of ferritins (HuHF, HL, and HosF) were studied in detail, using numerical differentiation of the change in optical density over time. In the presence of excess [O₂], the iron oxidation rates were continuously monitored until all iron(II) cations are completely depleted from solution. The observed iron oxidation reactions proceeded through two distinct phases (Phase I and Phase II), neither of which obeyed Michaelis-Menten kinetics. The initial and short Phase I reaction showed a rapid drop in reaction rates until approximately 2 Fe(II) ions have been oxidized per H-subunit. The subsequent and much slower Phase II reaction exhibited a significant decrease in reaction rates, proportionally to the concentration of remaining iron(II) cations in solution, but independently of the size of the iron core. A kinetic model is proposed in which the inhibition of the protein’s activity is caused by bound iron(III) cations at the ferroxidase center, with the rate limiting step corresponding to an exchange or a displacement reaction between incoming iron(II) cations and bound Fe(III) cations. On the other hand, and in the presence of limited [O₂], the kinetics of iron oxidation proceeded until all dissolved oxygen is fully depleted from solution, and exhibited Michaelis-Menten behavior, with K_m,O2 values in the low μM range (i.e. ~ 1 – 2 μM). The experimentally measured values of K_m,O2 are considerably lower than typical cellular oxygen concentrations in normoxic and hypoxic cells, indicating that the process of iron mineralization in ferritin should not be affected by hypoxic events.