Abstract
Fibroblast Growth Factor 2 (FGF2), an important regulator of angiogenesis, binds to endothelial cell (EC) surface fibroblast growth factor receptors (FGFR) and heparan sulfate proteoglycans (HSPG). FGF2 binding kinetics have been predominantly studied in static culture; however, the endothelium is constantly exposed to flow which may affect FGF2 binding. We therefore used experimental and computational techniques to study how EC FGF2 binding changes in flow. ECs adapted to 24 hours of flow demonstrated biphasic FGF2-HSPG binding, with FGF2-HSPG complexes increasing up to 20 dynes/cm2 shear stress and then decreasing at higher shear stresses. To understand how adaptive EC surface remodeling in response to shear stress may affect FGF2 binding to FGFR and HSPG, we implemented a computational model to predict the relative effects of flow-induced surface receptor changes. We then fit the computational model to the experimental data using relationships between HSPG availability and FGF2-HSPG dissociation and flow that were developed from a basement membrane study, as well as including HSPG production. These studies suggest that FGF2 binding kinetics are altered in flow-adapted ECs due to changes in cell surface receptor quantity, availability, and binding kinetics, which may affect cell growth factor response.
Keywords: fibroblast growth factor-2, endothelial cells, shear stress, fluid flow, binding kinetics, heparan sulfate proteoglycans, mass transport
I. Introduction
Fibroblast growth factor 2 (FGF2) is an 18–25 kDa protein that plays an important role in endothelial cell survival, proliferation, and migration under physiological and pathological conditions 1,2. FGF2, together with other growth factors such as vascular endothelial growth factor (VEGF), is critical to stimulating endothelial cells to initiate and maintain an angiogenic phenotype 3. While growth factor therapy has great potential to treat ischemic diseases such as myocardial infarction and wound healing, clinical successes have been modest partially because growth factor binding kinetics remain incompletely understood 4,5.
FGF2 binds to two types of receptors at the cell surface: FGF receptors (FGFR), which have high affinity (Kd 10−9 – 10−12) and low concentration (~104 binding sites per cell); or heparan sulfate proteoglycans (HSPG), which have lower affinity (Kd 10−8 – 10−9) but higher concentration (~106 binding sites per cell) 6–8. FGF2 bound to either an FGFR or an HSPG may be able to activate intracellular signaling pathways; however, FGF2 bound to both an FGFR and an HSPG in a triad is the widely accepted signaling complex 9–12. In addition to binding to the cell surface, FGF2 can also bind to HSPG in the basement membrane underneath endothelial cells, where it is thought to be protected and stored for later use 13.
FGF2 binding kinetics have predominantly been studied under static conditions. In vivo, the endothelium is constantly exposed to fluid flow velocities ranging from 0.3 mm/s to 400 mm/s 14. Fluid flow could alter FGF2 transport to the cell surface, endothelial expression of cell surface receptors, and bond association and dissociation rates. In fact, our group previously demonstrated that fluid flow increased FGF2 binding to basement membrane HSPG up to a shear stress of around 25 dynes/cm2 and then decreased FGF2 binding to basement membrane HSPG at higher shear stress levels 15. Our data suggested that increased FGF2 binding to basement membrane HSPG at moderate flow rates related to conformational changes in the basement membrane or HSPG themselves that exposed additional FGF2 binding sites. We and others have also used computational modelling to examine the effect of flow-induced transport on FGF2 binding to cell surface HSPG and FGFR. In our prior combined computational and experimental paper, flow decreased time to FGF2 equilibrium binding to endothelial cells, depending on receptor surface concentration, and had the largest effect on FGF2 capture during bolus delivery 16. Zhao et al. also studied FGF2 binding to HSPG and FGFR under fluid flow using a 3-dimensional computational model of endothelial cells seeded in a hollow-tube bioreactor 17. They found that FGF2 binding decreased with flow rates even slightly above capillary flow rates.
Despite the additional understanding of FGF2 binding kinetics in flow from these models, neither model considered the adaptive remodeling of the apical endothelial cell surface or changes in bond properties in response to fluid flow derived shear stress 18. Recent studies suggest that shear stress upregulates endothelial cell HSPG expression and regrowth as compared to cells in static culture 19,20. Furthermore, Sevim et al. used atomic force microscopy to demonstrate slip bond characteristics between FGF2 and heparin, introducing the possibility that the FGF2-HSPG bond itself may change under flow conditions 21. It is therefore important to explore how flow-adapted endothelial cells may differentially bind FGF2, including the mechanisms for this effect.
The goal of this study was to understand how steady laminar flow affects endothelial cell FGF2 binding. We hypothesized that steady laminar flow would increase FGF2 binding to cell surface HSPG in a similar manner to what we observed in our isolated basement membrane HSPG experiments. We first measured FGF2 binding to endothelial cell surface HSPG and FGFR, as well as basement membrane HSPG, in porcine aortic endothelial cells adapted to 24 hours of 20 dynes/cm2 laminar shear stress. We then built a finite element model of FGF2 binding kinetics under flow conditions. We conducted parametric studies to determine how alterations in FGF2 surface receptors and bonds would change binding kinetics, and then we used our prior basement membrane studies and evidence from the literature to fit the parameters in our computational model to the experimental data. We now show for the first time that FGF2 binding to cell surface HSPG peaks at moderate shear stress levels, and that this may relate to changes in HSPG availability, production, and dissociation with flow. These data suggest that endothelial cell surface remodeling in response to shear stress affects FGF2 binding kinetics, and that future studies of growth factor binding kinetics should be performed under physiological flow conditions.
II. Materials and Methods
FGF2 Experiments
Cell culture
Primary porcine aortic endothelial cells (PAEC) were isolated from porcine aortae obtained from a local abattoir. PAEC were cultured at 37°C and 5% CO2 in Dulbecco’s Modification of Eagle’s Medium (DMEM, 5 mM glucose) supplemented with 5% fetal bovine serum (Hyclone), 2% ʟ-glutamine, and 1% penicillin-streptomycin (Gibco). PAEC between passages four and nine were used for all experiments.
FGF2 binding kinetics
In all experiments, 1 × 106 PAEC were seeded onto sterile glass microscope slides and cultured for two days. For flow experiments, samples were exposed to 10, 20, or 40 dynes/cm2 shear stress (2.1, 4.2, or 8.4 mL/min, respectively) for 24 hours in a parallel plate flow chamber (Glycotech) at 37°C. A peristaltic pump (Ismatech) was used to drive steady flow, with a bubble trap upstream of the channel to dampen pulsatility in the recirculating medium. Steady rather than pulsatile flow was used in all experiments to isolate the effect of shear stress on FGF2 binding. Cell medium samples were collected during flow to quantify cellular FGF2 release and HSPG shedding. After flow, the medium was changed to 10 mL binding buffer (25 mM HEPES, 0.05% gelatin, pH 7.4) with 0 or 10 ng/mL FGF2 (Peprotech). Cells were then exposed to an additional two hours of flow at the same shear stress level at 37°C, with the binding buffer recirculating throughout the two hours. We previously demonstrated that equilibrium binding is reached by two hours 22. Samples were then removed from the parallel plate flow chamber and quickly washed in binding buffer. Cell surface HSPG-bound FGF2 was first extracted using a salt buffer (2 M NaCl, 20 mM Hepes, pH 7.4), after which FGFR-bound FGF2 was extracted using an acid buffer (2 M NaCl, 20 mM sodium acetate, pH 4.0). For static experiments, PAEC cultured on microscope slides were placed in low-binding Petri dishes (to minimize FGF2 loss from the binding buffer) and exposed to 10 mL binding buffer with 0 or 10 ng/mL FGF2 for two hours. For basement membrane HSPG-bound FGF2, cells were first lysed with 20 mM NH4OH with 0.5% Triton X-100 after which FGF2 was extracted using the salt buffer. FGF2 was quantified in all sample extracts using an FGF ELISA (R&D Systems) 23.
Endothelial permeability
Endothelial permeability was assessed through immunocytochemistry and a custom permeability assay. For immunocytochemistry, samples were exposed to 0, 8, or 24 hours of 20 dynes/cm2 shear stress. Cells were immediately fixed with 4% paraformaldehyde, permeabilized with 0.1% Triton X-100, and blocked with 1% bovine serum albumin. Samples were then incubated with a primary antibody for β-catenin (Invitrogen), followed by an Alexa Fluor 488 secondary antibody (Invitrogen) together with bisbenzimide (nuclei). Samples were imaged using an Olympus IX81 inverted confocal microscope (60X). In the custom permeability assay, cell permeability was assessed by quantifying FGF2 that moved through an intact endothelial monolayer and bound to the sub-endothelial basement membrane 23,24. PAEC exposed to 0, 8, or 24 hours of 20 dynes/cm2 shear stress were immediately incubated in serum-free DMEM supplemented with 0 or 10 ng/mL FGF2 at 37°C. After two hours, the cells were lysed in 20 mM NH4OH with 0.5% Triton X-100 after which basement membrane FGF2 was extracted and quantified as previously described. The amount of basement membrane bound FGF2 in samples that were not exposed to exogenous FGF2 was subtracted from these values to account for differences in basal FGF2 with flow.
Statistical analysis
Statistical analyses were conducted using GraphPad Prism. Data are presented graphically as mean ± standard deviation. Comparisons between two groups were analyzed by Student’s t-test, while comparisons among multiple groups were analyzed by ANOVA with a Tukey-Kramer post-hoc test. Experiments were repeated three times, and data represent one experiment out of three.
FGF2 Model Development
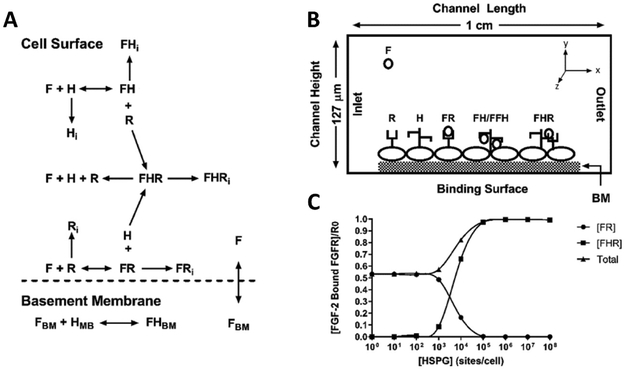
The computational model geometry was based on the Glycotech parallel plate flow chamber 16, which was 6 cm long, 1 cm wide, and 0.0127 cm high. Flow properties and species distribution were assumed constant along the channel width, allowing us to reduce the model to 2D with flow along the x axis and diffusion along the y axis. Diffusion along the x axis was ignored due to a calculated Peclet number of 60 25. Chamber length was reduced to 1 cm to reduce simulation time. Our prior studies showed that this did not significantly affect results 16. Fluid entered through the inlet boundary, passed over the bottom reactive surface with uniform reactive site (HSPG and FGFR) distribution, and exited through the outlet boundary (Figure 1B).
Figure 1:
Computational model reactions, schematics, and validation. (A) Model schematic showing reactive species and bound complexes. F = FGF2, R = FGFR, H = HSPG, FR = FGF2-FGFR, FH = FGF2-HSPG, FHR = FGF2-HSPG-FGFR (triad), BM = basement membrane. The subscript i indicates internalized species. (B) Computational model geometry showing parallel plate flow chamber and bottom reactive boundary with uniform H and R distribution. (C) Model validation at 4° C. Increasing cell surface HSPG concentration leads to increased FHR formation and decreased FR.
The model coupled three parts: (1) fluid flow, (2) FGF2 convective and diffusive mass transport, and (3) FGF2 binding kinetics.
Fluid flow
The fluid was defined as an incompressible Newtonian fluid with no-slip boundary condition at the walls and outlet to atmospheric pressure. The experimental flow chamber was modeled as two infinite parallel plates 26. The entrance length, defined as the distance required for fully developed flow, was calculated as less than 2.4% of channel length 16. Therefore, fully developed laminar flow was assumed through the chamber. The parabolic flow profile was given by:
where vmax is maximum flow velocity, h is total chamber height, and y is distance from the binding surface.
FGF2 convective and diffusive mass transport
FGF2 transport was defined using the standard convection–diffusion mass balance equation:
where [F] is FGF2 concentration, D is FGF2 diffusion coefficient and u is velocity vector. The diffusive term defines FGF2 transport due to the concentration gradient. The convective term describes FGF2 transport due to fluid flow down the chamber.
The outlet boundary was defined as a convective flux surface through which FGF2 exits the system. The upper chamber surface was defined as a non-binding insulation boundary, and the bottom chamber surface was defined as a binding insulating boundary.
FGF2 binding kinetics
In the model, FGF2 reacted with HSPG and FGFR to form a variety of complexes (Figure 1A). FGF2 could bind to FGFR to form an FGF2-FGFR complex (FR). FGF2 could bind to HSPG to form an FGF2-HSPG complex (FH). After FGF2 binds to FGFR or HSPG, this complex could then capture a free HSPG or FGFR, respectively, to form an FGF2-HSPG-FGFR triad (FHR; treated as the primary signaling complex.). FGF2 in the fluid could also permeate across the endothelial monolayer to bind basement membrane HSPG (HBM). All surface species could be internalized and degraded.
We also included in the model ways in which the cell surface receptors could vary with shear stress. In our prior research, we showed that basement membrane HSPG binding availability increased with shear stress 15. To simulate this effect, we introduced an availability parameter, α, which increases the proportion of available HSPG binding sites as shear stress increases. Our model also allows cell surface HSPG to increase through HSPG production (PH). We additionally included ways in which cell surface HSPG could decrease, including HSPG internalization (ki,H) and shedding (ks,H). Several of these parameters have previously been shown to vary with shear stress. For example, shear-induced HSPG shedding has been observed in ischemic conditions 27 and explored in a computational model studying HSPG regrowth following enzymatic degradation 28.
The model included several simplifications, either because the effects of specific processes were modest or because reaction rates have not been quantified. FGF2 in the fluid did not degrade or form homodimers, and no soluble HSPG or FGFR were initially present. HSPG shed from the cell surface did not bind FGF2 in the fluid since the base HSPG shedding rate is low. In addition, since FGF2-HSPG binding in the fluid has not been shown to be affected by shear stress, this process would similarly affect both static and flow conditions. FHR dimerization was not included in the model as there are no experimentally determined kinetic parameters in the literature. Internalized HSPG were only degraded, not recycled back to the cell surface, as there are no experimentally determined kinetic parameters in the literature and recycling has been shown to represent only about 0.2% of cell surface HSPG 29. At the binding surface, FGFR and HSPG were homogenously distributed, all complexes dissociated back to their constituent molecules and FGF2-HSPG-FGFR did not form dimers.
Cell surface species concentrations were defined to change with time in the computational model based on the possible reactions as described by:
| (1) |
| (2) |
where α is defined as the proportion of HSPG available to bind FGF2.
FGF2 complex concentrations were defined to change with time based on association, dissociation, and internalization rates as described by:
| (3) |
| (4) |
| (5) |
Internalized cell surface species concentrations were defined to change with time based on internalization and degradation rates as:
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
FGF2 volumetric concentration in the bulk fluid was coupled to the binding surface at y = 0. Dissociation of cell surface complexes released FGF2 into the fluid, while binding of FGF2 to cell surface species depleted FGF2 from the fluid:
| (11) |
FGF2 could additionally traverse the monolayer and bind to basement membrane HSPG as:
| (12) |
| (13) |
where PF is permeation rate and [F] – [FBM] is FGF2 concentration gradient across the monolayer. We assumed diffusion was negligible through the basement membrane, since basement membrane thickness is estimated to be ~50 nm 30,31. We therefore modelled the basement membrane as a flat surface, using the basement membrane thickness to convert volumetric species [F] to surface species [FBM] dimensions.
Parameters
Simulation parameters are listed in Table 1. The Glycotech flow chamber defined model geometry. Fluid FGF2 concentration was set at the experimental value of 10 ng/mL (5.56 × 10−4 µM). Initial FGFR and HSPG surface concentrations were set to experimentally determined values of 2.5 × 103 receptors/cell (4.15 × 10−12 mol/m2) and 1.3 × 105 receptors/cell (2.16 × 10−10 mol/m2), respectively, for cardiac microvascular endothelial cells 32,33. Basement membrane HSPG surface concentration was defined as the experimentally determined value (4.48 × 10−8 mol/m2) 16,34. Initial cell-surface FGF2 was 0, while initial basement membrane FGF2 concentration was 1.74 × 10−14 mol/m2 (volumetric FGF2 concentration of 0.35 pmol/cm3 converted to mol/m2 using basement membrane thickness of 50 nm) 32.
Table 1.
Base model parameter values
| Model Geometry | |||
| H | 1.27 × 10−4 m | Height of the chamber | Text |
| L | 0.01 m | Width of chamber | Text |
| HBM | 5 × 10−8 m | BM thickness | 32,64 |
| Initial Concentration | |||
| F0 | 10 ng/ml (5.56 × 10−4 µM) | FGF2 Concentration | Text |
| R0 | 4.15 × 10−12 mol/m2 | FGFR Concentration | 32,65 |
| H0 | 2.16 × 10−10 mol/m2 | HSPG Concentration | 32,65 |
| H0, BM | 4.48 × 10−8 mol/m2 | BM HSPG Concentration | 32,66 |
| F0, BM | 1.74 × 10−14 mol/m2 | BM FGF2 basal concentration | 32 |
| Diffusion Properties | |||
| DF | 1.32 × 10−8 m2/min | FGF2 Diffusivity | 32,35 |
| Surface Binding | |||
| kon,FR | 4.2 × 102 μM−1 min−1 | Association FGF2-FGFR | 32,35 |
| koff,FR | 0.79 min−1 | Dissociation FGF2-FGFR | 32,35 |
| kon,FH | 1.2 × 102 μM-1 min−1 | Association FGF2-HSPG | 32,35 |
| koff,FH | 1.37 min−1 | Dissociation FGF2-HSPG | 32,35 |
| kon,FHR | 1 × 108 (µmol/cm2)−1 min−1 | Association FGF2-HSPG-FGFR | 35 |
| koff,FHR | 0.038 min−1 | Dissociation FGF2-HSPG-FGFR | 32,35 |
| ks,H | 5.84 × 10−4 min−1 | HSPG shedding from cell surface | 36 |
| Internalization | |||
| ki,R | 0.005 min−1 | Internalization FGFR | 32,35 |
| ki,H | 0.0317 min−1 | Internalization HSPG | 36,67 |
| ki,FR | 0.078 min−1 | Internalization FGF2-FGFR | 32,35 |
| ki,FH | 0.0048 min−1 | Internalization FGF2-HSPG | 68 |
| ki,FHR | 0.043 min−1 | Internalization FGF2-HSPG-FGFR | 32,35 |
| Production | |||
| PR | ki,R*R0 | Production FGFR | 32,35 |
| PH | ki,H*H0 | Production HSPG | 32,35 |
| Degradation | |||
| kd,H | 5 × 10−3 min−1 | Degrade HSPG | 32,35 |
| kd,FR | 20 × 10−3 min−1 | Degrade FGF2-FGFR | 32,35 |
| kd,FH | 5.6 × 10−3 min−1 | Degrade FGF2-HSPG | 32,35 |
| kd,FHR | 5.6 × 10−3 min−1 | Degrade FGF2-HSPG-FGFR | 32,35 |
| Basement Membrane | |||
| kp | 7.2 × 10−7 m/min | BM Permeability | 32 |
| kon,BM | 25.2 μM−1 min−1 | Association FGF2-HSPG in BM | 69 |
| kon,BM | 0.6 min−1 | Dissociation FGF2-HSPG in BM | 69 |
| α | 1 | Total HSPG Availability | Text |
FGF2 diffusion (D) in water at 37˚C was calculated using the Stokes-Einstein equation, given by D=kT/(6πηa), where D is diffusivity (m2/s), k is Boltzmann’s constant (1.3807 × 10−23 J/K), T is absolute temperature (Kelvin), η is water viscosity (0.72 cP at 37°C), and a is FGF2 molecular radius (14.5 Å).
FGF2 association and dissociation rate constants at 37°C were obtained from Filion et al 35, in which the Arrhenius equation (14) was used to scale FGF2 binding kinetic rate constants that were experimentally determined at 4°C for Balb/c3T3 cells to 37°C:
| (14) |
where T1 = 4°C, T2 = 37°C, Ea is the reaction activation energy and R is the universal gas constant. HSPG shedding rate came from experimental data presented in the literature 36.
Unoccupied FGFR and HSPG, along with FR, FH and FHR complexes, were assumed to be internalized and degraded. Internalization and degradation rates were set to experimentally determined values at 37°C 37,38. FGFR and HSPG were assumed to be constitutive; therefore, production rates were set as the product of internalization rate and surface concentration35.
Finally, endothelial monolayer FGF2 permeability was approximated using comparably sized α-lactalbumin 39. FGF2 basement membrane association and dissociation rates were set to experimentally determined values within Descemet’s membrane at 37°C 32,40.
Model implementation and validation
The model was implemented in COMSOL Multiphysics®. COMSOL automatically optimized mesh quality over most of the model geometry, with a maximum element size of 670 µm and a minimum element size of 3 µm 16. At the binding surface, maximum element size was limited to 1 µm to provide a high-resolution prediction of FGF2 complex concentration 16. The final mesh was chosen as the minimum number of elements that converged to a stable equilibrium solution (less than 0.1% change when element number was increased). Unless otherwise specified, all simulations were run for 300 minutes in 1-minute step sizes.
To validate binding kinetics, we changed cell surface HSPG concentration under static conditions and measured FH and FHR formation at 4°C as described in the literature 35,41,42. Our model shows that as cell surface HSPG increase, FR complexes decrease, and FHR triads increase (Figure 1C). We additionally recreated model predictions from our own work 16 and the literature 35.
The model was fit to experimental data using a least-square objective function (SNOPT algorithm) in COMSOL. SNOPT allowed us to constrain parameter fits by defining upper and lower bounds as 1 × 102 and 1 × 10−2 times the base model parameter, respectively. We then used the best fit of specific shear stress data (0, 10, 20, 40 dyne/cm2) to estimate a generalized fit vs. shear stress for each parameter.
III. Results
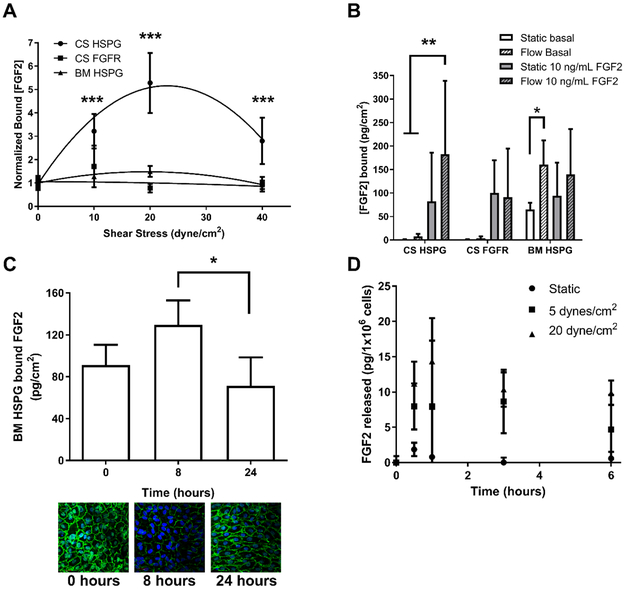
We first experimentally measured FGF2 binding to endothelial cells at 37°C under varied fluid flow conditions (Figure 2A). As shear stress increased from 0 to 20 dynes/cm2, FGF2 binding to cell surface HSPG increased five times and then decreased as shear stress increased to 40 dynes/cm2. FGF2 binding to cell surface FGFR showed no change with shear stress. Similar to previous results, FGF2 binding to basement membrane HSPG increased and then decreased with shear stress, although the magnitude of the change was smaller than for cell surface HSPG 15. Two-way ANOVA indicated that flow rate and receptor effects were both statistically significant, as was their interaction (p < 0.001). In addition, Tukey’s post-hoc test indicated that FGF2 binding to cell surface HSPG at 10, 20, and 40 dynes/cm2 were all statistically significantly different from static (p < 0.0001).
Figure 2:
FGF2 binding to cell surface and basement membrane HSPG peaks around 20 dynes/cm2 shear stress. (A) PAEC were adapted to varied shear stress levels (0 – 40 dynes/cm2) for 24 hours and then exposed to 10 ng/mL FGF2 at the same shear stress level for an additional two hours at 37°C. FGF2 bound to cell surface HSPG and FGFR, as well as basement membrane HSPG were extracted and quantified by ELISA. (B) PAEC adapted to 0 or 20 dynes/cm2 shear stress were treated with 0 (basal) or 10 ng/mL FGF2 for two hours at 37°C. FGF2 bound to cell surface HSPG and FGFR, as well as basement membrane HSPG was extracted and quantified by ELISA. (C) To assess permeability, PAEC were exposed to 0, 8 or 24 hours of 20 dynes/cm2 shear stress and then treated with 10 ng/mL FGF2. Cells were then lysed, and the FGF2 that permeated the endothelial monolayer and bound to the basement membrane was extracted and quantified by ELISA. Alternatively, cells were fixed and labeled for β-catenin (green) and nuclei (blue). (D) To assess FGF2 release from cells exposed to flow, FGF2 was quantified in media samples from PAEC exposed to 0 or 20 dynes/cm2 shear stress by ELISA. FGF2 was normalized for both media volume and cell number, and therefore is expressed as pg/1×106 cells. * p < 0.01; ** p < 0.001; *** p < 0.0001.
Endothelial cells also produce and release FGF2. We therefore measured FGF2 binding to the endothelial cell surface and basement membrane under static and flow conditions (20 dynes/cm2) without (basal) and with added FGF2 (10 ng/mL) to determine if changes in FGF2 binding with flow related to cell-released FGF2 or exogenous FGF2 addition. FGF2 bound to cell surface receptors (both HSPG and FGFR) was low under basal conditions but increased significantly when FGF2 was added (Figure 2B). FGF2 bound to cell surface HSPG only differed with flow when exogenous FGF2 was added, suggesting that flow-induced changes in cell surface bound FGF2 depend on exogenous FGF2 addition. In contrast, FGF2 bound to basement membrane HSPG was high under basal conditions, likely since the basement membrane has a large FGF2 binding capacity and is thought to serve as an FGF2 reservoir 34. FGF2 bound to basement membrane HSPG also increased significantly with flow (p < 0.05); however, FGF2 bound to basement membrane HSPG did not significantly increase when exogenous FGF2 was added. These data suggest that flow-induced changes in basement membrane bound FGF2 depend primarily on FGF2 released from cells.
We next experimentally examined the mechanism for increased basement membrane FGF2 with flow. Our data show that the endothelial monolayer became 50% more permeable after eight hours of flow, and monolayer permeability decreased after 24 hours of flow adaption (p < 0.05 for 8 vs 24 hours). The permeability increase was not FGF2 specific, since we similarly demonstrated that endothelial cells adapting to flow were more permeable to FITC-streptavidin (data not shown). Endothelial monolayers labeled for the cell-cell junction protein β-catenin showed decreased fluorescence intensity after 8 hours of flow, further suggesting that cell-cell junction integrity is compromised during flow adaptation (Figure 2C). PAEC also released more FGF2 under fluid flow (in pg/1×106 cells; normalized to both fluid volume and cell number to account for differences between static and flow conditions), with media FGF2 rising significantly in all flow conditions after 30 minutes (p < 0.01 by one-way ANOVA). These data suggest that basement membrane FGF2 storage increased with flow due to a combination of increased monolayer permeability and FGF2 release.
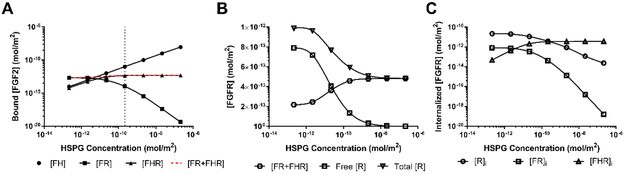
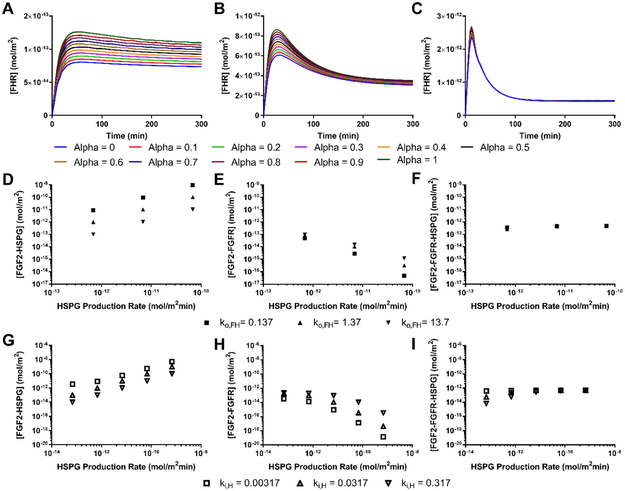
We then tried to experimentally determine the mechanism for increased FGF2 binding to cell surface HSPG with flow; however we were unable to obtain consistent results, specifically for available cell surface HSPG. We therefore used our computational model to predict which aspects of flow were likely to contribute to biphasic binding of FGF2 to cell surface HSPG under flow. The base computational model, run to equilibrium, failed to accurately reproduce the experimental results. Instead, FGF2 bound to cell surface HSPG remained constant at all shear stress levels, suggesting that it is not flow itself but cell adaptation to flow that alters FGF2 binding. We therefore hypothesized that flow-induced changes in HSPG binding sites contribute to the change in FGF2 bound to cell surface HSPG with flow. We varied HSPG cell surface concentration (H0) in the model three orders of magnitude above and below the base value, represented by the dotted line (Figure 3A). The model predicted that FGF2 bound to cell surface HSPG as FH would increase proportional to HSPG concentration. FGF2 bound to FGFR as FR was predicted to decrease with increasing HSPG, while FGF2 bound to both FGFR and HSPG as FHR was predicted to increase only slightly. Total FGF2 bound to FGFR in any form (FR + FHR) was predicted to remain nearly the same (Figure 3A, red dashed line), suggesting that FGFR was limiting. To further understand how HSPG concentration affected FGF2 binding to FGFR, we examined the amount of free, bound (FR + FHR), and total FGFR as HSPG increased (Figure 3B). At the highest HSPG concentrations, all FGFR were bound to FGF2 and no FGFR were free, confirming that FGFR are limiting as HSPG increases. While bound FGFR (FR + FHR) did increase with HSPG concentration, the increase was not of the same magnitude as the free FGFR decrease. This effect was explained by examining total FGFR, which also decreased with increasing HSPG. To understand decreased cell surface FGFR with increasing HSPG, we examined FGFR internalization as R, FR, and FHR (Figure 3C). As HSPG increased, FGFR internalization occurred primarily in the form of FHR. Since the FHR internalization rate is faster than the FR internalization rate, higher FHR formation with increased HSPG decreased total cell surface FGFR.
Figure 3:
Increased cell surface HSPG concentration increased FGF2-HSPG (FH) complexes and decreased FGF2-FGFR (FR) complexes but did not affect FGF2-HSPG-FGFR (HFR) complexes. (A) Predicted values of FH, FR, FHR, and FR+FHR as HSPG concentration was increased from 2.16 × 10−13 to 2.16 × 10−7 mol/m2 (α=1; ki,H, ksH, koFH at base values). (B) FGFR state as free FGFR (no bound FGF2), FGF2 bound FGFR (FR+FHR) and total FGFR with increasing HSPG concentration.. (C) FGFR internalization as free FGFR (R), FGF2-FGFR (FR), and FGF2-HSPG-FGFR (FHR) with increasing HSPG concentration. Flow rate 2.1 mL/min; [FGF2] = 10 ng/mL (5.56 × 10−5 µM); [FGFR] = 4.15 × 10−12 mol/m2.
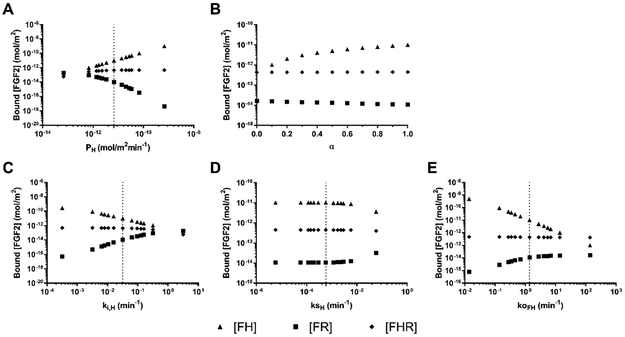
We then investigated several possible mechanisms that could increase cell surface HSPG binding sites to model increased FGF2 binding to HSPG at moderate flow rates, specifically HPSG production and availability. We did not vary FGF2-HSPG association rate (kon), since our previously published work and preliminary studies suggested that fluid flow did not change FGF2 association to basement membrane or cell surface HSPG 15. Instead we varied HSPG production rate several orders of magnitude above and below the base HSPG production rate (indicated by the dotted line) while keeping HSPG availability (α) at 1 and all other parameters at their base values (Figure 4A). Varying HSPG production rate had a large effect on HSPG concentration. The total amount of cell surface HSPG increased from ~10−12 mol/m2 at a production rate of 10−15 mol/m2min to ~10−8 mol/m2 at a production rate of 10−11 mol/m2min. When HSPG production rate was changed, the model predicted that FGF2 bound to HSPG (FH) would increase or decrease proportionally. FGF2 bound to only FGFR (FR) was predicted to decrease as HSPG increased, since FRs would quickly bind to an available HSPG. Triad formation was predicted to increase only slightly, since FHR internalization rate is higher than FR internalization rate and therefore the total FGFR concentration decreased as HSPG concentration increased (as shown in Figure 3). Changing HSPG production did not change the proportion of HSPG that were occupied by FGF2. Similarly, increasing cell surface HSPG availability (α) was predicted to increase the FH complex formation but not FHR triad formation (Figure 4B). These data suggest that increased cell surface HSPG availability could increase the FGF2 reservoir (as FH) rather than FGF2 signaling (as FHR).
Figure 4:
HSPG production, internalization, and FGF2-HSPG dissociation rate had the largest effect on cell surface bound FGF2. Bound FGF2 as FGF2-HSPG (FH), FGF2-FGFR (FR), and FGF2-HSPG-FGFR (FHR) with varied (A) HSPG production rate (PH) from 1.14 × 10−14 to 1.14 × 10−10 mol/m2min−1 (α=1; ki,H, ksH, koFH at base values); (B) HSPG availability (α) from 0 to 1 in 0.1 intervals (PH, ki,H, ksH, koFH at base values); (C) HSPG internalization rate (ki,H) from 3.17 × 10−4 to 3.17 × 100 min−1 (α=1; PH, ksH, koFH at base values); (D) HSPG shedding rate (ksH) from 5.84 × 10−7 to 5.84 × 10−1 min−1 (α=1; PH, ki,H, koFH at base values); and (E) FH dissociation rate (ko,FH) from 1.37 × 10−2 to 1.37 × 102 min−1 (α=1; PH, ki,H, ksH at base values). Initial model values: [FGF2] = 10 ng/mL (5.56 × 10−5 µM); [HSPG] =2.16 × 10−10 mol/m2; [FGFR] = 4.15 × 10−12 mol/m2; flow rate = 2.1 mL/min; simulation time = 300 min. Base values are indicated by dotted lines.
We next investigated several possible mechanisms that could decrease cell surface HSPG binding sites to model decreased FGF2 binding to HSPG at high flow rates, specifically HPSG internalization and shedding. Changing HSPG internalization rate over several orders of magnitude (while maintaining α = 1 and all other parameters at their base values) created the opposite effect on cell surface HSPG concentration and FGF2 binding as HSPG production. As HSPG internalization increased, FGF2 binding to HSPG (as FH) was predicted to decrease, FGF2 binding to FGFR (as FR) was predicted to increase, and FGF2 binding to both HSPG and FGFR (as FHR) was predicted to decrease only slightly (Figure 4C). While cell surface HSPG shedding was previously shown to increase in response to inflammation and shear stress, in our model it had little effect on FH, FR, or FHR formation unless the shedding rate increased by several orders of magnitude from the basal rate (dotted-line, Figure 4D) 36. Increasing ksH by four orders of magnitude only decreased cell surface HSPG concentration by about two times. Finally, it has recently been proposed that FGF2 and heparin demonstrate slip-bond characteristics 21. We therefore varied FGF2-HSPG koff several orders of magnitude above and below the base value (dotted line, Figure 4E). The model predicted a negative linear relationship between the koFH and FH complex formation along with a smaller increase in FR complex formation. Only increasing FH dissociation rate significantly decreased the proportion of occupied HSPG.
We next examined the interactions among model parameters. We systematically varied two model parameters at a time and selected those which we found most interesting. In our simulations, we found that decreasing FGF2 concentration decreased equilibrium FGF2 binding and increased the time to equilibrium. In addition, we found that decreasing FGF2 concentration altered the effect of the HSPG availability parameter, α (Figure 5A-C). At 10 ng/ml FGF2, the model predicted a large, early peak in FHR formation followed by a much lower equilibrium FHR concentration, with no apparent change in FHR concentration with α. However, at lower FGF2 concentrations (0.1 and 1 ng/ml), the early FHR peak significantly decreased in size and equilibrium FHR concentration noticeably increased with α. These data suggest that HSPG availability with flow may have larger effects at lower FGF2 concentrations.
Figure 5:
Interaction studies between model parameters. (A-C) FGF2-HSPG-FGFR (FHR) showed a larger transient peak at high FGF2 concentrations, whereas HSPG availability α had a larger effect on equilibrium FHR at lower FGF2 concentrations. Varied simulation parameters were FGF2 concentration (A) 0.1, (B) 1, and (C) 10 ng/ml; α = 0-10 in 0.1 increments. All other parameters at base values. (D-F) The highest HSPG production rate interacted with FH dissociation rate to decrease FGF2-FGFR formation, which FHR formation was unaffected by the parametric changes. (D) FH, (E) FR, and (F) FHR. All other parameters at base values. (G-I) At the lowest HSPG production and highest HSPG internalization rate, HSPG became limiting which decreased FH and FHR formation and increased FR formation. (G) FH, (H) FR, and (I) FHR. [FGF2] = 0.1-10 ng/mL (5.56 × 10−7 - 5.56 × 10−5 µM); [HSPG] =2.16 × 10−10 mol/m2; [FGFR] = 4.15 × 10−12 mol/m2; flow rate = 2.1 mL/min; Simulation time = 300 min.
We then studied the interaction between HSPG production and FH dissociation (Figure 5D-F). While there was no interaction between HSPG production and FH dissociation rate for FH formation, FR formation decreased more with HSPG production at the lowest FH dissociation rate. This condition resulted in the highest FH formation, causing fewer FGFR to remain in an FR complex rather than an FHR complex. Interestingly, FHR formation was essentially the same across all HSPG production and FH dissociation rates, likely reflecting the decreased total pool of FGFR as HSPG concentration increased. This suggests that if both HSPG production and FH dissociation were to increase in response to fluid-induced shear stress, as suggested by the literature, endothelial cell FGF2 signaling as FHR would not be affected; we would instead observe less FH forming an FGF2 storage reservoir at the cell surface.
The last interaction we examined was between HSPG production and internalization (Figures 5G-I). These two parameters largely balance each other out; however when HSPG production was decreased and HSPG internalization was increased, we observed that HSPG became limiting in FGF2 binding kinetics. At the lowest HSPG production rates, HSPG internalization had the largest decrease in FH formation, the smallest effect on FR formation, and a significant effect on FHR formation. While in most cases FGFR are limiting in FHR formation, when HSPG production decreases and internalization increases, HSPG can be the limiting factor.
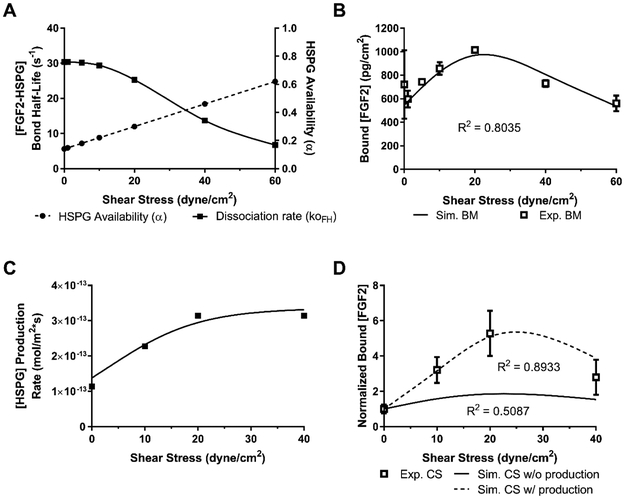
Finally, we used our prior study of FGF2 binding to basement membrane HSPG in flow as well as the computational model predictions from this study to create a model of FGF2 binding to the endothelial cell surface under flow conditions. In our prior work, we showed that binding of an HSPG antibody to the basement membrane increased linearly with flow 43. Since no HSPG can be produced by isolated basement membrane, we hypothesized that this increase was caused by increased HSPG availability (α) with flow. Using these data, we calculated α = 0.14 at a shear stress of 0 dynes/cm2, suggesting that only a small portion of HSPG is available in static conditions. We then estimated based on our data that all HSPG binding sites would be available at 100 dynes/cm2. Using these two data points, we created a linear fit and predicted the α value at all measured data points (Figure 6A). Increased HSPG availability with shear stress could model the increase in FH formation up to moderate shear stress levels but could not account for the decrease in FH at high shear stress levels. We therefore used COMSOL to estimate the FH dissociation rates (koff,FH) that would enable the model to best fit the decreased FH complex formation at high shear stress in our basement membrane data (Figure 6A; plotted as bond half-life). The combination of increased HSPG availability and decreased bond half-life produced a good fit to our data on the change in basement membrane FH formation in flow (Figure 6B, R2 = 0.80).
Figure 6:
The cell surface computational model was fit to the cell surface experimental data using the basement membrane-derived relationships between HSPG availability and FH dissociation with flow and also adding increased production with flow. (A) HSPG availability α was modeled to linearly increase with shear stress based on experimental basement membrane data. FH bond was modeled to decrease in response to shear stress like a slip-bond, with values developed by fitting to the basement membrane data. (B) The computational model with increased HSPG availability and increased FH dissociation closely matched the basement membrane experimental data. (C) A relationship between HSPG production and shear stress was developed to best fit the computational model to the experimental data. HSPG production increased by a factor of three at 20 dyne/cm2. (D) The computational model closely matched the experimental data only when increased HSPG production was included. [FGF2] = 10 ng/mL (5.56 × 10−5 µM); [HSPG] =2.16 × 10−10 mol/m2; [FGFR] = 4.15 × 10−12 mol/m2; flow rate = 2.1 mL/min; Simulation time = 300 min.
We then used just these changes in basement membrane FH formation with flow in the cell surface model. Unfortunately, HSPG availability and FH dissociation failed to accurately reproduce the change in FH formation with flow at the cell surface (Figure 6D, solid line; R2 = 0.51). We therefore added in a change in HSPG production, as has previously been reported in the literature, assuming that HSPG production would increase up to a shear stress of 20 dyne/cm2. When we fit HSPG production to the 10, 20, and 40 dyne/cm2 cell surface experimental data points, HSPG production rate increased by three times (Figure 6C). Including this production term allowed the model to match our experimental data (Figure 6D, R2 = 0.92). We therefore hypothesize that FGF2 binding to cell surface HSPG increases and then decreases with flow through alterations in HSPG availability and production as well as FGF2-HSPG dissociation rate.
IV. Discussion
FGF2 binding kinetics are essential to vascular processes, including angiogenesis, and should be studied under physiological flow conditions. We therefore used experimental and computational approaches to investigate how FGF2 binding to endothelial cell surface receptors and the sub-endothelial basement membrane changes under fluid flow. We now show experimentally that FGF2 bound to cell surface HSPG increased up to a shear stress of 20 dynes/cm2 and then decreased at higher shear stresses, whereas FGF2 bound to cell surface FGFR remained constant. FGF2 bound to the sub-endothelial basement membrane also increased with flow, likely due to a combination of increased monolayer permeability and FGF2 release during flow adaptation. A computational model of FGF2 binding under flow predicted that the change in FGF2 bound to cell surface HSPG related to cellular changes following flow adaptation, rather than transport effects. Specifically, model predictions suggest that the change in FGF2 binding to cell surface HSPG with flow relates to changes in HSPG production, availability, and FH dissociation. These data suggest that flow modifies FGF2 receptors at the cell surface as well as FGF2 binding rates, and therefore is important to consider when studying FGF2 binding kinetics.
In previous work, we showed that FGF2 binding to basement membrane HSPG similarly increased and then decreased with shear stress 15. We postulated and our data supported that the effect related to increased binding site availability and FGF2-HSPG dissociation. The current study on endothelial cells showed a much larger increase in FGF2 binding to cell surface HPSG in flow (500% increase) as compared to the increased in FGF2 binding to basement membrane HSPG in flow (100% increase). This change likely relates to active cell processes that modulate HSPG availability, in particular HSPG production.
Our experimental data further showed that whereas cell surface FGF2 depended on exogenous FGF2 addition, basement membrane FGF2 depended on a combination of endothelial cell released FGF2 and monolayer permeability. Studies have shown that endothelial monolayers exposed to flow in vitro increase permeability after flow initiation 44–47. At later times (~24 hours), endothelial monolayer permeability is lower in flow-adapted cells than cells in static conditions. FGF2 can be transported across the endothelium through leaky cell-cell junctions or via vesicles 48. While pinocytosis and endocytosis have been shown to increase with shear stress exposure 49,50, extensive data suggest that endothelial adherens and tight junctions remodel during flow adaptation, which increases monolayer permeability and transendothelial transport 51–54. In our previous work, we also showed that intercellular junction breakdown by high glucose increased basement membrane FGF2 23.
While we were not able to demonstrate a change in cell surface HSPG with flow, experimental and computational studies by others have suggested that cell surface HSPG availability is flow dependent. Giantsos-Adams et al. used fluorescence microscopy to show that the heparan sulfate content of the endothelial glycocalyx increased 1.4-fold after cells adapted to 15 dynes/cm2 shear stress 20. Flow-adapted EC also recovered their HSPG content more quickly following enzymatic degradation than did cells in static conditions. Liu et al. further showed that syndecan 1–4 and glypican-1 mRNA expression increased in EC exposed to 4, 10, or 15 dynes/cm2 shear stress 19. Experimental evidence also suggests that shear stress decreases endothelial HSPG internalization, which occurs via a clathrin- and caveolae-independent mechanism 43,55,56. Barkerfors et al. visualized HSPG internalization in endothelial cells cultured in static conditions or 11 dyne/cm2 shear stress 57. While endothelial cells internalized HPSG in static conditions, HSPG internalization was not detected in cells adapted to flow. HSPG are also shed from the endothelial cell surface in physiological and pathological situations, including under shear stress 27,58. While HSPG production and internalization rates affected HSPG-bound FGF2, our model showed little sensitivity to shedding, since the HSPG shedding rate is two orders of magnitude lower than HSPG production and internalization rates. Unless shedding rate increases substantially in flow, it is unlikely to significantly contribute to changes in FGF2-HSPG complex formation in flow adapted cells.
FGF2 binding kinetics to cell surface HSPG have also been suggested to change in response to forces similar to those experienced by cells in flow. FGF2 may dimerize on a single HSPG and possibly form higher order oligomers 10,59. Venkataraman et al. used MALDI-mass spectrometry to quantify FGF2 oligomer formation with heparin like glycosaminoglycans. Their results demonstrated that while monomers and dimers were most abundant, trimer, tetramer and pentamer formation was also possible. Computational studies of the endothelial glycocalyx have suggested that shear stress stretches cell surface HSPG 60–62, which would expose additional FGF2 binding sites and increase FGF2 capture by HSPG as FGF2 dimers in flow. Sevim et al. investigated the nanomechanics of the FGF2-HSPG bond itself using atomic force microscopy 21. Their data suggest that FGF2-HSPG dissociation rate was constant at loading rates of 101 to 106 pN/s but then increased approximately 4500 times at higher loading rates. In addition, bond lifetime decreased as clamping force increased, keeping with slip bond dissociation. Since it is difficult to estimate the actual flow-induced force experienced by an FGF2-HSPG bond using Bell’s equation 63, we modeled the potential effect of FGF2-HSPG slip bond characteristics by changing koff over several orders of magnitude.
While our model represents the first attempt, to our knowledge, to account for the effects of changes in endothelial cell surface HSPG with flow on FGF2 binding kinetics, it is not without limitations. In both the experiments and simulations, we only analyzed steady flow. It is possible that other mechanical stimuli, including flow pulsatility, cyclic stretch, and vascular wall compliance may also affect FGF2 binding kinetics. While we did not measure any differences in medium components in the flow vs. static conditions (e.g., FGF2 or HSPG), it is possible that differences in the medium may account for some of the flow-induced FGF2 binding differences. We assumed a general HSPG molecule at our cell surface and did not distinguish between the different molecules under the HSPG family (syndecans and glypicans). We did not include FHR dimerization, which has been postulated to be important in FGF2 signaling, since association and dissociation rates have not been experimentally determined. We assumed that FGF2 association to HSPG did not vary with flow, based on our prior work and unpublished data. For model simplicity or due to lack of binding parameters, we neglected several factors that may also affect FGF2 binding kinetics, including FGF2 degradation or dimerization in the fluid, soluble or shed HSPG and FGFR binding to FGF2 in the fluid, HSPG recycling after internalization, and FGF2-HSPG-FGFR dimers. Finally, we modeled the basement membrane as a flat surface and thereby neglected transport through the basement membrane.
We now present a flow-adapted endothelial cell model which includes an increase in HSPG production, HSPG availability, and FGF2-HSPG dissociation rate with shear stress. The model fits well with our experimental data and other published work on endothelial cell flow adaptation. Additional studies of HSPG dynamics under flow conditions are needed to confirm if the changes in FGF2 binding to HSPG in flow are indeed related to these three parameters alone or if other factors play an important role. It would also be valuable to examine the effects of other mechanical stimuli, including pulsatility, cyclic stretch, and vascular wall compliance, on HSPG dynamics and FGF2 binding kinetics. This model elucidates how flow-induced changes in endothelial cell surface receptors may impact FGF2 binding and signaling and highlights the need to conduct FGF2 binding and signaling studies in physiological mechanical environments.
Abbreviations:
- FGF2
Fibroblast Growth Factor 2, basic Fibroblast Growth Factor
- HSPG
Heparan Sulfate Proteoglycan
- FGFR
Fibroblast Growth Factor Receptor
- EC
Endothelial Cell
References:
- 1.Bikfalvi A, Klein S, Pintucci G, Rifkin DB. Biological roles of fibroblast growth factor-2. Endocr Rev. 18:26–45, 1997. [DOI] [PubMed] [Google Scholar]
- 2.Chua CC, Rahimi N, Forsten-Williams K, Nugent MA. Heparan sulfate proteoglycans function as receptors for fibroblast growth factor-2 activation of extracellular signal-regulated kinases 1 and 2. Circ Res. 94:316–323, 2004. [DOI] [PubMed] [Google Scholar]
- 3.Montesano R, Vassalli J-D, Baird A, Guillemin R, Orci L. Basic fibroblast growth factor induces angiogenesis in vitro. Proc Natl Acad Sci U S A. 83:7297–7301, 1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Laham RJ, Sellke FW, Edelman ER, et al. Local perivascular delivery of basic fibroblast growth factor in patients undergoing coronary bypass surgery: results of a phase I randomized, double-blind, placebo-controlled trial. Circulation. 100:1865–1871, 1999. [DOI] [PubMed] [Google Scholar]
- 5.Nugent MA, Iozzo RV. Fibroblast growth factor-2. Int J Biochem Cell Biol. 32:115–120, 2000. [DOI] [PubMed] [Google Scholar]
- 6.Moscatelli D, High and low affinity binding sites for basic fibroblast growth factor on cultured cells: Absence of a role for low affinity binding in the stimulation of plasminogen activator production by bovine capillary endothelial cells. J Cell Physiol. 131:123–130, 1987. [DOI] [PubMed] [Google Scholar]
- 7.Neufeld G, Gospodarowicz D. The identification and partial characterization of the fibroblast growth factor receptor of baby hamster kidney cells. The Journal of biological chemistry. 260:13860–13868, 1985. [PubMed] [Google Scholar]
- 8.Nugent MA, Edelman ER. Kinetics of basic fibroblast growth factor binding to its receptor and heparan sulfate proteoglycan: a mechanism for cooperactivity. Biochemistry. 31:8876–8883, 1992. [DOI] [PubMed] [Google Scholar]
- 9.Lin X, Buff EM, Perrimon N, Michelson AM. Heparan sulfate proteoglycans are essential for FGF receptor signaling during Drosophila embryonic development. Development. 126:3715–3723, 1999. [DOI] [PubMed] [Google Scholar]
- 10.Safran M, Eisenstein M, Aviezer D, Yayon A. Oligomerization reduces heparin affinity but enhances receptor binding of fibroblast growth factor 2. Biochemical Journal. 345:107–113, 2000. [PMC free article] [PubMed] [Google Scholar]
- 11.Yayon A, Klagsbrun M, Esko JD, Leder P, Ornitz DM. Cell surface, heparin-like molecules are required for binding of basic fibroblast growth factor to its high affinity receptor. Cell. 64:841–848, 1991. [DOI] [PubMed] [Google Scholar]
- 12.Zhang Z, Coomans C, David G. Membrane heparan sulfate proteoglycan-supported FGF2-FGFR1 signaling: evidence in support of the “cooperative end structures” model. The Journal of biological chemistry. 276:41921–41929, 2001. [DOI] [PubMed] [Google Scholar]
- 13.Vlodavsky I, Folkman J, Sullivan R, et al. Endothelial cell-derived basic fibroblast growth factor: Synthesis and deposition into subendothelial extracellular matrix. Proc Natl Acad Sci USA. 84:2292–2296, 1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sherwood L Human physiology: from cells to systems. 7th ed. ed: Cengage learning; 2010. [Google Scholar]
- 15.Reisig K, Clyne AM. Fibroblast growth factor-2 binding to the endothelial basement membrane peaks at a physiologically relevant shear stress. Matrix Biol. 29:586–593, 2010. [DOI] [PubMed] [Google Scholar]
- 16.Patel NS, Reisig KV, Clyne AM. A computational model of fibroblast growth factor-2 binding to endothelial cells under fluid flow. Ann Biomed Eng. 41:154–171, 2013. [DOI] [PubMed] [Google Scholar]
- 17.Zhao B, Zhang C, Forsten-Williams K, Zhang J, Fannon M. Endothelial cell capture of heparin-binding growth factors under flow. PLoS Comput Biol. 6:e1000971, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Davies PF. Flow-mediated endothelial mechanotransduction. Physiol Rev. 75:519–560, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu JX, Yan ZP, Zhang YY, Wu J, Liu XH, Zeng Y. Hemodynamic shear stress regulates the transcriptional expression of heparan sulfate proteoglycans in human umbilical vein endothelial cell. Cell Mol Biol (Noisy-le-grand). 62:28–34, 2016. [PubMed] [Google Scholar]
- 20.Giantsos-Adams KM, Koo AJ, Song S, et al. Heparan Sulfate Regrowth Profiles Under Laminar Shear Flow Following Enzymatic Degradation. Cell Mol Bioeng. 6:160–174, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sevim S, Ozer S, Jones G, et al. Nanomechanics on FGF-2 and Heparin Reveal Slip Bond Characteristics with pH Dependency. ACS Biomaterials Science & Engineering. 3:1000–1007, 2017. [DOI] [PubMed] [Google Scholar]
- 22.Reisig K, Clyne AM. Fibroblast growth factor-2 binding to the endothelial basement membrane peaks at a physiologically relevant shear stress. Matrix Biology. 29:586–593, 2010. [DOI] [PubMed] [Google Scholar]
- 23.Morss AS, Edelman ER. Glucose modulates basement membrane fibroblast growth factor-2 via alterations in endothelial cell permeability. The Journal of biological chemistry. 282:14635–14644, 2007. [DOI] [PubMed] [Google Scholar]
- 24.Figueroa DS, Kemeny SF, Clyne AM. Glycated Collagen Impairs Endothelial Cell Response to Cyclic Stretch. Cellular and Molecular Bioengineering. 4:220–230, 2011. [Google Scholar]
- 25.Cussler EL. Diffusion: mass transfer in fluid systems. Cambridge university press; 2009. [Google Scholar]
- 26.Bacabac RG, Smit TH, Cowin SC, et al. Dynamic shear stress in parallel-plate flow chambers. Journal of biomechanics. 38:159–167, 2005. [DOI] [PubMed] [Google Scholar]
- 27.Mulivor AW, Lipowsky HH. Inflammation-and ischemia-induced shedding of venular glycocalyx. American Journal of Physiology-Heart and Circulatory Physiology. 286:H1672–H1680, 2004. [DOI] [PubMed] [Google Scholar]
- 28.Giantsos-Adams KM, Koo AJ-A, Song S, et al. Heparan sulfate regrowth profiles under laminar shear flow following enzymatic degradation. Cellular and molecular bioengineering. 6:160–174, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bai X, Bame KJ, Habuchi H, Kimata K, Esko JD. Turnover of heparan sulfate depends on 2-O-sulfation of uronic acids. Journal of Biological Chemistry. 272:23172–23179, 1997. [DOI] [PubMed] [Google Scholar]
- 30.Liliensiek SJ, Nealey P, Murphy CJ. Characterization of endothelial basement membrane nanotopography in rhesus macaque as a guide for vessel tissue engineering. Tissue Eng Part A. 15:2643–2651, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Silver MD, Huckell VF, Lorber M. Basement membranes of small cardiac vessels in patients with diabetes and myxoedema: preliminary observations. Pathology. 9:213–220, 1977. [DOI] [PubMed] [Google Scholar]
- 32.Filion RJ, Popel AS. Intracoronary administration of FGF-2: a computational model of myocardial deposition and retention. Am J Physiol Heart Circ Physiol. 288:H263–279, 2005. [DOI] [PubMed] [Google Scholar]
- 33.Li J, Shworak NW, Simons M. Increased responsiveness of hypoxic endothelial cells to FGF2 is mediated by HIF-1alpha-dependent regulation of enzymes involved in synthesis of heparan sulfate FGF2-binding sites. J Cell Sci. 115:1951–1959, 2002. [DOI] [PubMed] [Google Scholar]
- 34.Clyne AM, Edelman ER. Vascular growth factor binding kinetics to the endothelial cell basement membrane, with a kinetics-based correction for substrate binding. Cytotechnology. 60:33, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Filion RJ, Popel AS. A reaction-diffusion model of basic fibroblast growth factor interactions with cell surface receptors. Ann Biomed Eng. 32:645–663, 2004. [DOI] [PubMed] [Google Scholar]
- 36.Dupree MA, Pollack SR, Levine EM, Laurencin CT. Fibroblast growth factor 2 induced proliferation in osteoblasts and bone marrow stromal cells: a whole cell model. Biophys J. 91:3097–3112, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fannon M, Forsten-Williams K, Dowd CJ, Freedman DA, Folkman J, Nugent MA. Binding inhibition of angiogenic factors by heparan sulfate proteoglycans in aqueous humor: potential mechanism for maintenance of an avascular environment. The FASEB journal. 17:902–904, 2003. [DOI] [PubMed] [Google Scholar]
- 38.Sperinde GV, Nugent MA. Heparan sulfate proteoglycans control intracellular processing of bFGF in vascular smooth muscle cells. Biochemistry. 37:13153–13164, 1998. [DOI] [PubMed] [Google Scholar]
- 39.Huxley VH, Williams DA. Role of a glycocalyx on coronary arteriole permeability to proteins: evidence from enzyme treatments. Am J Physiol Heart Circ Physiol. 278:H1177–1185, 2000. [DOI] [PubMed] [Google Scholar]
- 40.Dowd CJ, Cooney CL, Nugent MA. Heparan sulfate mediates bFGF transport through basement membrane by diffusion with rapid reversible binding. Journal of Biological Chemistry. 274:5236–5244, 1999. [DOI] [PubMed] [Google Scholar]
- 41.Fannon M, Forsten-Williams K, Dowd CJ, Freedman DA, Folkman J, Nugent MA. Binding inhibition of angiogenic factors by heparan sulfate proteoglycans in aqueous humor: potential mechanism for maintenance of an avascular environment. FASEB J. 17:902–904, 2003. [DOI] [PubMed] [Google Scholar]
- 42.Forsten KE, Fannon M, Nugent MA. Potential mechanisms for the regulation of growth factor binding by heparin. J Theor Biol. 205:215–230, 2000. [DOI] [PubMed] [Google Scholar]
- 43.Fuki IV, Meyer ME, Williams KJ. Transmembrane and cytoplasmic domains of syndecan mediate a multi-step endocytic pathway involving detergent-insoluble membrane rafts. Biochem J. 351 Pt 3:607–612, 2000. [PMC free article] [PubMed] [Google Scholar]
- 44.DePaola N, Phelps JE, Florez L, et al. Electrical impedance of cultured endothelium under fluid flow. Ann Biomed Eng. 29:648–656, 2001. [DOI] [PubMed] [Google Scholar]
- 45.Jo H, Dull RO, Hollis TM, Tarbell JM. Endothelial albumin permeability is shear dependent, time dependent, and reversible. Am J Physiol. 260:H1992–1996, 1991. [DOI] [PubMed] [Google Scholar]
- 46.Seebach J, Donnert G, Kronstein R, et al. Regulation of endothelial barrier function during flow-induced conversion to an arterial phenotype. Cardiovasc Res. 75:596–607, 2007. [DOI] [PubMed] [Google Scholar]
- 47.Sill HW, Chang YS, Artman JR, Frangos JA, Hollis TM, Tarbell JM. Shear stress increases hydraulic conductivity of cultured endothelial monolayers. Am J Physiol. 268:H535–543, 1995. [DOI] [PubMed] [Google Scholar]
- 48.Tarbell JM. Shear stress and the endothelial transport barrier. Cardiovasc Res. 87:320–330, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Davies PF, Dewey CF Jr., Bussolari SR, Gordon EJ, Gimbrone MA Jr. Influence of hemodynamic forces on vascular endothelial function. In vitro studies of shear stress and pinocytosis in bovine aortic cells. J Clin Invest. 73:1121–1129, 1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sprague EA, Steinbach BL, Nerem RM, Schwartz CJ. Influence of a laminar steady-state fluid-imposed wall shear stress on the binding, internalization, and degradation of low-density lipoproteins by cultured arterial endothelium. Circulation. 76:648–656, 1987. [DOI] [PubMed] [Google Scholar]
- 51.Colgan OC, Ferguson G, Collins NT, et al. Regulation of bovine brain microvascular endothelial tight junction assembly and barrier function by laminar shear stress. Am J Physiol Heart Circ Physiol. 292:H3190–3197, 2007. [DOI] [PubMed] [Google Scholar]
- 52.DeMaio L, Chang YS, Gardner TW, Tarbell JM, Antonetti DA. Shear stress regulates occludin content and phosphorylation. Am J Physiol Heart Circ Physiol. 281:H105–113, 2001. [DOI] [PubMed] [Google Scholar]
- 53.Kang H, Cancel LM, Tarbell JM. Effect of shear stress on water and LDL transport through cultured endothelial cell monolayers. Atherosclerosis. 233:682–690, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Noria S, Cowan DB, Gotlieb AI, Langille BL. Transient and steady-state effects of shear stress on endothelial cell adherens junctions. Circ Res. 85:504–514, 1999. [DOI] [PubMed] [Google Scholar]
- 55.Khan AG, Pickl-Herk A, Gajdzik L, Marlovits TC, Fuchs R, Blaas D. Entry of a heparan sulphate-binding HRV8 variant strictly depends on dynamin but not on clathrin, caveolin, and flotillin. Virology. 412:55–67, 2011. [DOI] [PubMed] [Google Scholar]
- 56.Yanagishita M, Hascall VC. Metabolism of proteoglycans in rat ovarian granulosa cell culture. Multiple intracellular degradative pathways and the effect of chloroquine. The Journal of biological chemistry. 259:10270–10283, 1984. [PubMed] [Google Scholar]
- 57.Barkefors I, Aidun CK, Ulrika Egertsdotter E. Effect of fluid shear stress on endocytosis of heparan sulfate and low-density lipoproteins. BioMed Research International; 2007:2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Christianson HC, Belting M. Heparan sulfate proteoglycan as a cell-surface endocytosis receptor. Matrix Biol. 35:51–55, 2014. [DOI] [PubMed] [Google Scholar]
- 59.Venkataraman G, Shriver Z, Davis JC, Sasisekharan R. Fibroblast growth factors 1 and 2 are distinct in oligomerization in the presence of heparin-like glycosaminoglycans. Proc Natl Acad Sci U S A. 96:1892–1897, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yao Y Three-dimensional flow-induced dynamics of the endothelial surface glycocalyx layer, Massachusetts Institute of Technology; 2007. [Google Scholar]
- 61.Han Y, Weinbaum S, Spaan JA, Vink H. Large-deformation analysis of the elastic recoil of fibre layers in a Brinkman medium with application to the endothelial glycocalyx. Journal of Fluid Mechanics. 554:217–235, 2006. [Google Scholar]
- 62.Pries A, Secomb T, Gaehtgens P. The endothelial surface layer. Pflügers Archiv. 440:653–666, 2000. [DOI] [PubMed] [Google Scholar]
- 63.Bell GI. Models for the specific adhesion of cells to cells. Science. 200:618–627, 1978. [DOI] [PubMed] [Google Scholar]
- 64.Ferrans VJ, Milei J, Tomita Y, Storino RA. Basement membrane thickening in cardiac myocytes and capillaries in chronic Chagas’ disease. Am J Cardiol. 61:1137–1140, 1988. [DOI] [PubMed] [Google Scholar]
- 65.Quere MA, Clergeau C, Fontenaille N. [The paralytic dyssynergies--the squint dyssynergies, and Cuppers’ syndrome (author’s transl)]. Klin Monbl Augenheilkd. 167:162–178, 1975. [PubMed] [Google Scholar]
- 66.East MA, Landis DI, Thompson MA, Annex BH. Effect of single dose of intravenous heparin on plasma levels of angiogenic growth factors. Am J Cardiol. 91:1234–1236, 2003. [DOI] [PubMed] [Google Scholar]
- 67.Egeberg M, Kjeken R, Kolset SO, Berg T, Prydz K. Internalization and stepwise degradation of heparan sulfate proteoglycans in rat hepatocytes. Biochim Biophys Acta. 1541:135–149, 2001. [DOI] [PubMed] [Google Scholar]
- 68.Sperinde GV, Nugent MA. Mechanisms of fibroblast growth factor 2 intracellular processing: a kinetic analysis of the role of heparan sulfate proteoglycans. Biochemistry. 39:3788–3796, 2000. [DOI] [PubMed] [Google Scholar]
- 69.Dowd CJ, Cooney CL, Nugent MA. Heparan sulfate mediates bFGF transport through basement membrane by diffusion with rapid reversible binding. The Journal of biological chemistry. 274:5236–5244, 1999. [DOI] [PubMed] [Google Scholar]