Comparison of Monoexponential, Biexponential, Stretched-Exponential, and Kurtosis Models of Diffusion-Weighted Imaging in Differentiation of Renal Solid Masses

Abstract

Objective

To compare various models of diffusion-weighted imaging including monoexponential apparent diffusion coefficient (ADC), biexponential (fast diffusion coefficient [D_f], slow diffusion coefficient [D_s], and fraction of fast diffusion), stretched-exponential (distributed diffusion coefficient and anomalous exponent term [α]), and kurtosis (mean diffusivity and mean kurtosis [MK]) models in the differentiation of renal solid masses.

Materials and Methods

A total of 81 patients (56 men and 25 women; mean age, 57 years; age range, 30–69 years) with 18 benign and 63 malignant lesions were imaged using 3T diffusion-weighted MRI. Diffusion model selection was investigated in each lesion using the Akaike information criteria. Mann-Whitney U test and receiver operating characteristic (ROC) analysis were used for statistical evaluations.

Results

Goodness-of-fit analysis showed that the stretched-exponential model had the highest voxel percentages in benign and malignant lesions (90.7% and 51.4%, respectively). ADC, D_s, and MK showed significant differences between benign and malignant lesions (p < 0.05) and between low- and high-grade clear cell renal cell carcinoma (ccRCC) (p < 0.05). α was significantly lower in the benign group than in the malignant group (p < 0.05). All diffusion measures showed significant differences between ccRCC and non-ccRCC (p < 0.05) except D_f and α (p = 0.143 and 0.112, respectively). α showed the highest diagnostic accuracy in differentiating benign and malignant lesions with an area under the ROC curve of 0.923, but none of the parameters from these advanced models revealed significantly better performance over ADC in discriminating subtypes or grades of renal cell carcinoma (RCC) (p > 0.05).

Conclusion

Compared with conventional diffusion parameters, α may provide additional information for differentiating benign and malignant renal masses, while ADC remains the most valuable parameter for differentiation of RCC subtypes and for ccRCC grading.

INTRODUCTION

Solid renal masses are the most common neoplasms of the urinary system, with renal cell carcinoma (RCC) accounting for nearly 90% of malignancies. Additionally, angiomyolipoma (AML) comprises 18–59% of resected benign solid tumors (1,2). Distinguishing benign and malignant renal lesions, different tumor types, and different grades has clinical significance in determining the appropriate treatment strategy and evaluating prognosis (3,4). Conventional computed tomography (CT) and magnetic resonance imaging (MRI) are routinely used in the evaluation of renal lesions. However, CT and MRI sometimes fail to provide reliable prediction when lesions lack typical imaging features. Moreover, approximately 16–33% of nephrectomies are performed on benign lesions (2).

Diffusion-weighted imaging (DWI) is a powerful technique for exploring biological microstructures. The apparent diffusion coefficient (ADC), obtained from DWI with the monoexponential model, has been widely used to characterize renal lesions (5,6,7). However, several studies have reported contradictory results using ADC to differentiate benign and malignant lesions (8,9). Previous studies have suggested that advanced fitting models, such as biexponential, stretched-exponential, or kurtosis models might provide more accurate information regarding water diffusion (10,11). The biexponential model, described by Le Bihan et al. (12), might allow separation of fast and slow diffusion components, which reflect capillary perfusion and tissue diffusion, respectively. The metrics derived from the biexponential model might be superior to ADC in renal tumor diagnosis, pathological subtyping, and grade prediction (13,14). Furthermore, Bennett et al. (15) proposed the stretched-exponential model, which was used to evaluate distributed diffusion and intravoxel heterogeneity. As one of the most popular non-Gaussian models, the diffusion kurtosis model has been used to reflect the complexity of tissue microstructure and provide a more comprehensive characterization of water diffusion in multiple organs such as the brain, prostate, and breast (16,17,18). These advanced models can fit the signal curve more precisely, reflecting tissue characteristics in greater detail. Although several studies on the role of DWI models in characterizing renal tumors have been done, they have generally used one or two models such as the monoexponential and/or biexponential models (19,20). Another recent research paper also investigated the stretched-exponential model but here the model was used simply to differentiate RCC and AML (21). In our study, we aimed to apply four signal attenuation models (monoexponential, biexponential, stretched-exponential, and kurtosis models) to DWI data from renal lesions to determine the optimal model fitting the multiple b-value signal decay curve and quantitatively compare the potential of diffusion parameters in differentiating benign and malignant renal lesions, RCC subtyping, and clear cell RCC (ccRCC) grading.

MATERIALS AND METHODS

Patients

This retrospective study was approved by our Institutional Review Board, and written informed consent was obtained from all patients. One hundred and sixteen patients with known or suspected renal lesions at ultrasonography (US), CT, or both US and CT were enrolled in the study from June 2014 to December 2015. The inclusion criteria were as follows: 1) patients had complete information and received no treatment before MRI and 2) surgery was performed within two weeks after MRI examination and a pathologic confirmation was made. The exclusion criteria were as follows: 1) poor-quality images with obvious artifacts (n = 8), 2) anti-tumor therapy and biopsy performed before MRI (n = 5), 3) no dynamic contrast-enhanced (DCE) data available (n = 10), 4) solid components that were difficult to characterize due to their small size (< 20 mm²) (n = 9), and 5) massive fat-containing masses that could easily have been diagnosed as AML (n = 3). Ultimately, a total of 81 patients (mean age, 57 years; range, 30–69 years), including 56 men (mean age, 55 years; range, 30–69 years) and 25 women (mean age, 64 years; range, 51–68 years), were included. Only one lesion was found in each included patient. Histopathologic results were obtained from pathology reports.

MRI Examination

Patients were instructed to fast for 4–5 hours before the examination. All scans were performed in the supine position using a 3T magnetic resonance scanner (Ingenia; Philips Medical Systems, Best, the Netherlands). The following sequences were used: axial turbo spin-echo T1-weighted imaging, axial and coronal turbo spin-echo T2-weighted imaging, axial DWI, and axial DCE imaging. DWIs with fat suppression were collected using a single-shot spin-echo echo-planar imaging sequence as follows: repetition time/echo time, 2000/86 ms; matrix, 152 × 137; in-plane resolution, 2 × 2 mm; section thickness, 5 mm; parallel acquisition with acceleration factor, 2; b-values, 0, 30, 50, 100, 250, 500, 1000, and 2000 sec/mm²; and acquisition time, 8 minutes 30 seconds. Sensitizing diffusion gradients were applied in the three orthogonal directions, and trace DWIs were generated. DCE imaging acquisitions were performed before and at three consecutive points after injection of gadolinium chelate (gadopentetate dimeglumine, Magnevist®; Bayer Healthcare, Berlin, Germany) at a dose of 0.1 mmol/kg at a rate of 2 mL/sec.

Image Analysis

DWI data were transferred to a personal computer and processed with software (MatLab; MathWorks, Natick, MA, USA). The corresponding mathematical expressions are shown as follows:

• 1) Monoexponential model:

S (b) = S₀ exp (−bADC)

where S (b) and S₀ denote signal intensities with and without diffusion weighting, respectively, and b is the diffusion-sensitizing factor.

• 2) Biexponential model:

S (b) = S₀ (f exp [−bD_f] + [1 − f] exp [−bD_s])

where D_f and D_s represent fast diffusion coefficient and slow diffusion coefficient, respectively. f represents the fraction of fast diffusion (0 ≤ f ≤ 1).

• 3) Stretched-exponential model:

S (b) = S₀ exp (−[bDDC]^α)

where DDC represents distributed diffusion coefficient, and α represents the anomalous exponent term (0 ≤ α ≤ 1).

• 4) Diffusion kurtosis model:

S (b) = S₀ exp (−bMD + b² MD² MK / 6)

where MD represents mean diffusivity, and MK represents mean kurtosis.

Images were independently analyzed by two renal radiologists (with 5 and 7 years of experience, respectively) who were blinded to patients' pathologic findings. For each lesion, three regions of interest (ROIs) (the slice with maximal tumor dimension and its upper and lower slices) were placed in different enhancing solid components on DWI b = 0 images, with reference to DCE to exclude areas of necrosis, cysts, hemorrhage and calcifications. The median size ROI was 65.7 mm² with range of 34.4–308.6 mm² (benign; median size 54.3 mm², size range 34.4–210.1 mm²: malignant; median size 81.6 mm², size range 45.4–308.6 mm²; p = 0.14 using Mann-Whitney U-test). The median value of each parameter from all pixels within the ROI was used for statistical analysis to reduce the sensitivity to outlier values.

Statistical Analysis

Statistical analyses were performed with MedCalc v. 12.7 (MedCalc Software, Mariakerke, Belgium). The goodness-of-fit of the four models was compared using the Akaike information criterion (22). For each voxel within the ROI, the best fitting curve was determined through calculating its vertical distances to the four curves (the shortest distance means the best fitting). The highest percentage of overall number of voxels indicated the optimal model. The interobserver variability for parameter measurements was assessed by using the intraclass correlation coefficient (ICC: 0.00–0.20, poor agreement; 0.21–0.40, fair; 0.41–0.60, moderate; 0.61–0.80, good; and 0.81–1.00, excellent) (23). A non-normal distribution was confirmed for all parameters except ADC, α, and D_S according to the Shapiro-Wilk test; nonparametric statistical tests were used for further analysis. Mann-Whitney U-tests were used to compare the diffusion parameters of patient subgroups assigned in terms of tumor types (benign and malignant), RCC subtypes (ccRCC and non-ccRCC), and ccRCC grading (low- and high-grade). Receiver operating characteristic (ROC) curves were created, and areas under the ROC curve (AUCs) were compared between ADC and other diffusion parameters by using the method developed by DeLong et al. (24). The maximum Youden index was used to determine the optimal sensitivity and specificity, as well as the corresponding cut-off value. A p value < 0.05 was considered significant.

RESULTS

Histopathologic Results

Of the 81 renal lesions, 18 lesions (22.2%) were categorized as benign and 63 lesions (77.8%) were categorized as malignant. The benign group comprised 15 AMLs (83.3%), two oncocytomas (11.1%), and one hyperplasia of fiber tissue (5.6%). Of the 63 malignant lesions, 46 ccRCCs (73.0%), 11 papillary renal cell carcinoma (pRCCs) (17.5%), and 6 chromophobe renal cell carcinoma (chRCCs) (9.5%) were identified. Patients with ccRCC were assigned to two groups according to the Fuhrman nuclear grading system: low-grade (25 in grade I and 14 in grade II) and high-grade (3 in grade III and 4 in grade IV). A pathologic examination confirmed type I pRCC in 5 patients (2 in grade I and 3 in grade II) and type II pRCC in 6 patients (2 in grade I and 4 in grade II). The average diameter of the 81 lesions was 4.1 cm, with a range of 1.2–12.7 cm (benign: median size 3.4 cm, range 1.2–6.4 cm; malignant: median size 4.9 cm, range 2.6–12.7 cm).

Goodness-of-Fit Assessment

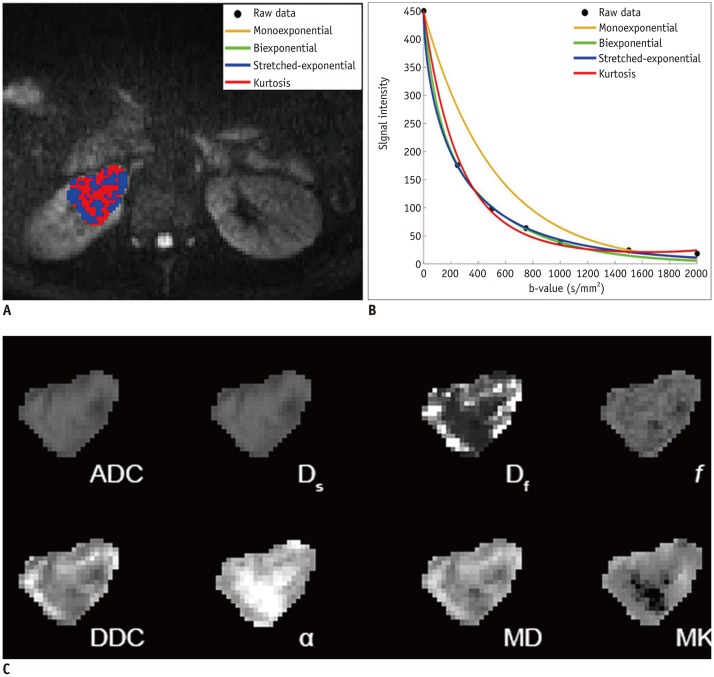
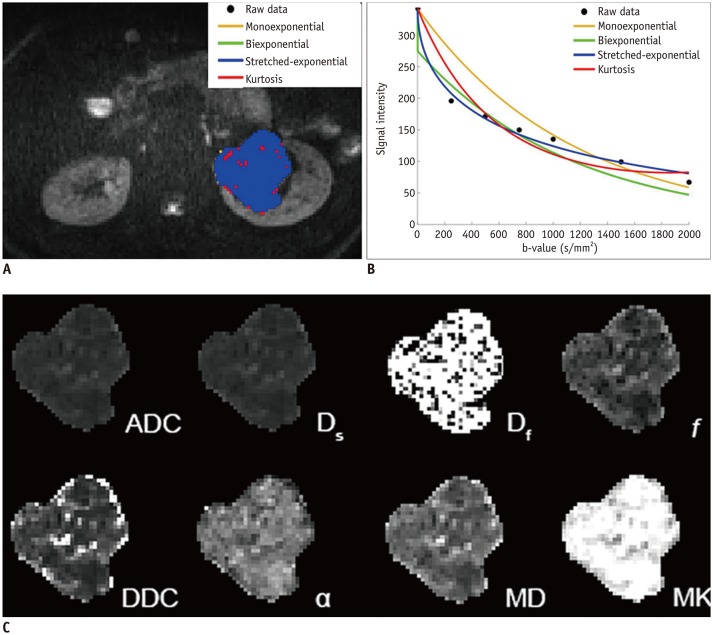
According to Table 1, the assessment of goodness-of-fit showed that the voxel percentages in benign and malignant lesions described by the stretched-exponential model were 90.7% and 51.4%, respectively. Monoexponential and biexponential models demonstrated relatively poor performance in fitting the diffusion-weighted (DW) dataset, with voxel percentages of 0.6% and 0%, respectively, for benign lesions and 2.0% and 0%, respectively, for malignant lesions. The kurtosis model fitted the voxels better but also had low voxel percentages of 3.9% and 30.3% for benign and malignant lesions, respectively. The fitting curves of different models and parameter maps for ccRCC and AML are displayed in Figures 1 and 2.

Table 1. Voxel Percentages Preferred by Four Models in Renal Lesions.

Model	Monoexponential	Biexponential	Stretched-Exponential	Kurtosis
Benign (%)	0.6 (6.5)	0 (8.5)	90.7 (38.4)	3.9 (13.9)
Malignant (%)	2.0 (11.0)	0 (14.1)	51.4 (24.4)	30.3 (32.8)

Data are medians with interquartile range in parentheses.

Fig. 1. Clear cell renal cell carcinoma (grade II) in right kidney in 39-year-old man.

A. Voxels preferred by monoexponential, biexponential, stretched-exponential, and kurtosis models in lesion. B. Plot of decay of diffusionweighted signal intensity as function of b-value from representative voxel within ROI. C. Multiparametric diffusion parameter maps within ROI. ADC = apparent diffusion coefficient, DDC = distributed diffusion coefficient, D_f = fast diffusion coefficient, Ds = slow diffusion coefficient, f = fraction of fast diffusion, MD = mean diffusivity, MK = mean kurtosis, ROI = region of interest, α = anomalous exponent term

Fig. 2. Angiomyolipoma in left kidney in 55-year-old woman.

A. Voxels preferred by monoexponential, biexponential, stretched-exponential and kurtosis models in lesion. B. Plot of decay of diffusion-weighted signal intensity as function of b-value from representative voxel within ROI. C. Multiparametric diffusion parameter maps within ROI.

Interobserver Agreement

All parameter measurements resulted in good to excellent interobserver agreement. Excellent interobserver agreement was found for ADC, D_s, DDC, α, MD, and MK (ICC = 0.881, 0.890, 0.904, 0.869, 0.898, and 0.852, respectively). Good interobserver agreement was found for Df and f (ICC = 0.712 and 0.795, respectively).

Association between Diffusion Parameters and Pathologic Diagnoses

Mann-Whitney U-tests revealed that ADC, D_s, α, and MK differed significantly between benign and malignant lesions (all Ps < 0.05). No significant difference was found between the two groups for f, D_f, DDC, and MD (p > 0.05). As shown in Table 2, AUC values were 0.731 for ADC, 0.752 for D_s, 0.567 for D_f, 0.496 for f, 0.543 for DDC, 0.923 for α, 0.568 for MD, and 0.803 for MK. α showed the highest diagnostic accuracy, the AUC value of which was significantly higher than that of ADC (p = 0.001).

Table 2. Diagnostic Performance of Diffusion Parameters in Differentiating Renal Lesions Types.

Parameter (x 10-3 mm2/sec)	ADC	Ds	Df	f*	DDC	α*	MD	MK*
Benign vs. Malignant
AUC (95% CI)	0.731 (0.621–0.824)	0.752 (0.644–0.841)	0.567 (0.452–0.677)	0.496 (0.383–0.609)	0.543 (0.429–0.654)	0.923 (0.842–0.971)	0.568 (0.453–0.678)	0.803 (0.700–0.883)
p †	Ref	0.313	0.042	0.007	< 0.001	0.001	< 0.001	0.217
Sensitivity (%)	60.3	58.7	98.4	39.7	68.3	96.8	60.3	63.5
Specificity (%)	88.9	88.9	27.8	77.8	61.1	72.2	61.1	88.9
Cut-off value	0.0014	0.0014	0.0416	0.3000	0.0019	0.5200	0.0025	0.7200
ccRCC vs. Non-ccRCC
AUC (95% CI)	0.918 (0.820–0.972)	0.903 (0.802–0.963)	0.621 (0.490–0.740)	0.791 (0.670–0.883)	0.920 (0.824–0.973)	0.631 (0.500–0.749)	0.898 (0.796–0.960)	0.851 (0.739–0.928)
p †	Ref	0.237	< 0.001	0.014	0.865	0.001	0.641	0.117
Sensitivity (%)	80.4	80.4	73.9	76.7	84.8	52.2	95.7	89.1
Specificity (%)	94.1	94.1	52.9	70.6	94.1	82.4	76.5	76.5
Cut-off value	0.0014	0.0014	0.0078	0.1800	0.0020	0.6600	0.0018	0.8000
Low-grade vs. high-grade
AUC (95% CI)	0.780 (0.634–0.889)	0.802 (0.658–0.905)	0.630 (0.475–0.768)	0.663 (0.509–0.796)	0.707 (0.554–0.832)	0.712 (0.560–0.836)	0.568 (0.412–0.715)	0.823 (0.680–0.920)
p †	Ref	0.297	0.397	0.443	0.592	0.509	0.047	0.456
Sensitivity (%)	84.6	89.7	35.9	64.1	89.7	43.6	94.9	71.8
Specificity (%)	71.4	71.4	100	71.4	57.1	100	42.9	100
Cut-off value	0.0014	0.0013	0.0083	0.2300	0.0021	0.6800	0.0019	0.6500

Data are medians with interquartile range in parentheses. ^*f, α, and MK have no units, ^†p value from statistical comparison between AUC values of ADC (Ref) and other diffusion parameters by using method of DeLong et al. (24). AUC = area under receiver operating characteristic curve, CI = confidence intervals, Ref = reference

For comparisons of pathologic subtypes, all parameters showed significant differences between ccRCC and non-ccRCC (p < 0.05), except D_f and α (p = 0.143 and 0.112, respectively) (Table 3). The AUC values of D_s, DDC, MD, and MK were 0.903, 0.920, 0.898, and 0.851, respectively, showing no significant differences compared with those of ADC (0.918) (Table 3). However, D_f, f, and α, whose AUC values were 0.621, 0.791, and 0.631, respectively, showed significantly lower diagnostic accuracy than did ADC (p < 0.05).

Table 3. Association between Diffusion Parameters and Pathologic Diagnoses.

Parameter (x 10-3 mm2/sec)	ADC	Ds	Df	f*	DDC	α*	MD	MK*
Benign (n = 18)	0.0010 (0.0004)	0.0010 (0.0004)	0.0138 (0.0414)	0.2300 (0.1400)	0.0016 (0.0023)	0.4450 (0.1600)	0.0022 (0.0013)	0.9750 (0.2900)
Malignant (n = 63)	0.0015 (0.0006)	0.0015 (0.0006)	0.0087 (0.0135)	0.2300 (0.1900)	0.0023 (0.0014)	0.6800 (0.1300)	0.0027 (0.0012)	0.6660 (0.3000)
p†	0.003	0.001	0.388	0.959	0.578	< 0.001	0.420	< 0.001
ccRCC (n = 46)	0.0016 (0.0004)	0.0016 (0.0004)	0.0095 (0.0172)	0.3250 (0.1800)	0.0024 (0.0005)	0.6550 (0.1400)	0.0028 (0.0006)	0.6200 (0.1800)
Non-ccRCC (n = 17)	0.0010 (0.0004)	0.0010 (0.0005)	0.0078 (0.0124)	0.1500 (0.1300)	0.0012 (0.0005)	0.7000 (0.0700)	0.0016 (0.0007)	0.9000 (0.1600)
p†	< 0.001	< 0.001	0.143	< 0.001	< 0.001	0.112	< 0.001	< 0.001
Low-grade (n = 39)	0.0017 (0.0003)	0.0017 (0.0003)	0.0087 (0.0170)	0.3300 (0.1700)	0.0025 (0.0006)	0.6700 (0.1400)	0.0028 (0.0006)	0.6000 (0.1900)
High-grade (n = 7)	0.0014 (0.0005)	0.0011 (0.0007)	0.0116 (0.0224)	0.2200 (0.1900)	0.0021 (0.0014)	0.6000 (0.1300)	0.0028 (0.0010)	0.7500 (0.1600)
p†	0.018	0.010	0.291	0.183	0.087	0.076	0.291	0.002

Data are medians with interquartile range in parentheses. ^*f, α, and MK have no units, ^†p value from statistical comparison between benign and malignant lesions, between ccRCC and non-ccRCC, between low-grade and high-grade ccRCC, respectively, by using Mann-Whitney U test. ADC = apparent diffusion coefficient, ccRCC = clear cell renal cell carcinoma, DDC = distributed diffusion coefficient, D_f = fast diffusion coefficient, D_s = slow diffusion coefficient, f = fraction of fast diffusion, MD = mean diffusivity, MK = mean kurtosis, α = anomalous exponent term

The results of comparative analysis of diffusion parameters between ccRCC with different grades were also displayed in Tables 2 and 3. ADC, D_s, and MK were significantly different between low-grade and high-grade groups (all Ps < 0.05). Other parameters did not show significant differences between the two groups (all Ps > 0.05). AUC values were 0.780 for ADC, 0.802 for D_s, 0.630 for D_f, 0.663 for f, 0.707 for DDC, 0.712 for α, 0.568 for MD, and 0.823 for MK. The AUC values for D_s and MK were slightly higher than those for ADC, but there was no significant difference (all Ps > 0.05). Other parameters did not show significantly higher AUC values than ADC.

DISCUSSION

In this study, the stretched-exponential model provided significantly better characterization of DW signal decay in both benign and malignant renal lesions than did the monoexponential, biexponential, or kurtosis model. This result was consistent with findings in other malignant tumors, including metastatic abdominal and pelvic tumors and endometrial cancer, indicating that significantly better fitting of the diffusion signals could be achieved by non-Gaussian models (25,26). Although both the biexponential and kurtosis models obtained much poorer fit performances in relation in both benign and malignant lesions, it might be partly due to the tumor types, which did not have an extremely significant intravoxel incoherent motion or kurtosis effect, or the choice of the number and range of b-values used in the study. Moreover, model performance changes based on the number and definitions of its parameters. For instance, the microstructural content of tumor tissue is conventionally divided into three parts, including the perfusion-related lesion, extravascular extracellular space, and cellular compartment, and the latter two are classified as slow compartments (27). The biexponential model may not be sufficient to handle two slow compartments because it provides only one parameter for the evaluation of the slow diffusion component.

We showed that α had significantly greater diagnostic value in differentiating benign and malignant renal lesions than did conventional or other non-Gaussian distribution parameters. However, none of the parameters from these advanced models showed significantly superior performance over ADC in discriminating subtypes or grades of RCC. In particular, α showed a much lower AUC value than did ADC in differentiating ccRCC and non-ccRCC. As an anomalous exponent term, α is considered to provide a means of assessing inter-lesion heterogeneity. Therefore, this result is unsurprising because the tissue architecture, cell density, and microcirculation may show large variations between benign and malignant lesions, while the deviation between certain kinds of malignant tumors or different grades of ccRCC might be quite modest, leading to lower diagnostic values for those non-Gaussian diffusion parameters. Although the diagnostic performance in differential RCC subtypes is less satisfactory, fewer differences within malignant tumors could be an important factor for the superior performance in discrimination between benign and malignant tumors with the stretched-exponential model.

The monoexponential model is valuable in the evaluation of renal masses (28,29). ADC is lower in malignant masses than in benign masses and this presumably indicates higher cellularity in malignancies (6). However, Ding et al. (20) reported that ccRCC had a significantly higher ADC value than did non-ccRCC and AML, consistent with our results. ccRCC tumor cells are often interspersed with cystic and hemorrhagic areas and separated by interstitial spaces; thus, water molecules could diffuse relatively freely. In contrast, benign lesions and non-ccRCC usually present with compact tissue architecture and greater cellular density, leading to decreased ADC values. As far as we know, ADC values are mainly affected by both tumor cellularity and vascularity, but in tumor tissue, no final conclusion has been made on the precise proportion of each component to constitute ADC. Our current study also showed that the results of ADC were consistent with those of D_s, which theoretically removes the influence of perfusion and may reflect the true diffusion coefficient. This finding suggests that the perfusion contribution to ADC was small and that ADC values can reflect the true diffusion coefficient to some extent, at least at the given b-values (b = 0–2000 sec/mm²) in the present study.

D_f and f, the other two important metrics in the biexponential model, are linked to perfusion and reflect the degree of tissue vascularity without the use of contrast agents. As for D_f, its diagnostic value has always been controversial (13,14,30). In our study, we did not find a significant difference between any subject subgroups for D_f values. Variations in the results might be related to the different sample sizes and the number and distribution of b-values in these studies. Additionally, artifacts from great vessels may also have an impact on this parameter. As such, further efforts are necessary to make this metric more reproducible and reliable. In contrast, the other perfusion-related parameter f performed more reliably in recent studies, suggesting that it is associated with the enhancement degree of renal lesions, accurately separating enhancing ccRCC from hypoenhancing pRCC and cystic RCC (31). Similar to prior investigations, we found higher f values in ccRCC than in non-ccRCC, indicating the hypervascularity of ccRCC.

Several studies using advanced diffusion models including the stretched-exponential and kurtosis models to probe the non-Gaussian water behavior in tissues, have been reported (32,33). In our current study, lower α and higher MK values were observed in benign lesions than in malignant ones. Although Fujima et al. (34) also suggested an inverse relationship between α and MK, and that the two metrics might be similar in describing the pathologic characteristics of tumors, this conclusion was controversial. The performance of these two metrics in assessing the pathophysiologic state is not always consistent (35), which also occurred in our study. The diffusion kurtosis model uses a quadratic equation, whereas the stretched-exponential model uses the exponential function, and there is no definite deductive formula between the two parameters. Therefore, as mentioned in previous studies, the exact meanings of α and MK in vivo are not fully understood and were mainly referenced as metrics that could assess the tissue “complexity”. Based on our results, we assume that α and MK may reflect information on a specific part of the “complexity”. However, as the definition and extent of “complexity” remain unclear, the precise underlying biological mechanism needs to be further explored.

Our study has several limitations. One is the relatively small number of non-ccRCCs and high-grade ccRCCs. Additional studies with a large sample size are necessary to confirm the results. Another limitation is the lack of research on the value of contrast-enhanced MRI in this study. However, contrast-enhanced imaging might be inferior to DWI in renal tumor diagnosis, especially for complicated renal lesions, hemorrhagic lesions, or tumors showing overlap in the enhancement pattern (28,36). Moreover, most patients with renal tumors are elderly individuals and may have renal dysfunction, which increases the risk of development of nephrogenic systemic fibrosis after contrast administration (37). Thus, DWI might be a reasonable alternative for these patients.

In conclusion, our results suggest that the stretched-exponential model provides the best fitting performance for DW-MRI data from both benign and malignant renal lesions. Compared with conventional diffusion parameters, α may provide additional information for differentiating benign and malignant renal masses, while ADC remains the most valuable parameter for the differentiation of ccRCC and non-ccRCC, as well as for ccRCC grading. However, at present, we have not identified a single DWI model that could be adequately powerful in characterizing renal masses. Therefore, combining these Gaussian diffusion and non-Gaussian diffusion parameters may be reasonable and helpful in improving therapeutic strategies and prognoses in clinical practice, however, these approaches need further research in the future.