Objectively Quantifying Walking Ability in Degenerative Spinal Disorder Patients using Sensor Equipped Smart Shoes

Abstract

Lumbar spinal stenosis (LSS) is a condition associated with the degeneration of spinal disks in the lower back. A significant majority of the elderly population experiences LSS, and the number is expected to grow. The primary objective of medical treatment for LSS patients has focused on improving functional outcomes (e.g., walking ability) and thus, an accurate, objective, and inexpensive method to evaluate patients’ functional levels is in great need. This paper aims to quantify the functional level of LSS patients by analyzing their clinical information and their walking ability from a 10 meter self-paced walking test using a pair of sensorized shoes. Machine learning algorithms were used to estimate the Oswestry Disability Index, a clinically well-established functional outcome, from a total of 29 LSS patients. The estimated ODI scores showed a significant correlation to the reported ODI scores with a Pearson correlation coefficient (r) of 0.81 and p < 3.5 × 10⁻¹¹. It was further shown that the data extracted from the sensorized shoes contribute most to the reported estimation results, and that the contribution of the clinical information was minimal. This study enables new research and clinical opportunities for monitoring the functional level of LSS patients in hospital and ambulatory settings.

1. Introduction

Lumbar spinal stenosis (LSS) is a condition closely related with age-associated degeneration of the lumbar (i.e., lower back) spinal disks [1]. It is known as the most common diagnosis leading to spinal surgery in elderly patients of age greater than 65 years [2], and approximately 40% of general adult populations are known to carry moderate conditions of LSS [3]. As a consequence of the worldwide trend of aging societies in developed and developing countries, a significant majority of the elderly population is expected experience LSS [4].

LSS is characterized by a narrowing of the spinal canal and compression of nerve roots in the lower back [1], which lead to various clinical symptoms including leg pain, numbness, and weakness [5]. Thus, patients with LSS have considerable walking limitation [6, 3, 1, 7], which is the leading cause of spinal surgery in Medicare recipients [3, 8]. The primary objective of medical treatment has been focused on improving functional outcomes, e.g., the walking ability [3]. Consequently, researchers and clinicians have focused their attention on the development of objective, inexpensive, and accurate assessment tools to quantify the level of functional capacity, which can be used to track the longitudinal progress of patient conditions.

Instrumented examination of walking ability has the potential to support such a need compared to traditional clinical tools such as radiographic testing (e.g., X-ray, Magnetic Resonance Imaging (MRI), and Computed Tomography (CT) images [1]) and self-reported functional outcomes (e.g., Oswestry Disability Index (ODI) [9], Swiss Spinal Stenosis Questionnaire, and Oxford Claudication Score [10]). Several observational studies recently validated the clinical efficacy of gait parameters recorded from self-paced walking tests (SPWT) or motorized treadmill tests (MTT) [6, 7, 11, 3]. In these works, patients were asked to walk on a flat surface (SPWT) and/or a treadmill (MTT) at preferred speeds until they voluntarily stopped due to symptoms of LSS or until they reached the predefined maximum time duration (e.g.,30 minutes). Two parameters related to walking capacity (i.e. time and distance traveled) were tested for their correlations to the perceived functional level obtained by using patient-reported outcomes. The work in [6] concluded that the traveled distance of SPWT had a statistically significant correlation with ODI scores. The work in [3] performed both SPWT and MTT, and concluded that gait parameters extracted from MTT has better correlation to the functional outcomes than SPWT. The work in [11] examined the changes in the value of ODI and the changes in the traveled distance of SPWT, and found a significant correlation between the two. The work in [6] also monitored levels of physical activity (i.e. activity count and maximum time of continuous activity) of LSS patients using a waist-worn accelerometer over several days, but their correlations to the patient-reported outcomes were not as significant as the gait parameters from walking tests.

The aforementioned works demonstrated the clinical effectiveness of gait parameters for their use as objective measures. However, SPWT and MTT are not fully automated and require presence of a clinical professional who needs to manually record the gait parameters. Moreover, these tests may require patients to walk for up to 30 minutes.>These may serve as barriers to use the SPWT and MTT in clinical and ambulatory settings, considering the patients’ adherence (or preference) to the testings for frequent and longitudinal tracking of functional level. Furthermore, all the aforementioned analyses investigate correlation between a single-dimensional gait parameter and the clinical score, rather than incorporating multi-dimensional gait parameters. This may restrict the quantification of motor function to be relatively simple and prohibit integrating multiple walking characteristics in the measure.

This paper introduces a fully automated system and its method that quantify the functional level of LSS patients by analyzing their walking ability using a pair of sensorized shoes equipped with pressure sensors. The method employed a self-paced walking test on a 10 meter flat trail, which took approximately six minutes to complete. A total of 76 spatio-temporal features that were extracted from the smart shoes and 12 clinical variables that were previously found to be relevant to the functional level were used to estimate the clinical scores obtained by using the ODI [12], a clinically well-established outcome measure in lower back pain patients [13]. This paper discusses two machine learning algorithms designed to estimate clinical scores collected during the preoperative and postoperative visits, respectively. The clinical efficacy of the system was investigated through a pilot involving 29 LSS patients.

2. Materials

2.1. Participants

A total of 29 patients (11 males and 18 female) with LSS were recruited from the UCLA Spine Center. The ages of the participants ranged from 28 to 78, with an average and standard deviation of 57.4 ± 15.9 at the time of surgery. All patients were diagnosed with LSS as a result of lumbar disk herniation, lumbar spondylolisthesis, or adjacent segment disease. All patients had radiculopathy or axial pain in the lower limbs, which affected their walking ability. Patients who had comorbidities that may affect their lower motor function and gait performance were excluded from the study. All patients received lumbar decompression and/or lumbar fusion surgery performed by a single neurosurgeon (DCL). The experimental procedure was approved by the UCLA institutional review board, and all patients provided consent to participate in the study.

2.2. Sensory Platform

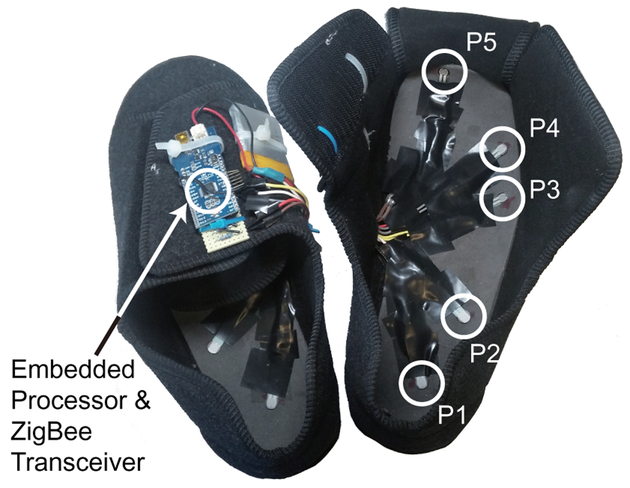
A pair of shoes equipped with an array of five pressure sensors was developed as shown in Fig. 1. The pressure sensors on the insole were positioned to detect heel-strike (P1), mid-lateral plantar pressure (P3), toe pressure (P5) and other spatio-temporal information (P2 and P4). An embedded system on each shoe collects sensory data at a sampling rate of 80 Hz and transmits the data in real-time to the base station (i.e. a laptop) via the IEEE 802.15.4 standard (i.e. ZigBee protocol) [14]. Each shoe establishes a wireless connection to the base station independently. A total of five shoes with different sizes were made for both males and females. The pressure sensors on the insole were positioned linearly proportional to the size of the shoe.

Figure 1:

A picture of the sensorized shoes containing an array of five pressure sensors and a wireless data transceiver. Pressure sensors on the insole were positioned to detect heel-strike (P1), mid-lateral plantar pressure (P3), toe pressure (P5) and other spatio-temporal information (P2 and P4).

2.3. Experimental Protocol

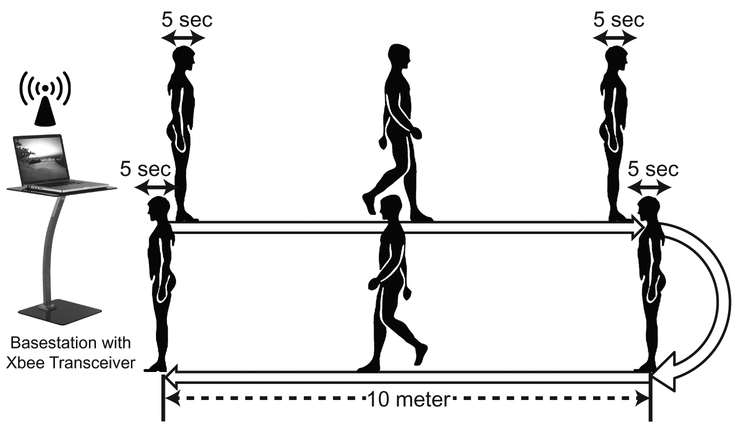
Fig. 2 illustrates the experimental protocol. A straight 10 meter long trail was marked on a level floor as was suggested in [15] for a stride analysis. Patients were asked to wear the sensorized shoes and walk on the trail at a self-paced speed, turn around, and walk back to the original position. Patients were asked to pause for five seconds before walking, before the turn, before walking back, and after reaching the final destination (Fig. 2); these five second defaults were used as annotations to segment the collected data. No further instruction was given to the patients regarding their gait performance and behavior. Patients repeated this procedure twice, which resulted in a maximum of four 10 meter walks per clinical visit (or per test).

Figure 2:

A graphical summary of the experimental procedure. Patients were asked to walk on a 10 meter trail at a self-paced speed, turn around, and walk back to the original position with five seconds of defaults between each transition in action.

All 29 patients performed the walking test approximately one hour before their surgical operation. In this work, the sensor and clinical data collected preoperatively are denoted as preoperative data. 15 of these patients had follow-up visits at least three months after the surgery, and performed the test again. A three-month period is known to be a clinically meaningful time for recovery in patients with lumbar spinal cord disorder [16]. The data collected during their follow-up visits are denoted as postoperative data.

2.4. Clinical Variables

Twelve clinical variables that were previously found to have close correlation to the functional level of LSS patients were collected. These variables included age, gender, presence of scoliosis [17], presence of acute injury, number of spinal vertebrae that were affected, number of previous spinal surgeries [18], duration of symptoms [19], height, weight, Body Mass Index (BMI) [17], and smoking status (smoker or nonsmoker) [20].

2.5. Patient Reported Outcome Measure

The ODI was collected from the participants after the walking test at each clinical visit (i.e. one ODI per clinical visit) in order to represent their functional level. The ODI is one of the very commonly used self-reported clinical outcome measures in patients with lower back pain [13]. The ODI, which was originally developed by Fairbank et al. [12], contains ten questions (or items) assessing the level of pain in the affected areas and the degree of interference in performing various daily activities such as personal care, lifting, walking, sitting, standing, sleeping, sex life, social life, and traveling. Each item has five or six answer choices describing different functional level. The overall score is computed by summing the scores of the answered items and linearly scaling the summed score from 0 (completely disabled condition) to 1 (completely healthy condition).

3. Methods

Two algorithms were independently designed to estimate the preoperative and postoperative clinical scores (i.e. ODI scores), respectively, due to different clinical information available at the two time points. Both algorithms employed the same data segmentation and feature extraction mechanisms to extract spatio-temporal features from the pressure sensors, which were used to train their machine learning models.

3.1. Data Segmentation

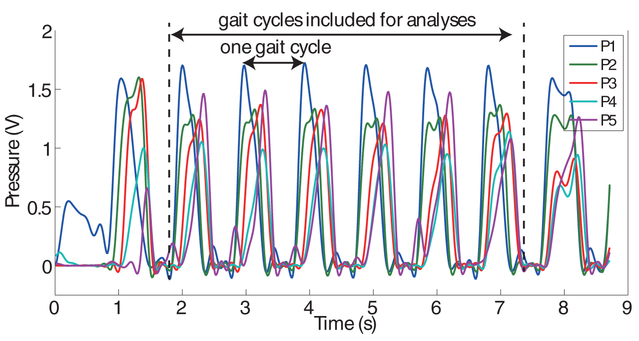
The data collected from a 10 meter walk was considered as a single data instance). For each instance, the first and the last gait cycles were discarded from further analyses due to possible abnormal gait patterns from the initiation and termination of walking. Fig. 3 illustrates a sample time series of pressure sensor data obtained from one of the participants. Since patients performed four 10 meter walks per clinical visit, the four data instances were labeled (assigned) with the same ODI score. Note that not all patients produced four data instances due to either mistakes during the data collection process or malfunction of the system. All patients, however, produced at least one instance per clinical visit. Consequently, a total of 137 data instances were obtained from 29 patients.

Figure 3:

Sample time series of pressure sensors that belong to one of the participated patients. This 10 meter walk was considered as a single data instance.

3.2. Spatio-Temporal Gait Features

A total of 76 spatio-temporal features were extracted from the pressure sensors. The gait cycle time, which represents the time it takes to complete one gait cycle, was computed by calculating the time between the peaks of the time series from pressure sensor P1 (Fig. 3). The mean and the standard deviation of the gait cycle time were computed to characterize the average duration and consistency of the gait cycles, respectively. The mean and the standard deviation of the gait cycle times, which were normalized to the height of the patients, were also computed in order to remove height-dependent variability. Stance time was calculated by measuring the time difference between the heel strike (local minima preceding the peaks of P1’s time series) and the toe-off (local minima followed by the peak of P5’s time series). The mean and the standard deviation of the stance time were included. The stance-to-stride ratio was computed by taking the ratio of the stance time to the gait cycle time. The mean and the standard deviation of the stance-to-stride ratio were included. The mean and the standard deviation of the time differences between the peaks of P1 & P2, P2 & P3, P3 & P4, and P4 & P5 were computed to investigate how fast and consistently patients distribute their weight on their foot. Similarly, the mean and the standard deviation of the peak amplitude of all pressure sensors were computed. Accumulated pressure amplitudes of all pressure sensors throughout the 10 meter walk were computed to investigate any abnormal distribution of the body weight while walking. The maximum cross correlation coefficient between the first half and the second half of each pressure time series was computed to investigate the consistency of weight distribution patterns. Furthermore, the cross correlations between all possible pairs of the pressure sensors were computed. The aforementioned features were extracted from both of the shoes. In order to investigate the bilateral symmetry between the two lower limbs, the symmetry index of gait, as introduced in [21], was computed. The symmetry index was computed by taking the ratio between the difference and the average of the mean gait cycle time of the left and the right feet. Furthermore, the maximum cross correlations between the pressure sensors located at the same position between the left and the right shoes were computed, e.g., correlation between left P1 and right P1.

3.3. Estimating Preoperative Clinical Scores

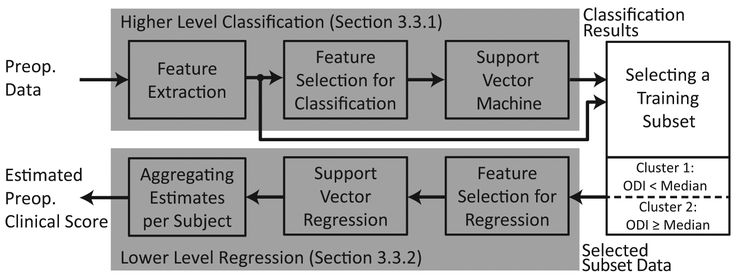
Fig. 4 shows the schematic representation of the algorithm used to estimate preoperative clinical scores. The independent variables of this estimation problem included the spatio-temporal features and the clinical variables that were introduced in Section 2.4. The dependent variable was the ODI score. All analyses presented in this paper were performed using a leave-one-subject-out cross validation (LOSOCV) technique. A LOSOCV technique leaves out data belonging to a subject when training the classification/regression model, and evaluates the trained model using the the left-out data. This process was iterated through all subjects.

Figure 4:

A schematic representation of the algorithm used to estimate preoperative clinical scores.

The algorithm employed a hierarchical (two-level) model composed of a classifier followed by a regression algorithm. The hypothesis behind this design was that the (regression) relationship between the input features and value range of ODI. Thus, the higher level classifier used a Support Vector Machine (SVM) with a highly flexible kernel function (Pearson VII function (PUK) [22, 23]) in order to provide a coarse estimate of the clinical score, i.e. determining if ODI was less than (or greater than or equal to) the median ODI score of the training set. This higher level classifier was discussed in detail in Section 3.3.1. Then, a Support Vector Regression (SVR) with a simpler kernel function (3^rd order polynomial kernel [24]) followed to provide more detailed estimation while minimizing the chances of over-fitting on the smaller training instances (Section 3.3.2).

3.3.1. HigherLevel Classification

The raw training and testing sensor data were processed to extract the spatio-temporal features. Then, the discretized labels (i.e. two clusters) of the training data were generated based on their ODI scores. These clusters were defined based on the empirical distribution of the training ODI scores to ensure the equal number of data points; the first cluster contained data points with ODI scores less than the median value and the second cluster contains those with ODI scores greater than or equal to the median. A feature selection algorithm was employed to reduce the feature dimensionality using the ReliefF algorithm [25] and the Davies-Bouldin (DB) index [26]. The ReliefF algorithm ranked the features based on their classification ability. This algorithm iteratively assigned weights of the features by sampling an instance and examining its K neighbors of the same and different classes. Then, the ranked features were progressively added and computed for the DB index, which evaluated the intra- and inter-cluster separability. The cardinality of the feature subset that produced the minimum DB index was selected. This feature subset, which was selected based on the analysis of the training dataset, was also applied to the testing dataset in order to reduce the dimensionality. The SVM with PUK followed to categorize the testing dataset into one of the two clusters. This work used the WEKA implementations of ReliefF and SVM [27], and the MATLAB implementation of the DB index [28].

3.3.2. Lower Level Regression

A subset of the training data belonging to the classified cluster was then used to construct a regression model for more refined estimation. A feature selection algorithm, which selected a feature subset that had a high correlation to the dependent variable (i.e. ODI scores) with low redundancy among the selected features [29], was employed to reduce the dimensionality. The SVR with polynomial kernel was trained based on the dimension-reduced training dataset, and was used to estimate the clinical scores of the testing dataset. Since more than one data instance was created per clinical visit per subject, the estimated scores of the instances belonging to the same clinical visit were averaged to provide a single estimated clinical score. This work employed the WEKA implementation of the feature selection algorithm [27] and the LibSVM implementation of the SVR [30].

3.4. Estimating Postoperative Clinical Scores

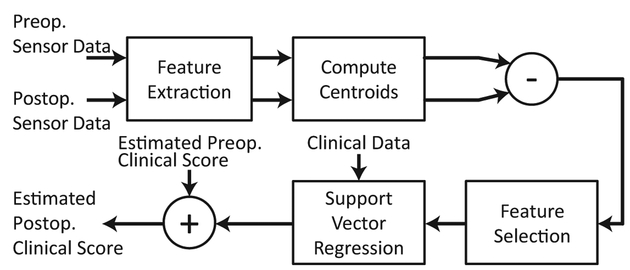
The postoperative dataset had access to additional information, other than the postoperative sensor data, that may significantly contribute in estimating the clinical score: its preoperative ODI scores. The algorithm was designed based on a hypothesis that the postoperative ODI score changes with respect to its preoperative value and thus, the postoperative score can be more accurately estimated by estimating the change in the ODI score rather than directly estimating the score using the sensor data. The schematic summary of the algorithm is provided in Fig. 5, which was again performed in a LOSOCV manner.

Figure 5:

A schematic representation of the algorithm used to estimate postoperative clinical scores. This algorithm estimates the changes in the ODI score after surgical operation rather than directly estimating the ODI score from the postoperative sensor data.

The preoperative and postoperative sensor data of patients, who had a follow-up visit, were processed to extract the spatio-temporal features. Then the feature values of the instances belonging to the same clinical visit were averaged to produce the centroid of the instances within the feature space. Then the differences between the values of preoperative and postoperative dependent variables to the postoperative estimation problem included these differences in feature values, the clinical variables introduced in Section 2.4, and the preoperative ODI scores. The difference between the preoperative and postoperative ODI scores of the training dataset were computed in order to serve as the target (dependent) variable. The correlation-based feature selection algorithm (i.e. [29]) was again employed to reduce the feature dimensionality. Then, SVR with 3^rd order polynomial kernel followed to construct a regression model based on the training dataset, and to estimate the change in the ODI score of the testing dataset. The SVR with polynomial kernel was used in order to avoid over-fitting of the regression model, considering relatively small number of patients with postoperative data (i.e. 15 patients). The estimated change in the ODI score was then added to the estimated preoperative value, i.e. the estimation of the preoperative ODI score of the testing subject that was produced by using the algorithm introduced previously in Section 3.3.

4. Results

4.1. Estimation Results of Preoperative Clinical Scores

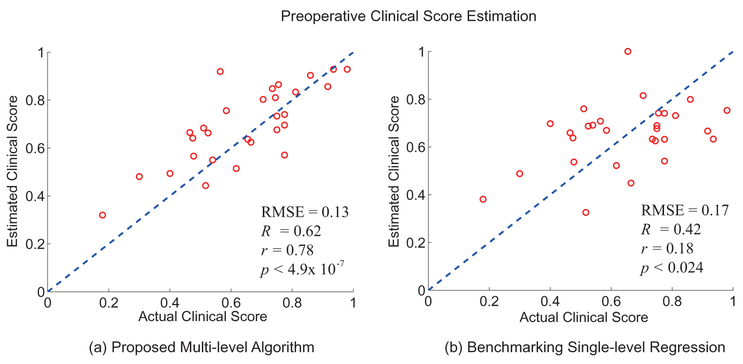
Fig. 6 (a) shows the scatter plot between the actual clinical scores reported preoperatively and the estimated scores produced by the proposed hierarchical algorithm. Fig. 6 (b) shows the estimation results of the benchmarking algorithm, which is based on a single-level regression algorithm (SVR with polynomial kernel); note that SVR with polynomial kernel yielded the best estimation results compared to other kernels and other regression algorithms such as random forest regression or multivariate linear regression. As discussed earlier, all results reported in this work were generated using the LOSOCV technique, which ensures the generalization of the model towards independent datasets and avoids the problem of over-fitting. The root mean square error (RMSE) between the actual scores and the estimated scores of the proposed algorithm was 0.13, and the RMSE of the benchmarking algorithm was 0.17. The coefficient of determination (R²), the Pearson correlation coefficient (r), and the p-value of the proposed algorithm were R² = 0.62, r = 0.78 and p < 4.9 × 10 ⁻⁷, respectively. The benchmaking algorithm produced R² = 0.42, r = 0.18, and p < 0.024.

Figure 6:

The estimation results of the preoperative ODI scores based on (a) the proposed hierarchical method and (b) the benchmakring single-level regression. The x-axis represents the actual ODI scores reported by the patients and the y-axis represents the estimated ODI scores.

4.2. Estimation Results of Postoperative Clinical Scores

The postoperative ODI scores have shown statistically significant difference compared to the associated preoperative scores (paired t-test produced p < 0.0040), which supports the necessity of a method for estimating postoperative ODI scores. The RMSE between the preoperative and postoperative ODI scores were 0.29, the R² was 0.25, the r was 0.50, and the p-value was 0.058. These can serve as the baseline of estimation results for postoperative clinical scores since the direct comparison between the preoperative and postoperative clinical scores is identical to having no estimation algorithm.

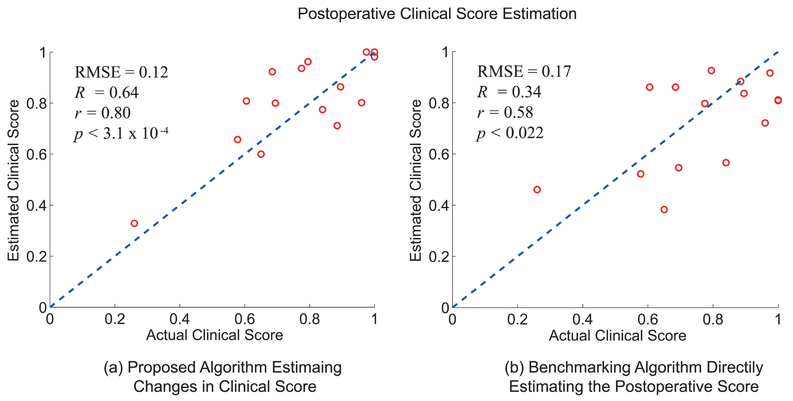
Fig. 7 (a) shows the estimation results of the postoperative clinical scores using the proposed algorithm, which estimates the change in the postoperative ODI score respect to its preoperative value. Fig. 7 (b) shows the results based on a benchmarking algorithm that directly estimates the post-operative clinical score using SVR with polynomial kernel. The proposed method produced postoperative estimations with RMSE = 0.12, R² = 0.64, r = 0.80, and p < 3.1 × 10⁻⁴. The benchmarking method had RMSE = 0.17, R² = 0.34, r = 0.58, and p < 0.022.

Figure 7:

The estimation results of the postoperative ODI scores based on (a) the proposed algorithm that estimates the changes in ODI score respect to the preoperative value, and (b) the benchmarking algorithm that directly estimates the postoperative ODI score from the sensor data using SVR with polynomial kernel.

4.3. Combined Estimation Results

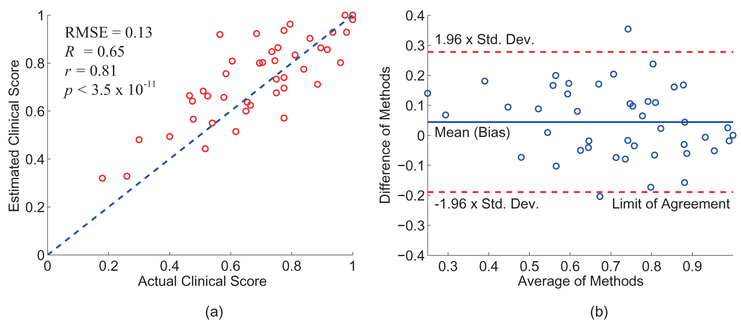
Fig. 8 (a) shows the scatter plot that combines the preoperative and postoperative estimation results of the proposed algorithms, and Fig. 8 (b) shows its Bland-Altman plot. The overall RMSE was 0.13, R² was 0.65, r was 0.81, and the p-value was 3.5×10⁻¹¹. The bias (mean of the difference) and the limit of agreement of the Bland-Altman plot were 0.044 ± 0.12.

Figure 8:

(a) The scatter plot of both preoperative and postoperative estimation results produced by the proposed algorithm, which shows RMSE = 0.13, R² = 0.65, r = 0.81, and p < 3.5 × 10⁻¹¹. (b) Its Bland-Altman plot with the bias of 0.044 and the magnitude of the limit of agreement of 0.12.

4.4. Contribution of the Spatio-Temporal Features in Estimation

To investigate the level of contribution of the spatio-temporal features and the clinical variables in estimating the clinical scores, the estimation results of using (1) the spatio-temporal features and the clinical information were compared to (2) using only spatio-temporal features as the input to the analytic methods and (3) using only the clinical information as the input to the analytic method. Table 1 summarizes the estimation results, which indicate that the spatio-temporal features extracted from the sensorized shoes contribute the most in estimating the ODI score.

Table 1:

A summary of the estimation results when (left) both spatio-temporal and clinical variables were considered as the input features, (center) only the spatio-temporal variables were considered, and (right) only the clinical variables were considered.

	Spatio-temporal & Clinical variables	Spatio-temporal only	Clinical variables only
RMSE	0.13	0.13	0.21
R2	0.65	0.65	0.36
r	0.81	0.80	0.13
p-value	3.5 × 10−11	5.1 × 10−7	0.15

5. Disscussion

This pilot study investigated the use of sensorized smart shoes to quantify the walking ability in LSS patients by estimating the ODI scores. The reported results demonstrate that the system has great potential to be used as a tool for screening the patients’ preoperative conditions as well as tracking their postoperative conditions. The system is non-invasive, easy-to-use, in-expensive, and takes approximately six minutes to complete, which supports the system’s potential as a tool for monitoring patients not only in clinical settings but also in remote (e.g., home and community) settings.

Fig. 6 illustrates that the proposed hierarchical estimation method out-performs the conventional regression approach in terms of the estimation accuracy. This may be due to the fact that the regression relationship between the clinical scores and the input features is highly complex and varies non-linearly depending on the value range of the ODI. To compensate for this, the proposed method employed a binary classifier that determined the coarse estimate of the testing instance (i.e. greater or less than the median ODI score) followed by a regression algorithm that provide more detailed estimation. This work considered only two subgroups in the higher level classifier due to the relatively small size of the study data. Investigating the optimal number of subgroups in our on-going clinical trial with a large-scale dataset remains as future work.

Fig. 7 shows that the proposed algorithm for postoperative estimation, which estimated the change in the ODI score, produce superior results compared to the algorithm that directly estimates the postoperative ODI scores. This may be due to the following. The estimations in Fig. 7 (b) were made by classification/regression models that used the combined set of preoperative and postoperative data as their training set. The relationship between the spatio-temporal features and the ODI scores may have changed after receiving surgical operation. For instance, ODI is known to have response shift following surgery for patients with lumbar spinal cord disorder [16], which may influence the results shown in Fig. 7 (b). On the other hand, the proposed method partially incorporated the presence of the response shift since the algorithm estimated the deviation of the postoperative ODI score from its preoperative value.

Fig. 8 shows the combined results of the preoperative and postoperative data. The estimation results (i.e. RMSE = 0.13, R² = 0.65, and r = 0.81) were comparable to other related works. Authors in [6] reported that the overall ODI score and the traveled distance of the SPWT showed correlation coefficient of r = −0.60. In [3], authors reported that the time length of MTT and the score of the walking item of the ODI showed a significant correlation with r = −0.63; the authors also reported, however, that the overall score did not show any significant correlations to the results of the walking tests. These are not surprising since both MTT and SPWT investigate the walking capacity, which is defined as the distance a person with LSS can walk before being forced to stop due to symptoms of LSS [31]. On the other hand, the presented work of this paper investigated the quality of walking in LSS patients by analyzing the gait parameters, balance, weight distribution, and symmetry of the limbs. This resulted in a higher correlation to the overall ODI score as the ODI assesses the level of pain and its interference in performing various daily activities. Furthermore, Fig. 8 (b) validates that there is no significant underestimation or overestimation; the value of the bias (mean) was 0.044. The magnitude of the limit of agreement was equal to 0.12, which shows the expected error range for the 95% (1.96 times the standard deviation) of estimation results.

The work presented in this paper estimated the overall ODI score that averaged the scores of ten items, which examined various dimensions of functional level of patients with lower back pain. Each individual item score was also estimated using the spatio-temporal features. Since items had only five or six answer choices whose value gradually changed according to the severity of the examining condition, a regression algorithm (without hierarchical design) was employed to estimate each item score. The estimated scores of items that investigate (1) pain intensity at the affected area, (2) ability to walk for a long distance, and the degree of interference of pain on (3) social life and (4) traveling showed statistical significance to the reported scores with p-values of 0.0031, 0.0057, 9.6 × 10⁻⁴, and 0.0093, respectively. The items that did not show significance included the degree of interference of pain on self-caring, lifting heavy weights, sitting for a long time, standing for a long time, sleeping, and sex life. It is interesting that the items that showed statistical significance involved some degree of walking ability; the definition of social life was not clearly stated in the questionnaire but one of the answer choice stated “pain has restricted social life to my home,” which may lead patients to consider their walking ability to travel outside of the home while answering.

Table 1 summarized the contributions of the spatio-temporal and clinical features in estimating the ODI scores. The estimation result produced by considering both the spatio-temporal and clinical variables as the input was comparable to when only the spatio-temporal variables were considered, and the contribution of the clinical variables was minimal. The most likely reason for this result is that the ODI quantifies the functional level based on many items that involve some degree of walking ability. Thus, the functional level, obtained by using the ODI can be more accurately estimated by analyzing the spatio-temporal data rather than the clinical information (e.g.,the number of previous spinal surgeries, symptom duration, presence of acute injury, or BMI). This further supports the need for a frequent, objective method to assess functional level in LSS population, which can be made possible using the proposed system.

6. Conclusion

This paper introduced a pair of pressure sensor equipped shoes and the associated algorithms that together can quantify the functional level in LSS patients by analyzing their walking ability and clinical information. The sensor data obtained from a pilot cohort of 29 LSS patients were used to estimate the Oswestry Disability Index, a clinically validated outcome measure. The estimation results based on the leave-one-out cross validation technique showed an RMSE of 0.13, an R² of 0.65, a r of 0.81, and a p-value of 3.5 × 10⁻¹¹. This pilot study enables new research and clinical opportunities for accurate quantification of functional capacity in LSS patients to track the level of disease severity before and after surgical operations. The quantification of walking ability can also be applied to stratifying patients for more personalized treatment and care. Furthermore, the pervasive nature of the proposed sensory platform can be used to ubiquitously monitor patients, which can potentially provide early alarming of any walking disorders.

Highlights.

• The functional level of LSS patients is quantified using a pair of sensorized shoes

• Machine learning algorithms were used to estimate the Oswestry Disability Index

• The functional level can be accurately quantified by analyzing walking ability