Association between divergence and interspersed repeats in mammalian noncoding genomic DNA

Abstract

The amount of noncoding genomic DNA sequence that aligns between human and mouse varies substantially in different regions of their genomes, and the amount of repetitive DNA also varies. In this report, we show that divergence in noncoding nonrepetitive DNA is strongly correlated with the amount of repetitive DNA in a region. We investigated aligned DNA in four large genomic regions with finished human sequence and almost or completely finished mouse sequence. These regions, totaling 5.89 Mb of DNA, are on different chromosomes and vary in their base composition. An analysis based on sliding windows of 10 kb shows that the fraction of aligned noncoding nonrepetitive DNA and the fraction of repetitive DNA are negatively correlated, both at the level of an entire region and locally within it. This conclusion is strongly supported by a randomization study, in which repetitive elements are removed and randomly relocated along the sequences. Thus, regions of noncoding genomic DNA that accumulated fewer point mutations since the primate–rodent divergence also suffered fewer retrotransposition events. These results indicate that some regions of the genome are more “flexible” over the time scale of mammalian evolution, being able to accommodate many point mutations and insertions, whereas other regions are more “rigid” and accumulate fewer changes. Stronger conservation is generally interpreted as indicating more extensive or more important function. The evidence presented here of correlated variation in the rates of different evolutionary processes across noncoding DNA must be considered in assessing such conservation for evidence of selection.

The rate of fixation of nucleotide substitutions and small insertions/deletions, collectively referred to as point mutations, varies substantially in different regions of mammalian genomes. The 1,000-fold difference in nonsynonymous substitution rates among genes has long been recognized as a reflection of different levels of selection on the protein products of genes (reviewed in refs. 1 and 2). However, the rate of fixation of synonymous substitutions, which seem to be effectively neutral, also varies about 10-fold locus to locus (3). The synonymous and nonsynonymous substitution rates are significantly correlated (4, 5). The variation in synonymous substitution rates has been attributed to differences in the rate and pattern of mutation in different regions of the genome (6). Recently, Matassi et al. (7) showed that the synonymous substitution rate is significantly more similar for neighboring genes than for randomly chosen genes, which argues for regional differences in substitution rates.

Regional differences in point mutation rates are also indicated by comparisons of long genomic DNA sequences. Examination of several loci reveals dramatic differences in the amount of noncoding nonrepetitive DNA that aligns between species in different mammalian orders (8, 9). Substantial differences are seen even for two loci that encode functionally equivalent proteins, the α- and β-globin subunits of hemoglobin (10). The amount of conservation in noncoding nonrepetitive DNA varies about 10-fold (11). Thus, a similar range of variation is seen both for the amount of aligning noncoding DNA and for synonymous substitution rates in coding DNA, showing local variation in the rate of fixation of substitutions and small insertions/deletions.

Striking differences in the distribution of repetitive DNA are also seen across the human genome (12–14). At one extreme are HOX gene clusters, which contain only about 2% interspersed repeats within 100 kb, whereas a 525-kb region of chromosome Xp11 has a repeat density of 89% (14). Thus, the frequency of fixation of these transposable elements varies enormously in different segments of the human genome.

Some potential explanations for these regional differences focus on particular sequences, such as target-site preference for transposition or base-composition biases in substitutions (6, 15). These explanations do not require a correlation between amount of point mutation and amount of transposition. A different model is that some segments of the genome are more tolerant of changes of any sort, whether they are point mutations or transpositions. In this case, a correlation should be seen between the number of point mutations (revealed by alignments of noncoding nonrepetitive DNA) and the amount of repetitive DNA in a locus.

We demonstrate such a correlation in four loci on different chromosomes for which substantial continuous DNA sequence is available in human and mouse. Quantitative and statistical analyses confirm a significant association between amount of divergence in noncoding nonrepetitive DNA and frequency of interspersed repeats in all four loci. Our results show that overall rates of evolution vary in different segments of the genome, with more “flexible” regions able to accommodate many point mutations and insertions, whereas more “rigid” regions tend to accumulate fewer changes of both types.

Methods

Sources of Sequences.

Information about the sources, chromosomal locations, and characteristics of the human and mouse sequences is summarized in Table 1. The human sequences for all four loci and parts of the mouse sequence homologous to the CD4 and velocardiofacial syndrome (VCFS) regions are finished. Other mouse sequences were compiled from searches of mouse draft sequences in GenBank. The pipmaker server can align a finished first sequence with multiple unordered and unoriented contigs from the second sequence (16).

Table 1.

Regions in human and mouse analyzed for noncoding conservation and density of repeats

Region	Human				Mouse			Ref.
	Sequences	Length	Chromosome	G + C content	Sequences	Length	Chromosome
VCFS	NT_001039	1.5 Mb	22q11.2	51.94%	AC003063, AC008020, AC010001, AC008019 contigs 5,3,6,4,1,2, AC003066, AC012399 contigs 9,8,4,7,3,1,2,5,6, AC003060, AC012526 contigs 2,1, AC006082 contigs 3,5,4,21, AF121882	1.47 Mb	16	12, 36
CD4	HSU47924	223 kb	12p13	51.14%	AC002397	227 kb	6	27
CFTR	AC000111, AC000061	498 kb	7q31	37.35%	AF162137	357 kb	6	28
MHC	http://www.sanger.ac.uk/HGP/ Chr6/MHC.shtml Oct. 1999 version, HLA-F to HSET	3.67 Mb	6p21	46.08%	NT_002588.2, AC025874.3, AC074150.1, AC087216.1, AC007080.2, AC005960	2.34 Mb	17	29

Contigs within a mouse draft sequence are listed in the order in which they align with human. 

Annotation.

To discriminate coding from noncoding sequences with high accuracy, we exhaustively reannotated the human sequences in a multistep process. First, the annotations from the authors were downloaded from GenBank or the Sanger Center (for the MHC, http://www.sanger.ac.uk/HGP/Chr6/MHC.shtml). Then additional genes were identified by matches to known genes and to spliced expressed sequence tags (ESTs) by using the program megablast to search databases at the National Center for Biotechnology Information (17) and The Institute for Genomic Research (http://www.tigr.org/tdb/tgi.shtml). As an example, in the VCFS/DiGeorge region, matches to ESTs identified four previously uncharacterized genes, homologous or identical to ESTs AK025539, BE234886, and AB045987 and protein KIAA1292 (18). Exons were assigned by SIM4 comparison of mRNAs and genomic sequence (19). Regions containing conserved sequences outside annotated genes were analyzed by the exon-prediction program genscan (20), but the predicted exons did not correspond to the highly conserved regions. Repetitive elements were identified by repeatmasker at http://ftp.genome.washington.edu/RM/RepeatMasker.html (21). Additional information, including full annotation of the human sequence, can be found at http://bio.cse.psu.edu/mousegroup/.

Alignment.

We used pipmaker (16) to align the complete human sequence with the draft mouse sequence. Previous studies have shown that alignment of a completed sequence with a draft sequence reveals much of the information found in alignment of two completed sequences (22). In cases where the mouse sequence was not finished, the pipmaker analysis was used to assess the extent of coverage. For example, the vast majority of the human VCFS/DiGeorge region sequence is covered by mouse sequence (see dotplot at http://bio.cse.psu.edu/≈elnitski/repeat_correlation/). However, regions of the human sequence for which no mouse sequence was available were excluded from the analysis. One of these is the CLTCL1/CLTD locus, which has no counterpart on the proximal end of mouse chromosome 16 (23, 24). We determined that portions of TR and DGCR5 were not covered by mouse sequence, because the ends of these genes align, but matches to internal exons are absent. For example, both ends of the TR homologue in mouse (Tnxrd2) are present in the contig AC003066 or contig 9 of AC012399. In contrast, exons 3–8 of TR do not align to the mouse sequence, whereas these exons are present in the reference cDNA for Tnxrd2, indicating that they are missing from the assembled mouse contigs (positions 1075–1100 kb in human). Each end of DGCR5 aligns with a different mouse contig (AC006082, contig 4, or AC003063) with no overlap between them, indicating that an internal region of the mouse Dgcr5 may not be in the current sequence. Of the 1.5 Mb of human sequence from the VCFS/DiGeorge region, 214.8 kb were omitted from the analysis because no corresponding mouse sequence was available.

Calculations of Aligning and Repetitive Nucleotide Fractions and Their Correlations.

Within each locus, we use a 10-kb sliding window to produce a local evaluation of the fraction of noncoding nonrepetitive human nucleotides aligning with mouse, and the fraction of repetitive nucleotides. For each position t we set:

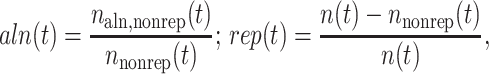1

where n(t), n_nonrep(t), and n_aln,nonrep(t) are, respectively, the number of nonexonic, nonexonic and nonrepetitive, and aligning nonexonic and nonrepetitive nucleotides in a 10-kb window about t. We then compute the locus-level correlation r(aln,rep) between the functions aln(t) and rep(t), extending the standard Pearson correlation formula

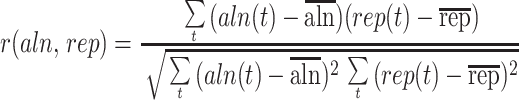2

to all positions (symbols with bars indicate averages). We also compute local correlation coefficients r(aln,rep;t) between the two functions, using again a 10-kb sliding window—the formula is extended to positions in a 10-kb window about t. Local correlations can be summarized in a histogram on [−1,1], and quantiles of the histogram (we consider the 10, 25, and 50%) help us gauge the concentration of local correlations on large negative values.

Note that the function aln(t) will not be defined when the number of nonexonic nonrepetitive nucleotides in the window about t is 0. Moreover, the local correlation r(aln,rep;t) will not be defined when all positions in the window about t have an undefined aln, or when one or both of the functions is constant throughout the window. We attempted the use of several window sizes on 22q11.2 (0.5, 1, 5, 10, 20, and 50 kb), obtaining different degrees of smoothness for the functions, but very similar correlation behaviors. On the other hand, small window sizes result in a larger number of undefined values for aln(t) and r(aln,rep;t), and thus decrease the reliability of the analysis. We selected 10 kb as the smallest size resulting in a negligible number of undefined alignment fractions and local correlations.

Randomization Analysis.

To assess the significance of the overall and local correlations observed in our four loci, we performed randomizations aimed at representing a hypothetical “null” scenario in which divergence by substitution and small insertions/deletions occurs independently of insertion of interspersed repeats. For each locus, we remove repetitive elements from the sequence and construct 100 artificial sequences by randomly and independently relocating the repeats. Each repeat has a uniform probability of being inserted anywhere along the sequence, except within a repeat that has been already inserted. This process makes the randomization independent of the order in which repeats are reinserted and simplifies computational and logical aspects (e.g., we do not need to specify an age, and thus an insertion order, for repetitive elements). For each of the artificial sequences, we then compute aligned and repetitive nucleotide fractions, their overall correlations, and their local correlations, which we summarize through a histogram and its 10, 25, and 50% quantiles.

Note that aligned nucleotides, as produced by pipmaker, may change slightly after reinsertion of repeats. We implemented the procedure with and without realigning the sequences on 22q11.2 and did not observe appreciable changes. Therefore, we performed the randomization analyses on the four loci maintaining the aligned nucleotides produced by pipmaker on the original sequences.

Through the randomization, we can compute empirical (left) P values for the overall correlation and the quantiles of the local correlation histogram. These P values represent the share of randomized sequences for which the overall correlation is more negative than the one computed on the original sequence, for which the 10% local correlation quantile is more negative than the one computed on the original sequence, etc. Moreover, we can calculate empirical envelopes for the local correlation histogram: for each value (actually, small interval) in [−1,1], we have 100 frequencies corresponding to the histograms produced by the 100 randomizations. We consider the smallest, 10, 25, 50, 75, and 90th, in increasing order, and the largest. Using these frequencies we produce a “median” frequency curve on [−1,1], a 50% envelope between the two “quartile curves” (this contains half of the frequencies generated by the randomization for each value in [−1,1]), an 80% envelope between the 10 and 90% “quantile curves” (this contains 80% of the frequencies for each value in [−1,1]), and a 100% envelope between the minimum and maximum curves (this contains all of the frequencies for each value in [−1,1]).

Results

Variation in Density of Interspersed Repeats and Amount of Noncoding Sequence Alignment.

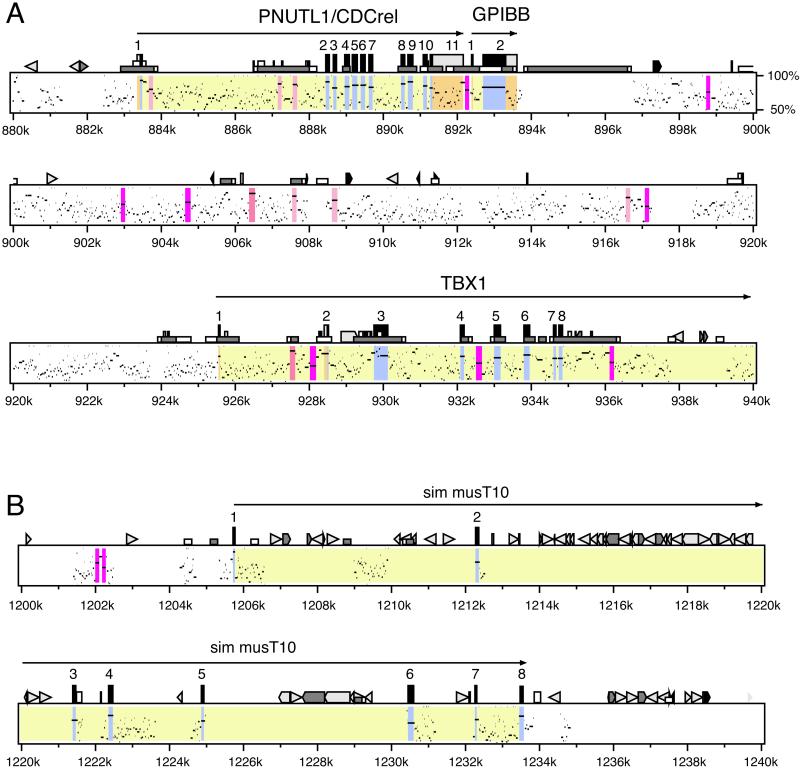
The four loci we analyzed are among the longest in the human genome with almost complete coverage with homologous sequence from mouse. The loci are a 1.5-Mb region of human chromosome 22q11.2 implicated in VCFS and DiGeorge Syndrome (25, 26), 223 kb around CD4 (27), 498 kb around CFTR (28), and 3.67 Mb containing the Class I and II regions of the major histocompatibility complex (29). They are located on four different chromosomes and range in their G + C content from 37% to 52% for the human sequences (Table 1). To accurately discriminate coding from noncoding portions, we accessed existing annotation and exhaustively reannotated the human sequence (see Methods). Fig. 1 presents percent identity plots (pips) for two portions of the 1.5-Mb region of human chromosome 22q11.2. (Pips for the four loci in their entirety can be found at http://bio.cse.psu.edu/∼elnitski/repeat_correlation/.)

Figure 1.

Pip for two portions of the 1.5-Mb region of human chromosome 22q11.2 implicated in DiGeorge Syndrome and VCFS, aligned with orthologous sequences from mouse chromosome 16. (A) The region from PNUT1 to part of TBX1. (B) The region containing a gene similar to mouse T10 (sim musT10). The positions of gap-free segments of alignments are plotted along the horizontal axis by using coordinates in the human sequence, and the percent identity is plotted along the vertical axis (from 50% to 100%). Features of the human sequence are annotated along the top of each graph. Genes are labeled above arrows showing the direction of transcription, and exons are shown as numbered rectangles (black if protein-coding, gray if untranslated). Low rectangles denote CpG islands, shown as white if 0.6 ≤ CpG/GpC < 0.75 and as gray if CpG/GpC ≥ 0.75. Interspersed repeats are shown by the following icons: light gray triangles are short interspersed repeats (SINEs) other than mammalian wide interspersed repeats (MIRs), black triangles are MIRs, black pointed boxes are long interspersed repeats 2 (LINE2s), and dark gray triangles and pointed boxes are other kinds of interspersed repeats, such as long terminal repeat elements and DNA transposons. Areas within the pip are colored yellow for introns, blue for coding exons, orange for noncoding exons, green for matches to expressed sequence tags that are not in known exons, and shades of red and pink for matches of various percent identities longer than 100 bp in noncoding nonrepetitive regions (pink for percent identities of at least 70% but less than 80%, light red for percent identities of at least 80% but less than 90%, red for percent identities of at least 90% but less than 100%).

Interspersed repeats are rare in some long segments of 22q11.2 (Fig. 1A), whereas they are highly clustered in others (Fig. 1B). The latter results from multiple repetitive elements integrating close to each other. Inspection of the pips indicated that segments with high repeat density are characterized by few matches in the noncoding nonrepetitive regions around the repeats (e.g., Fig. 1B), whereas segments with few repeats align with mouse throughout much of the noncoding nonrepetitive DNA (e.g., Fig. 1A). Most of the repetitive elements in human and mouse arose since the divergence of these two species (30), therefore it is unusual for repeats to align within orthologous chromosomal regions (31). In fact, we masked the repetitive human DNA before computing the initial hits with mouse, and although pipmaker can extend alignments that begin in nonrepetitive DNA through repeats, we excluded aligning repeats from the analysis, limiting ourselves to noncoding nonrepetitive aligned nucleotides.

Quantitative Results.

The next step was to quantify the association between conservation of noncoding nonrepetitive DNA and repeat density and compute this for all four loci in their entirety. To avoid biases in the extent of aligning segments due to adjacent coding and untranslated exonic regions, we masked the exons in the sequence files and recomputed alignments with pipmaker. This analysis provided all of the gap-free segments in the nonexonic regions of the human sequence that aligned with mouse with a percent identity of at least 50. Based on the repeatmasker results, each nucleotide was assigned as either repetitive (including repeats that predate the human–mouse divergence) or nonrepetitive.

For each position t in the four loci, we produce a local evaluation of the fraction of noncoding nonrepetitive human nucleotides aligning with mouse, aln(t), and the fraction of human nucleotides that are in interspersed repeats, rep(t), as detailed in Methods. The calculation of the aln(t) function is limited to the nonexonic nonrepetitive nucleotides, whereas the rep(t) function includes all nonexonic nucleotides. Thus, it is possible for a window to have a large fraction of repeats but still have a high value for aln(t); negative correlations between these functions are not forced by their definitions.

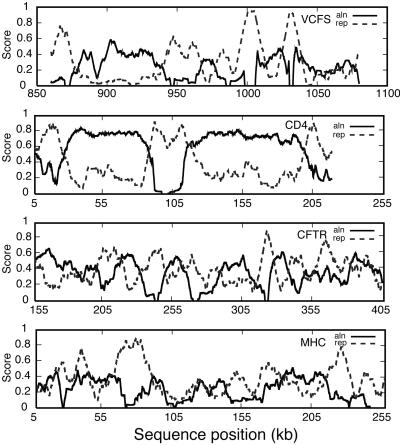
Fig. 2 shows the aln(t) and rep(t) functions on four regions of 250 kb selected from the four loci. In each case, the functions tend to oscillate in “counterphase,” with segments characterized either by strong conservation and little repetitive DNA or vice versa. This behavior translates into sizably negative overall correlations between aln(t) and rep(t); the r(aln,rep) coefficients for the four loci are reported in column 2 of Table 2.

Figure 2.

Local variation in the amount of DNA aligning with mouse and the density of repeats. The local fractions of noncoding nonrepetitive nucleotides aligning with mouse, aln(t) (black line), and those of noncoding repetitive nucleotides, rep(t) (dashed gray line), are computed with a 10-kb sliding window. Selected 250-kb regions are shown from the VCFS region of human 22q11.2 (first graph), CD4 (second graph), CFTR (third graph), and MHC (fourth graph).

Table 2.

Statistics of overall and local correlations between fraction of noncoding nonrepetitive aligning sequences and fraction of nucleotides that are repetitive

Region	Overall correlation	Left P value	10% Quantile local correlation	Left P value	25% Quantile local correlation	Left P value	50% Quantile local correlation	Left P value
VCFS	−0.458	<0.01	−0.882	<0.01	−0.736	<0.01	−0.382	<0.01
CD4	−0.858	<0.01	−0.962	<0.01	−0.876	<0.01	−0.610	<0.01
CFTR	−0.404	<0.01	−0.906	<0.01	−0.790	<0.01	−0.504	<0.01
MHC	−0.380	<0.01	−0.876	<0.01	−0.708	<0.01	−0.336	<0.01

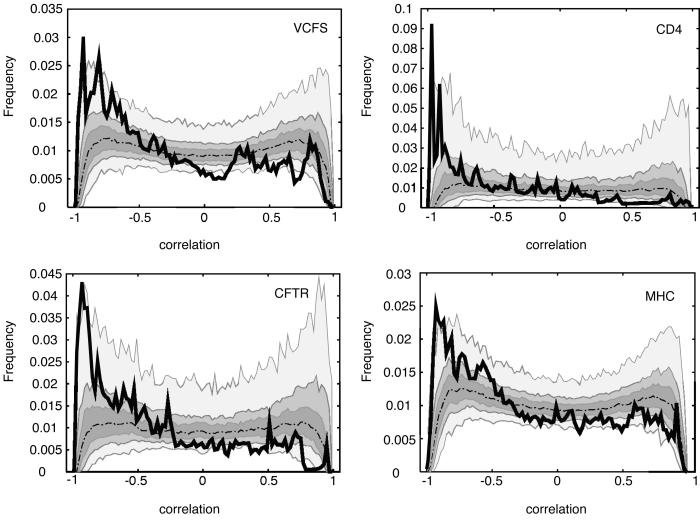
Next, we produced local correlation coefficients r(aln,rep;t), as detailed in Methods. The continuous lines in Fig. 3 represent the local correlation histograms for the four loci. Each shows a remarkable concentration on extreme negative values, as can be seen also from the values of the 10, 25, and 50% quantiles reported in columns 4, 6, and 8 of Table 2. Thus, along most of the regions under consideration, DNA segments that have sustained more insertions of repetitive elements also have diverged more from the mouse sequence.

Figure 3.

Histograms of local correlations between level of conservation and density of repeats. In each plot, the observed histogram of r(aln,rep;t) is shown as a continuous thick black line, accompanied by a “median curve” (dotted line) and envelopes (50%, darkest; 80%, lighter; and 100%, lightest) computed from the frequencies of histograms produced by repeat randomizations. For each correlation level between −1 and 1, the median of these frequencies lies on the dotted line, 50% of them fall in the most darkly shaded envelope, 80% in the lighter envelope, and all of them fall in the lightest envelop. Data are plotted for the VCFS region of human 22q11.2 (Left Upper), CD4 (Right Upper), CFTR (Left Lower), and MHC (Right Lower).

In each locus, a certain number of segments is characterized by small variations in the aln and rep functions. These produce positive or negative local correlations whose size is, by definition, insensitive to the size of the fluctuations in aln and rep. This “small-scale amplification” phenomenon is responsible for some of the observed local reversals in the dominant negative association. For instance, aln is much higher than rep over the interval 875–940 kb of 22q11.2 (see Fig. 2), but in three segments the local correlation is positive rather than negative. Two of these (centered around 910 and 920 kb) correspond to small in-phase fluctuations in aln and rep. More generally, amplification of small in-phase fluctuations in segments where one of the functions is high and the other low, and of small “counterphase” fluctuations in segments where the functions are both high or both low, is partly responsible for the differences in overall correlation coefficients among the four loci (Table 2, column 2), despite the similarity in their local correlation structures (Fig. 3). Although all of the association measurements we use are significantly negative and remain so after changing window sizes, one should realize that global and local analyses capture different aspects of the association, as gauged by the definition of “locality” implicit in the choice of window size.

Results of the Randomization Analysis.

We assessed the significance of our findings through a randomization analysis. For each locus, we removed interspersed repeats from the original sequence and generated 100 randomized sequences reinserting repeats at random locations. By using the alignment of nonexonic nonrepetitive nucleotides obtained on the original sequence and the new repeats locations, we then recomputed aln and rep functions, with their overall and local correlations, for each randomized sequence. Empirical (left) P values for the overall correlation and for the 10, 25, and 50% quantiles of the local correlations (see Methods) are reported in columns 3, 5, 7, and 9 of Table 2. In all cases, and for all loci, none of the quantities produced by the randomizations are more negative than the corresponding quantities in the original sequence. Therefore, all P values are <0.01. This expresses the significance of the negative overall correlations and of the concentration of local correlations on extreme negative values.

Also, Fig. 3 contains empirical “median curves” and envelopes for the local correlation histograms determined by the frequencies of histograms produced by the randomizations (see Methods). For all loci, the actual histogram frequencies (continuous line) are above most or all of the randomization frequencies on the left, and fall below most or all of the randomization frequencies as one moves toward the right (Fig. 3). Consistent with the P values in Table 2, this shows how extreme the negative association data are with respect to the null scenario represented by the randomizations (independence between divergence by point mutation and insertion of interspersed repeats).

Discussion

The frequency of nucleotide substitutions observed in comparisons of mammalian genomic DNA varies substantially among different regions (6, 7, 9, 11). Also, it is clear from this and other analyses (14) that repetitive elements are not free to integrate between any two base pairs along chromosomes; indeed, they show a propensity to cluster in some regions and to avoid others (Fig. 1). We show these two processes are highly correlated at four large loci that differ in chromosomal location and genomic context (such as G + C content). Thus, some genomic regions tend to accumulate change due to both point mutation and retrotransposition at a relatively high rate; these rapidly changing regions can be considered to be “flexible” with respect to evolutionary alteration. These flexible regions are not devoid of function, e.g., the T10 gene is in a flexible region of 22q11 (Fig. 1B), and the entire ERCC2 locus seems to be in a flexible region of chromosome 19 (9, 32). In contrast, other genomic regions are protected from these two different types of sequence alteration; they tolerate little change and can be considered “rigid” with respect to evolutionary change.

Selection solely on the coding regions could not generate these rigid segments, because the exons are a small portion of the sequence. Also, a long segment between GP1BB and TBX1 (897–924 kb in Fig. 1A) has no identifiable genes but retains a high level of conservation. Two different explanations can be offered for these rigid regions. One is that the matching sequences result from selection (33). By this model, the conservation in noncoding regions (such as 897–924 kb in 22q11.2) reflects a strong selection on a large number of gene regulatory elements (or sequences required for some other critical nuclear process) throughout a region. A similar explanation has been offered for the very small number of repeats in the HOX gene clusters (14). Alternatively, a region can be evolutionarily rigid because the local mutation rate is low, independently of selection. Distinguishing between these two classes of explanation will require more studies.

We further show that each of the four genomic regions is a mosaic of faster-changing segments interspersed with slower-changing segments. The mechanistic basis for this needs further study, too. Additional insight can be gained by using local evaluations of aln and rep to objectively segment large genomic regions and then determining the types of sequences that tend to be in rigid or flexible segments.

The variable amount of overall conservation in different genomic regions complicates the analysis of sequence alignments to find functional elements (34, 35). For instance, if the baseline conservation expected for neutral evolution varies from locus to locus, then different cutoffs should be applied to find DNA sequences that are significantly more conserved and hence likely functional. Better understanding of the variation can improve the accuracy of predictions of functional sequences. For instance, if the frequency of repeats is a significant predictor of the overall level of conservation, then a certain level of conservation in a repeat-rich region may be significant, whereas it may not be significant in a repeat-poor region. Furthermore, the most appropriate phylogenetic distance over which good candidates for functional sequences are revealed by matches in noncoding nonrepetitive DNA (34) may be predictable based on repeat density of a locus.

Tests of other genome-wide associations will also be informative. The variation in substitution rates correlates with the base composition of the locus in some (6, 15) but not all (7) existing studies. We find a positive correlation between point mutation frequency and density of repeats at four large chromosomal regions of differing base composition. However, further investigation is needed to assess whether the level of conservation correlates locally with base composition within each region. Tests of other possible correlations, e.g., with recombination frequency and position along a chromosome, will be feasible as more complete mouse genomic DNA sequence becomes available.

Abbreviations

VCFS

velocardiofacial syndrome

pip

percent identity plot