Shear Waves Reveal Viscoelastic Changes in Skeletal Muscles after Hemispheric Stroke

Abstract

We investigated alterations in material properties such as elasticity and viscoelasticity of stroke-affected muscles using ultrasound induced shear waves and mechanical models. We used acoustic radiation force to generate shear waves along fascicles of biceps muscles and measured their propagation velocity. The shear wave data were collected in muscles of thirteen hemiplegic stroke survivors under passive conditions at 90°, 120°, and 150° elbow flexion angles. In a viscoelastic medium, as opposed to a purely elastic medium, shear wave propagation velocity depends on the frequency content of the induced wave. Therefore, in addition to shear wave group velocity (GpV), we also estimated frequency dependent phase velocity (PhV). We found significantly higher GpVs and PhVs in stroke-affected muscles (p < 0.05). The velocity data were used to estimate shear elasticity and viscosity using elastic and viscoelastic material models. A pure elastic model showed increased shear elasticity in stroke-affected muscles (p < 0.05). The Voigt model estimates of viscoelastic properties were also significantly different between stroke-impaired and non-impaired muscles. We observed significantly larger model-estimated viscosity values on the stroke-affected side at elbow flexion angles of 120° and 150°. Furthermore, the creep behavior (tissue strain resulting from the application of sudden constant stress) of the model was also different between muscles of the paretic and non-paretic side. We speculate that these changes are associated with structural disruption of muscles after stroke and may potentially affect force generation from muscle fibers as well as transmission of force to tendons.

I. Introduction

MOTOR deficits after hemiparetic stroke are most evident in the contralesional limb and may involve muscle weakness, fatigue, abnormal muscle tone, spasticity, reflex hyperexcitability, and limited joint excursion, or contracture [1–5]. In addition to changes in the neural control properties related to motor neuron firing rates and recruitment thresholds, the muscle tissue in stroke survivors may also undergo abnormal alterations in its intrinsic properties [1, 6–8]. Such changes in muscle tissue post-stroke are likely caused by alterations in the composition, structure, and material properties of individual muscle fibers, and may potentially include a shift in fiber type (from type II to type I), increased variance in fiber size, and shortening of muscle fibers due to sarcomere loss [3, 4, 9–11]. Furthermore, deterioration in the quality and changes in the density of the extracellular matrix (ECM), infiltration of connective tissue, and an increased intramuscular fat are also possible mechanisms [4, 9, 11, 12].

Elasticity imaging or elastography is a technique to characterize tissue mechanical properties and structure. In shear wave elastography, the tissue is perturbed by the acoustic radiations/external force to generate shear waves. The resulting vibrations, i.e., propagation of shear waves, can be monitored due to changes in tissue acoustic impedance or magnetic properties, referred to as ultrasound elastography or magnetic resonance elasticity imaging, respectively [13]. The recorded shear wave velocity data can later be quantitatively linked to elastic and viscoelastic properties of the tissue using mathematical models. These models are based on elastic (spring) and viscous (dashpot) elements connected in various series/parallel combinations and assume specific properties including linearity, homogeneity, and isotropy of the medium [13].

A variety of ultrasound-based techniques and related mathematical models have been developed and used to estimate viscoelastic properties in biological tissues: the Voigt model has been linked with ultrasound-induced shear waves for skeletal muscles [14], anti-symmetric Lamb wave model with acoustic radiation force for bladder tissue [15], and the Voigt model with multi-push acoustic radiation force for canine muscle and renal allografts [16]. Another broadly related acoustic radiation force-based technique, Supersonic Shear Imaging (SSI), was developed recently to evaluate viscoelastic properties of soft tissues [17]. Using SSI, quasi-planar shear waves are generated with focused ultrasound beams, and transient propagation of these waves is measured through echographic images acquired at a high frame rate [17]. This technique has been applied to human organs such as liver and breast, as well as to skeletal muscles [17, 18].

Recently, two SSI studies from our group showed that skeletal muscles exhibited increased shear wave velocity after brain injuries such as stroke or cerebral palsy (CP) [6, 19]. Both studies employed SSI techniques to estimate muscle material properties such as elasticity with the assumption that the effect of changes in viscous properties was negligible, an assessment which may be somewhat premature. It has been shown, for example, that due to the viscoelastic nature of muscle tissue, measurement of both elastic and viscous properties is essential for comprehensive characterization of tissue mechanical behavior [16, [20–22]. The tissue viscosity may play a significant role in introducing frequency-dependent changes (dispersion) in muscle tissue and parallel changes in elasticity may significantly alter tissue mechanical behavior.

Our present study investigates differences in material properties of skeletal muscles of paretic and non-paretic sides of hemiplegic stroke survivors. Viscoelastic properties were estimated using shear wave velocity data. We estimated shear wave velocity (averaged over all frequencies), referred to as the group velocity (GpV), and the frequency dependent shear wave velocity called the phase velocity (PhV). We then related these velocity measurements to muscle viscoelastic properties using pure elastic and viscoelastic (Voigt) models. In a purely elastic medium, the velocity of the induced wave will not depend on its frequency, and thus, the PhV will converge to the GpV value. We hypothesized that both shear wave GpV and PhV would be significantly higher in stroke-affected muscles likely due to changes in material properties and increased muscle stiffness generally observed in joint-based measures. We further hypothesized that the elastic and viscous moduli estimated through mathematical models using GpV and PhV data would be significantly altered after stroke which are likely linked to viscous and elastic properties of stroke-affected muscles. These differences in viscoelastic properties between stroke-impaired and non-impaired muscles might potentially compromise force generation and transmission capacity of stroke-affected muscles. The force generation is linked to the contractile properties of individual muscle fibers while the force transmission is linked to the ECM network, connective tissue, and other non-contractile/fatty tissues.

II. Methods

A. Participants

Thirteen hemiplegic stroke survivors (8 male, 5 female) with the median age of 65 years and range of 39 to 70 years, participated in the study (Table I). The study was approved by the Institutional Review Board of Northwestern University, and all participants provided written consent. The participants had a broad range of functional impairment (upper-extremity Fugl-Meyer (FM) score range: 9 to 52) and spasticity (modified Ashworth scale (MAS): 0 to 3). Our inclusion criteria included: 1) 21 years of age and older, 2) a single hemispheric stroke that occurred at least six months before the study, 4) either hemorrhagic or thrombotic origin of stroke, 5) no structural limitations of joint motion, and 6) no surgery or botulinum toxin treatments within the past six months. Demographic data and clinical assessments of participants are presented in Table I.

TABLE I.

Stroke Participants’ Data

ID	Affected Arm	FM	MAS	Time Since Stroke (Yrs)	Age	Gender	Comments
1	Right	18	1	5	53	F
2	Left	27	2	12	47	M
3	Left	9	1+	22	66	F
4	Left	46	0	7	70	F	Data removed
5	Right	16	2	11	66	F
6	Left	18	1	9	60	M
7	Right	52	1+	11	59	M
8	Left	9	3	9	44	F
9	Left	21	1+	6	39	M	Data removed
10	Left	17	2	12	70	M
11	Left	18	3	2	66	M	Data removed
12	Right	22	1+	4	69	M
13	Left	19	1+	2	65	M

FM – Fugel-meyer score; MAS – Modified Ashworth Scale

B. Experimental Setup

Participants sat comfortably in a fully-adjustable chair (Biodex, Shirley, NY) to which the arm selected for ultrasound imaging was securely fastened using a plastic brace. The arrangement held the arm in a specified position for the whole duration of ultrasound imaging. The arm position was set at three elbow flexion positions 90°, 120°, and 150°. The shoulder abduction angle was set at 15∼20° and shoulder flexion at 15∼20°. Aixplorer ultrasound system (SuperSonic Imagine, Aix-en-Provence, France) with a linear transducer array (4–15 MHz, SuperLiner 15–4, Vermon, Tours, France) was used to generate and track shear wave propagation. This technology has been discussed in detail previously [23]. A region of interest (ROI), approximately 25mm × 10mm in size was selected for shear wave imaging. The ultrasound transducer was placed on the muscle in the longitudinal direction, parallel to muscle fascicles (Fig. 1(a)). The ROI was placed between the superficial and deep aponeuroses at the thickest section of the biceps muscle. Simultaneous B-mode ultrasound imaging ensured that the data were captured within the muscle fascicle plane.

Fig. 1.

(a) Schematic layout of the imaging setup with the ultrasound transducer, biceps brachii muscle, muscle fascicle direction, and region of interest (ROI). (b), (c), and (d) The propagation of planar shear waves (white color patches) in the ROI are shown at three different time points: 1ms, 2ms, and 3ms. All three subfigures are zoomed view of the ROI from subfigure (a) with the same orientation at three different time points. The propagation of shear waves towards the elbow on one side and towards shoulder on the other side is visually identifiable.

A shear wave imaging sequence using the SSI consisted of five automatically generated pushes along muscle fascicles within the ROI. Each push, in turn, consisted of multiple acoustic beams to create a Mach cone that produced quasi-planar shear waves [23]. The propagation of shear waves was recorded at 8000 frames per sec. At each joint angle (90°, 120°, and 150°), ten imaging sequences were performed for the stroke-affected and non-affected sides separately. After each imaging sequence, the probe was lifted by the experimenter and placed back again on the belly of the biceps brachii muscle for the next imaging sequence.

The propagation of planar shear waves inside the ROI is shown in Fig. 1(b)-(d). The propagation of shear waves from the center of ROI horizontally towards elbow on one side and shoulder on the other side is evident. The shear wave data were later processed in a custom-written graphical user interface (GUI) in Matlab (Mathworks Inc., Natick, MA).

C. Muscle Activity Monitoring

Shear wave velocity is sensitive to muscle activity [24]. Therefore, muscle activity was recorded using a single differential bar electromyogram (EMG) electrode from Delsys Inc. (Bagnoli System, Natick, MA). The electrode was placed on the medial side of the biceps brachii. The EMG data were monitored in real-time as well as recorded using a custom-written GUI in LabVIEW (National Instruments, Austin, TX). The EMG signals were recorded using an amplifier gain setting of 1000 and inbuild bandpass filtering of 20–450 Hz. A baseline EMG was established for the resting muscle state at the beginning of the experiment. The established baseline EMG was later monitored visually in real-time during imaging sequences. If EMG activity higher than the baseline was observed, the ultrasound imaging sequence was stopped and resumed after the EMG activity reduced to a value less than the established baseline.

All imaging sequences were time-synchronized with corresponding EMG data using an external trigger pulse. During offline processing, synchronized EMG signals were analyzed quantitatively to find traces of muscle activity. Various advanced statistical and mathematical tools have been proposed to detect muscle activity from the EMG data [25], [26]. However, in this particular application, we found that simple thresholding was sufficient, and a muscle was considered active if the root mean square EMG was larger than 3µV [8, 27]. The threshold value was established in previous studies and our preliminary data also confirmed its applicability [8, 27]. In cases where the muscle was found active, corresponding imaging sequences were removed. The shear wave velocity data from three stroke survivors (ID-4, 9, and 11) were excluded from analysis due to muscle activity.

D. Shear Wave Velocity Estimation

A single ultrasound imaging sequence produced data in the form of a displacement field u(z, x , t, n), where z represents depth, x lateral position, t time, and n push number. The displacement field consists of a time-history of pixel displacement values resulting from the push along the direction of muscle fascicles (Fig. 1(b), (c), and (d)).

1). Shear Wave GpV Estimation:

The displacement field was averaged along the z-axis to calculate a mean displacement image I (x , t, n) [17]. In Fig. 2(a), we present displacement images I (x , t) for n = 3, where lines of shear wave propagation originating from the focal plane of the acoustic beam are visually identifiable. A customized line detection algorithm using the Hough transform was used to detect these lines and calculate their slopes [8, 28]. Slopes of all detected lines from all n pushes were averaged to calculate a representative GpV value for an imaging sequence.

Fig. 2.

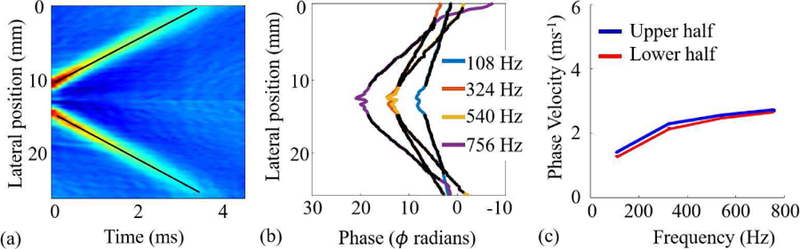
Estimation of GpV and PhV from the displacement field u(z, x, t) for the third push, i.e., n = 3. (a) The displacement field was averaged along the z-axis to calculate the displacement image I(x, t). Black lines were estimated using Hough transform and their slopes represent GpV. (b) Phase values at four different frequencies. After Fourier transformation of displacement images, phase data were extracted and unwrapped from the frequency image I(x, ω). (c) Estimated PhVs using phase data from subfigure (b).

2). Shear Wave PhV Estimation:

To estimate PhV, the displacement image I (x , t, n) was transformed to frequency domain using the Fourier transform. The resulting frequency image I (x , ω, n) was used to calculate the PhV:

$$c_{ph}(\omega )=\frac{\omega \Delta r}{\Delta \varphi },$$ (1)

where, c_ph (ω) is the PhV at the angular frequency ω, ∆r is the traveled distance by the phase, and ∆ϕ represents the change in the phase. The procedure can be implemented by retrieving and unwrapping phase data (ϕ) for different frequencies and performing a linear regression between phase and lateral position [17]. As there were more than two points available for the unwrapped phase, we used an optimization algorithm that produced the largest number of consecutive points with the minimum standard error of the linear fit [17]. The unwrapped phase (ϕ) and lateral position (x) are presented in Fig. 2(b) for a set of frequencies [14]. A shift in phase values near the point of origin of shear waves is evident in both images. The black dots shown in the figure over the phase lines are the points selected by the optimization algorithm that minimized the standard error of the linear fit. The slope of the line fitted to these points was used to estimate PhVs presented in Fig. 2(c).

E. Elastic and Viscoelastic (Voigt) Model Fitting

A linear model for the viscoelastic material consists of an elastic spring and a viscous dashpot arranged in parallel and is referred to as the Voigt model [29]. We preferred the Voigt model for its simplicity and acceptable performance in experiments with gelatin phantom and other tissue-like materials [30]. The propagation velocity, i.e., PhV of planar shear waves in a Voigt material is given by [30, 31]:

$$c_{ph}(\omega )=\sqrt{\frac{2(E^2+{\omega }^2{\eta }^2)}{\rho (E+\sqrt{E^2+{\omega }^2{\eta }^2})}},$$ (2)

where, E is the shear elasticity modulus measured in Pascals (Pa), ρ is the density of the medium in Kg·m⁻³ and η is the shear viscosity in Pa·s. The relation in (2) provides a link between material properties, i.e., shear elastic (E) and viscous (η) moduli and shear wave propagation velocity c_ph (ω). After estimation of c_ph (ω) at different frequencies using (1), shear elastic and viscous moduli were estimated using the nonlinear least square (NLS) algorithm and Eq. 2. The NLS algorithm is used to perform nonlinear regression for problems where the observed data, i.e., c_ph (ω) and ω are known to have a nonlinear relation with the unknown model parameters, i.e., E and η [32]. NLS is an iterative algorithm and its convergence may depend on the initialization due to non-convex nature of the problem [32]. We used Matlab’s inbuilt function lsqnonlin which in turn employs the trust-region-reflective algorithm for iteratively estimating unknown model parameters [33]. Both moduli (E and η) were estimated for each subject and at all three joint angles separately using corresponding PhV and frequency data. The NLS algorithm was initialized with a set of random values of elasticity and viscosity and one hundred repetitions were performed for better convergence. Estimated values with the minimum norm of the error were chosen as the representative moduli.

For a pure elastic medium, the viscosity is negligible, i.e., η = 0, or in case E ≫ ωη, the relation in (2) reduces to:

$$c_{gp}=\sqrt{E/\rho }\Rightarrow E=c_{gp}^2\rho ,$$ (3)

where, c_gp represents the GpV.

We used (3) to estimate shear elasticity (E) from the GpV data. The density ρ for the muscles was considered 1060 Kg/m³ for both elastic and viscoelastic cases [34]. It is important to note that the phase velocity is affected by both the intrinsic properties and tension in the muscles. Therefore, the shear elasticity and viscosity estimated using these models cannot be interpreted as a direct measure of the material properties of the muscle.

F. Creep Behavior for the Voigt Model

The creep phenomenon represents strain behaviors of material under conditions when constant stress is applied and removed suddenly, i.e., the step response of the system. The stress-strain relationship of the Voigt model is given as:

$$\sigma =Eϵ+\eta \dot{ϵ}(t),$$ (4)

where σ represents the stress, ϵ strain and ‘dot’ is first derivative with respect to time. For constant stress σ₀, we have:

$$\dot{ϵ}(t)=\frac{1}{\eta }[{\sigma }_o-Eϵ(t)].$$ (5)

The resulting relation is an ordinary differential equation of first order and can be solved for the creep behavior:

$$ϵ(t)=\frac{{\sigma }_o}{E}\left[1-e^{-\frac{E}{\eta }t}\right]=\frac{{\sigma }_o}{E}[1-e^{-t/\tau }].$$ (6)

The relation in (6) is an exponential function with the time constant τ = η/E in units of seconds. The exponential behavior of (6) is controlled by the time constant, while the scaling (along ordinate) is determined by the initial applied stress (σ₀) and shear elasticity modulus (E). The creep behavior describes the evolution of strain ϵ(t) over time once the Voigt material is subject to a sudden constant stress. We calculated creep values for all participants and compared stroke-affected muscles with non-affected muscles using a constant stress σ₀ = 1K Pa applied at t = 0 ms and removed at t = 8 ms.

In summary, GpV data were used to estimate elastic moduli considering muscle a purely elastic material. The PhV data were used to estimate elastic and viscous moduli using Voigt model and NLS algorithm. The estimated moduli were later used to calculate creep values and simulate creep behavior.

G. Statistical Analysis

The estimated PhV, GpV, elastic and viscous moduli data were tested for normality (Gaussian distribution) using the Kolmogorov–Smirnov test, where the null hypothesis was that the standardized data were following a standard normal distribution. We were unable to reject the null hypothesis at 95% significance. Therefore, for all later analyses, parametric statistics were used to analyze data with the probability of type-I error α = 0.05. For each participant, imaging sequences were considered independent observations and comparisons of PhV, GpV, elasticity, and viscosity moduli were performed between stroke-affected and non-affected muscles using the two-tail Student’s t-test with unequal variance. One-way ANOVA was used to analyze the effect of joint angle on PhV, GpV, elasticity, and viscosity data in stroke-affected and non-affected muscles separately. Results of the statistical test are represented with standard notations, i.e., M = Mean, SD = Standard Deviation, t = t-statistic, and F = F statistic.

The PhV data were fit to an exponential model f (x ) = αe^βx and parameters α and β with 95% confidence interval, and the coefficient of determination (r²) were calculated.

The time constant (τ) data of the Voigt model did not follow the Gaussian distribution and nonparametric statistics were used to analyze and report the time constant (τ) data. The statistical tests were performed in Matlab and IBM SPSS 21 (IBM, Armonk, NY).

III. Results

A. Shear Wave GpV Data

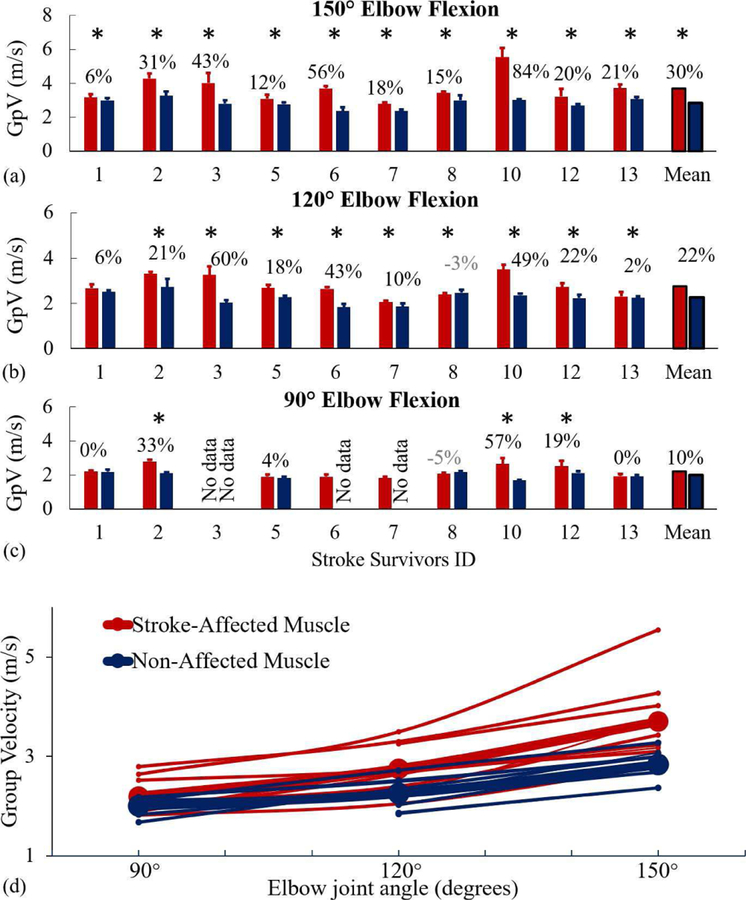
The shear wave GpV data of all stroke survivors from three elbow joint angles (150°, 120°, and 90°) is presented in Fig. 3(a), (b), and (c) respectively. At elbow flexion angle of 150°, there was a significant difference between stroke-affected (M = 3.70, SD = 0.79) and non-affected muscles (M = 2.84, SD = 0.30); t (11) = 3.25, p = 0.01. At an angle of 120°, there was again a significant difference between stroke-affected (M = 2.75, SD = 0.47) and non-affected muscles (M = 2.26, SD = 0.28); t (15) = 2.87, p = 0.01. However, at an angle of 90°, there was no significant difference between stroke-affected (M = 2.20, SD = 0.13) and non-affected muscles (M = 2.01, SD = 0.19); t (13) = 1.36, p = 0.20.

Fig. 3.

GpV data of stroke-affected muscles (red bars/lines) and non-affected muscles (blue bars/lines) at three joint angles (90°, 120°, and 150°). (a), (b), and (c) GpV of individual subjects. Capped lines over the bars show a single standard deviation. The percentage increase in GpV in stroke-affected muscles is indicated with statistical significance (*), p < 0.05. The last set of bars represent pooled mean. At 90°, data of three stroke survivors (ID-3 both sides, ID-6 and 7 non-affected muscles) were removed due to muscle activity detected in off-line processing. (d) GpV data of all stroke participants and mean (bold lines) at all three joint angles.

At the joint angle of 150° (Fig. 3(a)), GpVs were on average 30% higher (range: 6% to 84%) in stroke-affected muscles as compared to non-affected muscles. At the joint angle 120° (Fig. 3(b)), GpVs were 22% higher on the stroke-affected side (range: 2% to 60%). We noted a small reduction in the GpV (0.08 ms⁻¹) on the stroke-affected side (highlighted in gray color) in one stroke participant. At 90° (Fig. 3(c)), we observed 10% average increase (range: 0 to 57%) in GpVs on the stroke-affected side.

In Fig. 3(d), we present pooled GpV data of all stroke survivors. The effect of joint angle on the GpV is visually evident for both stroke-affected and non-affected muscles. On the stroke-affected side, there was significant effect of joint angle (p < 0.05) for three conditions [F(2,26) = 16.71, p < 0.001]. Post hoc comparisons using the Tukey HSD test indicated that the mean score for the joint angle of 150° was significantly different from 120° and 90°. However, mean scores of 120° and 90° were not significantly different from each other. Similarly, on the non-affected side, there was significant effect of joint angle (p < 0.05) for three conditions [F (2,24) = 22.07, p < 0.001]. Post hoc comparisons using the Tukey HSD test indicated the mean score for the joint angle of 150° was significantly different from 120° and 90° (p < 0.05). However, mean scores of 120° and 90° were not significantly different (p > 0.05).

B. Shear Wave PhV Data

PhV data for a range of frequencies (0–800 Hz) for all stroke survivors at three joint angles are presented in Fig. 4. At all three joint angles, the dependence of the PhV on the frequency of the induced wave is evident in both stroke-affected as well as non-affected muscles.

Fig. 4.

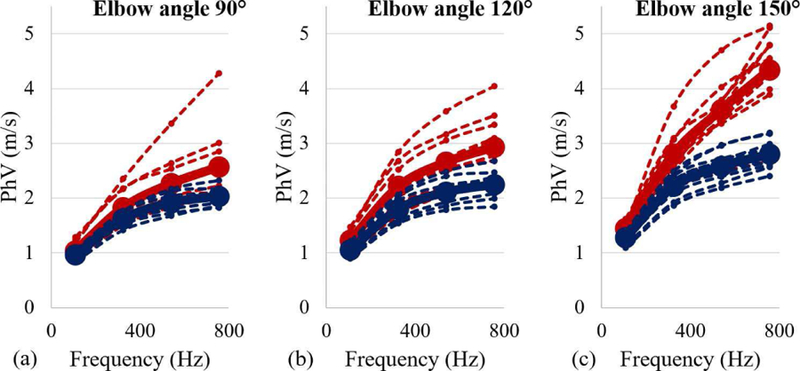
The PhV data from both stroke-affected muscles (red) and non-affected muscles (blue) for a range of frequencies. (a) PhV at 90°. (b) 120°. (c) 150°.

Parameter estimates for the exponential model fitting to the PhV data are presented in Table II. We note that PhVs increased with increasing joint angles (Fig. 4); however, the amount of increase was significantly more in stroke-affected muscles and at large joint angles (exponential parameter β in Table II).

TABLE II.

Exponential Parameter Estimates for Phase Velocity Data

Estimated parameter	90°		120°		150°
	SA	NA	SA	NA	SA	NA
α (95% CI)	1.804 (1.758, 1.850)	1.587 (1.556, 1.619)	2.160 (2.106, 2.214)	1.748 (1.716, 1.779	2.917 (2.845, 2.989)	2.135 (2.099, 2.172)
β (95% CI)	0.236 (0.211, 0.261)	0.225 (0.206, 0.245)	0.257 (0.233, 0.281)	0.227 (0.209, 0.244)	0.340 (0.317, 0.364)	0.232 (0.215, 0.248)
r2	0.71	0.67	0.59	0.66	0.69	0.69

CI – Confidence interval, SA – Stroke-affected, NA-Non affected

Using two-tailed Student’s t-test with unequal variance, we found significant differences between PhV values of stroke-affected and non-affected muscles at all measured frequencies (p < 0.0005 for all cases).

C. Elastic Model Fitting

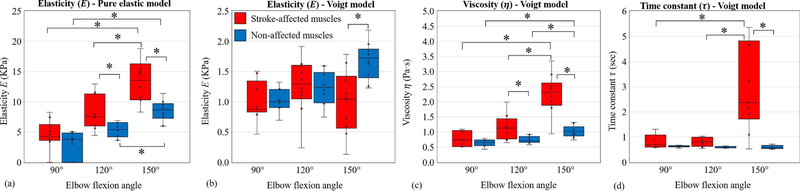
Shear elasticity values calculated from GpVs (3) are pre-sented in Fig. 5(a) for both stroke-affected and non-affected muscles at all three joint angles. We note that stroke-affected muscles exhibited higher shear elasticity as compared to non-affected muscles at all three joint angles. At an elbow flexion angle of 150°, there was a significant difference between stroke-affected (M = 14.8, SD = 6.86) and non-affected muscles (M = 8.56, SD = 1.70); t (10) = 2.79, p = 0.02. Similarly, at an angle of 120°, there was a significant difference between stroke-affected (M = 8.23, SD = 2.79) and non-affected muscles (M = 5.38, SD = 1.19); t (12) = 2.97, p = 0.01. However, at an angle of 90°, there was no significant difference between stroke-affected (M = 5.11, SD = 1.74) and non-affected muscles (M = 4.30, SD = 0.80); t (12) = 2.24, p = 0.24.

Fig. 5.

Elastic and viscoelastic (the Voigt) model fitting results in the form of box plots for stroke-affected muscles (red) and non-affected muscles (blue) with statistical significance (*), p < 0.05. (a) Pure elastic model. (b) Viscoelastic (the Voigt) model: shear elasticity data. (b) Viscoelastic model: shear viscosity data. (d) Viscoelastic model: time constant (τ = η/E) data.

On the stroke-affected side, there was significant effect of joint angle (p < 0.05) for the three conditions [F (2, 26) = 11.81, p = 0.0002]. Post hoc comparisons using the Tukey HSD test indicated the mean score for the joint angle of 150° was significantly different from 120° and 90°. However, the mean scores of 120° and 90° were not significantly different from each other. On the non-affected side, there was again significant effect of joint angle (p < 0.05) for three conditions [F (2, 24) = 24.64, p < 0.001]. Post hoc comparisons using the Tukey HSD test indicated that the mean score for the joint angle of 150° was significantly different from 120° and 90°. However, the mean scores of 120° and 90° were not significantly different.

D. Viscoelastic Model Fitting Using the Voigt Model

The Voigt model elastic moduli data are presented in Fig. 5(b). At an angle of 90°, there was no significant difference between stroke-affected (M = 1.00, SD = 0.34) and non-affected sides (M = 1.02, SD = 0.20); t (13) = 0.16, p < 0.88. At an angle of 120°, there was again no significant difference between stroke-affected (M = 1.26, SD = 0.47) and non-affected muscles (M = 1.22, SD = 0.28); t (15) = 0.20, p = 0.84. However, at 150°, there was a significant difference between stroke-affected (M = 0.99, SD = 0.52) and non-affected sides (M = 1.68, SD = 0.30); t (14) = 3.62, p = 0.003. We note that differences between elastic moduli of stroke-affected and non-affected muscles are not as distinct as those of the pure elastic model.

We observed a significant increase in the model-based estimates of viscous moduli in stroke-affected muscles as compared to non-affected muscles (Fig. 5(c)). At elbow flexion angle of 150°, there was a significant difference between stroke-affected (M = 2.26, SD = 0.66) and non-affected sides (M = 1.03, SD = 0.19); t (11) = 5.67, p < 0.001. At an angle of 120°, there was again a significant difference between stroke-affected (M = 1.15, SD = 0.41) and non-affected muscles (M = 0.74, SD = 0.12); t (11) = 3.02, p = 0.01. However, at 90°, there was no significant difference between stroke-affected (M = 0.87, SD = 0.48) and non-affected sides (M = 0.64, SD = 0.12); t (9) = 1.47, p = 0.20. Furthermore, on the stroke-affected side, there was significant effect of joint angle (p < 0.05) for three conditions [F(2, 26) = 18.71, p < 0.0001]. Post hoc comparisons using the Tukey HSD test indicated that the mean score for the joint angle of 150° was significantly different from 120° and 90°. However, the mean scores of 120° and 90° were not significantly different from each other. On the non-affected side, there was again significant effect of joint angle (p < 0.05) for three conditions [F (2,24) = 15.69, p<0.001]. Post hoc comparisons using the Tukey HSD test indicated that the mean score for the joint angle of 150° was significantly different from 120° and 90°. However, the mean scores of 120° and 90° were not significantly different.

The time constant represents the ratio of shear viscosity and elasticity moduli, i.e., $\tau =\eta /E$. The estimated time constant values for the Voigt model are presented in Fig. 5(d). A Wilcoxon signed-rank test showed that at elbow flexion angles of 150° and 120° stroke had a significant effect on the time constant (Z = 3.10, p = 0.002 and Z = 2.35, p = 0.02 respectively). However, at 90°, the effect of stroke was not significant (p = 0.22). The time constant exhibited a minimal dependence on the joint angle in non-affected muscles. A Kruskal-Wallis test showed that there was no statistically significant difference in time constant between different joint angles on the non-affected side, χ²(2) = 2.26, p = 0.32. However, in stroke-affected muscles, the time constant varied significantly between joint angles χ²(2) = 8.85, p = 0.01.

We demonstrate simulated creep behavior of stroke-affected and non-affected muscles in Fig. 6. We applied a constant stress of σ₀ = 1 KPa at time t = 0 ms and removed the same at t = 8 ms. Each curve was normalized to its maximum value to eliminate the scaling effect and highlight exponential behavior. We observed remarkable similarity in the behavior of non-affected muscles under constant stress for all three measured joint angles. On the other hand, stroke-affected muscles exhibited a different behavior and took more time to adapt to the changed stress levels at all three measured joint angles.

Fig. 6.

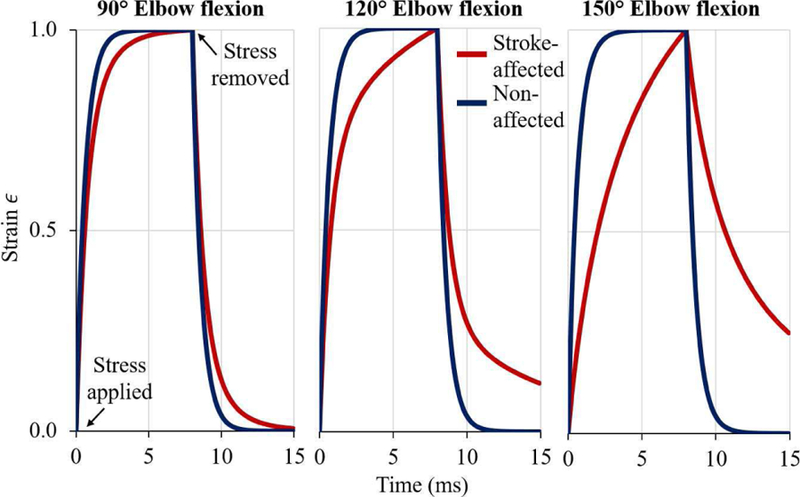
Normalized creep curves (simulated strain behavior under a constant stress of σo = 1 KPa applied at t = 0 ms and removed at t = 8 ms) are presented at three different joint angles (90°, 120°, and 150° elbow flexion). Stroke-affected (red) muscles, being more viscous, take a longer time to adapt to changed stress environment than non-affected muscle (blue).

IV. Discussion

After a brain injury such as stroke, many of the subsequent neurological changes are well-known [4]. In this study, we set out to demonstrate the nature and magnitude of local soft tissue changes in skeletal muscles after stroke. Our objective was to quantify changes in viscoelastic properties of stroke-affected muscles in a passive state, using both the group and phase velocities of shear waves. We augmented our analysis with a pure elastic and a viscoelastic (Voigt) model. The elastic model produced elasticity data, while the Voigt model produced both elasticity and viscosity data. The Voigt model also helped us investigate the creep behavior of muscle tissue, i.e., the time evolution of strain in the tissue when constant stress is suddenly applied or removed.

Our findings demonstrated significantly higher GpV in stroke-affected muscles at two joint angles (average increase of 30%, and 22% at elbow flexion angles of 150° and 120°, Fig. 3). These findings are supported by previous work in stroke and CP muscles [6, 19] where only GpVs were investigated, and viscous components were considered negligible. Other studies using the SSI technique typically report shear modulus calculated using the GpV data [6, 19]. The GpV values are averaged values over all induced wave frequencies and can be misleading if there are significant viscous elements in the tissue. The shear wave velocity data can be correctly translated to mechanical properties only after a mathematical model for the material is introduced that provides a relationship between velocity values and material elastic/viscous moduli.

Considering the joint angle as an independent parameter, we observed a length-dependent increase in both the GpV and PhV. These observations are related to length-dependent structural and mechanical properties of skeletal muscles. Previous studies have also reported an increase in the shear wave velocity with muscle length in upper-/lower-extremity skeletal muscle; however, these studies limited their analysis to reporting velocities only, and mechanical parameters, i.e., elasticity and viscosity were not explored [35, 36].

We observed a significant dependence of PhV on the frequency of the induced wave (Fig. 4). Using an exponential model, we found that PhV data were a function of the frequency of the induced wave for both stroke-affected and non-affected muscles at all joint angles (parameter β in Table II). The dispersive behavior of the muscle tissue, i.e., dependence on frequency, is related to the viscous properties of the biological material [31]. We noted that the frequency-dependence of PhV was increasing with increasing joint angle in both stroke-affected and non-affected muscles.

However, we observed relatively stronger dependence of the PhV on frequency in stroke-affected muscles at all three joint angles, i.e., higher values of parameter β in Table II in stroke-affected muscles as compared to non-affected muscles. This finding suggests that after stroke estimated viscous components in the muscle tissue may have significantly increased.

For the pure elastic model, i.e., assuming no viscosity, we observed significantly higher elasticity in stroke-affected muscles. In this model, elasticity is directly related to the GpV, i.e., $E=\rho c_{gp}^2$ (Eq. 3) [23].

For the Voigt model, shear elasticity values were not significantly different in stroke-affected muscles (Fig. 5(b)). At 150°, the stroke-affected muscles showed comparatively lower elasticity. The apparent discrepancy between elasticity estimates from both models is related to the structure of these models. For the elastic model, the GpV data directly translate into elastic modulus. However, for the Voigt model, the relationship between elasticity and PhV is highly nonlinear, and parameter estimation was performed using NLS algorithm. The general functional form of estimation problem is not convex, and a unique global minimum is not guaranteed. The NLS algorithm iteratively converges to a local minimum which may change due to the initialization of the unknown parameters every time the algorithm is run. We performed 100 repetitions with different random initializations and the solution with a minimum error norm was chosen. The local minimum found using an iterative algorithm, i.e., NLS may be far from the global optimal solution.

Model-based estimates of viscosity using PhV measured in the muscles of the paretic side were high than that of the non-paretic side (Fig. 5(c)). Considering both moduli together for the Voigt model, we can argue that the effect of stroke was mainly evident in the viscous parameter. Furthermore, we can also conclude that the differences between stroke-affected and non-affected muscles were more evident at large joint angles.

The time constant (τ) of the Voigt model is an important parameter as it encompasses both shear elastic and viscous moduli. It is the same time constant (τ) that appears in the solution of first-order ordinary differential equations (ODE). A small time constant value would result in a quick response from the material to a suddenly applied/removed stress (step input) and vice versa. The estimated time constant was found to be significantly different between the models of stroke-affected and non-affected muscles (Fig. 5(d)). The same effect is visually evident in Fig. 6, where creep behavior of the models of stroke-affected and non-affected muscle is shown. The normalized creep behavior of the non-affected muscles was consistent across joint angles. However, stroke-affected muscles exhibited a changed behavior and took more time to adapt to the changed stress levels at all three joint angles. In our simulation study of creep behavior, stroke-affected muscles were significantly slower in their reaction to changed stress levels especially at large joint angles (120°, and 150°), which is a typical characteristic of a material with relatively high viscosity. Furthermore, the simulated creep behavior of stroke-affected muscles was not consistent across joint angles as observed in non-affected muscles.

The observation of altered creep behavior (through Voigt model simulations) of stroke-affected muscles might be linked to the force generation and transmission capacity of these muscles. Because of neural excitation, muscle fibers contract and generate a pulling force that is transmitted to tendons. However, due to changes in mechanical characteristics, elastic as well as viscous, individual muscle fibers and bundles of fibers (fascicles) would react slowly to the changed stress level. The force generated at single fiber level will be relatively slowly transmitted to tendons in stroke-affected muscles due to the changed creep behavior of the muscle tissue. Furthermore, some of the generated energy will also be dissipated as heat due to increased viscosity. Therefore, we speculate that the viscoelastic changes in stroke-affected muscle tissue may compromise their capacity to generate and transmit force to tendons. Increased muscle viscosity would result in more energy absorption which would not only decrease the efficiency of force transmission; it could also impact the necessary neural input required to activate the muscle and to generate the same amount of force. In stroke survivors, the excitatory neural input of the descending pathways may initially decline immediately after the injury [37, 38]. Later, even if the individual regains regular neural inputs, these changes in the muscle’s mechanical properties can potentially limit its functionality.

Changes in viscoelastic properties could potentially be attributed to alterations in individual muscle fibers, to an increased amount of connective tissue, changes in the quality and quantity of ECM, to the accumulation of extracellular fat in the muscle, and to quantifiable fibrosis [3, 4]. Moreover, post-stroke abnormalities in muscle tissue, i.e., energy dissipative elements, time delays, and even water motion may induce phase shifts between acoustic wave input and the estimated shear wave response and potentially contribute to estimated changes in viscosity in stroke-affected muscles. The collective effect of these fundamental alterations in the muscle tissue may induce changes in its mechanical behavior, which can be directly linked to its primary function of force generation and transmission.

Currently, the origins of such changes in mechanical properties of stroke-affected muscles are unclear. One possibility is that there has been a progressive loss of spinal motoneurons as an indirect consequence of the hemispheric stroke. Such motoneuron loss could result from a process called “trans-synaptic degeneration” by which stroke-related damage to major cerebral cortical pathways projecting to spinal motoneurons gives rise to degeneration and death of those spinal neurons. As these motoneurons die, the muscle fibers that they innervate also begin to degenerate, and are replaced by fibrous connective tissue [39]. A second, related possibility, is that the damage to spinal neurons alters the command signal to muscle instructing muscle stem cells (called satellite cells) to switch from regenerating injured muscle fibers towards generating collagenous connective tissue. Finally, there is some recent evidence for an inflammatory mechanism in muscles of stroke survivors, which may damage muscle fibers selectively, and give rise to muscle fiber loss and eventually to damage of regional motor axons [40]. We are presently unable to distinguish between these three possibilities; however, the advent of higher resolution ultrasound imaging, coupled with precision shear wave measurements, may help us map the spatial distribution of these changes. These data may help us determine the mechanisms and origins of altered mechanical properties in muscle post-stroke.

One of the limitations of the study is related to the mathematical models used for estimation of elastic and viscous moduli. The models assume homogeneity and isotropy of the medium. There is the assumption that muscle composition (e.g., tissue composition, density, and structure) are consistent within the ROI and is representative of the whole muscle. There is also the assumption that muscle is isotropic whereas muscle is an anisotropic material. We assume that the effects of anisotropy were not significant due to the quasi-planar shear waves [14]. Besides, it is important to consider that the estimated parameters may only be relevant in the direction from which the shear wave propagation is measured, the longitudinal direction along the fascicles. Lastly, in this study, we focused primarily on quantitative comparisons between stroke-affected and non-affected muscles. Therefore, small deviations in the estimated data originating from the assumption (homogeneity, isotropy, and linearity of the medium) and estimation errors related to indirect measures, e.g., the NLS algorithm, may not radically alter our interpretations of the results.

V. Conclusion

We demonstrated that model-based estimates of viscoelastic properties from PhV in stroke-impaired muscles were different from those of the contralateral non-impaired muscles under passive conditions at three tested elbow angles. We noted that potential differences in the material properties of stroke-affected muscles might be related to altered elasticity and even more to increased viscosity. These changes, in turn, can potentially modify the functions of the muscle and may compromise force generation as well as transmission capacity of muscle fiber force to the tendon in stroke-affected muscles. The changes may be related to alterations in individual mechanical properties of muscle fiber cells, to changes in fiber architecture or to changes in the ECM; however, the origin of these various changes is still unknown. With methodological advances, there is great potential to identify sources of these changes to improve rehabilitative interventions.