Deriving Risk Adjustment Payment Weights to Maximize Efficiency of Health Insurance Markets

Abstract

Risk-adjustment is critical to the functioning of regulated health insurance markets. To date, estimation and evaluation of a risk-adjustment model has been based on statistical rather than economic objective functions. We develop a framework where the objective of risk-adjustment is to minimize the efficiency loss from service-level distortions due to adverse selection, and we use the framework to develop a welfare-grounded method for estimating risk-adjustment weights. We show that when the number of risk adjustor variables exceeds the number of decisions plans make about service allocations, incentives for service-level distortion can always be eliminated via a constrained least-squares regression. When the number of plan service-level allocation decisions exceeds the number of risk-adjusters, the optimal weights can be found by an OLS regression on a straightforward transformation of the data. We illustrate this method with the data used to estimate risk-adjustment payment weights in the Netherlands (N=16.5 million).

1. Introduction

Health insurance markets are vulnerable to market failures related to adverse selection (Einav, Finkelstein, and Cullen 2010; Glazer and McGuire 2000; Geruso and Layton 2017). Risk adjustment (aka “risk equalization”) of payments to health plans is a widely used policy intended to counter adverse selection problems and is a fundamental component of the regulated private health insurance markets that serve as the basis of national health policy in Germany, Israel, the Netherlands, Switzerland, and other countries, as well as of key sectors in the U.S., including the Medicare Advantage program for Medicare beneficiaries and the state-level Marketplaces created by the Affordable Care Act (2010). Each of these individual health insurance markets includes a payment system, which, depending on the country, adjusts plan payments to age, gender, geographic area, past or current medical diagnoses, past spending, and other characteristics of enrollees.

To date, the payment weights attached to the different individual characteristics included in a risk adjustment model used in a given health plan payment system have been generated using regression techniques, typically via an individual-level ordinary least squares (OLS) regression of total annual health care spending on the variables included in the model (risk adjustors). The payment to the insurer for a given enrollee is then effectively set equal to the predicted value the regression model generates for that enrollee. Such a method chooses payment weights that maximize the statistical “fit” (i.e., the R-squared) of plan revenues to costs at the individual level. However, as has been pointed out in previous work, it is unclear whether a statistical measure such as the R-squared is the “correct” objective function to maximize given the goals of either the regulator or the social planner (Glazer and McGuire 2002).

Indeed, empirical studies evaluating different risk adjustment models imply that maximizing the R-squared is not the regulator’s objective. Such studies tend to emphasize group-level fit of plan revenues to costs rather than individual-level fit. For example, Kautter et al. (2014) first estimated the federal model proposed for the U.S. Marketplaces using OLS, and then evaluated it by creating subgroups of individuals with particular characteristics and simulating average fit for each of these groups. McGuire et al. (2014) performed a similar evaluation of the Marketplace model. With data from the Netherlands, Van Kleef et al. (2016) first estimated a risk adjustment model, and then merged survey information with health claims to check fit for various groups of people, including those with low physical self-rated health status and those reporting chronic conditions. As far as we know, however, no explicit underlying framework describes insurer behavior and market efficiency underlying the evaluation methods and measures used in these papers and by researchers and policymakers generally. In other words, there has been no explicit objective function for risk adjustment design.

In this paper we attempt to develop a framework to describe how insurer behavior and market efficiency relate to the risk adjustment payments and the payment weights that underlie them. We then use this framework to derive an objective function that can be used to estimate risk adjustment payment weights that produce efficient market outcomes according to our framework. We start with Glazer and McGuire (2002) which uses a model of the behavior of a profit-maximizing insurer to (1) study incentives faced by insurers to inefficiently ration certain services and (2) develop a method for estimating risk adjustment weights that neutralize these incentives when the number of services for which plans make separate decisions in terms of allocation is smaller than the number of variables in the risk adjustment model. Our key innovations are to (1) move beyond incentives and solve for the equilibrium service-level allocations insurers will offer in a symmetric competitive equilibrium under a given plan payment system and (2) extend the model to relate these (distorted) allocations (as well as the payment system that generated them) to consumer utility and social welfare. These innovations allow us to make a number of novel and important advances. First, we are able to transparently show the set of (implausible) conditions under which the R-squared is the correct objective function to be maximized by the regulator. Second, we are able to relax some (but not all) of the implausible assumptions underlying the use of the R-squared as an objective function and derive a new, more welfare-grounded objective function. Even under our new objective function implausible assumptions remain in order to make the function computationally feasible under standard data constraints. However, we still believe this objective function represents a major contribution because under our framework these assumptions are now both transparent and fewer in number than when using the R-squared, representing a first step toward truly “optimal” risk adjustment. Finally, we are able to develop simple, general, and easy-to-implement methods for deriving risk adjustment payment weights that maximize our new objective function, even in the entirely plausible, but previously unexplored, case where the number of services exceeds the number of risk adjusters.

These methods can effectively replace the conventional two-step “estimate-then-evaluate” approach, where policymakers and researchers first estimate payment weights for a given risk adjustment model using a statistical objective function and then second evaluate the weights using a different set of criteria, with a relatively simple one-step “estimate-to-maximize-the-objective” approach, where the regulator’s true objective function is used to estimate the payment weights. For any risk adjustment model for which the number of risk adjustor variables exceeds the number of decisions plans make about service allocations, a simple constrained regression of healthcare spending on the risk adjustors in the model produces the payment weights that maximize the objective function. In other, typically more common cases, where the risk adjustment model includes fewer risk adjustors than services, there is typically no set of payment weights that fully eliminate incentives for service-level distortion. Under these circumstances the optimal (second-best) payment weights can be found via a standard OLS regression on a transformation of the data and the risk adjustors. Thus, while our methods are not perfect and still rely on strong assumptions, they improve on both the status quo and the more sophisticated methods developed in the academic literature (i.e., Glazer and McGuire 2002) while maintaining the simplicity and minimal computational burden of those methods.

In addition to providing a new approach for deriving risk adjustment payment weights, our analysis turns up a fundamental issue in the economics of health plan payment. In order to construct measures of welfare loss, we need, unsurprisingly, a characterization of the efficient allocation of health care services with which to compare the equilibrium allocation. In the theoretical parts of the paper, we distinguish between efficient and equilibrium allocations, but when it comes to the empirical application, we need additional assumptions about an efficient allocation to apply our welfare metrics. Some of these assumptions are implicit in existing methods for estimating risk adjustment weights, and there is value to making them explicit. Specifically, we model our initial empirical analyses on the presently used assumption that does not distinguish between the efficient and the observed allocations. Later in the paper we propose an alternative approach to defining efficiency that makes use of researcher knowledge of areas of pre-existing distortions of health care services in the market.

Following our modeling exercise in Section 3, we use data from the Netherlands to illustrate the use of our welfare-grounded measure of payment system performance (the value of the new objective function given a set of payment weights) and to demonstrate the implementation of our new optimal payment weight estimation methods. We note that this is an illustrative demonstration and not an attempt to make any inferences about the Dutch health insurance market which involves more complexity (e.g. finer relevant service categories) than that which is captured in our data. The data for our empirical demonstration, described in Section 4, are the actual data used to estimate risk adjustment payment weights in the Netherlands, and include multiple years of information on medical care use and individual demographic and risk characteristics, on the full 16.5 million Dutch population. We replicate the payment weights used in the 138-variable risk adjustment model in place for 2015, and compare these weights, and the welfare implications of the weights, to the weights produced by our efficiency loss-minimizing approach. For estimation, we take the set of risk adjustor variables as given, using the actual risk adjustors employed in the Dutch model.¹ In Section 4 we also describe how we operationalize assumptions about the level at which plans make allocation decisions, how (expected) individual spending relates to total spending on a service, and how we interpret the data in terms of efficiency of the current system.

Empirical methods to estimate risk adjustment payment weights and results are described in Section 5 (and an associated appendix). We describe model fit, equilibrium service-level allocations, and overall welfare loss according to our framework associated with the weights generated by the current methods and the weights generated by the welfare-maximizing methods. Section 6 contains what we believe to be a promising extension suggested by our model of insurer behavior and market efficiency. As noted above, an estimation approach based on efficiency calls for an explicit statement of what is meant by efficiency and how this is manifest in the data. In Sections 4 and 5 we assume that the levels of spending observed in the data are efficient, which we show to be a key implicit assumption underlying the use of the R-squared as the objective function in the existing risk adjustment literature. In Section 6 we modify our procedure for deriving payment weights by allowing the regulator or researcher to specify an efficient level of spending for each service for each individual that differs from what is observed in the data. The idea is very simple and operational. Suppose a public authority believes that plans currently (and in the data) spend too much on inpatient care for certain disease groups and too little on office-based care for the same conditions. Our analysis shows that the public authority can use the risk adjustment component of a health plan payment system to achieve its desired goals for spending targets due to the explicit link between risk adjustment payment weights and service-level spending revealed under our framework. First, the regulator should modify individual-level spending in the data to be equal to the desired level. Then, the regulator should use modified spending, rather than actual spending, to estimate the payment weights. In simple terms, we propose that regulators risk adjust for the system they want, not the system they’ve got. We introduce this idea and leave its further development for future research. Section 7 comments on some additional directions for research and policy.

2. Objectives for Health Plan Payment

Although risk-adjustment researchers acknowledge that risk adjustment is intended to reduce incentives for risk selection, in practice, statistical, not economic, criteria are used in estimation of payment weights used in risk adjustment models. In the two-step “estimate-then-evaluate” method of risk adjustment design referred to above, when done for policy, the first, “estimate” step is universally an OLS regression of individual-level spending on a set of risk-adjustor variables, with the estimated coefficients becoming the payment weights used in the risk adjustment component of the health plan payment system.² Researchers have studied alternatives to maximizing R-squared with an OLS regression, with the most commonly proposed alternative being minimizing the Mean Absolute Prediction Error (MAPE) which applies a linear rather than a quadratic loss function to the actual-prediction gaps.³ Arguments for the less-common alternatives to R-squared, however, are generally made on statistical rather than economic grounds, and none, so far as we know, have been put into practice.⁴

Research papers concerned with the economics of health insurance markets and the inefficiencies due to adverse selection tend not to draw explicit implications for risk adjustment payment weights.⁵ In one strand of this literature, building on earlier work by Cutler and Reber (1998), Einav and Finkelstein and colleagues study the adverse selection inefficiency which results from sicker individuals tending to join more generous plans.⁶ This type of adverse selection forces the more generous plans to increase premiums in order to cover costs of the sicker enrollees, not just to cover costs due to more generous benefits. Consequently, the premium for the generous plan is “too high” and too few consumers choose it.

One option to deal with this form of adverse selection is risk rating of the premiums faced by enrollees, for example, charging sick people their full incremental costs (Bundorf, Levin, Mahoney, 2012). From a social point of view, however, this is often regarded as undesirable due to objectives related to affordability of health plans for the sick, equity in health plan pricing, and a desire to provide insurance against the “reclassification risk” of deteriorating health status (Handel, Hendel, and Whinston 2015). It is common in regulated competition policy settings to strictly limit allowed premium groups, sometimes even requiring each plan to charge only a single premium, as is true in the Dutch national health insurance system, and the Medicare Advantage program.⁷

Another option is risk adjustment. By transferring funds to the more generous plan when sicker individuals enroll, risk adjustment dampens the component of plan premium differences due to selection. The optimal policy transfers a set amount of funding to the more generous plan so as to offset the selection effect on the incremental premium. Given that the number of risk adjustor variables exceeds the number of plans and given that the risk composition of health plans is known when the risk adjustment model is estimated, there are innumerable combinations of risk adjustment payment weights that would succeed in effecting this transfer. A well-chosen simple subsidy set in advance for the generous plan would solve the problem – risk adjustment is not required to solve the Einav-Finkelstein sorting inefficiency.⁸

The second strand of the literature on adverse selection, and the one relevant here, is concerned with plans distorting their products to attract/deter individuals who are financial winners/losers, an activity referred to as “cream-skimming,” “service-level selection,” or “indirect selection.” Even when nominal coverage is regulated, plans, through network structure, provider payment, managed care algorithms and other measures, can favor or disfavor certain population groups or service areas. Theoretical papers in health economics have “solved” this problem in simple cases by finding payment weights to correct for selection incentives.⁹ We make two advances in relation to previous research. First, we specify an explicit loss function that can guide choice of payment weights when selection incentives cannot be fully eliminated. Second, our solution can be implemented empirically in a real-world risk adjustment payment context.

In this paper we follow the second strand of the literature on adverse selection – the strand where risk adjustment is necessary to improve efficiency – and assume the goal of risk adjustment is to incentivize plans towards first-best service-level allocations. A crucial difference with the existing literature is that the one-step method proposed in this paper supplies the efficiency loss function to be minimized to find the second-best risk adjustment payment weights when the first best is infeasible.

3. Risk Adjustment Payment Weights to Minimize the Welfare Loss from Health Plan Payments

In the presence of premium regulation, incentives related to selection may lead health plans to distort their contracts away from the efficient allocation of health care services, undermining welfare. Our framework for measuring welfare loss due to inefficient allocations of health care spending is based on costs and benefits of health care. Welfare loss is driven by the gap between the efficient allocation to an individual and the allocation the individual would receive in equilibrium under a given health plan payment system. The measure thus applies to inefficiencies related to the services offered by health plans, and not to inefficiencies related to advertising or other plan actions distinct from the distortion of the health insurance contract itself and the benefits and costs of health care under that contract.¹⁰ Throughout this paper, we maintain the assumption that health plans compete in a market.¹¹ We also assume that consumer participation in the market is mandatory.¹²

After presenting the welfare metric, we start with a (very) special case of plan behavior where a plan can decide how much of a homogenous service, “health care,” to provide to each enrollee. While this case is clearly overly simplistic – health care is more than one product – and unrealistic – plans cannot set spending person-by-person – it provides intuition for how we approach the problem. Furthermore, this case establishes a set of assumptions under which a conventional OLS regression provides the efficient risk adjustment payment weights. We then consider the more general (and realistic) case where a plan can make spending decisions at the service level.

3.1. Welfare Loss

We envision a setting in which health insurance contracts are annual and plan premiums and demand-side cost sharing are regulated, and do not vary with the alternative risk adjustment payment weights we consider. This setting exactly matches many state Medicaid Managed Care markets in the U.S., and it comes close to fitting the Dutch national health insurance system, U.S. Marketplaces and other health insurance markets in which premiums and demand-side cost sharing are also highly regulated.¹³ The efficiency issue we focus on is the allocation of resources across various services provided to plan enrollees as a function of the risk adjustment payments.

In our model, each plan offers an annual health insurance contract consisting of N vectors of individual-level annual allocations of health care services measured in dollars. Individuals are indexed by i, with i = 1,…, N, and services by s, with s =1, …, S. A contract or allocation specifies the spending each person receives for each service:

$$\mathbf{X}=\left[\begin{array}{ccc}{\text{x}}_{11}& \cdots & {\text{x}}_{1\text{S}}\\ ⋮& \ddots & ⋮\\ {\text{x}}_{\text{N}1}& \cdots & {\text{x}}_{\text{NS}}\end{array}\right]$$

Let ${\text{x}}_{\text{i}}={\sum }_{\text{s}}{\text{x}}_{\text{is}}$ be the sum of spending across all services for person i. Individuals value service s according to ${\text{v}}_{\text{is}}({\text{x}}_{\text{is}})$, with ${\text{v}}_{\text{is}}^{\prime }({\text{x}}_{\text{is}})>0$ and ${\text{v}}_{\text{is}}^{\prime \prime }({\text{x}}_{\text{is}})<0$.^14,15 Let ${\text{x}}_{\text{is}}^{\ast }$ be the first-best level of x_is such that ${\text{v}}_{\text{is}}^{\text{'}}\left({\text{x}}_{\text{is}}^{\text{*}}\right)=1$. Also let ${\text{x}}_{\text{is}}^{\text{e}}$ be the level of x_is the insurer provides individual i in equilibrium, partly in response to the risk-adjusted plan payment. Thus, ${\text{x}}_{\text{i}}^{\text{e}}={\sum }_{\text{s}}{\text{x}}_{\text{is}}^{\text{e}}$ and

$${\mathbf{X}}^{\mathbf{e}}=\left[\begin{array}{ccc}{\text{x}}_{11}^{\text{e}}& \cdots & {\text{x}}_{1\text{S}}^{\text{e}}\\ ⋮& \ddots & ⋮\\ {\text{x}}_{\text{N}1}^{\text{e}}& \cdots & {\text{x}}_{\text{NS}}^{\text{e}}\end{array}\right]$$

Net welfare for individual i under equilibrium contract X^e is then ${\text{W}}_{\text{i}}\left({\mathbf{X}}^{\mathbf{e}}\right)={\sum }_{\text{s}}{\text{v}}_{\text{is}}\left({\text{x}}_{\text{is}}^{\text{e}}\right)-{\text{x}}_{\text{i}}^{\text{e}}$. Define ${\text{ΔW}}_{\text{i}}({\mathbf{X}}^{\mathbf{e}})=\left[{\sum }_s{\text{v}}_{\text{is}}\left({\text{x}}_{\text{is}}^{\text{e}}\right)-{\text{x}}_{\text{i}}^{\text{e}}\right]-\left[{\sum }_{\text{s}}{\text{v}}_{\text{is}}\left({\text{x}}_{\text{is}}^{\text{*}}\right)-{\text{x}}_{\text{i}}^{\text{*}}\right]$ as the welfare loss for individual i in equilibrium relative to the first-best. To make ΔW operational, we take a (second-order) Taylor-series expansion of ${\text{ΔW}}_{\text{i}}({\mathbf{X}}^{\mathbf{e}})$ around ${\text{x}}_{\text{is}}^{\text{*}}$ to yield

$${\text{ΔW}}_{\text{i}}({\mathbf{X}}^{\mathbf{e}})\approx \frac{1}{2}\sum _{\text{s}}{\text{v}}_{\text{is}}^{\prime \prime }\left({\text{x}}_{\text{is}}^{\text{*}}\right){\left({\text{x}}_{\text{is}}^{\text{e}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2$$ (1)

We can then sum the welfare loss described by (1) across the entire population as follows:

$$\text{ΔW(}{\mathbf{X}}^{\mathbf{e}}\text{)}\approx \frac{1}{2}\sum _{\text{i}}\sum _{\text{s}}{\text{v}}_{\text{is}}^{\prime \prime }\left({\text{x}}_{\text{is}}^{\text{*}}\right){\left({\text{x}}_{\text{is}}^{\text{e}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2$$ (2)

Approximation (2) describes the total welfare loss given the equilibrium contract X^e. Welfare loss is proportional to the weighted sum of squared differences between the equilibrium and the first-best allocations where the weight is the second-derivative of the individual’s valuation function of service s at the optimal level of service s for person i.

Equilibrium spending, as described by X^e, results from plan decisions to maximize profit. Consumers choose plans on the basis of plan choices about services, but consumers do not choose the services directly. Plan choices of the elements of X^e are a function of the payments received by the plan. The payment system generates payment r_i for person i, determined by the payment weights, β_k, on the k risk adjustors, z_k, included in the risk adjustment model taken as given. Thus, ${\text{r}}_{\text{i}}={\sum }_{\text{k}}{\text{β}}_{\text{k}}{\text{z}}_{\text{ik}}$, where z_ik is the value of risk adjustor k for individual i. In this section we explain how we solve for each element of X^e, ${\text{x}}_{\text{is}}^{\text{e}}$, (noting the necessary assumptions) given the risk adjustment model and its associated payment weights, using conditions of profit maximization and market equilibrium. In Section 4 below we explain how we use observed patterns of spending to define the optimal spending targets.

3.2. One Homogenous Service, Perfect Foresight and Individual-level Discrimination: an OLS Regression Selects Optimal Payment Weights

The risk-adjustment payment weights β_k that minimize (2) depend on what actions plans take; specifically, on the level at which health plans can set spending allocations. We begin with the unrealistic but instructive case in which there is one homogeneous service, consumers have perfect foresight (i.e. know exactly which line of the contract applies to them) and plans can discriminate at the individual level (e.g. shift a dollar of spending from individual 1 to individual 2). Specifically, assume a health plan can set the level of “health care spending” for each individual, x_i. In this case, competition forces each insurer to profit maximize at the zero-profit contract person-by-person, so in equilibrium, ${\text{x}}_{\text{i}}^{\text{e}}={\text{r}}_{\text{i}}$. Applying the welfare metric (2),

$$\text{ΔW(}{\mathbf{X}}^{\mathbf{e}}\text{)}=\frac{1}{2}\sum _{\text{i}}{\text{v}}_{\text{i}}^{\prime \prime }\left({\text{x}}_{\text{i}}^{\text{*}}\right){\left({\text{r}}_{\text{i}}-{\text{x}}_{\text{i}}^{\text{*}}\right)}^2$$ (3)

If we substitute ${\text{r}}_{\text{i}}={\sum }_{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}$ we get

$$\text{ΔW(}{\mathbf{X}}^{\mathbf{e}}\text{)}=\frac{1}{2}\sum _{\text{i}}{\text{v}}_{\text{i}}^{\prime \prime }\left({\text{x}}_{\text{i}}^{\text{*}}\right){\left(\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}-{\text{x}}_{\text{i}}^{\text{*}}\right)}^2$$ (4)

It is straightforward to see that the coefficient estimates from a weighted least squares regression of ${\text{x}}_{\text{i}}^{\ast }$ on z_ik, ${\widehat{\mathrm{\beta }}}_{\text{k}}$, where the individual-level regression weights are given by ${\text{v}}_{\text{i}}^{\prime \prime }\left({\text{x}}_{\text{i}}^{\text{*}}\right)$, minimize (4) and, thus, minimize the welfare loss. Furthermore, if we make the assumption that ${\text{v}}_{\text{i}}^{\prime \prime }\left({\text{x}}_{\text{i}}^{\text{*}}\right)$ is the same for all individuals, (4) further reduces so that the risk adjustment payment weights estimated from an (unweighted) ordinary least squares regression minimize the welfare loss.¹⁶ This implies that with one service, individual-level discrimination, and constant ${\text{v}}_{\text{i}}^{\prime \prime }\left({\text{x}}_{\text{i}}^{\text{*}}\right)$ across individuals the coefficients that minimize the sum of squared errors minimize welfare loss. These coefficients can be found with an OLS regression in which ${\text{x}}_{\text{i}}^{\ast }$ is the dependent variable. This also implies that under these assumptions the R-squared statistic is an appropriate metric for assessing the performance of a risk adjustment model and its associated payment weights. While some of these assumptions may seem implausible, it is not our goal here to defend a set of assumptions; rather, our goal is to make transparent the set of assumptions, plausible or implausible, underlying the use of the R-squared as an objective function, and to then relax some of the less plausible assumptions while leaving others in place to take a first step toward a more realistic and welfare-founded objective function. We proceed by relaxing the “one homogeneous service” and “individual-level” discrimination assumptions, as well as the assumption that consumers have perfect foresight, and then derive a more general loss function and methods for minimizing that function.

3.3. Risk Adjustment and Equilibrium Service-Level Plan Allocations

This section relaxes some assumptions from Section 3.2. Specifically, we make the more realistic assumption that plans discriminate over a variety of services rather than at the individual level and that consumers no longer have perfect foresight (i.e., they no longer know with certainty which line of the contract applies to them). Discrimination at the service level is general in that plans might have a large or a small number of service decisions to make. It is also general in the sense that a “service” could be defined not only on the basis of the type of health care (e.g., office-based care) but also on the basis of diagnosis within that type, or even on the basis of groups of patients, such as those living in a certain city, or on the basis of providers, such as mental health specialists or a particular specialty cancer hospital. Thus, a “service” could in principle be office-based care by nephrologists in Rotterdam. The right definition of “service” in a particular application depends on what level of discrimination is open to plans, where discrimination may be limited by regulation, information constraints, and the set of tools available to insurers. For example, if a plan can increase/decrease funding to primary care, but is unable to differentiate between pediatric and adult primary care in its contracts, then although pediatric and adult care are distinct services in a clinical sense, they can be aggregated and funding considered as one “decision” in terms of efficiency and the effect of risk adjustment on equilibrium spending.

Plan decisions about resource allocation at the service level flow down to services received by individuals. As with the special case described in Section 3.2, here we want to again describe the individual-by-service allocations, ${\text{x}}_{\text{is}}^{\text{e}}$, an insurer will offer in a competitive equilibrium as a function of the risk adjustment payments. Finding the equilibrium allocations as a function of the risk adjustment payments requires characterization of a plan’s profit maximizing decision with respect to spending on particular services. Profit maximization takes into account the costs of spending on a particular service as well as the net revenue of members that are expected to enroll in a plan as a function of service-level spending (i.e., selection). Some services attract members whose revenue exceeds their cost, incentivizing the plan to fund these services more generously. Other services attract members whose cost exceeds their revenue, incentivizing the plan to tighten rationing for these services. We maintain the assumption that competition enforces zero profits among plans.¹⁷

We also relax the assumption that consumers have perfect foresight of their healthcare spending under a particular contract. Given the spending decisions of all other plans, the probability that a particular consumer enrolls in plan j is a function of the individual’s valuation of the services the consumer expects to be provided by plan j. We assume that an individual’s valuation of a plan depends additively on the sum of the valuations of the s services, ${\text{v}}_{\text{i}}(\widehat{\mathrm{X}})={\sum }_{\text{s}}{\text{v}}_{\text{is}}({\widehat{\mathrm{X}}}_{\text{is}})$, where the “hat” indicates this is spending they expect to receive. Then, the probability of membership in plan j is ${\text{Pr}}_{\text{i}}^{\text{j}}({\text{v}}_{\text{i}}(\widehat{\mathrm{X}}))$. In the empirical applications below, consumers’ predictions about what they receive will be service-specific and based on patterns of prior spending. We assume equilibrium in the health plan market is symmetric so that in equilibrium all plans make the same decision about service-level spending and each plan has the same probability of enrolling each individual.¹⁸ Symmetry allows us to suppress plan j superscripts.¹⁹

In terms of the effect of a plan’s decision about spending on service s, we distinguish between what a consumer actually gets, which determines plan costs, profitability of individuals, and welfare, and what a consumer expects to get, which determines the consumer’s enrollment decisions. We introduce a parameter ${\text{σ}}_{\text{is}}\left({\sum }_{\text{s}}{\text{σ}}_{\text{is}}=1\right)$, that defines the share of total spending on service s allocated to individual i such that x_is = σ_isx_s where x_s is the total spending on service s across all consumers, ${\text{x}}_{\text{s}}={\sum }_{\text{i}}{\text{x}}_{\text{is}}$. However, enrollment decisions do not depend on what consumers actually get (x_is) but on what they expect to get $({\widehat{\mathrm{x}}}_{\text{is}})$. To deal with this we introduce a second parameter, ${\widehat{\mathrm{\sigma }}}_{\text{is}}({\sum }_{\text{s}}{\widehat{\mathrm{\sigma }}}_{\text{is}}=1)$, that defines the share of total spending on service s that individual i expects to be allocated to her such that ${\widehat{\mathrm{x}}}_{\text{is}}={\widehat{\mathrm{\sigma }}}_{\text{is}}{\text{x}}_{\text{s}}$.²⁰ To maintain tractability, we make the assumption that σ_is and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$ are fixed given all relevant insurer choices about total service-level allocations, x_s. We note that σ_is is not determined by the insurer nor by equilibrium, but is instead set by outside forces. The assumption that σ_is is fixed effectively implies that an increase in the overall level of spending on a service is distributed across consumers according to the observed distribution of service-level spending across consumers. Therefore, if an insurer increases mental health spending by $100, then most of the additional $100 will go to consumers who were already consuming high levels of mental health care and none of the $100 will go to consumers who were previously consuming no mental health care. This assumption seems reasonable in a world where contracts consist of service-specific coinsurance rates that do not vary across individuals, as a decrease in the coinsurance rate for a particular service will (1) lead to higher overall spending on the service which will (2) likely be distributed across consumers according to the prior distribution of spending on that service across consumers. This would also be consistent with a contract that consists of a provider network that varies at the service level but not the service-by-individual level. We also note that while fixed, σ_is is in reality flexible in that the researcher can define services in whatever way she believes insurers can manipulate spending. For example, if the researcher believes that the insurer can use some tool to modify mental health spending for males independently from females, then the researcher can just define mental health services for males and mental health services for females as separate services.

Given these assumptions, profits for a representative plan are

$$\text{π}=\sum _{\text{i}}{\text{Pr}}_{\text{i}}\left({\text{v}}_{\text{i}}\left(\widehat{\mathbf{X}}\right)\right)\left({\text{r}}_{\text{i}}-{\text{x}}_{\text{i}}\right)$$ (5)

Plans choose x_s to maximize profits leading to S first-order conditions of the form

$$\sum _{\text{i}}{\text{Pr}}_{\text{i}}\prime \left({\text{v}}_{\text{i}}\left(\widehat{\mathbf{X}}\right)\right){\text{v}}_{\text{is}}^{\prime }{\widehat{\mathrm{\sigma }}}_{\text{is}}\left({\text{r}}_{\text{i}}-{\text{x}}_{\text{i}}\right)-\sum _{\text{i}}{\text{Pr}}_{\text{i}}\left({\text{v}}_{\text{i}}\left(\widehat{\mathbf{X}}\right)\right){\text{σ}}_{\text{is}}=0$$ (6)

Denote ${\mathrm{\alpha }}_{\text{is}}={\text{Pr}}_{\text{i}}\prime \left({\text{v}}_{\text{i}}\left(\widehat{\mathrm{X}}\right)\right){\text{v}}_{\text{is}}^{\prime }{\widehat{\mathrm{\sigma }}}_{\text{is}}$, so that the S equations become

$$\sum _{\text{i}}{\mathrm{\alpha }}_{\text{is}}\left({\text{r}}_{\text{i}}-{\text{x}}_{\text{i}}\right)=\frac{1}{\text{J}}$$ (7)

where J is the number of plans competing in the market.²¹ Equation (7) implies that under profit maximization, the following S-1 equations will hold. With service s′ as a numeraire, for s ≠ s′:

$$\sum _{\text{i}}{\mathrm{\alpha }}_{\text{is}}\left({\text{r}}_{\text{i}}-{\text{x}}_{\text{i}}\right)=\sum _{\text{i}}{\mathrm{\alpha }}_{\text{is}\prime }\left({\text{r}}_{\text{i}}-{\text{x}}_{\text{i}}\right)$$ (8)

Following Glazer and McGuire (2002) and subsequent papers in the literature on service-level selection, we assume a symmetric equilibrium so that (8) holds for each (representative) plan. In addition, competition implies that plans make zero profit in equilibrium:

$$\sum _{\text{i}}{\text{r}}_{\text{i}}=\sum _{\text{i}}{\text{x}}_{\text{i}}$$ (9)

The S equations in (8) and (9) describe equilibrium as a function of the risk adjusted plan payment.

Substituting in for the risk adjusted payment, the S-1 service equations can be re-written as follows:

$${\mathrm{\beta }}_1\sum _{\text{i}}{\text{z}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{is}}\right)+{\mathrm{\beta }}_2\sum _{\text{i}}{\text{z}}_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{is}}\right)+\cdots +{\mathrm{\beta }}_{\text{K}}\sum _{\text{i}}{\text{z}}_{\text{iK}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{is}}\right)={\text{x}}_1^{\text{e}}\sum _{\text{i}}{\text{σ}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{is}}\right)+{\text{x}}_2^{\text{e}}\sum _{\text{i}}{\text{σ}}_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{is}}\right)+\cdots +{\text{x}}_{\text{S}}^{\text{e}}\sum _{\text{i}}{\text{σ}}_{\text{iS}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{is}}\right)$$ (8′)

And the budget constraint can be written as:

$$\sum _{\text{i}}\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}=\sum _{\text{s}}{\text{x}}_{\text{s}}^{\text{e}}$$ (9′)

These S equations can, in turn, be re-written as matrices as follows: $\left[\begin{array}{cccc}\sum _{\text{i}}{\text{z}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}2}\right)& \sum _{\text{i}}{\text{z}}_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}2}\right)& \cdots & \sum _{\text{i}}{\text{z}}_{\text{iK}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}2}\right)\\ \sum _{\text{i}}{\text{z}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}3}\right)& \sum _{\text{i}}{\text{z}}_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}3}\right)& \cdots & \sum _{\text{ig}}{\text{z}}_{\text{iK}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}3}\right)\\ ⋮& ⋮& \ddots & ⋮\\ \sum _{\text{i}}{\text{z}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{iS}}\right)& \sum _{\text{i}}{\text{z}}_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{iS}}\right)& \cdots & \sum _{\text{i}}{\text{z}}_{\text{iK}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{iS}}\right)\\ \sum _{\text{i}}{\text{z}}_{\text{i}1}& \sum _{\text{i}}{\text{z}}_{\text{i}2}& \cdots & \sum _{\text{i}}{\text{z}}_{\text{iK}}\end{array}\right]\left[\begin{array}{c}{\mathrm{\beta }}_1\\ {\mathrm{\beta }}_2\\ ⋮\\ {\mathrm{\beta }}_{\text{K}}\end{array}\right]\left[\begin{array}{cccc}\sum _{\text{i}}{\text{σ}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}2}\right)& \sum _{\text{i}}{\sigma }_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}2}\right)& \cdots & \sum _{\text{i}}{\sigma }_{\text{iS}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}2}\right)\\ \sum _{\text{i}}{\text{σ}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}3}\right)& \sum _{\text{ig}}{\text{σ}}_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}3}\right)& \cdots & \sum _{\text{i}}{\text{σ}}_{\text{iS}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{i}3}\right)\\ ⋮& ⋮& \ddots & ⋮\\ \sum _{\text{i}}{\text{σ}}_{\text{i}1}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{iS}}\right)& \sum _{\text{i}}{\text{σ}}_{\text{i}2}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{iS}}\right)& \cdots & \sum _{\text{i}}{\text{σ}}_{\text{iS}}\left({\mathrm{\alpha }}_{\text{i}1}-{\mathrm{\alpha }}_{\text{iS}}\right)\\ 1& 1& \cdots & 1\end{array}\right]\left[\begin{array}{c}{\text{x}}_1^{\text{e}}\\ {\text{x}}_2^{\text{e}}\\ ⋮\\ {\text{x}}_{\text{S}}^{\text{e}}\end{array}\right]$ Or, in matrix notation,

$$\mathrm{\Omega }\beta =\mathbf{\Gamma }{\mathbf{X}}^{\mathbf{e}}$$

Note that given knowledge of the α terms, all elements of Ω and Γ are either known or found in the data. For now, we will leave the α terms general. In the empirical section of the paper, we will make a set of assumptions that allows us to determine the αs from the data. Multiplying both sides by Γ⁻¹, the equilibrium values of the group-by-service-level allocations can be expressed as a linear function of β and data:

$${\mathbf{\Gamma }}^{-1}\mathbf{\Omega }\beta ={\mathbf{X}}^{\mathbf{e}}$$ (10)

The left hand side of this equality will be an S × 1 vector where each element of the vector consists of the summation of the product of each risk adjustment payment weight times the element determined by the multiplication of Γ⁻¹ and Ω. This summation can be written as:

$${\text{x}}_{\text{s}}^{\text{e}}=\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}$$

where ${\tilde{\mathrm{z}}}_{\text{sk}}$ is the transformed value of z_k determined by the matrix product. This implies that the individual-level equilibrium allocation of service s for individual i can be written as

$${\text{x}}_{\text{is}}^{\text{e}}={\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{\text{e}}={\text{σ}}_{\text{is}}\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}$$

This can be plugged into Equation (2) above to produce an expression for the welfare loss as a function of the risk adjustment payment weights, β_k:

$$\text{ΔW(}{\mathbf{X}}_{\mathbf{i}}^{\mathbf{e}}\text{)}=\frac{1}{2}\sum _{\text{i}}\sum _{\text{s}}{\text{v}}_{\text{is}}^{\prime \prime }{\left({\text{σ}}_{\text{is}}\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2$$ (11)

The task is to find the risk adjustment coefficients β_k that minimize (11). As noted earlier, the solution can take one of two forms depending on whether the number of services on which a plan makes decisions, S, is greater or less than the number of risk adjustors, K. We proceed by describing each case.

3.4. More Risk Adjustors than Services: Constrained Least-Squares Hits First Best

In this case, the regulator’s goal for risk adjustment is to induce insurers to offer the levels of service-level spending that result in optimal individual allocations. Thus, the regulator desires to set the payment weights, β_k, so that in equilibrium plans provide service level allocations ${\text{x}}_{\text{s}}^{\ast }$ that satisfy ${\text{x}}_{\text{i}}^{\text{*}}={\sum }_{\text{s}}{\text{x}}_{\text{is}}^{*}={\sum }_{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{is}}^{*}$.²²

Equilibrium conditions (8) and (9) can be regarded as a system of S unknowns, x_s, with K variables, β_k. When S < K, the β_ks that lead plans to set service allocations efficiently in equilibrium can be characterized by substituting ${\text{x}}_{\text{i}}^{\text{*}}={\sum }_{\text{s}}{\text{x}}_{\text{is}}^{*}={\sum }_{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{*}$ and ${\text{r}}_{\text{i}}={\sum }_{\text{s}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}$ into (8) and (9) yielding the following S equations:

$$\sum _{\text{i}}{\mathrm{\alpha }}_{\text{is}}\left(\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}-\sum _{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{*}\right)=\sum _{\text{i}}{\mathrm{\alpha }}_{\text{is}\prime }\left(\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}-\sum _{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{*}\right)$$

$$\sum _{\text{i}}\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}=\sum _{\text{i}}{\text{x}}_{\text{i}}^{\text{*}}$$ (12)

If the α_is terms are independent from the overall service-level allocations x_s (as they would be if the marginal consumer valuation of services is constant in the level of the service, which we assume is true in the empirical illustration below), then the S equations in (12) are linear in the payment weights, β_k.²³ Payment weights that satisfy (12) ensure that when plans can only discriminate on the basis of services the first-best allocations will be offered in equilibrium. If there are more risk adjustors than there are services (i.e., K>S), there will be an infinite number of combinations of payment weights that satisfy (12).

One practical method for choosing payment weights to satisfy the S equations is a constrained least-squares regression, fitting a linear regression of ${\text{x}}_{\text{i}}^{\ast }$ on z_ik, with the S equations in (12) as constraints. This is first-best because the constraints are satisfied. The solution also has the property of maximizing fit at the person level subject to the first-best allocation. Finally, least-squares guarantees the zero-profit constraint is satisfied. We apply this method in Section 5. Note that in this case, the full set of α terms are necessary for estimation of the optimal risk adjustment payment weights. Given estimates of all the components of α (${\text{Pr}}_{\text{i}}\prime \left({\text{v}}_{\text{i}}\left(\widehat{\mathrm{x}}\right)\right)$, ${\text{v}}_{\text{is}}^{\prime }$, and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$), estimation is straightforward. In the absence of estimates of these parameters, assumptions are necessary. We discuss in Section 4.6.1 the specific assumptions we use to operationalize α in our setting. Again, we leave σ_is and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$ general for now, and we will introduce the assumptions we use to produce values for σ_is and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$ when we apply this method in Section 5.²⁴

3.5. More Services than Risk Adjustors: OLS with Transformed Data Minimizes Welfare Loss

When there are more services than risk adjustors, the regulator’s objective is unchanged: to induce insurers to offer the service-level allocations that minimize welfare loss. When K < S, however, the regulator has too few “instruments” to achieve first-best allocations, implying that typically only a “second-best” set of allocations can be achieved and some welfare loss will remain. This presents a more difficult problem in that the regulator needs to choose the risk adjustment payment weights that efficiently trade off the welfare losses across services.

Equation (11) shows the way forward. It is straightforward to see that if the α_is terms are independent of the overall service-level allocations x_s (as they would be if the marginal consumer valuation of services is constant in the level of the service, which we assume is true in the empirical illustration below) a weighted least squares regression at the individual-by-service (is) level of ${\text{x}}_{\text{is}}^{\ast }$ on ${\text{σ}}_{\text{is}}{\tilde{\mathrm{z}}}_{\text{sk}}$ where the individual-by-service regression weights are equal to ${\text{v}}_{\text{is}}^{\prime \prime }$ will generate the set of risk adjustment payment weights that minimize ΔW(X^e).²⁵ Making the simplifying assumption that ${\text{v}}_{\text{is}}^{\prime \prime }({\text{x}}_{\text{is}}^{\ast })=\text{v}\prime \prime$ for all is (the same simplifying assumption made when using R-squared as the objective function) so that (11) can be rewritten as $\text{ΔW(}{\mathbf{X}}^{\mathbf{e}}\text{)}=\frac{1}{2}\text{v}\prime \prime {\sum }_{\text{i}}{\sum }_{\text{s}}{({\text{σ}}_{\text{is}}{\sum }_{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}-{\text{x}}_{\text{is}}^{\text{*}})}^2$, the welfare-minimizing risk adjustment payment weights can be estimated by unweighted rather than weighted least squares. Thus, for the S>K case, with a straightforward transformation of the data, researchers or regulators can estimate the efficiency-maximizing risk adjustment payment weights using either weighted or unweighted least squares. If the α_is terms are not independent of the overall service-level allocations x_s, then other optimization methods can be used to find the set of payment weights that minimize the welfare loss function.

Policymakers can often “choose” the number of risk adjustor variables so as to exceed the number of service dimensions (in order to make first-best payment weights feasible). We consider the S<K to be the more relevant case, at least in a setting like the Netherlands with an extensive set of risk-adjustor variables. The S<K case is the one we implement for purposes of illustration with data from the Netherlands.

3.6. Imperfect Information about ${\mathbf{X}}_{\mathbf{i}s}^{*}$

So far, we have implicitly assumed that the Regulator knows the optimal spending allocations,${\text{x}}_{\text{is}}^{\ast }$. As shown in Section 3.2, this assumption is also implicit in the use of the R-squared as an objective function when estimating risk adjustment payment weights. Here, we briefly discuss the possibility that the Regulator only observes ${\text{x}}_{\text{is}}^{\ast }$ with error, leaving a more thorough examination of this assumption for Section 6 and a separate paper (Bergquist et al. 2018).

Let ${\ddot{\mathrm{x}}}_{\text{is}}={\text{x}}_{\text{is}}^{\text{*}}+{ϵ}_{\text{is}}$ be the level of spending for person i on service s assumed by the Regulator to be the optimal level of spending for the person-service combination. ϵ_is represents the “error” in the Regulator’s assumed optimal level of spending. In the S>K case, our proposed method involves using ${\text{x}}_{\text{is}}^{\ast }$ as the dependent variable in an OLS regression where the independent variable is the transformed service-level spending,${\text{σ}}_{\text{is}}{\tilde{\mathrm{z}}}_{\text{sk}}$. This implies that error in ${\text{x}}_{\text{is}}^{\ast }$ is analogous to measurement error in the dependent variable. Thus, as long as the error is “classic” measurement error with E[ϵ] = 0 and with ϵ being orthogonal to variation in the transformed service-level spending, this type of error will not bias the risk adjustment payment weights (though it will make the estimates of the weights less precise). If the error is not classic and is in some way correlated with the transformed service-level spending, ${\text{σ}}_{\text{is}}{\tilde{\mathrm{z}}}_{\text{sk}}$, bias will be introduced to the risk adjustment payment weights, with the extent of the bias related to the strength of the correlation. It is conceivable that in some cases the bias could be severe enough that the welfare loss under the risk adjustment payment weights estimated by OLS on the non-transformed data (the conventional method) would be closer to the optimal weights than the weights estimated by the method described in Section 3.5.

4. Demonstration of Methods Using Data from the Netherlands

National health insurance in the Netherlands has been operating in roughly its current form since 2006. Health insurance is mandatory for all residents and based on principles of regulated competition. In 2015 about 60 plans were offered by about 25 insurers who compete on price and quality within a regulatory framework intended to promote individual affordability of health plans both for the healthy and the chronically ill. The regulatory framework includes a standard benefit package, premium rating restrictions, and risk adjustment. Open enrollment provisions ensure that plans accept every applicant.

Risk adjustment is used in the Dutch system in an attempt to weaken insurer selection incentives. The risk adjustment model provides a prediction of total annual spending for each individual; the risk adjustment payment from the health insurance fund to a health plan for an enrollee then equals that enrollee’s predicted spending minus a fixed amount (set by the government) that must be covered by the enrollee’s premium together with the loading fee.

In our empirical application we first replicate the Dutch risk adjustment model and its associated payment weights for 2015 and characterize the incentives for service-level distortion. Because we employ an explicit model of plan behavior as a function of the risk adjustment payment weights, we can derive the gaps between first-best and equilibrium spending that would occur under profit maximization and perfect competition. We next apply a constrained least-squares regression to find the payment weights that eliminate these gaps (and the welfare loss). In the remainder of this section, we briefly describe the Dutch risk adjustment model of 2015, the data available for this study, the way we operationalize “services,” how we interpret the data in relation to the first-best allocations $({\text{x}}_{\text{is}}^{\ast })$, how individuals’ (expected) spending on a service relates to the total spending on that service (σ_is and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$) and the measures we use to evaluate alternative risk adjustment models. We note throughout that this is an illustrative demonstration based on the data currently used for risk adjustment in the Netherlands. Effective application of our measures and methods should likely take place with many more than the ten services we use here.

4.1. Risk Adjustment Model 2015

The basic Dutch risk adjustment model of 2015 includes risk adjustors based on age, gender, region, source of income, socioeconomic status, and health indicators. The latter include disease groups based on prior utilization of specific pharmaceuticals (PCGs), diagnostic groups based on prior utilization of inpatient and outpatient hospital care (DCGs), groups based on prior utilization of durable medical equipment (DMECGs) and groups based on high health care spending in multiple prior years (MYHCGs). In total, the 2015 model contains 138 indicator variables, i.e., 40 classes for an interaction between age and gender, 10 regions, 19 classes for an interaction between age and source of income, 12 classes for an interaction between age and socioeconomic status, 25 PCGs, 16 DCGs, five DMECGs, seven MYHCGs, and four classes for an interaction between age and a dummy indicating whether PCG+DCG+DMECG+MYHCG>=1. The model is “prospective” in that the data for the health indicators (i.e. PCG, DCG, DMECG, and MYHCG) comes from years prior to the payment year. In practice, the payment weights for these 138 indicators are estimated by a least-squares regression of medical spending on the 138 dummy variables.²⁶ Predicted spending for an enrollee equals the sum of the product of the dummy-values and the regression coefficients for the 138 indicators. We note that in spite of years of research and model refinement, Van Kleef et al. (2017) have shown that the current risk adjustment model undercompensates insurers for particular groups of unhealthy consumers and overcompensates them for some healthy groups, leaving incentives for risk selection.

4.2. Data

To stay close to the actual Dutch health plan payment system we use exactly the same data as was used by the regulator for estimation of the risk adjustment model of 2015. These data include individual-level health care spending in 2012 and risk indicators for the Dutch population of approximately 16.5 million. The three-year time lag between the data and the year to which the risk adjustment model applies is due to the fact that when risk adjustment payment weights for year t are estimated (i.e. late summer t-1) t-3 is the most recent year for which complete spending information is available. The indicators for age/gender, region, source of income and socioeconomic status are based on information from 2012, whereas the PCGs, DCGs, DMECGs and MYHCGs are based on information from 2009–2011. Table 1 provides the population frequency of some risk indicators and the distribution of medical spending. Overall average medical spending equals 1,848 Euro per person per year. Not surprisingly, average spending is relatively high for people age 65 or older, those receiving a disability benefit, people living at an address with more than 15 residents (a proxy for being in an institution for long-term care) and those in a PCG, DCG, DMECG and/or MYHCG. Nearly 23 percent of the population is classified by at least one PCG, DCG, DMECG or MYHCG.

Table 1:

Population frequency and medical spending (in Euros, 2012) at aggregated levels of risk characteristics (N=16.5 million)

		Population frequency	Mean spending
Male, <65		42%	1,207
Male, >=65		8%	4,612
Female, <65		41%	1,487
Female, >=65		9%	4,123
Region, clusters 1–5		50%	1,979
Region, clusters 6–10		50%	1,719
Source of income if 18≤age<65: disability benefits		5%	3,817
Source of income if 18≤age<65: social security benefits		2%	2,321
Source of income if 18≤age<35: student		3%	588
Source of income if 18≤age<65: self-employment		4%	1,012
Source of income if 18≤age<65: other (e.g. employment)		48%	1,282
Other (i.e. age<18 or ≥65)		38%	2,477
Socioeconomic status, street address with >15 residents		1%	4,507
Socioeconomic status, income deciles 1–3		30%	1,842
Socioeconomic status, income deciles 4–7		40%	1,869
Socioeconomic status, income deciles 8–10		30%	1,721
Pharmacy-based Cost Group (PCG)	No	82%	1,212
	Yes	18%	4,751
Diagnoses-based Cost Group (DCG)	No	91%	1,353
	Yes	9%	6,855
Durable Medical Equipment Cost Group (DMECG)	No	99%	1,772
	Yes	1%	10,933
Multiple-year High Cost Group (MYHCG)	No	94%	1,378
	Yes	6%	9,536
PCG, DCG, DMECG and/or MYHCG	No	77%	984
	Yes	23%	4,784
Total population		100%	1,848

Note: the risk adjustor variable “Source of income” only applies to people with ages 18 to 65. PCGs, DCGs and DMECGs are based on prior-year use of selected of drugs, hospital treatments and durable medical respectively.

4.3. Defining Services

In the Dutch data used for risk adjustment medical spending is categorized according to ten types of medical services, with information on spending per person shown in Table 2.²⁷ Hospital care (which includes both facility and professional in-hospital costs) is by far the largest category at 61 percent, followed by pharmaceuticals (14 percent) and primary care (8 percent). Not surprisingly, for each service the distribution of spending is skewed. While these ten services are plausible levels of discrimination available to plans through their provider contracting decisions, ultimately, practical implementation of our methods would likely require a more refined categorization when health plans are believed to discriminate within some of these categories. For example, the large category of hospital care might be disaggregated into particular services, such as care for patients with cancer or kidney failure, and other services. However, in the data available to us, we are unable to disaggregate services beyond the ten shown in Table 2.

Table 2.

Average per person spending per service category (in Euros, 2012; N=16.5 million)

	Mean	Std Dev	75th Pctl	95th Pctl	Share of total spending
Hospital care	1132	5612	608	4779	61%
Pharmaceuticals	267	1309	186	1163	14%
Primary care	139	148	160	315	8%
Durable medical equipment	91	581	2	368	5%
Geriatric physical therapy	46	1145	0	0	3%
Dental care (18-)	44	238	2	197	2%
Paramedical care	42	242	0	127	2%
Sick transport	35	331	0	8	2%
Obstetrics and maternity care	29	283	0	0	2%
Other a	23	503	0	27	1%
Total	1848	6595	1392	7342	100%

^aIncluding very small categories of spending such as ‘ambulatory care for people with auditive or visual impairments’.

4.4. Defining First-Best Spending

The empirical methods for deriving the optimal risk adjustment payment weights described in Section 3 call for specification of the efficient spending levels, denoted ${\text{x}}_{\text{is}}^{\text{*}}$. The data available, however, are the actual spending patterns by person and service under the risk adjustment model and corresponding weights applicable at the time, which may or may not be regarded as optimal. Before we discuss our approach to this issue, it is worth noting that the statistics and simulations applied in existing approaches to risk adjustment implicitly treat the existing patterns in the data as the target for desired spending.²⁸

Highlighting the implicit assumption about the optimality of current spending patterns exposes a logical problem with risk adjustment methodology. If the current spending pattern is optimal, and it is also an equilibrium response to the current payment system, why change the payment system? This status-quo logic would lead to the obviously incorrect conclusion that the payment system should never be changed.

If the optimal service-level allocations, ${\text{x}}_{\text{s}}^{\text{*}}$, differ from the observed service-level allocations, we propose that before estimating or evaluating a risk adjustment model we should first alter the observed allocations so that they reflect the desired rather than the observed distribution of spending across services. ²⁹ In other words, we propose that the risk adjustment model be estimated using a regression of a modified spending variable on the risk adjuster variables. Suppose, for example, that there were a consensus that the health care system should spend more on primary care for persons with a set of chronic illnesses, possibly with the idea of offsetting some institutional care.

For the basic empirical analyses in Section 5 we follow conventional practice of risk adjustment and estimate the payment weights based on the data “as-is,” thereby invoking the implicit assumption that the observed patterns of spending are, in fact, optimal. In Section 6 below, we illustrate how this assumption can be relaxed by estimating payment weights “for the system we want rather than the system we have” by transforming the data before estimation of the payment weights.

4.5. Assumptions Regarding σ_is and ${\widehat{\mathrm{\sigma }}}_{\mathbf{i}s}$

In order to apply the methods described in Section 3 to derive the optimal set of risk adjustment payment weights in the case where S<K, we need to know the values of σ_is and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$. As discussed above, we assume that σ_is is fixed across all relevant service-level allocations and use the observed share in the data to determine what an individual actually gets in terms of a share of the total service-level allocation:${\text{σ}}_{\text{is}}=\frac{{\text{x}}_{\text{is}}}{{\text{x}}_{\text{s}}},{\sum }_{\text{i}}{\text{σ}}_{\text{is}}=1$. For example, if we observe that an individual receives $100 of diabetes-related care in the claims data and that the total allocation of diabetes-related care across all individuals is $10,000, then ${\text{σ}}_{\text{is}}=\frac{100}{10,000}=0.01$. We then assume that if the plan chooses to increase spending on diabetes-related care overall by $5,000 to $15,000, the individual’s allocation of diabetes care will increase in proportion such that her new allocation of diabetes-related care will be x_is = σ_is x_s = (0.01)(15,000) = $150. Thus, given σ_is we can determine what an individual gets as a function of the plan’s decision about the total service-level allocation, x_s.

In addition to the actual allocation of spending across individuals, our method also requires each consumer’s expected allocation,${\widehat{\mathrm{x}}}_{\text{is}}$. In the empirical illustration, we determine ${\widehat{\mathrm{x}}}_{\text{is}}$ in two steps. First, we estimate a prediction equation for each service, under the assumption that individuals can use information about past spending to predict future spending on a service.³⁰ In these prediction equations we require the sum of predicted spending to be equal to the sum of observed spending, i.e.${\sum }_{\text{i}}{\widehat{\mathrm{x}}}_{\text{is}}={\text{x}}_{\text{s}}$. The empirical model for ${\widehat{\mathrm{x}}}_{\text{is}}$ then determines the fixed allocation rule that distributes plan-level spending on service s, x_s, to individuals. Specifically, define ${\widehat{\mathrm{\sigma }}}_{\text{is}}=\frac{{\widehat{\mathrm{x}}}_{\text{is}}}{{\text{x}}_{\text{s}}}$ at the observed spending levels. In a second step, with ${\widehat{\mathrm{\sigma }}}_{\text{is}}$ fixed, we can state how ${\widehat{\mathrm{x}}}_{\text{is}}$ varies with different levels of x_s.³¹ For example, if the individual from the previous example expects $500 spending on diabetes-related care then ${\widehat{\mathrm{\sigma }}}_{\text{is}}=\frac{500}{10,000}=0.05$. If the plan chooses to increase spending on diabetes-related care overall by $5,000 to $15,000, the individual’s expected allocation of diabetes care will increase in proportion such that ${\widehat{\mathrm{x}}}_{\text{is}}={\widehat{\mathrm{\sigma }}}_{\text{is}}{\text{x}}_{\text{s}}=(0.05)(15,000)=\$750$. Thus, given a ${\widehat{\mathrm{\sigma }}}_{\text{is}}$ we can determine what an individual expects to get as a function of the plan’s decision about the total service-level allocation, x_s.

4.6. Measures

We use several measures to compare conventional risk adjustment and the constrained regression method outlined in Section 3.4. These measures follow from our model of plan profit maximization and are thus model-driven and motivated by efficiency. We also report the conventional R-squared measure for each set of risk adjustment payment weights. Finally, in Appendix A we report measures of selection incentives (predictability and predictiveness) from the prior literature on service-level selection.

4.6.1. Equilibrium vs. Optimal Spending Allocations

Our model of consumer and plan behavior allows us to go beyond the incentives to the implications for equilibrium spending, and to compare this to the spending patterns specified as optimal, but this requires an additional assumption (this assumption is also necessary for implementing our proposed estimation method). Recall that (10) provides the equilibrium service-level allocations as a linear function of the risk adjustment payment weights, β_k:

$${\mathbf{\Gamma }}^{-1}\mathbf{\Omega }\beta ={\mathbf{X}}^{\mathbf{e}}$$

As discussed in Section 3, this expression shows that given knowledge of α_is equilibrium service-level allocations can be calculated from the data. Recall that ${\mathrm{\alpha }}_{\text{is}}={\text{Pr}}_{\text{i}}\prime ({\text{v}}_{\text{i}}(\widehat{\mathbf{X}})){\text{v}}_{\text{is}}^{\prime }{\widehat{\mathrm{\sigma }}}_{\text{is}}$. In order to illustrate the implementation of the methods we describe above, we make the assumption that ${\mathrm{\alpha }}_{\text{is}}={\mathrm{Pr}}_{\text{i}}\prime ({\text{v}}_{\text{i}}(\widehat{\mathbf{X}})){\text{v}}_{\text{is}}^{\prime }{\widehat{\mathrm{\sigma }}}_{\text{is}}=\text{γ}{\widehat{\mathrm{\sigma }}}_{\text{is}}$ for all individuals and services.³² This assumption effectively implies that consumer-choice of health plans is driven entirely by the expected total healthcare spending allocation the consumer expects to receive under a given plan. While this assumption may be inconsistent with some evidence from behavioral economics that consumers make poor health plan choices (Abaluck and Gruber 2011; Ericson and Sydnor 2017), absent empirical estimates of the relationship between demand for a health plan and service-specific allocations, this seems like the most reasonable assumption we could make.³³ It is also consistent with the prior literature on service-level distortions to health insurance contracts (Frank, Glazer, and McGuire 2000). We also point out that even if consumer health plan choices are biased in some way, as long as choices are at least partially determined by service-level allocations, service-level distortions will exist, even if they are not as severe as our model may suggest.

It is straightforward to show that given this assumption, α_is reduces to $\text{γ}{\widehat{\mathrm{\sigma }}}_{\text{is}}$. Because γ is constant across individuals and services, it can be pulled out of the summation on each side of equation (8‘) and cancels out, allowing us to replace α_is with ${\widehat{\mathrm{\sigma }}}_{\text{is}}$ in the matrices Γ and Ω. Given our assumption that ${\widehat{\mathrm{\sigma }}}_{\text{is}}=\frac{{\widehat{\mathrm{x}}}_{\text{is}}}{{\text{x}}_{\text{s}}}$, where ${\widehat{\mathrm{x}}}_{\text{is}}$ and x_s are the expected individual-by-service- and actual service-level allocations, the elements of Γ⁻¹ and Ω are now all observable in the data except for ${\widehat{\mathrm{x}}}_{\text{is}}$. In order to determine ${\widehat{\mathrm{x}}}_{\text{is}}$ we estimated an individual0-level least-squares regression with actual spending for service s as the dependent variable and the following two independent variables: prior-year spending on service s (continuously) and the sum of prior-year spending on all services other than s (also continuously).^34,35 Finally, for a given payment system the full vector of risk adjustment weights, β, is also known. This implies that for any payment system, we can calculate the full vector of service-level equilibrium allocations, x^e.

In Section 5, we form the matrices, Γ⁻¹, Ω, and β, and apply them to solve for x^e. We compare those allocations for different sets of payment weights to illustrate how patterns of equilibrium service-level spending compare across different risk adjustment models.

4.6.2. Welfare Loss Metric

The expression for welfare loss in (11) provides a natural metric to use to compare risk adjustment models:

$$\text{ΔW(}{\mathbf{X}}_{\mathbf{i}}^{\mathbf{e}}\text{)}=\frac{1}{2}\sum _{\text{i}}\sum _{\text{s}}{\text{v}}_{\text{is}}^{\prime \prime }{\left({\text{σ}}_{\text{is}}\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2$$ (11)

If we assume that ${\text{v}}_{\text{is}}^{\prime \prime }=\text{v}\prime \prime$ for all i and s (the same assumption necessary for interpretation of an R-squared as a welfare measure in the context of individual-level discrimination) this can be re-written as

$$\text{ΔW}\left({\mathbf{X}}_{\mathbf{i}}^{\mathbf{e}}\right)=\frac{1}{2}\text{v}\prime \prime \sum _{\text{i}}\sum _{\text{s}}{\left({\text{σ}}_{\text{is}}\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2$$

Note that this measure relies on the solution for equilibrium spending by service derived in the previous section. Expression (11) for welfare loss is non-positive with a lower bound that depends on the covered population, the number of services, as well as the properties of the risk adjustment system in terms of risk adjustor variables and their coefficients.³⁶ In order to compare alternative risk adjustment payment weights, and to put our measure in a form analogous to the familiar R-squared statistic, we measure the efficiency properties of a given set of payment weights in terms of the improvement gained over a payment system with no risk adjustment, that is, when a plan is paid the simple population average for each member. This case is identical to the case where there is only one risk adjustment variable z_1i which is equal to 1 for all individuals. In this case the matrix Ω becomes a S-by-1 vector:

$${\mathbf{\Omega }}^{\mathbf{n}ora}=\left[\begin{array}{c}\sum _{\text{i}}{\text{z}}_{\text{i}1}\left({\widehat{\mathrm{\sigma }}}_{\text{i}1}-{\widehat{\mathrm{\sigma }}}_{\text{i}2}\right)\\ \sum _{\text{i}}{\text{z}}_{\text{i}1}\left({\widehat{\mathrm{\sigma }}}_{\text{i}1}-{\widehat{\mathrm{\sigma }}}_{\text{i}3}\right)\\ ⋮\\ \sum _{\text{i}}{\text{z}}_{\text{i}1}\left({\widehat{\mathrm{\sigma }}}_{\text{i}1}-{\widehat{\mathrm{\sigma }}}_{\text{iS}}\right)\\ \sum _{\text{i}}{\text{z}}_{\text{i}1}\end{array}\right]$$

Thus, the equilibrium service-level allocations, x^e,nora, can be expressed as

$${\mathbf{\Gamma }}^{-1}{\mathbf{\Omega }}^{\mathbf{n}ora}{\mathbf{\beta }}^{\mathbf{n}ora}={\mathbf{X}}^{\mathbf{e},\mathbf{n}ora}$$

Now, define ${\tilde{\mathrm{z}}}_{\text{s}}^{\text{nora}}$ such that ${\text{x}}_{\text{s}}^{\text{e},\text{nora}}={\tilde{\mathrm{z}}}_{\text{s}}^{\text{nora}}$. Then, we can write the welfare loss for the “no risk adjustment” case as

$$\text{ΔW}\left({\mathbf{X}}_{\mathbf{i}}^{\mathbf{e}}\right)=\frac{1}{2}\text{v}\prime \prime \sum _{\text{i}}\sum _{\text{s}}{\left({\text{σ}}_{\text{is}}{\tilde{\mathrm{z}}}_{\text{s}}^{\text{nora}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2$$

We thus define our loss measure as:

$$\varphi =1-\frac{\frac{1}{2}\text{v}\prime \prime {\sum }_{\text{i}}{\sum }_{\text{s}}{\left({\text{σ}}_{\text{is}}{\sum }_{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2}{\frac{1}{2}\text{v}\prime \prime {\sum }_{\text{i}}{\sum }_{\text{s}}{\left({\text{σ}}_{\text{is}}{\tilde{\mathrm{z}}}_{\text{s}}^{\text{nora}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2}=1-\frac{{\sum }_{\text{i}}{\sum }_{\text{s}}{\left({\text{σ}}_{\text{is}}{\sum }_{\text{k}}{\mathrm{\beta }}_{\text{k}}{\tilde{\mathrm{z}}}_{\text{sk}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2}{{\sum }_{\text{i}}{\sum }_{\text{s}}{\left({\text{σ}}_{\text{is}}{\tilde{\mathrm{z}}}_{\text{s}}^{\text{nora}}-{\text{x}}_{\text{is}}^{\text{*}}\right)}^2}$$

Note that ϕ mimics an R-squared statistic. ϕ will equal zero in the extreme case of no risk adjustment and it will equal one when the welfare loss is fully eliminated.

5. Empirical Methods and Results

This section presents our illustrative demonstration of the potential practical implementation of the methods and measures derived in Sections 3 and 4. We estimate two sets of payment weights using data on the entire Dutch population (N=16.5 million). For each set of weights, we use the same set of 138 risk adjustor variables but different estimation methods. The first payment weight estimates replicate the conventional estimation method used to derive payment weights in the Dutch risk adjustment model for 2015: a least-squares regression (OLS) of total spending on the 138 risk indicators plus an intercept.³⁷ The coefficient estimates for this model can be found in the Appendix.

The second set of weights is estimated using the methods we developed in Section 3. Recall that when plans discriminate at the service level, a set of equilibrium equations describes plan allocation decisions as a function of the risk adjustment payment weights. Substituting the efficient level of spending in these equations transforms them into a system of S equations and K unknowns. Because S < K, there exist an infinite number of solutions to this system of equations, all maximizing the social welfare function. We use a constrained OLS regression to find the solution that maximizes the conventional R-squared conditional on achieving the optimal service-level allocations.³⁸ Coefficient estimates for this model can also be found in the Appendix.

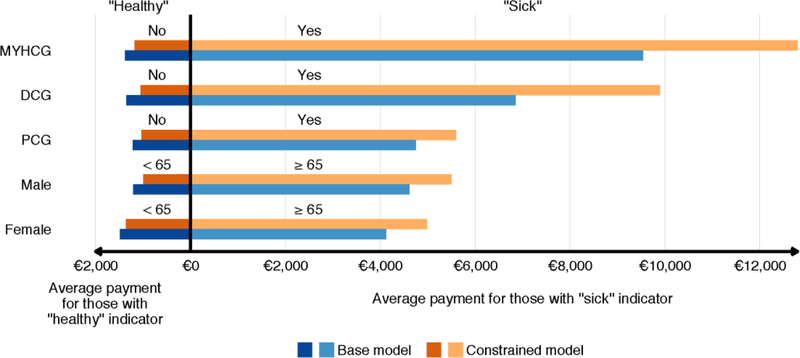
The two sets of payment weights differ in important and interesting ways. Compared to the base set of weights, the constrained regression method leads to an increase of mean predicted spending for people 65 or older and those in a PCG, DCG, DMECG and/or MYHCG (i.e., those with a chronic condition) and a decrease of mean predicted spending for the complementary groups. This can be seen in Figure 1.³⁹ The figure shows the payments for 5 stratifications of the population. For each stratification, the average payment for the healthier of the two groups is shown on the left while the average payment for the sicker group is shown on the right. The figure shows average payments under the conventional Dutch risk adjustment model (orange bars) and the constrained model (blue bars). Generally, the constrained model tends to encourage more spending on sick people. This is consistent with Glazer and McGuire’s (2000) analytic result that an optimal risk adjustment model will “overpay” (i.e. pay more than average spending) for individuals with a “sick signal” and underpay for individuals with a “healthy” signal. Nonetheless, the correlation in individual-level predicted spending between the base model and the constrained model is high at 0.94. This suggests that at least in this illustrative application, shifting payments to sicker people in the way suggested by the constrained regression would not be a highly disruptive change with respect to the flow of funds across insurers.

Figure 1:

Average Payments for Enrollees with Selected “Healthy” and “Sick” Indicators in Two Models

Notes: MYHCG: multiple-year cost group: DCG: any DCG; PCG; any PCG.

The male and female rows charaterize these two groups separately.

Table 3 compares the two models in terms of R-squared and our welfare loss measure ϕ. Compared to the base model, the constrained model led to a drop in R-squared, which of course must be true since the constraints will bind. However, as we showed in Section 3, the R-squared is the appropriate measure of payment system performance only in a very special case. In terms of our alternative welfare loss measure, the constrained model completely eliminates the welfare loss remaining from the base model. This also must be true, given that the estimation method used for the constrained model can fully solve the resource allocation problem with only ten service-level spending targets and 138 risk adjustor variables. From these results we can conclude that if the ten services we use here to illustrate these methods and measures were the relevant dimensions on which plans could discriminate, the constrained model clearly outperforms the base model.

Table 3.

R-squared and welfare loss measure for two models in relation to no risk adjustment

Measure	No risk adjustment	Base model	Constrained model
R-squared	0,000	0,226	0,129
Welfare loss measure (ϕ)	0,000	0,828	1,000

5.1. Equilibrium Service-level Allocations Implied by Plan Profit Maximization

In addition to a measure of overall payment system performance, our model from Section 3 allows us to derive equilibrium service-level allocations implied by the different payment models. We interpret our predictions about service-level allocations under the alternative set of risk adjustment payment weights as indicating the general pattern of mismatches between equilibrium spending and optimal spending as well as the direction in which profit maximization is pushing health plans to distort service-level spending. The gaps between the “optimal” and “equilibrium” allocations we present below should be interpreted as rough measures of the force of the distortionary incentive.

Figure 2 presents the equilibrium service-level allocations under the two payment models, the conventional Dutch model (blue bars) and the constrained model (orange bars) along with the optimal level of service-level spending (purple bars), which, as we explained above, we assume in this section to be equal to the spending observed in the data. All allocations are presented as a percent of total spending, which is constrained to be constant across payment models. The purple bars show that the optimal (and observed) level of spending on primary care is less than 10%. Our model, however, implies that under the conventional Dutch risk adjustment model, plans have incentives to drive the level of spending on primary care above 30%. This suggests that plans are incentivized to distort substantial resources toward primary care and away from other services as they compete for low-cost (and profitable) enrollees.⁴⁰ This distortion is largely due to the fact that an individual’s use of primary care does not predict unprofitability as strongly as their use of hospital care (as shown in Figure 3 below). On the other hand, our model implies that the conventional Dutch risk adjustment model pushes plans to allocate “too few” resources to hospital care.⁴¹

Figure 2:

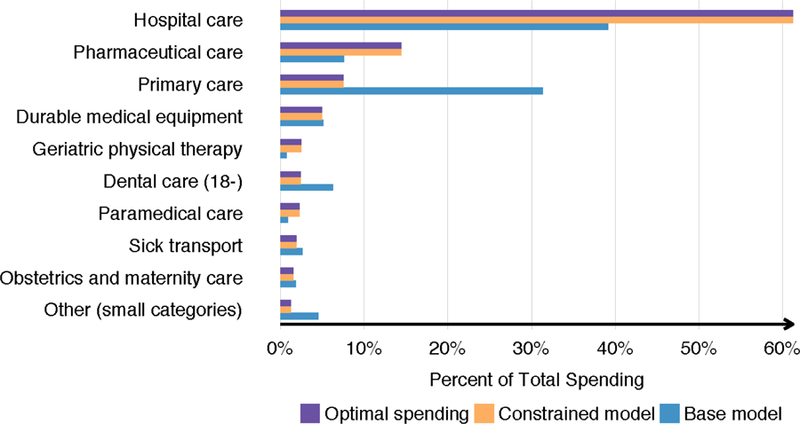
Equilibrium Service Level Allocation

Figure 3:

Difference in Payments for Enrollees with Selected “Healthy” and “Sick” Indicators with and without Changing the Data

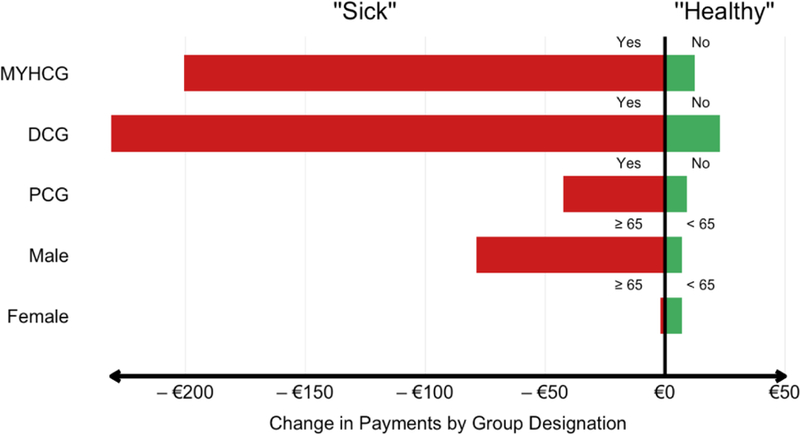
Notes: MYHCG multiple-year high cost group; DCG: any DCG; PCG. For each mutually exclusive partitioning of the population the payment changes weighted by group size sum to zero. Change in payments for the four groups, male < 65, male ≥, female < 65, and female ≥, must sum to zero.

Finally, Figure 2 confirms that equilibrium service-level allocations are moved to match the optimal allocations by the constrained risk adjustment model. As expected, the orange and purple bars are equal, indicating that the constrained model completely solves the service-level distortion problem by inducing plans to offer the optimal allocations of spending across services.

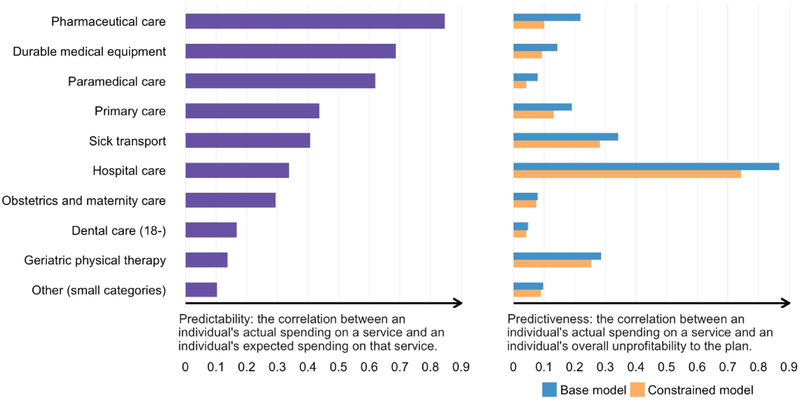
In Appendix A we present results on other measures of insurer selection incentives, namely the predictability and predictiveness introduced by Ellis and McGuire (2007). Again, these measures indicate that the constrained model represents a marked improvement over the base model in terms of providing insurers with appropriate incentives for offering efficient insurance contracts.

6. Redefining Efficient Spending for Purposes of Risk Adjustment: An Illustration

As discussed in Section 4.4, to implement our methods and measures we assume that the patterns of spending observed in the data represent the optimal levels of spending. This assumption, implicit in much of the risk adjustment literature, is problematic for a variety of reasons described above. We now illustrate how this assumption can be (and sometimes is) relaxed, more thoroughly examining this question in a separate paper (Bergquist et al. 2018).⁴²

In the Netherlands, regulators already effectively partially relax this assumption. Prior to estimating the payment weights for the Dutch risk adjustment model, data for risk adjustment are modified in order to more accurately capture trends in costs. Risk adjustment payment weights in the Netherlands for year t are estimated prospectively using medical spending from year t-3 as the dependent variable. Anticipated changes in spending levels between year t-3 and year t (e.g. due to changes in demography), are taken into account by a linear correction of the original service-level spending from t-3. This linear correction may vary across services at the discretion of the analyst. In addition, the data are corrected for changes in the benefit package between year t-3 and year t, which could mean, for instance, that if a certain drug was introduced in year t-1, spending on that drug is added to the risk adjustment data. These modifications are an example of regulators re-defining first-best optimal spending, ${\text{x}}_{\text{is}}^{\text{*}}$, to account for differences between observed spending patterns and the spending patterns regulators believe to be optimal.

In addition to altering the data because of changes in the benefit package or in anticipation of exogenous trends in service use and cost, the data might also be modified prior to estimation to improve the performance of the health care system. Suppose that for reasons unrelated to adverse selection the regulator believes that overall levels of primary care are inefficiently low relative to overall levels of hospital care.⁴³ In this setting, the regulator would want to move money from the overall hospital care allocation to the overall primary care allocation, allowing the individual-specific allocation rules to determine how this shift in funds affects each individual. Our insight is that the regulator can encourage this reallocation of funds via the risk adjustment model when using the constrained regression model. Instead of estimating the risk adjustment payment weights using observed spending levels as the outcome variable, the regulator can alter the overall levels of spending for each service, use the allocation rules (the σ_iss) to map from the overall service-level allocations to individual spending, and then use the modified individual spending variable in a constrained regression to estimate the payment weights. Such an adjustment would result in higher payments for groups of individuals more likely to use primary care at the cost of payments for groups more likely to use hospital care.

As a demonstration we implement this method by shifting 900 million Euros (3% of total spending) from hospital care to primary care and then re-estimating the constrained regression model. Figure 3 shows how this affects payments for various groups of individuals. The figure presents the same five stratifications of the population from Figure 1. The bars represent the change in payments for each group with the red bars showing changes in payments for the sicker group and the green bars showing changes in payments for the healthier group for each stratification. Note that in all cases, when the data are adjusted to shift resources from hospital care to primary care, payments for the sick go down while payments for the healthy go up. This type of shift in payments implies a shift in incentives, where plans will provide more primary care and less hospital care in order to attract more of the healthy groups who are now more profitable than before.

Under estimation methods that take into account health plans’ decisions on health care spending, transforming the data prior to deriving risk adjustment payment weights would likely improve incentives for resource allocation. When paired with a constrained regression, transformation of data can ensure that the payment model provides incentives to supply exactly the desired pattern of care in equilibrium.

7. Discussion

In this paper, we have developed new estimation methods and performance measures for risk adjustment models that generate optimal payment weights according to an explicit economic model of insurer behavior and social welfare as alternatives to the conventional estimation methods and measures that generate payments based on statistical criteria. We assumed the objective is efficiency of resource allocation across medical services. We showed that in this context the only case in which the R-squared is the “right” welfare measure is when 1) health care is regarded as one homogeneous service and 2) health plans can discriminate at the individual level. Since these assumptions are unrealistic, we have proposed a more general welfare measure and alternative estimation methods. Specifically, we have proposed to replace the two-step “estimate-then-evaluate” approach in risk adjustment for health plan payment with a one-step “estimate-to-maximize-the-objective” approach. Since this one-step approach forces regulators to make their objective regarding health plan payment explicit, we believe it is less vulnerable to subjective judgments about the “performance” of a risk adjustment model than the conventional two-step approach.

Our methodology is an application of the principal-agent or mechanism design approach using concepts of economic equilibrium and efficiency. In order to evaluate the performance of a policy tool like health plan payment, it is necessary to anticipate how it will affect market behavior. This calls for a model relating the risk adjusted payments to economic equilibrium. We have adapted approaches from the literature on health plan and consumer behavior to construct a workable model relating the payment weights to equilibrium service allocations decided by plans. Our paper proposes what we argue is a plausible and practical metric for welfare loss. Our methods for deriving payment weights minimize welfare loss subject to equilibrium behavior by plans in an empirically operational fashion. In each of the two major cases, when the number of available risk adjustors exceeds or falls short of the number of potential plan actions, we show that the solution to this problem can be found using relatively straightforward variants on the conventional least-squares regression: the addition of constraints to the regression model in the case of few plan actions and a straightforward transformation of the data in the case of many plan actions.

We have empirically illustrated the case where the number of adjustors exceeds the number of plan actions (few plan actions), using data from the Netherlands. Our empirical results are consistent with earlier papers, indicating that under our economic model the Dutch risk adjustment model (of 2015) and its corresponding weights leave substantial incentives for service-level distortions. We show that by adding a set of linear constraints when estimating the payment weights of the Dutch risk adjustment model, incentives for service-level distortion can be eliminated so that the risk adjustment payments push plans toward first-best service allocations.

The solution illustrated in our empirical illustration applies to any setting where the number of adjustors exceeds the number of plan actions. This may be the case for the Dutch risk adjustment model, the German risk adjustment model and the U.S. federal risk adjustment models used in Medicare Advantage and the Marketplaces, which all include over 100 risk adjustor variables. When the number of relevant services exceeds the number of risk adjustor variables this first-best allocation cannot be achieved. In that case the risk adjustment payment weights that minimize, but do not necessarily eliminate, the welfare loss can be found by a linear regression of first-best allocations, ${\text{x}}_{\text{is}}^{\text{*}}$, on the K-by-S transformed z variables (risk adjustors), ${\sum }_{\text{s}}{\text{σ}}_{\text{is}}{\tilde{\mathrm{z}}}_{\text{gsk}}$, derived in our analytical framework. Switzerland, with its simple risk adjustment model is a potential candidate for implementing this method empirically.

In a setting where regulators are concerned with service-level distortions the concepts of “equilibrium” and “efficiency” applied in this paper are powerful tools not only for estimating risk adjustment payment weights, but also for guiding the choice of risk-adjustor variables to include in the payment model. Presently, risk adjustor variables are included or excluded based on considerations of clinical meaningfulness, game-ability and contribution to fit (Kautter et al., 2014). There are several reasons to reconsider the specification of a risk-adjustment model. Recent research and policy experience implies that, in the US at least, “upcoding” clinically related variables is a serious and costly issue (Geruso and Layton, 2015). Furthermore, application of alternative estimation techniques based on machine learning indicates that statistical fit as measured by R-squared may be achieved with many fewer variables than presently in use (Rose, 2016). Our analyses add an additional reason to reconsider the specification. With a measure of efficiency in hand, the contribution of an additional set of risk adjustors can be evaluated in relation to its ability to improve economic efficiency. A simple and direct way to do this would be to supplement the R-squared fit criteria with the welfare loss criteria in evaluating the contribution of a set of variables. The contribution of a new set of variables will depend on the present set of adjustors and how well they do in directing incentives for each of the services plans can discriminate on. Our framework implies that – in the case of service-level distortion – risk adjustors should not be evaluated only by the extent to which they reduce “under/overcompensations”, but also by their potential to reduce variation in predictability and predictiveness across services. The stronger a risk adjustor variable correlates with spending on a particular service, the larger will be its potential to mitigate the welfare loss from allocative inefficiency.

When it comes to a practical implementation of our approach it will be important for regulators to carefully reconsider the assumptions made in this paper. More specifically, the beliefs on how health plans and consumers act in a particular setting may differ from those adopted here. For example, this paper assumes plans set service spending in response to incentives, whereas there might be other limits on service-level spending, such as when regulators require a minimum level of access to health care. Additionally, our economic model is based on assumptions of perfect competition, profit-maximization, a fixed premium and symmetric equilibrium. For several reasons these assumptions may deviate from how the market operates in a particular setting. Furthermore, the regulator’s objective may differ from the one adopted here. In the Netherlands, for instance, the regulator is not only concerned with service-level distortions but also with other types of selection actions such as specific marketing strategies of health plans. Finally, regulators are concerned with objectives other than economic efficiency, including “fairness” (i.e. premium differences between plans should not reflect differences in health risk), and “quality of care” (e.g. the risk adjustment payments should encourage plans to invest in the quality of care for particular treatments), among others. A formal incorporation of these objectives within a single social welfare function is probably unrealistic. Despite all of the additional objectives, however, regulators still use the R-squared as the primary metric for payment model performance, a measure which also ignores these other objectives and, as we’ve shown here, has the additional disadvantage that it does not accurately assess the objective it is intended to capture: incentives for service-level selection. Thus, a metric for economic efficiency with respect to service-level allocations of health care spending, such as one constructed here, can still be useful as a way to help policymakers assess the performance of different payment models.

Appendix A: Predictability and Predictiveness

A profit-maximizing health plan has incentives to skimp on services that are predictable by enrollees and predictive of financial losses. As shown by Ellis and McGuire (2007), profit maximization implies that the combination of measures of predictability and predictiveness is a summary index for service-level selection incentives. Our model produces a similar result. Equation (12) shows that an insurer’s incentive to ration a service is described by the following expression:

$$\sum _i{\widehat{\mathrm{\sigma }}}_{is}\left(\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}-\sum _{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{*}\right)$$

This expression can be written as:

$$\sum _{\text{i}}\left[\frac{{\widehat{\mathrm{\sigma }}}_{\text{is}}}{{\text{σ}}_{\text{is}}}\right]\left[{\text{σ}}_{\text{is}}\left(\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}-\sum _{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{*}\right)\right]$$

This expression can be divided into two components, one representing “predictability” and the other representing “predictiveness.” We operationalize these two components as follows. The first component, $\frac{{\widehat{\mathrm{\sigma }}}_{\text{is}}}{{\text{σ}}_{\text{is}}}$, captures the “predictability” of the service. Predictability measures how well consumers can anticipate what spending, ${\widehat{\mathrm{x}}}_{\text{is}}$, they will receive, given the plan’s decision about total spending on a service, x_s. We follow Ellis and McGuire (2007) and use the correlation between σ_is and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$ as a measure of predictability:

$${\text{Predictability}}_{\text{s}}={\text{Corr(σ}}_{\text{is}},{\widehat{\mathrm{\sigma }}}_{\text{is}}\text{)}$$

Recall that σ_is represents the portion of the total spending allocated to service s that is actually allocated to individual i.${\widehat{\mathrm{\sigma }}}_{\text{is}}$, on the other hand, represents the portion of the total spending allocated to service s that individual i expects to be allocated to her. Given these definitions of σ_is and ${\widehat{\mathrm{\sigma }}}_{\text{is}}$, this correlation is the correlation between an individual’s actual spending on a service and her expected spending on that service. If the service is strongly (weakly) predictable, the correlation between actual and expected spending will be high (low). Predictability does not vary across payment systems since the expected portion of spending (${\widehat{\mathrm{\sigma }}}_{\text{is}}$) as well as the actual portion of spending (σ_is) spending are independent of payment weights (see Section 3).

The second component, ${\text{σ}}_{\text{is}}({\sum }_{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}-{\sum }_{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{*})$, represents the “predictiveness” of the service. Predictiveness is related to the correlation between an individual’s share of spending on a service and her overall profitability to the plan. We find it more intuitive to depict predictiveness in terms of the correlation of service-level spending with losses rather than profits. We again follow Ellis and McGuire (2007) and use this correlation as our measure of predictiveness:

$${\text{Predictiveness}}_{\text{s}}=\text{Corr}\left({\text{σ}}_{\text{is}},\sum _{\text{s}}{\text{σ}}_{\text{is}}{\text{x}}_{\text{s}}^{*}-\sum _{\text{k}}{\mathrm{\beta }}_{\text{k}}{\text{z}}_{\text{ik}}\right)$$

In contrast to predictability, predictiveness will vary as risk adjustment payment weights vary. We report our measures of predictability and predictiveness in order to show that our new method for estimating risk adjustment payment weights improves performance not only on the metrics derived from our model but also on metrics derived in the previous literature on service-level selection.

Figure A1 shows our measures of predictability (left panel) and predictiveness (right panel) for each of the ten services. As described above, predictability is calculated as the correlation between individuals’ expected spending on service s and their actual spending on that service. The figure reveals substantial heterogeneity in predictability across services with pharmaceutical spending being the most predictable and “other” and geriatric physical therapy spending being the least predictable. Since actual spending (as reflected in σ_is) and expected spending (as reflected in ${\widehat{\mathrm{\sigma }}}_{\text{is}}$) are independent of payment weights, the predictability of services is independent of the payment model.

The right panel of Figure A1 shows our predictiveness measure for each of our ten services under two payment models: the conventional Dutch risk adjustment model and the new constrained model. The bars show the correlation between an individual’s spending on service s and their overall unprofitability to the plan. Bigger bars signify a higher correlation. Risk adjustment, by transferring funds to more costly enrollees should cause some convergence among these service-specific correlations such that spending on service s has a similar relationship with total profitability as spending on service s’.⁴⁴ It is clear from the figure that the constrained model improves on the conventional Dutch model, driving down the correlation between spending on a service and unprofitability to the plan for all services.

Note that predictiveness only matters for selection incentives if the service is also predictable. Unless a potential enrollee anticipates their level of utilization of a given service, her demand for a given insurance contract is unlikely to respond to changes in the level of rationing of that service. In other words, if a service is not predictable, tight or loose rationing of that service should have no effect on enrollment and profitability. This implies that the results in the right and left panels of Figure A1 combine to form the overall selection incentives faced by insurers, with services that score high on both predictability and predictiveness being the most vulnerable to service-level distortions.

Figure A1:

Predictability and Predictiveness

Appendix B: Estimated Coefficients for Two Models

Risk adjustor variables	Population frequency	Base model	Constrained model
Intercept	100.00%	203	−790
Male. 0	0.55%	3716	5898
Male. 1–4	2.27%	425	−85
Male. 5–9	2.96%	289	−72
Male. 10–14	3.11%	172	410
Male. 15–17	1.81%	192	629
Male. 18–24	4.29%	−15	−38
Male. 25–29	2.94%	−42	−58
Male. 30–34	2.95%	−39	−34
Male. 35–39	3.08%	0	0
Male. 40–44	3.83%	75	114
Male. 45–49	3.89%	187	263
Male. 50–54	3.67%	333	499
Male. 55–59	3.33%	584	936
Male. 60–64	3.19%	813	1364
Male. 65–69	2.73%	1278	1643
Male. 70–74	1.90%	1661	2041
Male. 75–79	1.37%	2104	2401
Male. 80–84	0.89%	2248	2351
Male. 85–89	0.43%	2364	2105
Male. 90+	0.15%	2542	1433
Female. 0	0.52%	3069	5207
Female. 1–4	2.17%	199	−154
Female. 5–9	2.82%	153	158
Female. 10–14	2.97%	142	514
Female. 15–17	1.72%	324	416
Female. 18–24	4.18%	305	145
Female. 25–29	2.96%	774	985
Female. 30–34	2.99%	935	1549
Female. 35–39	3.14%	546	977
Female. 40–44	3.83%	309	439
Female. 45–49	3.86%	352	387
Female. 50–54	3.68%	463	578
Female. 55–59	3.34%	573	773
Female. 60–64	3.18%	733	1110
Female. 65–69	2.78%	1043	1162
Female. 70–74	2.07%	1362	1534
Female. 75–79	1.71%	1703	2019
Female. 80–84	1.37%	1955	2296
Female. 85–89	0.89%	2165	2341
Female. 90+	0.48%	2125	1181
No PCG a	82.03%	201	637
Glaucoma	0.85%	279	346
Thyroid disorders	1.64%	83	−181
Mental disorders	0.53%	95	1243
Depressive disorder	2.67%	184	−636
Peripheral neuropathy	0.38%	1159	157
Hypercholesterolemia	5.30%	178	−620
Diabetes II without hypertension	0.63%	531	−1868
COPD / severe asthma	1.16%	1565	1165
Asthma	2.16%	573	643
Diabetes II with hypertension	1.40%	845	−1511
Epilepsy	0.48%	834	−245
Crohn’s disease / Colitis ulcerosa	0.20%	818	2881
Heart diseases	2.21%	1500	1242
Rheumatoid arthritis (TNF-α)	0.19%	14164	14623
Rheumatoid arthritis (other)	0.32%	1478	2813
Parkinson’s disease	0.14%	2176	3527
Diabetes type I	1.29%	1361	649
Transplantations	0.15%	89	6361
Cystic fibrosis / Pancreatic disease	0.04%	3021	15999
Disorders of brain/ spinal cord	0.07%	1511	4128
Cancer	0.09%	3697	9279
Hormone-sensitive tumors	0.35%	−712	−2226
HIV/AIDS	0.08%	2826	29936
Kidney disorders	0.07%	7201	15969
No DCG b	91.00%	0	0
DCG1	0.67%	391	400
DCG2	1.49%	560	750
DCG3	1.11%	635	659
DCG4	1.80%	1011	3436
DCG5	1.16%	1618	2657
DCG6	1.26%	2002	3813
DCG7	0.55%	3225	9061
DCG8	0.12%	3989	9721
DCG9	0.30%	3847	6950
DCG10	0.33%	7307	14332
DCG11	0.04%	8722	14286
DCG12	0.07%	8608	20788
DCG13	0.04%	15876	32097
DCG14	0.04%	65152	63374
DCG15	0.01%	51005	140811
ZIP-code cluster 1	9.91%	169	479
ZIP-code cluster 2	9.88%	124	351
ZIP-code cluster 3	9.97%	101	254
ZIP-code cluster 4	9.86%	84	215
ZIP-code cluster 5	10.01%	68	203
ZIP-code cluster 6	9.91%	64	171
ZIP-code cluster 7	9.98%	50	129
ZIP-code cluster 8	9.98%	38	78
ZIP-code cluster 9	10.17%	24	44
ZIP-code cluster 10	10.32%	0	0
Age = 0–17 or 65+	37.67%	0	0
Disability beneficiaries. 15–34	0.91%	647	−969
Disability beneficiaries. 34–44	0.77%	803	−50
Disability beneficiaries. 45–54	1.30%	720	88
Disability beneficiaries. 55–64	2.02%	596	362
General beneficiaries. 15–34	0.57%	267	−260
General beneficiaries. 34–44	0.55%	353	−214
General beneficiaries. 45–54	0.60%	412	43
General beneficiaries. 55–64	0.48%	368	327
Students. 18–34	3.20%	−238	−233
Self-employed. 15–34	0.78%	−116	−155
Self-employed. 34–44	1.27%	−111	−112
Self-employed. 45–54	1.32%	−146	−156
Self-employed. 55–64	0.79%	−152	−148
Other. 15–34	14.84%	0	0
Other. 34–44	11.29%	0	0
Other. 45–54	11.88%	0	0
Other. 55–64	9.75%	0	0
No MYHCG c	94.24%	0	0
2x costs in top-10%	1.01%	2661	6082
3x costs in top-15%	2.30%	2318	3155
3x costs in top-10%	1.05%	3680	4370
3x costs in top-7%	0.78%	5692	6085
3x costs in top-4%	0.46%	9661	9066
3x costs in top-1.5%	0.15%	25836	37142
No DMECG d	99.17%	0	0
Insulin pumps	0.12%	422	−3319
Catheters	0.39%	1308	−1212
Stoma	0.31%	1801	−929
Trachea-stoma	0.02%	6546	2464
Address >15 residents. 0–17	0.06%	244	−1059
Address >15 residents. 18–64	0.38%	169	480
Address >15 residents. 65+	0.72%	321	5820
Income deciles 1–3. 0–17	6.25%	27	−110
Income deciles 1–3. 18–64	18.57%	53	12
Income deciles 1–3. 65+	4.81%	200	−269
Income deciles 4–7. 0–17	8.34%	−5	−115
Income deciles 4–7. 18–64	24.79%	48	23
Income deciles 4–7. 65+	6.41%	44	−166
Income deciles. 8–10. 0–17	6.25%	0	0
Income deciles. 8–10. 18–64	18.59%	0	0
Income deciles. 8–10. 65+	4.81%	0	0
65-. no morbidity e	70.38%	0	0
65-. morbidity	12.86%	618	1541
65+. no morbidity	6.89%	0	0
65+. morbidity	9.88%	642	2272

^aPCG = Pharmacy-based Cost Group

^bDCG = Diagnostic-based Cost Group

^cMYHCG = Multiple-Year High Cost Group

^dDMECG = Durable Medical Equipment Cost Group

^eMorbidity is operationalized as having at least one PCG, DCG, MYHCG or DMECG.