Causal Inference About Good and Bad Outcomes

Abstract

People learn differently from good and bad outcomes. We argue that valence-dependent learning asymmetries are partly driven by beliefs about the causal structure of the environment. If hidden causes can intervene to generate bad (or good) outcomes, then a rational observer will assign blame (or credit) to these hidden causes, rather than to the stable outcome distribution. Thus, a rational observer should learn less from bad outcomes when they are likely to have been generated by a hidden cause, and this pattern should reverse when hidden causes are likely to generate good outcomes. To test this hypothesis, we conducted two experiments (N = 80, N = 255) in which we explicitly manipulated the behavior of hidden agents. This gave rise to both kinds of learning asymmetries in the same paradigm, as predicted by a novel Bayesian model. These results provide a mechanistic framework for understanding how causal attributions contribute to biased learning.

People are motivated to maximize rewards and minimize punishments, but when updating their beliefs, they often weigh good and bad news differently. The nature of this differential weighting remains puzzling. In some cases, animals and humans attend more to bad events and learn more rapidly from punishments than from rewards (Baumeister, Bratslavsky, Finkenauer, & Vohs, 2001; Taylor, 1991). Similarly, some studies of reinforcement learning have found that learning rates are higher for negative than for positive prediction errors (Christakou et al., 2013; Gershman, 2015a; Niv, Edlund, Dayan, & O’Doherty, 2012). However, other work has demonstrated the opposite pattern of results—greater learning for positive outcomes, not only in reinforcement-learning tasks (Kuzmanovic, Jefferson, & Vogeley, 2016; Lefebvre, Lebreton, Meyniel, Bourgeois-Gironde, & Palminteri, 2017; Moutsiana, Charpentier, Garrett, Cohen, & Sharot, 2015), but also in procedural-learning (Wachter, Lungu, Liu, Willingham, & Ashe, 2009) and declarative-learning tasks (Eil & Rao, 2011; Sharot, Korn, & Dolan, 2011).

Here, we explored the hypothesis that the direction of valence-dependent learning asymmetries depends on beliefs about the causal structure of the environment. To provide some insight, we borrow an example from Abramson, Seligman, and Teasdale (1978): Consider a group of researchers who receive a rejection for a manuscript submission. The researchers’ inferences about the cause of that feedback will influence whether they modify the paper or appeal the decision. If the researchers believe that their submission was rejected because the paper was bad, they will revise the paper and take this new information into consideration for future submissions. However, if they believe that the rejection was due to the opinion of an unfair reviewer, they will be less likely to update their beliefs about the quality of the paper. In other words, they will explain away the rejection, attributing it to a hidden cause (the reviewer’s caustic temperament) rather than to their own ability.

Abramson et al. (1978) argued that “failure means more than merely the occurrence of a bad outcome” (p. 55). Rather, attribution of negative outcomes to oneself is what constitutes failure. According to learned-helplessness theory, individuals with an optimistic explanatory style tend to attribute negative events to external forces, whereas those with a pessimistic explanatory style believe that the causes of negative events are internal. Given this view, optimistic and pessimistic cognitive biases might arise from both (a) differing experiences of reinforcements and (b) beliefs about the causes of those reinforcements. In other words, both the availability of rewards and punishments in the environment and the degree to which these consequences are attributed to oneself determine to what extent positive and negative outcomes influence learning.

Valence-dependent learning asymmetries are important because they may give rise to systematic biases with real-world consequences. On the one hand, learning more from positive outcomes can give rise to unrealistic optimism (Sharot et al., 2011) and risk-seeking behavior (Niv et al., 2012). On the other hand, learning more from negative outcomes can lead to unrealistic pessimism (Maier & Seligman, 1976) and risk aversion (Smoski et al., 2008). Thus, understanding the determinants of these asymmetries may provide insights into a wide range of behavioral phenomena and provide necessary information to curtail their harmful consequences.

One limitation of many past studies examining valence-dependent learning asymmetries is that they do not directly measure or control participants’ beliefs about causal structure, and hence they are not ideal for testing our hypothesis. In the present research, we conducted a more direct test by manipulating the causal structure of a reinforcement-learning task to induce both positively biased and negatively biased learning asymmetries in the same participants. Participants were asked to choose between two options with unknown reward probabilities and were informed that an agent could silently intervene to change the outcome positively (benevolent condition), negatively (adversarial condition), or randomly (neutral condition). Relying on a Bayesian model of causal inference, we expected that participants in the benevolent condition would update their beliefs about the reward probabilities more from negative than positive outcomes. We expected them to do so because negative outcomes could not have been caused by an interfering external agent but instead must have been a result of participants’ enacted choice (i.e., sampled from the option’s reward distribution). Likewise, we expected that participants would learn more from positive compared with negative outcomes in the adversarial condition. To examine the robustness and flexibility of our model, we explored a more realistic scenario in Experiment 2, in which the probability of latent agent intervention was unknown to participants.

Experiment 1

In Experiment 1, we manipulated the causal structure underlying a reinforcement-learning task so that a hidden agent occasionally intervened to produce particular outcome types (good, bad, or random). This allowed us to test our primary hypothesis that positive outcomes would be weighed more heavily when the hidden agent was adversarial, whereas negative outcomes would be weighed more heavily when the hidden agent was benevolent. Importantly, if participants made no causal attributions in the task, they should learn equally well from positive and negative outcomes in all three experimental conditions. However, any disproportionate learning of positive or negative outcomes could be attributed to the experimental manipulation of the causal structure. We formalized this hypothesis in terms of a Bayesian model that incorporates the underlying causal structure by rationally assigning credit to the different possible sources of feedback. This model describes participants’ beliefs about latent agent interventions, while also providing a mechanistic account for how beliefs are formed and how they influence learning from positive and negative feedback.

Method

Participants

Eighty participants (25 female, 52 male, 3 unreported) were recruited from Amazon Mechanical Turk. The sample size was chosen in order to exceed sample sizes from previous, related work (Lefebvre et al., 2017; Sharot et al., 2011). Participants were excluded from analyses if they failed to choose the stimulus with the higher reward probability on more than 60% of trials, leaving data from 72 participants (20 female, 49 male, 3 unreported) for subsequent analyses; 90% of participants met the accuracy criterion. Participants gave informed consent, and the Harvard University Committee on the Use of Human Subjects approved the experiment.

Procedure

Participants were instructed to imagine that they were mining for gold in the Wild West. On each trial, participants had to choose between two different-colored mines by clicking on a button underneath the mine of their choice (Fig. 1b, left). After making a decision, participants either received gold (reward) or rocks (loss; Fig. 1b). Each mine in a pair produced a reward with either 70% or 30% probability. Each reward yielded a small amount of real bonus money ($0.05), and each loss resulted in a subtraction of real bonus money ($0.05). Bonuses were summed, revealed, and paid out at the end of the task.

Fig. 1.

Illustration of the behavioral task. At the start of each block, participants were told which of three hidden agents can intervene (a): the bandit (adversarial condition), the tycoon (benevolent condition), or the sheriff (neutral condition). Participants then chose between two different-colored mines (b, left). After receiving feedback, participants answered whether or not they believed that the hidden agent intervened on that trial (b, right).

Participants completed three blocks of 50 trials each (150 total trials) in different “mining territories” (Fig. 1a). Participants were instructed that different agents frequented each territory: a bandit who will steal gold from the mines and replace it with rocks (adversarial condition), a tycoon who will leave extra gold in the mines (benevolent condition), and a neutral sheriff who will try to redistribute gold and rocks in the mines (neutral condition). Participants completed each of the three conditions once, in randomized order. The agents intervened on 30% of the trials, and participants were told this percentage explicitly at the start of the task, though they did not know unambiguously whether the agent intervened on any particular trial. While the underlying reward distributions (i.e., absent intervention) for the mines were 70% or 30%, the hidden agent intervened on 30% of trials (or 15 out of 50 trials). For example, the benevolent intervention produced rewards on 15 out of 50 trials, the adversarial intervention produced losses on 15 out of 50 trials, and the random intervention produced either losses or rewards on 15 out of 50 trials. After feedback on each trial, participants were asked whether they believed the outcome they received was a result of hidden-agent intervention (binary response of “Yes” or “No”; Fig. 1b, right). To ensure that participants understood the task instructions, we asked them comprehension questions. Correct answers were required before participants could proceed.

Bayesian reinforcement-learning model

The problem facing participants during the task is to choose the option yielding the highest reward. Because they do not know the reward probabilities of the two mines, they must estimate them from experience, while taking into account possible intervention from the hidden agent. We developed a Bayesian reinforcement-learning model that jointly infers the hidden-agent interventions and the reward probabilities. Here, we summarize the model (see the Supplemental Material available online for a full mathematical description).

After choosing an action and observing reward rt on trial t, participants updated their estimates of the action’s intrinsic reward probability θt according to a reinforcement-learning equation that depends on inferences about latent causes: θt + 1 = θt + αt (rt – θt), where αt is a learning rate. The learning rate changed across trials depending on the posterior probability of the hidden-agent intervention, as computed by Bayes’s rule. When the posterior probability was high, the learning rate was low. Intuitively, the model predicted that participants would suspend learning about the reward probabilities when they believed that the outcome was generated by an external force. Although the model was derived from Bayesian principles, at a mechanistic level, it closely resembles standard reinforcement-learning models that update reward predictions on the basis of prediction errors. Like other Bayesian reinforcement-learning models, the dynamic learning rate was derived from probabilistic assumptions about the environment (e.g., Frank, Doll, Oas-Terpstra, & Moreno, 2009; Gershman, 2015b; Gershman & Niv, 2015) rather than left as a free parameter. However, we enriched typical reinforcement-learning models by rationally assigning credit to different possible sources of feedback. In other words, the learning rate in the Bayesian model was calculated by integrating one’s cumulative past beliefs about intervention into one’s value estimate of a particular choice.

Critically, the learning rate exhibited asymmetries depending on whether the hidden agent tended to produce positive or negative outcomes. For example, when the agent was adversarial, positive outcomes could be generated only from the intrinsic reward probabilities, whereas negative outcomes could be generated by either the hidden agent or the intrinsic reward probabilities. Consequently, negative outcomes were less informative about the reward probabilities in this scenario, inducing a lower learning rate.

The Bayesian model was fitted using maximum a posteriori estimation with empirical priors based on previous research (Gershman, 2016). We computed a posterior over the underlying parameters and then input the expected values into a softmax function to model choice probabilities, with a response stochasticity (inverse temperature) parameter and a “stickiness” parameter to capture choice autocorrelation (Gershman, Pesaran, & Daw, 2009).

A valence-dependent learning asymmetry is built into the structure of the Bayesian model. Thus, the model itself cannot be used to test for the existence of such an asymmetry. To provide evidence for asymmetric learning, we also fitted a reinforcement-learning model in which we modeled separate, fixed learning rates for positive and negative outcomes in each of the three experimental conditions (six learning rates total). This model is heuristic in the sense that it characterizes, but does not explain mechanistically, learning-rate asymmetries in our task. Importantly, this model allowed for differential weighting of positively and negatively valenced outcomes without taking into account hidden-agent interventions.

We used random-effects Bayesian model selection (Rigoux, Stephan, Friston, & Daunizeau, 2014; Stephan, Penny, Daunizeau, Moran, & Friston, 2009) to compare models. This procedure treats each participant as a random draw from a population-level distribution over models, which it estimates from the sample of model evidence values for each model. We used the Laplace approximation of the log marginal likelihood to obtain the model evidence values. For our model-comparison metric, we report the protected exceedance probability (PXP), the probability that a particular model is more frequent in the population than all other models under consideration, taking into account the possibility that some differences in model evidence are due to chance.

Results

Behavioral analyses

As a preliminary manipulation check, we verified that participants’ beliefs about hidden causes varied with the outcome valence in a condition-specific manner (Fig. 2a). Participants were more likely to believe that a hidden cause resulted in negative outcomes, as opposed to positive outcomes, overall, t(71) = 16.82, p < .0001, d = −0.32, 95% confidence interval, or CI = [−0.55, −0.08]. Importantly, participants were more likely to believe that the hidden agent had intervened after negative than after positive outcomes in the adversarial condition, t(71) = 66.24, p < .0001, d = −0.28, 95% CI = [−0.51, −0.04], and after positive than after negative outcomes in the benevolent condition, t(71) = −71.35, p < .0001, d = −0.99, 95% CI = [−1.23, −0.74]. Participants were also slightly more likely to believe that the hidden agent had intervened after negative outcomes in the neutral condition, t(71) = 6.83, p < .0001, d = −0.31, 95% CI = [−0.55, −0.08]. We will revisit this effect in the context of our computational model.

Fig. 2.

Average beliefs (a) and Bayesian model predictions (b) about hidden-agent intervention for each condition and feedback type in Experiment 1. Intervention probability in (a) was calculated by taking the mean of each participant’s guess of whether or not the hidden agent caused a given outcome for each trial. Error bars represent standard errors of the mean.

Computational modeling

To characterize the effects of outcome valence and agent type on learning, we first fitted a reinforcement-learning model with six separate learning rates. As shown in Figure 3a, participants generally learned more from positive than from negative outcomes across all conditions, t(71) = 5.56, p < .0001, d = 0.66, 95% CI = [0.32, 0.99]. By treating the positivity bias in the neutral condition, t(71) = 3.08, p < .003, d = 0.36, 95% CI = [0.03, 0.70], as a participant-specific baseline and subtracting it from the other conditions, we obtained a relative measure of learning rates for the adversarial and benevolent conditions (Fig. 3b), revealing an underlying sensitivity to condition and valence. A 2 (condition: adversarial vs. benevolent) × 2 (valence: positive vs. negative) repeated measures analysis of variance on relative learning rates revealed no significant main effects (p = .57 for condition, p = .84 for valence), but a significant interaction, F(1, 71) = 4.91, p < .05. Consistent with our hypothesis, results showed that the learning-rate advantage for positive versus negative outcomes reverses depending on the causal structure of the task.

Fig. 3.

Learning rates in Experiment 1. Predictions of the reinforcement-learning model (a) are shown for each condition (adversarial, benevolent, neutral) and outcome valence (positive, negative). In (b), predictions of the reinforcement-learning model are shown after the learning rates for the neutral condition (which serves as a participant-specific baseline) was subtracted from the other conditions. Relative learning rates from the Bayesian model (c) are shown for the adversarial and benevolent conditions, averaged across trials. Error bars represent standard errors of the mean.

Although the interaction effect is significant, the effects are small and noisy because the model is overparametrized. Modeling learning rates separately for each condition and outcome valence cannot capture a common learning mechanism, and the model has only a small amount of data from which to estimate each parameter. We therefore developed a Bayesian reinforcement-learning model that makes the common learning mechanism explicit. Learning rates in the Bayesian model are determined entirely by the causal structure, which is known to the participant. The only free parameters in the model are those governing the choice policy—response stochasticity and stickiness. We fixed the prior probability of hidden-agent intervention in the Bayesian model at 30% to replicate the instructions that participants received in the task. Importantly, a variant of the model in which this probability was treated as a free parameter for each participant yielded a value very close to the ground truth of 30% probability of intervention: M = 29.6%, SEM = 3.8%.

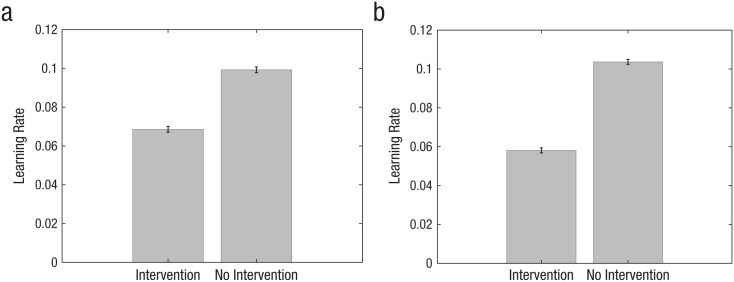
As expected, the Bayesian model showed a strong interaction between condition and outcome valence (Fig. 3c), a direct consequence of causal inference. To bolster our claim that causal inference predicts the valence-dependent learning-rate asymmetry, we examined the relationship between intervention judgments and learning rates (derived from the Bayesian model). We found that learning rates were significantly lower for trials in which participants believed that the hidden agent intervened, compared with trials in which participants believed that the hidden agent did not intervene, t(71) = −6.94, p < .0001, d = −0.82; see Figure 4a.

Fig. 4.

Learning rates for trials in which participants did or did not believe the outcome was a result of hidden-agent intervention, separately for (a) Experiment 1 and (b) Experiment 2. Learning rates were derived from the Bayesian model (Experiment 1) and the empirical Bayesian model (Experiment 2). Error bars represent standard errors of the mean.

Quantitative metrics also supported the Bayesian model. First, the model could predict intervention judgments even though it was not fitted to these judgments: A signed-ranks test between the participants’ guesses about intervention and the model’s posterior over intervention showed a significant median point-biserial correlation (r_pb = .45, p < .0001). Second, the Bayesian model received unequivocally stronger support than the reinforcement-learning model with six learning rates, according to a random-effects model-selection procedure (PXP = 0.97 and PXP < 0.001). This model was also strongly favored over the Bayesian model with a free intervention-probability parameter (PXP < 0.001) and a non-Bayesian reinforcement-learning model with separate learning rates for positive and negative feedback (PXP = 0.03).

Discussion

Participants in Experiment 1 demonstrated asymmetric learning from positive and negative outcomes that reversed depending on the nature of a hidden intervening agent: When the hidden agent intervened to produce negative outcomes, learning was greater for positive outcomes, and when the hidden agent intervened to produce positive outcomes, learning was greater for negative outcomes. A Bayesian model captured this pattern and could also accurately predict participants’ trial-by-trial judgments about interventions. As predicted by the model, learning rates were lower when participants believed that the hidden agent intervened. These results support our hypothesis that causal inference plays a central role in determining valence-dependent learning asymmetries.

Note that our data are not consistent with a model in which participants follow a simple rule of ignoring negative feedback in the adversarial environment and positive feedback in the benevolent environment. If they were in fact following such a rule, then we would expect learning rates in those cases to be 0, whereas in fact they are significantly greater than 0. The Bayesian model captures the differential sensitivity to positive and negative feedback in a more graded manner than a simple rule-based model.

Experiment 2

One of the broader questions motivating this research is how the environment shapes learning-rate asymmetries. We addressed this question in Experiment 2 by creating a subtle ambiguity in our experimental task: Instead of informing participants of the exact intervention probability, we simply told them that hidden agents occasionally intervene. We reasoned that this ambiguity more directly reflects real life; in the real world, probabilities for interventions and outcomes are often unknown, and decisions are dependent on one’s prior expectations.

Method

Participants

Two groups of participants (total N = 299) were recruited from Amazon Mechanical Turk—Sample A: n = 110, 49 female, 56 male, 5 unreported; Sample B: n = 194, 90 female, 96 male, 8 unreported. Sample B was collected as part of a preregistered replication, though for the purposes of these analyses we have aggregated the two samples. (See the Supplemental Material for further information on the preregistered replication. Registration details can be found at https://osf.io/cx4u9/ on the Open Science Framework.) Participants were excluded from model fitting if they did not choose the stimulus with the higher reward probability for over 60% of trials; of all participants, 85.3% met the accuracy criterion (86.4% of Sample A, 84.7% of Sample B). Participants were also excluded if they did not properly respond to an attention-check question (n = 6). We included data from 255 participants in the model fits (n = 95 for Sample A, n = 160 for Sample B). Participants gave informed consent, and the Harvard University Committee on the Use of Human Subjects approved the experiment.

Procedure

Behavioral-task procedures were identical to those in Experiment 1, except that participants were told that the hidden agents would intervene “sometimes.” Actual intervention remained fixed at 30% (15 of 50 trials per block).

Computational model

Because participants were not told the intervention probability, we explored models that either estimated the probability directly (the adaptive Bayesian model) or treated it as a free parameter (the fixed Bayesian model). In addition, we fitted a model in which the intervention probability was derived empirically by averaging the binary intervention judgments. We refer to this model as the empirical Bayesian model.

Results

Behavioral analyses

Results of Experiment 2 replicated those of Experiment 1: Participants believed that the hidden agent caused negative outcomes more often than positive outcomes across all conditions, t(254) = 6.26, p < .0001, d = −0.06, 95% CI = [−0.18, 0.06], and there was a significant difference between belief in the hidden agent for good outcomes in the benevolent and neutral conditions and for bad outcomes in the adversarial and neutral conditions, t(254) = 7.03, p < .0001, d = 0.29, 95% CI = [0.17, 0.41].

Computational modeling

Model comparison overwhelmingly (PXP > 0.999) supported the empirical Bayesian model (in which the intervention probability was derived from the binary intervention judgments) compared with a more sophisticated adaptive Bayesian model (which estimated the intervention probability from experience) and a fixed Bayesian model (which treated the intervention probability as a free parameter).

Once again, we found that participants had significantly higher learning rates for positive outcomes than for negative outcomes, t(254) = 4.73, p < .0001, d = −0.82, 95% CI = [−0.95, −0.69]. In a further replication of our results from Experiment 1, we also found that learning rates were significantly lower for trials in which participants believed that the hidden agent intervened, compared with trials in which they believed that the hidden agent did not intervene, t(252) = 16.77, p < .0001, d = −0.80, 95% CI = [−0.93, −0.67] (Fig. 4b).

A signed-ranks test between the participants’ actual guess about intervention and the intervention predicted by the model showed a significant median point-biserial correlation (r_pb = .55, p < .0001), demonstrating that intervention judgments can be accurately predicted by the adaptive Bayesian model.

Discussion

By modifying the behavioral task and the computational model to include an unknown probability of hidden-agent intervention, we were able to gain insight into individual differences in prior expectations that govern valence-dependent learning asymmetries. First, a version of the Bayesian model that derived the intervention probability from the average of participants’ binary judgments was favored by model selection among the models we considered. We conjecture that our task taps into prior expectations about the nature and frequency of hidden agents, possibly formed over a lifetime of learning.

General Discussion

Across two experiments, we found that the direction of valence-dependent learning asymmetries could be influenced by manipulating beliefs about causal structure. Specifically, participants learned more from positive than from negative outcomes when hidden agents intervened adversarially; conversely, they learned more from negative than from positive outcomes when hidden agents intervened benevolently. A Bayesian model explained the complete pattern of asymmetries, and an extension of the model that inferred the probability of hidden-agent intervention could capture performance in the more complex scenario in which the intervention probability was unknown.

Our findings are consistent with the long-standing idea that optimistic biases are not exclusively a consequence of increased salience of positive outcomes but also involve external attribution of negative outcomes (Miller & Ross, 1975). Across two independent samples, people displayed a generalized tendency to attribute positive outcomes to themselves and negative outcomes to others. Numerous studies have provided evidence for the prevalence of a self-serving bias (the attribution of good outcomes to oneself and bad outcomes to external forces; Campbell & Sedikides, 1999; Hughes & Zaki, 2015). For example, people are more likely to think a third party influenced a gamble when the outcome was a loss instead of a win (Morewedge, 2009), they are more likely to take credit for positive as opposed to negative outcomes (Bradley, 1978), and they demonstrate decreased intentional binding for monetary losses compared with gains as well as negative versus positive affect cues (Takahata et al., 2012; Yoshie & Haggard, 2013). Our computational model does not take into account a self-preservation bias, but removing individual variance by subtracting the bias in the neutral condition from the other two conditions resulted in our hypothesized asymmetry. In addition, our data show that participants have higher learning rates for positive outcomes. This discrepancy between learning rates for good and bad news is consistent with the well-studied phenomenon of an inherent optimism bias (Weinstein, 1980). Therefore, it may be more difficult for individuals to discount their agency over rewards, even when they are provided with explicit instructions about the structure of the environment.

While our model can account for our experimental findings and the related phenomena reviewed above, we have not demonstrated that it provides a comprehensive account of optimism bias in general. It is difficult to attribute optimism bias to causal structure without knowing (or manipulating) participants’ structural beliefs, which was the starting point of the present research. Nonetheless, it is possible to speculate (see Gershman, 2018, for more details). If people have a strong belief in their self-efficacy, then observing failure will favor the hypothesis that a latent cause was responsible, resulting in less updating compared with observing success. One suggestive source of data comes from studies of psychiatric disorders, in which beliefs about self-efficacy and agency are disrupted.

Previous work has shown that learning asymmetries are associated with depression, anhedonia, and pessimism and optimism. For example, research demonstrates that depressed patients with anhedonia exhibit blunted learning for both rewards and punishments (Chase et al., 2010) and that depressed participants accurately recall negative outcomes whereas healthy participants underestimate the frequency of negative outcomes (Nelson & Craighead, 1977). It should be noted, however, that other studies have also found no relationship between optimism and asymmetric updating (Stankevicius, Huys, Kalra, & Seriès, 2014). Our findings suggest that optimistic and pessimistic traits should depend on the interaction between imbalanced learning and beliefs about agency. We propose that a latent factor, such as agency inference, may be mediating inconsistent findings in the literature regarding imbalanced learning for positive and negative outcomes. This idea is supported by research that shows that optimistic and pessimistic biases can be manipulated by changes in outcome controllability. For example, greater perceived control is associated with increased optimism bias (Weinstein, 1980), and this finding has also been shown in a large meta-analysis (Klein & Helweg-Larsen, 2002). In a seminal study by Alloy and Abramson, nondepressed participants exhibited an agency bias for desired outcomes and a nonagency bias for undesired outcomes, while depressed participants showed no such bias (Alloy & Abramson, 1979). This work suggests that biased beliefs of control may protect against depression and that these cognitive distortions arise not solely from a belief that individuals have control over positive outcomes, but that negative outcomes can be attributed to someone or something outside of oneself (though see Msetfi, Murphy, Simpson, & Kornbrot, 2005, for evidence that abnormal beliefs about control in depression may be attributable to an impairment in contextual processing).

Conclusion

In sum, we provide evidence that valence-dependent learning asymmetries arise from causal inference over hidden agents. This idea, formalized in a simple Bayesian model, was able to quantitatively and qualitatively account for both choices and intervention judgments. An important task for future researchers will be to understand the limits of this framework: to what extent can we understand self-serving biases, learned helplessness, and other related behavioral phenomena in terms of a common computational mechanism? More generally, the real world is typically less well behaved than the idealized experimental scenarios studied in the present research; people constantly face causally complex and ambiguous inferential problems, where simple attributions to “good” and “bad” hidden agents may not be applicable. We foresee an exciting challenge in extending the Bayesian framework to tackle these more realistic settings.