D3R Grand Challenge 3: Blind Prediction of Protein-Ligand Poses and Affinity Rankings

Abstract

The Drug Design Data Resource aims to test and advance the state of the art in protein-ligand modeling, by holding community-wide blinded, prediction challenges. Here, we report on our third major round, Grand Challenge 3 (GC3). Held 2017–2018, GC3 centered on the protein Cathepsin S and the kinases VEGFR2, JAK2, p38-α, TIE2, and ABL1; and included both pose-prediction and affinity-ranking components. GC3 was structured much like the prior challenges GC2015 and GC2. First, Stage 1 tested pose prediction and affinity ranking methods; then all available crystal structures were released, and Stage 2 tested only affinity rankings, now in the context of the available structures. Unique to GC3 was the addition of a Stage 1b self-docking subchallenge, in which the protein coordinates from all of the cocrystal structures used in the cross-docking challenge were released, and participants were asked to predict the pose of CatS ligands using these newly released structures. We provide an overview of the outcomes and discuss insights into trends and best-practices.

2. Introduction

Computer-aided drug design (CADD) technologies have enormous potential to speed the discovery of new medications, and to lower the costs of drug discovery. When the three-dimensional structure of a targeted protein is known, two key goals of CADD are to predict the bound conformation (pose), of candidate ligands; and to predict, or at least correctly rank, the binding affinities of candidate ligands for the target^1–3. Today, multiple technical approaches to these problems are available in various software packages^4,5 and computational chemists routinely face the challenge of deciding which method is best to use in a given scenario and how best to use it. Similarly, those developing new methods must put their innovations in the context of existing approaches. However, evaluations of CADD methods are typically retrospective, which is decidedly suboptimal method given that these methods must work prospectively in actual drug discovery project. Moreover, different methods are frequently benchmarked using different datasets, making it difficult to compare multiple methods on an equal footing.

The Drug Design Data Resource (D3R; www.drugdesigndata.org) was founded to address these problems by providing the research community with opportunities to compare CADD methods on shared, prospective datasets. Building on the prior Community Structure Activity Resource (CSAR)^6–9, D3R has now held three major challenges^10,11, and we report here the outcome of Grand Challenge 3 (GC3). This challenge is the largest to date, focusing on seven high quality datasets across five subchallenges for pose and affinity ranking predictions. It also includes a new self-docking stage, designed to evaluate docking program performance using the protein structure solved with the query ligand. The conclusions provided by GC3 largely overlap with those of prior studies^7–17, with a few novel observations. In all, 28 research groups participated in GC3, submitting a total of 375 predictions. Here, we detail the datasets, challenge submission assessment procedures, and prediction results, while seeking lessons regarding best practices and trends in the field. A complementary set of articles from individual challenge participant labs accompanies this overview in the present special issue of the Journal of Computer-Aided Molecular Design.

3. Methods

3.1. Datasets and subchallenges

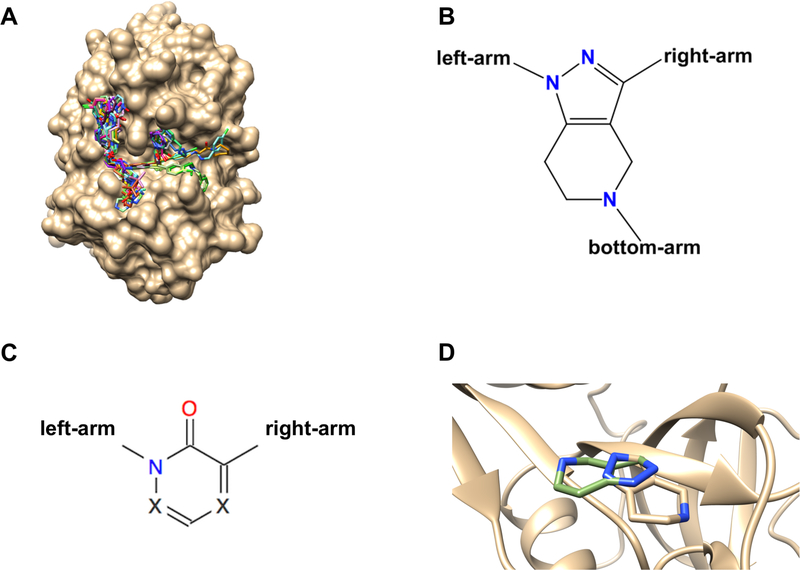
Grand Challenge 3 comprised five subchallenges (Supplementary Table 1). Subchallenge 1 included both pose-prediction and affinity ranking components and was based on 24 Cathepsin S (CatS) ligand-protein cocrystal structures (Figures 1A and 1B), along with the CatS IC50s of 136 compounds, which included many in the cocrystal structures. A histogram of the pIC50 values is provided in Supplementary Figure 1. Experimental details pertaining to the CatS dataset can be found in the supplementary materials¹⁸. Both the affinity and pose prediction CatS ligands are large and flexible with molecular weights of 530 to 810 Da and with 6 to 14 rotatable bonds. The 24 compounds with available cocrystal structures fall into two chemical series. The first series contains 22 of the 24 pose prediction CatS ligands (all but CatS_4 and CatS_6) that contain a tetrahydropyrido-pyrazole core. All members of the second series (CatS_4 and CatS_6) contain a pyridinone core. The tetrahydropyrido-pyrazole and pyridinone cores are demonstrated in Figures 1B and C, respectively. Compounds in the first series display consistent binding modes with CatS, except that CatS 7, CatS 9, and CatS 14 bind with the core flipped relative to the other members of the series (Figure 1D). CatS_11 was omitted from Pose 1 RMSD statistics because it was found during analysis to be present in PDB entry 3kwn. This was missed initially due to an incorrect bond order assignment. Further details regarding all CatS compounds are provided in the supplementary material (Supplementary Table 2). Assay and crystallization conditions for the CatS subchallenge data are also provided in the supplementary material (folder SM_CatS_expt).

Figure 1: A.

Binding poses of all 24 CatS ligands used in GC3 with the crystallographic surface displaying shallow and surface-exposed nature of the CatS binding pocket. B. Tetrahydropyrido-pyrazole core scaffold found in 22 of the CatS ligands and C. Pyridinone core scaffold found in 2 of the CatS ligands. D. Core scaffold flip in the Tetrahydropyrido-pyrazole core exemplified for ligands CatS_1 (brown) and CatS_7 (green).

Subchallenges 2–5 included only affinity predictions or ranking and are based on dissociation constants (K_d) of various ligands for five kinases. To construct these datasets, the D3R team selected ligand-kinase pairs for K_d measurements from a large matrix of available ligand/kinase screening data (single concentration percent inhibition) that has since been published¹⁹. Histograms of the pK_d values are provided in Supplementary Figure 1. Details of the experimental K_d measurement procedures may be found in the supplementary material folder SM_KinaseData_DiscoverX. Prior to the challenge, some of the dissociation constants and the full set of percent inhibition data were unblinded by Drewry et al.¹⁹. As the challenge pertains to the prediction of K_ds, we omitted the disclosed K_ds from our evaluation statistics. We further note that, given that the submitted predictions in general correlated worse with the K_d values than did the experimental percent inhibition data in Drewry et al. (Table 7), our assessment is that the availability of the percent inhibition data did not significantly affect the results of the challenge.

Table 7.

Correlations, in terms of Kendall’s t and Matthews correlation coefficient, of measured ligand-kinase K_d values with their respective measured percent inhibition values from the prior high-throughput screening study.

Target	Kendall’s τ	Matthews Corr. Coeff.
ABL1	0.24	−0.43
JAK SC2	0.76	0.54
JAK SC3	0.82	0.74
p38-α	0.77	0.83
TIE2	0.79	0.78
VEGFR2	0.82	0.72

That said, this partial unblinding should be kept in mind when assessing the kinase results. Subchallenge 2 involved 85, 89, and 72 diverse ligands for kinases vascular endothelial growth factor receptor 2 (VEGFR2), Janus Kinase 2 (JAK2), and p38-α (mitogen-activating protein kinase 14 (MAPK14), respectively; 54 of these ligands were assayed for all three kinases. Subchallenges 3 and 4 aimed to generate activity cliffs²⁰ and include, respectively, 17 congeneric compounds with K_d values for JAK2, and 18 congeneric compounds with K_d values for the kinase Angiopoietin-1 receptor (TIE2). Because GC3 contains two different subchallenges involving JAK2, we will use the terms JAK2 SC2 and JAK2 SC3 to differentiate between the two corresponding datasets. Finally, subchallenge 5 consisted of K_d values for two compounds for the wild type and five mutants of the nonphosphorylated ABL1 protein: ABL1(F317I), ABL1(F317L), ABL1(H396P), ABL1(Q252H), and ABL1(T315I).

Although GC3 included components designed to test explicit solvent alchemical free energy methods, as done in prior Grand Challenges^10,11, only one submission used such an approach, so these components are not discussed in the present paper.

3.2. Posing the Challenge

Similar to GC2015¹¹ and GC2¹⁰, GC3 followed a two stage format for the CatS dataset, including a docking component in Stage 1 and affinity ranking components in both Stages 1 and 2. In addition, for the first time, Stage 1 was split into two parts, Stages 1a and 1b. In Stage 1a, participants were asked to dock 24 CatS ligands into a CatS structure of their choosing from the Protein Data Bank (PDB) archive (https://rcsb.org); this constituted a cross-docking challenge because participants did not have the protein coordinates from the cocrystal structure with each ligand. At the end of Stage 1a, all 24 protein structures, without ligands, were released publicly, and participants were again invited to dock all 24 CatS ligands to their respective protein cocrystal structures from the released set; this constituted a self-docking challenge. In both Stages 1a and 1b, participants were allowed to submit up to five poses per ligand, where their single best guess was designated as Pose 1. Because the kinases subchallenges did not include any new cocrystal structures, they were included only in the Stage 2 affinity component of GC3. Prior to the start of the challenge, participants were notified that the cocrystal structure with ligand CatS_14 has a dimethylsulfoxide (DMSO) molecule in a critical bridging location; and six other cocrystal structures with six other ligands, CatS_2, CatS_17, CatS_20, CatS_22, CatS_23, and CatS_24, have a sulfate (SO4) ion in a critical bridging location. In order to facilitate the docking of these ligands, representative structures of Cathepsin S, with the key SO4 and DMSO, but no ligands, were provided in the dataset, and participants were invited to use this information in their docking calculations. In addition, we asked participants to use the provided SO4-bound structure as the reference structure for superposition of all pose predictions, in order to facilitate evaluation.

3.3. EVALUATION OF POSE AND AFFINITY PREDICTIONS

Predictions were evaluated with the approach used for GC2015¹¹ and GC2¹⁰, as summarized below. The scripts used to evaluate pose and affinity predictions evaluation scripts are available at Github (drugdesigndata.org/about/workflows-and-scripts). Pose predictions were evaluated in terms of the symmetry-corrected RMSD between predicted and crystallographic poses. These were calculated with the binding site alignment tool in the Maestro Prime Suite (align-binding-sites), where a secondary structure alignment of the full proteins is performed, followed by an alignment of the binding site Cα atoms within 5 Å of the ligand atoms²¹. Evaluations in this article are limited to the best guess poses (Pose 1, see above), unless otherwise noted. However, we also generated statistics for the pose with lowest RMSD to the crystallographic pose (“Closest Pose”), and for the mean across all ≤ 5 poses provided (“All Poses”); these additional analyses are provided on the D3R website.

Affinity predictions were evaluated in terms of the ranking statistics Kendall’s τ^22,23 and Spearman’s ρ²⁴. Compounds with experimental K_d values reported only as ≥10 μM were excluded from these ranking evaluations, but were used in an alternative classification metric, which is described in the following paragraph. (Ranking statistics for the full set of compounds are reported in Supplementary Table 3) The number of ligands per target including or excluding K_d or IC50 > 10 μM and their respective highest affinities are reported in Table 1. Uncertainties in these statistics were obtained by recomputing them in 10,000 rounds of resampling with replacement, where, in each sample, the experimental IC50 or K_d data were randomly modified based on the experimental uncertainties. Experimental uncertainties were added to the free energy, ΔG, as a random offset δG drawn from a Gaussian distribution of mean zero and standard deviation RTln(I_err). In this evaluation, the value of I_err was set to 2.5, based on the estimated experimental uncertainty. For this challenge we do not compute the Pearson’s correlation metric or root-mean square error (RMSE) given that we ask participants to consistently provide only their ranking of compounds. The present article focuses on the Kendall’s τ results, which is regarded as having advantageous statistical properties²⁵, and the Spearman’s ρ results may be found on the D3R website (drugdesigndata.org).

Table 1.

Number of ligands for each target, excluding or including K_d and IC50 >10 μM, as indicated. The highest affinity of any ligand in each set is also provided. For CatS, these data are provided for all ligands (CatS All), and for only the 19 ligands with associated ligand-protein crystal structures (CatS Xtal). The asterisk denotes that the dataset consists of K_d values for two compounds for the wild type and five mutants of the nonphosphorylated ABL1 protein: ABL1(F317I), ABL1(F317L), ABL1(H396P), ABL1(Q252H), and ABL1(T315I).

		No Kd or IC50
Target	All Kd Or IC50	>10 μM	Highest Affinity [μM]
CatS All	136	136	0.003
Cats Xtal	19	19	0.015
ABL1*	2	2	0.049
JAK2 SC2	89	37	0.00066
JAK2 SC3	17	11	0.053
p38-α	72	31	0.00028
TIE2	18	8	0.0034
VEGFR2	85	43	0.00062

Compounds with experimental K_d values reported only as ≥10 μM were considered in GC3 by defining these compounds as “inactive”, while compounds with reported K_d values were defined as “active”. We then used the Matthews correlation coefficient²⁶, a metric of classification accuracy, to assess how well each submission performed at distinguishing these two sets of compounds. Thus, if a given subchallenge comprised N_a known actives and N_i known inactives, by the present criterion, we assigned the top-ranked N_a compounds in the prediction set as “predicted actives” and the remaining N_i compounds as “predicted inactives” and compared this classification with the experimental classification.

As in previous challenges, two null models were used as performance baselines for ranking ligand potencies; the null models were then evaluated using Kendall’s τs and Matthews correlation coefficient in the same manner as the submitted predictions. The null models are “Mwt”, in which the affinities were ranked by decreasing molecular weight; and clogP, in which affinities were ranked based on increasing octanol–water partition coefficient estimated computationally by RDKit²⁷. Null models were not calculated for the ABL1 target since this subchallenge only contains two ligands.

Results

In GC3, 28 unique participants submitted a total of 375 prediction sets, as detailed in Table 2. The following subsections provide an overview of outcomes. Details of the methods and their performance statistics may be found in Supplementary Tables 4, 5, 7, and 8; further information, including raw protocol files, identities of submitters (for those that are not anonymous), and additional analysis statistics can be found on the D3R website (https://drugdesigndata.org). Many submissions and methods are further discussed in articles in this special issue by the participants themselves.

Table 2.

Number of submissions (N_submissions) and participants (N_participants) in each sub-challenge.

Sub-challenge	Nsubmissions	Nparticipants
CatS Stage 1a Pose Prediction	52	24
CatS Stage 1b Pose Prediction	47	18
CatS Stage 1 Affinity Prediction	54	20
CatS Stage 2 Affinity Prediction	81	17
ABL1	11	5
JAK2 SC2	31	10
JAK2 SC3	18	7
P38-α	29	11
TIE2	18	7
VEGRF2	34	12

3.4. Pose predictions

3.4.1. Overview of pose prediction accuracy

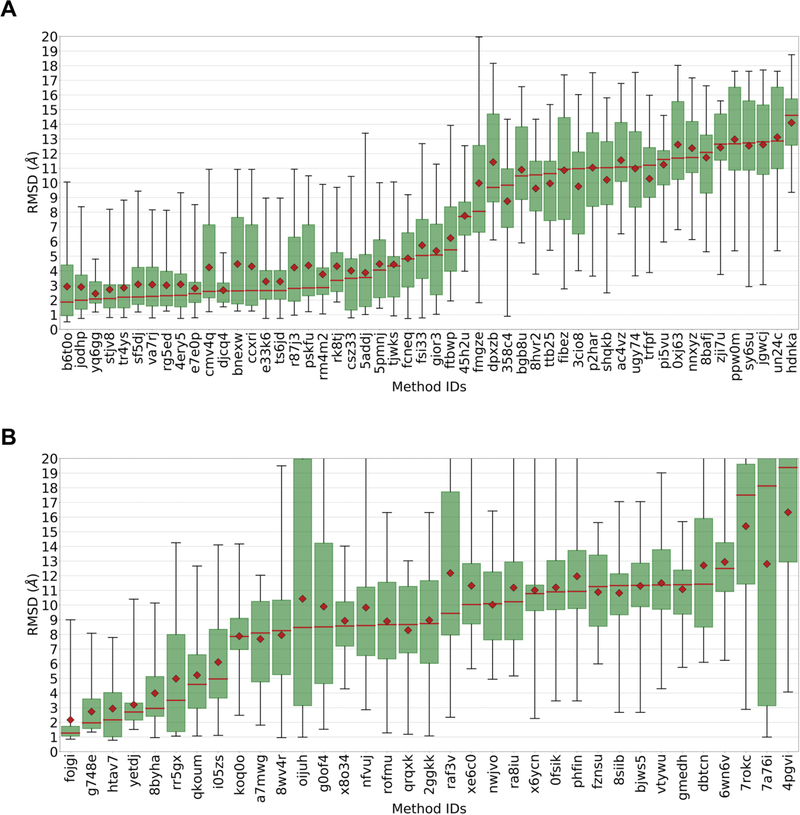
The CatS ligands appear to have presented a difficult docking challenge, as few submissions had a mean or median Pose 1 RMSD below 2.5 Å (Figure 2). By comparison, roughly half of the submissions met one of these criteria for the HSP90 and FXR pose prediction challenges in GC2015¹¹ and GC2¹⁰, respectively. Nonetheless, the best prediction sets did well, with lowest median RMSDs of 1.87 Å and 1.01 Å, in Stages 1a and 1b, respectively.

Figure 2 A.

Box plots of pose 1 RMSD statistics for all Stage 1a pose prediction submissions. B. Box plots of pose 1 RMSD statistics for all Stage 1b pose prediction submissions. Data labels are submission IDs. Red diamonds: means. Red lines: medians. Green boxes: interquartile ranges. Whiskers: minimum and maximum RMSDs. The results are ordered from left to right by increasing median RMSD.

The differences between mean and median RMSD values were often large (Figure 2), suggesting that the RMSD probability distributions have fat tails and are asymmetric. This is confirmed by inspection of the boxes and whiskers in Figure 2 and of the RMSD distributions themselves in Supplementary Figure 2. Indeed, even some of the top performing methods still generate rather inaccurate poses. These observations demonstrate the value of considering both mean and median in evaluating docking performance. For example, although not the top performing method in Stage 1a (Figure 2) as judged by median, submissions yq6gg and djcq4 both have low means and have the smallest pose prediction standard deviations of all top performing methods. Interestingly, both submissions used OMEGA and ROCS; but while yq6gg coupled these tools with the GLIDE docking code, djcq4 used Rosetta ligand.

3.4.2. Analysis by docking methodology

A variety of methods yielded either a mean or median RMSD≤2.5 Å across all ligands, in both Stage 1a (Table 3A) and Stage 1b (Table 3B). Given the relatively wide spread of RMSD values within each submission (see prior paragraph), it is not clear that any one of these high-performing methods should be considered “best”. Multiple software packages are represented in these relatively successful approaches, including Glide^28,29, ICM³⁰, LeadFinder³¹, POSIT³², and SMINA³³, and in-house codes from the Kozakov³⁴ and Bonvin groups³⁵. Much as previously observed^10,11, a given docking code could generate widely varied levels of accuracy when used in multiple submissions, as shown in Table 4 for several software packages that appear in multiple prediction sets. Thus, success was not determined only by what software was used, but also how it was used.

Table 3.

Top-performing pose predictions for CatS Stage 1a (A) and Stage 1b (B). Results are evaluated in terms of the RMSD (Å) of Pose 1 for each ligand. This table includes the union of the top 10 submissions, by both median and mean RMSD of Pose 1 across all ligands, excluding submissions where neither median nor mean was <2.5Å. The standard deviations (SD RMSD) of the Pose 1 RMSDs are also provided as measure of scatter. Software lists the software listed by the participants in their protocol files. Submitter/PI: names of submitter and principal investigator (PI) provided with submission. Organization: institution of PI provided with submission. Visual Inspection lists the participant’s response to the standard question “Did you use visual inspection to select, eliminate, and/or manually adjust your final predicted poses?” Similar Ligands lists the participant’s response to the standard question “Did you use publicly available co-crystal structures of this protein with similar ligands to guide your pose predictions?” The asterisk denotes that the organization for this submission was submitted as Molecular Technologies, LLC.

(A)
Median RMSD	Mean RMSD	SD RMSD	Software	Submitter/PI	Organization	Visual Inspection	Similar Ligands	Submission ID
1.87	2.92	2.78	molsoft icm 3.8–5	P.Lam/M. Totrov	Molsoft	no	yes	b6t0o
1.99	2.89	2.23	smina feb 28 2016, based on autodock vina 1.1.2 openbabel 2.3.2 pymol 1.8.4.2 omega2 2.5.1.4 python 2.7.11 matplotlib 1.5.1 scipy 0.17.0 click 6.6	B.Wingert/C. Camacho	University of Pittsburgh	yes	yes	jodhp
2.08	2.44	0.93	omega 2.5.1 rocs 3.2.0 glide 6.1	A.Kumar/K. Zhang	RIKEN	yes	yes	yq6gg
2.1	2.72	2.00	posit v3.2.0.2	G.Warren	Openeye Scientific Software	yes	yes	stjv8
2.2	2.84	2.15	posit v3.2.0.2	G.Warren	Openeye Scientific Software	yes	yes	tr4ys
2.21	3.07	2.06	haddock webserver 2.2 openeye omega 2017.6.1 openeye shape 2017.6.1 openeye rocs 3.2.2.2 chemminer 2.26 fmcsr 1.16	A.Bonvin/A. Bonvin	Utrecht University	yes	yes	sf5dj
2.3	3.01	1.87	omega 2.5.1 rocs 3.2.0 ligprep 2.8 glide 6.1	A.Kumar/K. Zhang	RIKEN	yes	yes	rg5ed
2.33	3.07	2.31	in house montecarlo/ligsift/rdkit	D.Kozakov/D. Kozakov	Stony Brook University	no	yes	4ery5
2.44	2.8	1.80	posit v3.2.0.2; szybki v1.9.0.3; smzap 1.2.1.4	G.Warren	Openeye Scientific Software	yes	yes	e7e0p
(B)
Median RMSD	Mean RMSD	SD RMSD	Software	Submitter/PI	PI Organization	Visual Inspection		Submission ID
1.01	2.31	2.86	molsoft icm 3.8–5	P.Lam/M. Totrov	Molsoft	no		dgsd5
1.27	2.17	2.18	leadfinder/buildmodel	O.Stroganov	BioMolTech, LLC*	yes		fojgi
1.94	2.95	2.6	in-house monte-carlo, in-house minimization, rdkit, vina	D.Kozakov/Dima Kozakov	Stony Brook University	no		pj0v7
1.97	2.73	1.65	haddock webserver 2.2 openeye omega 2017.6.1 openeye shape 2017.6.1 openeye rocs 3.2.2.2 chemminer 2.26 fmcsr 1.16	A.Bonvin/A. Bonvin	Utrecht University	yes		g748e
2.17	2.94	2.37	smina feb 28 2016, based on autodock vina 1.1.2 openbabel 2.3.2 pymol 1.8.4.2 omega2 2.5.1.4 python 2.7.11 matplotlib 1.5.1 scipy 0.17.0 click 6.6	B.Wingert/C. Camacho	University of Pittsburgh	yes		htav7

Table 4.

Performance of submissions using several commonly used docking programs, analyzed by their locations in the four quartiles of median pose 1 RMSD across all ligand, where Q1 is the lowest median RMSD and Q4 is the highest, for Stages 1a and 1b. Glide is not listed in Stage 1b because only one Stage 1b submission mentioned it. The bottom row of each table lists the total number of predictions in each quartile, across all methods and software packages.

Stage 1a
Software	Q1	Q2	Q3	Q4
Glide	2	2	0	1
Vina	0	1	9	2
Smina	3	0	1	2
All submissions	14	13	13	13
Stage 1b
Software	Ql	Q2	Q3	Q4
Vina	2	6	6	5
Smina	1	3	1	4
All submissions	12	12	12	12

Interestingly, all but two of the top-performing submissions in Stage 1a (Table 2a) used visual inspection to help with their pose predictions; the exceptions are b6t0o (MolSoft) and 4ery5 (in-house Monte Carlo). In contrast, only one of the ten lowest-performing methods, based on Pose 1 median RMSD, used visual inspection (data not shown). This is in agreement with results previously found in GC2015¹¹, where the more successful methods tended to use visual inspection, though GC2 reported the opposite finding¹⁰. Thus, it is not clear whether visual inspection is a significant determinant of success; presumably, its value will depend on the expertise of the scientist. It is also worth noting that the use of visual inspection makes it difficult to use these challenges to assess the accuracy of the computational methods used, since it depends on factors outside the algorithms.

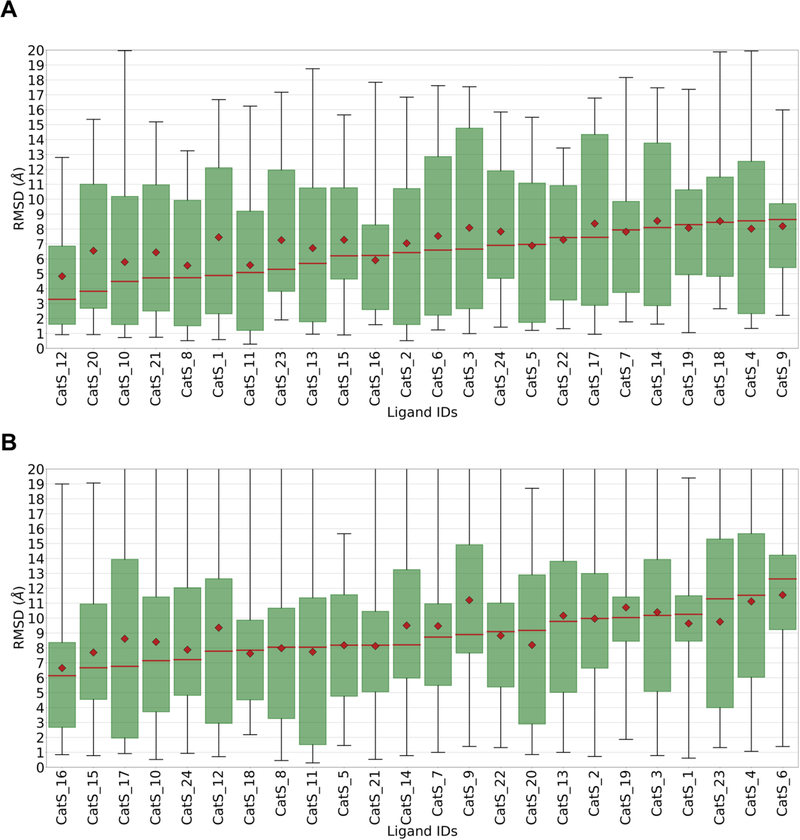
3.4.3. Analysis by ligand

An evaluation of pose prediction accuracy by ligand, rather than by docking method (Figure 3), suggests that some ligands are more difficult to dock correctly than others, although the large data ranges (see boxes and whiskers in Figure 3) make this assessment uncertain. The two pyridinone ligands, CatS 4 and CatS 6, fall toward the right in these graphs, and were the worst overall performing ligands in Stage 1b. Similarly, the ligands with the flipped binding mode, CatS 7, CatS 9, and CatS 14, fall to the right in the Stage 1a RMSD distribution, though only in the center of the Stage 1b distribution. Thus, the poses of the pyridinones and the flipped-mode tetrahydropyrido-pyrazoles may have been more difficult to predict on average. We further analyzed the statistics of the flipped binding mode ligands, CatS_7, CatS_9, and CatS_14, by calculating pose 1 RMSD statistics for each submission on only these cases (Supplementary Table 9). Of the 5 submissions that obtained a median Pose 1 RMSD < 2.5 Å, all were already present in the top submitter category in Table 3. This demonstrates that methods that performed well overall also tended to perform well in the difficult binding mode flip case. However, the results become less clear when considering the results of Stage 1b. The submission rr5gx, which employed a Medusa docking protocol, was the second ranked submission by mean Pose 1 RMSD on the flipped binding mode ligands, with an impressive RMSD of 1.4 Å, but with a 3.37 Å median pose 1 RMSD on the full set. Another interesting example is CatS_11, whose structure was available in in PDB entry 3kwn. (This entry is now superseded by 5qc4 as a result of our refinement process, which revealed that a pyrrole group in 3kwn was non-planar.) Nonetheless, the predicted poses of CatS_11 were not especially accurate, as CatS_11 was the 7th ranked ligand in Stage 1a and the 9^th in Stage 1b, with median RMSDs of 5.1 and 8.8 Å, respectively.

Figure 3. A.

Box plots of RMSD statistics, across submissions, for each ligand in Stage 1a. B. Box plots of RMSD statistics across submissions, for each ligand in Stage 1b. Data labels are ligand IDs. See Figure 2 for details.

3.4.4. Use of related crystal structures

The structure of a protein binding site can vary significantly in response to the binding of varied ligands, and the inability to adequately capture such responses is regarded as an important limitation in molecular docking^36–38. One method to reduce the resulting errors is to dock each ligand into a protein structure that was solved with a similar ligand, as the binding site is likely to have already adopted a suitable conformation. Indeed, prior grand challenges^11,10 as well as prior works by others^32,39,40 support a view that docking into an available receptor structure solved with a similar ligand increases the probability of correctly predicting ligand poses. This result seems to have percolated into the strategies employed in GC3, as 64% of submissions (34 of 53) in Stage 1a docked to the publicly available structure with the most similar ligand, in contrast to 45% (23 of 51) in GC2¹⁰. During GC3, approximately 28 CatS crystal structures were present in the PDB. We performed a 2D Tanimoto coefficient (tc) comparison between the challenge compounds and those present in available cocrystal structures of CatS. The results (Supplementary Table 10) show that six of the 24 CatS ligands had a tc greater than 0.6 with a ligand in the PDB at the time of the challenge. Results of GC3 provide continued support for the benefit of using ligand similarity to guide the selection of the receptor for docking (Table 3, and Supplementary Table 6 discussed below), as all of the top submissions in Table 3 are listed as having used available crystal structures to guide docking. The submissions in Table 3 that used ligand similarity used either the ROCS method⁴¹ or unspecified methods to do so. As a control, we also inspected the use of available crystal structures in the 10 submissions with largest median RMSD. Here, of the 10 submissions with largest median pose 1 RMSD, 6 used ligand similarity guided docking. We visually inspected a handful of the poses from these submissions and observed that the ligands were docked to the wrong portion of the binding pocket. If an incorrect subpocket is chosen for docking, ligand similarity guided receptor selection is not sufficient to prevent erroneous predictions.

The problem of accounting for binding site conformational adaptation does not obtain in the setting of self-docking, where a ligand is fitted back into the protein crystal structure with which it was cocrystallized. We, therefore, anticipated higher accuracy pose predictions in Stage 1b, where participants were provided with the precise protein structure determined with each bound ligand. It was, therefore, unexpected that overall accuracy was lower in Stage 1b than in Stage 1a (Section 3.4.1). However, this broad comparison may be hard to interpret because the participants and methods are not matched between these two stages. For a more meaningful comparison, we identified 13 participants who submitted predictions in both Stages 1a and 1b (Supplementary Table 6). Of these 13 participants, six used the same docking methodology in Stage 1a and 1b. For these participants, we quantified the performance change on going from Stage 1a to Stage 1b as R = 100(X_a − X_b)/X_a, where X_a is the median Pose 1 RMSD in Stage 1a, and X_b is the median pose 1 RMSD in Stage 1b. Across the six submissions, the mean improvement, <mi>, was modest, at 9.06%. However, the range of R was large, −9.05% to +46%, indicating significant improvement in some cases. (See Supplementary Table 6 for details.) These results support the value of similarity-guided docking but also emphasize the persistent importance of other factors. Thus, even a method that could reliably model the effects of binding on the receptor structure might not, in itself, yield large improvements in docking accuracy.

3.5. Affinity predictions

In this section, we evaluate the accuracy of predicted potency rankings for six different protein targets: CatS and the kinases ABL1, JAK2, p38-α, TIE2, and VEGFR2 (Table 5, Fig. 4). For CatS, the availability of 23 crystallographic poses in Stage 2 but not Stage 1 allows an examination of the role of structural data as a determinant of ranking accuracy. For the kinase measurements, some experimental K_d values were reported as ≥ 10 μM, making them difficult to include in standard metrics of ranking accuracy. We made use of these data by categorizing these compounds as “inactive”, and using the Matthews correlation coefficient, a classification statistic, to quantify the ability of the prediction methods to classify compounds as active or inactive. Finally, we examine the correlation of the kinase K_d measurements with corresponding single-concentration percent inhibition data available to us when we were choosing which K_d measurements to purchase. This analysis allows an interesting comparison between the accuracy of an experimental high-throughput (single-concentration) screen and the computational methods deployed in GC3.

Table 5.

Top 3 submissions, based on Kendall’s τ, for each affinity ranking challenge. Submission ID in bold font indicates a method that used machine learning. See Table 3 for details.

Kendall’s Tau	Software	Submitter/PI	Organization	Submission ID
Cats Stage 1
0.45	molsoft icm 3.8–5	P. Lam/M.Totrov	Molsoft	vtuzm
0.36	chemminer, libsvm 3.21	A. Bonvin/A. Bonvin	Utrecht University	kevrd
0.35	ligprep v33013 scaffopt	T. Evangelidis/T. Evangelidis	Central European Institute of Technology	kb2du
Cats Stage 2
0.39	molsoft icm 3.8–7	P. Lam/M.Totrov	Molsoft	q2k8y
0.34	ligprep v33013 scaffopt	T. Evangelidis/T. Evangelidis	Central European Institute of Technology	m6yb2
0.32	ligprep v33013 scaffopt	T. Evangelidis/T. Evangelidis	Central European Institute of Technology	e4emg
ABL1
0.52	rhodium 380e9–x9/openbabel 2.3.90 / pymol 1.3	J. Bohmann/Medicinal and Process Chemistry	Southwest Research Institute	3o8xi
0.52	schrodinger, gold, autodock vina, r-tda, javaplex, sci kit-learn	Z. Cang/W. Guo-Wei	Michigan State University	rdn3k
0.43	ri-score/tdl-bp/autodock vina	D. Nguyen/W. Guo-Wei	Michigan State University	c4xt7
JAK2 SC2
0.55	docking performed with gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina, conformer generation performed with rdkit via https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	zdyb5
0.36	molsoft icm 3.8–6	P. Lam/M.Totrov	Molsoft	7yjh3
0.23	amber11	X.Zou/X. Zou	University of Missouri-Columbia	qnq6x
JAK2 SC3
0.71	itscore2	X. Zou/X. Zou	University of Missouri-Columbia	87mci
0.6	docking performed with gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina, conformer generation performed with rdkit viahttps//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	7bi2k
0.56	docking performed with smina static binary available at https//sourceforge.net/projects/smina/files/ with default scoring function, then rescoring performed using gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina and the default cnn affinity model, conformer generation performed with rdkit via https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	yghq5
p38-α
0.21	molsoft icm 3.8–6	P. Lam/M. Totrov	Molsoft	8b6kk
0.2	smina feb 28 2016, based on autodock vina 1.1.2 openbabel 2.3.2 pymol 1.8.4.2 python 2.7.11 matplotlib 1.5.1 scipy 0.17.0 click 6.6	B. Wingert/C. Camacho	University of Pittsburgh	u48q2
0.13	smina feb 28 2016, based on autodock vina 1.1.2 openbabel 2.3.2 pymol 1.8.4.2 python 2.7.11 matplotlib 1.5.1 scipy 0.17.0 click 6.6	B. Wingert/C. Camacho	University of Pittsburgh	5vy6c
TIE2
0.57	ri-score/tdl-bp/autodock vina	D. Nguyen/W. Guo-Wei	Michigan State University	uuihe
0.57	schrodinger, gold, autodock vina, r-tda, javaplex, scikit-learn	Z. Cang/W. Guo-Wei	Michigan State University	y7qxv
0.5	docking performed with smina static binary available at https//sourceforge.net/projects/smina/files/ with default scoring function, then rescoring performed using gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina and the default cnn affinity model, conformer generation performed with rdkit via https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	xpmn7
VEGFR2
0.43	molsoft icm 3.8–6	P. Lam/M. Totrov	Molsoft	y0048
0.4	itscore2	X.Zou/X. Zou	University of Missouri-Columbia	uv5tc
0.38	chemminer, libsvm 3.21	A. Bonvin/A. Bonvin	Utrecht University	7smbe

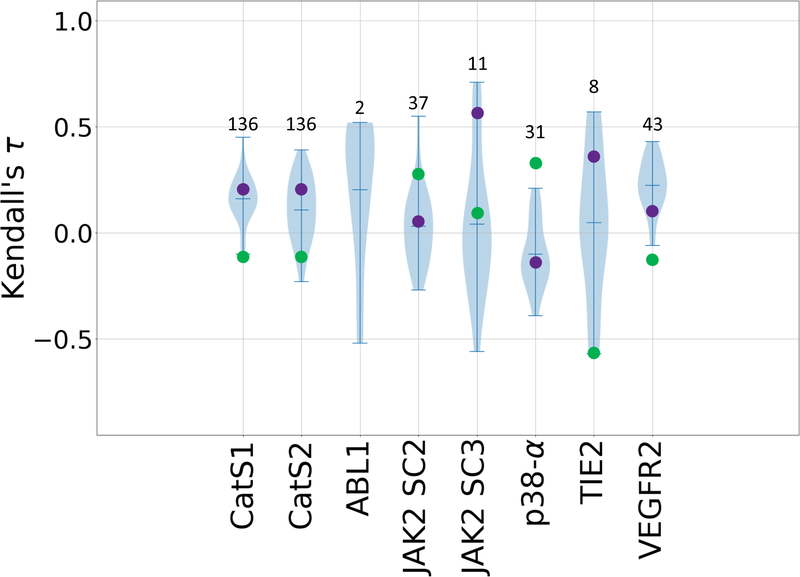
Figure 4.

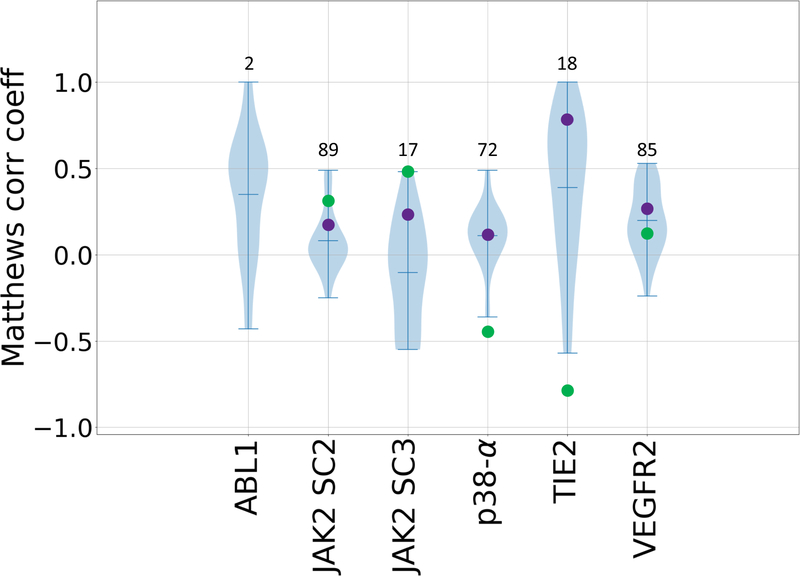
Violin plots of Kendall’s τ ranking correlation coefficients between predicted rankings and experimental IC50 rankings for the CatS dataset in Stages 1 and 2, and for predicted and experimental K_d values for all six kinase datasets: ABL1, JAK2 SC2, JAK2 SC3, p38-a, TIE2, and VEGFR2. Mean, minimum, and maximum Kendall’s τs for each target are shown by whiskers. Null models based on clogP and molecular weight are shown in green and purple, respectively. Null models were not calculated for the ABL1 target since this subchallenge only contains two ligands. The number of ligands for each subchallenge is given above each column.

3.5.1. Overview of potency ranking and active/inactive classification

Most of the ranking predictions correlate positively with the experimental data (Fig. 4, and Supplementary Table 7). Indeed, among all three Grand Challenges to date, GC3 yields the highest potency ranking accuracy, with values of Kendall’s τ exceeding the highest prior GC2 value of 0.46, for ABL1 (0.52 +/− 0.3), JAK2 SC2 (0.55 +/− 0.08), JAK2 SC3 (0.71 +/− 0.16), and TIE2 (0.57 +/− 0.24). This boost in performance is not attributable to differences in the ranges of affinities, as both challenges have a similarly wide range of affinities in each of their datasets. Nonetheless, this trend is also followed by a boost in null model performance, for JAK2 SC3 (Mwt 0.56 +/− 0.16) and TIE2 (clogP 0.57 +/− 0.28). The molecular weight and clogP models outperform the mean Kendall’s τ values in five and three of the seven targets, respectively. Additionally, some targets appear to have been more challenging than others. This is particularly evident for the VEGFR2, JAK2 SC2, and p38-α subchallenge, which involved a set of 55 ligands that are common between three kinases, yet the average Kendall’s τ values range from −0.1 for p38-α, to 0.02 for JAK2 SC2, and 0.22 for VEGFR2 (Fig. 4). Similarly, looking at the performance across the two ligand sets for JAK2 (SC2 and SC3), we observe a slight increase in Kendall’s τs of the top-performing methods for JAK2 SC3 (Fig. 4). Similar to the kinase targets, most of the ranking predictions for the CatS target also yield positive correlations with experimental data in both Stages 1 and 2. The large errors associate with the Kendall’s τ statistics in some of the targets is due in large part to the differences in number of ligands; in particular, ABL1, JAK2 SC3, and TIE2 include relatively small numbers of compounds (Table 1).

For the first time, GC3 included many compounds with experimental K_d values reported only as ≥10 μM. These were excluded from our Kendall’s τ ranking evaluations. However, we further evaluated all submissions against the full compound sets, using the Matthews correlation coefficient (Fig. 5, Supplementary Table 8), a classification metric. Most of the ranking predictions yield favorable Matthews correlation coefficients for the classification of active versus inactive compounds. This trend is followed by above average null model performances, where the molecular weight and clogP models outperform the mean Kendall’s τ values in five and four of the five targets, respectively, if we account for the reverse ranking performance of clogP in the case of p38-α and TIE2. Surprisingly, for TIE2, we see a notable performance across many of the methods with 56% of submissions reaching a Matthews correlation coefficient ≥ 0.55. Interestingly, TIE2 was designed as an activity cliff subchallenge to test the ability of current methods in detecting large changes in affinity due to small changes in chemical structure. Thus, the outstanding performance in TIE2 may reflect the ability of scoring function to classify congeneric ligands with a large activity cliff between actives and inactives. Furthermore, simple null models in which potency ranked by clogP and molecular weight have Matthews correlation coefficients of −0.8 and 0.78, respectively. JAK2 SC3 was also designed as an activity cliff subchallenge. However, the results are not as favorable in this case, which may be because it doesn’t have as sharp distinction between actives and inactives; i.e., the pK_d (−log(K_d)) distribution of TIE2 is bimodal with peaks near the extremes, while the pK_d distribution of JAK2 SC3 is unimodal, and has a smaller range.

Figure 5.

Violin plots of Matthews correlation coefficients between predicted classifications and experimental K_d classifications of active and inactive compounds for all six kinase datasets: ABL1, JAK2 SC2, JAK2 SC3, p38-a, TIE2, and VEGFR2. Mean, minimum, and maximum Matthews correlation coefficients for each target are shown by whiskers. Null models based on clogP and molecular weight are shown in green and purple respectively. Null models were not calculated for the ABL1 target, since this subchallenge only contains two ligands. The number of ligands for each subchallenge is given above each column.

3.5.2. Analysis by affinity prediction methodology

As in GC2¹⁰, the majority of submissions used structure-based approaches to rank the ligands, while a minority used ligand-based approaches. The two approaches performed similarly across most subchallenges, in terms of both Kendall’s τ and Matthews correlation coefficients. The most notable exception was JAK2 SC2, where multiple structure-based methods (max τ = 0.55) outperformed the top-performing ligand-based approach (nzud3; τ = 0.15) (Supplementary Table 7).

As noted above, a number of methods exceeded the top performing methods in GC2. Here, the top-performing methods, based on Kendall’s τ (Table 5) and Matthews correlation coefficient (Table 6), are now reviewed. For ABL1, the top-performing methods include the Rhodium docking and scoring algorithm developed by Southwest Research Institute (τ= 0.52 +/− 0.3; 3o8xi), and a topology-based machine-learning method by Guo-Wei Wei group⁴² (τ = 0.52 +/− 0.3; rdn3k) (Table 5). For JAK2 SC2, among the top-performing methods is a combination method of gnina docking and a convolutional neural network scoring model from the group of David Koes (τ = 0.55 +/− 0.08;zdyb5)⁴³. This method noticeably outperformed all other methods for this target, where the next top-performing method has a Kendall’s τ of 0.36 +/− 0.09 (7yjh3) and uses a custom ICM-score and 3D atomic property field quantitative structure–activity relationships (QSAR) model developed by Molsoft LLC (Table 5). For JAK2 SC3, three methods scored above the top-performing Kendall’s τ in previous challenges. These include a knowledge-based scoring function, itscore2, from the group of Xiaoqin Zou (τ = 0.71 +/− 0.16; 87mci) and two variations of a convolutional neural network docking and scoring method from the group of David Koes group⁴³ (τ = 0.60 +/− 0.17 and 0.56 +/− 0.17; bi2k and yghq5) (Table 5). Lastly, for TIE2, the top-performing methods include two topology-based machine-learning methods from the group of Guo-Wei Wei group⁴² (τ = 0.57 +/− 0.24 and 0.57 +/− 0.22; uuhe and y7qxv), and a convolutional neural network docking and scoring method from the group of David Koes⁴³ (τ= 0.5 +/− 0.23; xpmn7) (Table 5). Another notable prediction set for the CatS dataset in Stage 1 was submitted by Molsoft LLC (vtuzm); this exceeded all other methods by at least one standard deviation of 0.06 for that dataset (Table 5). We further report on the top-performing methods based on the classification metric, Matthews correlation coefficient (Table 6). As noted above TIE2 sees a notable performance across many of the methods employed. One method, in particular, was able to achieve a Matthews correlation coefficient of 1, thus classifying eight actives and 10 inactives perfectly. This was done at Southwest Research Institute using their proprietary Rhodium docking and scoring algorithm.

Table 6.

Top 3 submissions, based on Matthews correlation coefficient, for each affinity ranking challenge. Submission ID in bold font indicates a method that used machine learning. See Table 3 for details.

Matthews Corr. Coeff.	Software	Submitter/PI	Organization	Submission ID
ABL1
1.0	rhodium 380e9–x9/openbabel 2.3.90 / pymol 1.3	J. Bohmann/Medicinal and Process Chemistry	Southwest Research Institute	3o8xi
0.52	rhodium 380e9–x9/openbabel 2.3.90 / pymol 1.3	J. Bohmann/Medicinal and Process Chemistry	Southwest Research Institute	ktfzk
0.52	ri-score/tdl-bp/autodock vina	D. Nguyen/W. Guo-Wei	Michigan State University	c4xt7
JAK2 SC2
0.49	molsoft icm 3.8–6	P. Lam/M.Totrov	Molsoft	7yjh3
0.49	chemminer, libsvm 3.21	A. Bonvin/A. Bonvin	Utrecht University	nzud3
0.44	docking performed with gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina, conformer generation performed with rdkit via https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	j4kto
JAK2 SC3
0.48	itscore2	X.Zou/X. Zou	University of Missouri-Columbia	87mci
0.23	docking performed with smina static binary available at https//sourceforge.net/projects/smina/files/ with default scoring function, then rescoring performed using gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina and the default cnn scoring model, conformer generation performed with rdkit via https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	vshma
0.23	docking performed with gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina, conformer generation performed with rdkit via https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	7bi2k
p38-α
0.49	smina feb 28 2016, based on autodock vina 1.1.2 openbabel 2.3.2 pymol 1.8.4.2 python 2.7.11 matplotlib 1.5.1 scipy 0.17.0 click 6.6	B. Wingert/C. Camacho	University of Pittsburgh	5dbkc
0.43	molsoft icm 3.8–6	P. Lam/M. Totrov	Molsoft	8b6kk
0.26	amber11	X. Zou/X. Zou	University of Missouri-Columbia	vkpk7
TIE2
1.0	rhodium 380e9–x9/openbabel 2.3.90 / pymol 1.3	J. Bohmann/Medicinal and Process Chemistry	Southwest Research Institute	mey8v
0.78	docking performed with smina static binary available at https//sourceforge.net/projects/smina/files/ with default scoring function, then rescoring performed using gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina and the default cnn affinity model, conformer generation performed with rdkit via https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.	J. Sunseri/D. Koes	University of Pittsburgh	xpmn7
0.78	itscore2	X. Zou/X. Zou	University of Missouri-Columbia	fn2qt
VEGFR2
0.53	docking performed with smina static binary available at https//sourceforge.net/projects/smina/files/ with default scoring function, then rescoring performed using gnina commit b3fa6ae13fc6b42924f49b2d751d68f1bc14bc08 available from https//github.com/gnina/gnina and the default cnn scoring model, conformer generation performed with rdkit via	J. Sunseri/D. Koes	University of Pittsburgh	8civr
	https//github.com/dkoes/rdkit-scripts/rdconf.py, ensemble of receptors chosen via pocketome.
0.48	ri-score/tdl-bp/autodock vina	D. Nguyen/W. Guo-Wei	Michigan State University	rtv8m
0.48	ri-score/tdl-bp/autodock vina	D. Nguyen/W. Guo-Wei	Michigan State University	qikvs

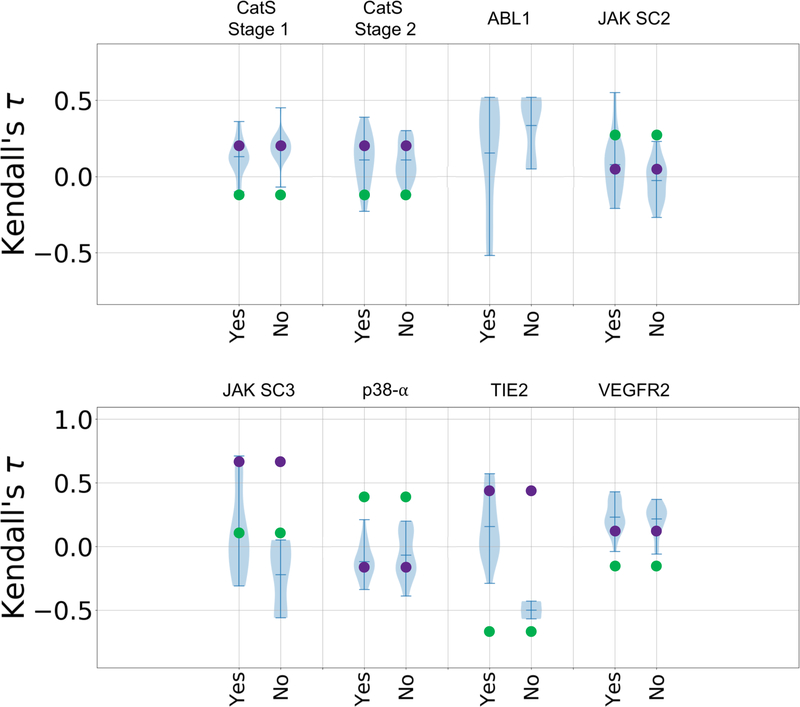
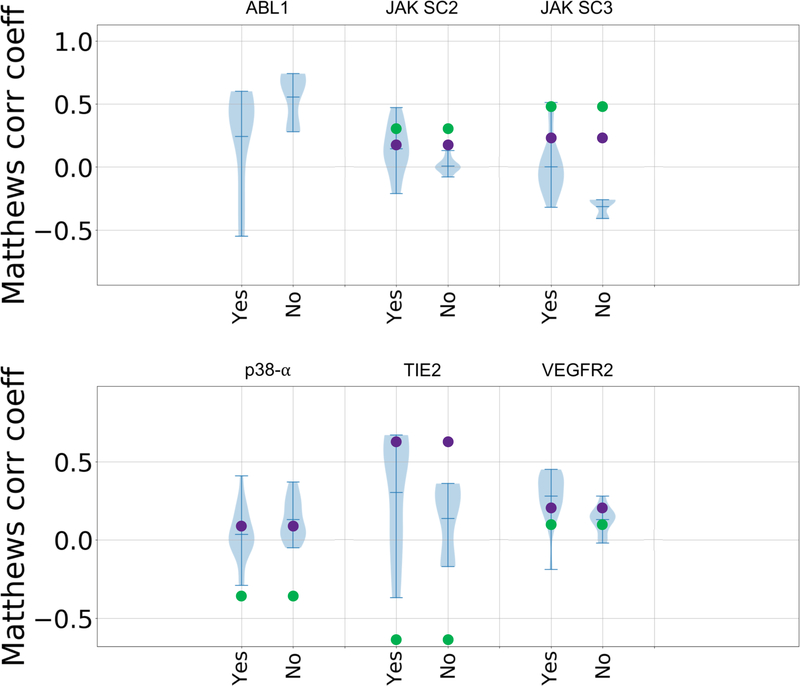
In GC3, we also observed increased use of machine- and deep-learning methods. These methods spanned conventional machine-learning methods, topology-based machine-learning, convolutional neural networks, and methods that combine physics-based and machine-learning models. However, based on the violin plots it is not clear that such methods performed better overall than methods using alternative approaches, as machine-learning methods appear in the top and bottom tails of the distribution (Figures 7 and 8). Both types of approaches, provided similar overall performance for all targets, with the exception of TIE2, for which all but three submissions used machine-learning (Figures 7 and 8).

Figure 7.

Violin plots of Kendall’s τ ranking correlation coefficients between predicted rankings and experimental rankings for submissions that use machine learning (“yes”) and those that do not (“no”) in each target dataset: CatS dataset in Stages 1 and 2, ABL1, JAK2 SC2, JAK2 SC3, p38-a, TIE2, and VEGFR2. Mean, minimum, and maximum Kendall’s τs for each target are shown by whiskers. Null models based on clogP and molecular weight are shown in green and purple, respectively. Null models were not calculated for the ABL1 target, since this subchallenge only contains two ligands.

Figure 8.

Violin plots of Matthews correlation coefficients between predicted classifications and experimental K_d classifications of active and inactive compounds for submissions that use machine learning and those that don’t in each target dataset: ABL1, JAK2 SC2, JAK2 SC3, p38-a, TIE2, and VEGFR2. Mean, minimum, and maximum Matthews correlation coefficients for each target are shown by whiskers. Null models based on clogP and molecular weight are shown in green and purple, respectively. Null models were not calculated for the ABL1 target, since this subchallenge only contains two ligands.

3.5.3. Relationship between affinity ranking accuracy and pose prediction

We used the CatS subchallenges to examine whether knowledge of the crystallographic poses of the ligands to be ranked would improve affinity rankings. Thus, we evaluated the Stage 1 and Stage 2 Kendall’s τ statistics for the 18 CatS ligands for which affinity data were available and crystallographic poses were released between the two stages. (CatS 1 to CatS 24, excluding CatS 7, 9, 11, 14, 19, and 21) (Supplementary Table 11). Much as seen in prior Grand Challenges^10,11 and prior literature⁴⁴, Stage 2 affinity rankings were no more accurate overall than Stage 1, even though crystallographic poses had been revealed for every ligand (Fig. 6). However, Fig. 6 does show a slight increase in the top Kendall’s τ in Stage 2 relative to Stage 1. For example, the topology-based machine-learning methods from the group of Guo-Wei Wei⁴² yielded values of Kendall’s τ in Stage 2 of 0.15 – 0.56 (median 0.36; submissions 6jekk, ymv87, yf20t, sdrvf, pgrod, mht0p, and 5d0rq), compared with Stage 1 values of −0.11 – 0.21 (median 0.03; submissions (04kya, t3dbz, tq8gb, xyy85, m7oq4, and hn0qy) (Supplementary Table 8).

Figure 6.

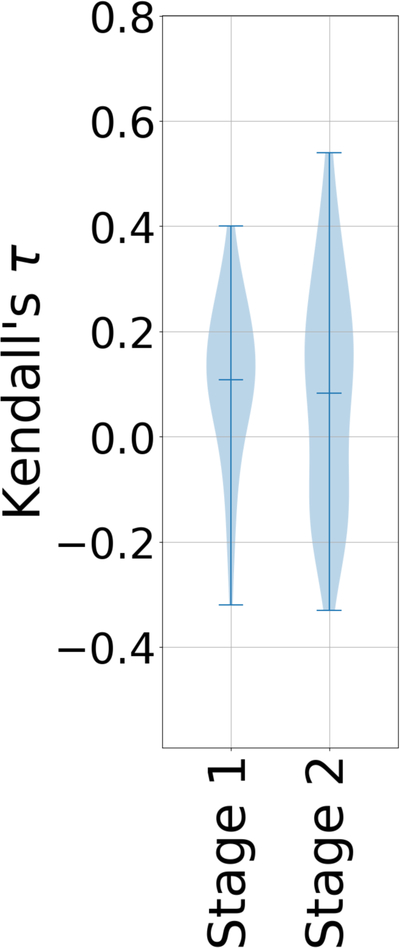
Violin plots of Kendall’s τ ranking correlation coefficients between predicted rankings and experimental IC50 rankings for the CatS dataset in Stages 1 and 2, using only the 18 ligands for which crystallographic poses had been provided in Stage 2 (CatS 1 to CatS 24, excluding CatS 7, 9, 11, 14, and 21). Mean, minimum, and maximum Kendall’s τs for each CatS stage are shown by whiskers.

3.5.4. Comparison of experimental high-throughput kinase screening data and computational predictions

As noted in the Methods section, the kinase K_d datasets were measured specifically for use in GC3. In choosing the measurements to be carried out, we referred to a much larger matrix of existing compound-kinase interaction data that had been obtained based on high throughput screening (HTS), single-concentration measurements of percent inhibition¹⁹. Such measurements are less reliable than K_d values derived from titration curves, and it is of interest to consider how their reliability compares with that of the computational methods used in this challenge. We, therefore, evaluated the correlation of the HTS percent inhibition data with the Kd data in terms of Kendall’s τ and the Matthews correlation coefficient (MCC) (Table 7) and compared these with the best results from the computational methods. For JAK2 SC3, p38-α, TIE2, and VEGFR2, the correlation coefficients for HTS versus K_d are ~0.8 (better than the computational results). However, the HTS results correlate poorly with K_d for ABL1 (τ 0.24, MCC −0.43), and here computational methods performed well relative to single shot experiments. However, it is possible that this outcome reflects in part the fact that ABL1 has a small ligand set, so good agreement with the measured Kd values could more readily occur by chance, given the variance of the computational methods. In addition, the calculations yield a Matthews correlation coefficient value of 0.49 for JAK2 SC2, which is close to the HTS result of 0.54.

4. DISCUSSION

This was the largest D3R GC to date in term of datasets, with six different protein targets and 5 subchallenges, and with a total of 465 prediction sets submitted by 28 research groups. It was encouraging to see the highest performance to date on affinity rankings, though it is not clear how much this improvement is due to methodological improvements and how much to the nature of the systems used in the challenge. For unknown reasons, only one submission used full free energy methods, in contrast with extensive use of this approach in prior challenges¹⁰. (GC3 included challenge components specifically designed for such methods.) We observed increased use of machine-learning methods married to structure-based modeling, though such methods did not, overall, perform better than those without machine learning.

New to GC3 was inclusion of an initial cross-docking challenge, which was then converted to a self-docking challenge for the same set of ligands and protein. On one hand, the general lack of improvement on going to self-docking was unexpected, since there is no longer uncertainty regarding the protein conformation corresponding with each ligand. On the other hand, it is perhaps encouraging that the cross-docking methods employed here approached self-docking accuracy. Other broad observations from GC3 largely reprise those of prior GCs. Thus, making full use of available structural data tended to improve the accuracy of pose prediction, and, in most cases, little to no improvement in ranking accuracy was obtained when protein-ligand crystal structures are provided. The difficulty of obtaining accurate rankings despite having what are arguably bona fide poses highlights the pressing need for improved scoring or energy functions.

Two new evaluation issues arose in this challenge. First, we suggest that the quality of a docking method be assessed not only in terms of its mean or median RMSD, but also through metrics that quantify the width of pose RMSD distributions, such as standard deviation. Thus, a method which yields a median RMSD of 1 Å but a maximum RMSD of 6 Å might be considered less desirable than one with a worse median RMSD of 2 Å but a lower maximum of 3.5 Å. Second, this is the first GC to assess ligand rankings for their ability to classify compounds as active versus inactive, via the Matthews correlation coefficient. Given that more effective identification of experimentally-verified hit compounds from large compound libraries is a prime application of docking and scoring methods, future blinded challenges designed specifically to test this capability could be of significant interest.

The present challenge also provides a unique comparison of computational accuracy with the accuracy of experimental high throughput screening data. Because we selected the kinase K_d measurements to be carried out based on available high throughput measurements, GC3 allowed a new comparison of computational methods with HTS. (It is remarkable that prior studies comparing HTS with docking and scoring have used different metrics, because they have focused on identification of active compounds within large, diverse libraries of putative inactives⁴⁵.) Although HTS data were generally more predictive of the K_d values, this was not universally true. For two datasets, the best computational methods did well relative to the HTS measurements. This encouraging observation lends support to the value of available computational methods and to the prospects for further improvement in modeling technologies.

5. Conclusions

1. Docking a ligand into a receptor conformation from a cocrystal structure determined with a similar ligand tended to improve docking accuracy.

2. Conversion of a cross-docking challenge into a self-docking challenge led to modest overall improvement in pose predictions, with some methods showing marked improvement.

3. The accuracy of the poses used in affinity rankings did not correlate well with the accuracy of the affinity predictions.

4. Docking results can be quite inconsistent, often generating skewed distributions of pose RMSDs with fat tails. Therefore, reporting both mean and median is informative, and it is of interest to explore ways of narrowing RMSD distributions.

5. It is not clear that machine-learning methods performed better overall than alternative approaches.

6. Although experimental HTS data were generally more predictive of K_d values than current computational methods, the best computational methods outperformed the HTS measurements for two of the datasets.

7. A given docking algorithm can yield a wide range of accuracies, depending on how it is used.