A Revised Look at Relativistic Electrons in the Earth's Inner Radiation Zone and Slot Region

Abstract

We describe a new, more accurate procedure for estimating and removing inner zone background contamination from Van Allen Probes Magnetic Electron Ion Spectrometer (MagEIS) radiation belt measurements. This new procedure is based on the underlying assumption that the primary source of background contamination in the electron measurements at L shells less than three, energetic inner belt protons, is relatively stable. Since a magnetic spectrometer can readily distinguish between foreground electrons and background signals, we are able to exploit the proton stability to construct a model of the background contamination in each MagEIS detector by only considering times when the measurements are known to be background dominated. We demonstrate, for relativistic electron measurements in the inner zone, that the new technique is a significant improvement upon the routine background corrections that are used in the standard MagEIS data processing, which can “overcorrect” and therefore remove real (but small) electron fluxes. As an example, we show that the previously reported 1‐MeV injection into the inner zone that occurred in June of 2015 was distributed more broadly in L and persisted in the inner zone longer than suggested by previous estimates. Such differences can have important implications for both scientific studies and spacecraft engineering applications that make use of MagEIS electron data in the inner zone at relativistic energies. We compare these new results with prior work and present more recent observations that also show a 1‐MeV electron injection into the inner zone following the September 2017 interplanetary shock passage.

Key Points

• A new background correction algorithm for relativistic inner zone electrons is developed

• We find important differences versus the standard algorithm, with several new/clarified features revealed

• Data from the new algorithm should be used for quantitative inner zone studies at energies >0.7 MeV

1. Introduction

Obtaining accurate charged particle measurements in the Earth's inner radiation zone (L values $\lesssim 2.5$) is a challenging task, as space‐borne particle detectors suffer from background contamination in this region of geospace. Energetic inner belt protons (approximately tens to hundreds of megaelectron volts [MeV]) are often the source of this contamination, as they are energetic enough to penetrate thick layers of instrument shielding and can register as valid counts in the detector system. This leads to ambiguities and uncertainties regarding inner zone particle measurements and their interpretation, particularly when foreground signals are low relative to the large background signals. In addition to their scientific necessity, accurate inner radiation belt particle measurements are also important for informing empirical models of the space radiation environment, such as the AE9 model (Ginet et al., 2013; Johnston et al., 2015; O'Brien et al., 2018). These models are used in spacecraft and mission design to mitigate the potential hazards that these particles pose to Earth‐orbiting spacecraft and their subsystems (e.g., spacecraft charging and total radiation dose). Inaccuracies in the empirical models can lead to uncertainties in the design margins, unnecessarily driving up development costs.

NASA's Van Allen Probes mission is equipped with instrumentation designed to overcome these observational challenges, and the high‐quality measurements have transformed and refined our understanding of the particle dynamics in the inner zone and slot region. For example, a series of studies (Claudepierre et al., 2015, 2017; Fennell et al., 2015) used background‐corrected measurements from the Magnetic Electron Ion Spectrometer (MagEIS) on the Van Allen Probes to firmly establish the transient nature of the most energetic electrons (∼1 MeV) observed in the Earth's inner radiation zone. Electrons at these energies can be injected into the inner zone following the passage of strong interplanetary shocks. In the absence of subsequent shock injections into the inner zone, these electrons remain stably trapped and decay slowly over long timescales, on the order of 1 year. Interestingly, electrons with kinetic energies $\gtrsim$1.6 MeV have not been observed in the inner zone during the Van Allen Probes era (2012–present), above instrument detection limits (Claudepierre et al., 2017; Li et al., 2015). At lower radiation belt energies (hundreds of kiloelectron volts [keV]), several Van Allen Probes studies have revealed unexpected features in inner zone electron observations, including the preponderance of 90° ‐minimum pitch angle distributions (Zhao et al., 2014), rapid flux enhancements (Turner et al., 2017), and the prevalence of regular, highly structured features in the energy spectra (Ukhorskiy et al., 2014).

These advances in our knowledge of the electron dynamics in the inner zone and slot region, enabled by the Van Allen Probes, have spurred on and motivated new avenues of research, with a particular emphasis on the electric field in the inner zone and how it organizes the particles (Lejosne & Mozer, 2016, 2018; Selesnick et al., 2016; Su et al., 2016), and inner belt modeling capabilities (Cunningham et al., 2018; O'Brien et al., 2016; Ripoll et al., 2017). The advances made at relativistic energies have prompted other researchers to revisit historical inner zone data sets to better understand the intricacies of these earlier measurements (e.g., Boscher et al., 2018; Selesnick, 2015). In many of the aforementioned studies, the physical processes that govern the observed electron dynamics have yet to be uniquely and conclusively identified (e.g., Lejosne & Roederer, 2016; Liu et al., 2016; Sauvaud et al., 2013).

The purpose of this paper is to revisit the series of studies noted above documenting the ∼1‐MeV electron injections into the inner zone observed during the Van Allen Probes era. One of the primary findings of Claudepierre et al. (2017) was that the background correction algorithm used to reveal the newly formed inner belt also removed valid foreground counts at these energies, an undesirable but necessary consequence of the algorithm design. Additional context data (MagEIS “histogram” data) were presented that suggested that the newly formed ∼1‐MeV inner belt was in fact distributed more broadly in L shell and persisted longer than suggested by the background‐corrected flux measurements. However, the extent of these differences could not be fully quantified at that time. In the following, we describe a new, specialized background correction algorithm that is designed to more accurately resolve this inner zone foreground signal at relativistic energies. This new algorithm is necessary because at higher energies, the MagEIS energy channel passbands are relatively wide, which can cause the assumption of a straight‐line background interpolation across the passband to breakdown. We emphasize that the background‐corrected flux variables in the standard MagEIS data files allow analysis with a high degree of confidence that the reported fluxes are free of background contamination but may not reflect the optimal balance between background insensitivity and foreground sensitivity.

The remainder of this paper is organized as follows. In section 2, we describe the data set and the specialized background correction algorithm, with additional details given in Appendix A. Section 3 presents the results using the new algorithm, revisiting and comparing with earlier work. Finally, we offer summarizing and concluding remarks in section 4.

2. Data and Methods

The data used throughout this work are from the MagEIS instrument suite (Blake et al., 2013; Spence et al., 2013) on NASA's Van Allen Probes spacecraft (Mauk et al., 2013). The two Van Allen Probes (Probe A and Probe B) orbit the Earth with a period of ∼9 hr in highly elliptical trajectories, taking them through apogee at roughly 5.8 R _E geocentric and perigee near 700‐km altitude. The spacecraft traverse the radiation belt region five to six times per day, usually within ±10° of the magnetic equatorial plane. The MagEIS spectrometers measure electrons throughout this orbit over a wide energy range (30 keV ‐ 4 MeV), with high energy resolution (ΔE/E≈30%), and high angular resolution (≤10° in pitch angle). Each probe carries four MagEIS electron spectrometers, which we refer to as the “LOW, MED35, MED75, and HIGH” units, distinguished by their energy coverage: LOW ∼30–200 keV, MED35/MED75 ∼200–1,000 keV, and HIGH ∼1–4 MeV. As the MED35 unit is redundant in energy with the MED75 unit and is oriented in a different direction from that of the other three units, it is not typically included in the standard MagEIS data products and is not considered further here.

Figure 1 presents MagEIS electron fluxes in six energy channels that span nearly the entire range of the MagEIS suite: two channels from the LOW unit (32 and 102 keV), two from the MED75 or “M75” unit (350 and 600 keV), and two from the HIGH unit (1.01 and 2.60 MeV). These data are from Van Allen Probe B, which is the probe that is used throughout this study. Contextual solar wind speed and D _st data are also shown. The electron fluxes are plotted in L versus time format, where the McIlwain L parameter is calculated from the Olson and Pfitzer (1977) quiet magnetic field model (used throughout). The data are extracted near the magnetic equator when B/B _eq ≤ 1.1, where B/B _eq is the ratio of the magnetic field strength at the spacecraft to that at the magnetic equator (both obtained from the model). The fluxes are averaged around 90° local pitch angle (α _L = [80,100]°) which, for this B/B _eq range, corresponds to equatorial pitch angles between 70° and 110°. This is the pitch angle and B/B _eq range that will be considered throughout this work. The MagEIS fluxes in Figure 1 are background corrected, and the new correction algorithm that is the subject of the present work has been used at low L (L ≤ 3) on the two highest energy channels shown. We note that the new correction algorithm is only utilized at low L (L ≤ 3) on the highest‐energy MagEIS channels (∼0.7–4.0 MeV), the reasons for which will be discussed in the subsequent sections. Finally, note that as energy increases, electron injections through the slot and into the inner zone become less frequent (Reeves et al., 2016; Turner et al., 2017).

Figure 1.

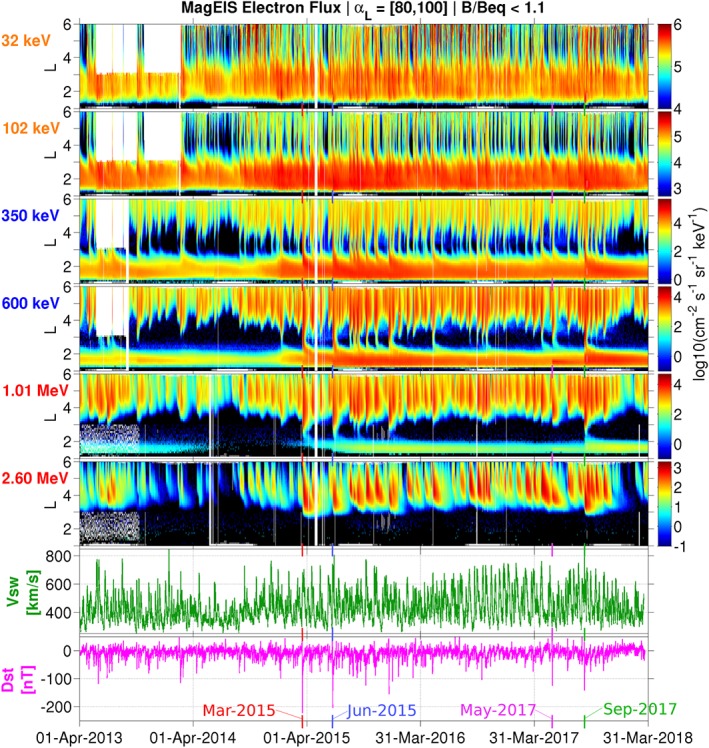
An overview of MagEIS electron flux measurements for the time interval under investigation. Six MagEIS energy channels are shown, ranging from 32 keV to 2.6 MeV, from the LOW (orange labels), M75 (blue labels), and HIGH units (red labels). Daily averaged solar wind speed (V _SW) and D _st data are shown for context. The daily averaged MagEIS fluxes have been corrected for background contamination, with the alternative correction algorithm (see text) used for L≤ 3 on the two highest energy channels shown (1.01 and 2.60 MeV). The long data gaps early in the time interval at L≥ 3 are due to the unavailability of MagEIS histogram data, which are required for the background corrections. MagEIS = Magnetic Electron Ion Spectrometer.

2.1. Alternative Background Correction: Overview

The new background correction technique makes use of the fact that the energetic inner proton belt (energies  $\gtrsim$ 100 MeV) is relatively stable over long timescales, on the order of months to years. For example, Van Allen Probes observations show that 100‐MeV proton fluxes are stable to within a factor of ∼2 in the heart of the inner belt (L = [1.3, 2.4]) over the course of the mission to date (see supporting information). Thus, we expect that the background contamination produced by these inner belt protons remains stable over these same timescales. We exploit the stability of these particles to produce an estimate of the background contamination due to inner belt protons in each MagEIS detector or energy‐“pixel.” Specifically, we construct a model of the background contamination in each pixel by binning the MagEIS pulse‐height data in time and L, when the measurements are known to be background dominated. In what follows, we refer to the background‐corrected flux obtained from the new algorithm as the “alternative” background‐corrected flux, to distinguish it from the “standard” background corrected flux that is part of the routine MagEIS data processing and data products. We note that the standard background‐corrected flux is what was used in the inner zone studies of Fennell et al. (2015) and Claudepierre et al. (2017).

As a brief aside, we note that there are additional potential sources of background contamination from more transient particle populations in the inner magnetosphere. For example, lower‐energy inner belt protons (∼10–50 MeV) are more dynamic than their higher‐energy counterparts, particularly at the outer edge of the inner zone, L = 2–3. However, these protons are mostly shielded out by the MagEIS instrument and do not contribute as significantly to the background response as the higher‐energy protons. In addition, solar proton events can produce transient changes in the energetic proton environment at Earth and thus constitute a transient source of background contamination. However, there have been very few intense proton events during the Van Allen Probes era, and none that have resulted in energetic proton ( $\gtrsim$ 100 MeV) enhancements at L ≤ 3. Another transient source of background contamination in the MagEIS instrument comes from bremsstrahlung‐producing ultrarelativistic electrons, but such particles are not observed below L≈2.8 during the Van Allen Probes era (Baker et al., 2014; Li et al., 2015). Thus, for the purposes of the present study, we assume that the primary source of background contamination at L ≤ 3 is the relatively stable energetic inner proton belt.

Figure 2 shows MagEIS histogram data, the count rate registered on each MagEIS pixel in each pulse‐height analyzer (PHA) channel. To meet telemetry constraints, the 256 PHA channels are downsampled via onboard lookup tables into 64 histogram channels, with the downsampling typically done using a 2‐1 mapping (i.e., two PHA channels combine into one histogram channel) across the range of PHA channels that encompass each pixel's nominal energy response. In Figure 2, the count rates are plotted versus histogram channel number, which is converted to energy deposits in keV. The histogram data are available as a complementary data product to the standard “main channel” data, which are obtained by summing the PHA data across the main channel passband, before the downsampling into the histogram data. The histogram data thus provide a much higher energy resolution than the main channel data, typically with ∼10 histogram channels in the main channel passband, that is, roughly an order of magnitude in ΔE/E. The details of the histogram data and the MagEIS measurement technique in general can be found in Blake et al. (2013) and Claudepierre et al. (2015, 2017).

Figure 2.

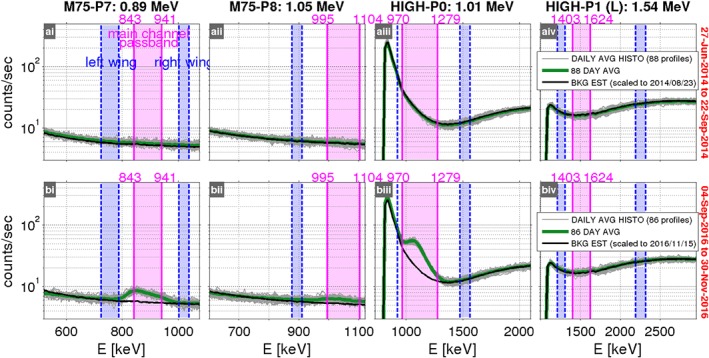
Magnetic Electron Ion Spectrometer histogram data from the four pixels that span the energy range 0.89 to 1.54 MeV, illustrating the alternative background correction technique. In each panel, the gray traces are daily averaged histogram count rates plotted versus energy in the inner zone (L = [1.5, 1.6]), near the magnetic equator (B/B _eq ≤ 1.1), and centered on 90° local pitch angle (α = [80, 100]°). Each green trace is the average of the ∼90 gray traces. The assumed background due to inner belt proton contamination in each pixel is shown as the black trace, which is the green trace from row a, scaled to match a particular gray trace at the right wing. The histogram data are compared for two ∼90‐day time intervals: when there are no foreground electrons detectable above background (row a) and when there are foreground electrons detectable above background (row b). In the latter case, a peak appears within the main channel passband (highlighted in magenta), as in panels bi–biii. Valid foreground electrons can only appear in the magenta passband. Note that in a given pixel in row a, the gray traces do not vary significantly around the black trace, indicating that the assumed backgrounds are stable over these timescales.

Figure 2 illustrates the concept behind the alternative background correction technique. Each panel shows MagEIS histogram data extracted between L = [1.5,1.6] near the magnetic equator (B/B _eq ≤ 1.1) and centered on 90° local pitch angle (α = [80,100]°). Each column displays histogram data from the indicated MagEIS unit (M75 or HIGH) and pixel (P7 and P8 from M75; P0 and P1 from HIGH). The centroid of the main channel passband for a given pixel is indicated above each column, in MeV (passband response highlighted in magenta). We note that valid foreground electrons can only appear in the magenta passband. Row a shows data taken during a 3‐month interval when there were no foreground MeV electrons observed in the inner zone above the background levels, 27 June 2014 through 22 September 2014. Row b shows data taken during a subsequent 3‐month interval when foreground MeV electrons were observed in the inner zone above background, 4 September 2016 through 30 November 2016 (Claudepierre et al., 2017). In each panel, the gray traces are daily averaged histogram count rates in the L, α, and B/B _eq range noted above, so that there are ∼90 gray traces in each panel. In both rows, the energetic inner belt protons produce substantial backgrounds in each pixel, influencing the shape of the histogram profiles. We note that histogram profiles from M75‐P6, HIGH‐P2, and HIGH‐P3 are not shown in Figure 2 but are provided in the supporting information.

We now describe the mechanics of the new algorithm by focusing on the 0.89‐MeV energy channel in Figure 2 (panels ai and bi). The procedure is essentially the same for all other energy channels under consideration. We begin by noting that foreground electrons are not observed in this L, α, and B/B _eq range over the first ∼90‐day interval, as there is no appreciable peak within the main channel passband (panel ai). In addition, we see that there is very little variability in the ∼90 gray traces, indicating that the background contamination in this pixel is relatively stable and varies by less than a factor of 2 over this ∼90‐day interval (i.e., the spread in the gray traces). Thus, we calculate an estimate of the expected background profile for this pixel in this L, α, and B/B _eq range by averaging the ∼90 gray traces to produce the green trace. We assume that this is the background profile for this pixel in this L, α, and B/B _eq range for all times, with slight modifications that are described in Appendix A.

With the background estimate obtained (panel ai, green), the background correction is then performed on each individual daily profile (gray) by comparing the background estimate with the daily profile. To account for the slight variability in the day‐to‐day background levels, the background estimate is first scaled to match the daily profile's average value in the right wing before the correction is made (the location of the right wing is indicated by a shaded blue box). This scaling of the background estimate is shown in black, scaled to the individual daily gray trace on 23 August 2014 in row a and to 15 November 2016 in row b (these 2 days are chosen arbitrarily, for illustration). We note that the scaling is done using the right wing rather than the left wing, because the right wing contains almost exclusively background signal. When there is foreground signal, the left wing count rate is a combination of both background and backscatter (Claudepierre et al., 2015) so that if the scaling is done with the left wing, valid foreground signal will also be removed.

We now estimate the background counts within the main channel passband by summing the black trace over the passband, using the accumulation time interval to convert histogram count rates back to counts. Similarly, we estimate the foreground counts in the channel passband by summing an individual gray trace over the channel passband. When the summed foreground counts in the channel passband are greater than the summed background counts, we subtract the two to produce the background‐corrected counts. When the summed foreground counts are less than the estimated background counts, we set the counts to 0. We emphasize that the background estimates are obtained from times when there are no peaks within the main channel passband (row a) and then used as the background estimate for other times when there may be peaks in the passband (row b); for example, compare panels ai and bi, where the black trace is the same apart from a scaling factor.

The entire procedure described yields background‐corrected counts for the indicated α and B/B _eq range, on a time cadence of one day in a given L bin. We then convert these counts to flux via the usual flux conversion factors. The process is repeated in 0.1L‐width bins for all L between L = 1 and 3, and all energies ≥700 keV, to produce the alternative background‐corrected flux. We note that the alternative correction is only performed on the seven highest‐energy MagEIS pixels: the last three pixels on M75 (P6–P8; ∼0.7–1.0 MeV), and all four pixels on HIGH (P0–P3; ∼1.0–4.0 MeV). The reason for correcting only these high‐energy pixels and only in the L = [1,3] range is essentially that a foreground‐free time interval must be identified in order to construct the background estimate, which is only possible at higher energies in the inner zone. This is described in greater detail in Appendix A. We note that in the analysis that follows for energies ≥700 keV, the alternative‐corrected data are a combined data product: Above L = 3, they are the standard background‐corrected data, while below L = 3, the alternative algorithm is used.

3. Results

3.1. Comparison at 0.74 MeV

We now present the results from the new, alternative algorithm, using a sequence of figures that are all in the same format as Figure 3. Here we compare the uncorrected fluxes (top), the standard background‐corrected fluxes (middle), and those obtained from the alternative correction algorithm (bottom). Henceforth, we will refer to the three types of data as the “UNCORR, CORR‐STD, and CORR‐ALT,” for the uncorrected, standard background‐corrected, and alternative background‐corrected data, respectively. The displayed data are from pixel 6 on M75, which has an energy passband of 0.70–0.79 MeV and a centroid energy of 0.74 MeV (all passbands and centroids are given in the supporting information). The data gap (white) at L ≥ 3 early in the time interval for both types of corrected data is due to the operation of the unit in a special high angular resolution mode that is mutually exclusive with the histogram mode. The patchy nature of the CORR‐ALT data at L ≤ 3 early in the time interval is due to the coarse histogram sampling parameters that were used at this time (low time and low angular resolution—see Appendix A). Four geomagnetic storm intervals are marked in the figure: March 2015 (max(|D _st|) ≈ 225 nT), June 2015 (≈200 nT), May 2017 (≈125 nT), and September 2017 (≈125 nT).

Figure 3.

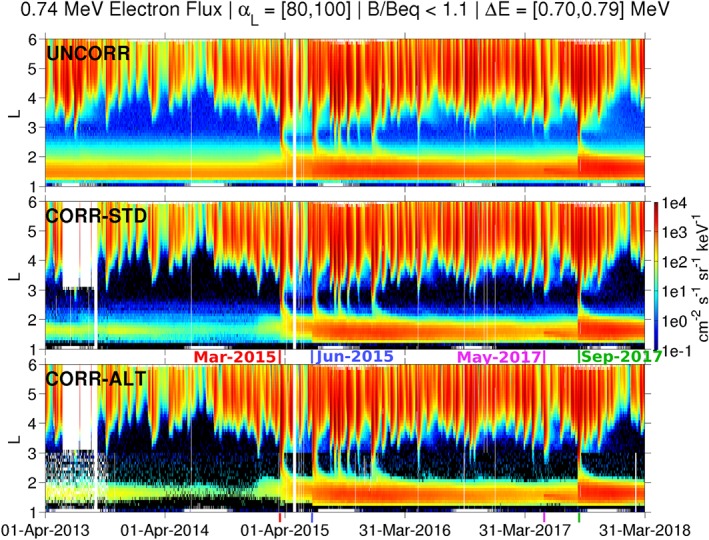
Electron flux at 0.74 MeV (M75 unit, pixel 6). Three levels of refinement of the data are shown: raw, uncorrected flux (UNCORR), background‐corrected fluxes using the standard algorithm (CORR‐STD), and fluxes corrected with the alternative algorithm (CORR‐ALT), the subject of this work. Note that the alternative correction algorithm is only used for L≤ 3; above L = 3 the standard algorithm is used, so that the CORR‐ALT data are the same as the CORR‐STD here. Below L = 3, we see that when the fluxes are low, the inner belt is more cleanly resolved with the alternative algorithm (e.g., in 2014), as compared to the standard algorithm. When the inner zone fluxes are high (e.g., in 2016), the standard and alternative algorithm reproduce similar intensity levels at this energy. We emphasize that the standard correction algorithm (CORR‐STD) has been used in all previous inner zone studies using MagEIS data (e.g., Claudepierre et al., 2015, 2017; Fennell et al., 2015).

Several interesting features are readily apparent in Figure 3. First, it is clear that early in the time interval, prior to 2015, the inner zone flux appears very stable in the uncorrected data, whereas the corrected data (CORR‐STD or CORR‐ALT) show that the flux is in fact steadily decaying. Thus, the background levels due to inner proton belt contamination are high relative to the low foreground flux during these early times (pre‐2015) and mask the true belt dynamics. Second, in the corrected data (CORR‐STD or CORR‐ALT), we see that beginning in early 2015, there are several enhancements of the inner electron belt during geomagnetically active times. The inner belt is progressively built up throughout 2015 by a series of deep injections and then begins to slowly decay once the injection activity subsides. Third, in the corrected data (CORR‐STD or CORR‐ALT), we note an apparent sporadic enhancement in the inner zone in May 2017, seemingly unaccompanied by any injection through the slot. This is discussed in greater detail below. Finally, we note that the strongest inner zone enhancement over the entire 5‐year interval occurs following the September 2017 event.

Overall, the agreement between the CORR‐STD data and the CORR‐ALT data at L ≤ 3 is quite good at this energy, lending confidence to the alternative algorithm. Again, we emphasize that above L = 3 the CORR‐ALT and the CORR‐STD fluxes are the same, by design. However, some differences between the two are worth noting. In particular, there is a clear discontinuity in the CORR‐ALT fluxes at L = 3, where the algorithm switches from the standard to the alternative technique. When the fluxes are low near L = 3, for example, during 2014, this discontinuity is essentially the different background flux levels in the two correction algorithms. The low‐flux/background discontinuity can also be seen more prominently in mid‐2015, where the color changes abruptly from a light blue above L = 3, to black below L = 3. Here above L = 3, there is remnant background contamination from bremsstrahlung (due to outer belt electrons) that is not completely removed by the standard algorithm, while below L = 3, the alternative correction algorithm entirely removes this contamination. (We note that the alternative algorithm is not designed to remove transient bremsstrahlung contamination but does so because it removes any background that has a consistent, relatively flat shape across the passband). In spite of these discontinuities when the foregrounds are low, we emphasize the numerous examples of high foreground fluxes that are continuous across the L = 3 boundary, when injections penetrate through the slot to very low L (particularly clear during 2015). The important point is that when significant foreground flux spans the artificial L = 3 boundary between the two algorithms, the CORR‐ALT fluxes show no discontinuities. This has been confirmed in detail for many injections on a case‐by‐case basis (not shown here). Thus, the discontinuity at L = 3 only arises when comparing the background levels between the CORR‐ALT algorithm and the CORR‐STD algorithm. Neither flux level has any true geophysical meaning and both are artifacts of the measurement technique and the two algorithms. Finally, we also note that between L = 2 and 2.5, the CORR‐STD fluxes have a low level of contamination from inner belt protons that is not completely removed by the standard algorithm (discussed in greater detail in Claudepierre et al., 2015), while this contamination is nearly entirely removed in the CORR‐ALT fluxes.

3.2. Comparison at 0.89 MeV

We now proceed to the next highest energy channel from M75, the 0.89‐MeV channel (pixel 7). Figure 4 displays the data in the same format as Figure 3 and many of the same features noted above are seen here as well. As at 0.74 MeV in Figure 3, there is remnant inner belt contamination in the CORR‐STD fluxes between L = 2 and 2.5, which is significantly cleaned up in the CORR‐ALT fluxes. More importantly, at this energy there are more significant differences between the CORR‐STD and the CORR‐ALT fluxes in the heart of the inner zone. In the CORR‐ALT data, we see that a new inner electron belt begins to form near L = 2 following the March 2015 event, while in the CORR‐STD data it is difficult to say conclusively whether any electrons are actually trapped here, due to the preexisting band of contamination at this L. There is also evidence of slow earthward transport of this newly injected population, as the CORR‐ALT fluxes slowly penetrate to lower L values as time progresses from March 2015. Subsequently, the CORR‐ALT data show that the June 2015 event further enhances the heart of the inner belt, after which the entire belt slowly decays. Finally, we see a rapid enhancement of the entire L ≤ 3 region following the September 2017 event, where the electrons in the slot decay rapidly, leaving a new population of stably trapped electrons in the inner zone. Note that nearly all of these dynamical features are obscured by inner proton belt contamination in the UNCORR data.

Figure 4.

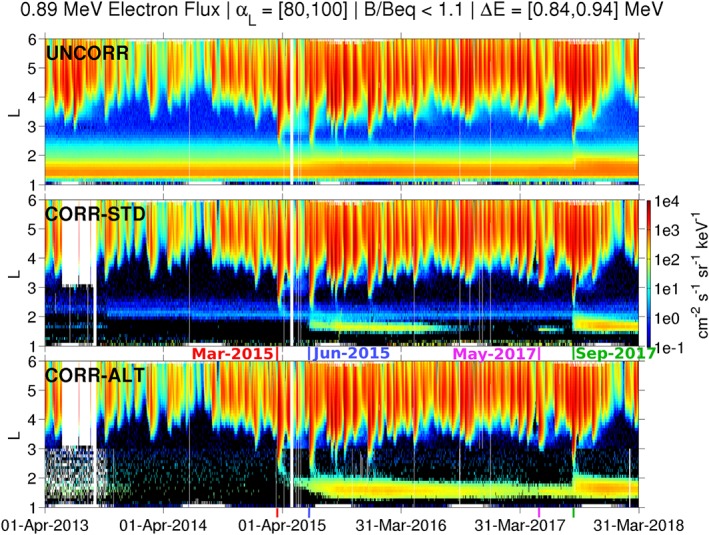
Same format as Figure 3 but for 0.89‐MeV electrons from pixel 7 on the M75 unit (M75‐P7). Note the much cleaner data in the inner zone with the alternative technique (CORR‐ALT).

In Figure 4, in both the CORR‐STD and CORR‐ALT fluxes, we again see a peculiar, apparent electron enhancement near L = 1.5 in May 2017, which was also noted above at 0.74 MeV. This enhancement appears to occur without any observable electron transport through the slot region. We briefly consider several possible explanations for this. First, it is possible, though unlikely, that the inner proton belt that produces background contamination is enhanced at this time and in this specific location. We have discounted this possibility by examining the inner belt proton data from both the Relativistic Electron Proton Telescope (Baker et al., 2013) and the Relativistic Proton Spectrometer (Mazur et al., 2013) on Van Allen Probes, and we find no evidence of any inner proton belt enhancement at this time (see supporting information). Furthermore, we have also examined MagEIS histogram data in the inner zone at this time and find that a histogram peak is clearly observed in the main channel passband without any appreciable change in the background levels in the left and right wings (not shown here). This strongly suggests that the observed electron enhancement near L = 1.5 in May 2017 is due to real, foreground electrons, and not due to background contamination. This then invites the question: Why is there no electron transport observed across the slot region at this time? One possibility is that the “missing flux” that should be observed across the slot region in May 2017 is somehow removed by the correction algorithm(s). Here we simply note that there is no evidence even in the UNCORR fluxes of any low intensity foreground signal through the slot, so that the absence of flux in the slot region at this time cannot be due to the background removal process.

This leaves at least two possible explanations regarding the apparent local flux enhancement near L = 1.5: Either the slot‐region fluxes are unobservable at this time due to some combination of instrumental and/or orbital effects, or it results from an adiabatic energization through first‐invariant‐conserving radial transport. For the latter, we note that electrons can double their energy over very short distances in the slot/inner zone (e.g., from L = 2.25 to L = 1.75) due to the steep magnetic field gradient (e.g., Su et al., 2016). This could readily produce a localized flux increase at ∼1 MeV as a result of deep injections at lower energy. For the former, were this an orbital/instrumental effect, it would mean that the flux intensity of the injection into the slot and down into the inner zone was very weak, below the detection capabilities of the instrument. We note that during other inner zone enhancements observed at this energy (e.g., June 2015 and September 2017), there is typically a “disconnect” between the flux intensity that penetrates into the slot and the resulting flux intensity in the inner zone (i.e., there is typically a local minimum in flux intensity in the slot region). The fact that the flux intensity is not continuous all the way into the inner zone in these events suggests that poor counting statistics and/or orbital effects might hinder the ability to measure the injection continuously, down through the slot into the inner zone. In fact, it may be the case that both adiabatic energization and orbital effects are playing a role here. Given that the profile of flux versus L for an event is made up of just a few traversals over a long time, it is plausible that the inward‐moving electrons are at such low intensity that they are not observable. This could thus produce the disconnect in L, as the fluxes at L∼1.5 are accumulated over many hours where their lifetimes are much longer, allowing a flux buildup. We also note that an in situ acceleration process could be operating in the inner zone that produces a localized increase in flux. We cannot conclusively support or refute this explanation at this time and a more in‐depth analysis is warranted. On the whole, though, the apparent local enhancement of the electron flux near L = 1.5 in May 2017 remains somewhat puzzling and we leave it for future investigation.

3.3. Comparison at 1.01 MeV

We now proceed to the next highest energy channel from HIGH, the 1.01‐MeV channel (pixel 0). Figure 5 displays the data in the same format as the previous two figures. We note that M75‐P8, which nominally measures the same energy electrons as HIGH‐P0, is omitted from the analysis due to its low sensitivity relative to HIGH‐P0 (see Appendix A). The analogous figure to Figure 5 for M75‐P8 is, however, provided in the supporting information.

Figure 5.

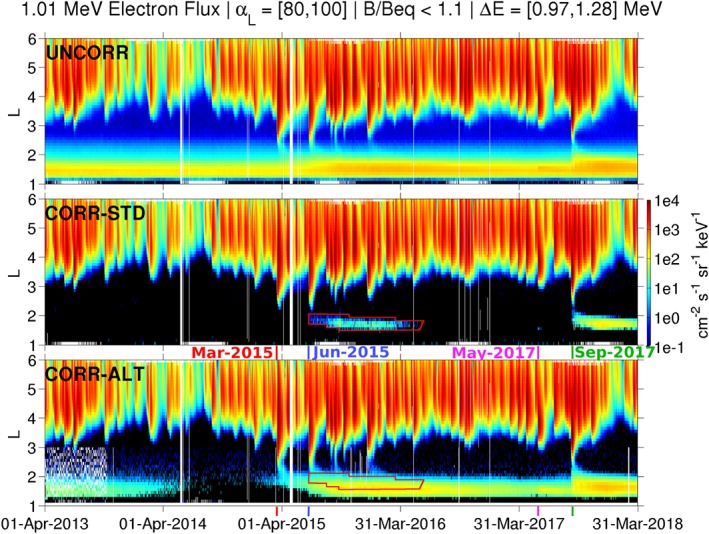
Same format as Figure 3 but for 1.01‐MeV electrons from pixel 0 on the HIGH unit (HIGH‐P0). We draw attention to the middle panel (CORR‐STD), where a newly formed inner belt appears following the June 2015 storm, as detailed in Claudepierre et al. (2017). The inner belt structure is highlighted with a red polygon, which is also shown for comparison in the bottom panel, where the alternative background correction algorithm is used in the inner zone. It is clear that the alternative correction algorithm is able to resolve the 1‐MeV inner electron belt with much greater accuracy than is obtained with the standard algorithm.

In Figure 5, we see many of the same features at 1.01 MeV that were noted at lower energies, such as the enhancement of the entire inner zone in 2015, the peculiar, local enhancement in May 2017, and a strong, isolated enhancement during the September 2017 event. And we again see significant differences between the CORR‐STD and CORR‐ALT data. For example, the newly formed inner belt that appears following the June 2015 storm, as detailed in Claudepierre et al. (2017), is highlighted with a red polygon in the middle panel. This same red polygon is shown for comparison in the bottom panel, where the alternative background correction algorithm is used in the inner zone. In the CORR‐ALT data, the new inner belt is observed to begin forming following the March 2015 event (and perhaps even slightly earlier) and not during the June 2015 event as suggested by the CORR‐STD data. A series of injections in 2015 then progressively enhances the inner belt, which slowly decays throughout 2016 and into 2017. Thus, the radial extent of the inner belt is significantly underestimated by the standard algorithm, and it is clear that the decay timescales are much longer in the CORR‐ALT data (compare bottom panel with the middle). Through a detailed examination of the histogram data, we have confirmed that the inner belt fluxes that are resolved with the CORR‐ALT algorithm, and not resolved in the CORR‐STD data, are valid foreground signals (this was in fact demonstrated in Claudepierre et al., 2017). We emphasize that many of the features noted using the CORR‐ALT data are not readily apparent in either the UNCORR data (top) or the CORR‐STD data (middle).

The significant differences between the CORR‐STD and CORR‐ALT data for HIGH‐P0 (Figure 5, middle and bottom) are in large part due to the histogram shapes that are produced by proton contamination in the inner zone and the impact that these shapes have on the correction algorithms. We note in Figure 2 that the background‐dominated histogram profiles for HIGH‐P0 have a shape that is considerably different from those for M75, with a local minimum in the profiles near the right edge of the passband (see also Appendix A). The standard correction algorithm attempts to fit a straight line across the channel passband, from the left wing to the right wing, and then to use this as the background contribution to the main channel passband. Thus, in the inner zone where the HIGH‐P0 histogram profiles exhibit a local minimum/concave‐up shape, valid foreground counts are only resolved in the standard algorithm when there are very large peaks in the passband that “overcome” the concavity, such as those that occur following the June 2015 and September 2017 events. Low‐intensity foreground signals are thus not well resolved in the standard algorithm, which leads to the underestimation of the CORR‐STD fluxes noted in Figure 5. The alternative correction algorithm does not suffer from this issue, since it uses the entire histogram profile as the assumed background level. In fact, the challenge of mitigating and circumventing this concavity issue in the HIGH unit was the motivation and driving force behind the design of the alternative correction algorithm. Note that M75 does not exhibit differences this significant between the CORR‐STD and CORR‐ALT data, due to the fact that the background‐dominated histogram profiles for M75 are typically monotonically decreasing, rather than concave up as for the HIGH unit (e.g., Figure 2). Thus, for M75 the standard correction algorithm, which uses straight line fits between the left and right wings, performs much better than it does for the HIGH unit in the inner zone.

Returning to Figure 5, there are several important points to be noted when comparing this, the first pixel on the HIGH unit, with the last few pixels on the M75 unit. For example, the CORR‐ALT data suggest that the inner zone is populated with ∼1‐MeV electrons at the beginning of the time interval. For a monotonically decreasing inner zone electron spectrum, one would expect there to be significant fluxes at 0.89 MeV at this time, but in Figure 4, it is not clear that there are. As discussed in greater detail in Appendix A, this is due to the much greater detector sensitivity of HIGH‐P0 when compared with M75 P6‐P8, where there is roughly an order of magnitude difference in geometry factor. Thus, the superior counting statistics on HIGH‐P0 means that the correction algorithm performs better for this pixel in the inner zone than for the similar‐energy pixels on M75. Accordingly, HIGH‐P0 is able to resolve the inner zone fluxes more cleanly, which is clear when comparing Figure 5 with the similar results from M75 (Figures 3 and 4). Also, when examining the UNCORR fluxes in Figure 5, it appears as though some of the inner zone background contamination is mitigated by the use of coincidence logic in the HIGH unit, as the foreground electrons injected at various times are more readily distinguishable from the background, when compared with the higher‐energy pixels on M75 that do not use coincidence. The sum of all of these effects means that the inner zone CORR‐ALT fluxes are more accurate for HIGH‐P0 than the similar‐energy pixels on M75.

3.4. Comparison at 1.54 MeV

As a final comparison of the UNCORR, CORR‐STD, and CORR‐ALT, in Figure 6 we present the 1.54‐MeV data from HIGH‐P1 (left channel). Left channel here refers to the fact that the channel passbands on the last three pixels on the HIGH unit, P1–P3, are each subdivided into two main channels, denoted “left (L)” and “right (R).” At 1.54 MeV, the CORR‐ALT data suggest that there are no foreground electrons observed in the inner zone above the background levels over the entire time interval under consideration. Any foreground electrons present in the inner zone at this energy must be of very low intensity, below the detection threshold limit set by the correction algorithm. There is faint, residual contamination in the CORR‐ALT data that is periodically observed in the inner zone throughout the interval, most clear in late 2015 and late 2016. This is likely an orbital/seasonal effect that is not entirely removed by the alternative algorithm. We have examined the histogram data in detail during these times and find no evidence of any foreground peaks within the main channel passband, thus confirming that this is indeed residual contamination. We also note a faint band of residual contamination in the CORR‐STD data near L = 2 (middle) that is removed in the CORR‐ALT data. On the whole, we conclude that the highest‐energy electrons observed by MagEIS in the inner zone during the Van Allen Probes era have kinetic energies $\lesssim$1 MeV (analogous plots at energies >1.54 MeV are provided in the supporting information).

Figure 6.

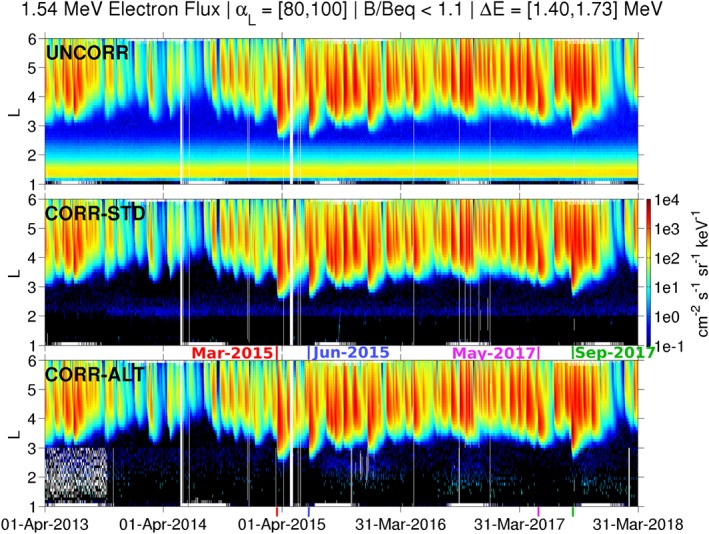
Same format as Figure 3 but for 1.54 MeV electrons (HIGH‐P1, left channel). Note that no foreground inner zone electrons are observed at this energy in the corrected data over the entire time interval displayed (the sporadic, low‐intensity signals are residual contamination). As shown in the supporting information, this is true up to ∼4 MeV, the measurement end point energy of the MagEIS suite. Thus, the highest‐energy electrons observed by MagEIS in the inner zone during the Van Allen Probes era to date are ∼1 MeV.

3.5. Comparison With Prior Results and AE9

Several recent studies have examined ∼1‐MeV electrons in the inner zone (Claudepierre et al., 2015, 2017; Fennell et al., 2015), all of which used MagEIS data from the standard correction algorithm. It is clear that these earlier works should be revisited in light what has been revealed above using the alternative correction algorithm in the inner zone.

Figure 7 shows flux‐versus‐energy spectra at L = 1.5 from the MagEIS CORR‐ALT data, averaged over two 7‐day intervals: A “quiet” interval when no MeV electrons are observed in the inner zone and an “active” interval when there are MeV electrons in the inner zone. We note that the use of quiet and active here refers to the absence/presence of MeV injection activity into the inner zone and not the usual meaning of geomagnetically quiet/active. The quiet spectrum is nearly identical to what was calculated using the standard correction algorithm in Fennell et al. (2015), and thus, the essential findings of that work remain valid when the inner zone is devoid of MeV electrons. On the other hand, during the active interval, we see that the fluxes are enhanced relative to the quiet interval by roughly a factor of 2 at the lower energy end and by roughly an order of magnitude at the higher‐energy end. Exponential fits to both MagEIS spectra are shown, with the fitting parameters indicated in the figure. The quiet spectrum has an e‐folding energy of ∼85 keV, while the active interval spectrum is slightly harder and rolls off more gradually, with an e‐folding energy of ∼120 keV. We note that at 1 MeV, the MagEIS active spectrum is a factor of 10 larger than the exponentially extrapolated value from the MagEIS quiet spectrum.

Figure 7.

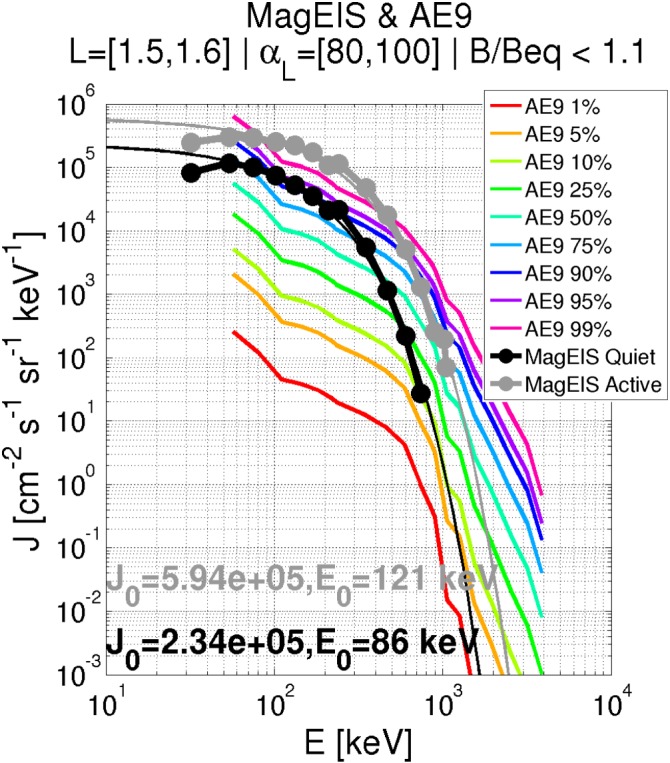
A comparison of MagEIS spectra with those obtained from V1.0 of the AE9 empirical model (Ginet et al., 2013). Two MagEIS spectra are shown, both computed with the alternative background correction algorithm: one averaged over a 7‐day “quiet” interval, when no MeV electrons are observed in the inner zone (black; 21 July 2014 to 28 July 2014) and another averaged over an “active” 7‐day interval when MeV electrons are observed in the inner zone (gray; 1 January 2016 to 8 January 2016). The MagEIS quiet spectrum is nearly identical to that presented in Fennell et al. (2015), and the same AE9 model data are shown for comparison, where the 50th percentile corresponds to the median. Exponential fits are made to the MagEIS spectra (thin black and gray traces), with the fitting parameters indicated in the figure. MagEIS = Magnetic Electron Ion Spectrometer.

Figure 7 also shows data from V1.0 of the AE9 empirical radiation belt model (Ginet et al., 2013), now known as the International Radiation Environment Near Earth (IRENE) model. The different percentiles shown represent the variability in the model fluxes and the 50th percentile corresponds to the median. These are the same AE9 profiles that were presented in Fennell et al. (2015). Thus, the conclusions reached in Fennell et al. (2015) regarding the AE9/MagEIS (quiet) comparisons remain valid: MagEIS fluxes are higher than AE9 at lower energies (<500 keV) and lower than AE9 at higher energies (>1 MeV). This holds true for the active spectrum as well, but here we see that the MagEIS fluxes below 500 keV are above AE9 99th percentile, suggesting that this variability is not captured by this version of the empirical model. The MagEIS spectral shapes are also dissimilar from those of AE9, with the AE9 model predicting much harder spectra. This could be due to proton contamination in the observations at higher energies in this version of the AE9 database, or differences in the inner belt electron environment during the earlier epochs when these observations were made, when solar and geomagnetic activity was enhanced relative to solar cycle 24. We note that this version of AE9 does not include any Van Allen Probes data, while later versions of AE9 have been informed by Van Allen Probes data. In particular, AE9 V1.2 (Johnston et al., 2015) is the first version to be informed by MagEIS data, where the data are used to guide the extrapolations that are used in the inner zone. AE9 V1.5 (O'Brien et al., 2018) is the first version to actually ingest the MagEIS fluxes into the empirical database.

4. Summary and Conclusions

We detail the development of a new, alternative algorithm that is used to correct Van Allen Probes MagEIS electron fluxes for inner zone proton contamination. This new algorithm is limited to L≤ 3, energies greater than 700 keV and fluxes that are output on a daily time cadence. The new technique is demonstrated to provide more accurate estimates of the inner zone fluxes than those obtained with the standard background corrections that are part of the routine data processing. As there are considerable postprocessing steps involved, the alternative algorithm cannot be made part of the standard MagEIS data processing or data products. However, we provide these new data in the supporting information as a Common Data Format file.

The present study was motivated by our earlier work, where the formation of a new inner belt was detailed following the strong shock events of March and June 2015. Claudepierre et al. (2017) presented auxiliary data (MagEIS pulse height, or histogram, energy spectra) that suggested that the new inner belt was wider in L and persisted longer than was suggested by the standard background‐corrected data. However, it was not possible to fully quantify those differences and discrepancies at that time. The goal of the present study is to quantify these differences, and the primary findings are as follows:

1. Due to a number of factors, MagEIS data that are corrected for background contamination using the standard algorithm can underestimate the inner zone flux intensities at relativistic energies, particularly when the foreground fluxes are low relative to the background signals (which is often the case in the inner belt and slot).

2. When compared with the standard background corrected data, the 1‐MeV inner zone electron injection and newly formed inner belt observed in mid‐2015 (i) is revealed to form earlier, (ii) is more intense, (iii) is distributed more broadly in L, and (iv) decays on longer timescales.

3. The strong interplanetary shock of September 2017 also injected ∼1‐MeV electrons into the inner zone, producing an inner belt enhancement with morphological features similar to those observed following the 2015 injections.

4. We find no observable level of $\gtrsim$1.5‐MeV electrons in the inner zone during the interval considered, April 2013 through April 2018.

5. The inner zone electron spectrum is steeply falling, with e‐folding energies on the order of 100 keV, during both quiet and active periods.

The differences between the standard and alternative background corrected data have important implications for both scientific studies and empirical radiation belt modeling. For example, diffusive timescales estimated empirically from the MagEIS measurements using the standard background correction algorithm will be inaccurate at relativistic energies in the inner zone. Similarly, empirical radiation belt models, such as AE9, that use MagEIS data may underestimate the relativistic electron flux in the inner zone when the standard background‐corrected fluxes are used. Thus, quantitative investigations of relativistic electron dynamics in the inner zone should be undertaken using the alternative background‐corrected fluxes described and provided here. However, the general results obtained in previous works (Claudepierre et al., 2017; Fennell et al., 2015) have not changed significantly: that the inner zone is devoid of electrons $\gtrsim$1.5 MeV during the Van Allen Probes era; that the inner zone electron spectrum is steeply falling; that ∼1‐MeV electrons can be injected into the inner zone following the passage of strong interplanetary shocks; and that MagEIS electron observations are out of family with the AE9 model in the inner zone.

Erratum

In the originally published version of this article, several mentions of MeV were incorrectly copyedited. The following have since been corrected, and this version may be considered the authoritative version of record: In section 2.1, fourth paragraph, “no foreground dropped volts electrons” has been changed to “no foreground MeV electrons.” In section 2.1, fourth paragraph, “foreground megaelectron electrons” was changed to “foreground MeV electrons.” In Figure 7 caption, “no megaelectron volts electrons” was changed to “no MeV electrons.” In Figure 7 caption, “when megaelectron volts electrons are observed” was changed to “when MeV electrons are observed.” In section 3.5, second paragraph, “A “quiet” interval when no megaelectron volts electrons are observed” was changed to “A “quiet” interval when no MeV electrons are observed.” In section 3.5, second paragraph, “there are megaelectron volts electrons in the inner zone.” Was changed to “there are MeV electrons in the inner zone.” In section 3.5, second paragraph, “of megaelectron volts injection activity” was changed to “of MeV injection activity.” In section 3.5, second paragraph, “devoid of megaelectron volts electrons.” Was changed to “devoid of MeV electrons.”

Supporting information

Supporting Information S1

Appendix A. Further Details on the Alternative Background Correction Technique

A.1.

We now describe several specific details that were omitted in the general overview of the algorithm as outlined in section 2.1 (in Appendix A.1), along with several caveats and limitations to the alternative correction algorithm (in Appendix A.2).

A1. Data Processing Details

When examining the raw fluxes obtained from the alternative correction algorithm, spurious features are sometimes found, which are then cross‐checked with the histogram data to refute or validate any such features (e.g., by looking for main channel passband peaks when questionable looking foreground fluxes are found). Many of these spurious features are found when the counting statistics are poor, which can lead to residual contamination due to Poisson fluctuations in the counting rates. To account for the effects due to Poisson noise, we compute the standard deviation of the individual daily histogram profiles that go into the background estimate. For example, if the background estimate is computed from 90 daily histogram profiles (e.g., Figure 2), then, in addition to computing the background estimate as the mean profile of those 90 profiles, we also retain the standard deviation profile, σ, of those 90 profiles. Then, when performing the background subtraction, the main channel passband counts are compared with 1σ times the estimated background counts in the passband. If the main channel counts are less than the 1σ‐scaled background counts, then the background‐corrected count rate is set to 0.

We have also observed that the shape of the background profiles obtained from the histogram data has a slight orbital dependence. For example, we have found that the ratio of the left‐wing histogram count rate to the right‐wing rate varies slightly in time, so that in some sense, the “tilt” of the background estimates shown in Figure 2 varies slightly, on long (seasonal) timescales. This “orbital season” effect appears to be related to spacecraft proximity to the magnetic equator in a given L bin, even within the low B/B _eq range considered here. While these effects are small, typically only a factor of 2 in count rate, the slight change in the background histogram shape or tilt can considerably alter the background counts within the main channel passband. This can in turn produce an artificially enhanced (or diminished) background flux estimate during times when the histogram shape is slightly different from that in the time interval used to obtain the baseline estimate. The consequence of this is that it is not possible to use the same background profile for all times, for a given pixel and L bin (e.g., the background profiles shown in Figure 2 cannot be used for the entire time interval under consideration). Through experimentation and an examination of trends in the B/B _eq time series, we have defined four distinct orbital seasons throughout the 6‐year time interval. A separate background estimate is derived for each of the four orbital seasons, and it is then used to correct all data that lie within the same orbital season. The dates corresponding to the four orbital seasons are shown in Table A1, along with the specific time intervals that are used to compute the background estimate for each season. Note, for example, that the background estimate profiles shown in Figure 2 correspond to orbital season 3. We also note that the large gyroradii of the inner belt protons (approximately hundreds of kilometers) that produces the well‐known East‐West effect (e.g., Mazur et al., 2014) may also contribute to the observed time dependence in the background shape.

Table A1.

Orbital Season Definitions

Orbital	Time intervals
Season	(yyyy/mm/dd)
1	2012/11/16–2013/01/19; 2013/12/21–2014/02/23; 2015/01/25–2015/03/30;
	2016/02/29–2016/05/03; 2017/04/04–2017/06/07
2	2013/01/20–2013/05/22; 2014/02/24–2014/06/26; 2015/03/31–2015/07/31;
	2016/05/04–2016/09/03; 2017/06/08–2017/10/08
3	2013/05/23–2013/08/19; 2014/06/27–2014/09/23; 2015/08/01–2015/10/28;
	2016/09/04–2016/12/01; 2017/10/09–2018/01/05
4	2013/08/20–2013/12/20; 2014/09/24–2015/01/24; 2015/10/29–2016/02/28;
	2016/12/02–2017/04/03; 2018/01/06–2018/05/08

Note. The time intervals that are used to compute the background estimate for each season are shown in bold.

Another challenge is that it is not possible to identify a satisfactory time interval in which inner zone electrons are not observed at 0.74 MeV (M75‐P6). The overarching assumption on which the alternative algorithm relies is that, in order to derive the background estimate, a time interval can be identified in which there are no foreground electrons observed above background levels. Such a time interval must be identified for every L in the inner zone (L = [1,3]) and over the entire energy range of interest (0.74–4.0 MeV). The four orbital seasons identified in Table A1 satisfy these criteria except for the lowest energy under consideration, the 0.74‐MeV channel (M75‐P6). Here we find low‐intensity foreground passband peaks in several L bins in each of the orbit seasons. Thus, to produce the background estimate for this pixel in these cases, we linearly interpolate (in log space) the average background profile across the main channel passband, from the left wing to the right wing. Thus, in these instances, the background estimate is constructed using the averaged histogram profile outside of the wings, while in between the wings a linearly interpolated profile is used.

For the 1.01‐MeV channel from the HIGH unit (HIGH‐P0), the situation is more complicated, due to two factors: (i) the greater sensitivity of this detector when compared with the higher‐energy pixels from M75 and (ii) the fact that the background histogram profiles are not strictly monotonically decreasing. With regard to the first factor, note that the main channel passband for HIGH‐P0 is ∼300 keV wide, which is much wider than the M75 channels from P6–P8, which are all ∼100 keV wide (see table in the supporting information). In addition, note that HIGH‐P0 and M75‐P8 nominally measure the same energy electrons, with nearly identical centroid energies of ∼1 MeV (see Figure 2), albeit with different passband widths. However, when ∼1‐MeV electrons are present in the inner zone at these energies, the passband count rates are nearly an order of magnitude larger in HIGH‐P0 than M75‐P8, as can be seen in panels bii and biii in Figure 2. This is due to the much greater sensitivity of HIGH‐P0 when compared with M75‐P8, with effective geometry factors of ∼1 × 10⁻² and ∼1 × 10⁻³ cm²·sr, respectively. A similar difference in detector sensitivity is noted between HIGH‐P0 and the other M75 pixels considered here (P6 and P7). With regard to the second factor, it is clear that the M75 and HIGH units respond differently to penetrating protons, which is readily seen by comparing the M75 and HIGH histogram profiles in Figure 2, row a. The penetrating protons produce monotonically decreasing profiles in the M75 unit, in stark contrast to the shapes in the HIGH unit. Specifically, in panel aiii, the histogram profile for HIGH‐P0 first decreases monotonically with energy (above the noise threshold) and then increases with energy above the main channel passband (note that the same is true for HIGH‐P1). These differences were noted in Claudepierre et al. (2017) and have been investigated using both MagEIS HIGH unit direct event data (full‐resolution pulse‐height data from both the front and rear detectors) and Geant4 simulations (Allison et al., 2016) of the HIGH unit response convolved with an assumed inner belt proton spectrum. Through these analyses, we have confirmed that the peculiar histogram shapes in the HIGH unit in the inner zone are due to the instrument's complex response to penetrating protons (not shown here).

This detection‐sensitivity discrepancy between HIGH‐P0 and M75 P6‐8, coupled in with the nonmonotonically decreasing background shapes in HIGH‐P0, impacts the computation of the background estimates from the histogram profiles. Due to the (relatively) high sensitivity of HIGH‐P0, the background estimates computed for all four orbital seasons show very slight inflections in the main channel passband in portions of the inner zone. While these are not passband peaks, and only inflections, they could be interpreted as evidence of very low intensity foreground signals (not shown here). These signals are not measured by M75‐P8 due to the lower sensitivity. If the background profiles for HIGH‐P0 were monotonically decreasing, like they are on M75, then this would not be an issue and we would simply linearly interpolate across the HIGH‐P0 passband to mitigate the effect of the low‐intensity signal. However, interpolating from the left wing to the right wing is clearly not an option for HIGH‐P0, due to the nonmonotonically profile. Doing so would also “chop off” significant foreground peaks that exist in the channel passband (e.g., Figure 2, panel biii). Moreover, since there may be very low‐intensity foreground electrons in the four orbital seasons that are used to construct the background estimates for HIGH‐P0, and since the intensity of these electrons could be slightly different in each orbital season, it is not possible to use different orbital seasons for HIGH‐P0. Thus, for HIGH‐P0 (only), the background estimate computed from orbital season 3 is used throughout, as it has the lowest intensity in the main channel passband.

To summarize these final two rather technical points related to the data processing: (i) For HIGH‐P0 (only), orbital season 3 is used as the background estimate for all times; for all other pixels under consideration, the orbital seasons are used as defined in Table A1; (ii) For M75‐P6 (only), we must linearly interpolate the background estimate across the passband for several L bins in the inner zone; for all other pixels, the entire histogram profile is used as the background estimate.

A2. Caveats and Limitations

It should be clear that the alternative background‐corrected flux cannot be calculated as part of the routine data processing, due to its reliance on a considerable number of postprocessing steps. The background estimate is constructed from multimonth averages of the histogram data, and thus cannot be made part of the routine processing. It should also be clear that, by design, the algorithm operates on daily averaged data, so that Δt = 1 day is the time resolution of the alternative background corrected data. This is because significant time is needed to accumulate counts in low‐flux regions of the radiation belt to produce the accurate histogram profiles that are required to construct the background estimates. For the same reason, at present, we have only attempted the alternative technique for near‐equatorially mirroring electrons, as this is where the radiation belt intensity maximizes. Future work will attempt to extend the pitch angle coverage to all equatorial pitch angles.

We note that the temporal range that we consider only goes back to April 2013, as we cannot easily go back to the beginning of MagEIS science operations in September 2012. This is because the MagEIS instrumental settings were modified and reconfigured regularly early in the mission, to optimize sensor performance. In particular, the detector biases were changed considerably up until late December 2012, which significantly affects the shape of the histogram profiles, whereas the algorithm relies on these being stable and consistent. Furthermore, because of its relatively large detectors, the HIGH unit uses coincidence to mitigate background contamination and spurious signals from side penetrators. These coincidence settings (and detector threshold settings) were similarly changed frequently early in the mission. In addition, the MagEIS lookup tables (and thus energy channel definitions) were also changed regularly early on and did not become stable until April 2013. We also note that prior to October 2013, the histogram sampling parameters were rather coarse, as the data were accumulated at a ∼2‐min time cadence (12 spacecraft spins) with low angular resolution (27 sectors per spacecraft spin for LOW/M75 and 16 sectors/spin for HIGH). On October 2013, these sampling parameters were improved to a roughly 1‐min time cadence (six spacecraft spins) with 25 sectors/spin for LOW/M75 and 16 sectors/spin for HIGH, which then increased to 25 sectors/spin in January 2014 to match LOW/M75. Finally, in June of 2014, the final histogram accumulation parameters were set to a ∼22‐s time cadence (two spacecraft spins) with 32 sectors/spin (LOW/M75/HIGH). The sum of all of these configuration changes precludes us from making accurate estimates of the foreground fluxes prior to April 2013 with the alternative correction technique as described, though future work may attempt to overcome some of these challenges.

As noted above, the construction of the background estimate requires that an extended period of time (several months) can be identified in which there is no foreground signal in a given pixel in a given L bin. Due to the rich electron dynamics at lower energy, it is not possible to find these required time intervals for energies below ∼700 keV, as electrons are present in the inner zone at these energies throughout the Van Allen Probes mission (see Figure 1). The difficulty with constructing a background estimate for the lower‐energy pixels centers on the fact that when there are significant foreground counts in the passband, the left‐wing count rate levels are influenced by backscatter, in addition to contamination from inner belt protons (see Claudepierre et al., 2015). Thus, in order to estimate the true background level due only to penetrating protons, the low wing must be scaled down in some way before the interpolation across the passband, to account for backscatter. This is not possible without an accurate knowledge of the percentage of particles that are measured on a given detector due to backscatter, a difficult quantity to estimate. As noted above, interpolation is used in a few L bins to estimate the background profile for M75‐P6. However, in these few instances, the foreground peak in the passband is of low intensity, which minimizes the backscatter influence on the background profile's shape. At energies below this, the inner zone foreground fluxes are higher, and the backscatter issue becomes more influential on the histogram shape. Thus, the lower limit of the energy coverage for the alternative technique is ∼700 keV. And for these same reasons, the spatial coverage of the algorithm is restricted to L≤ 3, since the construction of the background estimate requires a very stable source of background (the inner proton belt) in the absence of foreground fluxes. Clearly, this situation is essentially never the case in the outer zone, as foreground electrons exist at all energies at essentially all times and are highly dynamic (Figure 1). Thus, in all of the results presented, the alternative corrected data is a combined data product: Above L = 3, it is the standard background corrected data, while below L = 3, the alternative algorithm is used.

Claudepierre, S. G. , O'Brien, T. P. , Looper, M. D. , Blake, J. B. , Fennell, J. F. , Roeder, J. L. , et al. (2019). A revised look at relativistic electrons in the Earth's inner radiation zone and slot region. Journal of Geophysical Research: Space Physics, 124, 934–951. 10.1029/2018JA026349