Interrogating metabolism as an electron flow system

Abstract

Metabolism is generally considered as a neatly organised system of modular pathways, shaped by evolution under selection for optimal cellular growth. This view falls short of explaining and predicting a number of key observations about the structure and dynamics of metabolism. We highlight these limitations of a pathway-centric view on metabolism and summarise studies suggesting how these could be overcome by viewing metabolism as a thermodynamically and kinetically constrained, dynamical flow system. Such a systems-level, first-principles based view of metabolism can open up new avenues of metabolic engineering and cures for metabolic diseases and allow better insights to a myriad of physiological processes that are ultimately linked to metabolism. Towards further developing this view, we call for a closer interaction among physical and biological disciplines and an increased use of electrochemical and biophysical approaches to interrogate cellular metabolism together with the microenvironment in which it exists.

Highlights

• •Cell metabolism represents an interconnected network rather than isolated pathways.
• •Capturing the interconnected nature of metabolism makes experimental and theoretical analysis of metabolism very challenging.
• •We highlight kinetic and thermodynamic constraints arising from a view of metabolism as an electron flow as a fundamental approach to study and understand metabolism.
• •We call for the development of experimental tools and models that focus on capturing redox and ion fluxes connected to electron flows through metabolism.

Metabolism refers to the collective set of biochemical reactions that occur within a cell. Early pioneering studies, crowned by several Nobel prizes, have mapped the so-called core metabolism that includes glycolytic and pentose phosphate pathways (PPP), Calvin–Benson cycle, gluconeogenesis and the tricarboxylic acid (TCA) cycle ^{1, 2}. In parallel, the chemiosmotic theory of energy generation through the respiratory electron transport chain has been formulated and proven correct [3] (even though the mechanistic details are still a matter of debate ^{4∗∗, 5}). These productive lines of research elucidating individual enzymatic reactions continue to make important contributions to our understanding of metabolism [6]. In this opinion article, we argue that it is now time to use this accumulating knowledge to develop an explanatory theoretical framework based on electron flows for interrogating cellular metabolic structure and dynamics at systems level.

Pathway-centric views of metabolism and its shortcomings

Following the early pioneering studies on the biochemistry of enzymes, a pathway-centric framework has dominated the description of metabolism ^{7∗, 8, 9}. This textbook view organizes cellular metabolism into modular pathways that link sugars to pyruvate (i.e. the glycolysis pathways of pentose-phosphate (PP), Entner–Doudoroff (ET), and Embden–Meyerhof–Parnas (EMP)), and those that link pyruvate to the generation of the key reductive equivalents via the TCA (a.k.a. Krebs) cycle and associated glyoxylate and glutamate cycles. These pathways and their interactions with the biosynthesis pathways of lipids and amino acids are considered to give rise to a higher organisation of metabolism as catabolic (energy generating) and anabolic (energy consuming) reactions ^{7∗, 8, 9}. Such organisational view is further enforced by graph-theory analyses that suggest a hierarchical and modular organisation of metabolism ^{10, 11} (although it is important to note that identifying appropriate null models is challenging when studying metabolism as a graph ^{12, 13} and different graph representations can give different results [14]).

This pathway-centric framework, thus, draws a picture of cellular metabolism as consisting of well-defined flows through modularly organised pathways. The pathways themselves are suggested to represent historical contingencies in evolution, where a key set of metabolites and metabolic conversions emerged as first forms of “life” [15] and subsequently maintained and expanded through an evolutionary process that is commonly seen as driven by cellular growth under diverse conditions. While this adaptive view of metabolism gives us one possible way of rationalising it, it ignores other possible driving forces and constraints in the evolution of metabolism (e.g. osmotic or toxic effects, trade-offs, cell stability) ^{16, 17}, and falls short in explaining and predicting many of the key structural and dynamical features of metabolism. We list below some of these as open questions, and argue for the development of a new explanatory framework, which can offer starting points towards addressing them.

Why are metabolic systems diverse across different species? Pathways that offer alternative routes for glucose consumption are present or absent in different microbes [18]. Biosynthesis pathways for essential co-factors, such as thiamine or vitamin B12, are lacking in different algae and fungi species ^{19, 20}, and even the TCA cycle structure can be varied in different organisms [21]. While the pathway-centric view tends to explain such structural diversity as “adaptations to different conditions”, we need a more predictive theory that can directly link specific environmental factors to specific metabolic structures (e.g. lack of a given enzyme predicted under a certain environment). For example, loss of metabolic pathways in some organisms is explained as an adaptive process under the provision of specific metabolites by other organisms [22], but it is left unclear why and under what conditions any organism would excrete any such metabolites. Similarly, functionally equivalent pathways are suggested to be adaptive under different conditions due to their different energetic costs ^{7∗, 18∗}, but it is left unclear what those conditions might be. An ideal theoretical framework for metabolism should provide experimentally testable predictions about where and when to find which structural variants of metabolism.

What are the design principles of common metabolic system structures? While metabolic systems show some diversity, there are common structures that are conserved across many species, and that can be presented as key metabolic pathways. It is still not clear why these common pathways are structured in the way that they are. Several studies have tried to answer this question based on biophysical and energetic aspects ^{18∗, 23, 24∗}, but did so while treating individual pathways as isolated units. These approaches should be further developed, given the fact that no pathway (and its reactions and metabolites) exists in isolation in a cellular environment, but instead operates under high interconnectedness through metabolites and common electron shuttles (Figure 1). Developing a system-level framework that could naturally explain the emergence of interconnected pathways as a whole remains to be an open challenge.

Figure 1.

Common metabolic pathways, shown in their broader context, and highlighting their interconnected nature. Reactions are compiled from Ref. [7] and do not represent the full list of known metabolic reactions in the cell. Metabolites are shown using their common names, while reactions are indicated with arrows. Yellow and green arrows indicate oxidation and reduction reactions, respectively, with arrow type indicating the involved electron shuttle; solid, dashed, and double dashed lines for NADH, NADPH, and FADH₂. Reactions releasing and consuming ATP are shown in red and blue, respectively. Where multiple reactions are involved when going from one metabolite to another, this is indicated by multiple arrows. Involvement of co-factors and release of small molecules (such as carbon dioxide) are indicated partly (with smaller arrows). Metabolites involved in multiple reactions, and therefore forming additional metabolic cycles, are indicated with a grey backdrop.

Why do cells excrete metabolites and enzymes to their environment? Many metabolites are readily excreted from cells despite still carrying energy value, and many enzymes are known to operate outside of the cell. A pathway-centric view focused on optimization of growth does not provide any explanations for these observations, nor does it allow any predictions about which metabolites or enzymes might be secreted under which conditions. Adaptive arguments have been made about some metabolic excretions (i.e. ethanol) providing a mechanism to inhibit or kill competing species [25]. This particular example also highlights a broader issue with adaptive arguments in that they can readily be formulated for many different observations, but lack a clear sequential evolutionary path; in this case, for example, the killing argument does not explain how small amounts of metabolic excretions, that would not yet function as a toxic agent, could have emerged and stabilised. A series of recent studies indicate that metabolic excretions, in particular those involving organic acids, can arise from cellular trade-offs linked to biophysical constraints on enzymatic reactions such as space (i.e. cytosolic vs. membrane–bound reactions) ^{26∗∗, 27, 28} and protein capacity ^{29, 30}. These studies highlight the importance of considering the biophysical basis and limits as directing evolutionary processes when explaining and predicting specific features of metabolic systems.

How does metabolism exhibit non-linear dynamics as a whole? The pathway-centric view of metabolism does not consider the dynamics of fluxes across pathways. This dynamic nature is evident from the interconnectedness of key metabolic pathways through common electron and energy shuttles such as NADH and ATP (Figure 1), and the fact that many of their constituting reactions are close to thermodynamic equilibrium under standard conditions [31] (Figure 2). These reactions could thus be operating reversibly with changing cellular conditions, such as pH and redox potential, as shown for some pathways ^{32, 33∗∗, 34∗}, and lead to non-intuitive flux dynamics. In addition, the sharing of (or competition for) metabolites and enzymes across many reactions can lead to complex temporal dynamics such as oscillations and multi-stability, as theoretically shown for even simplified biochemical reaction systems ^{35∗, 36, 37∗, 38∗∗}. Indeed, where measured, periodic oscillations are found to be present in central metabolism ^{39, 40, 41∗∗, 42}. These oscillations are well studied in continuous yeast cultures, in which they have been shown for virtually all metabolites and coincide with a separation of oxidative and reductive phases [43]. Similarly, combined levels of NADH and NADPH in Escherichia coli, measured fluorimetrically, were found to oscillate in line with the cell division cycle [41]. It has been furthermore suggested that these oscillations are crucially linked to other biological oscillations, such as cell cycle and circadian rhythms ^{44, 45}. While some models ^{46, 47, 48} and metabolic mediators ^{39, 49} have been proposed to explain these oscillations, a detailed and predictive understanding of metabolic oscillations still needs to be developed. Besides oscillations, bistable dynamics have been predicted and experimentally shown for isolated enzymatic reactions and pathways ^{36, 50, 51, 52, 53}. These dynamics are still challenging to analyse at the single-cell level, but emerging fluorescence approaches offer a promising route [54]. Finally, the dynamics arising from (seemingly) futile enzymatic cycles have been discussed theoretically as a mechanism for achieving robustness against perturbations [37], but have not been studied in the context of temporal dynamics. Theoretical models of futile cycles have shown that these can give rise to bistability and oscillations under certain parameter regimes [50], but these ideas have not been explored experimentally. Overall, the dynamics of metabolism either at the whole system level or at the level of commonly observed dynamical modules (like futile cycles) is understudied.

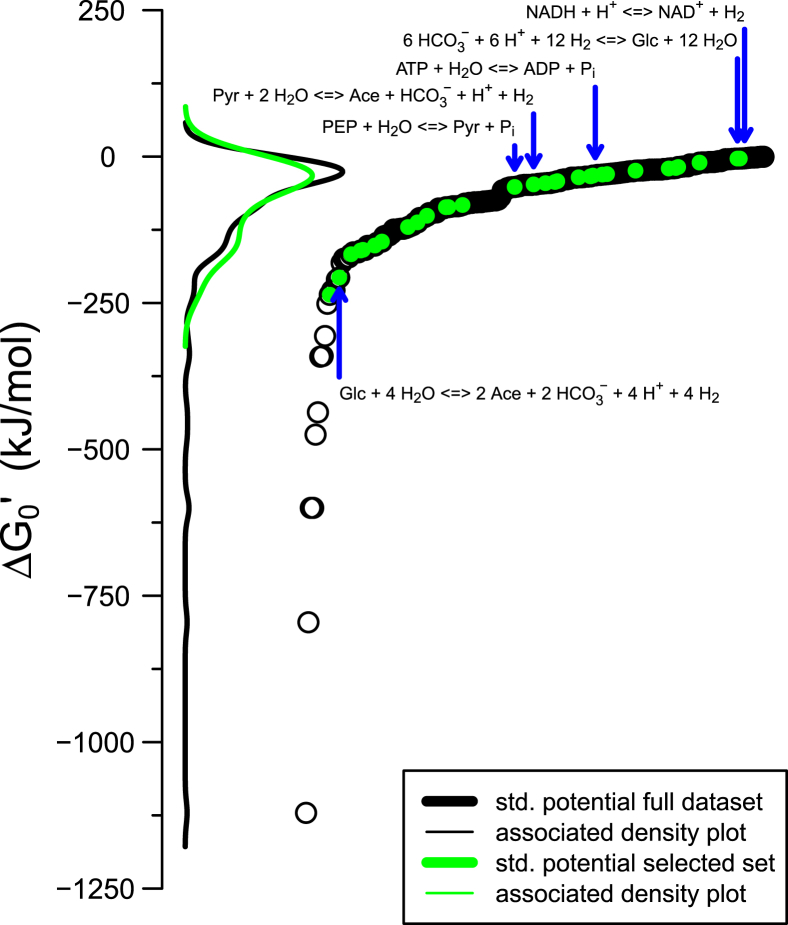
Figure 2.

Thermodynamics of common metabolic conversions as collated from references 31∗, 73∗. The y-axis shows the standard Gibbs free energy at physiological conditions (ΔG⁰′), while the x-axis is used for reaction index (ordering them from lowest to highest ΔG⁰′). In calculating the ΔG⁰′, reactions are considered in their spontaneous direction and the H⁺/H₂ pair is used for electron balancing (in the case of redox reactions). Each reaction is shown as a single data point, while lines are for the density distribution (as indicated in the inset). Reactions that were included in Fig. 1 are shown as green filled points and their distribution by the green line. This figure suggests that most metabolic conversions have a ΔG⁰′ value close to zero (see distributions), but calls for a further mapping of metabolites and reactions in order to allow more general conclusions to be drawn (with regards to how these distributions compare to those of all possible reactions). We note that reactions with the most negative ΔG⁰′ (<-250 kJ/mol, left side in plot) are those involving the reduction of nitrate, oxygen, and sulphite; common terminal electron acceptors.

Metabolism as a thermodynamically driven electron flow system

Life depends on free energy gradients [55]. Organisms, or cells, act as “disequilibrium converters” [56] that exploit these energy gradients and couple thermodynamically spontaneous and nonspontaneous reactions through a defined path, the metabolic reaction network. The ratio of the forward and reverse kinetic constants of a reaction equals to the equilibrium constant K_eq, which in turn determines its standard Gibbs free energy at a dynamical steady state (ΔG⁰ = —R⋅T⋅ln(K_eq), where R is universal gas constant and T is temperature in Kelvin) ^{56, 57, 58}. The actual reaction free energy (and hence the spontaneous direction of a reaction) at a given condition is based on ΔG⁰ (Figure 2), which relates to the concentrations of substrates and products under that condition. Thus, changing concentrations through one reaction can make another reaction feasible, allowing metabolism to couple external gradients to internal ones in a turnstile-like mechanism [56]. For example, light-energy drives photosynthetic reactions forward (i.e. water-oxidation with carbon dioxide reduction), and once a pool of metabolites is generated, the reverse reaction (e.g. glucose oxidation with oxygen reduction) becomes spontaneous (i.e. energy releasing), allowing excess energy for other non-spontaneous reactions.

These dynamics of metabolic flows can be formalised through non-equilibrium thermodynamics, which is well developed for simplified enzymatic reaction networks ^{58, 59}. The use of this formalism as a general theoretical framework for studying the entire cellular metabolism, however, has not been fully explored. This is mainly due to a lack of information about thermodynamic properties (i.e. standard Gibbs energies) and intracellular concentrations of many metabolites. The former issue can be approached computationally using statistical (e.g. group contribution) or quantum chemical methods, however, these are currently limited and can only cover a fraction of cellular metabolites ^{60∗, 61}. The intracellular metabolite concentrations can be increasingly determined using technological developments in high-throughput mass spectrometry and ion chromatography [33], hence, with knowledge of a reaction's ΔG⁰, allowing direct assessment of the thermodynamic state of the reaction.

Development of a dynamical thermodynamic framework for cellular metabolism can benefit from a special focus on redox reactions. These reactions hold a key interconnecting role among different pathways and offer electrochemical interrogation of their dynamics ^{62, 63}. Redox reactions interlink for example glucose oxidation via PP, ET, and EMP pathways, pyruvate oxidation through the TCA cycle, and biosynthesis of many of the amino acids (Figure 1), through the shared use of conserved moieties acting as electron shuttles, such as NAD⁺/NADH, NADP⁺/NADPH, FAD/FADH₂, ferredoxins, and quinones. This, crucially, makes the ratio of the concentration of the oxidised and reduced forms of these molecules a key factor in determining the thermodynamics of (and flows through) different metabolic paths.

Considering this interconnected set of redox reactions can crucially allow us to consider electronic circuits as an analogy to metabolic systems [64] on one hand, and to attempt their manipulation by electrochemical means on the other ^{65, 66, 67}. Indeed, it has been shown that influencing the ratio of key electron shuttles (e.g. NAD⁺/NADH) through enzymatic and electrochemical means can directly influence metabolic pathway fluxes and the dynamics of metabolic excretions ^{63, 68, 69, 70∗}.

Potential explanatory powers of viewing metabolism as electron flows

We argued so far that considering metabolism as a thermodynamically driven flow system, rather than isolated pathways, can provide an overarching theoretical framework and that focusing this framework to redox reactions can further allow the formulation of new explanatory and predictive theories. We list below some of the key areas where this electrical view of metabolism can make immediate impact in our understanding of metabolism.

Energetic barriers in electron flow driving metabolic pathway diversity and utilization. When strong electron acceptors are not available in the environment, cells have to use weaker electron acceptors such as organic acids or inorganic molecules (such as H⁺) as electron sinks (i.e. to maintain electron flow). The result is a smaller free energy available from the overall redox reaction that the cell implements, and an increased risk of the system reaching equilibrium by product accumulation (i.e. thermodynamic inhibition). Recently, it has been shown theoretically that this type of thermodynamic inhibition due to product accumulation can lead to diversity of microbial growth-supporting metabolic reactions and possibly internal metabolic pathways [71]. This theory aligns well with the observation that organisms, such as methanogens and sulfate reducers, adapted to weak or fluctuating electron acceptors show diverse respiratory and fermentative pathways and enzymes ^{55∗, 72, 73∗}. It would be interesting to see if theories relating to thermodynamic inhibition could be developed further to link the diversity of broader organization of metabolic systems (in particular redox shuttle and respiratory enzyme usage) to environmental conditions, and in particular availability and ecological dynamics of common electron acceptors.

Metabolic excretions to maintain electron flows. Thermodynamic inhibition could also be a driving force beyond observed metabolic excretions. For example, oxidation of certain metabolites can become thermodynamically inhibited if the reduced forms of their paired electron shuttle have reached a low concentration. Such an inhibition would be lifted if another metabolite could be reduced using the oxidized form of the same shuttle molecule. This coupling can be further facilitated if one (or some) of the metabolites can be made to act as a sink, e.g. by excreting them from the cell. The increased rate of formation and excretion of organic and amino acids through reductive reactions can be understood within this view, as a mechanism to combat shifts in the NAD⁺/NADH ratio. Indeed, experimental manipulation of the NAD⁺/NADH ratio in E. coli and yeast were found to directly influence the dynamics of metabolic excretions through fermentative pathways (i.e. acetate and ethanol excretion) ^{69, 70∗}. Thus, furthering a theoretical framework based on thermodynamically driven redox paths might allow us to predict metabolic excretions under different conditions.

Enzymatic excretions combatting toxic effects arising from redox reactions involving electron sinks (i.e. respiration). Redox reactions with compounds that act as final electron acceptors (i.e. electron sinks), should ideally involve strong electron acceptors so to provide a significant energy gradient (see Figure 2). This, however, creates an additional constraint on metabolic system structure and dynamics in that strong terminal redox reactions can also result in the generation of even stronger redox active compounds [74]. The respiration (i.e. reduction) of O₂, for example, is found to lead to a generation of reactive oxygen species (ROS) at a rate up to 20% [75], while sulfate and nitrate respiration results in ‘toxic’ sulfide and nitrite, respectively. To avoid additional, uncontrolled redox reactions by these strong oxidizing agents, cells must have evolved ways to generate enzymes and redox metabolites that can act as effective neutralizers against strong redox agents. While catalases and peroxidases are known enzymes that can combat ROS toxicity [76], the generation of ROS from respiration could have been a strong driver also for the overall metabolic structure and dynamics. Indeed, connections between resistance to ROS and metabolic flux changes have been shown ^{77, 78, 79, 80, 81}, and ROS mitigation is suggested as an explanation for excretions of metal oxidizing enzymes in bacteria ^{82, 83}.

Compartmentalization of electron flows in space or time. Spatial compartmentalization of metabolism can be seen in form of specialized organelles within an individual cell ^{84, 85} (e.g. mitochondria and chloroplasts) and in form of subpopulations within an isogenic cell population ^{54, 86}. Such compartmentalization could be understood in the context of thermodynamic inhibition due to product accumulation and the associated issue of maintaining electron flows: local microenvironments that can maintain a disequilibrium through separation or flow of products from their reactions can allow overcoming thermodynamic inhibition. A similar effect could also be achieved by separation of processes over time, i.e. by implementing oscillatory dynamics that can balance the impact of opposing processes (e.g. on the NAD⁺/NADH ratio). Indeed, theoretical analyses suggest that oscillations, as observed for example in the NAD⁺/NADH ratio in yeast and eukaryotic cells ^{39, 44, 49}, may enhance the thermodynamic efficiency of glycolysis [87] or, more broadly, coupled chemical reaction systems [88]. This is in line with experimental observations of periodic NADH/NADPH concentration oscillations correlating with cell cycle phases ^{41∗∗, 43}, which could be an adaptation to alternately maximize thermodynamic driving force through pathways of interest with temporal separation.

Testing and establishing the electrical view of metabolism – the road ahead

It has been long-recognized that metabolism is a prime example of a system obeying non-equilibrium thermodynamics [89]. Bringing this view to practical study and engineering of metabolism, however, remains a challenge. We believe that the presented framework highlighting a view of metabolism that is based on maintenance of electron flows, under constraints arising from thermodynamics, kinetics, and interconnectedness of pathways through common electron and energy shuttles, can initiate further studies towards overcoming this challenge. This framework calls for more interaction between experimental and modelling disciplines and the development of new theoretical and experimental tools.

On the theoretical side, we note that efforts have been made to expand the stoichiometric, constraint-based optimization models of metabolism (i.e. flux balance analysis, FBA) with thermodynamics ^{90, 91, 92, 93} and also with overall constraints that can mimic some of the biophysical constraints arising from resource and space limitations ^{27, 94, 95, 96}. It would be important to continue these developments, and also consider coupling FBA with the modelling of cell environment dynamics ^{95, 97} towards incorporating possible thermodynamic inhibitions and electron acceptor availabilities in these environments. Inevitably, however, capturing the full dynamics of metabolism as electron flows will require kinetic and even spatial models that account for physiological parameters such as pH and membrane potential. To achieve this, current kinetic models, which usually assume fixed ratios for common electron and energy shuttles, and tend to consider pathways in isolation, need to be further developed. Dynamics of electron shuttles and the possibility of reaction reversibility will need to be incorporated to account for thermodynamics. Statistical thermodynamics simulations, as used recently to simulate TCA cycle dynamics [98], can be useful in this context but would need to be expanded and further developed to account for the larger parts and interconnected nature of metabolism. Similarly, emerging thermodynamic models for modelling overall metabolic conversions embedded through metabolism (i.e. thermodynamic microbial growth models) [99] can be possibly adapted to model cellular metabolism. As kinetic models incorporate more biochemical realism through reaction reversibility, electron and energy shuttle dynamics, and pathway interconnectedness, the major challenge will be to maintain models as tractable and ‘simple enough’ so that they can still generate experimentally testable insights and predictions.

On the experimental side, approaches integrating physiological, metabolomic, and electrochemical techniques will need to be developed to better understand electron flows in metabolism and constraints on these flows. In particular, we note that combined application of fluorescent reporters (as being increasingly used to interrogate cellular redox states and physiology (e.g. ^{41∗∗, 100, 101, 102, 103, 104})) and emerging nano-scale electrochemical probing methods [105] can provide powerful insights into the electron flow dynamics at cellular and population levels. These methods can be particularly suited to link metabolic dynamics to higher–level complex physiological processes such as cellular differentiations. Intriguingly, cellular differentiation is often associated with specialization of metabolism (e.g. bacterial spores ^{106, 107}, T cells [108], cancer cells [109]). We envision that development of the electron-flow based view to metabolism may provide a novel insight to these cellular differentiation processes as arising from thermodynamic limits and imbalances in metabolism. This, in turn, can open up novel means of controlling these processes using electrochemistry, and opening up new medical intervention methods.

Conflict of interest statement

Nothing declared.

This review comes from a themed issue on Systems ecology and evolution

Edited by Eörs Szathmáry and Ferenc Jordán