An information theoretic phase I–II design for molecularly targeted agents that does not require an assumption of monotonicity

Summary

For many years phase I and phase II clinical trials have been conducted separately, but there has been a recent shift to combine these phases. Although a variety of phase I–II model‐based designs for cytotoxic agents have been proposed in the literature, methods for molecularly targeted agents (TAs) are just starting to develop. The main challenge of the TA setting is the unknown dose–efficacy relationship that can have either an increasing, plateau or umbrella shape. To capture these, approaches with more parameters are needed or, alternatively, more orderings are required to account for the uncertainty in the dose–efficacy relationship. As a result, designs for more complex clinical trials, e.g. trials looking at schedules of a combination treatment involving TAs, have not been extensively studied yet. We propose a novel regimen finding design which is based on a derived efficacy–toxicity trade‐off function. Because of its special properties, an accurate regimen selection can be achieved without any parametric or monotonicity assumptions. We illustrate how this design can be applied in the context of a complex combination–schedule clinical trial. We discuss practical and ethical issues such as coherence, delayed and missing efficacy responses, safety and futility constraints.

1. Introduction

The primary objective of a phase I trial is to identify the maximum tolerated regimen (dose–combination–schedule), i.e. the regimen corresponding to the highest acceptable toxicity probability ϕ. Subsequently, a phase II clinical trial with the objective of finding a safe regimen corresponding to a prespecified efficacy probability is planned. For many years these phases were conducted separately, but there has been a recent shift to integrate both phase I and phase II clinical trials in a single study. The integration of phases enables an acceleration of the development and reduces costs (Yin, 2013; Wages and Conaway, 2014) while more observations for both toxicity and efficacy end points become available. The goal of a phase I–II clinical trial is to find the so‐called optimal biologic regimen (OBR). There are different definitions of the OBR which depend on the context of the trial. The OBR can be defined as the safest regimen with a toxicity probability below the upper toxicity bound ϕ and the highest efficacy above the lowest efficacy bound ψ (see for example Riviere et al. (2018)). It can, however, be challenging to find a single regimen having the safest toxicity and maximum efficacy simultaneously. In this case, the OBR can be alternatively defined as the regimen with the highest efficacy rate while still safeguarding patients (see for example Wages and Tait (2015)). In this work we use both definitions and call the regimen satisfying the first definition the optimal regimen and the regimen satisfying the second definition the correct regimen.

Historically, Gooley et al. (1994) were one of the first to consider two dose–outcome models. Similarly to later works on phase I–II clinical trials (e.g. Thall and Russell (1998), O’Quigley et al. (2001), Braun (2002), Thall and Cook (2004) and Yin et al. (2006), among others), this design is based on the paradigm ‘the more the better’—i.e. an agent has a greater activity but also a greater toxicity as the dose increases. This holds for cytotoxic agents but can be violated for molecularly targeted agents which include hormone therapies, signal transduction inhibitors, gene expression modulators, apoptosis inducers, angiogenesis inhibitors, immunotherapies and toxin delivery molecules, among others. For targeted agents either efficacy or toxicity curves can have a plateau (Morgan et al., 2003; Postel‐Vinay et al., 2011; Robert et al., 2014; Paoletti et al., 2014) or exhibit an umbrella shape (Conolly and Lutz, 2004; Lagarde et al., 2015).

Several designs for either single‐agent or combination therapy trials that relax the assumption of monotonicity for the dose–efficacy relationship have been proposed in the literature: see for example Polley and Cheung (2008), Hoering et al. (2013), Yin et al. (2013), Zang et al. (2014), Cai et al. (2014), Wages and Tait (2015) and Riviere et al. (2018) for a binary efficacy end point and Hirakawa (2012) and Yeung et al. (2017, 2015) for a continuous efficacy end point. The majority of current proposed designs are model based and the selection of the OBR is governed either by

• (a)a trade‐off function (e.g. Thall and Cook (2004) and Yeung et al. (2017, 2015)) or
• (b)a two‐stage procedure in which the safe subset is firstly defined and the most efficacious dose is then estimated (e.g. Thall and Russell (1998), Yin et al. (2013) and Wages and Tait (2015)).

Regardless of the approach used, the number of parameters to be included in the underlying model increases considerably if the monotonicity assumption is relaxed (Cai et al., 2014; Riviere et al., 2018). The design that was proposed by Wages and Tait (2015) employs a one‐parameter model but uses the idea of different orderings (Wages et al., 2011) to overcome the uncertainty about monotonicity. This idea can be extended to a range of problems (see for example Wages and Conaway (2014) for cytotoxic drug combination trials), although the extension to more complex settings, for instance, combination–schedule trials, can also be challenging because of a large number of possible orderings. Consequently, designs for such more complex trials have not been extensively studied yet. In contrast, an approach that does not use any parametric or monotonicity assumptions gives more flexibility and is a good candidate for both simple and complex phase I–II clinical trials.

This work is motivated by an on‐going phase I clinical trial at the Hospital Gustave Roussy for patients with high risk neuroblastoma, for which the authors contributed as statistical collaborators. Neuroblastoma is the most frequent individual type of solid tumour in children (Steliarova‐Foucher et al., 2017). Although different chemotherapy regimens of increasing intensities have been evaluated, the 5‐year overall survival remains around 50% for the high risk group (Kreissman et al., 2013). A recent preclinical study has suggested that the use of a particular immunotherapy targeting the disialoganglioside GD2 which is expressed in all neuroblastoma cells, in combination with conventional chemotherapy (etoposide and cisplatin) can improve the induction treatment. The first part of the high risk neuroblastoma treatment aims to reduce the tumour burden to facilitate surgery and subsequent treatments. Combinations of the newly developed immunotherapy and chemotherapy are given under different schedules:

• (a)immunotherapy for 2 days after the chemotherapy (S ₁);
• (b)immunotherapy for 3 days after the chemotherapy (S ₂);
• (c)immunotherapy for 4 days together with the chemotherapy and overlap 1 day (S ₃);
• (d)immunotherapy for 4 days together with the chemotherapy and overlap 2 days (S ₄).

The combination of treatments is given for two cycles (3 weeks). In each cycle the combination is given under one of schedules S ₁,…,S ₄. Six different regimens are considered in the study and are given in Table 1. The toxicity outcome is evaluated by the end of the second cycle. The efficacy data are available after two more cycles (after 6 weeks from the start of the treatment) only. If a patient has experienced toxicity he will be treated off the protocol and the efficacy outcome cannot be observed. A maximum of 40 patients will be recruited to the study and it is expected that two patients can be recruited each month. Consequently, it is expected that the next two patients are assigned a regimen before efficacy outcomes for the previous two patients have been observed.

Table 1.

Range of regimens considered in the motivating trial

Regimen	Cycle 1	Cycle 2
T 1		S 1
T 2	S 1	S 2
T 3	S 2	S 2
T 4	S 3	S 3
T 5	S 3	S 4
T 6	S 4	S 4

Clinicians are certain that toxicity probabilities of T ₃, T ₄ and T ₅ are greater than of T ₁ and T ₂ and smaller than of T ₆. However, toxicity probabilities of T ₃, T ₄ and T ₅ cannot be put in the order of increasing toxicity before the trial. Therefore, there are six possibilities how regimens T ₁,…,T ₆ can be ordered with respect to the toxicity probabilities:

$$\left.\begin{array}{cc}& T_1,T_2,T_3,T_4,T_5,T_6,\hfill \\ \hfill & T_1,T_2,T_3,T_5,T_4,T_6,\hfill \\ \hfill & T_1,T_2,T_4,T_3,T_5,T_6,\hfill \\ \hfill & T_1,T_2,T_4,T_5,T_3,T_6,\hfill \\ \hfill & T_1,T_2,T_5,T_3,T_4,T_6,\hfill \\ \hfill & T_1,T_2,T_5,T_4,T_3,T_6.\hfill \end{array}\right\}$$ (1)

Additionally, a plateau or umbrella shape for the dose–efficacy relationship is plausible because of the novel agent mechanism. This results in 48 efficacy orderings to be considered so traditional designs cannot be applied directly.

The aim of this paper is to propose a practical phase I–II design that can be used for regimens with both monotonic and non‐monotonic regimen–toxicity and regimen–efficacy relationships. We derive a novel trade‐off criterion that governs the regimen selection during the study. The form of the trade‐off function proposed is motivated by recent developments in the theory of weighted information measures (Mozgunov and Jaki, 2017) and in the estimation on restricted parameter spaces (Mozgunov et al., 2017). Although model‐based estimates can be used together with the proposed trade‐off function, we show that highly accurate optimal and correct regimens recommendations can be achieved without parametric assumptions because of the trade‐off function's special properties. It is demonstrated how practical issues such as safety, futility or information about any pair of the regimens can be incorporated in the design proposed.

The rest of the paper is organized as follows. The information theoretic approach, the trade‐off function and its estimation are given in Section 2. The novel regimen finding design and its illustration are presented in Section 3. Safety and futility constraints are introduced in Section 4. Section 5 presents the application of the proposed design to the motivating trial. Further discussion is given in Section 6.

2. Methods

2.1. Trade‐off function

Following Mozgunov and Jaki (2017), we consider a random variable Y that takes one of three values corresponding to

• (a)‘efficacy and no toxicity’,
• (b)‘no efficacy and no toxicity’ and
• (c)‘toxicity’.

Outcomes ‘toxicity and no efficacy’ and ‘toxicity and efficacy’ are combined as efficacy can be observed only when no toxicity occurs. Let $\mathbf{Z}=(Z^{(1)},Z^{(2)},Z^{(3)})\in {\mathbb{S}}^2$ be a random probability vector defined on the triangle

$${\mathbb{S}}^2=\{\mathbf{Z}:Z^{(1)}>0,Z^{(2)}>0,Z^{(3)}>0;\sum _{i=1}^3{Z}^{(i)}=1\}.$$

Random variables Z ⁽¹⁾,Z ⁽²⁾ and Z ⁽³⁾ correspond to probabilities of each of the three outcomes. As ${\mathrm{\Sigma }}_{i=1}^3{Z}^{(i)}=1$, the problem is, indeed, two dimensional. A common question in a phase I–II trial is ‘what is the probability vector Z?’. We use a Bayesian framework to answer this question.

Assume that Z has prior Dirichlet distribution Dir(v + J), $\mathbf{v}={(v_1,v_2,v_3)}^{\mathrm{T}}\in {\mathbb{R}}_{+}^3$, where v _i>0, i=1,2,3, and J is a three‐dimensional unit vector. After n realizations in which x _i outcomes of i, i=1,2,3, are observed, the posterior probability density function f _n of a random vector Z ⁽ⁿ⁾ takes the Dirichlet form

$$f_n(\mathbf{p}|\mathbf{x})=\frac{1}{B(\mathbf{x}+\mathbf{v}+\mathbf{J})}\prod _{i=1}^3{p}_i^{x_i+v_i}$$ (2)

where p=(p ₁,p ₂,p ₃)^T, x=(x ₁,x ₂,x ₃), ${\mathrm{\Sigma }}_{i=1}^3{x}_i=n$, 0<p _i<1, ${\mathrm{\Sigma }}_{i=1}^3{p}_i=1$ and

$$B(\mathbf{x}+\mathbf{v}+\mathbf{J})=\frac{\prod _{i=1}^3\mathrm{\Gamma }(x_i+v_i+1)}{\mathrm{\Gamma }\left\{\sum _{i=1}^3(x_i+v_i+1)\right\}}$$

is the beta function and Γ(x) is the gamma function. The quantitative amount of information that is required to answer the estimation question can be measured by the Shannon differential entropy of f _n (Cover and Thomas, 2012)

$$h(f_n)=-{\int }_{{\mathbb{S}}^2}{f}_n(\mathbf{p}|\mathbf{x})\text{log}\{f_n(\mathbf{p}|\mathbf{x})\}\mathrm{d}\mathbf{p}$$ (3)

with the convention 0 log (0)=0. However, an investigator has a particular interest in regimens which are associated with desirable efficacy and acceptable toxicity probabilities and the measure (3) does take this into account (Kelbert et al., 2016).

Assume that the OBR is defined as the regimen with probabilities of the three outcomes equal $\mathit{\gamma }=({\gamma }_1,{\gamma }_2,{\gamma }_3)\in {\mathbb{S}}^2$ where γ ₁, γ ₂ and γ ₃ are the target probabilities of no toxicity and efficacy, no toxicity and no efficacy and toxicity respectively. These target characteristics are to be defined by clinicians. Then, we would like to find the regimen whose characteristics (probability of these events) are as close as possible to the targets. Because of the specific interest in the regimens with characteristics close to γ, we consider a twofold experiment in which, when the sample size is large, an investigator seeks to answer

1. what the probability vector is whereas, for the small sample size, he is interested in

2. whether the probability vector lies in the neighbourhood of γ so that subsequent patients can be allocated to regimens with the characteristics close to the OBRs.

The amount of the information that is required for this twofold experiment can be measured by the weighted Shannon differential entropy (Belis and Guiasu, 1968; Clim, 2008; Kelbert and Mozgunov, 2015; Kelbert et al., 2016) of f _n with a positive weight function ${\varphi }_n(\mathbf{p})$:

$$h^{{\varphi }_n}(f_n)=-{\int }_{{\mathbb{S}}^2}{\varphi }_n(\mathbf{p})f_n(\mathbf{p}|\mathbf{x})\text{log}\{f_n(\mathbf{p}|\mathbf{x})\}\mathrm{d}\mathbf{p}.$$ (4)

The weight function ${\varphi }_n(\mathbf{p})$ emphasizes an interest in the neighbourhood of γ rather than on the whole space. We shall use a weight function of the Dirichlet form,

$${\varphi }_n(\mathbf{p})=C(\mathbf{x},\mathit{\gamma },n)\prod _{i=1}^3{p}_i^{{\gamma }_i\surd n}$$ (5)

where the rate √n emphasizes an interest in question (b) for the small sample size only. Here C(x,γ,n) is a constant satisfying the normalization condition ${\int }_{{\mathbb{S}}^2}{\varphi }_n(\mathbf{p})f_n(\mathbf{p}|\mathbf{x})\mathrm{d}\mathbf{p}=1.$

Because of ethical constraints and a limited sample size, an investigator is interested in the accurate estimation not for all regimens, but only for those with characteristics that are close to the target. This goal corresponds to question (ii) alone. The quantitative measure of the information that is required to answer (ii) only equals the difference of weighted $h^{{\varphi }_n}(f_n)$ and standard h(f _n) differential entropies (Mozgunov and Jaki, 2017). Denote the vector in the neighbourhood of which the probability density function f _n concentrates as n→∞ by θ=(θ ₁,θ ₂)^T, where θ ₁ is the probability of efficacy and no toxicity, θ ₂ is the probability of no efficacy and no toxicity and 1−θ ₁−θ ₂ is the probability of toxicity with corresponding targets γ ₁, γ ₂ and 1−γ ₁−γ ₂. It was shown by Mozgunov and Jaki (2017) that the difference in the entropies tends to

$$\delta \left(\mathit{\theta },\mathit{\gamma }\right):=\frac{{\gamma }_1^2}{{\theta }_1}+\frac{{\gamma }_2^2}{{\theta }_2}+\frac{{(1-{\gamma }_1-{\gamma }_2)}^2}{1-{\theta }_1-{\theta }_2}-1,\text{as}n\to \infty :$$ (6)

the sum of three contributions corresponding to each of three events considered.

Although result (6) is limiting, we propose to use this quantity as a measure of distance between θ and γ and, consequently, as a trade‐off function for selecting a regimen. Clearly, δ(·) ⩾ 0, δ(·)=0 if and only if θ=γ and boundary values θ _i=0, i=1,2, or θ ₁+θ ₂=1 correspond to infinite values of δ(·). The former property is argued to be fundamental for restricted parameter spaces (Aitchison, 1992; Mateu i Figueras et al., 2013; Mozgunov et al., 2017) and enables us to avoid parametric assumptions. Terms in result (6) have the following interpretations.

• (a)When θ ₁→0 the regimen is either inefficacious or (and) highly toxic. Then, the value of the trade‐off function tends to ∞, meaning that the treatment should be avoided.
• (b)When θ ₂→0 the regimen is either highly efficacious or (and) highly toxic. Then, this term penalizes the high toxicity regardless of high efficacy as the trade‐off function tends to ∞. This term prevents too quick escalation to highly toxic regimens.
• (c)When 1−θ ₁−θ ₂→0, the regimen is associated with nearly no toxicity. However, the optimal regimen is expected to be associated with non‐zero toxicity. Then, this term drives allocation away from the underdosing regimens.

All terms are dependent—an increase in one leads to decreases in others. The optimal value is attained at the point of target characteristics only. The denominators drive away the selection from inefficacious and highly toxic regimens and concentrate the allocation in the neighbourhood of the OBR.

The trade‐off function (6) depends on probabilities θ ₁ and θ ₂ whereas the goal of a phase I–II clinical trial is conventionally formulated in terms of toxicity α _t and efficacy α _e probabilities and corresponding targets γ _t and γ _e. Thus, we reparameterize function (6) by using θ ₁=(1−α _t)α _e, θ ₂=(1−α _t)(1−α _e), γ ₁=(1−γ _t)γ _e and γ ₂=(1−γ _t)(1−γ _e) and denote the trade‐off function by δ(α _t,α _e,γ _t,γ _e). This measure can be computed for each of the M regimens under study with parameters α _t,1,…,α _t,M and α _e,1,…,α _e,M respectively. Given δ(α _t,i,α _e,i,γ _t,γ _e), i=1,…,M, the target regimen j satisfies

$$\delta ({\alpha }_{\mathrm{t},j},{\alpha }_{\mathrm{e},j},{\gamma }_{\mathrm{t}},{\gamma }_{\mathrm{e}})=\underset{i=1,\dots ,M}{min}\delta ({\alpha }_{\mathrm{t},i},{\alpha }_{\mathrm{e},i},{\gamma }_{\mathrm{t}},{\gamma }_{\mathrm{e}}).$$ (7)

Efficacy–toxicity trade‐off contours for various combinations of toxicity and efficacy probabilities and γ _t=0.01 and γ _e=0.99 are given in Fig. 1. The contours of the trade‐off function are concave. The most desirable point α _t=0.01, α _e=0.99 (bottom right‐hand corner) corresponds to the minimum of the trade‐off function. As probabilities move away from this point the trade‐off function grows with an increasing rate that can be seen by contours that are closer to each other.

Figure 1.

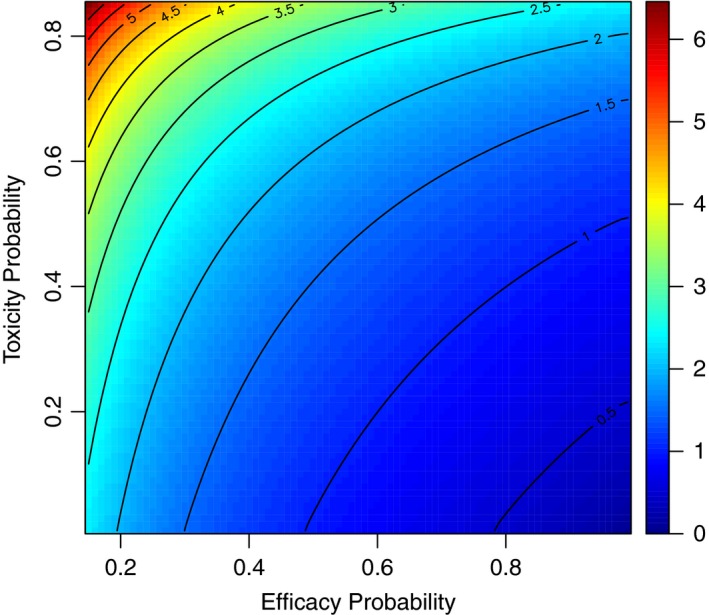
Contours of the efficacy–toxicity trade‐off function δ(α _t,α _e,γ _t,γ _e) for ${\alpha }_{\mathrm{t}}\in (0,0\text{.}85)$ and ${\alpha }_{\mathrm{e}}\in (0\text{.}15,1)$, γ _t=0.01 and γ _e=0.99

2.2. Estimation

The proposed trade‐off function for regimen i depends on unknown parameters α _t,i and α _e,i. Although these could be estimated by using model‐based approaches such as the continual reassessment method (O’Quigley et al., 1990), we can also consider each toxicity and efficacy probability independently as a beta random variable estimated directly from the observed number of toxicities or efficacies. This enables the design to avoid the monotonicity assumption which motivated this work initially.

Consider an estimator for regimen i. The toxicity probability has prior distribution $\mathcal{B}({\nu }_{\mathrm{t},i}+1,{\beta }_{\mathrm{t},i}-{\nu }_{\mathrm{t},i}+1)$, ν _t,i,β _t,i>0. After $n_i$ patients and x _t,i toxicities, we obtain the beta posterior $\mathcal{B}(x_{\mathrm{t},i}+{\nu }_{\mathrm{t},i}+1,n_i-x_{\mathrm{t},i}+{\beta }_{\mathrm{t},i}-{\nu }_{\mathrm{t},i}+1)$ which concentrates in the neighbourhood of 0<α _t,i<1. Similarly, given prior beta parameters ν _e,i,β _e,i>0 and x _e,i efficacy responses the beta posterior $\mathcal{B}(x_{\mathrm{e},i}+{\nu }_{\mathrm{e},i}+1,n_i-x_{\mathrm{e},i}+{\beta }_{\mathrm{e},i}-{\nu }_{\mathrm{e},i}+1)$ for the efficacy probability can be found. The posterior modes of these beta distributions are

$$\begin{array}{cc}& {\widehat{p}}_{\mathrm{t},i}^{(n_i)}=\frac{x_{\mathrm{t},i}+{\nu }_{\mathrm{t},i}}{n_i+{\beta }_{\mathrm{t},i}},\hfill \\ & {\widehat{p}}_{\mathrm{e},i}^{(n_i)}=\frac{x_{\mathrm{e},i}+{\nu }_{\mathrm{e},i}}{n_i+{\beta }_{\mathrm{e},i}}\hfill \end{array}$$ (8)

respectively. We then use the ‘plug‐in’ estimator $\delta ({\widehat{p}}_{\mathrm{t},i}^{(n_i)},{\widehat{p}}_{\mathrm{e},i}^{(n_i)},{\gamma }_{\mathrm{t}},{\gamma }_{\mathrm{e}})={\widehat{\delta }}_i^{(n_i)}$ as the criterion that governs the selection of a subsequent regimen to be studied in a phase I–II regime finding trial.

We emphasize that the trade‐off function (6) is derived in the general form without assuming independence between toxicity and efficacy. Whereas estimators (8) do not account for the interaction between toxicity and efficacy, the derived trade‐off function does.

3. Regimen finding algorithm

3.1. Non‐randomized design

We propose the following novel regimen finding design that does not require the assumption of monotonicity for trials looking to identify a regimen with toxicity probability γ _t and efficacy probability γ _e. Assume that N patients and M regimens are available in a trial. Patients are assigned sequentially cohort by cohort, where a cohort is a small group of typically 1–4 patients. Let ${\widehat{\delta }}_i^{(n_i)}$ be the plug‐in estimator for regimen i after $n_i$ patients have been treated on regimen i. The procedure starts from ${\widehat{\delta }}_i^{(0)}$ and the starting regimen depends on the prior only. After $n_i$ patients on regimen i (i=1,…,M) the next cohort of patients is allocated to a regimen m such that

$${\widehat{\delta }}_m^{(n_m)}=\underset{i=1,\dots ,M}{\text{min}}{\widehat{\delta }}_i^{(n_i)}.$$ (9)

The method proceeds until the maximum number of patients, N, have been treated. We adopt the regimen that is selected after N patients as the final recommended regimen.

Note that the estimators (8) require a vector of prior probabilities for each regimen to be specified before the trial. This choice implies a specific ordering of the regimens before trial data are available and can be considered as an initial ordering. However, as the trial progresses this ordering can change. We refer to the proposed design as the weighted entropy (WE) design, as the WE motivated the criterion.

3.2. Randomized design

For the WE design all previous outcomes are taken into account for the current selection decision. In this case designs can ‘lock in’ which means that one regimen would be tested regardless of further outcomes and the true optimal regimen can never be tested. It might happen because of certain sequences of observations in combination with the choice of the prior. Thus, one can benefit from the allocation rule based on a randomization (Thall and Wathen, 2007; Wages and Tait, 2015). We propose randomization within a safety set with probabilities proportional to the inverse of the trade‐off function. For ethical considerations we restrict randomization to the two best regimens only. Formally, assume that regimen m is the estimated best regimen (has the minimum value of ${\widehat{\delta }}_m^{(n_m)}$) and j is the second‐best regimen (i.e. has the second‐smallest value of ${\widehat{\delta }}_j^{(n_j)}$). Then, randomization probabilities ${\widehat{w}}_i^{(n_i)}$ for a regimen i=1,…,M are

$${\widehat{w}}_i^{(n_i)}=\left\{\begin{array}{cc}{\displaystyle \frac{1/{\widehat{\delta }}_i^{(n_i)}}{1/{\widehat{\delta }}_m^{(n_m)}+1/{\widehat{\delta }}_j^{(n_j)}},}\hfill & \text{if}i=m,j\text{and}{\widehat{\delta }}_m^{(n_m)},{\widehat{\delta }}_j^{(n_j)}\ne 0,\hfill \\ 1,\hfill & \text{if}{\widehat{\delta }}_i^{(n_i)}=0,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right.$$ (10)

The method proceeds until the maximum number of patients, N, have been treated. The regimen m satisfying equation (9) is adopted as the final recommendation. We refer to this design as ‘WE(R)’. This randomization technique enables us to obtain a more spread allocation, while assigning only few patients to suboptimal regimens. We shall focus on these two allocation rules only although other alternatives are possible. For instance, one might assign the first patients by using randomization and the rest by using allocation to the ‘best’ as suggested by Wages and Tait (2015).

3.3. Delayed responses

So far, it has been implied that efficacy responses are available at the same time as the toxicity information is. However, in practice this is unlikely to be true. Whereas toxicity is usually quickly ascertainable, the efficacy end point may take longer to be observed (Riviere et al., 2018) and waiting for both end points increases the length of a trial substantially. However, the criterion proposed still can be applied in the trial with delayed responses as ${\widehat{p}}_{\mathrm{t},\mathrm{i}}^{(n_i)}$ and ${\widehat{p}}_{\mathrm{e},i}^{(n_i)}$ can be estimated on the basis of a different number of observations. Consequently, the design can proceed before the full response has been observed and would only use the information that is available at the time that the regimen for the next cohort is selected.

For instance, in the motivating trial it takes twice as long to observe the efficacy outcome than the toxicity outcome (6 weeks versus 3 weeks). To conduct the trial in a timely manner, the next cohort of patients is expected to be assigned on the basis of the toxicity data only for the previous cohort and both toxicity and efficacy data for earlier patients. For instance, the recommendation for the third cohort is based on both toxicity and efficacy outcomes for cohort 1 but only the toxicity outcomes for cohort 2. The design proposed accommodates this by computing toxicity and efficacy estimates on the basis of different numbers of observations, but on all the available information up to the time of the next patient allocation. If an efficacy outcome is available earlier, it can (and should) be included in the design. Doing so can improve the performance of the design as illustrated in the on‐line supplementary materials. Note also that there may be situations in which auxiliary information about efficacy is available (e.g. through a short‐term end point). Accounting for this information is beyond the scope of this paper.

3.4. Coherence

In practice, a clinician might be very cautious about further escalation if a toxicity was observed in the previous cohort. For this reason, we force the WE designs to satisfy principles of the coherent escalation or de‐escalation (Cheung, 2005) with respect to known orderings. Assume that there are S known monotonic partial orderings. Denote the position of a regimen for cohort i in the partial ordering s by _[s] T ⁽ⁱ⁾ and the sum of the corresponding toxicity outcomes by Q ⁽ⁱ⁾. Then the coherent escalation means that

$$\mathbb{P}{(}_{[s]}{T}^{(i)}{-}_{[s]}{T}^{(i-1)}>0|Q^{(i-1)}\ge q)=0,s\in S,$$ (11)

where q is a threshold number of toxicities after which the escalation should be prohibited. The coherent de‐escalation means that

$$\mathbb{P}{(}_{[s]}{T}^{(i)}{-}_{[s]}{T}^{(i-1)}<0|Q^{(i-1)}<q)=0,s\in S.$$ (12)

For instance, in the motivating example the following partial orderings are known:

$$\left.\begin{array}{c}\hfill {\alpha }_{\mathrm{t},1}\le {\alpha }_{\mathrm{t},2}\le {\alpha }_{\mathrm{t},3}\le {\alpha }_{\mathrm{t},6},\\ \hfill {\alpha }_{\mathrm{t},1}\le {\alpha }_{\mathrm{t},2}\le {\alpha }_{\mathrm{t},4}\le {\alpha }_{\mathrm{t},6},\\ \hfill {\alpha }_{\mathrm{t},1}\le {\alpha }_{\mathrm{t},2}\le {\alpha }_{\mathrm{t},5}\le {\alpha }_{\mathrm{t},6}.\end{array}\right\}$$ (13)

It follows that if more than q toxicity outcomes are observed for T ₃ the next cohort can be still allocated to T ₄. Moreover, these coherence principles are used to incorporate the information about pairs of regimens that can be ordered (e.g. T ₁ and T ₂). Although it is not taken into account in the estimation step of the original design, it is reflected in allocation restrictions.

3.5. Illustration

Below, we demonstrate the performance of the non‐randomized WE design in the context of the motivating trial. The major challenge of the motivating trial is the uncertainty in the regimen–toxicity relationship for T ₃, T ₄ and T ₅ which results in six possible toxicity orderings (1). Furthermore, for each of these toxicity orderings either a monotonic, plateau or umbrella regimen–efficacy relationship can be expected. Despite this complex setting, the WE design can be applied as both toxicity and efficacy end points are binary.

We consider the regimen finding clinical trial with M=6 regimens, T ₁,…,T ₆, N=36 patients and cohort size c=2. The regimens are ordered (on the basis of clinicians’ beliefs) with increasing toxicity and efficacy. The trial is to be started at regimen T ₁ and no regimen skipping is allowed. The coherence parameter is fixed to be q=1 and the escalation–de‐escalation is required to be coherent with respect to known partial orderings (13). Following the motivating trial, toxicity is evaluated after two cycles of treatment (3 weeks) and efficacy data are available after four cycles (6 weeks) only. Since it is expected to recruit two patients per month, we assume that the next cohort is assigned after the toxicity outcome is available for the previous cohort. Moreover, efficacy is observed only for patients without toxicity.

True probabilities of toxicity and efficacy are α _t=(0.05,0.10,0.45,0.15,0.30,0.55)^T and α _e=(0.10,0.40,0.70,0.70,0.70,0.70)^T. This scenario corresponds to a plateau in the regimen–efficacy relationship starting at T ₃ and to the misspecified ordering of toxicities—regimen T ₃ is more toxic than regimens T ₄ and T ₅. We study the ability of the WE design to recommend the optimal and correct regimens. The safest regimen with a toxicity probability below the upper toxicity bound ϕ and the highest efficacy above the lowest efficacy bound ψ is called optimal and the regimen with the highest efficacy rate while still safeguarding patients (irrespectively of also having lowest toxicity) is called correct. Then, for a maximum toxicity probability bound ϕ=0.35 and a minimum efficacy probability bound ψ=0.20, regimen T ₄ is optimal and regimens T ₄ and T ₅ are correct. To ensure that a regimen with the same efficacy but lower toxicity is preferred over a regimen with higher toxicity we set γ _t=0.01 and, similarly, we set γ _e=0.99 to prefer a regimen with a higher efficacy if the toxicity is the same. To see that T ₄ is indeed the OBR by using these targets, we can compute the true values of the trade‐off function (9.48,1.77,1.59, 0.67,1.03,2.16)^T. The minimum (0.67) among all regimes corresponds to T ₄ as desired and the second‐smallest value corresponds to the correct regimen T ₅.

Prior parameters of toxicity ${\widehat{p}}_{\mathrm{t}}^{(0)}={(0.10,0.175,0.25,0.325,0.40,0.475)}^{\mathrm{T}}$, efficacy ${\widehat{p}}_{\mathrm{e}}^{(0)}={(0.60,0.65,0.70,0.75,0.80,0.85)}^{\mathrm{T}}$ and β _t,i=β _e,i=1, i=1,…,6, are chosen. Note that the purpose of this prior is to specify in which order the regimens are trialled. The allocation of 18 cohorts in a single simulated trial is given in Fig. 2. Note that the no toxicity and efficacy and no toxicity and no efficacy outcomes in Fig. 2 can be observed after four cycles only. Until an efficacy outcome is available the design uses information about no toxicity only.

Figure 2.

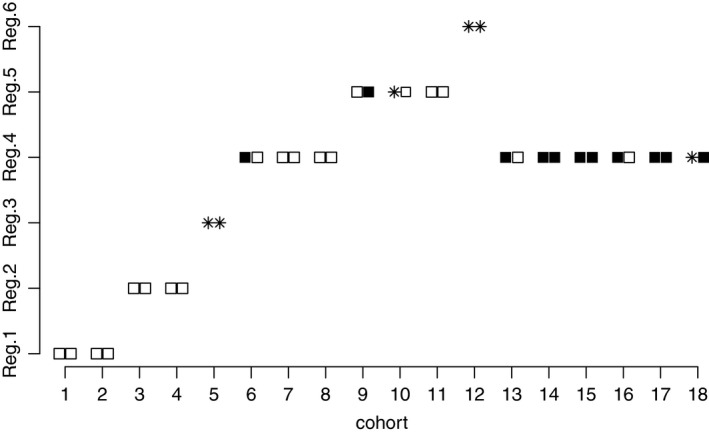
Allocation of 18 cohorts in the individual trial: □, no toxicity and no efficacy; , toxicity; , no toxicity and efficacy

The allocation starts at T ₁ with no toxicities. As no efficacy has been observed yet and T ₁ has ‘promising’ prior efficacy probability, it is selected again. Following no efficacies for cohort 1, cohort 3 is assigned to T ₂ at which no patients have toxicities. This leads to selecting T ₂ again until the efficacy data are available. After no toxicity (cohort 4) and no efficacy (cohort 3), cohort 5 is assigned to T ₃ for which both patients experience toxicities. As there is uncertainty whether T ₃ is more toxic than T ₄ and (or) T ₅, cohort 6 is assigned to T ₄. After no toxicity outcomes have been observed, cohort 7 is allocated to regimen T ₄ again. Because of no toxicity (cohort 7) and one efficacy (cohort 6), regimen T ₄ is chosen for cohort 8 as well. However, after no efficacy for cohort 7, the design escalates to regimen T ₅. Again, as no toxicity outcomes have been observed for cohort 9, cohort 10 is assigned to T ₅ also, at which one patient experiences a toxicity. However, by the time that cohort 11 has been allocated, an efficacy outcome for cohort 9 becomes available and the allocation remains at regimen T ₅. As no further efficacy has been observed for regimen T ₅, the design escalates further to regimen T ₆ for which two toxicities are observed. Then, the design de‐escalates to the optimal regimen T ₄ for which one efficacy and no toxicity has been previously observed (against one efficacy and one toxicity for regimen T ₅). All the consequent patients (up to cohort 18) are assigned to the optimal regimen T ₄ which is finally recommended in the trial. Clearly, a delayed efficacy response requires two cohorts to be assigned to each dose conditionally on no toxicity. It leads to fewer patients at the OBR, but also to more reliable recommendation due to better exploration of the available regimes.

Whereas the regimen finding algorithm in an individual trial is considered above, allocation probabilities for each cohort in 10⁶ replicated trials are given in Fig. 3. Using the WE design, first and second cohorts are to be assigned to the first regimen with probability 1. As was illustrated above, the design stays at T ₁ if no toxicity was observed (due to a ‘promising’ efficacy) or if a toxicity is observed (due to the coherence principle). The probability of allocating a cohort to the optimal regimen T ₄ starts to increase after cohort 5 and reaches nearly 60% for cohort 18. Considering the probability of regimen recommendations, we compare the performance with an equal allocation of six patients per each regimen. For the equal allocation, the trade‐off functions for each regimen are estimated at the end of the trial and the dose with a smallest value is recommended. The optimal regimen T ₄ is recommended in 62.5% of trials and the correct regimen T ₅ in 18.6% of trials by the WE design against 31% and 29% by equal allocation respectively. It means that the design proposed recommends one of the correct regimens in more than 80% of the trials and clearly favours the optimal regimen.

Figure 3.

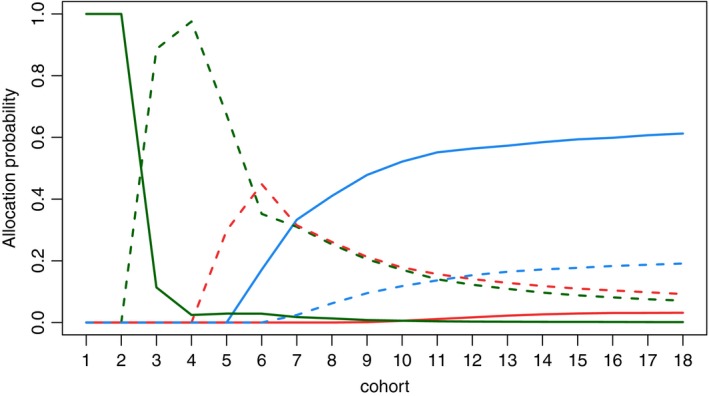
Probabilities to allocate each of 18 cohorts to T ₁ (), T ₂ (), T ₃ (), T ₄ (), T ₅ () and T ₆ () in the motivating trial setting: the optimal regimen is regimen T ₄ and the correct regimens are regimens T ₄ and T ₅; results are based on 10⁶ replications

Overall, the design proposed appears to be able to recommend the optimal regimen with high probability and the escalation–de‐escalation algorithm in the individual trial is intuitive. A comprehensive study comparing the proposed method with alternative approaches and across different scenarios is given in Section 5.

4. Ethical constraints

Not borrowing information across regimens is a key feature of the design proposed. However, some regimens might have high toxicity and/or low efficacy. Then, a design can result in a high or small number of toxicity or efficacy responses respectively or in an unsafe or inefficacious recommendation. For ethical reasons it is required to control the number of patients who are exposed to such regimens and two time varying constraints are introduced.

4.1. Safety constraint

Absence of the monotonicity assumption for toxicity makes the problem of the highly toxic regimen selection even more crucial. A conventional (constant) safety constraint (e.g. as in Riviere et al. (2018)) cannot be applied because no parametric model is used (Mozgunov and Jaki, 2017). On the one hand, a reliable safety constraint should give the hypothetical possibility of testing all regimens if data suggest so. On the other hand, a recommendation should be made with a high confidence in safety. A time varying safety constraint meets both of these requirements. A regimen i is safe if after $n_i$ patients

$${\int }_{{\varphi }^{*}}^1{f}_{\mathrm{t},i}^{(n_i)}(p)\mathrm{d}p⩽{\zeta }^{(n_i)}$$ (14)

where $f_{\mathrm{t},i}^{(n_i)}$ is the beta posterior density function of the toxicity probability, ${\varphi }^{*}$ is the toxicity threshold and ${\zeta }_{n_i}$ is the probability that controls overdosing. As information increases, we gain confidence about a regimen's safety and hence consider the constraint that becomes more strict as the trial progresses. We therefore use a non‐increasing function of $n_i$ for ${\zeta }^{(n_i)}$. We choose ζ ⁽⁰⁾=1 initially to allow all regimens to be tested whereas the final recommendation is made with probability ζ _N. Subsequently we use a linear decreasing function ${\zeta }^{(n_i)}=\text{max}(1-r_{\mathrm{t}}{n}_i,{\zeta }_N)$ where r _t>0. These safety constraint parameters can either be specified by experts or alternatively calibrated with respect to a trial's goals by using simulations.

4.2. Futility constraint

The same reasoning is applied to a time varying futility constraint. Regimen i is efficacious if after $n_i$ patients

$${\int }_{{\psi }^{*}}^1{f}_{\mathrm{e},i}^{(n_i)}(p)\mathrm{d}p⩾{\xi }^{(n_i)}$$ (15)

where $f_{\mathrm{e},i}^{(n_i)}$ is the beta posterior density function of the efficacy probability, ${\psi }^{*}$ is the efficacy threshold and ${\xi }^{(n_i)}$ is the controlling probability. This probability is an increasing function of $n_i$ and the recommendation is made with probability ξ _N. We use a linear increasing function ${\xi }^{(n_i)}=min(r_{\mathrm{e}}{n}_i,{\xi }_N)$ where r _e>0.

5. Numerical results

5.1. Setting

In this section we study the performance of the proposed design in the context of the motivating trial under various scenarios. Following the motivating trial, we consider M=6 regimens and N=36 patients who are enrolled in cohorts of c=2. The setting as stated in Section 3.5 remains unchanged. The upper toxicity and the lowest efficacy bounds are ϕ=0.35 and ψ=0.20 respectively. The goal is to study the ability of the WE design to identify the optimal and correct regimens as defined above.

The major challenge of the motivating trial is the uncertainty in both regimen–toxicity and regimen–efficacy relationships. This increases the number of possible scenarios to be investigated enormously. Therefore, we start by defining scenarios on which the assessment will be based. Firstly, we specify 14 scenarios with increasing regimen–toxicity relationships and different shapes of regimen–efficacy curves (Fig. 4): eight plateau regimen–efficacy scenarios (1–8) by Riviere et al. (2018), four umbrella‐shaped scenarios (9–12) by Wages and Tait (2015) and two scenarios with no optimal and correct regimens (13 and 14, due to inefficacy and toxicity respectively). These scenarios were originally used to test the WE approach for phase I–II dose finding designs with a single targeted agent and compare its performance with the methods by Wages and Tait (2015) and Riviere et al. (2018). The results of this evaluation are given in the on‐line supplementary materials. Secondly, to allow for the uncertainty in the toxicity ordering, we consider six permutations of each scenario with respect to toxicity orderings (1). For instance, six permutations of scenario 1 are given in Table 2. Overall, this results in 84 scenarios that cover a large variety of possibilities and allows the design proposed to be assessed in the setting of the motivating trial adequately. In the analysis we focus on

Figure 4.

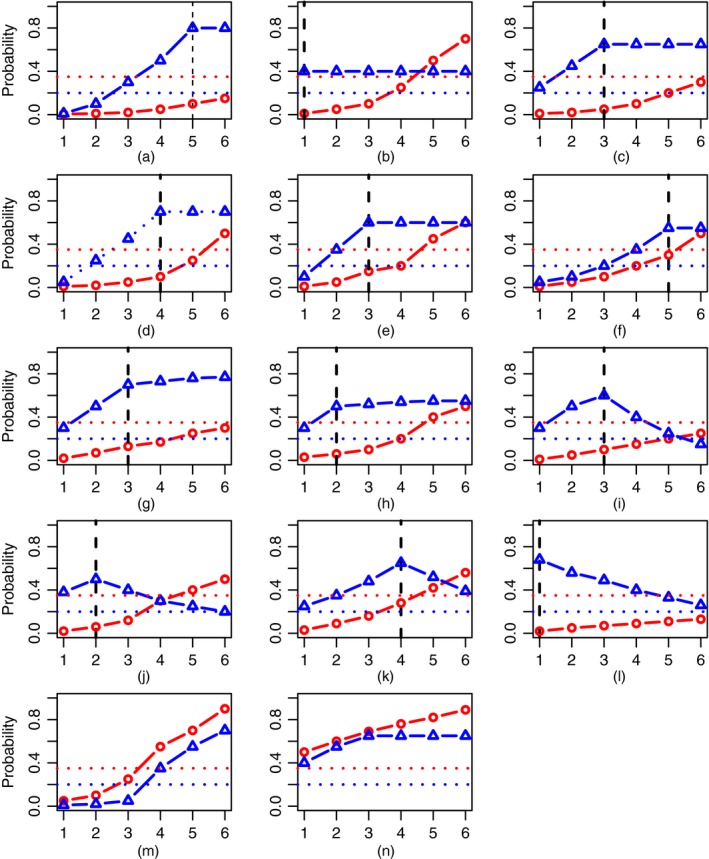
Eight plateau regimen–efficacy scenarios (1–8), four umbrella regimen–efficacy scenarios (9–12) and two scenarios with no correct regimens (13 and 14) in the trial with M=6 regimens (, toxicity probabilities; , efficacy probabilities; , upper toxicity bound ϕ=0.35; , lowest efficacy bound ψ=0.20; , optimal regimen): (a) scenario 1; (b) scenario 2; (c) scenario 3; (d) scenario 4; (e) scenario 5; (f) scenario 6; (g) scenario 7; (h) scenario 8; (i) scenario 9; (j) scenario 10; (k) scenario 11; (l) scenario 12; (m) scenario 13; (n) scenario 14

Table 2.

Six permutations of scenario 1^†

Scenario	T 1	T 2	T 3	T 4	T 5	T 6
1.1	(0.005;0.01)	(0.01;0.10)	(0.02;0.30)	(0.05;0.50)	(0.10;0.80)	(0.15;0.80)
1.2	(0.005;0.01)	(0.01;0.10)	(0.02;0.30)	(0.10;0.80)	(0.05;0.50)	(0.15;0.80)
1.3	(0.005;0.01)	(0.01;0.10)	(0.05;0.50)	(0.02;0.30)	(0.10;0.80)	(0.15;0.80)
1.4	(0.005;0.01)	(0.01;0.10)	(0.10;0.80)	(0.02;0.30)	(0.05;0.50)	(0.15;0.80)
1.5	(0.005;0.01)	(0.01;0.10)	(0.05;0.50)	(0.10;0.80)	(0.02;0.30)	(0.15;0.80)
1.6	(0.005;0.01)	(0.01;0.10)	(0.10;0.80)	(0.05;0.50)	(0.02;0.30)	(0.15;0.80)

† The optimal regimen is in bold and correct regimens are in italics.

• (a)the proportion of optimal/correct recommendations,
• (b)the average number of toxicity responses and
• (c)the average number of efficacy responses.

The study is performed by using R (R Core Team, 2015) and 10000 replications for each scenario. We compare the characteristics with an extended design ‘WT’ by Wages and Tait (2015); WT's specification is given below.

5.2. Design specification

As in the illustrative example above, we use a target toxicity of γ _t=0.01 and a target efficacy of γ _e=0.99. This implies that an investigator targets the most efficacious yet the least toxic regimen. Because of the partially unknown toxicity ordering, the design was restricted to satisfy the coherence conditions (11) and (12) with respect to partial orderings (13) and q=1. The randomized design is presented here as it has been shown in the evaluations of single‐agent trials (see the on‐line supplementary materials) to have more potential benefits when more than one correct regimen is expected in the trial.

Parameters β _t,i=β _e,i=1 of the prior beta distributions in expression (8) are chosen for all regimens i=1,…,6 to emphasize a limited amount of information that is available to clinicians. Parameters ν _t,i and ν _e,i (which coincide with prior toxicity efficacy probabilities for chosen values of β _t,i and β _e,i) are calibrated such that the optimal regimen can be found in various scenarios with high probability. The design is fully driven by the values of the trade‐off function and, therefore, there are two requirements to the prior parameters. The prior should dictate starting the trial at the lowest regimen T ₁ and the design should follow the escalation order of regimens that are specified by clinicians (with no regimen skipping). To preserve a gradual escalation, the prior should assume that the higher regimens have greater efficacy, but also greater toxicity. To restrict the number of prior parameters to be calibrated, we would assume a linear increase in prior toxicity and efficacy probabilities. Through extensive calibration, prior vectors of toxicity probabilities ${\widehat{\mathbf{p}}}_{\mathrm{t}}^{(0)}={(0.10,0.14,0.18,0.22,0.26,0.30)}^{\mathrm{T}}$ and efficacy probabilities ${\widehat{\mathbf{p}}}_{\mathrm{e}}^{(0)}={(0.60,0.62,0.64,0.66,0.68,0.70)}^{\mathrm{T}}$ were chosen for subsequent analysis in all scenarios. Despite the increasing prior probabilities, the ordering of the regimes is not fixed and can change as the trial progresses.

Regarding the ethical constraint, parameters of the safety constraint ζ _N=0.30, r _t=0.02 and ${\varphi }^{*}=0.4$ and of the futility constraint ${\xi }_N=0.50,r_{\mathrm{e}}=0.05\text{and}{\psi }^{*}=0.35$ were calibrated. Further guidelines on the prior parameters choice together with the calibration of safety and futility constraints are given in the on‐line supplementary materials.

We compare the performance of the novel approach with the extension of WT by Wages and Tait (2015). We extend the original WT to allow the randomization between toxicity orderings. Following Wages and Tait (2015), a trial with a monotonic regimen–toxicity relationship and six regimens is associated with 11 efficacy orderings: one strictly monotonic, five cases of a plateau location and five cases of an umbrella peak. Similarly, one can deduce all possible efficacy orderings that are associated with each toxicity ordering. For instance, for the toxicity ordering T ₁, T ₂, T ₃, T ₅, T ₄, T ₆ we specify

• (a)0.10, 0.20, 0.30, 0.50, 0.40, 0.60 (monotonic with respect to regimen–toxicity),
• (b)0.20, 0.30, 0.40, 0.60, 0.50, 0.60 (plateau starting at T ₄),
• (c)0.30, 0.40, 0.50, 0.50, 0.60, 0.40 (peak at T ₅),
• (d)0.20, 0.30, 0.40, 0.60, 0.50, 0.50 (peak at T ₄),
• (e)0.40, 0.50, 0.60, 0.40, 0.50, 0.30 (peak at T ₃),
• (f)0.50, 0.60, 0.50, 0.30, 0.40, 0.20 (peak at T ₂) and
• (g)0.60, 0.50, 0.40, 0.20, 0.30, 0.10 (peak at T ₁).

Other orderings as a ‘plateau starting at T ₁/T ₂/T ₃/T ₅’ are already included in the first regimen–toxicity case. Applying the same procedure to the rest of the toxicity orderings in equation (1) leads to 48 efficacy orderings. The design proceeds as follows. Firstly, given the available data, one of six toxicity orderings is selected as proposed by Wages et al. (2011). Secondly, one of 48 efficacy orderings is chosen as in the original design. The parameters of the designs are chosen as in the specification by Wages and Tait (2015) with an exception of using cohort size c=2 and 80% confidence intervals for stopping rules. Note that WT waits for both toxicity and efficacy responses to allocate the next cohort and assumes that an efficacy outcome is observed regardless of the toxicity outcome.

Variations of the extended WT design were also explored. A reduced number of efficacy orderings (plateau cases only) were investigated, but no significant difference was found, and the specification with the full number of orderings was found to be more robust. Additionally, the ‘conditional’ choice of the efficacy orderings was also studied. Using this approach, once the toxicity orderings have been selected, that choice of the efficacy orderings is restricted to 11 orderings with respect to the toxicity profile. However, it was found to result in less accurate optimal and correct regimen recommendations across all scenarios.

5.3. Operating characteristics

The results of the comparison in scenarios 1–12 by using six permutations are summarized in Fig. 5. The length of the bar corresponds to the proportion of the optimal (full) and correct (light) regimen recommendations by WE(R) (black) and WT (red). Overall, both designs are robust to toxicity ordering permutations under all scenarios. The difference of minimum and maximum proportions of the optimal and correct recommendations within one scenario does not exceed 5% and 8% for either design respectively. Regarding the proportion of correct recommendations, the designs perform comparably (no more than 5% difference) in scenarios with several correct regimens (scenarios 2–5, 7 and 8) with scenario 1 being an exception (8% difference in favour of WT). Regardless of the large number of orderings, WT preserves its accuracy in terms of the correct regimen recommendation.

Figure 5.

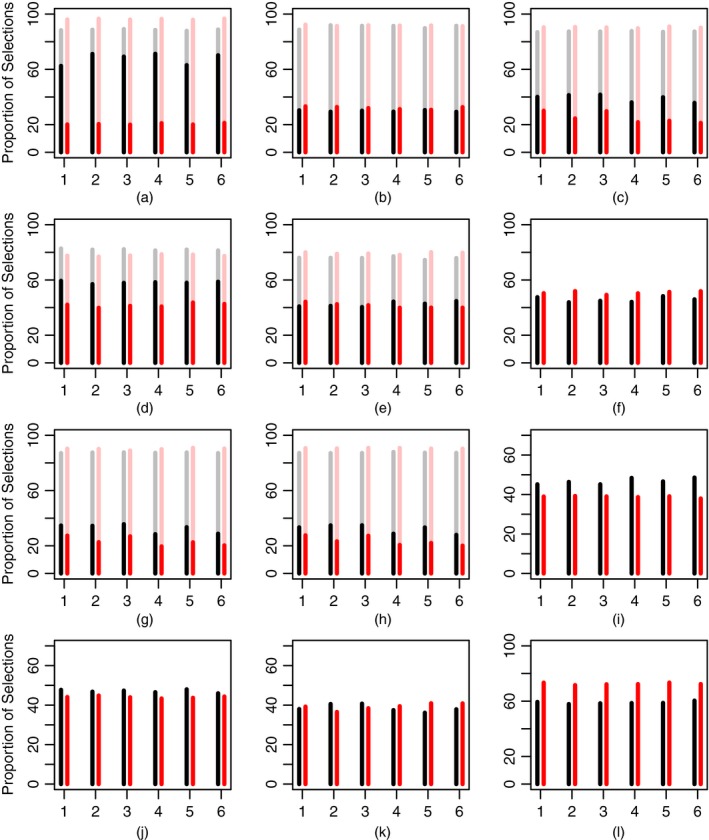
Proportion of optimal (full) and correct (light) recommendations by WE(R) (black) and WT (red) designs in scenarios 1–12 across six permutations (the results are based on 10⁴ replications): (a) scenario 1; (b) scenario 2; (c) scenario 3; (d) scenario 4; (e) scenario 5; (f) scenario 6; (g) scenario 7; (h) scenario 8; (i) scenario 9; (j) scenario 10; (k) scenario 11; (l) scenario 12

Comparing optimal regimen recommendations, WE(R) favours the optimal regimen over other correct regimens systematically. It results in superior characteristics in half of all scenarios: 1, 3, 4 and 7–9 with the minimum difference across permutations ranging from 7% (scenario 7) up to 45% (scenario 1) and the maximum difference varying between 11% and 52% respectively. Generally, WT is less conservative as it favours safe regimens with higher toxicity that results in a lower proportion of optimal recommendations in these scenarios. Both designs perform comparably in scenarios 2, 5, 10 and 11 within the maximum difference of 2–4%. At the same time, the less conservative nature of WT enables it to outperform WE(R) by 3–8% under scenario 6 in which the optimal regimen is the highest safe regimen. WT also shows better performance in scenario 12 with the difference in the proportion of optimal recommendations ranging by 10–13%. Regimen 1 is optimal and 36 patients are not enough for WE(R) to investigate all regimens and to come back to T ₁, but it is enough for WT to identify the decreasing ordering.

Regarding scenarios 13 and 14 with no correct and no optimal regimens because of futility and high toxicity, WE(R) terminates the trial earlier in nearly 72% and 85% of the trials against 68% and 79% respectively. WE(R) results in 10.5 and 10.3 toxic responses on average in scenarios 13 and 14 against 10.4 and 10.5 by WT respectively. Regarding efficacy outcomes, WE(R) results in 7.0 and 8.7 responses versus 7.4 and 9.0 by WT. It follows that both designs can terminate the trial with high probability and prevent unethical patient allocations. Investigating further ethical aspects of the design, the average numbers of toxicity and efficacy responses across all permutations in the rest of the scenarios are given in Table 3.

Table 3.

Mean number of toxicity and efficacy responses in scenarios 1–12 across six permutations by using N=36 patients and M=6 regimens^†

Scenario	Toxicity responses		Efficacy responses
	WE(R)	WT	WE(R)	WT
1	2.5	4.1	19.8	24.5
2	6.4	5.0	14.4	14.4
3	3.2	4.5	20.8	21.0
4	4.4	7.1	19.5	21.4
5	7.0	7.9	18.2	19.0
6	7.7	8.7	12.5	13.8
7	5.1	5.9	22.8	23.4
8	5.1	6.0	22.8	23.5
9	3.9	3.3	15.4	15.8
10	5.9	4.2	13.7	14.4
11	7.8	7.5	16.7	16.7
12	2.4	1.5	18.1	21.5

†Figures corresponding to the best performance are in italics. The results are based on 10⁴ replications.

WE(R) is generally more safe and results in at least nearly one fewer toxic response in scenarios 1 and 3–8 with the largest difference of 2.7 in scenario 4. WT results in fewer toxicities in scenarios where the target regimen is among the first (scenarios 2, 10 and 12). Whereas the prior toxicity vector chosen for WE(R) suggests proceeding escalation, the model‐based approach can identify the correct ordering faster. The average number of efficacy outcomes does not differ by more than 1 in the majority of scenarios (2, 3, 5 and 7–11). Because WT waits for the complete efficacy response and because of its model‐based nature, it results in 1–5 more average efficacy responses in scenarios 1, 4, 6 and 12. At the same time, WE(R) waits for the efficacy outcome and escalates more slowly as was shown in Section 3.5.

Summarizing, the design proposed is robust to the possible true toxicity and efficacy orderings. WE(R) is found to be a good and comparable alternative to the model‐based design when large numbers of orderings are to be considered and the randomization might be difficult to justify in an application. Although all possible toxicity and efficacy orderings are still feasible to specify, it can be challenging to convince a clinician to randomize between them given the limited sample size of N=36 patients. WE(R) can identify optimal and correct regimens with high probability while being more safe than the model‐based design and has a comparable number of efficacies in the majority of realistic scenarios.

5.4. Sensitivity analysis

In the simulation study above, the toxicity and efficacy outcomes were assumed to be uncorrelated, which may not hold in an actual trial. In this section, we investigate the robustness of WE(R) to the correlation in toxicity and efficacy under scenarios given in Fig. 4. The study was also conducted for various toxicity orderings permutations and the same qualitative results were obtained (which are not shown).

We follow the procedure that was proposed by Tate (1955) to generate correlated binary toxicity and efficacy outcomes. The procedure generates a binary normal vector with unit variances and prespecified correlation coefficient ρ. The random variable generated is then transformed into a binary response by applying the cumulative distribution function and a quantile transformation, subsequently.

The results of the WE(R)'s performance in the case of high negative correlation (ρ=−0.8), an absence of correlation (ρ=0.0) and high positive correlation (ρ=0.8) under scenarios 1–12 are summarized in Table 4. In the majority of scenarios, WE(R) is robust to both negative and positive correlations. The differences between the proportion of optimal recommendations in positively and negatively correlated cases do not exceed 8% in 10 out of 12 scenarios with scenarios 2 and 8 being exceptions. Moreover, the proportions of optimal recommendations in correlated cases never differ by more than 10% compared with the uncorrelated one. A noticeable difference in the performance can be seen in plateau scenarios 2 and 8 in which the optimal regimens are among low regimens (T ₁ and T ₂ respectively). In these scenarios efficacy probabilities are nearly the same. The negative correlation biases the recommendations to higher regimens which worsen the proportion of optimal recommendations by nearly 9% in scenarios 2 and 8. In contrast, the positive correlation biases selections to lower regimens and leads to an increase by 10% and 6% in the proportion of optimal recommendations in these scenarios. There are no noticeable changes in the rest of the scenarios as the bias that is caused by the correlation is smaller than the difference in true toxicity and efficacy probabilities.

Table 4.

Operating characteristics of WE(R) in scenarios 1–12: proportion of optimal and correct recommendations for different values of toxicity and efficacy outcomes correlation r={−0.8,0.0,0.8}^†

Scenario	Proportion of optimal recommendations			Proportion of correct recommendations
	ρ=−0.8	ρ=0.0	ρ=0.8	ρ=−0.8	ρ=0.0	ρ=0.8
1	70.7	66.5	65.5	90.9	88.1	88.4
2	22.5	31.0	41.2	81.2	89.7	96.6
3	37.7	39.5	42.4	91.4	87.2	84.8
4	59.8	59.3	61.4	91.8	86.7	84.5
5	40.0	40.5	42.7	78.0	73.2	73.6
6	52.8	46.8	47.5	52.8	46.8	47.5
7	36.2	33.2	33.5	91.6	86.7	86.2
8	24.7	32.8	38.3	75.4	77.5	80.9
9	51.1	44.8	43.6	51.1	44.8	43.6
10	45.9	47.7	51.4	45.9	47.7	51.4
11	45.1	38.5	37.3	48.1	38.5	37.3
12	56.0	59.1	63.6	56.0	59.1	63.6

†The largest deviations are in italics. Results are based on 10⁴ replications.

Overall, the design proposed is robust to the highly correlated toxicity and efficacy outcomes. The proportion of optimal and correct recommendations in the correlated cases never differs by more than 10% compared with the uncorrelated case. Despite assumed independence in the estimates, WE(R) can find the optimal and correct regimens in highly correlated cases.

6. Conclusions

In this paper, we have introduced a novel phase I–II design for molecularly targeted agents that does not require an assumption of monotonicity. The design is based on the simple and intuitively clear trade‐off function which can be easily computed by non‐statisticians. The simulation results demonstrate that the novel approach can identify the optimal regimen with high probability and leads to ethical patient allocations. Therefore, it can be recommended for clinical application with a limited sample size and missing, delayed efficacy responses. The novel design is applied to the challenging combination–schedule trial with uncertainty in both toxicity and efficacy ordering. The proposal is shown to be a good alternative to the model‐based designs when the ordering specification is challenging.

In this paper we have considered the setting where efficacy can be observed only if no toxicity is observed in a patient. At the same time, a setting with four possible outcomes can be also considered by using the same information theoretic approach. The only difference is the form of the Dirichlet distribution (2) which is used to obtain the trade‐off function (Mozgunov and Jaki, 2017). Additionally, the influence of various techniques of the missing and delayed efficacy outcomes implementation can be of interest in a setting with no parametric model. Although only binary outcomes are considered, a continuous efficacy end point becomes the more common choice in a clinical practice. An extension of the proposed design for this case is the subject for future research.

7. Supplementary materials

Refer to the on‐line supplementary materials which provide details on the calibration of design parameters and on the performance of the WE design in the context of a single‐agent trial including the case of efficacy data that are available earlier.

Supporting information

‘An information‐theoretic Phase I/II design for molecularly targeted agents that does not require an assumption of monotonicity. Supplementary Materials’.