Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2018 Oct 25;45(20):10874–10882. doi: 10.1029/2018GL079786

Fast Diffusion of Ultrarelativistic Electrons in the Outer Radiation Belt: 17 March 2015 Storm Event

A N Jaynes 1,✉, A F Ali 2,3, S R Elkington 3, D M Malaspina 3, D N Baker 3, X Li 3, S G Kanekal 4, M G Henderson 5, C A Kletzing 1, J R Wygant 6
PMCID: PMC6472651  PMID: 31007304

Abstract

Inward radial diffusion driven by ULF waves has long been known to be capable of accelerating radiation belt electrons to very high energies within the heart of the belts, but more recent work has shown that radial diffusion values can be highly event‐specific, and mean values or empirical models may not capture the full significance of radial diffusion to acceleration events. Here we present an event of fast inward radial diffusion, occurring during a period following the geomagnetic storm of 17 March 2015. Ultrarelativistic electrons up to ∼8 MeV are accelerated in the absence of intense higher‐frequency plasma waves, indicating an acceleration event in the core of the outer belt driven primarily or entirely by ULF wave‐driven diffusion. We examine this fast diffusion rate along with derived radial diffusion coefficients using particle and fields instruments on the Van Allen Probes spacecraft mission.

Keywords: magnetosphere, radiation belts, radial diffusion, ULF waves

Key Points

  • Fast radial diffusion of ultrarelativistic electrons is observed days after storm main phase

  • Event‐specific radial diffusion can be orders of magnitude higher than statistical values

  • ULF‐wave driven acceleration can account for intense particle enhancement observed in inner magnetosphere

1. Introduction

ULF waves in the inner magnetosphere are known to play a significant, even dominant, role in particle energization at times (e.g., Mann et al., 2013; Ozeke, Mann, Turner, et al., 2014). These waves are created through a variety of processes, including direct solar wind input through the interaction with the magnetopause boundary (Engebretson et al., 1991; Kepko et al., 2002). Interplanetary shocks cause global mode oscillations in the ULF frequency regime (Zong et al., 2009), and high‐speed solar wind can increase the energy transfer to the magnetosphere and generate ULF waves via Kelvin‐Helmholtz instabilities (Claudepierre et al., 2008; Kavosi & Raeder, 2015; Mathie & Mann, 2001). ULF oscillations can also be produced by particle injections deeper in the magnetosphere (James et al., 2013; Yeoman et al., 2010; Zolotukhina et al., 2008) that occur during elevated substorm activity and can access regions close to Earth. Inward radial diffusion, driven by fluctuating electromagnetic fields in drift resonance with trapped particles, serves to energize particle populations by transporting them to drift paths nearer to Earth (e.g., Barker et al., 2005; Elkington et al., 2003; Hudson et al., 2000; Schulz & Lanzerotti, 1974).

In recent times, the role of the radial diffusion mechanism in outer belt electron acceleration has been debated actively. Some studies conclude that energy diffusion enacted by higher‐frequency VLF waves (local acceleration; e.g., Chen et al., 2007; Green & Kivelson, 2004) can be the more significant process, particularly during the main phase of Coronal Mass Ejection (CME)‐driven storms (Reeves et al., 2013; Thorne et al., 2013). However, radial diffusion driven by low‐frequency waves likely plays the leading role in radiation belt acceleration events during the absence of intense VLF chorus. The open question that remains is under what conditions the ULF‐wave driven energization process described here is dominant over VLF local acceleration (which violates the first adiabatic invariant instead of the third).

Early on 17 March 2015, one of the largest geomagnetic storms of the Van Allen Probes period was triggered in Earth's magnetosphere, resulting in a minimum Dst of −222 nT (provisional). The interplanetary shock impact resulted in abrupt and dramatic dynamics in the trapped particle populations from plasmasheet to ultrarelativistic energies. Moderately intense VLF chorus waves were observed during the main phase and particle energization from source (few kiloelectron volts) to seed (tens to hundreds of kiloelectron volts) to relativistic (>500 keV) energies took place over the ensuing hours and days. Impulsive increases in ULF wave power were seen at the time of the shock impact, as well as during scattered time periods over the following few days, far into the relaxation phase of this intense magnetospheric storm. In this paper, we investigate the radial diffusion timescales of ultrarelativistic (multi‐MeV) electrons and their associated energization as uniquely observed during this storm event.

2. Relativistic Electron Observations

The 17 March storm was characterized by a strong interplanetary shock, which impinged upon the magnetosphere at approximately 04:45 UT when the propagated solar wind pressure (OMNI data) reached over 20 nPa (Figure 1e). The Van Allen Probes apogees were in the premidnight sector at the time of the shock; Probe A was heading into perigee, while Probe B was near L = 5 on the way to apogee. The Energetic Particle, Composition, and Thermal Plasma (ECT) suite (Spence et al., 2013) of particle instruments observed energization of the electron population across a broad range of energies throughout the remainder of the day, which resulted in an overall enhancement of particle fluxes above prestorm levels for all but the highest electron energies. The ultrarelativistic electron population (>5 MeV) exhibited a dropout at the time of the shock (Figure 1) and did not reappear at accelerated levels until 19 March and later (depending on energy). Characteristics of the response of medium‐ and high‐energy electrons to this storm are variously studied in recent work (Baker et al., 2016; Foster et al., 2016; Hudson et al., 2017; Kanekal et al., 2016; Z. Li, Hudson, et al., 2016; Z. Li et al., 2017; W. Li, Ma, et al., 2016).

Figure 1.

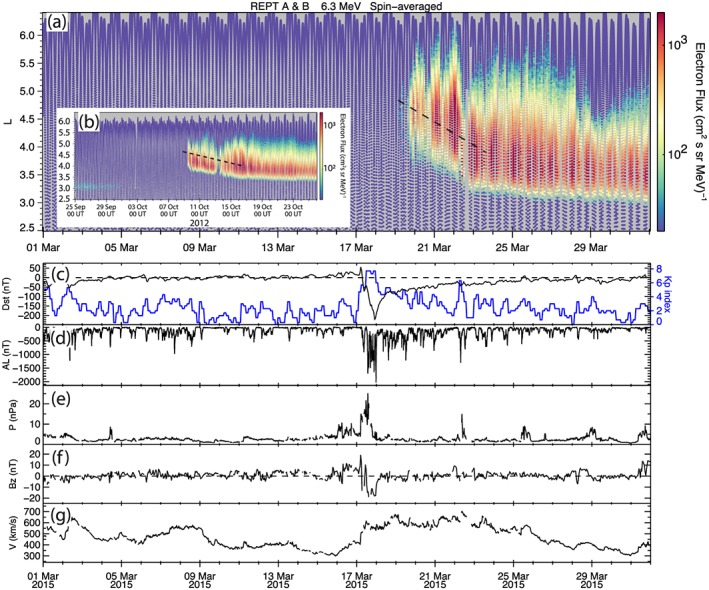
grl58040-fig-0001

Open in a new tab

(a) Fast radial diffusion of ultrarelativistic electrons in the 6.3‐MeV range, crossing 1.5 L‐shell radial distance in 2 days. Compare to much slower diffusion seen in previous strong storm in October 2012—inset (b). Black‐dashed lines in (a) and (b) are included to guide the eye, and each panel is plotted on the same y scale for an equal number of days. OMNIweb solar wind parameters and geomagnetic indices: (c) Dst (storm time ring current) index and Kp (geomagnetic storm) index in blue, (d) AL (substorm activity) index, (e) solar wind dynamic pressure, (f) solar wind Bz, and (g) solar wind speed.

The Dst index reached a minimum of −222 nT (provisional value) at ∼22:00 UT on 17 March (Figure 1c) and began to recover very quickly over the ensuing 16 hr, before slowing to a gradual recovery that returned to a baseline level about 8 days later. The solar wind speed jumped to over 600 km/s along with the intense, structured pressure pulse that indicated the shock approach. Strong, southward interplanetary magnetic field (negative B z) was observed during several extended periods of the storm main phase, accompanied by intense substorm activity as exhibited by a minimum AL value (measure of westward auroral electrojet) of less than −2,200 nT (reached near the end of 17 March, as currently reported in 1‐min OMNI data). However, B z quickly quieted to very small fluctuations around 0 nT by the start of 18 March, and substorm activity dropped off concurrently, with only occasional spikes in activity over the following days. The Kp index was between 2 and 5 for the time period of 19–22 March. Midway through the day on 22 March, Kp spiked to just over 6 (with no appreciable corresponding drop in Dst) and afterward quickly dropped, fluctuating between 1 and 4 for the remainder of the month of March.

A quick recovery and intensification was notable in the seed energy and relativistic energy flux observations up to 1.8 MeV by the end of the 17th (not shown). For these populations, the acceleration was likely due to local heating via VLF waves energized by substorm injections and directly injected “seed energy” electrons (cf. W. Li, Ma, et al., 2016). In contrast, the ultrarelativistic electron acceleration was not observed until after the start of 19 March. Here we briefly note the evolution of VLF chorus waves during this interval, although the data are not shown. Direct wave measurements on the Van Allen Probes' Electric and Magnetic Field Instrument Suite and Integrated Sciences (EMFISIS) instruments showed an increase in wave power within the chorus frequency band following the shock impact on 17 March. Within ∼2 days the chorus power dropped substantially (along with a diminished substorm activity index AL) and remained at low levels for the following days.

Beginning on 19 March, the ultrarelativistic populations were observed to increase in intensity and quickly diffuse inward. At that point, fast inward radial diffusion is observed in multiple energy channels from the REPT instrument onboard both Van Allen Probes A and B following the rapid energization to these energies. These dynamics are illustrated by showing both the electron flux intensity (Figure 2a) at E = 6.3 MeV and the electron phase space density (Figure 2b) at μ = 10,000 MeV/G as a function of L‐shell and L∗ parameter calculated using the TS04D magnetic field model (Tsyganenko & Sitnov, 2005), respectively, with color representing time. At one point, the peak intensity of 6.3‐MeV electrons moves inward over a distance of ∼0.5 in L∗ within 9 hr, corresponding to an estimated diffusion rate of DLL=(ΔL)22Δt = 0.33 days-1. We note that the estimate given here is only a crude approximation, since it is based solely upon particle flux at one energy related to the L∗ parameter although flux is not necessarily conserved; we explore a more rigorous analysis of diffusion rate in section 3. Based on flux observations as shown in Figure 1a, this diffusion rate appears to be the highest in the Van Allen Probes era as confirmed by visual inspection, with rapid energization and diffusion occurring clearly for up to >8‐MeV electrons in the outer zone (supporting information Figure S1) and, as we will show, occurring in concert with brief but repeated intense enhancements of ULF power. For comparison to another strong storm of the Van Allen Probes era, we include an inset panel (Figure 1b) from the 8–9 October 2012 storm.

Figure 2.

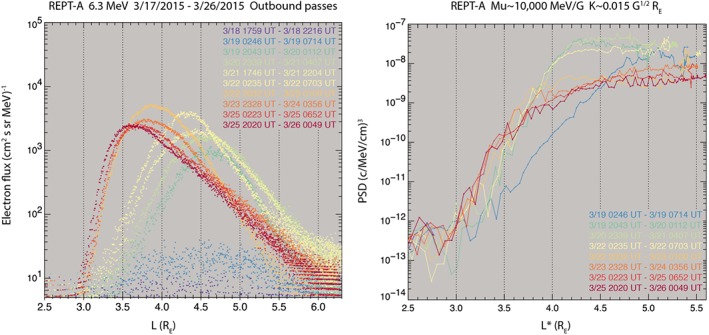
grl58040-fig-0002

Open in a new tab

(left) Electron flux versus L‐shell for all outbound passes covering 18 March to 26 March for 6.3‐MeV electrons, color‐coded by date where cool colors are earlier times and warm colors are later times. (right) Phase space density versus L* (TS04D model) for the same time period (as data coverage allows) representing nearly equatorially mirroring electrons with μ = 10,000 MeV/G, with same color coding by time.

Quantification of radial diffusion coefficients is central to quantifying the amount of acceleration that occurs in various energy populations. Average and statistical radial diffusion rates have been calculated previously (Ali et al., 2015, 2016; Brautigam & Albert, 2000; Brautigam et al., 2005; Ozeke, Mann, Murphy, et al., 2014; Ozeke et al., 2012). This event shows clearly, however, that during intense storm times, rates of radial diffusion can be orders of magnitude higher than typical estimates. We present here a study of this event to quantify this radial diffusion rate and to highlight the effect of ULF‐wave driven diffusion on energetic electron enhancements in the inner magnetosphere when VLF wave activity is largely absent.

3. ULF Wave Observations and Radial Diffusion

While the reduced Fokker‐Planck equation for radial diffusion describes the evolution of phase space density in time (Schulz & Lanzerotti, 1974), it is often times useful to distill coefficients of radial diffusion due to magnetic and electric field fluctuations, DLLB and DLLE. To further investigate the role of ULF‐wave driven radial diffusion in this event, we quantify the radial diffusion coefficients derived directly from in situ magnetic and electric field data from the EMFISIS (Kletzing et al., 2013) and the Electric Field and Waves (EFW) (Wygant et al., 2013) instruments. Following Brizard and Chan (2001) and Elkington et al. (2003) and using the treatment developed in Fälthammar (1965), Fei et al. (2006) derived expressions for radial diffusion coefficients for relativistic charged particles:

DLLB=M28q2γ2BE2RE4L4∑mm2PmB(mωd), (1)
DLLE=18BE2RE2L6∑mPmE(mωd). (2)

In this formulation, M (or μ) is the first invariant of the particle, q is the charge of the particle, γ is the Lorentz factor, B E is the equatorial magnetic field strength at the Earth's surface, R E is the radius of the Earth, L is the Roederer (1970) L ∗ parameter, m is the azimuthal wave mode number, and ω d is the drift frequency of the particle. PmB and PmE are the power spectral densities of the compressional component of the magnetic field and the azimuthal component of the electric field, respectively. The data processing methodology follows from Ali et al. (2016) and can be summarized as such: High‐resolution electric and magnetic field data are resolved into components, using the E→·B→=0 assumption with appropriate error analysis based on magnetic field and spacecraft observing geometry to obtain the unavailable E x measurements (aligned with the spacecraft spin axis which points generally sunward). All problematic data resulting from thruster firings, spacecraft charging events, and eclipse times are omitted. Data are resampled to a constant cadence in radial and azimuthal coordinates to estimate the drift‐averaged power spectral density of the ULF waves along each spacecraft orbit. Radial diffusion coefficients are then estimated using the Fei et al. (2006) expressions. The reader is referred to Ali et al. (2015) and Ali et al. (2016) for more detail.

The power spectral density information is estimated as the spacecraft move through radial distance along their eccentric orbits. The estimated magnetic field power spectral density from 0.28‐ to 8.03‐mHz frequencies do clearly show periods of enhanced ULF wave power often occurring across the entire frequency band shown (Figure 3). As expected, much of the ULF power is concentrated at the very start of the storm main phase and continues with similar intensity through the beginning of 18 March through the period when the Dst index is first rapidly falling and then rapidly recovering (Figure 1c). When the Dst index begins to flatten out for the slower long‐term recovery, ULF wave power dies down. However, bursts of transient but intense wave power are seen throughout the duration of ∼18 March 12 UT to 23 March 02 UT, potentially due to fluctuations in solar wind dynamic pressure (Eriksson et al., 2006). Van Allen Probe B observes very similar characteristics in the magnetic field power spectral density (Figure S2), although at different times due to the high time lag in their nearly identical orbits during this phase of the mission (ΔL of up to 5.3 RE and ΔMLT of up to 6.6 hr), indicating that the overall ULF wave occurrence was higher than observed on either one of the spacecraft. (See Figure S3 for more example orbit configurations during the event.) Intense enhancements up to over 3 nT2/Hz in ULF wave power can be seen in Figure 3 sporadically during the time of fast diffusion noted in the particle observations.

Figure 3.

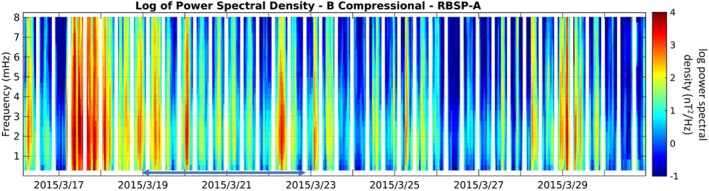
grl58040-fig-0003

Open in a new tab

Power spectral density of in situ magnetic field measurements within the ULF frequency range from 0.28 to 8.03 mHz for Van Allen Probe A from 16 March through 30 March 2015 for the compressional component of B. Blue arrow indicates time of fast radial diffusion as observed in high‐energy particle data.

As detailed in this section, radial diffusion coefficients can be estimated from the ULF wave power spectral density data. We show our estimates of DLLB in Figure 4 plotted against L‐shell for μ = 8,011‐MeV/G electrons (equivalent to 4.8 MeV at L = 4.5, with corresponding drift frequency of ω d∼3 mHz for the m = 1 mode), where color indicates evolution in time from 16 March to just after the start of 27 March. (The derived DLLE coefficients are shown in Figure S4 with data quality caveats described in detail.) At the beginning of 18 March, ULF power is still very intense during the main recovery phase of the storm, and radial diffusion rates are high. From 20 March through 24 March, or the teal, green, and yellow traces, radial diffusion coefficients vary drastically from one orbit to the next and can also be quite high, approaching the level of DLLB on 18 March particularly at L‐shell of 4.5 and above. These orbits cover the time of the overall fast inward motion of the bulk flux as seen in Figures 1a and 2. We will compare these to statistical DLLB coefficients in the next section, though it is worth noting now that the derived coefficients in this case study can be orders of magnitude higher than averaged results for the same μ and storm activity (Kp) level. There is also a large variation in radial diffusion coefficient values over this time period of over 8 days beginning after 19 March (dark blue traces), with DLLB ranging from 0.8 × 10−5 to 0.9 × 10−2 days-1 at L = 3.5 and ranging from 0.3 × 10−4 to 0.3 days-1 at L = 5.5.

Figure 4.

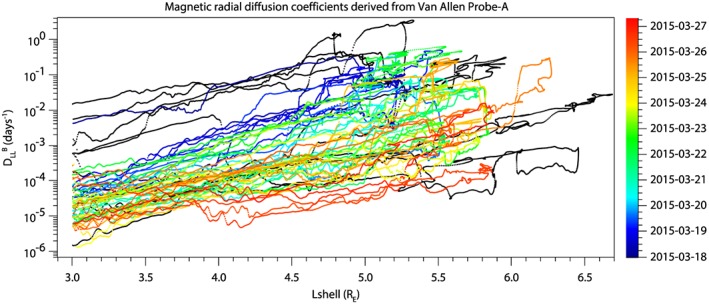
grl58040-fig-0004

Open in a new tab

Magnetic radial diffusion coefficients, DLLB, for first adiabatic invariant μ = 8,011 MeV/G derived from in situ magnetic field measurements on Van Allen Probe A plotted against L‐shell and shown for the time period of 18 March 00 UT through 27 March 06 UT 2015, indicated by change in color. This μ corresponds to roughly 7.2‐ and 3.4‐MeV electron energy at L = 3.5 and 5.5, respectively.

4. Discussion

Here we note some limitations to our data set, before comparing to other radial diffusion coefficients derived from both statistical data sets and simulations. There are severe limitations in making the assumption that the wave power spectral density is drift‐averaged, as we have done here, which is not always valid since the azimuthal distribution can depend on the source location and mechanism of the ULF wave generation (Claudepierre et al., 2008, 2009). We do also assume that ULF wave power is concentrated in the lowest mode (m = 1), which may not be accurate but is at least a well‐founded assumption based on previous work that contends most magnetic wave power is confined in the m = 1 mode, particularly during the recovery period of a storm (Elkington et al., 2013; Z. Li, Hudson, et al., 2016; Tu et al., 2012). With dual‐point space‐based measurements in nonstationary orbits, it is not possible to definitely determine wave power in higher modes. Sophisticated modeling studies using full MHD simulations would be useful to study the distribution of wave power over mode number for this event in particular.

Comparing radial diffusion coefficients among multiple methods is always problematic since the details of each analysis are different (e.g., ground‐based estimates vs. in situ measurements or deriving values from different times in a solar cycle). Regardless, we can compare the coefficients derived in this event‐specific study to the myriad statistical averages published previously to get an idea of the scope of this event compared to a typical Kp = 5 event. Ali et al. (2016), in fact, compares DLLB and DLLE derived from 3 years of Van Allen Probes data to previous averaged results binned by Kp, μ, and L‐shell. They found variation between previous radial diffusion coefficients and those derived with Van Allen Probes data. The magnetic coefficients generally fall in the middle of previously reported values at Kp = 5. The electric coefficients tend to be higher by one to two orders of magnitude than the magnetic coefficients for both Kp = 1 and Kp = 5 scenarios, falling more in line with the previous ground‐based (Ozeke, Mann, Murphy, et al., 2014; Ozeke et al., 2012) and CRRES (Brautigam et al., 2005) estimates, but diverging from the results of Brautigam & Albert, (2000; referred to hereafter as D LL[BA]). The coefficients derived in this study for the period following the 17 March 2015 storm can be 1 to 1.5 orders of magnitude higher than the reported Van Allen Probes average DLLB for Kp = 5. Consistently with all but the D LL[BA] results, our study shows that the DLLE coefficients are dominant over the DLLB coefficients (Figure 4 compared to Figure S4). This may be due to the difference in calculation of D LL[BA] where the coefficients were derived as electromagnetic and electrostatic contributions, rather than taking the full electric field without separating the inductive and convective components. This difference in method can be resolved by comparing the total D LL; however, the electric field coefficients for the March 2015 event are noisy and erratic (likely due to spacecraft charging during elevated electron flux levels), and while it is clear they are overall dominant over the magnetic field coefficients, we do not believe they are suitable to use for a quantitative comparison. Germane to this discussion, Murphy et al. (2015) concluded that ULF wave power and associated radial diffusion coefficients acting in the heart of the outer radiation belt can diverge significantly from the empirical models and Kp‐binned statistical averages, depending on local time and latitude, often far exceeding predicted values during times of most active driving. Additionally, their study found that ULF wave power is seen to have a strong dependence on magnetopause location indicating a need for a multiparameter determination of empirical wave power and D LL estimates or an event‐specific approach.

Another technique can be used to derive radial diffusion coefficients using global MHD simulations since the resolution is capable of capturing field fluctuations on the ULF timescale. Tu et al. (2012) used Lyon‐Fedder‐Mobarry (LFM) MHD simulations (Lyon et al., 2004) to compare the model D LL values to those calculated from the empirical D LL[BA] coefficients during a Coronal Interaction Region (CIR) storm in March 2008. The D LL[BA] coefficients were found to be higher than the LFM MHD‐derived D LL values. The modeled field of compressional B and azimuthal E were also compared to in situ field measurements from the Time History of Events and Macroscale Interactions during Substorms (THEMIS) and GOES spacecraft. GOES and THEMIS magnetic fields lined up fairly well with the MHD output, but the simulation underestimated the electric field power when compared with that from THEMIS. It is worth noting here that the DLLE values computed from THEMIS measurements fall in between those derived by other means (Liu et al., 2016). Z. Li, Hudson, et al. (2016) calculated radial diffusion coefficients for the March 2015 storm using LFM‐MIX (Merkin & Lyon, 2010) simulation results. They found that the electric component was dominant and that the coefficient values varied widely over the course of the storm. They also concluded that the wave power was dominated by the m = 1 mode but significantly distributed through m = 2 and m = 3 as well; however, the results only cover the first few days of the storm after 17 March. The D LL values of Z. Li, Hudson, et al. (2016) are lower by about two orders of magnitude than those presented here. Although we do not have full validation of simulation‐derived radial diffusion coefficients, global MHD simulations may be a key data set to compare with event‐specific studies such as the one presented here. The simulations can also highlight the limitations in the observational data (e.g., assuming all wave power is contained in the m = 1 mode).

We have not included any discussion of potential losses due to wave‐particle interactions, specifically with hiss and electromagnetic ion cyclotron waves, though these processes may contribute to the differences between the instantaneous in situ wave‐derived D LL values and the estimated average D LL coefficients derived from particle data. The precipitation losses due to these wave‐particle interactions have been shown to be important for the energy of electrons considered in this work (Drozdov et al., 2017; Glauert et al., 2014; Ma et al., 2015) and warrant further study in event‐specific cases such as this one.

5. Conclusions

Local acceleration due to high‐frequency VLF waves plays a vital role in the energization of source energy electrons up to relativistic energies deep in the heart of the outer belt (Jaynes et al., 2015). However, strong energization can occur fairly quickly even in the absence of higher frequency waves. We present here a case of rapid inward radial diffusion and subsequent energization to multi‐MeV energies due to resonant ULF wave interactions with an initial source electron population at higher L‐shells. Fast radial diffusion of ultrarelativistic electrons is observed by the REPT instrument onboard the Van Allen Probes in the days following the 17 March 2015 storm, where inward transport is confirmed by both the flux measurements and phase space density data. A population of >7.7‐MeV electrons is shown to have been accelerated to these energies quite quickly, in the absence of higher‐frequency plasma waves that might contribute to the energization. This population can be observed to step inward to lower radial distances in a short time, while subsequently higher energy electrons are created in the course of the event.

Average radial diffusion rates of 0.33 days-1 are estimated from the particle flux data alone. The diffusion coefficients computed directly from ULF wave activity measured by Van Allen Probes using the Fei et al. (2006) method are found to be about 0.3 days-1 on average (with spikes up to higher values, particularly in DLLE, Figure S4). Strong enhancements of ULF wave power up to 3 nT2/Hz are observed during this same time period within the in situ magnetic field data. Comparing the diffusion rates derived here to previous periods of high geomagnetic activity, we find that this ultrafast radial diffusion of ultrarelativistic electrons may be unique so far in the Van Allen Probes era. Additionally, this is a clear example of intense radial diffusion alone producing a high‐energy outer radiation belt and shows the extent to which radial diffusion can play a role in the overall energization and dynamics of the electron belt.

While VLF chorus may have energized a lower portion of the energy spectrum up to higher energies immediately after the 17 March storm impact, here we emphasize that ULF waves alone can (and in this case clearly do) energize and transport the ultrarelativistic population that we observe in the inner magnetosphere. W. Li, Ma, et al. (2016) performed a comprehensive analysis of the March 2015 storm event using a 3‐D diffusion simulation and found evidence that inward radial diffusion is the driver that produces the very highest multi‐MeV electrons observed. The likely scenario in most radiation belt acceleration events involves varying contributions from both ULF‐wave driven inward diffusion and VLF‐driven local acceleration. In addition to the balance of loss and acceleration, an added layer of complexity is present due to the many drivers of each process that are acting (at times) simultaneously. Events such as the one detailed here can create a better understanding of the extent to which one kind of acceleration mechanism can affect a given population, but there is more work yet to be done to uncover the interplay between various mechanisms and understand when each is dominant over the other. Event‐specific studies must be performed in order to build a more convincing conclusion; including those events in which ULF waves appear to be the significant actor and those in which high‐frequency VLF chorus waves act as the significant or sole driver. Only then can we sort out the conditions under which each process is more central to radiation belt electron enhancements.

Supporting information

Supporting Information S1

Click here for additional data file. (2.6MB, pdf)

Acknowledgments

A. N. Jaynes acknowledges the use of funds from NASA's Van Allen Probes ECT project, through JHU/APL contract 967399 under prime NASA contract NAS5‐01072. All data are publicly available from NASA SPDF CDAWeb, including the Van Allen Probes and OMNI solar wind data.

Jaynes, A. N. , Ali, A. F. , Elkington, S. R. , Malaspina, D. M. , Baker, D. N. , Li, X. , et al. (2018). Fast diffusion of ultrarelativistic electrons in the outer radiation belt: 17 March 2015 storm event. Geophysical Research Letters, 45, 10,874–10,882. 10.1029/2018GL079786

References

  1. Ali, A. F. , Elkington, S. R. , Tu, W. , Ozeke, L. G. , Chan, A. A. , & Friedel, R. H. W. (2015). Magnetic field power spectra and magnetic radial diffusion coefficients using CRRES magnetometer data. Journal of Geophysical Research: Space Physics, 120, 973–995. 10.1002/2014JA020419 [DOI] [Google Scholar]
  2. Ali, A. F. , Malaspina, D. M. , Elkington, S. R. , Jaynes, A. N. , Chan, A. A. , Wygant, J. , et al. (2016). Electric and magnetic radial diffusion coefficients using the Van Allen Probes data. Journal of Geophysical Research: Space Physics, 121, 9586–9607. 10.1002/2016JA023002 [DOI] [Google Scholar]
  3. Baker, D. N. , Jaynes, A. N. , Kanekal, S. G. , Foster, J. C. , Erickson, P. J. , Fennell, J. F. , et al. (2016). Highly relativistic radiation belt electron acceleration, transport, and loss: Large solar storm events of March and June 2015. Journal of Geophysical Research: Space Physics, 121, 6647–6660. 10.1002/2016JA022502 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barker, A. B. , Li, X. , & Selesnick, R. S. (2005). Modeling the radiation belt electrons with radial diffusion driven by the solar wind. Space Weather, 3, S10003 10.1029/2004SW000118 [DOI] [Google Scholar]
  5. Brautigam, D. H. , & Albert, J. M. (2000). Radial diffusion analysis of outer radiation belt electrons during the October 9, 1990, magnetic storm. Journal of Geophysical Research, 105, 291–310. 10.1029/1999JA900344 [DOI] [Google Scholar]
  6. Brautigam, D. H. , Ginet, G. P. , Albert, J. M. , Wygant, J. R. , Rowland, D. E. , Ling, A. , et al. (2005). CRRES electric field power spectra and radial diffusion coefficients. Journal of Geophysical Research, 110, A02214 10.1029/2004JA010612 [DOI] [Google Scholar]
  7. Brizard, A. J. , & Chan, A. A. (2001). Relativistic bounce‐averaged quasilinear diffusion equation for low‐frequency electromagnetic fluctuations. Physics of Plasmas, 8, 4762–4771. 10.1063/1.1408623 [DOI] [Google Scholar]
  8. Chen, Y. , Friedel, R. H. W. , Reeves, G. D. , Cayton, T. E. , & Christensen, R. (2007). Multisatellite determination of the relativistic electron phase space density at geosynchronous orbit: An integrated investigation during geomagnetic storm times. Journal of Geophysical Research, 112, A11214 10.1029/2007JA012314 [DOI] [Google Scholar]
  9. Claudepierre, S. G. , Elkington, S. R. , & Wiltberger, M. (2008). Solar wind driving of magnetospheric ULF waves: Pulsations driven by velocity shear at the magnetopause. Journal of Geophysical Research, 113, A05218 10.1029/2007JA012890 [DOI] [Google Scholar]
  10. Claudepierre, S. G. , Wiltberger, M. , Elkington, S. R. , Lotko, W. , & Hudson, M. K. (2009). Magnetospheric cavity modes driven by solar wind dynamic pressure fluctuations. Geophysical Research Letters, 36, L13101 10.1029/2009GL039045 [DOI] [Google Scholar]
  11. Drozdov, A. Y. , Shprits, Y. Y. , Usanova, M. E. , Aseev, N. A. , Kellerman, A. C. , & Zhu, H. (2017). Emic wave parameterization in the long‐term verb code simulation. Journal of Geophysical Research: Space Physics, 122, 8488–8501. 10.1002/2017JA024389 [DOI] [Google Scholar]
  12. Elkington, S. R. , Chan, A. A. , & Wiltberger, M. (2013). Global Structure of ULF Waves During the 24–26 September 1998 Geomagnetic Storm (pp. 127–138). Washington, DC: American Geophysical Union; 10.1029/2012GM001348 [DOI] [Google Scholar]
  13. Elkington, S. R. , Hudson, M. K. , & Chan, A. A. (2003). Resonant acceleration and diffusion of outer zone electrons in an asymmetric geomagnetic field. Journal of Geophysical Research, 108, 1116 10.1029/2001JA009202 [DOI] [Google Scholar]
  14. Engebretson, M. J. , Lin, N. , Baumjohann, W. , Luehr, H. , Anderson, B. J. , Zanetti, L. J. , et al. (1991). A comparison of ULF fluctuations in the solar wind, magnetosheath, and dayside magnetosphere. I—Magnetosheath morphology. II—Field and plasma conditions in the magnetosheath. Journal of Geophysical Research, 96, 3441–3464. 10.1029/90JA02101 [DOI] [Google Scholar]
  15. Eriksson, P. T. I. , Blomberg, L. G. , Schaefer, S. , & Glassmeier, K.‐H. (2006). On the excitation of ULF waves by solar wind pressure enhancements. Annales Geophysicae, 24, 3161–3172. 10.5194/angeo-24-3161-2006 [DOI] [Google Scholar]
  16. Fälthammar, C.‐G. (1965). Effects of time‐dependent electric fields on geomagnetically trapped radiation. Journal of Geophysical Research, 70, 2503–2516. 10.1029/JZ070i011p02503 [DOI] [Google Scholar]
  17. Fei, Y. , Chan, A. A. , Elkington, S. R. , & Wiltberger, M. J. (2006). Radial diffusion and MHD particle simulations of relativistic electron transport by ULF waves in the September 1998 storm. Journal of Geophysical Research, 111, A12209 10.1029/2005JA011211 [DOI] [Google Scholar]
  18. Foster, J. C. , Erickson, P. J. , Baker, D. N. , Jaynes, A. N. , Mishin, E. V. , Fennel, J. F. , et al. (2016). Observations of the impenetrable barrier, the plasmapause, and the VLF bubble during the 17 March 2015 storm. Journal of Geophysical Research: Space Physics, 121, 5537–5548. 10.1002/2016JA022509 [DOI] [Google Scholar]
  19. Glauert, S. A. , Horne, R. B. , & Meredith, N. P. (2014). Three‐dimensional electron radiation belt simulations using the BAS Radiation Belt Model with new diffusion models for chorus, plasmaspheric hiss, and lightning‐generated whistlers. Journal of Geophysical Research: Space Physics, 119, 268–289. 10.1002/2013JA019281 [DOI] [Google Scholar]
  20. Green, J. C. , & Kivelson, M. G. (2004). Relativistic electrons in the outer radiation belt: Differentiating between acceleration mechanisms. Journal of Geophysical Research, 109, A03213 10.1029/2003JA010153 [DOI] [Google Scholar]
  21. Hudson, M. K. , Elkington, S. R. , Lyon, J. G. , & Goodrich, C. C. (2000). Increase in relativistic electron flux in the inner magnetosphere: ULF wave mode structure. Advances in Space Research, 25, 2327–2337. 10.1016/S0273-1177(99)00518-9 [DOI] [Google Scholar]
  22. Hudson, M. , Jaynes, A. , Kress, B. , Li, Z. , Patel, M. , Shen, X.‐C. , et al. (2017). Simulated prompt acceleration of multi‐MeV electrons by the 17 March 2015 interplanetary shock (Vol. 122, pp. 10,036–10,046). 10.1002/2017JA024445 [DOI] [Google Scholar]
  23. James, M. K. , Yeoman, T. K. , Mager, P. N. , & Klimushkin, D. Y. (2013). The spatio‐temporal characteristics of ULF waves driven by substorm injected particles. Journal of Geophysical Research: Space Physics, 118, 1737–1749. 10.1002/jgra.50131 [DOI] [Google Scholar]
  24. Jaynes, A. N. , Baker, D. N. , Singer, H. J. , Rodriguez, J. V. , Loto'aniu, T. M. , Ali, A. F. , et al. (2015). Source and seed populations for relativistic electrons: Their roles in radiation belt changes. Journal of Geophysical Research: Space Physics, 120, 7240–7254. 10.1002/2015JA021234 [DOI] [Google Scholar]
  25. Kanekal, S. G. , Baker, D. N. , Fennell, J. F. , Jones, A. , Schiller, Q. , Richardson, I. G. , et al. (2016). Jaynes prompt acceleration of magnetospheric electrons to ultrarelativistic energies by the 17 March 2015 interplanetary shock. Journal of Geophysical Research: Space Physics, 121, 7622–7635. 10.1002/2016JA022596 [DOI] [Google Scholar]
  26. Kavosi, S. , & Raeder, J. (2015). Ubiquity of Kelvin‐Helmholtz waves at Earth's magnetopause. Nature Communications, 6, 7019 10.1038/ncomms8019 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kepko, L. , Spence, H. E. , & Singer, H. J. (2002). ULF waves in the solar wind as direct drivers of magnetospheric pulsations. Geophysical Research Letters, 29(8), 1197 10.1029/2001GL014405 [DOI] [Google Scholar]
  28. Kletzing, C. A. , Kurth, W. S. , Acuna, M. , MacDowall, R. J. , Torbert, R. B. , Averkamp, T. , et al. (2013). The Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) on RBSP. Space Science Reviews, 179, 127–181. 10.1007/s11214-013-9993-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Li, Z. , Hudson, M. , Paral, J. , Wiltberger, M. , & Turner, D. (2016). Global ULF wave analysis of radial diffusion coefficients using a global MHD model for the 17 March 2015 storm. Journal of Geophysical Research: Space Physics, 121, 6196–6206. 10.1002/2016JA022508 [DOI] [Google Scholar]
  30. Li, Z. , Hudson, M. , Patel, M. , Wiltberger, M. , Boyd, A. , & Turner, D. (2017). ULF, wave analysis and radial diffusion calculation using a global MHD model for the 17 March 2013 and 2015 storms. Journal of Geophysical Research: Space Physics, 122, 7353–7363. 10.1002/2016JA023846 [DOI] [Google Scholar]
  31. Li, W. , Ma, Q. , Thorne, R. M. , Bortnik, J. , Zhang, X.‐J. , Li, J. , et al. (2016). Radiation belt electron acceleration during the 17 March 2015 geomagnetic storm: Observations and simulations. Journal of Geophysical Research: Space Physics, 121, 5520–5536. 10.1002/2016JA022400 [DOI] [Google Scholar]
  32. Liu, W. , Tu, W. , Li, X. , Sarris, T. , Khotyaintsev, Y. , Fu, H. , et al. (2016). On the calculation of electric diffusion coefficient of radiation belt electrons with in situ electric field measurements by THEMIS. Geophysical Research Letters, 43, 1023–1030. 10.1002/2015GL067398 [DOI] [Google Scholar]
  33. Lyon, J. G. , Fedder, J. A. , & Mobarry, C. M. (2004). The Lyon‐Fedder‐Mobarry (LFM) global MHD magnetospheric simulation code. Journal of Atmospheric and Solar‐Terrestrial Physics, 66, 1333–1350. 10.1016/j.jastp.2004.03.020 [DOI] [Google Scholar]
  34. Ma, Q. , Li, W. , Thorne, R. M. , Ni, B. , Kletzing, C. A. , Kurth, W. S. , et al. (2015). Modeling inward diffusion and slow decay of energetic electrons in the Earth's outer radiation belt. Geophysical Research Letters, 42, 987–995. 10.1002/2014GL062977 [DOI] [Google Scholar]
  35. Mann, I. R. , Lee, E. A. , Claudepierre, S. G. , Fennell, J. F. , Degeling, A. , Rae, I. J. , et al. (2013). Discovery of the action of a geophysical synchrotron in the Earth's Van Allen radiation belts. Nature Communications, 4, 2795–2795. 10.1038/ncomms3795 [DOI] [Google Scholar]
  36. Mathie, R. A. , & Mann, I. R. (2001). On the solar wind control of Pc5 ULF pulsation power at mid‐latitudes: Implications for MeV electron acceleration in the outer radiation belt. Journal of Geophysical Research, 106(A12), 29,783–29,796. 10.1029/2001JA000002 [DOI] [Google Scholar]
  37. Merkin, V. G. , & Lyon, J. G. (2010). Effects of the low‐latitude ionospheric boundary condition on the global magnetosphere. Journal of Geophysical Research, 115, A10202 10.1029/2010JA015461 [DOI] [Google Scholar]
  38. Murphy, K. R. , Mann, I. R. , & Sibeck, D. G. (2015). On the dependence of storm time ULF wave power on magnetopause location: Impacts for ULF wave radial diffusion. Geophysical Research Letters, 42, 9676–9684. 10.1002/2015GL066592 [DOI] [Google Scholar]
  39. Ozeke, L. G. , Mann, I. R. , Murphy, K. R. , Jonathan Rae, I. , & Milling, D. K. (2014). Analytic expressions for ULF wave radiation belt radial diffusion coefficients. Journal of Geophysical Research: Space Physics, 119, 1587–1605. 10.1002/2013JA019204 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Ozeke, L. G. , Mann, I. R. , Murphy, K. R. , Rae, I. J. , Milling, D. K. , Elkington, S. R. , et al. (2012). ULF wave derived radiation belt radial diffusion coefficients. Journal of Geophysical Research, 117, A04222 10.1029/2011JA017463 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Ozeke, L. G. , Mann, I. R. , Turner, D. L. , Murphy, K. R. , Degeling, A. W. , Rae, I. J. , et al. (2014). Modeling cross L shell impacts of magnetopause shadowing and ULF wave radial diffusion in the Van Allen belts. Geophysical Research Letters, 41, 6556–6562. 10.1002/2014GL060787 [DOI] [Google Scholar]
  42. Reeves, G. D. , Spence, H. E. , Henderson, M. G. , Morley, S. K. , Friedel, R. H. W. , Funsten, H. O. , et al. (2013). Electron acceleration in the heart of the Van Allen Radiation Belts. Science, 341(6149), 991–994. 10.1126/science.1237743 [DOI] [PubMed] [Google Scholar]
  43. Roederer, J. G. (1970). Dynamics of Geomagnetically Trapped Radiation, Physics and Chemistry in Space. Berlin:Springer; 10.1007/978-3-642-49300-3 [DOI] [Google Scholar]
  44. Schulz, M. , & Lanzerotti, L. J. (1974). Particle Diffusion in the Radiation Belts, Series: Physics and Chemistry in Space. Berlin, Heidelberg: Springer‐Verlag. [Google Scholar]
  45. Spence, H. E. , Reeves, G. D. , Baker, D. N. , Blake, J. B. , Bolton, M. , Bourdarie, S. , et al. (2013). Science goals and overview of the Radiation Belt Storm Probes (RBSP) Energetic Particle, Composition, and Thermal Plasma (ECT) Suite on NASA's Van Allen Probes Mission. Space Science Reviews, 179, 311–336. 10.1007/s11214-013-0007-5 [DOI] [Google Scholar]
  46. Thorne, R. M. , Li, W. , Ni, B. , Ma, Q. , Bortnik, J. , Baker, D. N. , et al. (2013). Evolution and slow decay of an unusual narrow ring of relativistic electrons near L 3.2 following the September 2012 magnetic storm. Geophysical Research Letters, 40, 3507–3511. 10.1002/grl.50627 [DOI] [Google Scholar]
  47. Tsyganenko, N. A. , & Sitnov, M. I. (2005). Modeling the dynamics of the inner magnetosphere during strong geomagnetic storms. Journal of Geophysical Research, 110, A03208 10.1029/2004JA010798 [DOI] [Google Scholar]
  48. Tu, W. , Elkington, S. R. , Li, X. , Liu, W. , & Bonnell, J. (2012). Quantifying radial diffusion coefficients of radiation belt electrons based on global MHD simulation and spacecraft measurements. Journal of Geophysical Research, 117, A10210 10.1029/2012JA017901 [DOI] [Google Scholar]
  49. Wygant, J. R. , Bonnell, J. W. , Goetz, K. , Ergun, R. E. , Mozer, F. S. , Bale, S. D. , et al. (2013). The Electric Field and Waves instruments on the Radiation Belt Storm Probes Mission. Space Science Reviews, 179, 183–220. 10.1007/s11214-013-0013-7 [DOI] [Google Scholar]
  50. Yeoman, T. K. , Klimushkin, D. Y. , & Mager, P. N. (2010). Intermediate‐m ULF waves generated by substorm injection: A case study. Annales Geophysicae, 28, 1499–1509. 10.5194/angeo-28-1499-2010 [DOI] [Google Scholar]
  51. Zolotukhina, N. A. , Mager, P. N. , & Klimushkin, D. Y. (2008). Pc5 waves generated by substorm injection: A case study. Annales Geophysicae, 26, 2053–2059. 10.5194/angeo-26-2053-2008 [DOI] [Google Scholar]
  52. Zong, Q.‐G. , Zhou, X.‐Z. , Wang, Y. F. , Li, X. , Song, P. , Baker, D. N. , et al. (2009). Energetic electron response to ULF waves induced by interplanetary shocks in the outer radiation belt. Journal of Geophysical Research, 114, A10204 10.1029/2009JA014393 [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information S1

Click here for additional data file. (2.6MB, pdf)

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES