Mutation frequency and biological cost of antibiotic resistance in Helicobacter pylori

Abstract

Among the several factors that affect the appearance and spread of acquired antibiotic resistance, the mutation frequency and the biological cost of resistance are of special importance. Measurements of the mutation frequency to rifampicin resistance in Helicobacter pylori strains isolated from dyspeptic patients showed that ≈1/4 of the isolates had higher mutation frequencies than Enterobacteriaceae mismatch-repair defective mutants. This high mutation frequency could explain why resistance is so frequently acquired during antibiotic treatment of H. pylori infections. Inactivation of the mutS gene had no substantial effect on the mutation frequency, suggesting that MutS-dependent mismatch repair is absent in this bacterium. Furthermore, clarithromycin resistance conferred a biological cost, as measured by a decreased competitive ability of the resistant mutants in mice. In clinical isolates this cost could be reduced, indicating that compensation is a clinically relevant phenomenon that could act to stabilize resistant bacteria in a population.

Helicobacter pylori is a Gram-negative, microaerophilic spiral bacterium that colonizes the human gastric mucosa of ≈50% of the world's population (1). In all infected individuals there is an inflammation that in a subpopulation of infected hosts can lead to the development of peptic ulcer or stomach cancer (1–4). To eradicate a bacterial infection, treatment usually includes two antibiotics, one proton pump inhibitor and/or a bismuth compound that has both acid-suppressing and antimicrobial activity (1, 5). Resistance acquired during therapy is common and a major cause of treatment failure (5). Resistance has been reported to most antibiotics used in treatment, including clarithromycin, metronidazole, tetracycline, and amoxicillin (1, 5). One mechanism of clarithromycin resistance has been elucidated, where either of two 23S rRNA mutations (A₂₁₄₂ or A₂₁₄₃ → G) confer resistance by altering the ribosomal target (6).

The rate by which antibiotic resistance emerges in a bacterial population within a patient will be determined by several factors, including the rate of formation of the resistant mutants, the biological cost of resistance (7, 8), and the rate and pattern of antibiotic use (9). The rate by which the resistant mutants form will be determined by the mutation rate (for chromosomally encoded resistance) and the population size. In this context, mutator bacteria might be important because their higher mutation rate would increase the supply of resistance mutations. Mutator strains usually owe their increased mutation rate to a defective methyl-directed mismatch DNA repair (MMR) system where proteins encoded by the mutH, mutL, mutS, dam, and uvrD genes play important roles (10, 11). After the appearance of resistant mutants, their spread and maintenance will be influenced by the rate and pattern of antibiotic use (selective pressure) and the effect of the particular resistance on bacterial fitness. In experimental systems resistance usually confers a cost, as measured by a decreased growth rate. However, evolution to reduce these costs, without a concomitant loss of resistance, has been shown to occur and could potentially be important in stabilizing the resistant bacteria in a natural population (7, 8). The rate and trajectory of compensatory evolution depends on the specific resistance mutation and the environment in which it occurs (12, 13). It is unclear how significant compensation is in clinical settings because only two examples have been reported (14, 15).

Here we have examined the mutation frequency in H. pylori by using rifampicin resistance as a mutational marker. Results showed that hypermutable strains were common and that the strains exhibited a wide range of mutation frequencies. In addition, results showed that the high fitness cost associated with clarithromycin resistance mutations was reduced in some clinical isolates.

Materials and Methods

Bacterial Strains, Growth Conditions, Minimal Inhibitory Concentration Determinations, and Selection for Resistant Mutants.

Isolates of H. pylori were obtained from antral biopsies from adult patients enrolled in a treatment study (16, 17). Twenty-nine clinical isolates were examined of which 13 were from peptic ulcer patients, 13 from non-ulcer dyspepsia patients, and three from gastric cancer patients (Table 1). They included 20 clarithromycin-sensitive strains that were randomly chosen from the above collection of clinical isolates. In this collection of strains were included ten isolates obtained from five patients where clarithromycin resistance was developed during antibiotic treatment (16, 17). From each of these five patients, biopsies were acquired immediately before and 3 months after treatment, representing clarithromycin-sensitive bacteria (ClaS) and clarithromycin-resistant bacteria (ClaR), respectively. The pre- and posttreatment strain (ClaS-ClaR) pair from each patient was clonally related as shown by arbitrarily primed (AP)-PCR of ten independent colonies from each biopsy. Isolate 67:21 used for in vitro selection of a clarithromycin-resistant mutant was acquired from a gastric ulcer patient included in a case-control study of gastric cancer (15, 16). Bacteria were grown on chocolate agar plates in a microaerophilic atmosphere at 37°C. The MIC values to the different antibiotics was determined by using E-test (AB Biodisk, Solna, Sweden). Clarithromycin-resistant mutants were selected by plating 10⁹ bacteria on chocolate agar plate containing 1 μg/ml clarithromycin. Resistant mutants were single-colony purified on a selective plate and then immediately frozen at −80°C to prevent any inadvertent selection.

Table 1.

Characteristics of H. pylori strains examined in this study

ClaS-ClaR strain pairs	Isolated from	MIC, μg/ml						23S rRNA mutation
		Amo	Met	Tet	Cef	Cip	Cla
67:21	Peptic ulcer	<0.016	ND	ND	ND	ND	<0.016	Wt
67:21 ClaR	In vitro	<0.016	ND	ND	ND	ND	8	A2143 → G
G6	Peptic ulcer	<0.016	0.38	0.094	0.19	0.094	<0.016	Wt
G44	Peptic ulcer	<0.016	0.125	0.047	0.5	0.047	8	A2143 → G
G47	Non-ulcer dyspepsia	<0.016	0.032	0.047	0.25	0.032	<0.016	Wt
G108	Non-ulcer dyspepsia	<0.016	ND	ND	ND	ND	8	A2143 → G
G142	Non-ulcer dyspepsia	<0.016	0.125	0.064	0.5	0.047	<0.016	Wt
G193	Non-ulcer dyspepsia	<0.016	0.047	0.047	0.38	0.047	8	A2143 → G
G34	Peptic ulcer	<0.016	0.094	0.19	0.38	0.047	<0.016	Wt
G49	Peptic ulcer	<0.016	0.094	0.064	0.5	0.047	>256	A2142 → G
G83	Non-ulcer dyspepsia	<0.016	64	0.064	0.38	0.064	<0.016	Wt
G162	Non-ulcer dyspepsia	<0.016	0.5	0.023	1.0	0.094	>256	A2142 → G
G16	Non-ulcer dyspepsia	<0.016	ND	ND	ND	ND	<0.016	Wt
G33	Peptic ulcer	<0.016	>256	0.064	0.75	0.125	<0.016	Wt
G36	Peptic ulcer	<0.016	0.023	0.047	0.25	0.032	<0.016	Wt
G54	Non-ulcer dyspepsia	<0.016	>256	0.032	0.064	0.047	<0.016	Wt
G59	Non-ulcer dyspepsia	<0.016	0.023	0.023	0.125	0.032	<0.016	Wt
G64	Non-ulcer dyspepsia	<0.016	0.125	0.023	0.047	0.023	<0.016	Wt
G66	Peptic ulcer	<0.016	<0.016	<0.016	0.25	0.023	<0.016	Wt
G67	Non-ulcer dyspepsia	<0.016	0.047	0.094	0.25	0.032	<0.016	Wt
G74	Peptic ulcer	<0.016	0.125	0.032	0.19	0.032	<0.016	Wt
G76	Peptic ulcer	<0.016	0.19	0.094	0.5	0.125	<0.016	Wt
G77	Peptic ulcer	<0.016	0.25	0.094	0.25	0.047	<0.016	Wt
G84	Non-ulcer dyspepsia	<0.016	0.19	0.094	0.5	>32	<0.016	Wt
G86	Non-ulcer dyspepsia	<0.016	0.19	0.064	0.25	0.032	<0.016	Wt
G88	Peptic ulcer	<0.016	<0.016	0.023	0.19	0.032	<0.016	Wt
G90	Non-ulcer dyspepsia	<0.016	0.032	0.047	0.5	0.064	<0.016	Wt
G117	Non-ulcer dyspepsia	<0.016	ND	ND	ND	ND	<0.016	Wt
K65	Peptic ulcer	ND	ND	ND	ND	ND	<0.016	Wt
K57	Gastric cancer	<0.016	<0.016	<0.016	0.047	0.023	<0.016	Wt
K59	Gastric cancer	<0.016	<0.016	<0.016	0.47	0.0047	<0.016	Wt
K66	Gastric cancer	ND	ND	ND	ND	ND	<0.016	Wt
26695	Gastritis	ND	ND	ND	ND	ND	<0.016	Wt

MIC, minimal inhibitory concentration; Cla, clarithromycin; Met, metronidazole; Tet, tetracycline; Amo, amoxicillin; Cip, ciprofloxacine; Cef, ceftazidime; ND, not determined; Wt, wild type. 

AP-PCR, 23S rDNA Sequencing, and Inactivation of the mutS Gene.

The AP-PCR (16, 17) and sequencing of the 23S rRNA gene (6) were performed as described. The mutS gene was inactivated by inserting the kanamycin resistance cassette from plasmid pJMK30 (18) into a SphI site (nucleotide 1953) of the PCR-amplified gene from strain G34. The mutS∷kanR construct was electroporated into the different strains. Bacteria were plated on chocolate agar plates for 2 days, resuspended, and then kanamycin resistant transformants were selected after plating on chocolate agar plates with 20 μg/ml of kanamycin. PCR and Southern hybridization confirmed that the mutS∷kanR construct was inserted into the correct location (data not shown).

Mutation Frequency Determinations.

For each strain, 10 μl (<10⁴ cells) of an overnight preculture was inoculated into 20 independent 1-ml Brucella broth cultures supplemented with 5% calf serum and grown for 36–48 h under microaerophilic conditions at 37°C. A viable count determination was performed on three of the tubes. To determine the number of resistant mutants, the whole amount of each tube was spread on GC plates containing rifampicin (15 μg/ml) or clarithromycin (10 μg/ml). The plates were incubated for 5 days and colonies were counted. The mutation frequency was calculated from the median number of mutants divided by the viable count. Typically the range from the lowest to highest number of mutants/culture varied between 10- and 50-fold for the different strains. Because the mutation frequencies were calculated from the median of 20 cultures for the respective strain, the occasional jackpot cultures had no impact on the calculation and the obtained values. To assure that the 10 μl of bacteria used to inoculate the 1-ml sample cultures was free of preexisting resistant mutants, 30 μl of the preculture was plated on a selection plate. The sample cultures were used to measure the mutation frequency only if no mutants were present in these 30 μl.

Competition Experiments in Mice and Cultures.

In competition experiments, transgenic α-1,3 Ft FVB/N mice expressing a H. pylori receptor, the human blood group antigen Lewis^b, in the pit and surface mucus cells of the stomach were used. It has been demonstrated that H. pylori establishes a chronic, high-density infection in this line of mice (19, 20). Equal amounts of ClaS wild type and ClaR mutant of each clonally related pair were mixed and orally inoculated in a volume of 50 μl into 6–10-week-old animals. For the in vitro selected mutant pair (67:21 ClaS/ClaR), the mice were inoculated with 10⁶, 10⁷, or 10⁸ CFUs and killed 15 min, 1 h, 1 day, 3 days, or 7 days after inoculation. For the three clinical pairs only the highest dose (10⁸) and the 1, 3, and 7 days time points were examined. In addition, two groups of animals were mono-inoculated with either of the two isolates at the 10⁸ dose and killed at day 7. The mono-inoculations served as controls of the ability of the isolates to colonize the mice in the absence of its isogenic counterpart (data not shown). In competition experiments, four animals/dose/time point were used and the experiments were performed twice. For all mouse experiments, H. pylori were recovered by homogenization of half of the stomach. Samples were cultured on chocolate agar plates containing vancomycin, polymyxin B, and trimetoprim with and without 1 μg/ml clarithromycin. In culture competitions, bacteria were resuspended from GC plates in Brucella broth to ≈10⁶ bacteria/ml, mixed at a 1:1 ratio, and then 200 μl of this suspension was used to inoculate 20 ml of Brucella broth supplemented with 5% FCS. Bacteria were grown overnight and sampled, and then 200 μl was transferred to 20 ml of fresh medium and grown overnight. This overnight culture was again sampled. Each growth cycle represented ≈6 generations of growth (growth from 10⁴ to 10⁶ cells/ml). After suitable dilutions of the samples, the bacteria were spread on GC plates with and without clarithromycin. The plates were incubated for 5 days before colonies were counted. Results from the competition experiments in mice and cultures were expressed as the ratio of the number of ClaS/ClaR colonies at the respective time points (competition ratio).

Results

In this study we addressed the following questions: (i) What is the variation in mutation frequency between isolates of H. pylori? (ii) Is MutS-dependent mismatch repair active in H. pylori? (iii) Does clarithromycin resistance confer a biological cost? (iv) Can this cost be genetically reduced in clinical isolates?

Mutation Frequency in H. pylori.

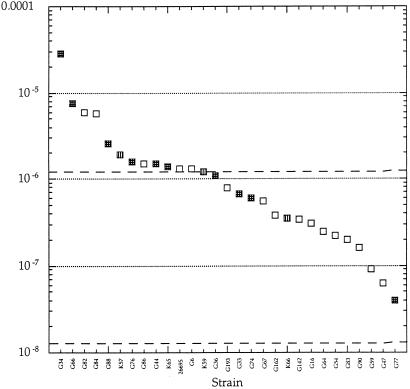
The mutation frequency was measured by using rifampicin resistance as a mutational marker. Rifampicin resistance in H. pylori is, as in most bacterial species, caused by point mutations in the rpoB gene (20, 21) and can therefore also in H. pylori be used as a convenient indicator of overall mutation frequency (23, 24). The mutation frequency to rifampicin resistance varied extensively between the strains, with the highest being 3 × 10⁻⁵, the lowest 4 × 10⁻⁸ and the median 10⁻⁶. There was no statistically significant correlation between the type of disease caused by the infection and the mutation frequency (Fig. 1). Most H. pylori strains showed higher mutation frequencies than wild-type Enterobacteriaceae, and ≈1/4 of the strains showed mutation frequencies higher than enterobacterial MMR-defective mutators (10, 11). To validate the rifampicin resistance mutation frequency measurements, the mutation frequency to clarithromycin resistance was determined for two strains, G34 and G83. The clarithromycin resistance mutation frequencies were 10⁻⁷ and 5 × 10⁻⁹, respectively, as compared with 2.8 × 10⁻⁵ and 2 × 10⁻⁷ for rifampicin, suggesting that rifampicin resistance provides a relevant measure of overall mutation frequencies, as has been shown in other bacteria (23, 24). Selection for antibiotic resistance can enrich for mutators (25). Furthermore, in isolates of P. aeruginosa from cystic fibrosis patients the presence of a mutator phenotype and antibiotic resistance were positively correlated, indicating that antibiotic use and selection for resistant mutants can enrich for mutators in clinical settings (24). However, in H. pylori we could not detect any correlation between antibiotic resistance (Table 1) and a high mutation frequency (Fig. 1).

Figure 1.

Mutation frequency to rifampicin resistance for H. pylori isolates. The dotted lines indicate the approximate mutation frequencies to rifampicin resistance for wild-type and mutator Enterobacteriaceae and P. aeruginosa (23, 24). Indicated are strains isolated from peptic ulcer patients (stippled), non-ulcer dyspepsia patients (open), and gastric cancer patients (vertical lines). The number of peptic ulcer and dyspepsia non-ulcer strains with mutation frequencies <10⁻⁶ were 3 and 11, respectively, and for strains with mutation frequencies >10⁻⁶ were 7 and 5, respectively. This difference is not statistically significant as calculated by Fischer's Exact test (P > 0.05).

What Causes the High Mutation Frequency?

The mutator phenotype in natural populations of Enterobacteriaceae and P. aeruginosa is usually caused by defects in MMR, in particular by mutations in the mutS gene (23, 24). To examine whether this could be the cause for the high mutation frequency in H. pylori the mutS gene was inactivated in three isolates. Inactivation of mutS had no substantial effect on the mutation frequencies (at most a 3-fold increase), irrespective of whether the parent strain had a low or high mutation frequency. This indicates that the mutS gene in H. pylori is not involved in MMR and that the variability in mutation frequencies seen among the strains is not caused by allelic differences in the mutS gene (Table 2). These data show that H. pylori lacks MutS-dependent MMR, as has been proposed (26).

Table 2.

Mutation frequency to rifampicin resistance in three strain pairs with an intact and insertion-inactivated mutS gene, respectively

Strain	Mutation frequency
	wt	mutS∷kanR	Ratio mutS∷KanR/wt
26695	1.3  × 10−6	1.3  × 10−6	1.0
G74	6  × 10−7	5  × 10−7	0.9
G77	4  × 10−8	13  × 10−8	3.2

Clarithromycin Resistance Confers a Biological Cost in Mice.

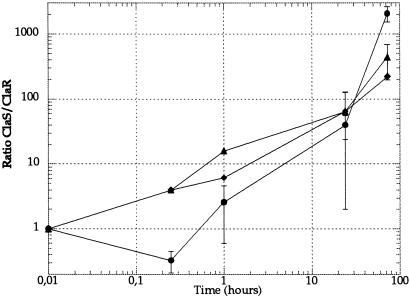
To estimate the fitness cost of clarithromycin resistance, we competed the spontaneous ClaR mutant isolated from strain 67:21 against the isogenic ClaS parent in mice (Table 1). In mice the resistant mutant was outcompeted by the sensitive parent at all three doses tested (Fig. 2). A considerable loss of the ClaR mutant was observed during the early phases of the infection (24 h), under which no net growth of bacteria has occurred. This finding suggests that the ClaR mutant might be defective in functions required for establishment in the stomach. We measured adhesion to mouse stomach tissue sections and acid sensitivity of the ClaS and ClaR strains, but no significant differences in adhesion or acid sensitivity were seen (data not shown).

Figure 2.

Competition between the in vitro isolated ClaS (67:21) and ClaR (67:21, A₂₁₄₂ → G) pair in mice. Three different doses of bacteria were used: 10⁶ (diamond), 10⁷ (triangle), and 10⁸ (circle). Standard errors are indicated. For some time points an insufficient number of mice were examined to allow a statistical analysis.

The Costs of Clarithromycin Resistance Can Be Reduced in Clinical Isolates.

We used five pairs of ClaS-ClaR strains isolated from individuals pre- and postantibiotic treatment to examine the cost of clarithromycin resistance in the clinical isolates and the defined in vitro pair. These patients had monoclonal H. pylori infections as judged by AP-PCR of several independent colonies examined from each stomach biopsy taken before and after treatment. Furthermore, for each pair the pretreatment (ClaS) and posttreatment (ClaR) isolates showed identical AP-PCR patterns (data not shown), indicating that they were clonally related and that the resistant strain had been selected from the sensitive population during treatment. We compared the fitness of ClaR isolates with the same resistance mutation by measuring each mutant's fitness by competition with the respective, clonally related, sensitive parent. If the cost of resistance had been reduced in a clinically isolated ClaR mutant, the fitness difference between the mutant and the sensitive parent should be lower than for the defined in vitro isolated ClaS-ClaR pair.

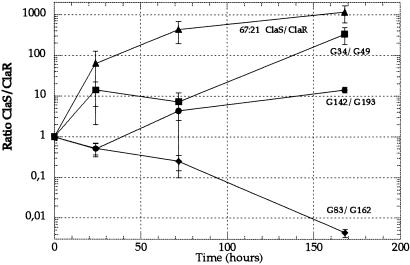
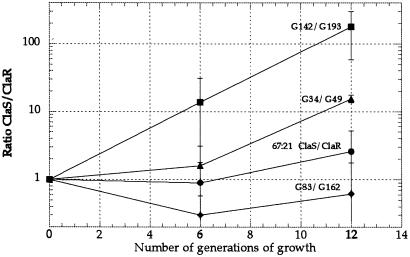
For two of the clinical pairs, G6-G44 and G47-G108, for unknown reasons no infection could be established in the mice. Thus, only three of the clinical pairs and the defined pair isolated in vitro are shown (Fig. 3). Comparison of the fitness in mice of the pair ClaS (67:21)-ClaR (67:21, A₂₁₄₃ → G) with the pair ClaS (G142)-ClaR (G193, A₂₁₄₃ → G) suggested that the cost of clarithromycin resistance had been reduced in the G193 mutant. The ratios of ClaS/ClaR bacteria at day 7 were 1167 and 14, respectively, indicating that most of the fitness cost of the A₂₁₄₃ 224 G mutation had been lost in strain G193. An even clearer example of the reduction of cost was demonstrated by the comparison between the ClaS (G34)-ClaR (G49, A₂₁₄₂ → G) and ClaS (G83)-ClaR (G162, A₂₁₄₂ → G) pairs. For the G34/G49 pair the posttreatment resistant mutant lost against the pretreatment sensitive strain; the competition ratio was 337 at day 7. In contrast, in the second pair (G83/G162) the posttreatment resistant mutant competed out the sensitive pretreatment strain; the competition ratio was 0.004 at day 7 (Fig. 3). Thus, in this case the cost of the A₂₁₄₂ → G mutation was completely eliminated in strain G162. We also examined the relative fitness of the ClaS-ClaR pairs during growth in cultures; a growth disadvantage was seen for the G49 and G193 mutants, whereas the G162 and 67:21 ClaR strains were not impaired, suggesting that growth rates in vitro and in mice are not generally correlated (Fig. 4).

Figure 3.

Competition between clonally related pre- and posttreatment (ClaS and ClaR) pairs in mice. Pairs G34-G49, G142-G193, and G83-G162 were clinically isolated pairs, whereas the 67:21 ClaS-67:21 ClaR pair was isolated in vitro. One dose of bacteria (10⁸) was used. Standard errors are indicated.

Figure 4.

Competition between clonally related pre- and posttreatment (ClaS/ClaR) pairs in laboratory medium. Pairs G34-G49, G142-G193, and G83-G162 were clinically isolated pairs, whereas the 67:21 ClaS-67:21 ClaR pair was isolated in vitro. Standard errors are indicated.

Discussion

Acquired clarithromycin resistance represents one major reason for clinical treatment failures of H. pylori infections (1, 5). One potential explanation for the common occurrence of acquired resistance is the high prevalence of hypermutable strains, which will increase the number of resistant bacteria and conceivably the rate of resistance development. We calculated the probability that resistant bacteria are present (and will become fixed) in an infected stomach when antibiotic treatment is initiated as a function of the population size and the mutation rate to resistance. This calculation suggests that during a typical H. pylori infection the probability of fixation of a resistant mutant depends on the mutation supply rate. This finding in turn implies that an increase in the mutation rate will increase the likelihood of acquired resistance developing (see Appendix 1).

Why Are Hypermutable Strains So Common Among H. pylori Isolates?

In natural populations of E. coli, S. typhimurium (23) and P. aeruginosa (24) mutators are found at frequencies much higher than expected from mutation–selection equilibrium. Variable and selective conditions are predicted from theoretical analysis, and shown in experimental studies, to enrich for bacteria with increased mutation frequencies (25, 27–29). Likewise, antibiotic use and selection for resistant mutants can enrich for bacteria with higher mutation frequencies (24, 25). However, there is no clear correlation between the level of resistance and the mutation frequency in H. pylori. In view of the above calculation (Appendix 1), this finding is unexpected. One possible explanation is that once adaptation to resistance is obtained, a low mutation rate is recovered. Alternatively, other selective pressures than antibiotics might dominate in selecting for strains with high mutation rates and could obscure a correlation to resistance. For example, during disease progression the exposure of the bacteria to a continuously changing environment in the gastric mucosa could conceivably cause an enrichment for mutators (1).

This analysis suggests that the mutS gene in H. pylori is not involved in DNA mismatch repair, indicating that the variation in mutation frequencies seen among the clinical isolates is not caused by variability in MutS-dependent MMR. We suggest that the 700-fold range of mutation frequencies seen among the strains examined here is caused by variation in the efficiency of DNA repair functions, other than the mutHLS pathway, or alternatively, in the accuracy of DNA polymerase. This finding also raises the question of the function of the mutS homologue in H. pylori. Interestingly, the H. pylori homologue belongs to a MutS subfamily (MutS2) that is inferred from phylogenetic analysis to be involved in chromosome segregation and crossing over (30).

Clarithromycin resistance confers a biological cost. Other 23S rRNA mutations that cause macrolide resistance impair translation and the fitness-decreasing effect of clarithromycin resistance is possibly caused by a reduction in protein synthesis efficiency (31). In two of three clinical strain pairs examined the cost was reduced, and in one ClaR strain the fitness was above that of the ClaS parent strain. At least two explanations can be proposed for the different costs of an identical resistance mutation in different isolates. One possibility, as has been shown to occur both in laboratory media (32) and in experimental animals (12), is that a compensatory mutation was selected after the resistance mutation occurred, resulting in a strain with increased fitness. Another possibility is that the cost depends on the genetic background of the clinical isolates in which the resistance mutation appeared. At present, we cannot distinguish between these two possibilities. However, with respect to the stabilization of resistance mutations it is less important whether the compensatory mutations were present before or appeared after the resistance mutation because in both cases the cost would be reduced and result in stabilization of the resistant clone in the population. Assuming that compensatory mutations were selected after the resistance mutation, we estimated the succession time from sensitive → resistant → compensated bacteria in the stomach (Appendix 2). We assumed that when an antibiotic is added all bacteria in the stomach, except a few that are resistant, die. The resistant bacteria grow slowly, and during growth a new compensated mutant can occur with a low probability. This new variant grows with a faster growth rate than the original resistant mutant. From this analysis we estimated a take over time of 40–120 days, similar to the 90 days between isolation of the pre- and posttreatment strains. Thus, these calculations are consistent with the possibility that there was a stepwise selection from sensitive to resistant to compensated mutant during the time between sampling of the pre- and posttreatment strains.

Abbreviations

MMR

mismatch DNA repair

ClaR

clarithromycin-resistant bacteria

ClaS

clarithromycin-sensitive bacteria

AP

arbitrarily primed

Appendix

Consider a population of N haploid individuals at steady-state growth. The population size is kept constant by random removal (death) of individuals at the same rate as growth. In each replication, a counterselected mutation appears with probability u. The growth rate of the mutant is a factor 1 + s (with s < 0) as large as that of the wild type. What is the probability, P_n, that the population contains n mutants? The state of the population is given by n (n = 0, 1, . . . , N) and can change according to a stochastic birth-and-death scheme:

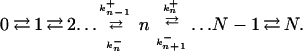1

The rate constants for change are

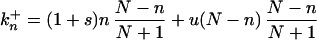2

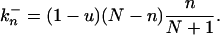3

Eq. 2 describes the change from n to n + 1. This can occur through the replication (with rate 1 + s) of one of the n mutants and subsequent removal [random probability (N − n)/(N + 1) of one wild-type individual]. Or it can occur through the replication (rate 1) of one of the N − n wild-type individuals that picks up a new mutation (probability u) followed by random removal of a wild-type individual. These two contributions give the two terms in Eq. 2. Similarly, the change from n to n − 1 described by Eq. 3 requires the replication of a wild type, without picking up a mutation, and subsequent random removal of a mutant.

At the stationary state, the net flux across any of the steps in the scheme must be zero. As a consequence the probabilities, P_n can be found by recursion of

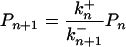4

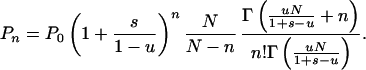This gives

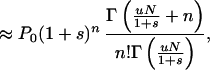5

where Γ( ) is the gamma function. The approximation is valid under the assumptions that u ≪ |s| and sN ≪ −1, and in this limit Eq. 5 is a negative binomial distribution. If the counterselection is sufficiently strong, the probability that n approaches N is vanishingly small and P₀ can be determined from the normalization condition that all probabilities P_n must sum to 1. This gives the probability that the population carries no mutant

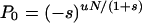6

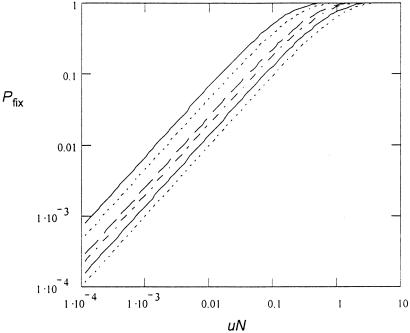
The approximate distribution in Eq. 5 gives the expectation value for the number of mutants in the population as ∑nP_n = uN/(−s), as expected for the mutation–selection balance of a counterselected mutant. When s approaches s = −1—i.e., when mutations occur but do not propagate, P₀ of Eq. 6 becomes P₀ = e^−uN. This simply corresponds to the probability that no mutation occurs in N replications, which is the expected result for a Luria–Delbruck distribution. When the mutation is causing antibiotic resistance, P_fix = 1 − P₀ corresponds to the probability that the population will survive treatment (see Fig. 5).

Figure 5.

Probability of fixation as function of uN. Curves from left to right: s = −0.001, s = −0.01, s = −0.1, s = −0.2, s = −0.5, s = −1.

The number of H. pylori cells in the mucosa and epithelial cell layers in an infected stomach is 10⁴–10⁵/mm³ and 10¹–10³/mm³, respectively (33, 34). Reasonable assumptions for the stomach volume and thickness of the mucosa layer in an average stomach is 1 dm³ and 2 mm, respectively. Thus, in a stomach where bacteria have infected 100% of the surface the total number of bacteria is 10⁹–10¹⁰. Because bacterial growth is localized to the antral part of the stomach and is focal in its nature, a more realistic assumption is that 1–10% of the surface contains bacteria, yielding a total population in the range of 10⁷–10⁹. The mutation rate to clarithromycin resistance is approximately 10⁻⁹ (22), resulting in a range of uN values (0.01–1) where the P_fix value is sensitive to the mutation supply rate. From these calculations we predict that an increase in the mutation rate of H. pylori will increase the rate of resistance development by increasing the likelihood that resistant mutants are present when treatment is initiated.

Appendix

Variant 0 is the wild type, variant 1 is the resistant, and variant 2 is the compensated. At time 0, antibiotic is added and all bacteria except a small number, n₁⁰, that is resistant die. The resistant bacteria grow slowly with rate k₁, so that their number at time t is n₁(t) = n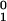e^k₁t. During the growth, a new, compensating mutation can occur with probability u₂ per replication. This new variant grows with rate k₂ > k₁. The rate of appearance of this new variant is

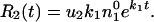7

The probability, P₀, that no compensatory mutation has appeared before time t is determined by the equation

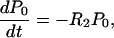8

which can be integrated to give

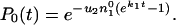9

The probability that the first occurrence of variant 2 takes place in the time interval (t,t + dt) is given by

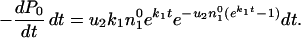10

If the first compensated mutant appears at time t, their numbers at time T will be n₂(T;t) = e^{k₂(T − t)}. Thus the ratio of compensated to resistant mutants at time T will be given by

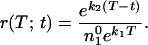11

When this ratio is larger than 1, we can consider variant 2 as having taken over. The probability P_to(T) that the ratio is larger than 1 at time T corresponds to the probability that the first compensated mutant appears before time t₂ = T(1 − k₁/k₂) − (1/k₂)ln(n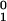). This can be calculated by integration of Eq. 10 from time 0 to time t₂, or from Eq. 9 as P₀(0) − P₀(t₂). Thus, the take-over probability at time T is

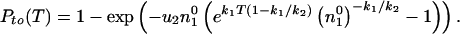12

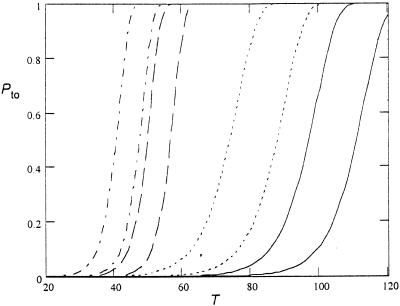
The largest uncertainty in the take-over time comes from the fact that the actual growth rates (k₁ and k₂) are unknown (see Fig. 6). Except for their difference which is ca k₂ − k₁ = 1 per day as measured from the competition experiments (k₂ − k₁ = 0.6 in case 1 and k₂ − k₁ = 1.6 in case 2). The time between sampling of the pretreatment (ClaS) and posttreatment (ClaR) strains was 90 days, suggesting that the fixation probability of a compensated mutant is high for most of the parameter values shown above.

Figure 6.

Take-over probability as a function of time (days) from Eq. 12. Data used: dash-dot, n₁⁰ = 10³, k₁ = 0.5, k₂=1.5; dashed, n₁⁰ = 10, k₁ = 0.5, k₂ = 1.5; dotted, n₁⁰ = 10³, k₁ = 0.2, k₂ = 1.2; solid, n₁⁰ = 10, k₁ = 0.2, k₂ = 1.2. For each pair of curves the left is with u₂ = 10⁻⁸ and the right one is with u₂ = 10⁻⁹.