Holistic Reinforcement Learning: The Role of Structure and Attention

Abstract

Compact representations of the environment allow humans to behave efficiently in a complex world. Reinforcement learning models capture many behavioral and neural effects, but do not explain recent findings showing that structure in the environment influences learning. In parallel, Bayesian cognitive models predict how humans learn structured knowledge, but do not have a clear neurobiological implementation. We propose an integration of these two model classes in which structured knowledge learned via approximate Bayesian inference acts as a source of selective attention. In turn, selective attention biases reinforcement learning towards relevant dimensions of the environment. An understanding of structure learning will help resolve the fundamental challenge in decision science: explaining why people make the decisions they do.

How do We Learn what to Learn About?

The complex, multidimensional nature of the external world presents humans with a basic challenge: learning to represent the environment in a way that is useful for making decisions. For example, a wine neophyte on her first trip to Napa could learn that white wines are more refreshing in hot weather. This experience would give rise to a useful distinction between white wines and all other wines, regardless of other dimensions such as the grape varietal or winery. Such representation learning (see Glossary) often involves dimensionality reduction — the pruning out of distinctions that are unlikely to be important [1]. For example, after multiple wine tastings, our wine enthusiast might start paying attention to the type of grape, but still ignore the color of the label on the bottle. For any given task, a learner should ideally form a compact representation of the environment that includes all relevant input from either the immediate sensory snapshot or memory. Making too few distinctions may lead to ignoring differences between situations that require different behavior. Making too many distinctions may lead to poor generalization to new, related situations. Understanding how learners arrive at a representation of their environment is a fundamental challenge in cognitive science.

Reinforcement learning algorithms are powerful descriptors of how humans learn from trial and error and substantial progress has been made in mapping these algorithms onto neural circuits [2–4]. Yet reinforcement learning approaches still lack an account of how humans learn task representations in multidimensional environments. In particular, recent work has highlighted two phenomena that current models do not fully capture: selective attention to a subset of features in the environment and the use of structured knowledge. These findings come from two literatures that have seen relatively little crosstalk, reinforcement learning models of decision-making and Bayesian models of category learning. We summarize recent advances at the intersection of the two literatures, with the goal of emphasizing parallels between them and motivating new research directions that can establish how neural circuits give rise to useful structured representations of the external world. We propose that representations of task structure learned through approximate Bayesian inference are the source of selective attention during learning. At the neural level, such structured representations in prefrontal cortex determine which aspects of the environment are learned about via dopaminergic modulation of corticostriatal synapses.

Probing How Humans Learn Task Representations

A burgeoning literature has begun to address the question of how humans learn task representations in two different, but related domains: reinforcement learning and category learning. In a typical multidimensional reinforcement learning task, participants are given a choice between stimuli that vary along several dimensions, and observe a reward outcome after every choice (Table 1, yellow). For example, the participant might be presented with a red square and a blue triangle, choose the red square, and receive a binary reward [5]. Often, reward probability does not uniformly depend on all features. For instance, one feature may be more predictive of reward than others [6,7]. Given only partial information about which features matter, participants are instructed to maximize reward in a series of sequential decisions. By contrast, in category learning tasks participants are required to sort multidimensional stimuli one at a time into one of several categories (Table 1, green). Category membership usually depends on the presence or absence of one or more features, as well as on the relationship between features. For example a red square would be classified as a “dax” if “all red objects are daxes” or as a “bim” if “all red circles are daxes” [8]. Finally, a related class of “weather prediction” tasks (Table 1, blue) ask participants to predict one of two outcomes (e.g. rain or shine) given multiple cues and a non-uniform mapping between cues and outcome probabilities [9,10].

Table 1. Studies addressing representation learning.

A representative set of studies that have addressed how humans learn mappings from percepts to states from trial and error. Shown here are distinctions between studies in the size of the observation space, the number of actions available to the subject, and the relationship between stimuli and rewards.

Paper	Observation space	Action space	Reward function
Akaishi et al. 2016 [9]	4 cues	2-alternative weather prediction task	Probabilistic binary outcome contingent on different cue combinations; 2 cues more predictive than the others
Ballard et al. 2017 [8]	3 dimensions × 2 features	2-alternative categorization task	Deterministic binary reward contingent on correctly categorizing stimulus based on 6 possible rules
Choung et al. 2017 [58]	3 dimensions × 2 features	2-alternative go-nogo task	Different cue combinations lead to deterministic positive (+10) or negative (−10) rewards, or to probabilistic rewards (+10 or −10)
Duncan et al. 2018 [10]	4 cues	2-alternative weather prediction task	Probabilistic binary outcome; 2 different environments: separable (both individual cues and combinations are predictive) vs. inseparable (only cue combinations are predictive)
Farashahi et al. 2017 [5]	2 dimensions × 2 features	2-alternative forced-choice task	Probabilistic binary reward; 2 different environments: generalizable (one dimension is on average more predictive) vs. non-generalizable (both dimensions are equally predictive)
Mack et al. 2016 [21]	3 dimensions × 2 features	2-alternative categorization task	Deterministic binary reward for correctly categorizing stimulus based on a diagnostic feature rule or a disjunctive rule
Niv et al. 2015 [7]	3 dimensions × 3 features	3-alternative forced-choice task	Probabilistic binary reward with high probability if subject selects “target feature”, and low probability otherwise

Such tasks differ in framing (e.g. decision-making vs. categorization), the size of the observation space (i.e. how many dimensions stimuli can vary on), the nature of the feedback (scalar reward vs. a category label; stochastic vs. deterministic) and the instructions the participant receives about the structure (Table 1). But they also are alike in that each trial consists of a perceptual observation, an action and a reward outcome. And they share the key property that the participant needs to disambiguate observations by learning and representing an appropriate mapping between perceptual observations and environmental states [4,11–13]. In other words, performance depends on learning to carve the perceptual observation space into a compact state representation appropriate for the task. In this review, we refer to the process of learning a mapping from observations to states as representation learning (note that there also exist other kinds of representation learning problems, such as that of learning the transition structure between states (i.e. model-based learning) [14]).

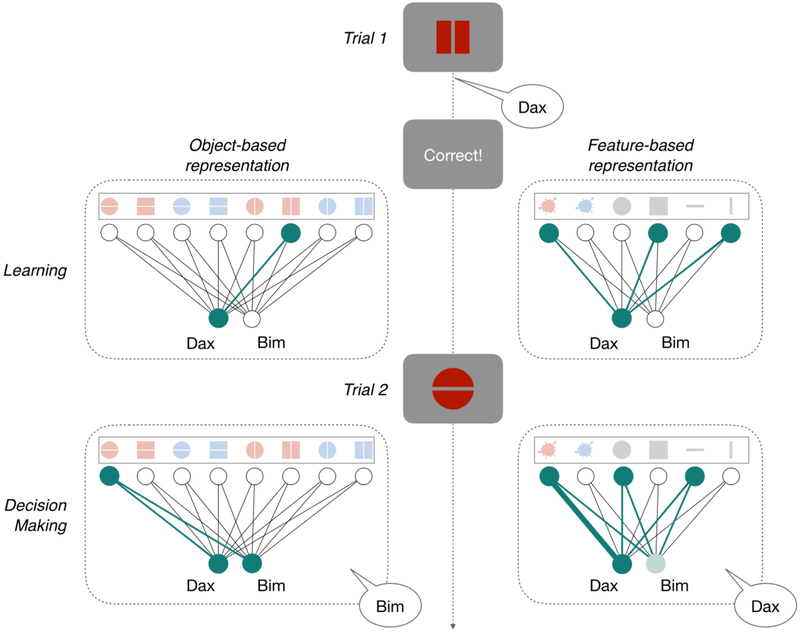
Several studies have tackled the question of what kinds of state representations humans use. These studies built reinforcement learning agents (“models”) that simulated actions trial-by-trial, and compared these predictions to human data [5,7–10,15–17]. Importantly, models that have been proposed vary in the state representation they learn over (Fig. I, Box 1). For example, in object-based reinforcement learning [5,18], the agent maintains a value for each combination of features (Fig. I left). In other words, there is a one-to-one correspondence between unique percepts and states. In feature-based reinforcement learning (a form of function approximation [19]), the agent maintains values for all possible features in the environment and generalizes across observations by combining the predictions of constituent features (e.g., by summing them; Fig. I right). Recent work on multidimensional reinforcement learning has suggested that humans do not use one strategy exclusively. Instead, participants tended to adopt feature-based learning when information about features is predictive and object-based learning when it is not [5,10], and did not rely on object-based representations in a task in which a single feature is more predictive of reward [7] (cf. [20]). These findings suggest that state representations can flexibly adapt to task structure.

Figure I: Possible state representations for a prototypical representation learning task.

Perceptual observations varying along 3 dimensions (color: red or blue, shape: circle or square, and orientation: horizontal or vertical) can be categorized as “daxes” or “bims”. On trial 1, the participant learns from correctly categorizing the red square with a vertical stripe as a “dax”. She can represent the stimulus either as an object (left) or a composition of features (right). An object-based representation leads to strengthening the association between the object and “dax”, while a feature-based representation leads to strengthening the association between the component features and “dax”. On trial 2, the participant must categorize the red circle with a horizontal stripe. If she has an object-based representation, she is indifferent between “dax” and “bim” (and hence might randomly choose “bim”), while if she has a feature-based representation, she would be more likely to say “dax” due to the previously learned association between red and “dax”. Thicker lines show a stronger association between an input-level representation and the output label; active input units, and their connection to output units, are shown in teal.

Box 1. State Representation Effects on Learning.

In addition to learning how to select appropriate actions, humans and animals learn from trial and error which features of our environment are relevant for predicting reward. Formally, this converts the space of perceptual observations into a state representation suitable for the problem at hand.

Imagine for example that on the first trial of a categorization task, you correctly name a red square with a vertical stripe a “dax” (Fig. I, adapted from [8]). The expected value associated with the action “dax” for the current stimulus, V(“dax”|stimulus), can be updated based on the difference between the reward and the initial expected value of that action, i.e., the reward prediction error RPE = R − V₀(“dax”|stimulus), scaled by a learning rate η.

But the update depends on the state representation. For instance, you could either update the entire object (Fig. I left)

$${\mathrm{V}}_{\text{new}}(‘‘\text{dax}"\mid \text{red circle with vertical stripe})={\mathrm{V}}_{\text{old}}(‘‘\text{dax}"\mid \text{red circle with vertical stripe})+\mathrm{\eta }\cdot \text{RPE}$$

or update individual features (Fig. I right):

$${\mathrm{V}}_{\text{new}}(‘‘\text{dax}"\mid \text{red})={\mathrm{V}}_{\text{old}}(‘‘\text{dax}"\mid \text{red})+\mathrm{\eta }\cdot \text{RPE}(\text{and equivalently for}‘‘\text{square}"\text{and}‘‘\text{vertical}")$$

These different assumptions about the state representation will lead to diverging reward expectations. If you next encounter a red circle with a horizontal stripe and you have an object-based state representation, you will not expect reward for saying “dax” because you have never encountered this stimulus before. If you have a feature-based representation, you will expect a reward for saying “dax”, because the same action in response to a different red stimulus previously led to reward.

Attention Shapes State Representations

How can it be that people use different representations in different learning tasks? One possible explanation is that selective attention dynamically shapes state representations. Selective attention is defined as the preferential processing of a subset of environmental features at any stage between perception and action. Several recent studies have reported that attended features influence actions more strongly than unattended features, and are learned about more readily [7,17,21,22]. Moreover, this interaction between attention and learning is bidirectional: attentional biases are dynamically adjusted as a function of reward history [22].

Selective attention could sculpt state representations for reinforcement learning via known neurobiological mechanisms. Reinforcement learning is thought to occur via dopamine-dependent plasticity of synapses from cortical neurons onto striatal neurons [23]. In response to an unexpected reward, dopamine neurons fire in proportion to the reward prediction error [2] and release dopamine onto their striatal targets [24], facilitating long-term potentiation of corticostriatal synapses [25]. If cortical neurons are firing in response to a sensory cue, such as a tone, at the same time as a surprising reward, then their synapses onto striatal neurons will strengthen (and vice versa for a negative prediction error, which causes long-term depression of synapses). If attention is directed to a subset of sensory features, then the cortical response to those features will be stronger and more precise [26]. Because these neurons are firing more, their synapses onto striatal neurons will be strengthened more in response to unexpected reward than those of unattended features. Attention could therefore bias reward-driven value learning towards a subset of features in the sensory environment.

If selective attention shapes the representations used for learning, then an important empirical question is, which aspects of the observation space are subject to attentional selection? Two prominent theories suggest different targets for attention in reinforcement learning. The Mackintosh model proposes that attention tracks stimulus features that are most predictive of reward [27]. The Pearce and Hall model suggests instead that attention is directed to features that learners are most uncertain about [28]. Hybrid approaches suggest that both processes occur independently [29,30], while integration models posit that a stimulus’ learned attentional salience is directed by both predictiveness and uncertainty [31,32], with the balance of the two possibly different at the choice versus learning stage of a decision [33,34]. Additionally, features of the stimulus, such as its visual salience, can capture attention in a bottom-up manner [35] and such features ought to be learned about more readily. While a topic of active debate, how the brain dynamically directs attention during either choice or learning remains an open question [36].

Insights from Structure Learning

Humans use knowledge about the world to scaffold learning. This knowledge can take the form of abstract concepts [37], domain knowledge [38], relational maps of the environment [39,40], or hierarchically structured knowledge of task rules [41]. Knowledge about structure endows humans with a remarkable ability to generalize behavior to new environments. It also enables rapid “one-shot” learning of new concepts and “learning to learn” [42,43], the ability to learn more quickly after experience with a class of learning problems. Cognitive psychology research has successfully modeled such structure learning phenomena using Bayesian cognitive models.

Probabilistic programming models (Fig. 1, top row) construct rules (or concepts) from compositions of features with simple primitives (e.g., “for all”, “if”, “and”, “or”) [37,42,44]. In category learning tasks, rules are constructed from the stimulus features and simple logical operations (e.g. “(blue and square) or red”) [8,37,45]. Given a hypothesis space of all possible rules, the posterior probability is calculated via Bayesian inference, considering both a rule’s complexity and the proportion of examples it correctly categorizes. Rules are, a priori, exponentially less likely as the expressive length of the rule increases. Probabilistic programming models are an instance of a class of models that describe concept-learning data by assuming a compositional rule-based structure (e.g., RULEX [46]). The unique contribution of probabilistic programming models is that they use statistical inference to build concepts that are appropriate for the learning problem. This flexibility allows them to explain phenomena outside of categorization, such as how people infer causal relationships between events [47,48] or how people infer others’ intentions from their actions [49] or choice of words [50].

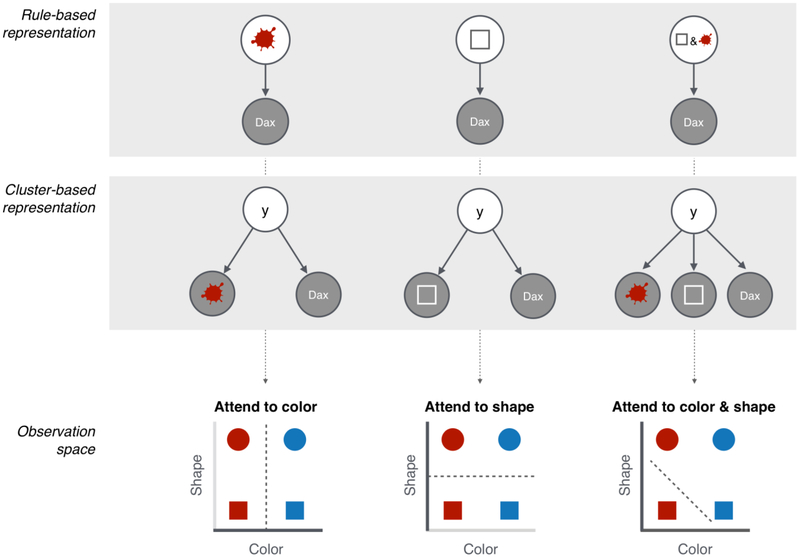
Figure 1: Structure learning guides selective attention.

Rules inferred by probabilistic programming models (top row) or clusters inferred by Bayesian non-parametric models (middle row) lead to different perceptual distinctions in observation space (bottom row). Left column: if the agent infers that red objects are “daxes”, or that red and “dax” cluster together, then she can ignore shape and only attend to color when categorizing a stimulus as a “dax” or a “bim”. Middle column: similarly if the agent infers that squares are “daxes” (middle left), or that square and “dax” cluster together, then she can ignore color and only attend to shape. Right column: finally if the agent infers that red squares are “daxes”, or that red, square and “dax” cluster together, then she should attend to both color and shape.

Yet category learning tasks only subtly differ from decision-making experiments that are modeled with reinforcement learning (Table 1). A recent study of human category learning highlighted this relationship by directly comparing a Bayesian probabilistic programming model with several reinforcement learning models that learn over different state representations [8,37]. While reinforcement learning models can learn categorization rules if given the correct state representation, the Bayesian model better predicted human choices. In contrast to reinforcement learning, which learns over a predefined state representation and updates uninformative states indefinitely, probabilistic programming models settle on the rules that parsimoniously describe observations.

Bayesian non-parametric models (Fig. 1, middle row) also highlight how Bayesian inference can explain learning phenomena that have eluded reinforcement learning (cf. [51]). Bayesian non-parametric models group perceptual observations into unobserved “latent causes” (or clusters) [52–55]. For example, consider a serial reversal learning task in which the identity of the high-reward option sporadically alternates. In such tasks, animals initially learn slowly and but eventually learn to rapidly respond to contingency changes [56]. Bayesian non-parametric models learn this task by grouping reward outcomes into two latent causes: one in which the first option is better, and one in which the second option is better. Once this structure is learned, the model displays one-shot reversals after contingency changes because it infers that the latent cause has changed. This inference about latent causes in the environment has also shed light on several puzzling conditioning effects. When presented with a neutral stimulus such as a tone followed by a shock, animals eventually display a fear response to the tone. The learned fear response gradually diminishes when the tone is later presented by itself (i.e. in extinction), but often returns after some time has passed. This phenomenon is known as spontaneous recovery. Bayesian non-parametric models attribute spontaneous recovery to the inference that extinction signals a new environmental state. This prevents old associations from being updated [57]. Bayesian nonparametric models also predict that gradual extinction will prevent spontaneous recovery, a finding borne out by empirical data [57]. In gradual extinction, the model infers a single latent state and gradually weakens the association between that state and aversive outcome, thereby abolishing the fear memory.

In both probabilistic programming and Bayesian nonparametric models, learning is biased by a prior that favors simpler representations over complex ones. For example, a probabilistic programming model is biased towards rules in which a single feature is relevant for classification. This simplicity prior is appropriate across tasks and domains. This stands in contrast to reinforcement learning models that require definition of an appropriate state space for each task. A simplicity bias is also consistent with findings that suggest that trial-and-error learning follows a pattern whereby simpler feature-based state spaces precede more complex object-based spaces [5,58], and explains why classification becomes harder as the number of relevant dimensions grows [59]. The findings outlined in this section illustrate both the importance of structured knowledge in learning and the utility of Bayesian cognitive models for explaining how this knowledge is acquired. However, they raise an important question: how does this knowledge about task structure interface with the neural systems that support reinforcement learning?

Bridging Structure Representations and Neural Models of Reinforcement Learning

We propose a conceptual model that links reinforcement learning with a structure learning system in a neurobiologically plausible architecture (Fig. 2). We base our framework on connectionist models of the basal ganglia-prefrontal cortex circuit [41,60,61]. These models describe how rules [41,62,63] or working memory content [61,64] are selected via known corticostriatal circuitry (see [61] for neuroanatomical detail). Antero-lateral prefrontal cortical pools can represent different rules, working memory content, or hypotheses about task structure. These different pools compete via mutual lateral inhibition. The outcome of this competition is biased by the relative strength of each pools’ connectivity with the striatum. Pools with stronger cortical-striatal connectivity will generate a stronger striatal response, which in turn increases the strength of thalamic feedback onto these pools. This recurrent circuit allows a pool representing a task rule to inhibit competing pools and control behavior [65]. If an unexpected reward occurs, dopamine release in the striatum strengthens the synapses from the most active cortical pool. In this way, rule representations that lead to reward are more likely to win over alternative representations in the future [41,66]. This model describes how a reinforcement learning system could gate the representation of a hypothesis about task structure into cortex. Our central proposal is that this hypothesis is the source of top-down selective attention during learning (Box 2).

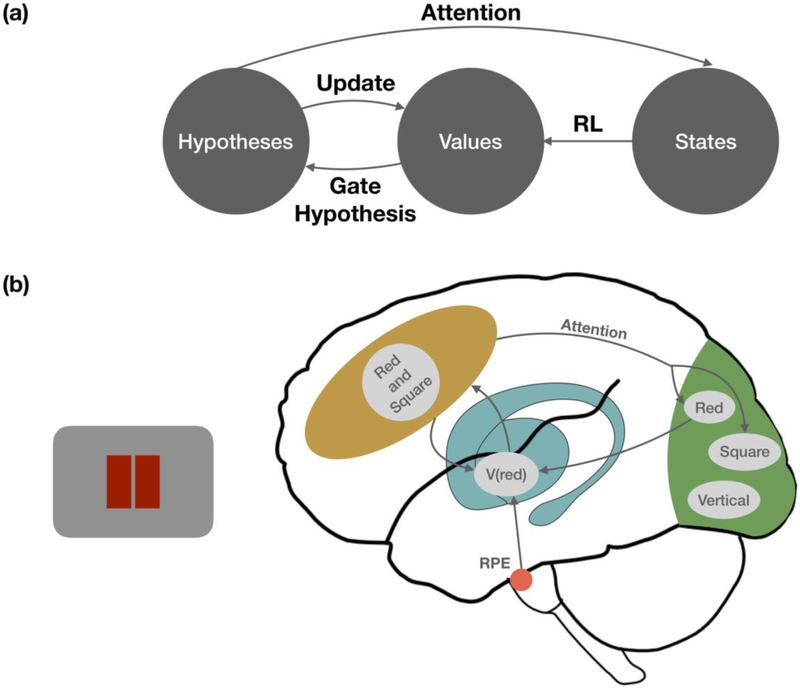
Figure 2: Conceptual model of structure learning.

(a). We propose that 1) hypotheses about task structure are the source of top-down attention and 2) attention sculpts the state representation by prioritizing some features of the environment for reinforcement learning. Existing models suggest that state values (or (state,action) pair values) are learned via reinforcement learning. In turn, learned values about states participate in the gating of which hypotheses are considered. Specifically, hypotheses that are consistent with the high-value (state, action) pairings are more likely to be considered. Finally, prediction errors in response to violations of these hypotheses help to update state values. (b) A simple model showing how the interacting systems architecture in (a) could be realized in different neural circuits. Yellow area corresponds to the lateral prefrontal cortex, blue to the basal ganglia, green to sensory cortex, and red to the dopaminergic midbrain. A prefrontal hypothesis that “red and square” is the correct categorization rule biases top-down attention to the “red” and “square” features in sensory cortex, which in turn increases learning about these features in response to reward prediction errors (RPE). In turn, values stored in the striatum influence prefrontal rule selection.

Box 2. How Selective Attention May Emerge from Structure Learning.

When stimuli are multidimensional, the state representation underlying reinforcement learning is shaped by selective attention [22]. Total reward expectation can be computed as a weighted sum of expectations from each component feature:

$$\mathrm{V}(‘‘\text{dax}"\mid \text{red circle})={\mathrm{\Phi }}_{\text{color}}\mathrm{V}(‘‘\text{dax}"\mid \text{red})+{\mathrm{\Phi }}_{\text{shape}}\mathrm{V}(‘‘\text{dax}"\mid \text{circle})$$

where V are reward expectations and Φ are attention weights. But how are the weights determined? These weights can be thought of as indexing the allocation of attention to each feature. We illustrate how these attention weights can emerge from inferring latent structure:

Probabilistic programming models (Fig. 1 top row) construct rules from compositions of perceptual features and logical primitives (e.g., “and”, “or”, “not”). Returning to the categorization problem from Fig. I reduced to 2 dimensions (color: red or blue, and shape: circle or square), say you observe evidence in favor of the rule that “red objects are daxes”. Given this rule, you can collapse across the shape dimension and only attend to the color of each object (Φ_color = 1, Φ_shape = 0, Fig. 1 left column, bottom panel). If on the other hand you believe that “squares are daxes”, you can ignore color and only attend to shape (Φ_color = 0, Φ_shape = 1, Fig. 1 middle column, bottom panel). Finally, if your rule is that “red squares are daxes”, you must be able to distinguish across both dimensions (Φ_color = 0.5, Φ_shape = 0.5, Fig. 1 right column, bottom panel).

Bayesian non-parametric models (Fig. 1 middle row) propose an alternative mechanism for structure learning, which is to group observations into clusters, or “latent causes” that generate linked observations. When a latent cause is “on”, it tends to emit linked observations. For example, if you infer that latent variable y causes both red and “dax”, you can ignore shape (Φ_color = 1, Φ_shape = 0, Fig. 1 left column, bottom panel), since only the presence of red is relevant for determining whether y is active and will also cause “dax”. If on the other hand you infer that latent variable y causes both square and “dax”, you can ignore color (Φ_color = 0, Φ_shape = 1, Fig. 1 middle column, bottom panel). Finally if both red and square are related to “dax” via y, attention should be allocated to both color and shape, as both dimensions provide information about the likelihood of y being active and also causing “dax” (Φ_color = 0.5, Φ_shape = 0.5, Fig. 1 right column, bottom panel).

Both probabilistic programming models and Bayesian non-parametric models offer normative solutions to the problem of learning to represent structure in the environment. Understanding whether and how the different representations they require (rules vs. clusters) map onto neural circuits may help adjudicate between the two model classes.

Hypotheses about task structure can constrain feature-based reinforcement learning by directing attention to specific component features and not others. For example, a hypothesis that “red stimuli are daxes” would increase the strength and fidelity of the representation of color in sensory cortex. If an unexpected outcome follows a red square, the heightened representation of “red” will cause a larger update to the corticostriatal projections from “red” neurons than from “square” neurons. As a result, reinforcement learning will operate over a feature-based representation with biased attention to the color “red”. If later in the task the hypothesis is updated to “red squares are daxes”, then both red and square features will be attended to more strongly than other features. In this way, rules can sculpt the state representation underlying reinforcement learning.

Reinforcement learning could, in turn, contribute to the selection of hypotheses via two mechanisms. First, learning can adjust the corticostriatal weights of projections from cortical pools representing alternative rules, as has been proposed by a recent neural network model [41]. Second, reinforcement learning over features represented in sensory cortex can contribute to rule selection. For instance, the rule “red squares are bims” will be influenced by simple reinforcement learning linking “red” with “bim” and “square” with “bim”. Even if the learner is using the rule “red objects are bims”, the incidental reinforcement of “square” every time a red square is correctly classified as “bim” will cause higher activation of “red squares” relative to “red circles” neural pools in the cortex. This differential activation will increase the likelihood that the subject switches to the correct rule. This mechanism is consistent with the finding that even when subjects are given the correct categorization rule, features of the stimulus that are not part of the rule exert an influence on decisions [20]. When a rule is discarded, reinforcement learning would also support the selection of an alternative rule that has explained past observations. This mechanism eliminates the need to remember all previous trials and evaluate alternative rules against these memories, thereby endowing the hypothesis testing system with implicit memory.

By designating hypotheses as the source of top-down attention, this model provides a mechanistic account of how reinforcement learning is influenced by both structured knowledge and attention. This idea is closely related to recent work suggesting that working memory contents in lateral prefrontal circuits act as the source of top-down attention to the constituent sensory circuits [67]. Indeed, working memory plays an important role in constraining reinforcement learning [68], and our model predicts that learning is influenced by the number of hypotheses that can be simultaneously considered [69].

Computational Feasibility of Bayesian Inference

Our model claims that hypotheses about task structure are considered in a manner consistent with Bayesian rational models. However, the computations underlying these models are generally intractable [70]. For instance, in probabilistic programming models, the agent must repeatedly compute the likelihood of all previous observations over all possible rules. Recent work has attempted to address this problem using sampling algorithms that approximate solutions to Bayesian inference [71,72]. One such algorithm is the particle filter.

A particle filter can approximate any given Bayesian model by using a finite number of particles, each of which expresses a particular hypothesis about the state of the world [73,74]. For example, in a category learning task, each particle represents a single categorization rule. After an observation, the particle either samples a new hypothesis or stays with the current one. This decision depends on how likely the observation is under the current hypothesis. A particle encoding the belief that “red stimuli are daxes” would be more likely to stay with its current hypothesis after observing a red square that is a “dax”, and more likely to switch to a new hypothesis after observing a red square that is a “bim”. This update algorithm is computationally simple because it only incorporates each particle’s belief about the world (e.g., one classification rule).

In addition to their computational simplicity, particle filters are an appealing model for representation learning because they can preferentially sample simpler rules. Moreover, they capture the phenomenological report that people consider alternative hypotheses [75]. Particle filters also closely resemble a serial hypothesis testing model that has previously been shown to describe human behavior in a multidimensional decision-making task [76]. In addition, they provide a single framework for implementing representation learning over different types of models, including both probabilistic programming models and Bayesian nonparametric models [69,71].

Given an infinite number of particles, particle filters converge to the true posterior probability. Remarkably, recent work has demonstrated that the use of a single or very few particles can describe human behavior well. This is because humans face a practical problem: rather than learning the true probability distribution over all possible rules, people need only find a rule that explains enough observations to make good decisions [77]. This could explain why behavior across an entire group may be Bayes-optimal, but individual choices are often not [78]. If each individual tracks just one or a few hypotheses, only the group behavior will aggregate over enough “particles” to appear Bayes-optimal [78].

Our neural model proposes that hypotheses are gated by corticostriatal circuitry that is, in turn, influenced by reinforcement learning. This architecture could form the basis of a particle filter algorithm. Specifically, particle filters sample hypotheses based on how well each hypothesis accounts for previous observations. Feature weights learned via reinforcement learning could enable the sampling of hypotheses that have already explained some observations. Unlike particle filter accounts of sensory integration, which propose that individual spikes of feature-selective neurons represent particles [79–82], in our model particles correspond to distributed prefrontal representations of rules. The particle filter algorithm is a flexible mechanism for inference that could apply to different timescales (from milliseconds to trials) and different types of problems (e.g., perception and categorization).

Although corticostriatal connectionist models can exhibit properties similar to a Bayesian structure-learning model [41], the corticostriatal gating mechanism need not perfectly implement a particle filter, and the differences may be informative [77]. For example, in a task where the motor response mapping varies (e.g., “bim” is sometimes the left-hand and sometimes the right-hand response), a corticostriatal gating model would correctly predict that if recent right-hand selections were rewarded, the subject is more likely to respond “right” regardless of category of the current stimulus [83]. A particle filter implementing a probabilistic programming model of representation learning would not predict this effect. A fruitful area for future research will be to examine other ways in which constraints imposed by the corticostriatal architecture can predict deviations from Bayesian inference.

Related Models

Our proposal that prefrontal cortex and striatum interact to support structure learning is related to the longstanding idea that the brain contains multiple, competing learning systems [84,85] (see COVIS for computational implementation [86]). Previous work has shown that in tasks where categorization rules are difficult to verbalize, (e.g., respond left to squares that are more red than they are circular), performance is supported by incremental learning in corticostriatal circuits [87,88]. In contrast, performance of explicit rule-learning tasks depends on prefrontal cortex [89]. Our proposal also relies on the distinction between the kinds of representations and learning supported by the prefrontal cortex and striatum. However, we propose that prefrontal rule representations act as a source of top-down attention that sculpts the state representation over which reinforcement learning operates.

Rule-based categorization models stand in contrast to clustering approaches to learning. In clustering models, stimuli are clustered according to the similarity of their features. This clustering can be biased by attention, such that stimuli that differ in unattended features nonetheless cluster together (e.g., in the attention-learning covering map model; “ALCOVE” [90]). An association between a cluster (e.g., all previous red stimuli) and a category label (e.g., “dax”) implicitly encodes a categorization rule (“red stimuli are daxes”). This mechanism for building representations has been proposed as a solution to the representation learning problem in reinforcement learning [91]. A related model, the supervised and unsupervised stratified adaptive incremental network (“SUSTAIN”), suggests that a single cluster is activated by each stimulus (akin to a single rule representation in our model) [92]. SUSTAIN shares many similarities to the Bayesian nonparametric models described above and more empirical work is necessary to adjudicate between their mechanisms for forming clustered representations. Importantly, both SUSTAIN and ALCOVE describe a bidirectional relationship between attention and representation learning that is influenced by prediction errors, in line with the framework we suggest here.

The critical difference between clustering models and the model that we describe is the nature of the representation (clusters versus concepts). Because probabilistic programming models perform inference over compositions of concepts, they can handle a broader range of tasks. Consider the task of learning to tie one’s shoelaces. Probabilistic programming models would treat each of the operations that can be applied to a shoelace as a concept, and could learn how to tie knots from compositions of these concepts. These compositions can be rapidly applied to solve new problems, such as tying a bow on a gift or triple-knotting one’s shoelaces before a hike. Categorization tasks may be a special case in which the predictions of cluster-based and rule-based models converge. Moreover, these models may map onto partially distinct neural systems, with the hippocampus and medial temporal lobe cortex supporting learning based on similarity to past exemplars [92,93], and the prefrontal cortex supporting learning based on concepts. Recent work showed that multivariate hippocampal representations of stimuli are similar to predictions of the SUSTAIN model [21]. In category learning, the top-down attention mechanism we propose may also influences hippocampal clustering. Indeed, there is elevated prefrontal-hippocampal functional connectivity during category learning [21].

The role of the hippocampus and surrounding cortex in representation learning is likely to extend beyond the clustering of past experiences. Conjunctive representations of multiple features in the hippocampus can support reinforcement learning over configurations of features [10,94] and the selection of hypotheses relating to conjunctions of features. Further, episodic retrieval of individual past choices and outcomes, as well as previous task rules, has a strong influence on decisions [95,96]. Retrieval is both influenced by and influences top-down attention. As a result, retrieval is likely to interact with the model we propose. For example, retrieval drives reinstatement of cortical representations of features [97], which could lead to reinforcement learning over features that are not present in the environment. Finally, the hippocampus and entorhinal cortex form spatial maps of the environment in the service of spatial learning [98]. Recent modeling and empirical work has emphasized a role for the hippocampus and entorhinal cortex in forming cognitive maps of tasks and a specific function for the hippocampus in signaling that the environment has changed enough to necessitate forming a new state representation [39,93,99]. Thus, a pressing question for the field is what distinguishes the representations of task structure between the hippocampus and prefrontal cortex.

Concluding Remarks

We have outlined recent findings showing the extent to which reinforcement learning is constrained by attention and by the underlying representation of the structure of the environment. We propose that attention is a key mechanism that sculpts the sensory representations supporting learning. Bayesian cognitive models explain unique aspects of behavior in categorization tasks that are very similar to the tasks used to study reinforcement learning. An exciting possible unification of these research threads is that abstract conceptual knowledge that forms the basis of these cognitive models drives top-down attention during learning. Our conceptual model makes several testable predictions. First, particle filter or related approximations to Bayesian cognitive models should describe the diversity of individual subject behaviors in representation learning tasks [69]. Second, application of a rule should be associated with increased sensory cortical responses to the constituent features of that rule, and increased reinforcement learning about them. Third, values learned via reinforcement learning should influence which rules are selected in rule learning tasks.

Manipulations that are known to influence attention and working memory should also influence representation learning. For example, interference from a dual task may reduce the number of hypotheses about task structure (e.g. rules in a categorization task) that can be considered simultaneously. A quantitative prediction of our model is that this would reduce the accuracy of rule learning. From a neuroscience perspective, dual tasks degrade the quality of representations held in working memory [100], which could cause learners to forget rules or implement them more noisily. Another possible consequence of a dual task is that attention is biased against complex rules. This could actually improve learning for tasks with a simple structure (e.g. tasks where a single feature is relevant for categorization or reward), because the dual task prevents the learner from considering complex hypotheses that may have otherwise interfered with learning. In addition, features that drive bottom-up attentional capture, such as exogenously salient or mnemonically important features, should be more likely be incorporated into hypotheses and, as a result, drive top-down attention. The impact of these features should depend on their rule-relevance: if salient features are relevant to the task rules, they should accelerate representation learning.

Answering these and related questions (see Outstanding Questions Box) will help to illuminate how rule representations in prefrontal cortex influence ongoing neural processing in the service of adaptive behavior. More broadly, it will help us to understand how humans build rich representations that are suited to both their environment and their goals, a question central to our understanding of cognition in both health and disease [101].

Outstanding Questions Box.

• How do reinforcement learning and cortical representations of structure interact to control behavior? Can systematic deviations from Bayesian rationality be explained by reinforcement learning? Can we model why different tasks bias the arbitration between learning systems?

• Are the predictions of corticostriatal connectionist models of rule learning borne out by neural and neuroanatomical data? For example, do anterior cortical projections influence the stimulus-response coding profiles of striatal neurons targeted by motor cortex? Do thalamocortical projections mediate the activation of cortical neurons representing task rules?

• What are the regional differences in task structure learning and representation across prefrontal cortex? In particular, what are the different roles for orbitofrontal cortex and lateral prefrontal cortex in representation learning?

• How does working memory affect representation learning? Specifically, does interference from working memory contents influence hypothesis selection and top-down attention? Do multiple hypotheses or rules interfere with one another due to working memory constraints? Do individual differences in working memory capacity relate to representation learning?

• How do relational, spatial, and episodic knowledge in the hippocampus support or compete with reinforcement learning? Under what conditions does retrieval interfere with or support representation learning?

• Can a union of Bayesian cognitive models with reinforcement learning provide new ideas about education and classroom learning? How can attention be directed to facilitate the discovery of a novel concept?

• Can structure learning account for maladaptive behaviors in psychiatric and substance abuse disorders?

Highlights.

• Recent advances have refined our understanding of reinforcement learning by emphasizing roles for attention and for structured knowledge in shaping ongoing learning.

• Bayesian cognitive models have made great strides towards describing how structured knowledge can be learned, but their computational complexity challenges neuroscientific implementation.

• Behavioral and neural evidence suggests that each class of algorithms describe unique aspects of human learning.

• We propose an integration of these computational approaches in which structured knowledge learned through approximate Bayesian inference acts as a source of top-down attention, which shapes the environmental representation over which reinforcement learning occurs.

Glossary

Action

A response the participant makes, e.g. choosing an option, labeling a stimulus or predicting an outcome.

Bayesian non-parametric models

A class of Bayesian cognitive models that group observations into sets of unobservable latent causes, or clusters.

Environmental state

A subset of environmental features relevant to the agent’s goal, e.g. the feature red being more predictive of reward.

Particle filters

A class of sampling methods for approximating arbitrary probability distributions in a sequential manner, by maintaining and updating a finite number of particles (hypotheses).

Perceptual observation

A stimulus, potentially with multiple features.

Probabilistic programming models

A class of Bayesian cognitive models that reason over structured concepts such as rules.

Reinforcement learning

A class of algorithms that learn an optimal behavioral policy, often through learning the values of different actions in different states.

Representation learning

The process by which learners arrive at a representation of environmental states.

Reward outcome

Consequence of an action, e.g. a reward or category label.

Reward prediction error

The difference between the reward outcome and what was expected, used as a learning signal for updating values of states and actions.

State representation

The agent’s internal representation of the environmental state.