Abstract
PET image reconstruction is challenging due to the ill-poseness of the inverse problem and limited number of detected photons. Recently deep neural networks have been widely and successfully used in computer vision tasks and attracted growing interests in medical imaging. In this work, we trained a deep residual convolutional neural network to improve PET image quality by using the existing inter-patient information. An innovative feature of the proposed method is that we embed the neural network in the iterative reconstruction framework for image representation, rather than using it as a post-processing tool. We formulate the objective function as a constrained optimization problem and solve it using the alternating direction method of multipliers (ADMM) algorithm. Both simulation data and hybrid real data are used to evaluate the proposed method. Quantification results show that our proposed iterative neural network method can outperform the neural network denoising and conventional penalized maximum likelihood methods.
Index Terms—: Positron emission tomography, Convolutional neural network, iterative reconstruction
I. Introduction
Positron Emission Tomography (PET) is an imaging modality widely used in oncology [1], neurology [2] and cardiology [3], with the ability to observe molecular-level activities inside the tissue through the injection of specific radioactive tracers. Though PET has high sensitivity compared with other imaging modalities, its image resolution and signal to noise ratio (SNR) are still low due to various physical degradation factors and low coincident-photon counts detected. Improving PET image quality is essential, especially in applications like small lesion detection, brain imaging and longitudinal studies. Over the past decades, multiple advances have been made in PET system instrumentation, such as exploiting time of flight (TOF) information [4], enabling depth of interaction capability [5] and extending the solid angle coverage [6], [7].
With the wide adoption of iterative reconstruction in clinical scanners, more accurate point spread function (PSF) modeling can be used to take various degradation factors into consideration [8]. In addition, various post processing approaches and iterative reconstruction methods have been developed by making use of local patch statistics, prior anatomical or temporal information. Denoising methods, such as the HYPR processing [9], non-local mean denoising [10], [11] and guided image filtering [12] have been developed and show better performance in bias-variance tradeoff or partial volume correction than the conventional Gaussian filtering. In regularized image reconstruction, entropy or mutual information based methods [13]–[15], segmentation based methods [16], [17], and gradient based methods [18], [19] have been developed by penalizing the difference between the reconstructed image and the prior information in specific domains. The Bowsher’s method [20] adjusts the weight of the penalty based on similarity metrics calculated from prior images. Methods based on sparse representations [21]–[27], have also shown better image qualities in both static and dynamic reconstructions. Most of the aforementioned methods require prior information from the same patient which is not always available due to instrumentation limitation or long scanning time, which may hamper the practical application of these methods. Recently a new method is developed to use information in longitudinal scans [28], but can only be applied to specific studies.
In this paper, we explore the potential of using existing inter-patient information via deep neural network to improve PET image reconstruction. Over the past several years, deep neural networks have been widely and successfully applied to computer vision tasks, such as image segmentation [29], object detection [30] and image super resolution [31], due to the availability of large data sets, advances in optimization algorithms and emerging of effective network structures. Recently, it has been applied to medical imaging, such as image denoising and artifact reduction, using convolutional neural network (CNN) [32]–[35] or generative adversarial network (GAN) [36]. It showed comparable or superior results to the iterative reconstruction but at a faster speed. In this paper, we propose a new framework to integrate deep CNN in PET image reconstruction. The network structure is a combination of U-net structure [29] and the residual network [37]. Different from existing CNN based image denoising methods, we use a CNN trained with iterative reconstructions of low-counts data as the input and high-counts reconstructions as the label to represent the unknown PET image to be reconstructed. Rather than feeding a noisy image into the CNN, we use the CNN to define the feasible set of valid PET images. To our knowledge, this is the first of its kind in the applications of neural network in medical imaging. The solution is formulated as the solution of a constrained optimization problem and sought by using the alternating direction method of multipliers (ADMM) algorithm [38]. The proposed method is validated using both simulation and hybrid real data.
The main contributions of this paper include (1) using dynamic data of prior patients to train a network for PET denoising and (2) proposing to incorporate the neural network into the iterative reconstruction framework and demonstrating better performance than the denoising approach. This paper is organized as follows. Section 2 introduces the theory and optimization algorithm. Section 3 describes the computer simulations and real data used in the evaluation. Experimental results are shown in Section 4, followed by discussions in Section 5. Finally conclusions are drawn in Section 6.
II. Theory
A. PET data model
In PET image reconstruction, the measured data can be modeled as a collection of independent Poisson random variables and its mean is related to the unknown image through an affine transform
| (1) |
where is the detection probability matrix, with Pij denoting the probability of photons originating from voxel j being detected by detector i [39]. denotes the expectation of scattered events, and denotes the expectation of random coincidences. M is the number of lines of response (LOR) and N is the number of pixels in image space. The log-likelihood function can be written as
| (2) |
The maximum likelihood estimate of the unknown image x can be found by
| (3) |
B. Representing PET images using neural network
Previously, the kernel method [24] used a kernel representation x = Kα to represent the image x, through which the prior temporal or anatomical information can be embedded into the kernel matrix . The kernel representation can be treated as a linear representation by the kernel matrix and the kernel coefficients. Inspired by this idea, here we represent the unknown image x through a nonlinear representation
| (4) |
where represents the neural network and α denotes the input to the neural network. Through this representation, inter-patient information and intra-patient information can be included into the iterative reconstruction framework through pre-training the neural network using existing data.
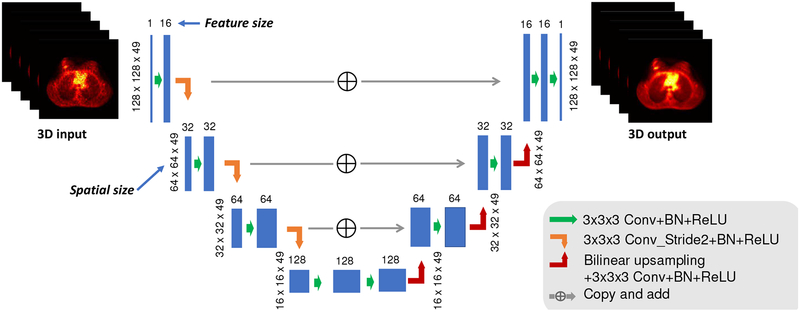
Our network implemented in this work is based on 3D version of the U-net structure [29] and also includes the batch normalization layer [40]. The overall network architecture is shown in Fig. 1. It consists of repetitive applications of 1) 3×3×3 convolutional layer, 2) batch normalization (BN) layer, 3) ReLU layer, 4) convolutional layer with stride 2 for down-sampling, 5) bilinear interpolation layer for upsampling, and 6) identity mapping layer that adds the left-side feature layer to the right-side. In our implementation, there are three major modifications compared to the original U-net:
Fig. 1:
The schematic diagram of the neural network architecture. The feature size after the first convolution is 16. Once the image is downsampled through the convolution operation with stride 2, the feature size will be multiplied by 2. The spatial size is based on the XCAT and lung patient studies. For brain patient study, the third dimension of the spatial size is 91. 3D convolution is used and the total number of trainable parameters is around 1.4 million.
using convolutional layer with stride 2 to down-sample the image instead of using max pooling layer, to construct a fully convolutional network;
use bilinear interpolation instead of transpose convolution for upsampling to remove the potential checkboard artifact [41];
directly adding the left side feature to the right side instead of concatenating, to reduce the number of training parameters.
The left-hand side of the architecture aims to compress the input path layer by layer, an “encoder” part, while the right-hand side is to expand the path, a “decode” part. Unlike the original 2D U-net which has four down-sampling operations, here we only use three down-sampling operations, to reduce the trainable parameters due to limited number of training pairs. After the last layer, ReLU activation function is added, which sets all the negative value to 0. Through ReLU activation, non-negative constraint is enforced on image x. This neural network has 15 convolutional layers in total and the largest feature size is 128. We have also tried a 2D Unet with input consisting of five axial slices, and found that the 3D structure can generate better image qualities. The network is trained with reconstructed images from low counts data as the input and the images reconstructed from high counts data as the label. The number of trainable parameters for this 3D CNN is around 1.4 million. The parameters mainly include the convolutional kernels, the bias terms and the parameters for each batch normalization.
When substituting the representation in (4) using the above mentioned network structure, the original PET system model shown in (1) can be rewritten as
| (5) |
The maximum likelihood estimate of the unknown image x can be calculated as
| (6) |
| (7) |
The objective function in (7) is difficult to solve due to the nonlinearity of the neural network representation. Here we transfer it to the constrained format as below
| (8) |
C. Optimization
We use the Augmented Lagrangian format for the constrained optimization problem in (8) as
| (9) |
which can be solved by the ADMM algorithm iteratively in three steps
| (10) |
| (11) |
| (12) |
Subproblem (10) is a penalized PET reconstruction problem. We solve it using the optimization transfer method [42]. As x in L(y|x) is coupled together, we first construct a surrogate function QL(x|xn) for L(y|x) as follows
| (13) |
Where and is calculated by
| (14) |
It can be verified that the constructed surrogate function QL(x|xn) fulfills the following two conditions:
| (15) |
| (16) |
After getting this surrogate function, subproblem (10) can be optimized pixel by pixel. For pixel j, the surrogate objective function for subproblem (10) is
| (17) |
The final update equation for pixel j after maximizing (17) is
| (18) |
Subproblem (11) is a non-linear least square problem. In order to solve it, we need to compute the gradient of the objective function with respect to the input α. As it is difficult to calculate the Jacobian matrix or Hessian matrix of the objective function with respect to the input in current network platform, we use a first-order method as follows
| (19) |
where β is the step size and non-negative constraint is added on the network input α, as all network inputs are nonnegative during network training. In our implementation, β is a scalar and was chosen so that the objective function in subproblem (11) can be monotonic decreasing. As the intensity of network input is normalized to be within a certain range, once a proper β is found, it can be used for different data sets. In order to accelerate the convergence speed, Nesterov momentum method was used in subproblem (11) [43]. In our implementation, we run one iteration for subproblem (10) and then run five iterations for subproblem (11). As subproblem (11) is a non-linear problem, it is very easy to be trapped into a local minimum and it is thus essential to assign a good initial for α. In our implementation, we first ran MLEM for 30 iterations and used its CNN output as the initial for α. The overall algorithm flowchart is presented in Algorithm 1.
D. Implementation details and reference methods
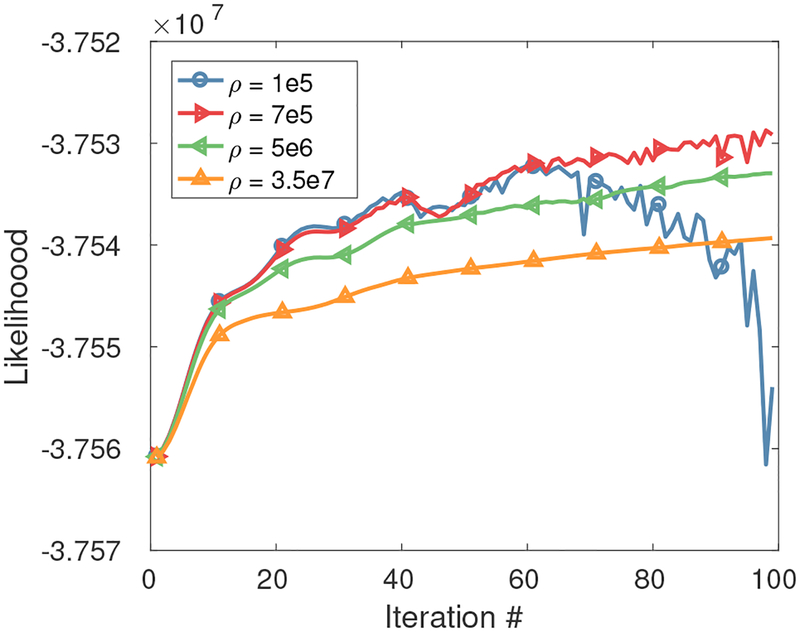
All image reconstructions in this work were performed in fully 3D mode. The neural network was implemented using TensorFlow 1.4 on a NVIDIA GTX 1080Ti. During training, Adam algorithm [44] with default parameter settings was used as the optimizer and the cost function was calculated as the L2 norm between the network outputs and the label images. The first-order gradient used in subproblem (11) was implemented using the tf.gradient function in TensorFlow, which uses “automatic differentiation”, breaking complex gradient calculation into simpler gradient calculations through chain rules. The running time of Subproblem (11) in GPU mode is 16.7% of Subproblem (10) in CPU mode with 16 threads (Intel Xeon E5-2630 v3) measured using the brain data introduced in Sec. III–C. For the proposed optimization framework, the penalty parameter ρ has a large impact on the convergence speed. As the final algorithm output is , we examined the log-likelihood to determine the proper penalty parameter. As an example, Fig. 2 shows the log-likelihood curve using different penalty parameters for the lung patient study mentioned in Section. III–B. Considering the convergence speed and stability of the likelihood, ρ = 5e6 was chosen. Example code for the proposed iterative CNN framework is available under the first author’s github.
Fig. 2:
The effect of penalty parameter ρ on the log-likelihood . Plot is based on the lung patient data described in section. III–B.

We compared the proposed method with the post-reconstruction Gaussian filtering, CNN denoising method [34], fair penalty based penalized reconstruction, and dictionary learning based reconstruction [21]. The CNN denoising method is directly applying the trained network to ML EM reconstruction. For the penalized reconstruction, the fair penalty was used with the form
| (20) |
The fair penalty approaches the L-1 penalty when σ ≪ |t| and is similar to the quadratic penalty when σ ≫ |t|. In our implementation, σ was set to be 1e−5 of the mean image intensity in order to have the edge preserving capability. MAP EM algorithm was used in the penalized reconstruction [42]. In order to accelerate the convergence, 10 iterations of MLEM algorithm was used for “warming up” before running the MAP EM algorithm for 100 iterations. For the dictionary learning based reconstruction, 3D patches were used with size 4×4×4 and the number of atoms was set to 300. The dictionary was pre-learnt using images reconstructed from high count data running K-SVD algorithm [45] for 20 iterations. During image reconstruction, the dictionary learning based penalized reconstruction was solved by alternating between the MAP EM reconstruction step and the orthogonal matching pursuit (OMP) algorithm based sparse coding step [21]. In our implementation, 30th iteration of MLEM algorithm was used as initialization. During each loop the MAP EM algorithm was run for 1 iteration.
III. Experimental setup
A. Simulation study
The computer simulation modeled the geometry of a GE 690 scanner [46]. The scanner consists of 13, 824 LYSO crystals forming a ring of diameter of 81 cm with an axial field of view (FOV) of 157 mm. The crystal size for this scanner is 4.2 × 6.3 × 25 mm3. Nineteen XCAT phantoms with different organ sizes and genders were employed in the simulation [47], seventeen were used for training, one for loss validation and the last one for testing. Apart from the major organs, thirty hot spheres of diameters ranging from 12.8 mm to 22.4 mm were inserted into eighteen phantoms as lung lesions for the training and validation. For the test image, five lesions with diameter 12.8 mm were inserted. The time activity curves (TAC) of different tissues were generated mimicking an FDG scan using a two-tissue-compartment model with an analytic blood input function [48]. In order to simulate the population difference, each kinetic parameter was modelled as a Gaussian variable with coefficient of variation equal to 0.1. The mean values of the kinetic parameters are presented in Table I [49], [50]. The TACs using the mean kinetic parameters are shown in Fig. 3. The system matrix P used in the data generation and image reconstruction was computed by using the multi-ray tracing method [51], which modelled the inter-crystal photon penetration. The image matrix size is 128 × 128 × 49 and the voxel size is 3.27 × 3.27 × 3.27 mm3. Noise-free sinogram data were generated by forward-projecting the ground-truth images using the system matrix and the attenuation map. Poisson noise was then introduced to the noise-free data by setting the total count level to be equivalent to an 1-hour FDG scan with 5 mCi injection. Uniform random and scatter events were simulated and accounted for 60% of the noise free prompt data in all time frames to match those observed in real data-sets. During image reconstruction, all the correction factors were assumed to be known exactly.
TABLE I:
The mean values of the simulated kinetic parameters of FDG for different organs. V stands for blood volume ratio.
| Tissue | K1 | k2 | k3 | k4 | V |
|---|---|---|---|---|---|
| Myocardium | 0.6 | 1.2 | 0.1 | 0.001 | 0 |
| Liver | 0.864 | 0.981 | 0.005 | 0.016 | 0 |
| Lung | 0.108 | 0.735 | 0.016 | 0.013 | 0.017 |
| Kidney | 0.263 | 0.299 | 0 | 0 | 0.438 |
| Spleen | 1.207 | 1.909 | 0.008 | 0.014 | 0 |
| Pancreas | 0.648 | 1.64 | 0.027 | 0.016 | 0.107 |
| Muscle/Bone/Soft tissue | 0.047 | 0.325 | 0.084 | 0 | 0.019 |
| Marrow | 0.425 | 1.055 | 0.023 | 0.013 | 0.04 |
| Lung lesion | 0.63 | 0.842 | 0.092 | 0.014 | 0.132 |
Fig. 3:
The simulated time activity curves based on the kinetic parameters shown in Table I.
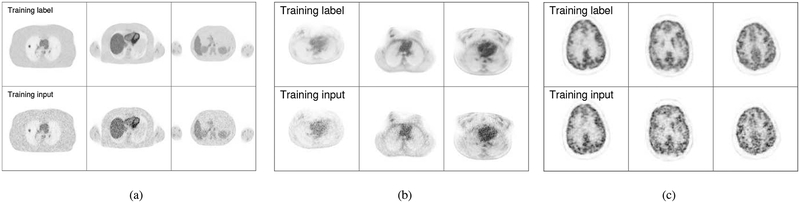
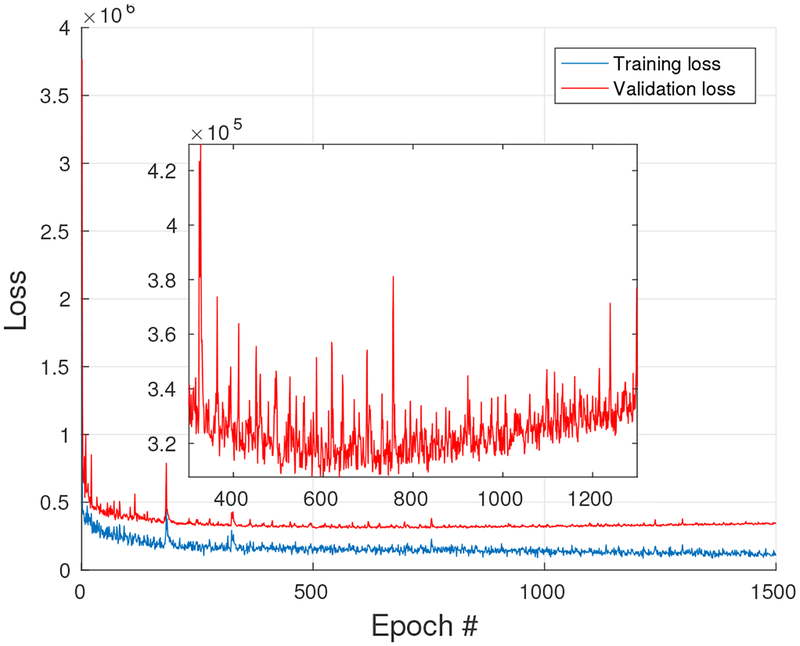
To generate the training data, forty-minutes data from 20 min to 60 min post injection were combined into a high count sinogram and reconstructed as the label image for training. The high count data was down-sampled to 1/10th of the counts and reconstructed as the input image. In order to account for different noise levels, images reconstructed at iteration 20, 40, 60 using ML EM algorithm were all used in the training phase. In total 51 (17 × 3) 3D training pairs were generated, each containing 49 axial slices. Three transaxial slices from different 3D training pairs are shown in Fig. 4(a). As our network needs 3D data as input, a whole patient phantom with 49 axial slices was used as network input for each batch, and correspondingly there were 51 batches in each epoch. Different rotations and translations were applied to each patient phantom to enable larger data capacity for the training. In order to choose the proper epoch number, the training and validation loss for each epoch was saved and shown in Fig. 5. We can see that the training loss is decreasing while the validation starts to increase after 600 iterations. In our experiment the epoch number was chosen as 600 and it took 7 hours for training.
Fig. 4:
(a) Three example training pairs used in simulation study described in section. III–A; (b) three example training pairs used in lung patient study described in section. III–B; (c) three example training pairs used in brain patient study described in section. III–C.
Fig. 5:
The training and validation loss for the simulation study.
During the evaluation, 20 low-counts realizations of the testing phantom, generated by pooling the last 40 min data together and resampling with a 1/10 ratio, were reconstructed using different methods. For quantitative comparison, contrast recovery (CR) vs. the standard deviation (STD) curves were plotted. The CR was computed from the lung lesion regions as
| (21) |
where R = 20 is the number of realizations, is the average uptake of all the lung lesions in the test phantom. The background STD was computed as
| (22) |
where is the average of the background ROI means over realizations, and Kb = 42 is the total number of background ROIs chosen.
B. Lung patient study
Six patient data sets of one hour FDG dynamic scan acquired on a GE 690 scanner with 5 mCi dose injection were employed in this study. Training and validation data were generated in the same way as that in the simulation. The system matrix used in the reconstruction is the same as the one used in the simulation. Normalization, attenuation correction, randoms and scatters were generated using the manufacturer software and included in image reconstruction. Five patient data sets were used in the training and the last one was left for validation. As no ground truth exist in the real data-sets, 5 lesions were inserted in the testing data to generate the hybrid real data-sets for quantitative analysis. The diameters for the lesions inserted in the testing data is 12.8 mm. To increase the training samples for fine-tuning, for each patient data set we have generated three low-dose realizations from the high-counts data. Training pairs of iteration 20, 40, 60 were also included to account for different noise levels. In total 45 3D training pairs composed of 5 (# of patients) × 3 (# of different iterations)× 3 (# of realizations) were generated, each 3D training pair containing 49 axial slices. Different rotations and translations were applied to each patient 3D image. Three transaxial slices from different 3D training pairs are shown are shown in Fig. 4(b). In the simulation set-up, though we tried to match the simulation with real data, there were still texture differences as the simulation is based on piecewise constant phantoms. Directly applying the network trained from simulated phantoms would not give the optimal results for real data sets. Fine-tuning the network trained from simulation is preferred as it can make use of the information from the simulation, while adapted to the real data sets. In our implementation, the network trained after 200 epochs using simulated phantoms described in section. III–A were employed as the initialization of the network used in the real data sets. Four hundred epochs were running during fine-tuning. The fine-tuning process took 4 hours.
Twenty realizations of the low dose data sets were resampled from the testing data and reconstructed to evaluate the noise performance. Forty-seven background ROIs were chosen in the liver region to calculate the STD as presented in (22). For lesion quantification, images with and without the inserted lesion were reconstructed and the difference was taken to obtain the lesion only image and compared with the ground truth. The lesion contrast recovery was calculated as in (21).
C. Brain patient study
Seventeen FDG brain scans acquired on a GE SIGNA PET/MR system were employed in this study [52]. The scan durations are 240 ± 56 s, and injected activity 305.2 ± 73.9 MBq. No pathology in the brain was reported for any of the subjects. Normalization, randoms and scatters were generated using the manufacturer software. Attenuation were generated using the CT information from separate PET/CT scans after co-registration. The brain image was reconstructed with an array size of 128×128×91 and voxel size of 2×2×2.78 mm3. In our implementation, fifteen data sets were used in training, one data set was used for loss validation, and the last one was used for testing. Images reconstructed at iteration 20, 40, 60 using ML EM algorithm were all used in the training phase. In total 45 (15 × 3) 3D training pairs were generated, each containing 91 axial slices. Different rotations and translations were applied to each patient 3D image. Three transaxial slices from different 3D training pairs are shown in Fig. 4(c). Based on observing the validation loss, 800 epochs were run for the training and it took 12 hours. Twenty realizations of the low dose data sets were resampled from the testing data and reconstructed to evaluate the noise performance. Eleven background ROIs were chosen in the white matter region to calculate the STD as presented in (22). As no ground truth exist in the real data-sets, one lesion was inserted in the white matter region of the testing data. The diameters for the lesion inserted in the testing data is 13.5 mm. For lesion quantification, images with and without the inserted lesion were reconstructed and the difference was taken to obtain the lesion only image and compared with the ground truth. The lesion contrast recovery was calculated as in (21).
IV. Results
A. Simulation results
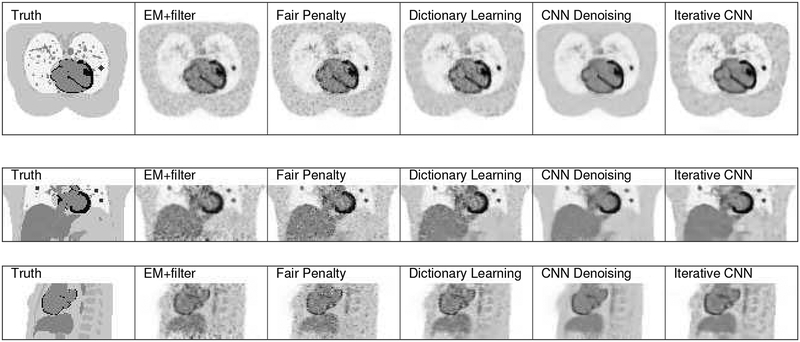
Fig. 6 shows three orthogonal slices of the reconstructed images using different methods. From the image appearance, we can see that the proposed iterative CNN method can generate images with a higher lung lesion uptake and reveal more vessel details in the lung region as compared with the CNN denoising method. Both CNN approaches are better than the traditional Gaussian post filtering method as the images have less noise but also keep all the detailed features, such as the thin myocardium regions. The fair penalty based method has a high lesion uptake, but also has some noise spots showing up in different regions. Dictionary learning method has a better noise reduction compared to the fair penalty based method. These observations are consistent with the quantitative results shown in Fig. 7. In terms of the CR-variance trade-off, the proposed iterative CNN method has the best performance among all methods.
Fig. 6:
Three views of the reconstructed images using different methods for the simulation data set. From left to right: ground truth, Gaussian denoising,fair penalty based penalized reconstruction, dictionary learning based reconstruction, CNN denoising, and the proposed iterative CNN reconstruction
Fig. 7:
The contrast recovery vs. STD curves using different methods for the simulated data sets. Markers are plotted every twenty iterations with the lowest point corresponding to the 20th iteration.
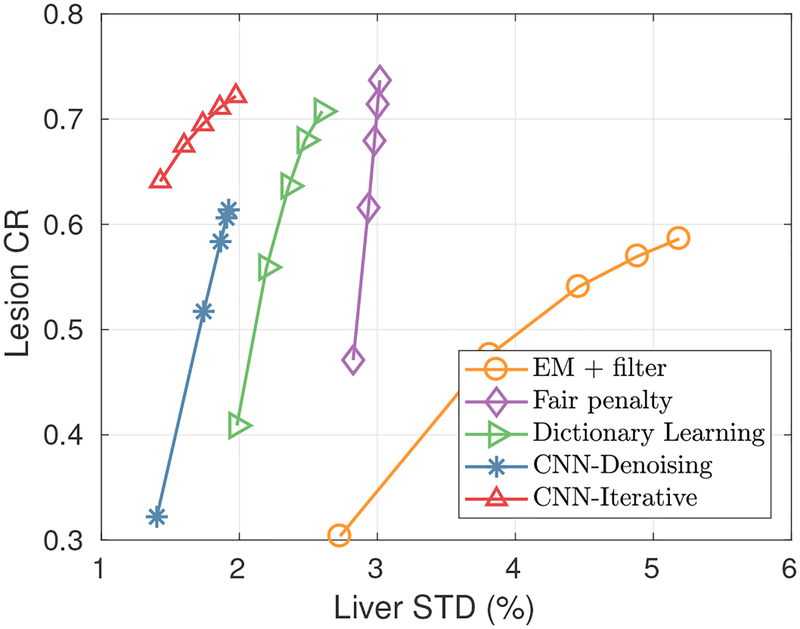
B. Lung patient results
Fig. 8 shows three orthogonal slices of the reconstructed images using the lung data-set by different methods. We can see that the uptake of the inserted lesion in the iterative CNN method is higher than the CNN denoising method, same conclusion as in the simulation study. In addition, the iterative CNN method produced the clearest image details in the spinal regions compared with all other methods. The fair penalty based method can preserve lesion uptake and reduce image noise, but can also present cartoon-like patterns, especially in the high uptake regions. Results from dictionary learning method is better than the fair penalty based method. Compared with other methods, the result using the iterative CNN method has high lesion contrast with lower noise. . The quantitative results are presented in Fig. 9. From the figure, we can see that about two-fold STD reduction can be achieved by the iterative CNN method, compared with the fair-penalty penalized reconstruction.
Fig. 8:
Three views of the reconstructed images using different methods for the lung patient set. From left to right: high count reference image, Gaussian denoising,fair penalty based penalized reconstruction, dictionary learning based reconstruction, CNN denoising, and the proposed iterative CNN reconstruction
Fig. 9:
The contrast recovery vs. STD curves using different methods for the real lung data sets. Markers are plotted every twenty iterations with the lowest point corresponding to the 20th iteration.
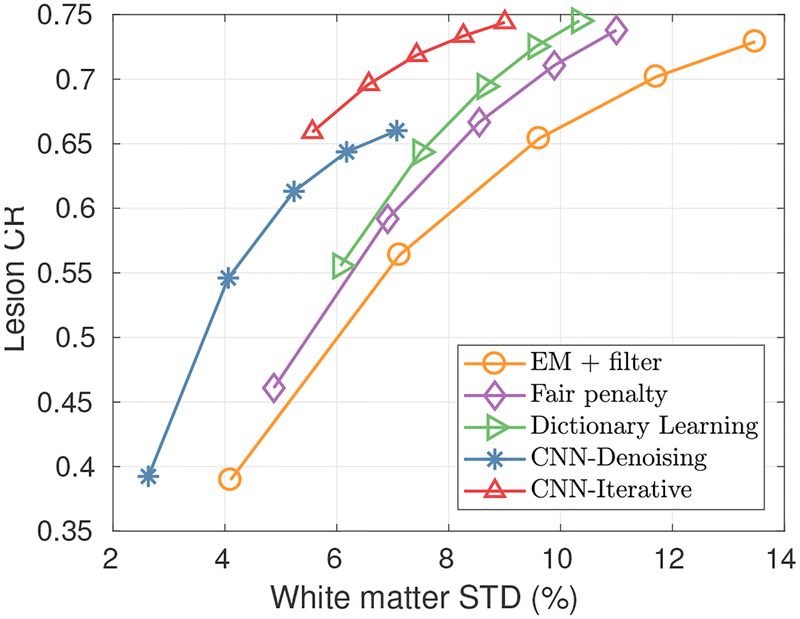
C. Brain patient results
Fig. 10 presents three orthogonal slices of the reconstructed images using the test brain data set with different methods. For the CNN based methods, the white matter region is clearer and more cortices details can be observed compared with other methods. Compared to the CNN denoising method, the proposed iterative CNN method has a higher lesion uptake. The quantitative results are presented in Fig. 9. We can see that the proposed iterative CNN method has the best performance among all methods.
Fig. 10:
Three views of the reconstructed images using different methods for the brain patient data. From left to right: high count reference image, Gaussian denoising,fair penalty based penalized reconstruction, dictionary learning based reconstruction, CNN denoising, and the proposed iterative CNN reconstruction.
V. Discussion
For denoising methods like toal variation and non-local mean, embedding them into reconstruction frameworks can generate better results [53], [54]. It is shown in prior arts that CNN is an effective denoising method. Here we used CNN as the image representation and embedded it into PET iterative reconstruction framework, trying to outperform the denoisng approach. Previously the kernel method has been applied successfully in both static and dynamic PET image reconstructions. When using the kernel method, we need to explicitly specify the basis function when constructing the kernel matrix. This is not needed for CNN and the whole network representation is more data-driven. The biggest advantage of the proposed method is that more generalized prior information, such as the inter-patient scanning information, can be included in the image representation. In addition, when the prior information is from multiple resources, such as both the temporal and anatomical information, it is hard to specify how to combine those information in the kernel method. For neural network, we can use multiple input channels to aggregate the information and let the network decide the optimum combination in the training phase.
One concern about applying neural network method is whether the bias will arise when the network come across new scenarios which it has never seen during training, which is often the case in practice. In the lung patient and the brain patient studies, there were no lesions in the training data. We can see that the lesion recovery is worse using the CNN denoising method compared with the fair penalty based method and the dictionary learning method, which demonstrates that the bias is introduced due to the imperfectness of the trained network. Compared with the CNN denoising approach, the proposed iterative CNN method has a constraint from the measured data, which can help recover some small features that are removed or annihilated by the image denoising methods. Higher contrast recovery of the lesions shown in the CR-STD plots demonstrated this benefit. We should also notice that the observation of better performance for the CNN approaches is relative to the chosen metric: CR-STD. Currently we are not sure about the performance of CNN approaches regarding other tasks, such as small lesion detection. We can notice some small fine features are lost in the brain images shown in Fig. 10 for the CNN and dictionary learning approaches. Further quantification based on other tasks are needed to test the robustness of CNN methods.
As for the optimization of the proposed iterative CNN method, the reason to use ADMM algorithm is to de-couple the image update step and the network input update step. The network input step needs more update steps than the iterative reconstruction step. If they are coupled together, every time the network input is updated, we need to compute the forward and backward projections. As the computation of forward and backward projections are very time-consuming for fully 3D PET, decoupling these two steps will save more computational time. Furthermore, after using ADMM algorithm, the image update step in subproblem (10) can re-use current PET image reconstruction packages, which makes the proposed method more adaptable to traditional iterative reconstruction framework. Apart from the MAP EM algorithm employed in this work, other algorithms, such as preconditioned conjugate gradient (PCG) algorithm [55], can also be used to solve subproblem (10). The most challenging part is subproblem (11) as it is a non-linear problem. As the computation of the Jacobian matrix is difficult due to the platform limitation, currently we choose a first-order method with Nesterov momentum to solve it. However, it is easy to get trapped in local minimums. In our experiment, we found that if the initial value of α is a uniform image, the result is very poor. In our proposed solution, we used the EM results after 30 iterations as the input, which can make the results more stable. Better optimization methods and more effective initial choosing strategies need further investigations. From Fig. 2 we can see that when a proper penalty parameter ρ is chosen, the likelihood function will increase steadily. We have compared the reconstruction results at 1000 iteration and 2000 iterations, the difference is very small. Based on these observations, we think that Algorithm 1 converges.
During the experiments, we found that if the noise level of the testing data is similar to the training data, the performance of the neural network is the best. If there was a mismatch between the training and testing data noise levels, the performance would be degraded. Hence to have the best improvement using neural network methods, a new training session is suggested if the dose level of the test data is outside of the training dose level range. In this study, images reconstructed using different iteration numbers were employed during network training as they cover different noise levels. This is not the optimum approach as noise controlled by iteration number is not the same as noise generated by different count level. Better strategies for network pre-training still need further investigations. The network structure used in this study is the modified 3D U-net structure, which is a fully convolutional network. One drawback of CNN is that it will remove some of the small structures in the final output. Though our proposed iterative framework can overcome this issue, better network structures, which can preserve more features, can make our proposed iterative framework work better. For example, our proposed approach can be also fit for GAN. After the generator network is trained through GAN, it can be included into the iterative framework based on the proposed method. Besides, though the data model used here is PET, it can also be used in CT or MRI reconstruction framework.
Currently only FDG data sets were employed in this study. In addition, in this study evaluations of the real data sets are based on inserted lesions. Further evaluations regarding other radioactive tracers, real tumor uptakes, as well as more clinical tasks such as quantifying target density or measuring blood flow, are our future work.
VI. Conclusion
In this work, we proposed an iterative PET image reconstruction framework by using convolutional neural network representation. Both simulated XCAT data and real data sets were used in the evaluation. Quantitative results show that the proposed iterative CNN method performs better than the CNN denoising method as well as the Gaussian filter and penalized reconstruction methods regarding contrast recovery vs. noise trade-offs. Future work will focus on exploring better network training approaches as well as further evaluations using more clinical data sets regarding different tasks.
Fig. 11:
The contrast recovery vs. STD curves using different methods for the brain data sets. Markers are plotted every twenty iterations with the lowest point corresponding to the 20th iteration.
VII. Acknowledgements
This work is supported by the National Institutes of Health under grant number R01EB000194, R01AG052653 and P41EB022544.
Contributor Information
Kuang Gong, Gordon Center for Medical Imaging, Massachusetts General Hospital and Harvard Medical School, Boston, MA 02114 USA, and with the Department of Biomedical Engineering, University of California, Davis CA 95616 USA..
Jiahui Guan, Department of Statistics, University of California, Davis, CA 95616 USA.
Kyungsang Kim, Gordon Center for Medical Imaging, Massachusetts General Hospital and Harvard Medical School, Boston, MA 02114 USA.
Xuezhu Zhang, Department of Biomedical Engineering, University of California, Davis, CA 95616 USA.
Jaewon Yang, Physics Research Laboratory, Department of Radiology and Biomedical Imaging, University of California, San Francisco, CA 94143 USA.
Youngho Seo, Physics Research Laboratory, Department of Radiology and Biomedical Imaging, University of California, San Francisco, CA 94143 USA.
Georges El Fakhri, Gordon Center for Medical Imaging, Massachusetts General Hospital and Harvard Medical School, Boston, MA 02114 USA.
Jinyi Qi, Email: qi@ucdavis.edu, Department of Biomedical Engineering, University of California, Davis, CA 95616 USA.
Quanzheng Li, Email: li.quanzheng@mgh.harvard.edu, Gordon Center for Medical Imaging, Massachusetts General Hospital and Harvard Medical School, Boston, MA 02114 USA.
References
- [1].Beyer T, Townsend DW, Brun T et al. , “A combined PET/CT scanner for clinical oncology,” Journal of nuclear medicine, vol. 41, no. 8, pp. 1369–1379, 2000. [PubMed] [Google Scholar]
- [2].Gunn RN, Slifstein M, Searle GE et al. , “Quantitative imaging of protein targets in the human brain with PET,” Physics in medicine and biology, vol. 60, no. 22, p. R363, 2015. [DOI] [PubMed] [Google Scholar]
- [3].Machac J, “Cardiac positron emission tomography imaging,” Seminars in nuclear medicine, vol. 35, no. 1, pp. 17–36, 2005. [DOI] [PubMed] [Google Scholar]
- [4].Karp JS, Surti S, Daube-Witherspoon ME et al. , “Benefit of time-of-flight in PET: experimental and clinical results,” Journal of Nuclear Medicine, vol. 49, no. 3, pp. 462–470, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yang Y, Qi J, Wu Y et al. , “Depth of interaction calibration for PET detectors with dual-ended readout by PSAPDs,” Physics in medicine and biology, vol. 54, no. 2, p. 433, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Poon JK, Dahlbom ML, Moses WW et al. , “Optimal whole-body PET scanner configurations for different volumes of LSO scintillator: a simulation study,” Physics in medicine and biology, vol. 57, no. 13, p. 4077, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Gong K, Majewski S, Kinahan PE et al. , “Designing a compact high performance brain PET scanner—simulation study,” Physics in medicine and biology, vol. 61, no. 10, p. 3681, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Gong K, Zhou J, Tohme M et al. , “Sinogram blurring matrix estimation from point sources measurements with rank-one approximation for fully 3-d PET,” IEEE transactions on medical imaging, vol. 36, no. 10, pp. 2179–2188, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Christian BT, Vandehey NT, Floberg JM et al. , “Dynamic PET denoising with HYPR processing,” Journal of Nuclear Medicine, vol. 51, no. 7, pp. 1147–1154, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Dutta J, Leahy RM, and Li Q, “Non-local means denoising of dynamic PET images,” PloS one, vol. 8, no. 12, p. e81390, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Chan C, Fulton R, Barnett R et al. , “Postreconstruction nonlocal means filtering of whole-body PET with an anatomical prior,” IEEE Transactions on medical imaging, vol. 33, no. 3, pp. 636–650, 2014. [DOI] [PubMed] [Google Scholar]
- [12].Yan J, Lim JC-S, and Townsend DW, “MRI-guided brain pet image filtering and partial volume correction,” Physics in medicine and biology, vol. 60, no. 3, p. 961, 2015. [DOI] [PubMed] [Google Scholar]
- [13].Nuyts J, “The use of mutual information and joint entropy for anatomical priors in emission tomography,” in 2007 IEEE Nuclear Science Symposium Conference Record, vol. 6 IEEE, 2007, pp. 4149–4154. [Google Scholar]
- [14].Tang J and Rahmim A, “Bayesian PET image reconstruction incorporating anato-functional joint entropy,” Physics in Medicine and Biology, vol. 54, no. 23, p. 7063, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Somayajula S, Panagiotou C, Rangarajan A et al. , “PET image reconstruction using information theoretic anatomical priors,” IEEE Transactions on Medical Imaging, vol. 30, no. 3, pp. 537–549, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Comtat C, Kinahan PE, Fessler JA et al. , “Clinically feasible reconstruction of 3D whole-body PET/CT data using blurred anatomical labels,” Physics in Medicine and Biology, vol. 47, no. 1, p. 1, 2001. [DOI] [PubMed] [Google Scholar]
- [17].Baete K, Nuyts J, Van Paesschen W et al. , “Anatomical-based FDGPET reconstruction for the detection of hypo-metabolic regions in epilepsy,” IEEE Transactions on Medical Imaging, vol. 23, no. 4, pp. 510–519, 2004. [DOI] [PubMed] [Google Scholar]
- [18].Ehrhardt MJ, Markiewicz P, Liljeroth M et al. , “PET reconstruction with an anatomical MRI prior using parallel level sets,” IEEE Transactions on Medical Imaging, vol. 35, no. 9, pp. 2189–2199, 2016. [DOI] [PubMed] [Google Scholar]
- [19].Knoll F, Holler M, Koesters T et al. , “Joint MR-PET reconstruction using a multi-channel image regularizer,” IEEE Transactions on Medical Imaging, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Bowsher JE, Yuan H, Hedlund LW et al. , “Utilizing MRI information to estimate F18-FDG distributions in rat flank tumors,” in Nuclear Science Symposium Conference Record, 2004 IEEE, vol. 4 IEEE, 2004, pp. 2488–2492. [Google Scholar]
- [21].Chen S, Liu H, Shi P et al. , “Sparse representation and dictionary learning penalized image reconstruction for positron emission tomography,” Physics in medicine and biology, vol. 60, no. 2, p. 807, 2015. [DOI] [PubMed] [Google Scholar]
- [22].Tahaei MS and Reader AJ, “Patch-based image reconstruction for PET using prior-image derived dictionaries,” Physics in Medicine and Biology, vol. 61, no. 18, p. 6833, 2016. [DOI] [PubMed] [Google Scholar]
- [23].Tang J, Yang B, Wang Y et al. , “Sparsity-constrained PET image reconstruction with learned dictionaries,” Physics in Medicine and Biology, vol. 61, no. 17, p. 6347, 2016. [DOI] [PubMed] [Google Scholar]
- [24].Wang G and Qi J, “PET image reconstruction using kernel method,” IEEE Transactions on Medical Imaging, vol. 34, no. 1, pp. 61–71, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Hutchcroft W, Wang G, Chen KT et al. , “Anatomically-aided PET reconstruction using the kernel method,” Physics in Medicine and Biology, vol. 61, no. 18, p. 6668, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Novosad P and Reader AJ, “MR-guided dynamic PET reconstruction with the kernel method and spectral temporal basis functions,” Physics in Medicine and Biology, vol. 61, no. 12, p. 4624, 2016. [DOI] [PubMed] [Google Scholar]
- [27].Gong K, Cheng-Liao J, Wang G et al. , “Direct patlak reconstruction from dynamic PET data using the kernel method with MRI information based on structural similarity,” IEEE transactions on medical imaging, vol. 37, no. 4, pp. 955–965, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Ellis S and Reader AJ, “Simultaneous maximum a posteriori longitudinal PET image reconstruction,” Physics in medicine and biology, vol. 62, no. 17, pp. 6963–6979, 2017. [DOI] [PubMed] [Google Scholar]
- [29].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2015, pp. 234–241. [Google Scholar]
- [30].Ren S, He K, Girshick R et al. , “Faster r-cnn: Towards real-time object detection with region proposal networks,” in Advances in neural information processing systems, 2015, pp. 91–99. [DOI] [PubMed] [Google Scholar]
- [31].Dong C, Loy CC, He K et al. , “Image super-resolution using deep convolutional networks,” IEEE transactions on pattern analysis and machine intelligence, vol. 38, no. 2, pp. 295–307, 2016. [DOI] [PubMed] [Google Scholar]
- [32].Wang S, Su Z, Ying L et al. , “Accelerating magnetic resonance imaging via deep learning,” in Biomedical Imaging (ISBI), 2016 IEEE 13th International Symposium on. IEEE, 2016, pp. 514–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Kang E, Min J, and Ye JC, “A deep convolutional neural network using directional wavelets for low-dose x-ray CT reconstruction,” arXiv preprint arXiv:1610.09736, 2016. [DOI] [PubMed] [Google Scholar]
- [34].Chen H, Zhang Y, Zhang W et al. , “Low-dose CT via convolutional neural network,” Biomedical optics express, vol. 8, no. 2, pp. 679–694, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Wu D, Kim K, Fakhri GE et al. , “A cascaded convolutional nerual network for X-ray low-dose CT image denoising,” arXiv preprint arXiv:1705.04267, 2017. [Google Scholar]
- [36].Wolterink JM, Leiner T, Viergever MA et al. , “Generative adversarial networks for noise reduction in low-dose CT,” IEEE Transactions on Medical Imaging, 2017. [DOI] [PubMed] [Google Scholar]
- [37].He K, Zhang X, Ren S et al. , “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [Google Scholar]
- [38].Boyd S, Parikh N, Chu E et al. , “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Foundations and Trends® in Machine Learning, vol. 3, no. 1, pp. 1–122, 2011. [Google Scholar]
- [39].Qi J, Leahy RM, Cherry SR et al. , “High-resolution 3D Bayesian image reconstruction using the microPET small-animal scanner,” Physics in medicine and biology, vol. 43, no. 4, p. 1001, 1998. [DOI] [PubMed] [Google Scholar]
- [40].Ioffe S and Szegedy C, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in International Conference on Machine Learning, 2015, pp. 448–456. [Google Scholar]
- [41].Odena A, Dumoulin V, and Olah C, “Deconvolution and checkerboard artifacts,” Distill, vol. 1, no. 10, p. e3, 2016. [Google Scholar]
- [42].Wang G and Qi J, “Penalized likelihood PET image reconstruction using patch-based edge-preserving regularization,” IEEE transactions on medical imaging, vol. 31, no. 12, pp. 2194–2204, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Nesterov Y, “A method of solving a convex programming problem with convergence rate o (1/k2),” in Soviet Mathematics Doklady, vol. 27, no. 2, 1983, pp. 372–376. [Google Scholar]
- [44].Kingma D and Ba J, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014. [Google Scholar]
- [45].Aharon M, Elad M, and Bruckstein A, “rmk-svd: An algorithm for designing overcomplete dictionaries for sparse representation,” IEEE Transactions on signal processing, vol. 54, no. 11, pp. 4311–4322, 2006. [Google Scholar]
- [46].Bettinardi V, Presotto L, Rapisarda E et al. , “Physical performance of the new hybrid PET/CT Discovery-690,” Medical physics, vol. 38, no. 10, pp. 5394–5411, 2011. [DOI] [PubMed] [Google Scholar]
- [47].Segars W, Sturgeon G, Mendonca S et al. , “4D XCAT phantom for multimodality imaging research,” Medical physics, vol. 37, no. 9, pp. 4902–4915, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Feng D, Wong K-P, Wu C-M et al. , “A technique for extracting physiological parameters and the required input function simultaneously from PET image measurements: Theory and simulation study,” IEEE Transactions on Information Technology in Biomedicine, vol. 1, no. 4, pp. 243–254, 1997. [DOI] [PubMed] [Google Scholar]
- [49].Qiao H and Bai J, “Dynamic simulation of FDG-PET image based on VHP datasets,” in Complex Medical Engineering (CME), 2011 IEEE/ICME International Conference on. IEEE, 2011, pp. 154–158. [Google Scholar]
- [50].Karakatsanis NA, Lodge MA, Tahari AK et al. , “Dynamic whole-body PET parametric imaging: I. concept, acquisition protocol optimization and clinical application,” Physics in medicine and biology, vol. 58, no. 20, p. 7391, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Zhou J and Qi J, “Fast and efficient fully 3D PET image reconstruction using sparse system matrix factorization with GPU acceleration,” Physics in medicine and biology, vol. 56, no. 20, p. 6739, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Gong K, Yang J, Kim K et al. , “Attenuation correction for brain PET imaging using deep neural network based on Dixon and ZTE MR images,” Physics in medicine and biology, vol. 63, no. 12, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Sidky EY and Pan X, “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Physics in Medicine & Biology, vol. 53, no. 17, p. 4777, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Adluru G, Tasdizen T, Schabel MC et al. , “Reconstruction of 3D dynamic contrast-enhanced magnetic resonance imaging using nonlocal means,” Journal of Magnetic Resonance Imaging, vol. 32, no. 5, pp. 1217–1227, 2010. [DOI] [PubMed] [Google Scholar]
- [55].Mumcuoglu EU, Leahy R, Cherry SR et al. , “Fast gradient-based methods for bayesian reconstruction of transmission and emission PET images,” IEEE transactions on Medical Imaging, vol. 13, no. 4, pp. 687–701, 1994. [DOI] [PubMed] [Google Scholar]