Spatial Resolution of Coherent Cathodoluminescence Super-Resolution Microscopy

Abstract

We investigate the nanoscale excitation of Ag nanocubes with coherent cathodoluminescence imaging spectroscopy (CL) to resolve the factors that determine the spatial resolution of CL as a deep-subwavelength imaging technique. The 10–30 keV electron beam coherently excites localized plasmons in 70 nm Ag cubes at 2.4 and 3.1 eV. The radiation from these plasmon modes is collected in the far-field together with the secondary electron intensity. CL line scans across the nanocubes show exponentially decaying tails away from the cube that reveal the evanescent coupling of the electron field to the resonant plasmon modes. The measured CL decay lengths range from 8 nm (10 keV) to 12 nm (30 keV) and differ from the calculated ones by only 1–3 nm. A statistical model of electron scattering inside the Ag nanocubes is developed to analyze the secondary electron images and compare them with the CL data. The Ag nanocube edges are derived from the CL line scans with a systematic error less than 3 nm. The data demonstrate that CL probes the electron-induced plasmon fields with nanometer accuracy.

Cathodoluminescence (CL) spectroscopy is a well-known technique for nanoscale optical materials characterization.¹⁻⁴ In CL, a high-energy (∼1–100 keV) electron beam is raster-scanned over a sample and a two-dimensional map is constructed of the emission spectrum at each electron excitation position, providing insights in optical properties at subwavelength scale. CL can result from incoherent emission processes induced by the incoming electrons such as electron–hole recombination in semiconductors or color center emission in wide-bandgap materials. In contrast, in coherent CL excitation, a material is directly polarized by the time-varying electric fields created by the electron as it passes by the material. The induced polarization then radiates into the far field where it is detected.^2,5 This coherent excitation is similar to that of a light beam that polarizes material and subsequently scatters, with the exception that the time-varying evanescent electron fields that couple to the polarizable object only make a single cycle in time, as opposed to commonly used light beams (see Supporting Information). The corresponding excitation energy spectrum spans a broad range from 0 to ∼40 eV making high-energy electrons an effective broadband source of excitation in the optical spectral range.^2,5,6

Coherent CL has gained great interest in recent years as it offers a method to characterize optical nanomaterials with three unique characteristics: (1) nanoscale probe size, (2) broadband excitation spectrum, and (3) attosecond excitation pulse. Coherent CL has been very successful in identifying optical modes in resonant plasmonic and dielectric nanostructures,⁷⁻⁹ hybridization of coupled nanoscale systems,^10,11 mapping the local density of states in photonic crystals,^12,13 and much more. A key question that has not been well addressed so far is what fundamentally determines the spatial resolution of CL in practical experimental conditions.

In conventional optical microscopy, the maximum spatial resolution is defined by Abbe’s diffraction limit and is ∼200 nm in the visible spectral range, depending on the numerical aperture. Optical super-resolution microscopy techniques achieve better spatial resolution through a specific preparation of the excitation state of the sample (STED microscopy, 30–80 nm)¹⁴ or using stochastic analysis to reconstruct an image (PALM, STORM, 10–50 nm).^15,16 In scanning optical near-field microscopy (SNOM), the probe can couple to near-field features at a resolution down to 10–20 nm.¹⁷ CL imaging brings together some of these features: it is a near-field probing technique in which the electron beam prepares an excited (polarized) state of matter of which the radiation is detected, creating optical excitation images with features that are far below the standard optical diffraction limit.

Previous measurements have shown CL maps with deep-subwavelength feature sizes, but the spatial resolution could not be accurately derived because of several reasons: plasmons were imaged on spherical samples in which the distance between beam and particle surface varies strongly along the trajectory,¹⁸ the measurement pixel size was too large to study nanoscale features in detail,¹⁹ the sample geometry was not well-defined enough, or the beam diameter was too large to perform analysis at the true nanoscale.¹³ We note that also electron energy loss spectroscopy (EELS) has been used to reveal nanoscale optical features in plasmonic nanostructures, also aided by the very small electron beam spot size in the transmission electron microscopes on which EELS microscopy is carried out.²⁰⁻²⁶ The exact spatial resolution that can be experimentally achieved with CL and how close plasmon field profiles, and optical mode profiles in general that are derived from the measurements, approach theoretical profiles has remained unresolved.

In this paper, we investigate the resonant plasmonic near-field distribution of Ag nanocubes with atomically flat edges (see Supporting Information) that serve as a model system with well-defined plasmonic resonances.^27,28 We show that the evanescent decay lengths of the near-field profiles derived from the CL data approach the calculated ones by 1 nm at 10 keV and 3 nm at 30 keV. The Ag nanocube edges can be derived from the CL maps with an accuracy better than 3 nm. The data demonstrate that CL probes the electron-induced plasmon fields with nanometer accuracy.

Fundamentally, the coupling strength of the electron beam and a resonantly polarizable object is determined by the overlap between the evanescent field of the electron with the polarizable charges in the object, and the strength with which the generated field acts back on the electron.^2,29 It has been shown that the associated energy loss probability is directly linked to the local density of optical states (LDOS).² By extension, CL is a direct probe of the radiative LDOS as it probes radiation. The extent of the evanescent field about the electron trajectory and the extent of the modal field thus determine the spatial extent of the CL image of the object. As the electron field extension increases with electron velocity, the CL image for a given resonant photonic object will be more extended if a higher-energy primary electron beam is used in the CL experiment.^2,7 Similarly, it will be more extended as lower-frequency optical modes are probed.²

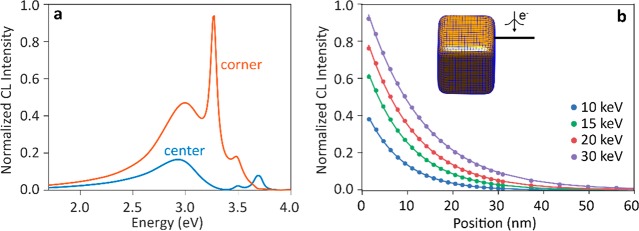
In our analysis, we use a scanning electron microscope (SEM) equipped with a CL collection system composed of a half-parabolic mirror that is placed between the sample and the electron column, with the mirror focus aligned with the electron spot on the sample using a micro actuation system.³⁰ The electron beam passes through a 600-μm-diameter hole in the mirror and the collected light is sent through a vacuum port to an optical analysis system (see Supporting Information). Figure 1a shows a high-angle dark-field 30 keV scanning transmission electron microscopy image of a Ag nanocube with a width D = 70 nm. The straight sidewalls are easily recognized in the image and enable a very accurate analysis of CL and secondary electron (SE) line scans across the particle.

Figure 1.

(a) High-resolution HAADF-STEM image of a 70 nm Ag nanocube. (C) CL spectra (30 keV) taken at the center and a corner of a 70 nm Ag nanocube on a 15 nm Si₃N₄ membrane. (b) CL spectra (30 keV) taken at the center and a corner of a 70 nm Ag nanocube on a 15 nm Si₃N₄ membrane. (c) Top, simultaneously collected SE intensity and CL intensity (1.3–5.4 eV spectral range, 1 nm step size) collected in a 25 nm wide rectangular region across the nanocube; bottom, laterally integrated CL and SE intensities along the nanocube. Solid lines are model fits. The dashed vertical lines indicate the nanocube boundaries derived from the SE (blue dashed line) and CL (red dashed line) models.

Figure 1b shows the 30 keV CL spectrum for central and corner excitation of the nanocube. Resonant localized surface plasmon modes with main peaks at 2.4 and 3.1 eV are clearly observed. Earlier work has shown these correspond to a vertical dipole mode centered in the particle, and a mode with field maxima at the corners, respectively.³¹⁻³⁴ To study the spatial extent of the CL maps with much more precision, we scan the electron beam in 1 nm steps over a narrow rectangular box (dimensions ∼25 × 600 nm²) across the particle and collect the CL intensity in the 1.3–5.4 eV spectral range to cover the full plasmon spectrum. The SE intensity is collected simultaneously. Figure 1c shows the CL and SE line profiles, made by integration of the data in the lateral direction of the rectangle. Clearly the extent of the CL profile is wider than that of the SE profile.

To analyze the shape of the SE profile, we used Casino V3.3, a Monte Carlo based computer code³⁵ to simulate electron trajectories in a Ag nanocube. Figure 2a and c show the distribution of inelastic scattering events for an electron beam incident at the center of the top facet (x′ = 0) at 10 and 30 keV. Figure 2b and d show the simulated SE coefficient, defined as the average number of secondary electrons escaping the sample per primary electron, as a function of the impact position x of the incoming electron beam in a plane through the center of the cube. We perform simulations for two effective electron beam widths of 2 nm and of 12 nm (full-width at half-maximum, fwhm; standard deviation σ_beam = 0.85 nm, σ_beam = 5.1 nm) that reflect the primary electron beam diameter on the cube and the effect of mechanical instabilities of the measurement system resulting in variations in alignment of the electron beam with the sample. Clear SE peaks are observed close to the edge of the cube, similar to what is observed in the experimental SE data of Figure 1c. Elevated SE signals are expected near the sharp edge as the escape probability is higher near the edge.³⁶

Figure 2.

Monte Carlo simulations of electron scattering in a 70 nm Ag nanocube (10 and 30 keV). (a, c) Distribution of inelastic scattering events for the electron beam incident at the center of the top facet (dots) and probability that a SE generated at a certain lateral position x′ escapes from the nanocube integrated over the nanocube height, per primary electron (blue dashed line, σ_beam = 0.85 nm; green dashed line, σ_beam = 5.1 nm). (b, d) Simulated probability that a secondary electron is generated and escapes from the nanocube for two effective beam widths (blue dots, σ_beam = 0.85 nm; green dots, σ_beam = 5.1 nm) as a function of the lateral position x of the incident electron beam, and model fits (blue and green drawn lines). The open circles indicate the nanocube edge as derived from the fits. The orange vertical dashed lines indicate the particle edges used in the Casino simulation.

Next, we reproduce the simulated profiles I_cube(x) of Figure 2b and d with an analytical model, where the SE density generated at position x′ by a primary electron incident at position x, C_SE(x′,x), is represented by a Gaussian distribution centered around x inside the cube with standard deviation σ_SE (see Supporting Information, Eq S1). The SE intensity detected for an electron impact position x is then given by the integration over the cube of C_SE(x′,x) multiplied by the probability P_det (x′,σ_esc) that a SE generated at a certain position x′ escapes from the nanocube. We then convolve this product with a Gaussian distribution B(x,σ_beam) that reflects the effective electron beam diameter on the cube:

1

In our analysis, we model P_esc(x′,σ_esc) by a component that is independent of x′, representing SEs escaping from the top of the cube, and a component that increases toward the facets that follows a cumulative distribution for a Gaussian centered at the edge, with a standard deviation σ_esc that reflects the electron escape depth from the cube (see Supporting Information, Eqs S2–S4). Eq 1 is then used to fit the simulated data for the two beam widths in Figure 2b and d. To fit the data, the positions of the edges were kept as a free parameters. As can be seen, the analytical model fits the simulated data for both beam widths very well. The nanocube edges derived from the model (open circles in Figure 2b,d) match well with the edges used in the simulations (dashed vertical lines): for the small beam spot size, they match within 1 nm. For the large spot size, they match within 2 and 7 nm for 10 and 30 keV, respectively, which is very small compared to the modeled beam spot size of 12 nm fwhm.

The escape probability P_esc(x,σ_esc) derived from the fits of eq 1 is displayed in Figure 2a and c for the two beam energies and beam widths. As expected, the curves for two different beam widths are similar, as SE detection is independent of the way in which SEs are generated. The P_esc(x) curve for 10 keV shows a higher intensity in the center because a higher fraction of SEs (integrated over the cube height) escapes through the top surface. For both beam energies we find σ_esc = 3 nm, which corresponds to the electron escape depth in Ag for SEs in the keV energy range.³⁷

Calculations of CL spectra and images were performed using the MNPBEM17 computer code that uses the boundary element method (BEM) to solve Maxwell’s equations in and outside the nanocube for a given electron trajectory.^38,39 The BEM method uses a Green’s function method to calculate the surface charges and currents and derives the corresponding far-field CL radiation spectrum. Figure 3a shows the calculated 30 keV CL spectra: a low-energy resonance is observed at 2.9 eV for excitation in the center; a sharp resonance appears at 3.4 eV for corner excitation. The small higher-energy peaks are assigned to higher-order resonances with more complex spatial field profiles.³⁴ These resonances can be compared with the center and corner resonances at 2.6 and 3.1 eV, respectively, found in Figure 1b. We ascribe the discrepancy in spectral shape between experiment and simulation to several factors: differences in particle dimensions and corner rounding that can strongly affect the spectral shape,^27,34 the effect of the substrate in the experiment (not included in the simulations), the formation of a thin oxide shell on the Ag surface after etching off the ligands, and carbon deposition during electron irradiation, all of which redshift and broaden the resonances.

Figure 3.

MNPBEM calculations for 70 nm Ag cubes. (a) 30 keV CL spectra for electrons incident at the center or a corner. (b) CL intensity as a function of beam position away from the nanocube, integrated over the 1.6–3.5 eV spectral range used in the measurements in Figure 1c, for 10, 15, 20, and 30 keV electrons. The drawn lines are exponential fits to the data.

Figure 3b shows the calculated CL intensity as a function of beam position away from the nanocube. The data are derived from BEM calculations integrated over the 1.6–3.5 eV spectral range that covers both resonances. The data are fitted with exponential curves, yielding effective 1/e decay lengths from 8 to 12 nm, as the energy is increased from 10 to 30 keV.

The spatial frequency of optical waves to which the electron couples in the direction along the trajectory k_z = ω/v is well above the free-space optical wave vector k₀ = ω/c (electron velocity v = 0.19–0.33c in the 10–30 keV energy range, ω the angular frequency, c the speed of light in vacuum), so that the electron induced field in the transverse directions is evanescent with a characteristic decay length L = γ × v/ω, with γ the Lorenz contraction factor (1 – v²/c²)^−1/2.² At 30 keV and 2.6 eV, this translates to L = 14 nm. We note that the precise shape of the profiles in Figure 3b is determined by the time-integrated convolution of the different resonant nanocube modal fields (in space and time) within the 1.6–3.5 eV spectral range with the evanescent electron fields.

Next, we analyze the measured CL line scan in Figure 1c. We fit the data with a model for the CL intensity I_CL(x) with an exponential decay with decay length L and maximum amplitude a outside the particle and two exponential terms with amplitude b and decay length L that describe the decaying intensity away from the edge on top of the particle (see Supporting Information; Eqn. S5). To obtain the measured data, the model for I_CL(x) is convoluted with a Gaussian distribution for the beam width. The nanocube size, D, is also a parameter in the fits. As can be seen, the model fits the data in Figure 1c very well.

We then performed a large number of measurements as in Figure 1c on different Ag nanocubes. We fit all data with the model for I_CL(x) to determine the decay length L and nanocube size D. A histogram of the distribution of decay lengths from a total of 159 measurements is shown in Figure 4 for four beam energies in the range 10–30 keV. Gaussian fits are made through the distributions. The decay length derived from the data is 9 nm at 10 keV, while it is 8 nm in the BEM simulation and 15 nm at 30 keV, while it is 12 nm in BEM.

Figure 4.

CL decay length L away from the cubes. Histograms of the decay length L derived by fitting the model for I_CL to 159 measured CL line scans as in Figure 1c. The green vertical lines show the decay lengths derived from the BEM calculations in Figure 3b. The dashed lines are Gaussian fits to the histograms.

These data show that the experimental artifacts captured in the beam width σ_beam can be fitted to yield the plasmonic field profiles with an accuracy of 1–3 nm. The remaining very small difference may be related to the difference between the experimental Ag cube geometry and the input parameters for the BEM simulations and the fact that the spectral range and detector response function for the CL line scans and spectral weight in the BEM simulations was slightly different.

Finally, to investigate the consistency between the SE and CL models introduced above, we compare the size of the nanocubes determined from the fits of I_cube to the SE data as described above with the size determined from the fits of I_CL to the CL data. This is illustrated in Figure 5, which shows SE and CL line scans at 10 keV with the corresponding fits of I_CL and I_cube. The dashed vertical lines show the position of the edge determined by the two methods. The difference Δd between these values for a total of 159 measurements (with two edges each) is plotted in the histograms of Figure 5b for four different energies.

Figure 5.

(a) SE and CL line scans at 10 keV with model fits for I_cube and I_CL. The vertical dashed lines indicate the nanocube edges derived from the two fits, with the difference Δd indicated. (b) Histograms of Δd for 159 measurements for four different energies. The dashed lines are Gaussian fits through the data.

Gaussian fits are made through the histograms of which the center values determine the accuracy with which the particle size is determined from the CL line scan; it varies from Δd = −3 nm to Δd = 1.5 nm when the beam energy increases from 10 to 30 keV. From this analysis, we conclude that the edge position of the cube can be derived from the CL line scan with an accuracy (systematic error) better than 3 nm. The width of the histograms of Figure 5b reflects the precision with which the edge position can be determined from a single CL line; the standard deviation is below σ = 3 nm in all cases. The strong correspondence between these experimental data and calculated data further confirms that the electron-induced field profiles can be accurately derived from the measured CL line profiles. It indicates that our measurement accuracy is not limited by distortions of the primary electron beam diameter due to the relatively large working distance, mechanical instabilities and misalignments, or errors in the data analysis determined by statistical variations in the CL data.

In conclusion, we have determined the factors that determine the spatial resolution of 10–30 keV cathodoluminescence imaging spectroscopy (CL). Using 70 nm Ag cubes as a model system with sharp edges, we coherently excite localized plasmons of which the CL radiation is collected. The half-width at half-maximum of the plasmon CL line scan at 10(30) keV is 7(10) nm wider than the physical nanocube size, directly reflecting the extent of the evanescent field around the electron trajectory and the plasmonic field distributions. The CL decay length derived from the data differs from the calculated value from boundary-element simulations by only 1 nm at 10 keV and 3 nm at 30 keV. A statistical electron scattering model describes the secondary emission line scans well and is used to determine the physical nanocube size. The Ag nanocube edge position derived from the CL line scans show an accuracy (systematic error) less than 3 nm compared to the secondary electron line scan. The nanoparticle edge position can be derived with a standard deviation below σ = 3 nm. The strong correspondence between experimental data and calculations proves that the electron-induced field profiles can be accurately derived and firmly establishes CL as an optical characterization technique with nanoscale spatial resolution.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.9b00164.

• Description of electron excitation energy spectrum, SEM/CL experiments, Ag nanocube synthesis, CASINO simulations, analytical SE model, MNPBEM simulations, analytical CL model (PDF)

Author Present Address

^§ S.M., CNRS, Centre d’Élaboration de Matériaux et d’Etudes Structurale (CEMES), Toulouse, France.

The authors declare the following competing financial interest(s): A.P. is co-founder and co-owner and T.C. is employee of Delmic BV, a company that produces the cathodoluminescence system that was used in this work.