Matrix‐Based Sensitivity Assessment of Soil Organic Carbon Storage: A Case Study from the ORCHIDEE‐MICT Model

Abstract

Modeling of global soil organic carbon (SOC) is accompanied by large uncertainties. The heavy computational requirement limits our flexibility in disentangling uncertainty sources especially in high latitudes. We build a structured sensitivity analyzing framework through reorganizing the Organizing Carbon and Hydrology in Dynamic Ecosystems (ORCHIDEE)‐aMeliorated Interactions between Carbon and Temperature (MICT) model with vertically discretized SOC into one matrix equation, which brings flexibility in comprehensive sensitivity assessment. Through Sobol's method enabled by the matrix, we systematically rank 34 relevant parameters according to variance explained by each parameter and find a strong control of carbon input and turnover time on long‐term SOC storages. From further analyses for each soil layer and regional assessment, we find that the active layer depth plays a critical role in the vertical distribution of SOC and SOC equilibrium stocks in northern high latitudes (>50°N). However, the impact of active layer depth on SOC is highly interactive and nonlinear, varying across soil layers and grid cells. The stronger impact of active layer depth on SOC comes from regions with shallow active layer depth (e.g., the northernmost part of America, Asia, and some Greenland regions). The model is sensitive to the parameter that controls vertical mixing (cryoturbation rate) but only when the vertical carbon input from vegetation is limited since the effect of vertical mixing is relatively small. And the current model structure may still lack mechanisms that effectively bury nonrecalcitrant SOC. We envision a future with more comprehensive model intercomparisons and assessments with an ensemble of land carbon models adopting the matrix‐based sensitivity framework.

Key Points

• One matrix equation reproduces spatial‐temporal dynamics of SOC from the vertically discretized ORCHIDEE‐MICT model

• The matrix representation enables comprehensive sensitivity analyses (e.g., Sobol's method) for complex models

• Active layer depth is critical for modeling SOC distribution in high latitudes

1. Introduction

Terrestrial biosphere models (TBM) play an important role in studying land carbon dynamics and their complex feedbacks to future climate changes (Ciais et al., 2013; Fisher et al., 2014; Friedlingstein et al., 2014). These TBMs normally capture multiple intricate soil‐vegetation‐atmosphere interactions across various spatiotemporal scales at the land surface and are computationally expensive especially when soil organic carbon (SOC) stocks require hundreds or thousands of simulation years to stabilize. The complexity and computational constraints on models limit our capacity in conducting thorough sensitivity analyses and tracking model behaviors. Improvements in modeling efficiency are becoming urgent as the slow, computationally expensive high‐latitude (permafrost) processes are critical in land carbon studies and have been incorporated in a growing number of TBMs (Barman & Jain, 2016; Burke et al., 2017; Chaudhary et al., 2017; Ekici et al., 2014; Guimberteau et al., 2018; Koven et al., 2013; Mcguire et al., 2016; Wania et al., 2009).

We lack comprehensive sensitivity analyses in current TBMs especially when it comes to long‐term belowground carbon dynamics. Sensitivity tests provide information on the importance of variables, parameters, or other inputs on model outputs. It is a common practice in order to understand model dynamics, trace uncertainty sources, calibrate model parameters, assess experimental plans and decision strategies, etc. (Lu et al., 2013; Xie et al., 2013). Varying parameters one at a time is one of the most straightforward methods to test parameter sensitivity but misses interactions among parameters. Variance‐based methods, such as the random‐sampling, high‐dimensional model representation method and the Sobol's method (Rabitz et al., 1999; Sobol, 2001), decompose uncertainties in model output and attribute these uncertainties to sensitivities associated with corresponding parameters. Variance‐based methods are advantageous over the brutal force one‐at‐a‐time approach by taking into account interactions among parameters but rely on hundreds of thousands of model simulations, for example, through the Monte Carlo random or quasi‐random sampling (Dantec‐Nedelec et al., 2017; Lu et al., 2013). Despite current ongoing efforts in improving sampling strategies and testing efficiency (Lu et al., 2013), variance‐based sensitivity analysis is still computationally heavy for TBMs when it comes to regional or global simulations. These models often track diverse processes ranging from minutes (e.g., half‐hourly time step for photosynthetic carbon uptake) to centuries or millennium (e.g., soil carbon processes) and incorporate a large number of parameters (Krinner et al., 2005; Oleson et al., 2013). The overall computational requirement to obtain a thorough picture of the whole system dynamics relies on slow soil carbon processes which take a long time to stabilize. Therefore, previous sensitivity studies on TBMs focused on fluxes in short time scales instead of pools (Lu et al., 2013) or local scales instead of regional or global scales (Tang & Zhuang, 2009), leaving the long‐term carbon pool dynamics less explored.

Soil carbon is the largest carbon pool in the terrestrial biosphere (Ciais et al., 2013; Scharlemann et al., 2014), and current model simulations are affiliated with large uncertainties that require great effort to improve. For example, models that participated in the Coupled Model Intercomparison Project Phase 5 reported a range from 510 to 3,040 Pg C for current global soil carbon stock and a source of 72 Pg C to a sink of 253 Pg C during the 21st century (Todd‐Brown et al., 2013; Todd‐Brown et al., 2014). The northern high latitudes (>50°N) or the permafrost regions contain at least twice as much carbon as it is currently in the atmosphere (Hugelius et al., 2013; Zimov et al., 2006). Carbon stored in the permafrost region is highly vulnerable and sensitive to warming as thawing permafrost exposes a large amount of SOC to decomposition and plays an important role in feeding back to future climate change with the release of greenhouse gases such as carbon dioxide and methane (Elberling et al., 2013; Schuur et al., 2015). As a result, a growing number of TBMs started to explicitly incorporate processes that are unique to permafrost regions (Barman & Jain, 2016; Burke et al., 2017; Chaudhary et al., 2017; Ekici et al., 2014; Guimberteau et al., 2018; Koven et al., 2013; Mcguire et al., 2016; Wania et al., 2009). Permafrost regions have distinctive vertical soil carbon dynamics and contain a large amount of soil carbon below the 1‐m depth routinely studied for middle and low latitudes (Hugelius et al., 2013). A vertical representation of soil carbon is therefore needed in order to realistically capture permafrost soil carbon dynamics. The vertical discretization of soil carbon in the permafrost region increases complexity of the soil module and the number of unconstrained parameters, further raises computational requirements with added soil carbon pools and slower turnover rate of soil carbon due to cold climate, and makes sensitivity tests more difficult.

Facing the challenge, we reorganize one of the TBMs that track high‐latitude processes, the Organizing Carbon and Hydrology in Dynamic Ecosystems (ORCHIDEE)‐aMeliorated Interactions between Carbon and Temperature (MICT) model, into the analytically traceable and structurally clear matrix form. The matrix representation reproduces the spatial‐temporal gradients of SOC from the original ORCHIDEE‐MICT. Meanwhile, it makes parameter sensitivity analyses of this complex model more flexible. We will first introduce the matrix representation of ORCHIDEE‐MICT and then illustrate the flexibility of our structured sensitivity assessment framework through examples focusing on sensitivities of long‐term SOC dynamics to model assumptions and parameterizations.

2. Materials and Methods

2.1. ORCHIDEE‐MICT Overview

ORCHIDEE‐MICT is a land surface model that couples carbon, water, and energy dynamics and has a specific representation of high‐latitude processes (Guimberteau et al., 2018). For example, ORCHIDEE‐MICT incorporates permafrost physics and seasonal freeze‐thaw cycles, captures the insulation impacts of snow on soil thermal dynamics, simulates high‐latitude climatic constraints on vegetation growth, and represents the accumulation of large soil carbon stocks by limited decomposition under cold conditions and through slow vertical mixing of carbon via processes such as cryoturbation (Gouttevin et al., 2012; Guimberteau et al., 2018; T. Wang et al., 2013; F. Wang et al., 2016).

For vegetation carbon dynamics, the model structure follows largely on Krinner et al. (2005). Global vegetation is divided into 13 plant functional types (PFTs). PFTs differ in their physiological and phenological parameterizations which regulate carbon transfers from the atmosphere to vegetation and soil. Carbon is taken up from the atmosphere by plants through photosynthesis that adopts the Farquhar approach (Farquhar et al., 1980; Yin & Struik, 2009) for leaf photosynthesis which is further scaled to canopy assuming a leaf area index‐dependent absorption of light. The fate of photosynthetically assimilated carbon is either returned to the atmosphere as carbon dioxide through plant respiration or allocated to eight plant biomass pools (foliage, root, aboveground/belowground sapwood and heartwood, fruit, and carbohydrate reserve) to support different vegetation activities. Vegetation carbon enters litter pools during processes such as leaf senescence, root and wood turnovers, and fire disturbance. ORCHIDEE‐MICT tracks four classes/types of litters, that is, the aboveground metabolic litter, belowground metabolic litter, aboveground structural litter, and belowground structural litter. And the model does not explicitly track coarse woody debris as a separate single carbon pool. Aboveground and belowground litters differ in the environmental conditions (temperature and moisture) that modify the rate of litter decomposition. Litter carbon (both aboveground and belowground) is transferred into vertically resolved soil carbon pools as litter decomposes. ORCHIDEE‐MICT currently divides soil carbon into 32 layers, up to a depth of 38 m. The thickness of soil layer increases from shallow to deep soil layers, and Table S1 provides the depth information of each soil layer. In each soil layer, ORCHIDEE‐MICT tracks three different types of soil carbon pools, that is, the active SOC with a default potential turnover time of 0.145 year and the slow and passive SOC pools with their potential turnover times of 5.48 and 241 years, respectively (Guimberteau et al., 2018). Once entering the soil, carbon is transferred among a complex network formed by either vertical or turnover time distinguished soil carbon pools. Ultimately, soil carbon can enter the atmosphere through respiration, be transformed into more recalcitrant pools with longer turnover times, or be buried into deep soil layers through cryoturbation or bioturbation, while advection is not considered in this model version (Figure 1).

Figure 1.

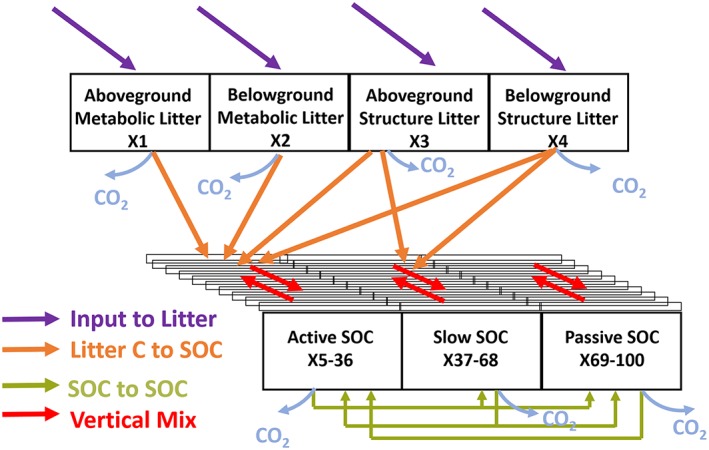
Litter and soil organic carbon (SOC) dynamics in ORCHIDEE‐MICT. ORCHIDEE‐MICT tracks four litter carbon types and three SOC types that differ in turnover time following the CENTURY modeling approach. For each SOC type (i.e., the active, slow, and passive SOC), ORCHIDEE‐MICT explicitly represents the vertical dynamics through dividing the soil profile into 32 layers. Litter pools receive carbon input (purple arrows) from plant residue and lose carbon through respiration (blue arrows) and transfer into SOC pools (orange arrows). Carbon entering SOC can be stored in soil for a period of time, respired out as carbon dioxide, transformed into different SOC types (green‐yellow arrows) within the same soil layer or transferred into different soil vertical layers (red arrows). Mathematically, the system dynamics are captured by tracking 100 carbon state variables (X1–100) and can be represented by one matrix equation (equation (9) in the main text). ORCHIDEE‐MICT=Organizing Carbon and Hydrology in Dynamic Ecosystems (ORCHIDEE)‐aMeliorated Interactions between Carbon and Temperature (MICT).

Litter and SOC decompositions and transfers among different organic matter types follow the structure of CENTURY model (Parton et al., 1987) except the vertical discretization, with modified decomposition rates and environmental response functions (Guimberteau et al., 2018; Krinner et al., 2005). Litter from leaf, aboveground sapwood, aboveground heartwood, fruit, and the carbohydrate reserve enters the aboveground litter pools, while the belowground litter pool is composed of litter from belowground sapwood, belowground heartwood, and root. The split of litter into metabolic and structural components is based on the lignin to nitrogen ratio (L/N) of plant residues,

$${\mathit{F}}_{\mathit{m}}=\mathbf{0.85}-\mathbf{0.018}*\mathit{L}/\mathit{N}$$ (1)

where F_m is the fraction that is allocated to metabolic litter. Decomposition of each type of dead organic matter (aboveground metabolic litter, belowground metabolic litter, aboveground structural litter, belowground structural litter, active SOC, slow SOC, and passive SOC) is modeled as a first‐order decay process with a potential turnover time (or decay rate) modified by soil temperature and moisture. The temperature and moisture dependence of the turnover time is represented by the temperature scalar (ξ_T) and moisture scalar (ξ_W; supporting information Figure S1),

$${\mathit{\xi }}_{\mathit{T}}=\mathit{\text{min}}\left(\mathbf{1},{\mathit{e}}^{\frac{\mathit{\text{temps}}*\left(\mathit{T}-\mathbf{303.15}\right)}{\mathbf{10}}}\right)$$ (2)

$${\mathit{\xi }}_{\mathit{W}}=\mathit{\text{max}}(\mathbf{0.25},\mathit{\text{min}}\left(\mathbf{1},-\mathbf{1.1}{\mathit{W}}^{\mathbf{2}}+\mathbf{2.4}\mathit{W}-\mathbf{0.29}\right)$$ (3)

where T is temperature in Kelvin, temps is the temperature sensitivity (the natural logarithm of q10) and W is the relative soil moisture content, that is, the ratio between the plant available water (the volumetric soil water content minus soil water content at the wilting point) and the plant available water capacity (water content at the field capacity minus water content at wilting point). W includes both ice and liquid fractions. For aboveground litter pools, T and W are the averages across the surface 4 soil layers (2 cm). And T and W for belowground litter are weighted averages within the maximum rooting zone. Detailed information about soil hydrology and thermal dynamics is available in Guimberteau et al. (2018).

Following Guimberteau et al. (2018), Krinner et al. (2005) and Parton et al. (1987), the decomposition rate of structural litter is also scaled by the lignin content through the lignin scalar ξ_L,

$${\mathit{\xi }}_{\mathit{L}}={\mathit{e}}^{-\mathit{lgc}*\mathit{L}}$$ (4)

where L is the fraction of the lignin in structural litter and lgc is the coefficient that regulates the lignin effect. The decomposition of active SOC is affected by the clay content through the clay scalar ξ_Cl,

$${\mathit{\xi }}_{\mathit{Cl}}=\mathbf{1}-\mathbf{0.75}*\mathit{\text{clay}}$$ (5)

As organic matter decomposes, certain fractions of the carbon fluxes are transferred into other types of carbon pools, and the remaining fractions are respired. Detailed pathways of carbon transfers are illustrated in Figure 1. Transfer fractions are generally prescribed at fixed levels with corresponding parameters and their default values available in Table 1. In the case of transferring carbon from the structural litter to active and slow SOC, the fraction is modified by the lignin content in structural litter. The final fraction transferred from the aboveground structural litter to slow SOC is the fraction parameter (fas2s) multiplied by the lignin content in the aboveground structural litter. And the final portion of the aboveground structural litter that goes into active SOC is the fraction parameter (fas2a) multiplied by 1 minus the lignin content. The same rule applies for the belowground structural litter. The fraction transferred from active to slow SOC (f_a2s) depends on the fraction transferred from active to passive SOC (f_a2p) and the clay content,

$${\mathit{f}}_{\mathit{a}\mathbf{2}\mathit{s}}=\mathbf{1}-{\mathit{f}}_{\mathit{a}\mathbf{2}\mathit{p}}-\left(\mathbf{0.85}-\mathbf{0.68}*\mathit{\text{clay}}\right)$$ (6)

Table 1.

Parameters Affecting Litter and SOC Dynamics in the ORCHIDEE‐MICT Model

	Name	Matrix source	Description	Default value	Range	Unit
1	ins	I	Input scalar	1	[0,1]
2	p4lf	I	Partition (structural versus metabolic) coefficient for leaf	0.6916	[0,1]
3	p4sa	I	Aboveground sapwood partition, structural versus metabolic	0.598	[0,1]
4	p4sb	I	Belowground sapwood partition, structural versus metabolic	0.598	[0,1]
5	p4ha	I	Aboveground heartwood partition, structural versus metabolic	0.598	[0,1]
6	p4hb	I	Belowground heartwood partition, structural versus metabolic	0.598	[0,1]
7	p4ro	I	Root partition, structural versus metabolic	0.6916	[0,1]
8	p4fr	I	Fruit partition, structural versus metabolic	0.6916	[0,1]
9	p4ca	I	Carbohydrate reserve partition, structural versus metabolic	0.6916	[0,1]
10	fam2a	A	Transfer fraction, aboveground metabolic litter to active SOC	0.45	[0,1]
11	fbm2a	A	Transfer fraction, belowground metabolic litter to active SOC	0.55	[0,1]
12	fas2a	A	Transfer fraction, aboveground structural litter to active SOC	0.45	[0,1]
13	fbs2a	A	Transfer fraction, belowground structural litter to active SOC	0.45	[0,1]
14	fas2s	A	Transfer fraction, aboveground structural litter to slow SOC	0.7	[0,1]
15	fbs2s	A	Transfer fraction, belowground structural litter to slow SOC	0.7	[0,1]
16	fa2p	A	Transfer fraction, active to passive SOC	0.004	[0,0.15]
17	fs2a	A	Transfer fraction, slow to active SOC	0.42	[0,0.5]
18	fs2p	A	Transfer fraction, slow to passive SOC	0.03	[0,0.5]
19	fp2a	A	Transfer fraction, passive to active SOC	0.45	[0,1]
20	zlit	A	Factor control vertical distribution of litter input to SOC	PFT dependent	[0.2, 1.25]
21	clay	A, ξCl	Clay content	0.2	[0,0.6]
22	lgc	A, ξL	Lignin coefficient on structural litter decomposition	3	[0,10]
23	lga	A, ξL	Aboveground lignin content	0.76	[0,1]
24	lgb	A, ξL	Belowground lignin content	0.72	[0,1]
25	temps	ξT	Temperature sensitivity	0.69	[0,1]
26	ms	ξW	Moisture scalar	1	[0.8,1.2]
27	tau4ml	K	Turnover time, metabolic litter	0.066	[0,0.066]	year
28	tau4sl	K	Turnover time, structural litter	0.245	[0,0.245]	year
29	tau4a	K	Turnover time, active SOC	0.149	[0,0.149]	year
30	tau4s	K	Turnover time, slow SOC	5.48	[0,5.48]	year
31	tau4p	K	Turnover time, passive SOC	241	[0,241]	year
32	cryo	V	Cryoturbation rate	0.001	[0,1]	m2/year
33	bio	V	Bioturbation rate	0.0001	[0,1]	m2/year
34	alt	A, V	Active layer depth of the last year	0.2	[0,3]	m

Note. SOC = soil organic carbon; ORCHIDEE = Organizing Carbon and Hydrology in Dynamic Ecosystems; PFT = plant functional type.

ORCHIDEE‐MICT explicitly simulates the vertical distribution of SOC, while the litter pools are not vertically discretized. Flux from each litter pool is allocated to different soil layers.

$${\mathit{r}}_i=\left\{\begin{array}{ll}\frac{\mathbf{1}}{\mathit{\alpha }\left(\mathbf{1}-{\mathit{e}}^{-\frac{\mathit{m}}{\mathit{\alpha }}}\right)}{\mathit{e}}^{-\frac{{\mathit{z}}_{\mathit{i}}}{\mathit{\alpha }}}& \mathit{\text{if}}{\mathit{z}}_{\mathit{i}}<\mathit{m}\\ \mathbf{0}& \mathit{\text{if}}{\mathit{z}}_{\mathit{i}}\ge \mathit{m}\end{array}\right.$$ (7)

where r_i is the relative fraction (fraction multiply thickness of each soil layer) of the transferring carbon flux from the litter pool allocated to the ith soil layer (supporting information Figure S1). The z_i is the vertical node location of the ith soil layer. The m is the integration length beyond which there is no input to soil carbon from litter flux. The m is set as the minimum between a fixed depth of 2 m and the active layer depth of the last year's alt. The active layer depth is defined as the depth above which soil temperature is greater than 0 °C. α is PFT dependent,

$$\mathit{\alpha }=\mathit{\text{min}}\left(\mathbf{0.5}\mathit{\text{zlit}},\mathbf{0.5}\mathit{alt}\right)$$ (8)

where zlit is a PFT‐dependent parameter that reflects the reference rooting and is a setup partly based on general understandings of rooting pattern, for example, the grass PFTs normally have relatively higher portion of root in the surface layers compared to tree PFTs and partly based on modeler's experience.

In addition to the vertical input into SOC pools, SOC is also redistributed among vertical soil layers through cryoturbation or bioturbation. If alt is no bigger than the preset depth of 3 m, cryoturbation is the main vertical mixing process. Otherwise, bioturbation is the main vertical mixing mechanism. The rate of cryoturbation is constant for soil layers with depth smaller than alt and linearly drops to 0 between alt and the depth that is 3 times alt. However, if the soil depth is bigger than the preset 3 m, the cryoturbation rate is 0. For the case of bioturbation, the bioturbation rate is constant for soil layers with the depth smaller than 2 m and 0 beyond 2 m. That is, there is no vertical mixing for soil with a depth deeper than 3 m (neither cryoturbation nor bioturbation; Guimberteau et al., 2018). With the 2‐m boundary of inputs from litter to SOC, the 3‐m boundary of mixing, the deepest layer where SOC can reach is the twelfth layer in the default setting, and the model is adaptable to have SOC in deeper soil layers with adjustment of these boundaries.

2.2. Matrix Representation

Litter and SOC dynamics in ORCHIDEE‐MICT can be organized into one matrix equation with 100 carbon state variables (X(t)), corresponding to four litter carbon pools and 32 × 3 soil carbon pools,

$$\frac{\mathit{d}\mathit{X}\left(\mathit{t}\right)}{\mathit{d}\mathit{t}}=\mathit{I}\left(\mathit{t}\right)+\mathit{A}\left(\mathit{t}\right){\mathit{\xi }}_{\mathit{\text{TWLCl}}}\left(\mathit{t}\right)\mathit{K}\mathit{X}\left(\mathit{t}\right)-\mathit{V}\left(\mathit{t}\right)\mathit{X}\left(\mathit{t}\right)$$ (9)

where I(t) (100 × 1) is the external carbon inputs into the litter and soil system. The second term (A(t)ξ_TWLCl(t)KX(t)) in the right side of the equation represents carbon dynamics that include organic matter decomposition, losses through respiration, transfers of decomposed litter fluxes into layered SOC pools, and transfers of SOC among different SOC pools in the same soil layer. A is the carbon transfer matrix, ξ_TWLCl is the environmental scalar matrix, K is the potential decomposition rate matrix, and X is a matrix describing the carbon state variables. The third term (V(t)X(t)) captures SOC mixing in the vertical soil profile through cryoturbation or bioturbation while V is the vertical mixing matrix. t in parentheses indicates that the corresponding element is time‐dependent.

In ORCHIDEE‐MICT, plant residues are allocated into four different litter pools, and no direct vegetation carbon goes into SOC pools. So I(t) has four nonzero elements,

$$\mathit{I}\left(\mathit{t}\right)=\left(\begin{array}{c}{\mathit{I}}_{\mathbf{1}}\left(\mathit{t}\right)\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}{\mathit{I}}_{\mathbf{2}}\left(\mathit{t}\right)\\ {\mathit{I}}_{\mathbf{3}}\left(\mathit{t}\right)\\ {\mathit{I}}_{\mathbf{4}}\left(\mathit{t}\right)\end{array}\\ \mathbf{0}\\ ⋮\end{array}\\ \mathbf{0}\\ \mathbf{0}\end{array}\end{array}\right)$$ (10)

K is a 100 × 100 diagonal matrix with each diagonal element representing the potential decomposition rate of each carbon pool. The potential decomposition rates differ for different types of organic pools but are the same for the same type of organic pool in different soil layers, that is, there are seven unique values in the matrix (four for litter and three for SOC). K is modified by the scalar matrix ξ_TWLCl(t), a 100 × 100 diagonal matrix with each diagonal element (ξ_TWLCl^′) denoting temperature (ξ_T), water (ξ_W), lignin (ξ_L), and clay (ξ_Cl) scalars that downregulate the potential decomposition rate,

$${\mathit{\xi }}_{\mathit{\text{TWLCl}}}\prime ={\mathit{\xi }}_{\mathit{T}}{\mathit{\xi }}_{\mathit{W}}{\mathit{\xi }}_{\mathit{L}}{\mathit{\xi }}_{\mathit{Cl}}$$ (11)

A is the carbon transfer matrix (100 × 100) that quantifies carbon transfers among different types of organic pools. The diagonal entries of A are negative ones, delegating the entire decomposition flux that leaves each carbon pool. The nondiagonal items represent the fraction of carbon that is transferred from one pool to another. In ORCHIDEE‐MICT, decomposition fluxes from aboveground and belowground metabolic litter pools are allowed to transfer into 32 active SOC pools. And part of carbon from decomposing aboveground and belowground structural litter ends in 32 active SOC pools and part in 32 slow SOC pools. Additionally, carbon is transferred from slow to active SOC, passive to active SOC, active to slow SOC, active to passive SOC, and slow to passive SOC (Figure 1) within the same soil layer. Therefore, the structure of A is illustrated through the block matrix,

$$\mathrm{A}=\left(\begin{array}{ccccccc}-1& 0& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0\\ \mathbf{A}\mathbf{51}& \mathbf{A}\mathbf{52}& \mathit{A}\mathbf{53}& \mathbf{A}\mathbf{54}& -1& A56& A57\\ 0& 0& \mathbf{A}\mathbf{63}& \mathit{A}\mathbf{64}& A65& -1& 0\\ 0& 0& 0& 0& A75& A76& -1\end{array}\right)$$ (12)

where A51, A52, A53, A54, A63, A64 (in bold in equation (12)) represent transfers of carbon from litter decomposition flux to SOC pools. Numbers from 1 to 7 are abbreviations for aboveground metabolic litter, belowground metabolic litter, aboveground structural litter, belowground structural litter, and active, slow, and passive SOC. A51, A52, A53, A54, A63, A64 are 32 × 1 vectors.

$$\mathit{A}\mathbf{51}={\mathit{f}}_{\mathit{am}\mathbf{2}\mathit{a}}\left(\begin{array}{c}\begin{array}{c}{\mathit{r}}_{\mathbf{1}}/{\mathit{z}}_{\mathbf{1}}\\ \begin{array}{c}{\mathit{r}}_{\mathbf{2}}/{\mathit{z}}_{\mathbf{2}}\\ ⋮\end{array}\end{array}\\ \begin{array}{c}{\mathit{r}}_{\mathbf{31}}/{\mathit{z}}_{\mathbf{31}}\end{array}\\ \begin{array}{c}{\mathit{r}}_{\mathbf{32}}/{\mathit{z}}_{\mathbf{32}}\end{array}\end{array}\right)$$ (13)

where f_am2a is the fraction parameter that tells the fraction transferred from aboveground metabolic litter to the active SOC and r_i is the relative fraction of carbon flux allocated to the ith soil layer from equation (7).

A56, A57, A65, A75, and A76 represent carbon transfers among different SOC pools in the same soil layer. A56, A57, A65, A75, and A76 are 32 × 32 diagonal matrices. For example, A₅₆ is a diagonal matrix with the identical diagonal entry f₅₆which denotes the fraction transferred from the slow SOC pool to the active SOC pool (fs2a).

$${\mathbf{A}}_{\mathbf{56}}\mathbf{=}\mathit{\text{diag}}\left({\mathit{f}}_{\mathbf{56}},{\mathit{f}}_{\mathbf{56}},{\mathit{f}}_{\mathbf{56}},\dots ,{\mathit{f}}_{\mathbf{56}}\right)$$ (14)

V(t) represents the vertical carbon mixing coefficient matrix,

$$\mathrm{V}\left(\mathrm{t}\right)=\left(\begin{array}{ccccccc}\mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathit{V}\mathbf{55}\left(\mathit{t}\right)& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathit{V}\mathbf{66}\left(\mathit{t}\right)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathit{V}\mathbf{77}\left(\mathit{t}\right)\end{array}\right)$$ (15)

Each of the diagonal block is a tridiagonal matrix that describes vertical redistribution of corresponding carbon pools among different soil layers. As the vertical transfer rates are not differentiated among different types of carbon pools, V55(t), V66(t), and V77(t) are identical with the following structure,

$$\mathit{V}\mathbf{66}=\mathit{diag}{\left({\mathit{z}}_{\mathbf{1}},{\mathit{z}}_{\mathbf{2}},\dots ,{\mathit{z}}_{\mathbf{32}}\right)}^{-\mathbf{1}}\left(\begin{array}{cccccccc}{\mathit{g}}_{\mathbf{1}}& -{\mathit{g}}_{\mathbf{1}}& \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ -{\mathit{h}}_{\mathbf{2}}& {\mathit{h}}_{\mathbf{2}}+{\mathit{g}}_{\mathbf{2}}& -{\mathit{g}}_{\mathbf{2}}& \mathbf{0}& \cdots & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& -{\mathit{h}}_{\mathbf{3}}& {\mathit{h}}_{\mathbf{3}}+{\mathit{g}}_{\mathbf{3}}& -{\mathit{g}}_{\mathbf{3}}& \cdots & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& -{\mathit{h}}_{\mathbf{4}}& {\mathit{h}}_{\mathbf{4}}+{\mathit{g}}_{\mathbf{4}}& \cdots & \mathbf{0}& \mathbf{0}& \mathbf{0}\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \cdots & {\mathit{h}}_{\mathbf{30}}+{\mathit{g}}_{\mathbf{30}}& -{\mathit{g}}_{\mathbf{30}}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \cdots & -{\mathit{h}}_{\mathbf{31}}& {\mathit{h}}_{\mathbf{31}}+{\mathit{g}}_{\mathbf{31}}& -{\mathit{g}}_{\mathbf{31}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}& -{\mathit{h}}_{\mathbf{32}}& {\mathit{h}}_{\mathbf{32}}\end{array}\right)$$ (16)

where the subscript numbers indicate soil layers; g and h are vertical mixing rates (in units of depth/time, e.g., m/year) of carbon between the current soil layer and the upper layer and between the current and the lower layer derived from the diffusion rate (cryoturbation or bioturbation). The z_i indicates the depth of each soil layer. And g_i = h_i + 1, i = 1…, 31.

2.3. Validation of the Matrix Calculation

To validate the matrix representation, we conduct two types of tests. The first series of tests are grid cell level simulations. We drive both the matrix and the original ORCHIDEE‐MICT by the same configuration (e.g., the same simulation time step) and climate forcing (CRUNCEP v7; Guimberteau et al., 2018; Kalnay et al., 1996; New et al., 2000) at one randomly chosen high latitude (161°E, 69°N) and one tropical grid cell (99°E, 1°S) to test how well the matrix simulation captures transient dynamics of the original ORCHIDEE‐MICT simulation. Since we only focus on litter and SOC from the matrix equation (equation (9)), vegetation dynamics are the same for the matrix and original ORCHIDEE‐MICT simulations. In the second test, we check the spatial pattern of long‐term carbon stocks. We first bring the original ORCHIDEE‐MICT into quasi steady state following the default ORCHIDEE‐MICT spin‐up procedure (Guimberteau et al., 2018). We use the term quasi steady state to differentiate between the numerical steady state and the true steady state. For the default ORCHIDEE‐MICT spin‐up, we run the full (coupled aboveground and belowground with 30‐min time step for photosynthesis and daily time step for SOC decomposition) ORCHIDEE‐MICT model for 150 years, followed by 100,000 years soil‐only simulations (with daily time step for SOC decomposition), and then 100 years full model simulation again. For demonstration purpose, we recycle only one year's (1961) climate forcing to drive the model. Meanwhile, we conduct the matrix simulation with the same setting as the original ORCHIDEE‐MICT. Instead of running the matrix for 100,250 years, we solve the matrix equation by inverse calculations, similarly as in Xia et al. (2012) and Huang, Lu, et al. (2018), which gives us the matrix carbon storage capacity or the SOC steady state after the stabilization of vegetation with several hundred years of simulation. To be specific, we calculate annual averages of matrix items obtained from the original ORCHIDEE‐MICT simulation driven by the climate forcing of 1961 and set equation (9) to be 0 to solve the state matrix X for each year.

2.4. Sensitivity Tests

We conduct three series of sensitivity tests to identify important parameters that regulate long‐term SOC stocks in ORCHIDEE‐MICT and to quantify sensitivities of different SOC pools to these parameters.

In the first sensitivity test, we focus on the relative importance of parameters based on Sobol's method (Sobol, 2001). Sobol's method provides an approach to assess the global parameter sensitivity and allows us to sample the whole parameter space as well as to discern model nonlinearity or parameter interactions through variance decomposition. The total variance of the model output can be represented as the sum of variance caused by each individual parameter and interactions among parameters. The first‐order Sobol sensitivity index (Si) quantifies the single contribution from the ith parameter (p _i), with no interaction effects included. And the total order Sobol sensitivity index (ST _i) measures the total effect of the parameter p _i on the variance of model output, including the single‐effect Si and different orders of interactions of p _i with other model parameters. The difference between Si and ST _i is a measure of interactions.

We scrutinize litter and SOC decomposition processes from the matrix equation (equation (9)) and select 34 relevant parameters as listed in Table 1. These parameters can be categorized into groups that affect carbon input (I in equation (9)), transfer (A), environmental scalar (ξ_TWLCl), potential decomposition rate (K), and vertical mixing (V). For the carbon input parameter group, we look into the total carbon input into litter and the partitioning of the input into metabolic and structural components. As a first step, we conduct idealized sensitivity analysis with constant carbon input from vegetation obtained from ORCHIDEE‐MICT simulation at one randomly chosen northern high‐latitude grid cell and rescale the total carbon input with the parameter ins (range, 0–1). The sensitivity to total carbon input is therefore reflected in ins. For partitioning of the input into structural versus metabolic litter, we do not put each item in equation (1) (the constants can also be set as parameters) into the sensitivity test. Instead, we use only one parameter, the fraction allocated to metabolic litter (F_m in equation (1), and p4lf, for example, in Table 1) to test the sensitivity to litter partitioning (metabolic versus structural litter). The transfer parameter group includes parameters that regulate allocation of litter fluxes into different SOC layers (e.g., zlit) and transfer fractions among different organic matter types. Clay content regulates both the transfer fraction (equation (6)) and the decomposition rate of the active SOC (equation (5)). Similarly, we do not test each parameter related to the regulation of clay on SOC dynamics. Instead, we put clay content as one parameter to understand the impact of clay on carbon dynamics (clay in Table 1). The environmental scalar parameter group takes into account parameters that alter different environmental scalars in equation (11). For the moisture scalar ξ_W, instead of incorporating three parameters that regulate soil moisture effect on decomposition (equation (3)), we use one parameter (ms) to rescale the magnitude of the moisture scalar. For the temperature scalar ξ_T, we test the temperature sensitivity parameter, temps, in equation (2). Aboveground lignin content in structural litter (lga), belowground structural litter lignin content (lgb), and the lignin coefficient (lgc, equation (4)) are related to the lignin scalar ξ_L. For the clay scalar ξ_Cl, we only focus on clay content. By appropriately lumping parameters, we reduce the parameter space without losing the main information on important parameters or processes. We also incorporate parameters (ranging from 0 to 1) to rescale potential turnover times for different carbon pools to quantify sensitivities to these parameters. For this idealized sensitivity test, we hold temperature and moisture constant. The alt controls both the vertical distribution of carbon from litter decomposition fluxes into SOC (related to A) and the vertical redistribution of SOC through cryoturbation or bioturbation (related to V). We are more interested in the direct impact of alt on carbon dynamics, and therefore we set alt as a parameter in the sensitivity analyses instead of simulating it dynamically through temperature.

To calculate Sobol indices, we randomly sample parameters within ranges provided in Table 1 assuming uniform distribution of each parameter. Parameter ranges are chosen based on model information, parameter meaning (e.g., the transfer fraction cannot be bigger than 1), and empirical knowledge. With these randomly chosen parameters, we conduct 34 × 100 × 100 simulations. The first‐order sensitivity index S_i for parameter i (p_i) is given by

$${\mathit{S}}_{\mathit{i}}=\frac{{\mathit{V}}_{{\mathit{p}}_{\mathit{i}}}\left({\mathit{E}}_{{\mathit{p}}_{-\mathit{i}}}\left(\mathit{Y}|{\mathit{p}}_{\mathit{i}}\right)\right)}{\mathit{V}\left(\mathit{Y}\right)}$$ (17)

where V(Y) denotes the total variance; Y ∣ p_i indicates simulation outputs given p_i; p_−i represents the parameter space excluding the ith parameter, and E corresponds to the expectation from multiple simulations. Similarly, the total order Sobol index is given by

$${\mathit{ST}}_{\mathit{i}}=\frac{{\mathit{E}}_{{\mathit{p}}_{-\mathit{i}}}\left({\mathit{V}}_{{\mathit{p}}_{\mathit{i}}}\left(\mathit{Y}|{\mathit{p}}_{-\mathit{i}}\right)\right)}{\mathit{V}\left(\mathit{Y}\right)}$$ (18)

To avoid the convergence issue, we repeat the previous step eight times (34 × 100 × 100 × 8 simulations in total) and calculate Sobol indices as the average from the eight replicates.

In the second test, we follow the first sensitivity test by holding total carbon input, temperature, and moisture constant. We select parameters that rank high in the first test and perturb these parameters one at a time to get detailed information about the model behavior.

The third test focuses on the northern high latitudes (>50°N) with spatially varying total carbon input, temperature, and moisture conditions the same as those during model spin‐up. While the first and second idealized tests gain insights on the overall behavior of ORCHIDEE‐MICT based on its structure, formulation, and parameter space, the third test puts the analysis into the context of spatially varying interactions among model parameters, environmental conditions, and ecosystem properties. We choose several highly sensitive parameters based on the first test and either increase or decrease these parameters by 20% its default value. For demonstration purpose, we only focus on the direction that reduces the overall total SOC stocks. For each of the new parameters, we conduct inverse matrix simulation, similarly as during the validation, for the northern high latitudes. We define the normalized sensitivity as the ratio between the relative change in total SOC and the relative change in the corresponding parameter (20% or −20%).

$${\mathit{S}}_{\mathit{\text{ratio}}}=\frac{\left({\mathit{\text{SOC}}}_{\mathit{\text{new}}}-{\mathit{\text{SOC}}}_{\mathit{ref}}\right)/{\mathit{\text{SOC}}}_{\mathit{\text{ref}}}}{\left({\mathit{P}}_{\mathit{\text{new}}}-{\mathit{P}}_{\mathit{\text{ref}}}\right)/{\mathit{\text{P}}}_{\mathit{\text{ref}}}}$$ (19)

where SOC_new is the total SOC with the new parameter and SOC_ref is the total SOC with the default parameter. P_new and P_ref correspond to new and default parameter values, respectively.

3. Results

3.1. Reproducing Original Model Dynamics by the Matrix

Matrix simulations reproduce both the transient dynamics and the global pattern of quasi steady state SOC stocks. Matrix simulations echo the transient dynamics of carbon accumulation (starting from the near‐zero initial condition) through time for both the high‐latitude (Figure 2) and tropical (supporting information Figure S2) grid cells, as illustrated through the overlapping of the 1:1 lines when plotting the matrix versus original model‐simulated active, slow, and passive SOC stocks.

Figure 2.

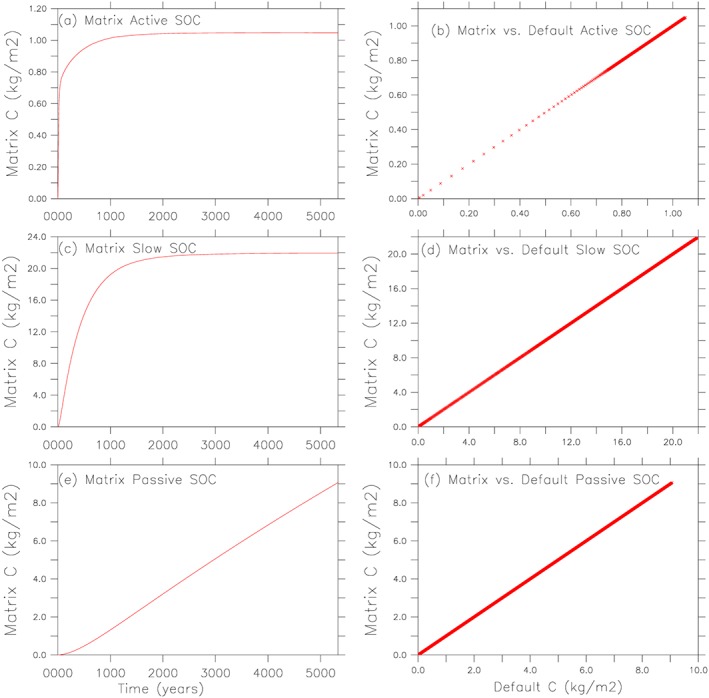
Validation of the matrix simulation at the high‐latitude grid cell (161°E, 69°N). (a, c, e) SOC dynamics (from cold start, i.e., near zero initial SOC) through the matrix simulation and (b, d, f) plot of the matrix SOC against original ORCHIDEE‐MICT simulated SOC, which overlaps with the 1:1 line. ORCHIDEE‐MICT=Organizing Carbon and Hydrology in Dynamic Ecosystems (ORCHIDEE)‐aMeliorated Interactions between Carbon and Temperature (MICT).

The quasi steady state carbon stocks are also comparable between the matrix calculation and the original model simulation (Figure 3). Total SOC stocks reach 2,564 Pg C after 400 years matrix simulation, which is close to 2,532 Pg C from the original ORCHIDEE‐MICT simulation after the default spin‐up through 150 years full model run plus 100,000 years soil‐only simulation followed by 100 years full ORCHIDEE‐MICT simulation. A large portion of SOC is stored in the northern high latitudes and in the form of passive SOC which has a relatively long turnover time. Most of the spatial pattern from the original simulation is reproduced by the matrix simulation except for the active SOC around Greenland. From the original simulation, the active SOC in some Greenland grid cells reach as high as 70 kg C/m², which is much higher than regions outside Greenland (with active SOC < 2.4 kg C/m²). From the matrix calculation, active SOC in these grid cells can reach as high as 10⁸ kg C/m² _. We excluded these Greenland grid cells for the global budget and provide explanation of the discrepancy in the supporting information.

Figure 3.

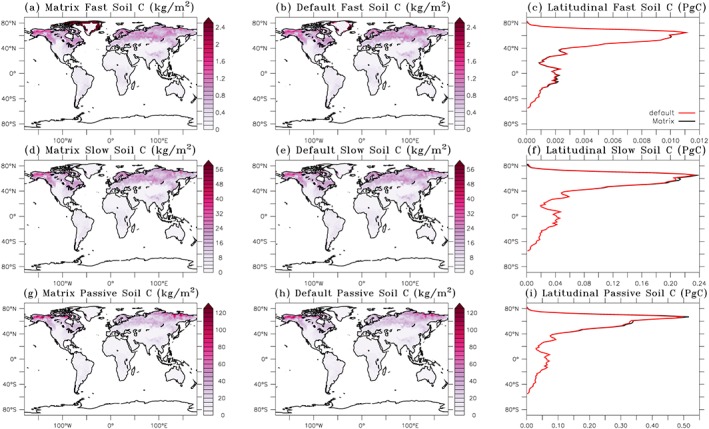
Quasi steady state C storages (fast (b), slow (e), and passive (h) SOC) after 100,250 years default ORCHIDEE‐MICT simulation (right column) and C storage diagnosed from 400 years inverse matrix calculation (through setting equation (9) equals 0 and solving the state variables, a, d, and g). (c, f, and i) Total fast, slow, and passive SOC along the latitudes. Results from panel (c) are calculated by excluding grid cells in Greenland with extremely high fast C (>2,000 kg/m²) diagnosed from the matrix calculation (supporting information). SOC = soil organic carbon; ORCHIDEE‐MICT=Organizing Carbon and Hydrology in Dynamic Ecosystems (ORCHIDEE)‐aMeliorated Interactions between Carbon and Temperature (MICT).

3.2. Overall Sensitivity Characteristic Derived From the Parameter Space

The total order Sobol sensitivity index points to a high sensitivity of total SOC stocks to the turnover time of passive SOC (tau4p, Figure 4a), followed by the parameter that rescales total carbon input into the system (ins), the temperature sensitivity of SOC decomposition (temps), the fraction of carbon transferred from slow SOC to passive SOC (fs2p), and the clay content (clay). For these highly sensitive parameters, the model is also sensitive to their individual effect (Figure 4b, the first‐order Sobol index). However, the first‐order Sobol sensitivity index is around only half of the total order index, indicating nonneglectable interactions among parameters. The sum of the first‐order Sobol index over all parameters is slightly smaller than 1 which is likely caused by a small deviation of randomly sampling scheme to cover the whole parameter space.

Figure 4.

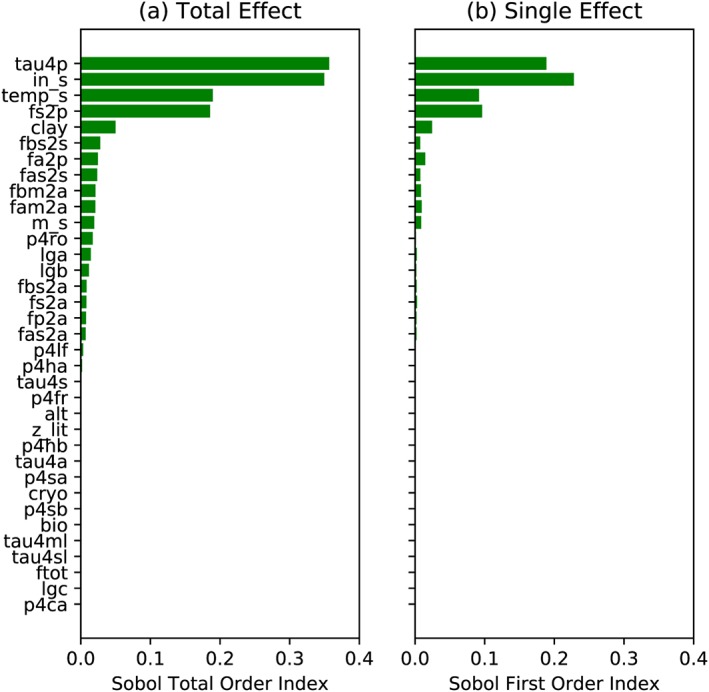
Sensitivities of total soil organic carbon to 34 relevant parameters (see Table 1 for detailed information about parameters). (a) Ranked sensitivities (the top‐to‐down direction corresponds to high‐to‐low sensitivities) based on Sobol total order sensitivity index which measures the single as well as the interaction effect. (b) The single effect based on Sobol first‐order sensitivity index. Ranks of parameters for the single effect are the same as in panel (a). The environmental settings are based on one random chosen grid cell, while the parameter space spans values designed for the global simulation.

Based on Sobol indices, the sensitivity rank differs for each SOC class and each soil layer (Figures 5 and 6). Generally, the sensitivity to ins, temps, and clay are still high. The active layer depth of the last year (alt) emerges as a highly sensitive parameter especially for surface and deep soil layers. The default setting precludes any carbon to reach a depth deeper than the twelfth layer (depth of the eleventh layer: 1.75 m; twelfth layer: 2.5 m; thirteenth layer: 3.5 m), with the 2‐m boundary of inputs from litter to SOC, the 3‐m boundary of cryoturbation, and the 2‐m boundary of bioturbation. Without the vertical SOC input in the twelfth soil layer, cryo comes out as a sensitive parameter (light blue bars, Z2.5005 in Figure 5), indicating that the vertical SOC input is relatively more important than cyro in the first 11 soil layers, caused by relatively small vertical mixing fluxes. The relatively high importance of vertical SOC input is also illustrated by the higher total sensitivity to zlit, a parameter that regulates the vertical distribution of litter fluxes into soil layers, with increasing soil depth (Figure 5). However, the impact of different parameters on the twelfth layer SOC is highly interactive, with relatively small first‐order Sobol index and strong increase in the total order Sobol index compared to other soil layers (Figures 5 and 6). Among different SOC classes, active and slow SOC are not sensitive to tau4p and fs2p (except in the twelfth layer) but are very sensitive to the parameter that controls their respective turnover time (tau4a and tau4p).

Figure 5.

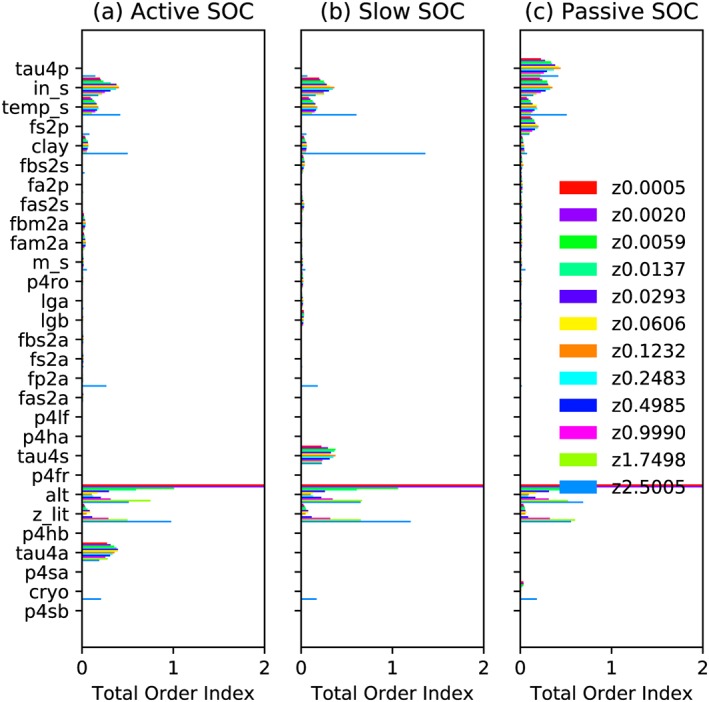
Sensitivities (Sobol total order index) of different SOC pools to 34 relevant parameters (see Table 1 for detailed information on parameters). Panels correspond to three SOC classes, that is, (a) active, (b) slow, and (c) passive. Different colors indicate different vertical soil layers with the legend numbers indicating the node depths in meters. The rank of parameters (y axis) is based on Figure 4a. Parameters ranked after cryo in Figure 4 are not shown here since their sensitivities are close to 0. SOC = soil organic carbon.

Figure 6.

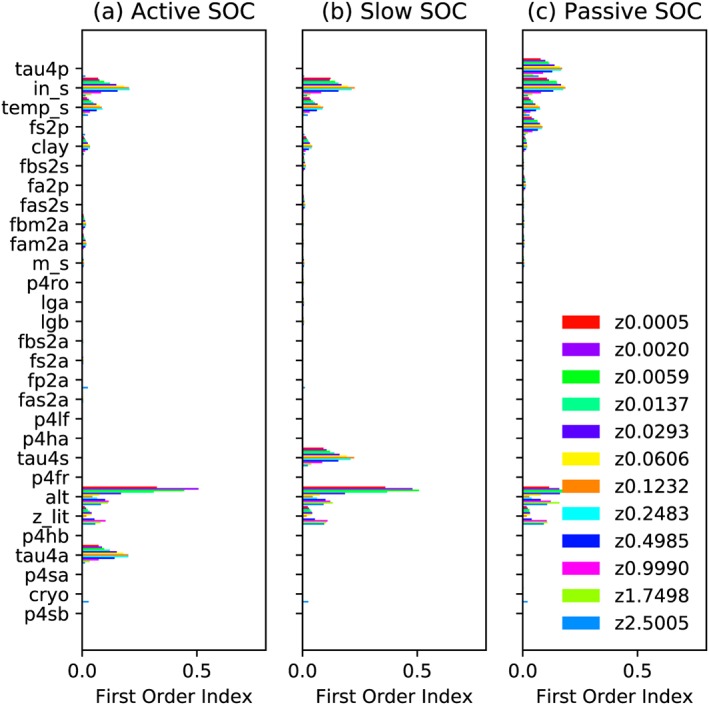
Sensitivities (Sobol first‐order index, single effect only) of different SOC pools to 34 relevant parameters. Symbols are the same as in Figure 5. SOC = soil organic carbon.

We select ins, tau4p, and alt, which are among the top sensitive parameters for either the total SOC stocks or based on each SOC class and soil layer. Figure 7 shows changes of SOC stocks for each SOC class and each soil layer in response to perturbing each parameter one at a time for a range of values. Higher ins results in higher carbon storage for each SOC class and each soil layer. Carbon pool size increases linearly with the carbon input scalar (ins). The passive SOC also unidirectionally increases with longer turnover time (tau4p). However, tau4p has no impact on active and slow SOC. In contrast, higher alt results in lower SOC stock in surface soil layers but more SOC locked in deeper soil layers. The sensitivity of SOC to alt is higher when alt is small for different soil layers.

Figure 7.

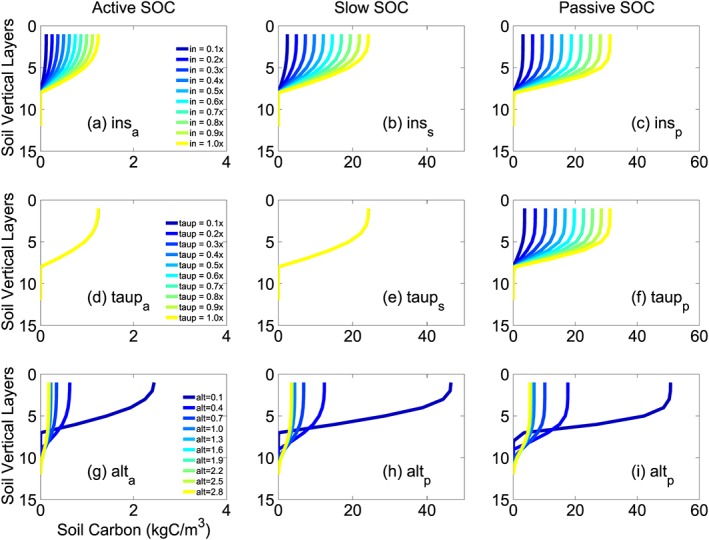
Sensitivities of different SOC pools to litter input scalar (a–c, ins), passive SOC turnover time scalar (d–f, tau4p) and the active layer depth of the last year (g–i, alt) through changing each parameter one at a time. The x axis corresponds to soil carbon content, and the y axis corresponds to soil vertical layers (larger numbers mean deeper soil layers). Different colors correspond to different parameter values. The unit of alt is meter. A similar figure with y axis representing the soil depth (instead of layer numbers) is provided in the supporting information. SOC = soil organic carbon.

3.3. Context‐Dependent Sensitivity From the Northern High Latitudes

We select parameters ins, tau4p, alt, fs2p, and temps in the test focusing on high latitudes. Total SOC stocks from the default model simulation is 1,453 Pg C in the high latitudes. The ins is still the most sensitive parameter, with a reduction of total SOC of 290 Pg C by 20% decrease in ins, followed by alt. Twenty percent decrease in alt reduces total SOC by 236 Pg C. Twenty percent decrease in tau4p, temps, and fs2p reduce total SOC by 190, 173, and 156 Pg C, respectively.

Spatially, the sensitivity to alt is highly variable. The most sensitive regions lie in regions with relatively low alt, for example, the northern end of North America, Asia, and some part of Greenland, where the sensitivity can reach as high as 3.2 times the reference carbon stocks per unit change of alt (Figure 8). And there are also grid cells; for example, some regions of northern Europe show negative sensitivity to alt. In contrast, the sensitivity to carbon input scalar (ins) is relatively uniform across grid cells. The range of sensitivity to temps is next to alt, from 0.02 to 0.92, and the northern part generally has higher sensitivity compared to the southern part of the study region. The sensitivity to tau4p ranges from 0.32 to 0.84, with stronger sensitivity at the northern end of North America, Asia, and part of Greenland. For fs2p, similarly to tau4p, the most sensitive region lies in the northern end of North America, Asia, and some Greenland grid cells.

Figure 8.

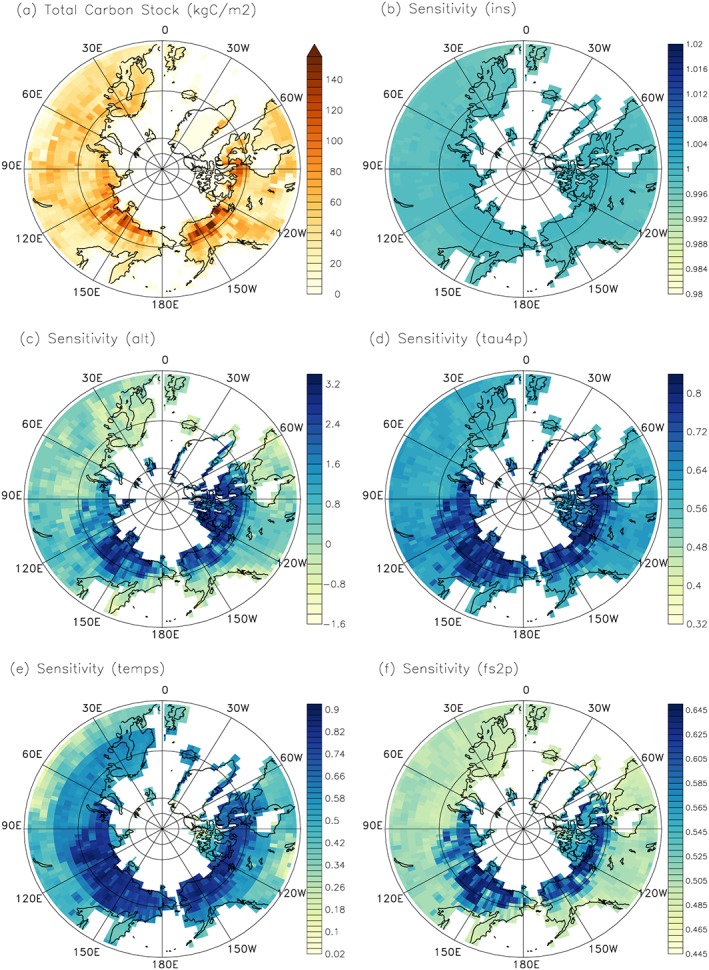
Sensitivity of the high‐latitude (>50°N) total SOC stocks to 20% change in the corresponding parameter. Sensitivity is quantified as the ratio between the change in total SOC and the parameter. (a) Total SOC stock. (b–f) The sensitivity to carbon input (ins), active layer depth (alt), turnover time of passive SOC (tau4p), and the temperature sensitivity (temps) and transfer fraction from slow SOC to passive SOC (fs2p), respectively. SOC = soil organic carbon.

4. Discussion

The matrix approach offers a structured and flexible sensitivity analyzing framework to systematically assess process/parameter sensitivities for complex global land carbon models. The matrix equation reorganizes the original ORCHIDEE‐MICT without simplifying any processes incorporated in the original model, and it is reasonable for the matrix simulation to well reproduce dynamics of the original ORCHIDEE‐MICT (Figures 2 and 3). Through reorganizing, the structure of ORCHIDEE‐MICT gets clearer, and it is relatively easy to isolate each individual process or parameter, to track and understand their complex interactions with other parameters, and to systematically locate relevant parameters that might affect system dynamics through the structured matrix equation (equation (9) and Table 1). For example, it is straightforward from the matrix equation that the sensitivity of the passive SOC to its turnover time interacts strongly with parameters that alter the temperature, moisture, lignin, and clay scalars (equation (9)). We group processes that affect active layer thickness as we are interested in the direct impact from the active layer thickness. Alternatively, it is relatively easy to incorporate the soil temperature‐active layer thickness function and conduct similar analyses to explore other scientific questions; for example, what would be the long‐term impact of a given amount of degrees Celsius warming on SOC stocks through thawing frozen permafrost soil? How much of the temperature response of the carbon cycle comes from direct temperature response of SOC decomposition, and how much of the contribution comes from altered carbon input into SOC pools (indirect response to warming)? In addition to the active layer thickness, we have the flexibility to group other parameters in different ways and trace their sensitivities through different components (carbon input (I in equation (9)), transfer (A), environmental scalar (ξ_TWLCl), potential decomposition rate (K), and vertical mixing (V)) that regulate SOC dynamics based on the skeleton of the system recorded by the matrix equation. Beyond getting piece‐by‐piece information about the sensitivity to a particular parameter, grouping in a process‐based manner provides the flexibility to look into relevant scientific questions through different hierarchy levels, revealing system information from different angles and avoiding misleading information from parameter interactions to a certain level.

On the other hand, the sensitivity analysis illustrated in this study takes advantage of the semianalytical approach to derive the system steady state (Xia et al., 2012), which greatly reduces the computational resource requirement, enables variance‐based sensitivity analysis for global carbon models, and allows to study the model parameter space through different sensitivity indices or for different state variables in great detail. Variance‐based sensitivity analysis provides a detailed picture on sensitivities and interactions among parameters across multidimensional parameter space but is computationally too expensive to apply to complex global land carbon models. Through the matrix representation, we obtain valuable and detailed information on the relative overall importance of each relevant parameter (Figure 4a) and the impact from parameter interactions (Figures 4a and 4b) and differences in sensitivities across SOC types and soil layers (Figures 5 and 6) with the Sobol's indices. In addition to indices illustrated in this study, the matrix representation is also adaptable to different sensitivity testing methods, broadening the range of sensitivity analyses.

Sensitivity analyses for the ORCHIDEE‐MICT model generally show strong controls of carbon input and turnover time on long‐term SOC storage. Litter and SOC representation in ORCHIDEE‐MICT is essentially the vertically discretized CENTURY model. In CENTURY‐like models, carbon input and turnover time are widely recognized as important components controlling soil carbon storage (Todd‐Brown et al., 2013; Xia et al., 2013). Despite the sensitivity analyses in this study being idealized, our sensitivity tests agree with previous understandings. For example, He et al. (2016) revealed that to better fit with the observed ¹⁴C data, the Coupled Model Intercomparison Project Phase 5 model should increase the turnover of the passive SOC (tau4p in our study) and decrease the flux of the slow to the passive SOC (fs2p in our study), both of which are sensitive parameters from our analysis. It also makes sense that the overall sensitivity rank for total SOC is predominantly controlled by passive SOC due to its proportionally large size. Although parameter ranges may affect the absolute value of Sobol indices, the sampling ranges for carbon input scalar we chose are relatively conservative (e.g., the upper range of the carbon input is smaller than what can potentially be produced by ORCHIDEE‐MICT across grid cells), and subsequent regional test also points to the strong model response to carbon input (section 3.3). Sampling ranges for potential turnover times are relatively arbitrary. However, there are no directly observable equivalents for active, slow, and passive SOC pools at the global scale. Sampling ranges are designed to be realistic to cover the space spanned by different grid cells across the globe when there is enough supporting empirical knowledge. For example, we sample the clay content within the minimal and maximum values from the global texture map that drives the simulation (Table 1). Although arbitrary sampling ranges of parameters that are not directly measurable may affect the sensitivity index, our matrix‐based sensitivity assessment approach provides the potential for more comprehensive sensitivity assessment with the accumulation of model‐relevant global scale observations, such as turnover times (e.g., incubation data), temperature and moisture modifiers, and transfer fractions among different SOC categories.

The active layer depth (alt) plays an important role in the vertical distribution of SOC and in the storage of SOC in the northern high latitudes. Despite the fact that the Sobol indices do not pick out alt as a sensitive parameter for total SOC, alt turns out to be important for SOC in different soil layers (Figures 5 and 6) and across the northern high latitudes (Figure 8c). The alt is the key parameter that controls both the vertical carbon input into SOC and the vertical redistribution of SOC through cryoturbation or bioturbation. But the impact of alt is highly interactive and nonlinear (Sobol's total versus single index, Figures 5 and 6). Sobol indices from the idealized simulation may not be adequate in capturing these complex interactions. A shallower alt corresponds to a higher long‐term storage of SOC in surface layers but lower carbon storage in deep soil layers (Figure 7). The impact of alt on the vertically integrated SOC stocks is therefore determined by the balance between the surface and lower layers. Therefore, despite the overall reductions in the total SOC storage over the northern high latitudes, there are also grid cells with enhanced total SOC storage in response to 20% shallower alt (Figure 8c). Note that here we focus on the long‐term (steady state) carbon storage instead of the short‐term response. From observations, the permafrost thaw (or an increase in the active layer depth) increases carbon release and reduces carbon storage (Schuur et al., 2015). This increase in carbon release from observations is a transient response, which is different from the long‐term sensitivity here. The increase in carbon release in thawing permafrost is reflected in the removal of the temperature constraints on decomposition instead of direct control of alt on carbon input and vertical redistribution in the model. And the sensitivity analysis on alt here simplifies the original model by isolating the impact of alt on SOC dynamics instead of simulating alt as a state variable that varies with soil temperature.

Relatively speaking, the model is not sensitive to vertical mixing processes, that is, the cryoturbation or bioturbation except in the deepest soil layer where SOC can reach (the twelfth soil layer), indicating that the original model may lack mechanisms that effectively bury nonrecalcitrant SOC. The vertical SOC distribution is affected by both the vertical input into SOC and the vertical mixing of SOC. Despite the fact that we chose a very high up limit for cryoturbation rate (1 m²/year compared to 0.3–17 cm²/year from empirical data compiled by Koven et al., 2013) or bioturbation rate, the vertical mixing‐incurred SOC flux is still smaller than the decomposition of the passive SOC at each time step. In other words, the turnover time (dividing the carbon pool size by the fluxes caused by vertical mixing) caused by vertical mixing is much longer than decomposition. Therefore, SOC accumulation in the original model is more likely to be associated with the accumulation of passive SOC than burying of fresh SOC, and the latter is supported by empirical evidence and may play an important role such as in SOC stocks in Yedoma (Koven et al., 2015; Strauss et al., 2012; Zhu et al., 2016). Incorporating advection and sedimentation processes into the model is one way to improve the effective burial of nonrecalcitrant SOC (Zhu et al., 2016). A realistic simulation of the environmental conditions as well as the environmental regulation on decomposition is also likely to improve the vertical distribution of SOC. Koven et al. (2013) incorporated a depth modifier, which creates a higher potential decomposition rate in surface soil layers compared to deep layers, to capture the vertical distribution of SOC in addition to the diffusion and advection mechanisms. The rationale behind a depth modifier is to account processes other than temperature, moisture, and anoxia that might limit decomposition. Detailed long‐term observation data, such as cryoturbation, bioturbation, and advection rates along the soil profile, vertical carbon input, decomposition fluxes, and SOC stocks from different soil layers, and their responses to environmental changes from different locations across the globe are valuable for validating these approaches attempted to improve vertical distribution of SOC.

Going beyond previous studies, the matrix sensitivity analyzing framework provides a new angle for future model assessment and intercomparisons. Xia et al. (2013) proposed a traceable framework that diagnostically decomposes the steady state carbon storage into ecosystem carbon input, baseline turnover time, and environmental modifications. Luo et al. (2017) extended the traceable framework and proposed a three‐dimensional parameter space (i.e., carbon input, residence time, and carbon storage potential) to diagnose transient carbon dynamics, which has been applied to analyze uncertainty sources with outputs from 25 models from three model intercomparison projects (MIPs; Zhou et al., 2018). Zhou et al. (2018) attributed more than 90% of the variations in transient carbon storage across three MIPs focusing on nonvertically resolved models to the baseline (climate impact excluded) residence time and ecosystem carbon input. This study expands previous matrix‐based studies by going beyond diagnosing model outputs and through linking original model parameters to model dynamics with a detailed sensitivity analysis. For example, in addition to identify the relative contributions from major components, such as the carbon input and residence time, the sensitivity analyses demonstrated here can potentially provide detailed information on key parameters that regulate the contribution from carbon input or residence time. The sensitivity framework illustrated in this study is therefore unique in providing detailed parametric information and can also easily take advantage of previous diagnosing and traceability theories. Future studies could compare the relative importance (ranks) of different parameters for different models or assess model differences through tracing essential model components (e.g., I, A, ξ_TWLCl,K, and V) and their corresponding key parameters, especially for the vertical component which is currently not fully represented in most MIPs but play a key role in high‐latitude carbon dynamics Mcguire et al., 2016). Different from Zhou et al. (2018) which diagnosed key variables from common model outputs, future applications of this study for model intercomparisons require tracking every detail of the original model, and rewriting the original model into its matrix equivalent is a first step. In addition to the ORCHIDEE‐MICT model, CLM4.5 (Huang, Lu, et al., 2018) and CABLE (Xia et al., 2013) have detailed matrix representations. More global models are planned to adopt the matrix representation after the minisymposium and short training course, New Advances in Land Carbon Cycle Modeling, held in the Northern Arizona University (http://www2.nau.edu/luo-lab/?workshop). With an ensemble of matrices representing carbon models differing in structures and parameterizations, we look forward to a more unified, detailed, and efficient future model intercomparison and assessment with the help of the matrix sensitivity analyzing framework.

5. Conclusions

We built a matrix‐based sensitivity assessment framework to help the land carbon community to better understand modeled carbon dynamics. Taking the ORCHIDEE‐MICT model as an example, we generated one matrix equation that reproduces the spatial‐temporal dynamics of the original model simulation. The matrix equation enabled systematic and complex sensitivity assessment with its clear structure and computational efficiency. The variance‐based sensitivity analysis (Sobol's method) reveals that similarly to the nondiscretized soil carbon model, ORCHIDEE‐MICT is highly sensitive to carbon input and turnover time. In addition, the active layer depth of the last year (alt) is critical in controlling the vertical distribution of SOC as well as the total SOC stock in the northern high latitudes. Regions currently with low active layer depth (e.g., the northernmost part of America, Asia, and some Greenland regions) is most vulnerable to alt‐associated SOC changes. And the impact of alt is highly interactive and nonlinear, which requires special attention in future model analyses. Cryoturbation plays a less important role due to its small impact compared to vertical litter carbon input represented in the original model. And current vertical mixing mechanisms need to be strengthened to realistically represent the effective burial of nonrecalcitrant SOC.

Supporting information

Supporting Information S1

Huang, Y. , Zhu, D. , Ciais, P. , Guenet, B. , Huang, Y. , Goll, D. S. , et al. (2018). Matrix‐based sensitivity assessment of soil organic carbon storage: A case study from the ORCHIDEE‐MICT model. Journal of Advances in Modeling Earth Systems, 10, 1790–1808. 10.1029/2017MS001237