Predicting ICU readmission using grouped physiological and medication trends

Abstract

Background:

Patients who are readmitted to an intensive care unit (ICU) usually have a high risk of mortality and an increased length of stay. ICU readmission risk prediction may help physicians to re-evaluate the patient’s physical conditions before patients are discharged and avoid preventable readmissions. ICU readmission prediction models are often built based on physiological variables. Intuitively, snapshot measurements, especially the last measurements, are effective predictors that are widely used by researchers. However, methods that only use snapshot measurements neglect predictive information contained in the trends of physiological and medication variables. Mean, maximum or minimum values take multiple time points into account and capture their summary statistics, however, these statistics are not able to catch the detailed picture of temporal trends. In this study, we find strong predictors with ability of capturing detailed temporal trends of variables for 30day readmission risk and build prediction models with high accuracy.

Methods:

We study physiological measurements and medications from the Multiparameter Intelligent Monitoring in Intensive Care II (MIMIC-II) clinical dataset. Time series of each variable are converted into trend graphs with nodes being discretized measurements of each variable. Then we extract important temporal trends by applying frequent subgraph mining on the trend graphs. The frequency of a subgraph is a good cue to find important temporal trends since similar patients often share similar trends regarding their pathophysiological evolution under medical interventions. Important temporal trends are then grouped automatically by non-negative matrix factorization. The grouped trends could be considered as an approximate representation of patients’ pathophysiological states and medication profiles. We train a logistic regression model to predict 30-day ICU readmission risk based on snapshot measurements, grouped physiological trends and medication trends.

Results:

Our dataset consists of 1,170 patients who are alive 30 days after discharge from ICU and have at least 12 hours of data. In the dataset, 860 patients were not readmitted and 310 were readmitted, within 30 days after discharge. Our model outperforms all comparison models, and shows an improvement in the area under the receiver operating characteristic curve (AUC) of almost 4% from the best comparison model.

Conclusions:

Grouped physiological and medication trends carry predictive information for ICU readmission risk. In order to build predictive models with higher accuracy, we should add grouped physiological and medication trends as complementary features to snapshot measurements.

1. Introduction

The cost of critical care is increasing annually. From 2000 to 2005, the annual cost of critical care in the US increased from $56.6 to $81.7 billion (by 44.2%) and in 2005, the critical care cost accounted for 13.4% of hospital costs [1]. While discharging patients from an Intensive Care Unit (ICU) at an early time may have a significantly impact on reducing hospital costs, premature discharges may lead to deterioration of patient health or adverse outcomes, and in turn, readmission. Previous studies have shown that almost a third of readmissions are due to premature discharge [2, 3]. Reducing the rate of premature discharge has become an important concern of hospitals and it has been used as one of the top indicators for ICU quality [4].

From a clinical perspective, patients who are readmitted to an ICU usually have a high risk of mortality and an increased length of stay, compared with the first admission [3]. Some readmissions might be avoided if physicians could re-evaluate patients who have high readmission risk before discharging them. On the other hand, physicians may discharge patients with low readmission risk from ICUs at the earliest appropriate time to reduce critical care costs and make room for more severely sick patients. Furthermore, eliminating unnecessary ICU stays may also help to reduce the rate of specific ICU-related complications [5]. Therefore, estimating the readmission risk of ICU patients is of critical importance for the consideration of both the health of patients and the critical care costs for hospitals. ICU readmission prediction is an effective way to determine the risk of a patient’s readmission and can be used to help physicians to make appropriate decisions of discharge.

In this work, we hypothesize that information hidden in temporal trends of physiological and medication variables is predictive for ICU readmission risk, as it could be considered as a representation of a patient’s health trend. We adapt the Subgraph Augmented Non-negative Matrix Factorization (SANMF) algorithm [6] and apply it for 30-day ICU readmission risk prediction. In addition, we perform comparisons between using temporal trends and using only snapshot measurements, and between using grouped temporal trends and using temporal trends directly. Our model, using a comprehensive feature set, including the snapshot measurements and the grouped temporal trends, outperforms other comparison models by demonstrating an improvement in AUC.

The contributions of this work are summarized as follows. To the best of our knowledge, grouped physiological and medication trends have not yet been used in ICU readmission risk prediction. Additionally, we perform a comprehensive comparison between models using different types of features including snapshot measurements, temporal trends and grouped temporal trends. As a result, we show that grouped temporal trends of physiological measurements and medications carry predictive information for ICU readmission risk and can be used as complementary features to improve performance of predictive models. Along the way, we study the impact of different imputation techniques and develop a tailored methodology that outperforms all other state-of-the-art approaches.

The remainder of this paper is structured as follows. Section 2 discusses related work while in Section 3, the proposed method is described, as well as the cohort selection and the strategy of model evaluation. The computational results and the underlying analyses are discussed in Section 4. Section 5 addresses the limitations of this study and future work, and the conclusions are drawn in Section 6.

2. Related Work

Research in building accurate ICU readmission prediction models has attracted growing interest in recent decades. Some early efforts in ICU readmission risk prediction consider a specific population, such as elderly patients (over 65 years old) or patients with cardiac or respiratory problems [7–19]. These specific populations may have limited the generalizability of the above methods. Several other studies predict ICU readmission mainly based on non-physiological variables [20–25]. These methods used patient characteristic variables, including race, income and social status (e.g., living alone). Most of the works above used their own institutional data [7–9, 11, 12, 14, 16, 18, 19, 23–25]. The rest of them used different public data sources, such as American Hospital Association Annual Survey Database and Statewide Planning and Research Cooperative System (SPARCS) database [10, 13, 15, 17, 20–22]. In recent years, research in seeking predictive physiological variables for readmission risk has drawn more interest and the MIMIC-II (The Multiparameter Intelligent Monitoring in Intensive Care) database [26, 27] has become a common choice for such studies. The MIMIC-II clinical database is a publicly available database containing physiological signals and comprehensive clinical data for a cohort of ICU patients. We use the MIMIC-II dataset in our study.

Previous studies in predicting ICU readmission risk using the MIMIC database build models mainly based on physiological measurements. Fialho et al [28] applied fuzzy modeling with tree search feature selection to the MIMIC-II clinical dataset for 24–72 hours ICU readmission risk prediction. The most predictive variables found by Fialho et al include: the mean heart rate, mean temperature, mean spO2, mean non-invasive arterial blood pressure, mean platelets and mean lactic acid. The mean values of these variables are calculated within the last 24 hours before discharge. Missing data of a variable are imputed with the last valid measurement. In the following few years, several methods were proposed to develop the application of fuzzy modeling on ICU readmission prediction. Fernandes et al [29] developed a multi-model approach using the 6 most predictive physiological variables found by Fialho et al [28]. Vieira et al [30] proposed a test-driven model where they used the medical text reports in the MIMIC-II dataset that presented some particular characteristics. They used a refined data selection process where patients with any variable missing from a predefined feature set were excluded. This predefined feature set consists of 23 manually selected physiological variables that are easily assessed in the 24 hours before discharge. They performed the tree search feature selection and found 6 best variables, which were the same as those found by Fialho et al in [28]. Curto et al [31] used another text resource -- bedside medical text notes written by physicians or nurses, to explore complementary features for a set of 7 physiological variables (heart rate, temperature, platelets, noninvasive blood pressure mean, oxygen saturation in the blood, lactic acid and creatinine), which were determined as important predictors for readmissions by Carvalho et al [32]. Curto et al also used the mean values of physiological measurements. These methods use manually selected physiological variables, related medical text reports or bedside medical text notes. Despite the improvement of AUCs, these methods suffer from neglecting predictive information within trends of physiological variables since they use the snapshot measurements or summary statistics such as mean values. Additionally, in the data preprocessing step of these methods, the elimination of patients with missing values and outliers might have biased their study. To address these problems, we study temporal trends of physiological measurements and medications, and use them to improve the performance of ICU readmission risk prediction models.

Recently, the PhysioNet/Computing in Cardiology Challenge 2012 developed methods for the prediction of in-hospital mortality on the MIMIC-II dataset [33–44]. The data consists of 36 physiologic time series. McMillan et al [33] used temporal pattern mining to explore the approach of discovering short characteristic patterns (i.e. time series motifs). Temporal pattern mining has been used in several ICU mortality prediction studies to discover time series patterns [45, 46]. Hug et al [45] manually selected a set of temporal patterns considering a comprehensive set of variables. Cohen [46] et al used pattern recognition to identify physiologic patient states with hierarchical clustering. Luo et al [6] proposed an unsupervised feature learning algorithm to predict 30-day ICU mortality risk. Instead of using temporal pattern mining, they adapted frequent subgraph mining to extract common temporal trends. A time series abstraction is used to capture the temporal trends of variables [47–51]. They represent the time series of each variable as a graph, where each node is the measurement of a variable at each time point. The same representation of time series is used in this work to capture the temporal trends. However, instead of predicting 30-day mortality risk, the goal of our study is to predict ICU readmission risk within 30 days after discharge. To this end, we additionally use the medication trends to complement the physiological trends. Furthermore, Luo et al used linear imputation to address missing values. In this work, we perform a comprehensive comparison between several widely-used imputation methods on their impact to our predictive models and develop a customized linear interpolation that is designed for the MIMIC-II dataset.

3. Methods

3.1. Patient Cohort

We use the MIMIC-II dataset [26] collected from a variety of ICUs between 2000 and 2008. The dataset consists of detailed information about ICU patients’ stays including time series of physiological measurements and medication variables. We select 53 physiological variables, 21 medication variables and age of patients. A detailed description of variables is given in Appendix A. We only include patients who have recorded readmission time after being discharged from their first admission. Each patient must have at least 12 hours of data since we use data from the last 12 hours before discharge to train our models. We select 1,170 patients that satisfy our criteria. In our cohort, 860 patients were not readmitted within 30 days and 310 were readmitted within 30 days.

3.2. Design

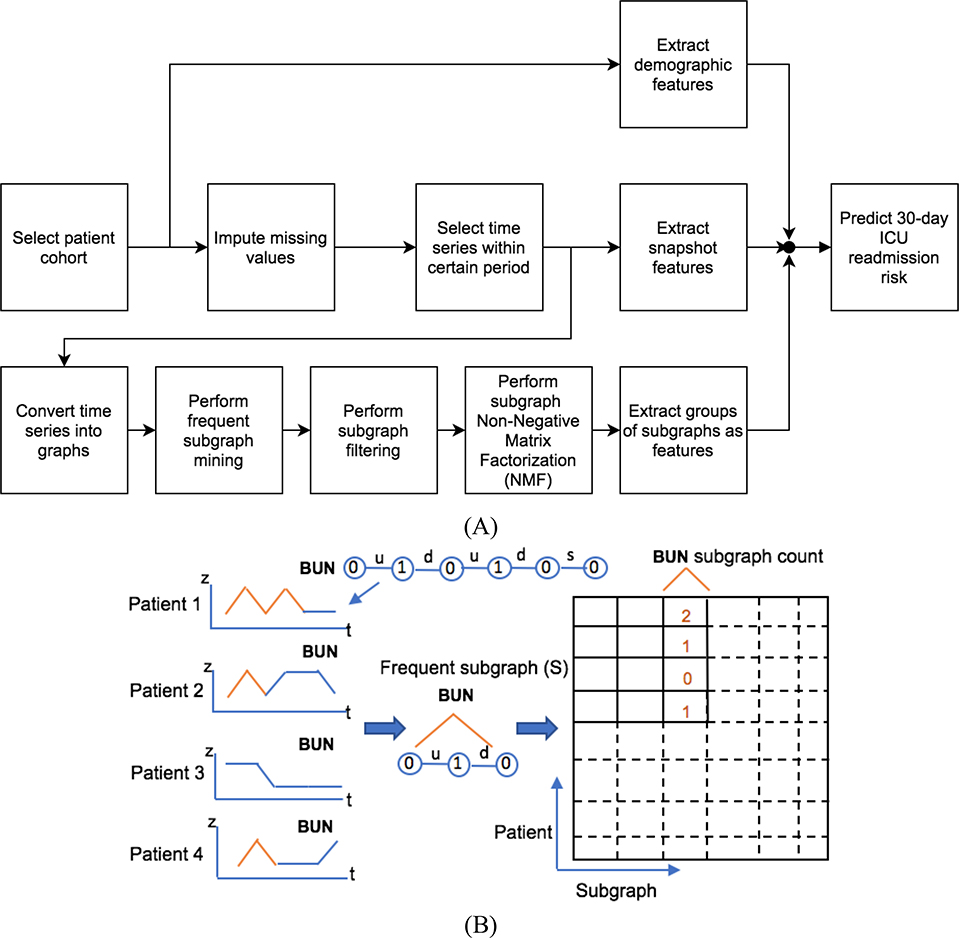
Intuitively, values from the last valid measurements of variables reflect patients’ health effectively and have been commonly used by researchers. Therefore, we build a baseline model that used the last measurements as predictors. This model serves as a baseline to evaluate the performance of other models in predicting 30-day ICU readmission. In this work, we study physiological and medication trends, and use a comprehensive feature set that combines snapshot measurements and temporal trends, in order to build more accurate machine learning models. The methodology of converting time series data into temporal trends follows the SANMF algorithm [6] and is detailed later, see Fig. 1(a). We convert patients’ time series into graphs, where each node represents a discretized measurement at a single point in time. Among these graphs, we discover the most important subgraphs and identify them as common temporal trends. In this representation, temporal trends are encoded by subgraphs and we use the terms “subgraph” and “temporal trend” interchangeably in later discussions. We study the correlation between the important subgraphs, group them and use the groupings as an augmentation to snapshot features in building predictive models.

Fig. 1.

(A) The flowchart of proposed approach, moving from selecting data to predicting readmission risk. (B) An example of creating matrix of common subgraphs. Only the Blood Urea Nitrogen (BUN) trend graph for patient 1 is shown (BUN 0 1 0 1 0 0). The frequent subgraph is (BUN 0-u-1-d-0), noted as S. Patient 1 has two frequent subgraphs S; patients 2 and 4 have one; and patient 3 has no S. The edge labels, “u,” “d” and “s,” are short for “up,” “down” and “same,” respectively.

3.3. Data Preprocessing and Imputation

Measurements in the collection of time series are often sparse. In total, about 23.6% of values in our dataset are missing. Eliminating patients with incomplete data may bias our study. Therefore, imputation becomes an essential step of the data preprocessing. We try several different imputation techniques, including mean value imputation and a more sophisticated imputation method called Multivariate Imputation by Chained Equations (MICE) [52]. The effectiveness of each imputation method is evaluated by the performance of our prediction models. In this work, we introduce an imputation method that is designed for temporal data, called customized linear interpolation.

Let X_p be the set of measurements of variable X for patient p and let m be the last valid measurement of X_p. Assuming m is the measurement at time t, we replace the missing values of X_p after time 𝑡 with measurement m; we use standard linear interpolation to replace the missing values of X_p that are before time t. For variables of patient p that have no valid measurement, we replace missing values with mean values. After imputation, we extract the last 12 hours of data before discharge for each patient.

3.4. Converting Time Series into Graphs

The basic idea of converting time series into graphs is to represent measurements with labeled nodes and connect them in order of time by labeled edges. Five different discrete levels (0, ±1 and ±2) are used to label the nodes and are discretized using the z-score [53] of the corresponding measurements of the nodes. The z-score _Zj of measurement X_j is calculated by:

$$Z_j=\left(x_j-{\mu }_x\right)/{\sigma }_x$$

where μ_x and σ_x are the mean and deviation of measurements of variable x across all patients and time points. If X_j is within the one σ_x range (−1 < _Zj < 1), we choose label of 0; if X_j is beyond the one σ_x range but within the two σ_x range (−2 < _Zj ≤ −1 or −2 < _Zj ≤ −1), we choose label ±1; otherwise we choose label ±2, which means X_j is beyond the two σ_x range. Three edge labels are used to indicate changes between two adjacent nodes: up, down and same. Considering the fact that the time series of physiological variables in the MIMIC-II dataset are often sparse and sampled irregularly, before converting them into graphs, we discretize the time axis by interpolating time series linearly and resampling them at equally spaced intervals. The length of intervals is determined by performing 5fold cross-validation over choices of 1,2,3,4,6 or 12 hour intervals, which yields the 2-hour interval as the best. As a result, the graphs are sequences of 6 time intervals, since we use 12 hours of data. An example of the graph for a patient is shown in Fig. 1(b).

3.5. Frequent Subgraph Mining

After representing time series (trends) with graphs, we explore important common trends across patients for each variable. Intuitively, similar patients tend to experience similar physiological trajectories during their ICU stays. Thus, common trends are helpful to characterize similar patients. The frequency of a subgraph is a good cue for seeking important common trends. The purpose of Frequent Subgraph Mining (FSM) is to discover subgraph structures that occur a significant number of times across a set of graphs. One essential concept in FSM is subgraph isomorphism. Assuming two graphs G and H are given, if G contains a subgraph that is isomorphic to, then H is subisomorphic to G. In our work, we use Molecular Substructure miner (MoSS) [54] to discover frequent subgraphs. The threshold of frequency is a parameter of MoSS and only the subgraph whose occurrence is above the threshold is selected. The threshold is determined by performing 5-fold cross-validation over choices from 1 to 12 for each model. It turns out that subgraphs that occur at least 11 times are the most suggestive for important common trends in our best model.

3.6. Subgraph Filtering

Next, we count the number of frequent subgraphs for each patient and create a patient-subgraph matrix, where each entry specifies the number of times that a certain temporal trend (subgraph) occurs during that patient’s stay, see Fig. 1(b). Note that the subgraphs of a frequent subgraph are also frequent. Since a larger frequent subgraph already contains the information in its own subgraphs, we only count maximal frequent subgraph that are not a subgraph of others. Another reason for using this counting strategy is that if we count both the larger subgraph and its own smaller subgraphs, the signal of the larger one might be overwhelmed by the signal from the smaller subgraphs thus yielding less predictive models.

3.7. Subgraph NMF (Non-Negative Matrix Factorization) and Groups

We may use temporal trends (columns of the patient-subgraph matrix in Fig. 1(b)) directly as features to train statistical models, however, using temporal trends directly has two drawbacks: 1) the huge number of temporal trends usually causes overfitting problems; 2) treating trends independently cannot effectively reflect a patient’s pathophysiological trajectory. The latter is because a patient often experiences an underlying pathophysiological condition involving multiple variables and even multiple organs. On the other hand, one abnormal physiological variable may have various implications. For example, a low hematocrit may be linked to blood loss, bone marrow problems, kidney problems, and a variety of other problems. Thus, it is more consistent with medical practice to establish a panel of pathophysiological trends as a feature for predictive modeling.

Inspired by the observation that a group of physiological trends usually shows a patient’s underlying pathophysiological evolution, we apply Non-Negative Matrix Factorization (NMF) on our patient-subgraph count matrix to group temporal trends. Another motivation of using NMF is that we aim at counting data which are non-negative numbers. Additionally, Hofree et al. [55] have shown that NMF is an effective method to cluster similar patients. Let V be our patient-subgraph count matrix, which has M patients and N subgraphs. NMF approximates V using two matrices W and H (V ≈ W ∙ H) by minimizing the error function: min_W,H||V − WH||_F, subject to W ≥ 0, H ≥ 0. Matrix W is an M × S matrix and H is an S × N matrix, where S is the number of subgraph groups. Parameter S is determined by performing 5-fold cross-validation over choices from 10 to 120 (in increments of 10) with the value of 110 being best for our best model. Each row of H can be interpreted as the composition of each subgraph group. Each column of W can be viewed as a mixture of subgraph groups for each patient.

The mixture of subgraph groups specified in weight matrix W are used as features in machine learning models. We split V into a training and validation part and calculate the weight matrix W_tr and W_va separately. Then our model is trained on the training set W_tr and evaluated on the validation set W_va. We tried several machine learning models, such as logistic regression, SVM (Support Vector Machine), random forest and an artificial neural network, with default parameters on our dataset. The logistic regression works best no matter what snapshot measurements or temporal trends are used as features. We decided to only focus on logistic regression as experiments on all these models involve too many parameters to tune.

3.8. Model Evaluation

3.8.1. Cross-validation

To evaluate the performance of our model, we perform 5-fold cross-validation. Our dataset with 1,170 patients is spilt into 5 folds. In one round of cross-validation, one of the five folds is treated as the validation set and the other four folds serve as the training set. The logistic regression model is built on the training set and evaluated on the validation set. Five rounds of cross-validation are performed, each time with one of the five different validation datasets, and the validation results are combined over rounds. Additionally, in order to make sure that our model does not gain any knowledge from the validation set in the subgraph mining procedure, we perform FSM on training and validation sets separately. To achieve this, we find frequent subgraphs from the training set first and treat them as a fixed subgraph set. Then we perform FSM on the validation set and only select those existing in the fixed subgraph set. Furthermore, the imputation is also done separately on training and validation sets.

3.8.2. Comparison Models

We evaluate our model by comparing its performance with the following comparison models: (1) the “baseline model,” a logistic regression model using only snapshot features, specifically the last measurements; (2) the “subgraph model,” using subgraphs directly as features; (3) the “subgraph + snapshot model,” combining features from the baseline and subgraph models; (4) the “grouping model,” using only grouped subgraphs as features. Our model uses both snapshot features and grouped subgraphs and thus it is labeled as “grouping + snapshot.” We do not use summary statistics (e.g. mean, max and min) as features because subgraphs capture detailed temporal trends. In other words, our model considers summary statistics implicitly.

4. Results

4.1. Model Evaluation

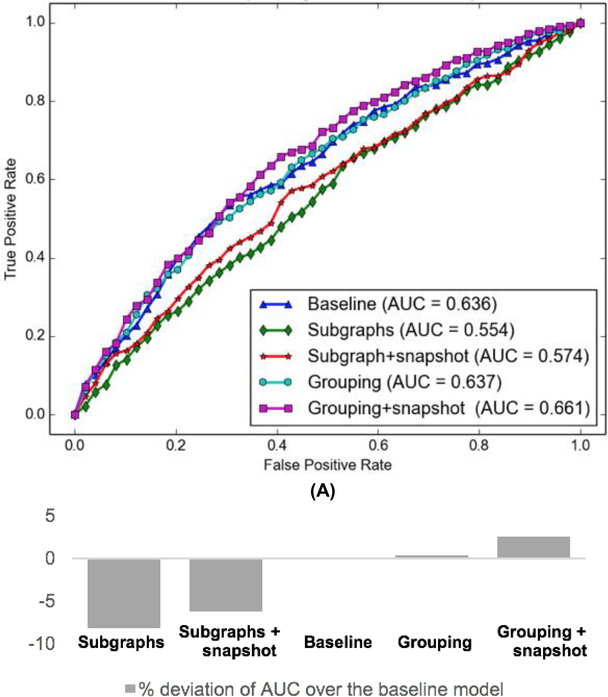
The receiver operating characteristic (ROC) curve of our model and comparison models are shown in Fig. 2(a). The baseline model achieves an AUC of 0.636 which is only outperformed by the “grouping” and “grouping + snapshot” models. The grouping model achieves an AUC of 0.637. Our model referred to as the “grouping + snapshot” model gives the best performance with an AUC of 0.661, significantly better (and statistically significant with p < 0.001 by the random permutation test [56]) than the second-best model with an AUC of 0.637. The AUC percentage deviation of all 5 models over the baseline model are shown in Fig. 2(b).

Fig. 2.

(A) ROC curves of different ICU readmission risk predictive models. (B) Percentage deviation of AUC over the baseline model.

All the experiments were done on a 32GB RAM Linux server with 4 2.8GHz cores with the code written in Python. NMF with 110 groups takes 607.7 seconds and FSM with the frequency of 11 takes 94.9 seconds in total for 5-fold cross-validation.

4.2. Important Groups

The important groups of temporal trends discovered by our model could not only be used as strong features to build predictive models, but also help physicians to determine the patients’ current health condition and make better discharge decisions. In Table 1, we list top ranked temporal trend groups based on the value of the coefficient of a group in the NMF matrix. Group 1 is the first ranked group relating to patients that were not readmitted within 30 days. Group 2 is the first ranked group relating to patients readmitted within 30 days. Variables in group 1 tend to have a trend to a better state, such as Saturation of arterial oxygen (SaO2) (0 1 1 0), Respiratory rate (−1 0) and Anticoagulant (1 1 1 1 1 0). There is no variable that indicates a severe health state as well, such as a sequence containing several nodes with label 2 or −2. Therefore, group 1 could be an effective predictor for non-readmission patients. Intuitively, a predictive trend group for patients with high readmission risk should contain trends toward a worse health state. For example, in Group 2, patient’s Lactate shows a severe trend (2 2 2 2 2 2), which likely reflects the buildup of lactate in the body. Although two trends going toward a better state are included in this group, the probable lactic acidosis condition together with continuously abnormal hemoglobin, red blood count etc. do not bode well for the patient. This analysis attests that discharging patients with deteriorating trends is an indicator for readmission.

Table 1.

Temporal trend groups with low and high readmission risk.

Group 1 - non-readmission group
0.0174	Location	1 1 1 1 1 1
0.0164	SaO2	0 1 1 0
0.0159	Respiratory rate	−1 0
0.0141	Respiratory rate	0 −1 0 −1
0.0114	Glucose	1 1 1 1 1 1
0.0113	Anticoagulant	1 1 1 1 1 0
0.0085	MetCarcinoma	1 1 1 1 1 1
0.0080	Heart Rate	−1 −1 0 −1 −1
0.0078	Systolic blood pressure	1 0
0.0078	SaO2	1 1 0 1
0.0068	Diastolic blood pressure	−1 −1 0 −1 −1
Group 2 - readmission group
0.2407	Hemoglobin	−1 −1 −1 −1 −1 −1
0.2043	Red blood count	−1 −1 −1 −1 −1 −1
0.0146	Hematocrit	−1 −1 −1 −1 −1 −1
0.0120	Mg	1 1 1 1 1 1
0.0099	Lactate	2 2 2 2 2 2
0.0092	Minute Ventilation	1 1 1 1 1 1
0.0069	Central Venous Pressure	0 1 0
0.0068	K	1 0
0.0066	SaO2	0 −1 −1
0.0064	Central Venous Pressure	−1 −1
0.0062	Heart Rate	1 1 1 1 1 1

Each trend is represented by a sequence, e.g. “0.2407 Hemoglobin −1 −1 −1 −1 −1 −1,” where 0.2407 is the membership coefficient (the component weight in NMF model), Hemoglobin is the name of measurement and “−1 −1 −1 −1 −1 −1” is the trend. Abbreviations used in the table include: SaO2 -- Saturation of arterial oxygen; MetCarcinoma -- Metastatic Carcinoma; Mg – Magnesium level; K – Potassium level.

4.3. Subgraph Analysis

In our early models, we count all frequent subgraphs and our grouping model only achieves an AUC of 0.602. This motivates us to perform an analysis on subgraphs and develop methods to enhance the strength of subgraphs.

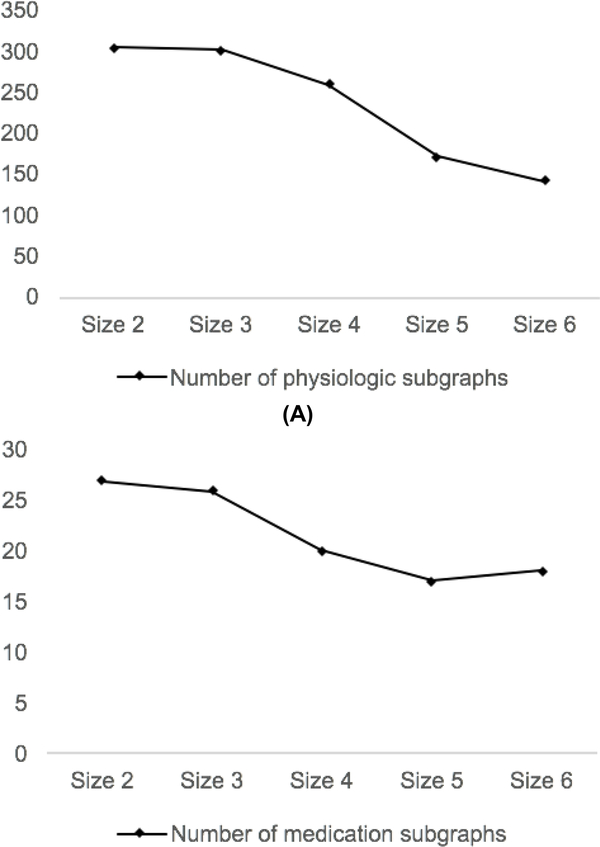
The numbers of frequent subgraphs of different sizes are shown in Fig. 3. The size of a subgraph is the number of nodes in the subgraph. Intuitively, it is much harder for larger subgraphs to become frequent than smaller subgraphs. However, the number of subgraphs decreases slower than we expect as the size increases, especially in medication subgraphs. To explain the unexpected trends, in Fig. 3, we perform an analysis on the frequent medication subgraphs. We observe that the frequent medication subgraphs could either indicate stable trends (e.g. “Insulin 0 0” and “BUN 1 1 1 1”) or unstable trends with one change (e.g. “Insulin 0 1” and “BUN 1 1 1 0”). None of the temporal trends that have more than one change are frequent. Overall, only about one fifth of the frequent medication subgraphs indicate unstable trends.

Fig. 3.

Relation between subgraph size and number of distinct subgraphs.

For medication subgraphs that have more than 3 nodes, almost all of them indicate stable trends. Having the knowledge that if a subgraph indicating a stable trend is frequent, its subisomorphic graphs are frequent as well, we should have a large number of subisomorphic subgraphs, due to the fact that most of the frequent subgraphs indicate stable trends. Therefore, one explanation for the unexpected trend of the number of frequent subgraphs shown in Fig. 3 is that most of the small subgraphs are subisomorphic to some larger frequent subgraphs. In this scenario, the large amount of smaller subisomorphic subgraphs could have a significant influence on the performance of our model, since the signals from the larger frequent subgraphs might be overwhelmed by those from smaller ones. Therefore, we only count the maximal frequent subgraph that are not a subgraph of others. As a result, the patients’ average count of subgraphs drops from 143 to 20. In our experiment, the AUC of our grouping model is improved from 0.602 to 0.637 by filtering out smaller subisomorphic subgraphs.

5. Discussion

5.1. Error Analysis

Our best model demonstrates a sensitivity of 57.1%, specificity of 65.7%, positive predictive value (PPV) of 37.5% and negative predictive value (NPV) of 80.9%. The confusion matrix from 5-fold crossvalidation is show in Table 2.

Table 2.

Confusion matrix of our best model.

	Predicted: Non-readmitted	Predicted: Readmitted
Actual: Non-readmitted	565	295
Actual: Readmitted	133	177

To have a better understanding of why our model sometimes fails in making correct predictions, we select 17 patients who have been wrongly classified by our best model, from all validation sets. Of these 17 patients 3 patients were readmitted and 14 were not readmitted (ground truth). Our best model predicted those, who were actually readmitted, as having a very low readmission risk (predictive score lower than 0.2) and predicted those, who were not readmitted, as having a very high readmission risk (predictive score higher than 0.8). We observe that the average length of stay of these 17 patients is 104 hours, while the average length of stay of all patients is 73 hours. The poor performance of our model on these 17 patients, whose average length of stay is above the average level of all patients, motivates us to analyze the impact of the length of stay on our model.

Fig. 4 shows the relationship between length of stay and the ratio of patients that are correctly classified. Despite an increment from 3- to 4-day stay, the overall trend of the ratio is decreasing. The ratio drops from 0.683 for patients who stayed in an ICU less than 1 day to 0.566 for patients whose length of stay were 7 days or more. Since our model only considers trends during the last 12 hours, the trends captured by our model might be less representative of the trends throughout the entire ICU stays, especially for patients having a longer length of stay.

Fig. 4.

Number of correctly and wrongly classified patients with different length of stay.

5.2. Impact of Imputation on Model Performance

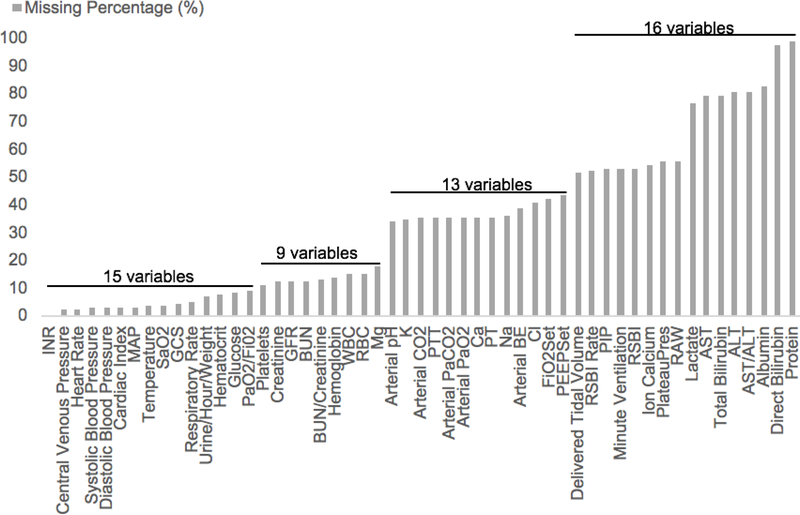
The dataset contains a large portion of missing values. Among the 53 physiological variables, only one of them has no missing values, 15 of them have less than 10% missing values and 29 (53.7%) of them have over 30% missing values. There are 16 variables that have even more than 50% missing values. The percentage of missing values for each physiological variable is shown in Fig. 5.

Fig. 5.

Percentage of missing values of each variable.

Using different imputation techniques could lead to different prediction results. To reduce variability of different imputation, we tried several widely-used imputation methods. The effectiveness of each imputation method is evaluated by the performance of our prediction models. We test the performance of imputation methods on both the grouping and “grouping + snapshot” models. The grouping model could work with missing values by discarding graphs that contain nodes without a value. Without imputation, the grouping model only achieves an AUC of 0.592, which motivates us to look for a proper imputation method. MICE (Multivariate Imputation by Chained Equations [52]) is a multivariate imputation model based on chained equations. Using MICE to replace missing values improves the performance of the grouping model to the AUC score of 0.619.

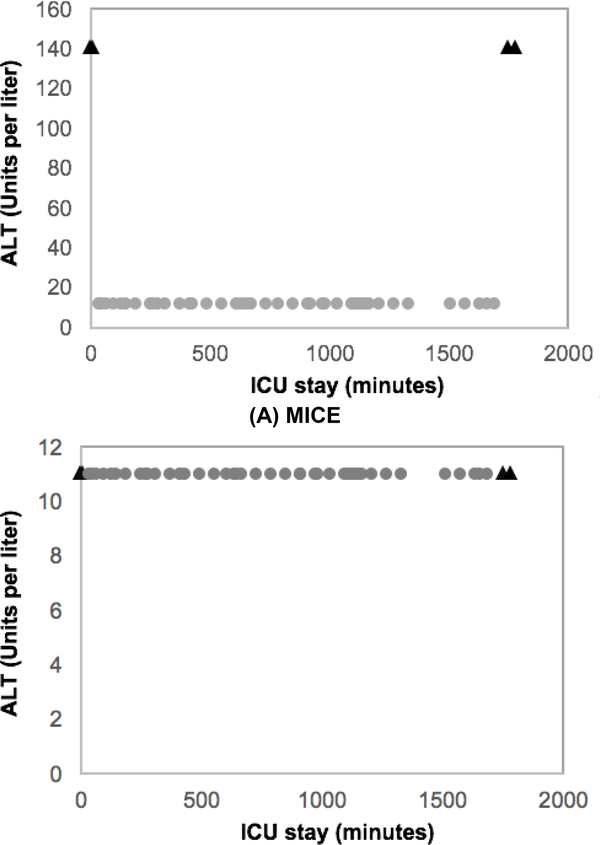
By manually checking the imputed values, we found that MICE failed to impute temporal data in many cases. As an example (see Fig. 6), the imputed values by MICE cause sharp changes in the trends, which might suggest that these imputed values are unreasonable, because the observed values show that the alanine aminotransferase in blood (ALT) of this patient is in a stable status. The observed measurements of a few variables, including the rapid shallow breathing index rate change (RSBI Rate), the prothrombin time international normalized ratio (INR) and the fraction of inspired oxygen set on ventilator (FiO2set), of this patient show sharp changes at the very beginning and end of the trends. We also noticed that a group of other patients experienced some sharp changes, which might be captured by MICE and used as a pattern to replace missing values in ALT. However, sharp changes seldom occur at the very beginning or end of the ALT trends in our dataset. The imputed values for another 10 variables of this patient show similar patterns as ALT. These sharp changes caused by the imputed values could be an explanation of the poor performance of the model using MICE imputation.

Fig. 6.

ALT measurements. X-axis is time and Y-axis is value. Triangles are imputed values. Circles are observed values.

To address this problem, we have tried several strategies of imputing missing values. One strategy is breaking up the time axis into intervals before performing MICE imputation. The value of an interval is the average of all measurements within this interval. By breaking the time axis into intervals, variable trends become smoother. We could expect less sharp changes caused by the imputed values if the patterns of time series captured by MICE are smoother. As shown in Table 3, by using this strategy, referred to as MICE-interval, the grouping model achieves an AUC of 0.612, which is worse than performing MICE directly. However, the “grouping + snapshot” model is improved to an AUC of 0.627 by using this strategy, compared to the AUC of 0.625 from the model where we perform MICE directly. We have also tried to perform MICE on standardized data. As a result, the performance of the “grouping + snapshot” model is slightly improved (0.630 of MICE-interval-norm vs. 0.627 MICE-interval and 0.639 of MICE-norm vs. 0.625 of MICE). Another strategy is to use the customized linear interpolation, so that we could maintain the current trends in the imputed values. In our experiment, the customized linear interpolation works better than MICE by showing an improvement in the AUC score of both the grouping model (0.637 vs. 0.619) and the “grouping + snapshot” model (0.661 vs. 0.639). A list of performances of the grouping and “grouping + snapshot” models based on different strategies of imputation are shown in Table 3.

Table 3.

Performance of the grouping and “grouping + snapshot” models based on different imputation methods.

Imputation Methods	AUC of Grouping Model	AUC of Grouping + Snapshot Model
No Imputation	0.592	NA
Mean	0.620	0.637
MICE-interval	0.612	0.627
MICE-interval-norm	0.610	0.630
MICE	0.619	0.625
MICE-norm	0.611	0.639
Customized Linear Interpolation	0.637	0.661

5.3. Summary, Limitation and Future Work

In this study, we use the MIMIC-II dataset and build logistic regression models to predict the risk of 30-day ICU readmission. We discover risk-predictive features in time series for readmission and provide a grouping method to enhance temporal trend features. Our model outperforms other comparison models by using augmented temporal features.

Our model can be considered as a pilot study that focuses extensively on physiologic variables’ predictive power on the long standing difficult readmission management problem. Besides physiologic variables, other features including procedures, medications, and length of stay (LOS) may also add to readmission prediction. On the other hand, our methodology is very general and if additional features are available, the same model and methodology would apply with necessary adaptation.

This study adds to the current knowledge in several ways. First, we build a logistic regression model that takes advantage of physiological and medication time series to predict 30-day ICU readmission risk. The state-of-the-art ICU readmission prediction methods use the last valid measurements or the summary statistics (e.g., mean, max, min) of physiological variables during a patient’s ICU stay. In this work, we provide a method to utilize the temporal trends in time series of physiological variables to build a more accurate predictive model. Our model outperforms the baseline model that only uses the snapshot features, suggesting that the temporal trends carry predictive information for ICU readmission risk.

Second, our model can discover important groups of temporal trends that could help physicians to determine the patients’ current health condition and make better discharge decisions. Physicians may re-evaluate patients who are predicted by our model as having a high risk of readmission before discharging them. In addition to simply relying on the predictions, physicians can also check the temporal trends in the important groups discovered by our model (e.g., continuous lactic acidosis). Discharging patients with deteriorating trends more likely leads to readmissions, even for patients that show some improvements at the time of discharge. Our model encourages physicians to take a closer look at those patients who have some physiological variables deteriorating, to make further inspections and to reconsider the decision of discharge.

Third, we perform extensive analyses on the impact of subgraph filtering on the predictive models. Subgraph filtering solves two major problems in predictive models that use subgraphs as features: model overfitting and signal overwhelming. Here, signal overwhelming is the problem that signals from important subgraphs are overwhelmed by redundant subgraphs and then hard to be captured by predictive models. Our experiments show that subgraph filtering is an essential step and has a significant impact on our predictive models.

Furthermore, we introduce an imputation method called customized linear interpolation that is designed for temporal data. Our experiments show that some imputation methods work well on replacing missing values in snapshot measurements but not on temporal data, suggesting that the temporal pattern needs to be taken into consideration in imputation. We also perform comparisons between several widely-used imputation methods and perform extensive analysis on the impact of imputation on predictive models.

Our study has some limitations, which could be the focus for future studies. We focus on physiological and medication variables, and our goal is to explore predictive trends in time series of these variables for ICU readmission risk. In particular, we do not consider other readmission risk factors including socioeconomic status, clinical notes [30, 31] and comorbidities [57, 58]. In this study, we focus on predicting 30-day readmission using last 12 hour measurements of a multivariate panel of physiologic variables, in order to elucidate subclinical deterioration of patient’s physiologic baselines that are predictive of readmission.

In addition, we want to strengthen our model with the ability to capture the trend-trend relative changes, rather than changes in single trends, considering that changes in one trend may affect others. This may require interconnecting sequences, which could be effectively represented by graphs. To make our model more extensible to such cases in the future, instead of just sequence mining, we used subgraph mining in the first place.

The dataset used in this study contains a large portion of missing values and the quality of imputation has a significant influence on our model’s performance. Either eliminating all patients with incomplete data or imputing too many missing values might bias our study. We could have misclassified patients whose missing measurements have been replaced by unreasonable values. There is an opportunity to develop a better imputation method for temporal data that is stronger than the customized linear interpolation in catching the patterns of time series and making more reasonable imputation. Besides the missing values issue, another problem that may limit our model’s performance is the false alarms and noise in some variables of our dataset. The physiological variables captured from the monitors and the ventilators may come with noise due to the potential failure or malfunction of these devices, or reading errors. Developing strategies to account for the innate noise of the data, such as adding a latent variable of noise to the predictors, may help to further improve our model.

The imbalance of our data could be another problem to address, where only 26.5% of patients were readmitted within 30 days. We should expect our model to discover stronger trend groups for the high readmission risk population, if our model is trained on a dataset with more readmitted patients. Although a patient cohort with a higher readmission ratio is probably difficult to obtain (most physicians are doing their best to effectively treat patients), recent development in Generative Adversarial Networks (GANs) [59] may offer ways to artificially generate readmitted patient cases to counter the data imbalance problem.

6. Conclusions

To predict 30-day ICU readmission risk, we present a “grouping + snapshot” model, where a subgraph mining based method is used to analyze temporal patterns in time series and to extract multivariate temporal trends. We use Nonnegative Matrix Factorization to group correlated temporal trends. Our experiments show that the groupings are informative features for ICU readmission risk and could be used as complementary features to snapshot measurements to improve the accuracy of predictive models and to provide clinical insights. Our model outperforms all the comparison models and in particular it demonstrates an AUC improvement from 0.636 to 0.661, compared to the snapshot only model. The extensive analysis on the impact of imputation and subgraph filtering to predictive models also shed light on how to improve the performance of models using temporal trends.

Appendix A.

Variable	Description	Missing percentage
Age	Age of the patient	0.034
Albumin	Albumin in blood	0.823
ALT	Alanine aminotransferase in blood	0.803
Arterial Base Excess	Excess in the amount of base present in arterial blood	0.385
Arterial CO2	Arterial carbon dioxide	0.349
Arterial PaCO2	Arterial carbon dioxide tension	0.350
Arterial PaO2	Arterial oxygen tension	0.351
Arterial pH	The pH level in arterial blood	0.336
AST	Aspartate aminotransferase in blood	0.794
AST/ALT	Aspartate aminotransferase / alanine aminotransferase	0.806
BUN	Blood urea nitrogen	0.125
BUN/Creatinine	Blood urea nitrogen / Creatinine	0.126
Ca	Calcium level	0.351
Cardiac Index	Relates the cardiac output from left ventricle in one minute to body surface area	0.027
Central Venous Pressure	Blood pressure in the thoracic vena cava	0.022
Cl	Chloride level	0.405
Creatinine	Level of creatinine in blood	0.124
Heart Rate	Heart Rate per minute	0.023
Delivered Tidal Volume	Air volume of lung without extra effort	0.513
Diastolic Blood Pressure	Minimum blood pressure during heartbeat	0.026
Direct Bilirubin	Level of bilirubin conjugated with glucuronic acid	0.972
GFR	Estimated glomerular filtration rate	0.124
FiO2Set	Fraction of inspired oxygen set on ventilator	0.422
GCS	Glasgow coma scale	0.044
Glucose	Glucose level	0.081
Hematocrit	Hematocrit level	0.077
Hemoglobin	Hemoglobin level	0.139
INR	Prothrombin time international normalized ratio	0
Ion Calcium	Ion Calcium level	0.538
K	Potassium level	0.347
Lactate	Lactate level	0.766
MAP	Mean arterial pressure	0.028
Mg	Magnesium level	0.173
Minute Ventilation	Volume of gas exchanged from lung per minute	0.526
Na	Sodium level	0.360
PaO2/FiO2	Partial pressure arterial oxygen / Fraction of inspired oxygen	0.087
PEEPSet	Positive end-expiratory pressure set on ventilator	0.430
PIP	Peak inspiratory pressure	0.525
Plateau Pressure	Pressure applied (in positive pressure ventilation) to the small airways and alveoli	0.557
Platelets	Platelets count	0.111
Prothrombin Time	Time for plasma to clot	0.354
PTT	Partial Thromboplastin Time	0.350
RAW	Airway Resistance	0.557
RBC	Red blood count	0.150
Respiratory Rate (RESP)	Respiratory rate per minute	0.049
RSBI	Rapid shallow breathing index	0.526
RSBI Rate	Rapid shallow breathing index rate change	0.523
SaO2	Saturation of arterial oxygen	0.035
Systolic Blood Pressure	Maximum blood pressure during heartbeat	0.025
Temperature	Body temperature	0.033
Total Bilirubin	Level of bilirubin	0.794
Protein	Total protein in blood plasma	0.990
Urine/Hour/Weight	Urine per hour per kg body weight	0.065
WBC	White blood count	0.148
Antiarrhythmic	Antiarrhythmic agents	0
Anticoagulant	Blood thinner	0
Antiplatelet	A class of drugs that decrease platelet aggregation and inhibit thrombus formation	0
Benzodiazepine	Used for sedation, inducing sleep, and muscle relaxation.	0
Beta Blocking	Beta blockers, used to slow the heart rate and lower blood pressure, by blocking adrenaline	0
Calcium Channel Blocking	Used to decrease blood pressure for hypertensive patients, also have the secondary effect of slowing heart rate in addition to relaxing blood vessels.	0
Diuretic	Used to increase the production of urine	0
Hemostatic	Drug that promotes hemostasis and stops bleeding	0
Inotropic	Drug that alters the muscular contraction force	0
Insulin	A hormone that helps manage blood sugar level	0
Nondepolarizing	Neuromuscular nondepolarizing agent, used as muscle relaxant	0
Sedatives	Sedative drugs	0
Somatostatin Preparation	Somatostatin inhibits insulin and glucagon secretion.	0
Sympathomimetic	Drugs that mimic the effects of neurotransmitters of the sympathetic nervous system	0
Thrombolytic	Used to dissolve dangerous clots in blood vessels	0
Vasodilating	Used to dilate blood vessels	0
AIDS	acquired immunodeficiency syndrome	0
HemMalig	Hematologic Malignancies	0
MetCarcinoma	Metastatic Carcinoma	0
Medtype	Clustered medication administration patterns	0
Location	ICU types	0