Abstract
Cardiac conduction disturbances are linked with arrhythmia development. The concept of safety factor (SF) has been derived to describe the robustness of conduction, but the usefulness of this metric has been constrained by several limitations. For example, due to the difficulty of measuring the necessary input variables, SF calculations have only been applied to synthetic data. Moreover, quantitative validation of SF is lacking; specifically, the practical meaning of particular SF values is unclear, aside from the fact that propagation failure (i.e., conduction block) is characterized by SF < 1. This study aims to resolve these limitations for our previously published SF formulation and explore its relationship to relevant electrophysiological properties of cardiac tissue. First, HL-1 cardiomyocyte monolayers were grown on multi-electrode arrays and the robustness of propagation was estimated using extracellular potential recordings. SF values reconstructed purely from experimental data were largely between 1 and 5 (up to 89.1% of sites characterized). This range is consistent with values derived from synthetic data, proving that the formulation is sound and its applicability is not limited to analysis of computational models. Second, for simulations conducted in 1-, 2-, and 3-dimensional tissue blocks, we calculated true SF values at locations surrounding the site of current injection for sub- and supra-threshold stimuli and found that they differed from values estimated by our SF formulation by <10%. Finally, we examined SF dynamics under conditions relevant to arrhythmia development in order to provide physiological insight. Our analysis shows that reduced conduction velocity (Θ) caused by impaired intrinsic cell-scale excitability (e.g., due to sodium current a loss-of-function mutation) is associated with less robust conduction (i.e., lower SF); however, intriguingly, Θ variability resulting from modulation of tissue scale conductivity has no effect on SF. These findings are supported by analytic derivation of the relevant relationships from first principles. We conclude that our SF formulation, which can be applied to both experimental and synthetic data, produces values that vary linearly with the excess charge needed for propagation. SF calculations can provide insights helpful in understanding the initiation and perpetuation of cardiac arrhythmia.
Keywords: cardiac safety factor, cardiac electrophysiology, conduction velocity, cardiac excitability, sodium channel, fibrosis, source-sink mismatch
1. Introduction
Propagation of electrical activity in cardiac tissue relies on the transfer of charge between myocytes. However, action potential conduction fails if the charge entering a downstream cell, generated by the upstroke of the neighboring cells, is insufficient to elicit excitation. The resulting disturbance in cardiac conduction is recognized as proarrhythmic under various conditions including slow conduction in the ventricles of patients with Brugada syndrome [1], tissue around infarcts [2, 3], and fibrotic regions in the atria [4]. Conceptually, the amount by which the charge delivered to a cell exceeds the minimum necessary to sustain action potential propagation is termed the safety factor (SF) for cardiac conduction.
Several SF formulations have been posited over the years [5–7], including one formulated by our group [8, 9]. Widespread adoption of SF metrics may have been hindered by the fact that some necessary input parameters (e.g., threshold charge as a function of stimulus duration [Qthr(tA)], transmembrane current over time [Im(t)], etc.) are difficult to derive from living cells or tissue via experimental measurements. Moreover, these studies have shown that propagation fails when SF drops below a critical value (SF < 1), but no formulation has explored whether the measure behaves quantitatively. For example, while it has been presumed that SF = 2 implies conduction that is twice as robust as SF = 1, it has never been confirmed that SF = 2 when the current injected into a downstream cell is 2× the minimal amount required to elicit an action potential. Our previously-published formulation showed evidence that more robust propagation is associated with higher SF values [8], but a formal quantitative relationship has not yet been established.
Electrophysiological changes arising from pathological conditions that disturb conduction have been assumed to precipitate reduced SF. For example, reduced tissue conductivity brought about by fibrotic remodeling [10], including gap junction lateralization [11], is associated with reduced conduction velocity (Θ) and might reduce the robustness of conduction due to exacerbated source-sink mismatch. Changes in cell-scale excitability are also associated with compromised conduction, including reduced expression of SCN5a (the gene that encodes for the α sub-unit of the voltage-gated Na+ channel) [1] and shifts in the activation curve for the fast Na+ current [12]. Currently, a precise quantification of how these different factors could lead to conduction block is wanting.
The goals of this paper are to show that our SF formulation can be applied to quantify robustness of conduction in cardiomyocyte monolayers, to perform quantitative validation to determine the meaning of specific SF values, and to compute SF to help understand the relationship between pathological remodeling and arrhythmogenesis. We first provide a roadmap for approximating SF from easily measurable experimental recordings, and show that the resulting values are consistent with those computed from synthetic data. Then, we establish that there is a sound and reasonable quantitative relationship between our SF formulation and the true robustness of conduction. Finally, we conduct simulations of tissue with altered conductivity and sodium channel properties to show exactly how these changes affect SF, producing insights that can aid in the interpretation of the changes in conduction seen in simulations or experimental/clinical recordings.
2. Methods
2.1. Formulation for calculating SF
Our formulation for quantifying the robustness of cardiac conduction supposes that a depolarizing current is applied to a myocyte, which leads to a rise in transmembrane voltage (Vm), which may or may not result in an action potential. The definition we proposed for SF [8] is:
| (1) |
where A is the take off interval, defined as the time between Vm reaching 1% of its peak value and transmembrane current (Im) crossing the Vm = 0 threshold (from positive to negative), Qstim is the charge delivered by an externally applied stimulus, and Qthr is the threshold charge, as a function of stimulus duration (tA = tIm,0 –t1%), that must be applied to an isolated cell to elicit an action potential. It should be noted that Qthr is implicitly dependent on the electrophysiological properties of the cell(s) in question, regardless of whether the data in question are experimental or synthetic. For example, two mathematical representations of the action potential with different parameters (e.g., normal vs. reduced conductance values for a particular ion channel) necessitate two different Qthr(tA) curves. Several example SF calculations are shown in Fig. 1.
Figure 1.
SF values calculated for action potentials simulated via the Mahajan-Shiferaw model of the rabbit ventricular myocyte [23] under three conditions: (a) normal (i.e., no changes to any cell-scale parameters), (b) sodium channel inactivation gate (τh) reduced to 50% of its default value, and (c) sodium channel conductance (GNa) reduced to 60% of its default value. For each configuration, the top panel shows transmembrane voltage (Vm) over the course of the entire action potential; blue shaded areas indicate the time ranges highlighted in subsequent rows. The middle and lower panels show zoomed-in views of Vm and transmembrane current (Im) focusing on the upstroke interval (tA). Red shading in lower panels indicates the area under the Im curve used to calculate the Qin value used in the SF calculation.
2.2. Calculation of SF from experimental recordings
Murine atrial phenotypic clones of HL-1 cells were used under experimental conditions as previously described [13]. The clone was maintained in culture in Claycomb medium (Sigma Aldrich) and passed once a week at a 1/3 density in 25cm2 flasks. All experiments were performed in modified Krebs-Ringer solution (in mmol/L): NaCl, 140; KCl, 4; CaCl2, 2; MgCl2, 1; HEPES, 5; sodium pyruvate, 2; glucose, 5 (pH 7.4). Details regarding single-cell electrophysiology measurements for this study were as described in the previous paper [13].
For tissue-scale measurements, cloned HL-1 cells [13, 14] were cultured on a Multi-Electrode Array (MEA) with 64 unipolar recording sites separated by 200 μ m, as shown in Fig. 2a. Extracellular electrograms ( φe(t) ) were recorded at 1kHz under physiological temperature conditions (37° C) from day 2 to day 4 post-seeding and analyzed using Python [15]. Raw electrograms were smoothed using a second order Savitsky-Golay filter with a window length of 11. Only electrograms with signal peaks 10 times greater than the root mean square of the noise magnitude were considered since the SF calculation involves numerical integration, which is sensitive to noisy input data. Local activation time was defined by the instant of the peak negative slope in the unipolar voltage signal, and point-by-point Θ estimates were computed by taking the inverse of the spatial gradient of activation times surrounding each electrode. To estimate Im, we assumed a locally planar wavefront and used the method described by Gray et al. [16] to convert spatial to temporal derivatives:
| (2) |
where σe is the extracellular conductivity, and β is the membrane surface to volume ratio which can be expressed as [17]:
| (3) |
where fvol is the fraction of the volume occupied by the cells on the MEA and ξ is the cellular surface-to-volume ratio. Exact values for the latter parameters were unknown and impossible to obtain using standard experimental techniques. Reported values of σe range from 33 to 160 mS/m [18, 19]; accordingly, we considered five plausible σe values (16.7, 33.3, 75.5, 117.8, 160 mS/m). fvol was estimated via manual analysis of photographs of cultured cells using ImageJ [20]; however, since different parts of the MEA had different densities of cell packing, we subdivided the visible domain into quarters, measured the lower and upper extrema of fvol and considered four possible values within that range: 0.145, 0.289, 0.427, and 0.565. Thus, for each usable (φe recording, we assessed the sensitivity of Im to 20 different permutations of σe and fvol. Finally, average cell surface area was determined by measuring the capacitance of cultured cells, but precise calculation of ξ was not possible because 3D cell geometry was not readily discernible. Thus, we assumed that cells were cylindrical with a 4:1 height to width ratio and derived ξ accordingly.
Figure 2.
Approximation of SF from experimentally recorded data. a. Photograph of HL-1 cells cultured on MEA. Black dots represent recording electrodes. b. Map of activation times for MEA. Squares marked with “X” represent sites that were ignored due to low signal-to-noise ratio. Squares with a circle indicate electrodes for which data are shown in panels d and e. c. Map of Θ values for MEA. d. Plots of φe over time show filtered signals recorded from for electrodes 9, 28, and 39. e. Plots of Im over time for electrodes 9, 28, and 39. The area under each Im curve in the intervals used to calculate Qin is highlighted by yellow shading. f. Histogram of SF values calculated at all electrodes over 23 beats with the following assumptions: σe = 75.5 mS/m, fvol = 0.565. Red-shaded histogram bars indicate SF values between 1 and 5.
The Qthr(tA) relationship for experimental SF calculations was derived by determining the charge associated with threshold currents required to elicit action potentials in isolated HL-1 cells. The threshold Ithr value was identified using current stimulation (square pulses, tA = 3ms) and a linear relationship between threshold charge and tA was assumed as suggested by Weiss [21] and observed previously [8]:
| (4) |
where r is the rheobase and c is the chronaxie.
2.3. Numerical validation and exploration of SF dynamics in synthetic data
To quantitatively gauge the accuracy of our SF formulation, we performed computer simulations in which we applied constant amplitude transmembrane current pulses (stimulus duration [ds] = 1–5ms) to 1D strands, 2D sheets, and 3D blocks of cardiac tissue. Stimuli were applied to rectangular regions (i.e., 1D: line segment, 2D: square, 3D: cube) at the center of each domain with variable spatial extent (i.e., electrode width [we] = 0.2–0.8mm in all directions). For each combination of ds and we, we first found the minimum current necessary for generation of a propagating wave, Ithr, using a binary search with a 100 nA/cm 2 resolution. Then, for a stimulus of the same duration and spatial extent but with arbitrary magnitude Istim, the true safety factor (SFtrue) was defined as:
| (5) |
which was compared to the SF value computed according to our formulation (Eqn. 1) at the edge of the stimulus.
All simulations were performed using CARP [22]. Regular finite element meshes were constructed with 100 μ m inter-node spacing for line elements in 1D, and tetrahedra in 3D. For 2D cases, the simulated tissue was actually a one element-thick 3D sheet. In all cases, membrane kinetics were represented by a rabbit ventricular myocyte model [23]. A time step of 25 μ s was used and results were output every 100 μ s for analysis.
To assess structural and electrophysiological effects on robustness of conduction, we ran further simulations in 2D tissue domains under a variety of conditions and computed SF. Specifically, we:
Explored the effects of gradual and abrupt changes in macroscopic geometry in a 4cm-long tissue sheet with thin-to-thick and thick-to-thin transitions;
Examined the effect of different degrees of fibrotic remodeling with conduction approaching the percolation threshold, by randomly removing a fixed percentage of finite elements (10%, 25%, 50%, and 75%) from the central third of a 15×7.5mm rectangular tissue sheet; and,
Characterized, in the same simulated tissue sheet as the fibrotic remodeling experiments described above, the influence on SF of modulating tissue- and cell-scale parameters that influence Θ (tissue-scale: 1/3, 1/4, or 1/6 of baseline tissue conductivity [σi]; cell-scale: time constant of sodium channel inactivation gate [τh] and sodium channel conductance [gNa], 50–90% in 10% increments).
3. Results
3.1. Calculation of SF from Experimentally Recorded Data
The average cell capacitance was measured as 14.0 ± 1.1 pF (n=16); the threshold current stimulus to elicit an action potential was 172.8 ± 10.2 pA (n=18) for pulse duration = 3ms. The membrane threshold potential was −36.1 ± 1.8 mV (n=18), and, thus, 404.6 fC of charge were needed to raise the membrane capacitance voltage to threshold. Based on these values and assuming Weiss’s equation [21], we obtained an estimate of Qthr(tA) = 404.6+37.9tA fC. Activity occurred spontaneously in cell culture, from a region outside the MEA coverage area, and excitation spread as a planar wavefront across the MEA (Θ ≈ 0.5±0.35cm/s). Failure of the wave to propagate across the MEA was never observed. After discarding electrodes with poor signal quality as described in Methods, SF was calculated for 36.1±3.3 (for n = 23 distinct propagation events) electrodes for each possible combination of σe and fvol parameters.
Maps of activation time and conduction velocity reconstructed for a representative activation sequence are presented in Figs. 2b and c, respectively. Black squares indicate electrodes where values could not be calculated due to poor signal quality. The filtered signals for recorded φe(t) (Fig. 2d) and reconstructed Im(t) (Figs. 2e) are shown for the sites corresponding to the highlighted locations in Figs. 2b and c (and for the same excitation interval shown in those panels). In general, SF values reconstructed from experimentally measured data were in the range from 1 to 5, although the specific distribution was dependent on the values of fvol and σe used in calculations (see: Fig. S1). A representative distribution of SF values derived from experimental data is shown in Fig. 2f. In this case, where fvol = 0.289 and σe = 33.3 mS / mm, 88.1% of all computed SF values were between 1 and 5; this was the highest proportion observed for all values of fvol and σe.
To explore the relationship between Θ and SF in experimental data from a similar HL-1 preparation, we examined MEA data for spontaneous behavior in a series of 60+ beats. Over time, a gradual increase in Θ from ~0.9cm / s to ~1.5cm / s (62% increase) was observed (Fig. 3a). Since this change in Θ was not prompted by application or washout of any exogenous pharmacological compound (e.g., channel blockers/agonists, uncoupling agents, etc.), it was unclear whether the distinct change in behavior was caused by enhanced gap junctional coupling, increased sodium channel excitability, or some synergistic combination of the two. To identify the causal mechanism, we examined the maximum second temporal derivative of transmembrane voltage (Fig. 3b), which is not affected by changes in σi [15]. The fact that did not increase as dramatically as the Θ values (increasing by 32% over the studied beats) is consistent with a functional increase in gap junctional coupling being chiefly responsible for increased Θ, and not a change in cell-scale excitability. This supposition is supported by the fact that even dramatic changes in cell-scale excitability (e.g., halving or doubling of GNa) have relatively subtle effects on Θ compared to proportional changes in σi [25]. Remarkably, SF remained relatively constant over time (~1.7) (Fig. 3c). Plotting SF vs. Θ showed no clear relationship (Fig. 3d), highlighting that Θ changes do not necessarily accompany SF changes.
Figure 3:
Properties of Θ and SF over time in experimentally recorded data from an HL-1 monolayer. In all panels, the values shown for each time point are the median of all valid electrodes from which signal was recorded during that beat. Best-fit (linear regression) lines, with corresponding equations and correlation coefficients ( r ) are shown in panels a and b. % increase/decrease values are derived by comparing values at the extremes of each best-fit line. a. Θ values over time, which increase by ~70% between the first and last beats observed. b. values over time, which stay relatively constant over time, suggesting that the increase in Θ is predominantly due to increased gap juction coupling (see text). c. SF values over time, which also stay relatively constant (~1.7). d. Beat-by-beat comparison of SF vs. Θ values, showing that Θ variability is not necessarily accompanied by a change in SF.
3.2. Validation of correspondence between SF and SFtrue
As described in Methods, a one dimensional tissue strand was stimulated at the midpoint for a range of different we and ds values. Complete spatio-temporal excitation sequences are shown side-by-side with plots of SF(x), derived using our formulation, for four different values of SFtrue in Fig. 4a. In general, there was reasonble correspondence between SFtrue and estimated SF. For the case where the stimulus was 25% higher than the threshold strength to elicit a propagating response (i.e., SFtrue = 1.25 ; top row), SF values in the vicinity of the electrode boundary ranged from 1 to 1.6. When SFtrue was exactly 1 (second row), SF was 1 under the electrode and 1.5 in the region where robust propagation had already been initiated. Interestingly, in this case, stimulation initiated a propagating unstable wavelet [26], which traveled along the strand at a much slower Θ until it transformed into full-fledged action potential-driven propagation at some distance from the electrode. Remarkably, for a stimulus that was only slightly weaker (SFtrue = 0.999; third row), SF(x) was uniformly less than 1 for all values of x. Finally, as anticipated, for the case of a stimulus that was 25% weaker than the value necessary to initiate propagation (SFtrue = 0.75; bottom row), SF(x) was bell-shaped with a peak of 0.75 at x = 0, under the center of the electrode. Similar behavior was observed for the entire range of SFtrue, regardless of we and ds values (see Fig. 4b). Notably, SF (x) profiles were smooth, gradually and continuously changing from the stimulated to the nonstimulated regions, even though the Qstim term in Eqn. 1 was only considered directly under the electrode.
Figure 4.
SF validation simulations conducted in a one-dimensional tissue strand. a. Strand geometry (top), along with spatio-temporal plots of transmembrane voltage (left) and profiles of SF distribution along the strand (right) for four different SFtrue values. Examples shown here are for we = 0.8mm and ds =5ms. b. SF(x) graphs for SFtrue values ranging from 0.125 to 2 for two combinations of we and ds. c. top: SF at electrode boundary versus SFtrue for all 1D experiments. The dashed line is the identity line. The inset shows detail around SFtrue =1. bottom: Percentage error of calculated between SF and SFtrue.
Overall, there was excellent correlation between SFtrue and SF at the electrode boundary (Fig. 4c). Deviation from the identity line was minimal, the percent error never exceeded 40%, with the dramatic majority of errors less than 20%. The error was minimal near SFtrue = 1, which is arguably the most important region since it corresponds to conditions near the critical point between successful and failed conduction. Furthermore, the relationship was monotonic so an increase in SF consistently corresponded to an increase in SFtrue.
For simulations conducted in 2D (Fig. 5a) and 3D (Fig. 5b), there was a similar trend towards strong correlation between estimated SF and known SFtrue. As in 1D, propagating unstable wavelets were observed at SFtrue =1, travelling along the direction of greatest conductivity.
Figure 5.
SF validation simulations conducted in a two-dimensional tissue sheet or a three-dimentional tissue slab. a. For 2D simulations, a one element-thick sheet (top left) was stimulated centrally. Stimulus parameters for the specific examples shown are we = 0.4mm and ds = 5ms. Maps of activation time (isoline spacing: 0.2 ms; gray = failed propagation) and SF (isoline spacing: 0.1) are presented for three SFtrue values from simulations (top right). Profiles of SF(x) (bottom left) and correlation between estimated SF (measured at the electrode boundary) and known SFtrue for all combinations of we and ds (bottom right) show findings consistent with 1D observations. b. Same as a but for 3D simulations. Examples shown are for we = 0.8mm and ds = 4ms. Isoline spacing for SF schematics is 0.2.
3.3. Relationship between variability in tissue geometry and SF
Different types of geometric variability (i.e., thick-to-thin and thin-to-thick transitions with varying degrees of abruptness; Fig. 6a) had the expected effects on the emergent property of Θ (Fig. 6b). Specifically, there was a localized Θ increase at points where the width of the propagation path decreased (i.e., thick-to-thin transitions). Conversely, in regions where the path of propagation became wider (thin-to-thick transitions), there was a transient Θ decrease because of reduced source-to-sink ratio. SF along the central profile followed Θ but the peaks were attenuated. Qualitatively, SF(x) appeared to be a low-pass filtered version of Θ(x), with smoother transitions at geometrical changes. The differences in SF were not as dramatic as those in Θ, especially at the openings of thin-to-thick transitions between the center and edge values.
Figure 6.
Simulations exploring how changes in geometry (i.e., thin-to-thick and thick-to-thin transitions) affect Θ and SF. a. The 2D geometry with activation times. Isochrone line spacing is 2.5ms. b. Θ map (top) and profile of Θ(x) along the vertical axis of symmetry (bottom). c. Same as b but for SF and SF(x).
3.4. Effect of fibrotic remodeling on SF
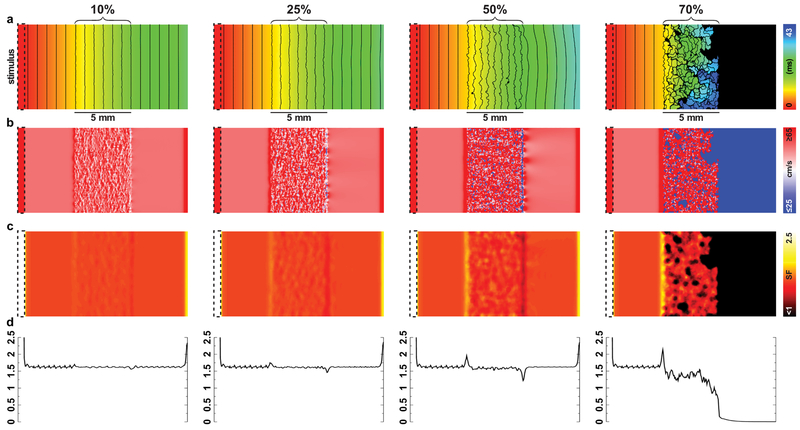
Action potentials propagated all the way through the fibrotic region for values < 70% tissue removal (Fig. 7a-b). The time required for the wavefront to percolate through the fibrotic region became longer as the extent of element removal increased, since propagation became more tortuous and propagation failure occurred within the fibrotic region. In all cases, a localized increase in SF was observed as the wave entered the diseased tissue (Fig. 7a-b); the magnitude of this increase was dependent on the extent of fibrotic remodeling, with higher levels of tissue removal corresponding to a larger localized increase (ranging from 1% to 8% higher than baseline SF ≈ 1.62). Within the fibrotic tissue region for < 70% tissue removal, there was a subtle decrease in SF ; in contrast, a dramatic drop in SF was seen within the fibrotic region for the 70% case. Finally, at the transition between fibrotic and non-fibrotic tissue, there was a localized decrease in SF, again with magnitude proportional to the severity of remodeling.
Figure 7.
Effect of fibrotic remodeling, simulated by removal of elements from the center third of the tissue, on SF. a. Maps of activation times for all four configurations simulated (10%-70% of elements removed; see Methods). Isochrone line spacing is 1.5ms. b Θ maps. c SF maps. d SF (x) profile for all four configurations, with each value representing the average of all SF values at that particular value of x.
3.5. Changes in SF under tissue- and cell-scale conditions that reduce Θ
As expected, reduced σi (i.e., tissue-scale change) resulted in decreased Θ (Fig. 8a), with larger σi reductions corresponding to more dramatic Θ decreases (Fig. 8b). There were significant localized changes in SF at the boundaries between regions of normal and reduced σi, but SF was approximately the same (~1.6) regardless of σi despite obvious reductions in Θ (Fig. 8c). Specifically, there were regions of increased and decreased local SF at sites where the wavefront entered and exited the low-σi domain, respectively, with the extent of this change larger for greater differences in σi.
Figure 8.
Changes in Θ and SF resulting from reduced σi in the central third of a simulated tissue slab. a. Maps of local activation time. Isoline spacing is 2 ms. b. Θ profiles from the center line (i.e., vertical axis of symmetry). c. Same as b but for SF.
As shown in Fig.9a, cell-scale excitability changes imposed in similar simulations also resulted in reduced local Θ as expected. For the example shown, reduction of τh to 50% of its nominal value resulted in Θ≈ 32.6cm/ s in the central part of the corresponding region, which was ~40% lower than the value in tissue without compromised excitability ( 56.1cm/ s ). Likewise, reduction of gNa to 50% of its baseline level led to Θ≈ 42.0cm/ s (~25% lower than normal Θ). However, in stark contrast to the observed SF-to-Θ relationship in low-σi tissue, SF was reduced in regions with slower Θ arising from impaired cell-scale excitability. This observation held true for all values of τh or gNa and plotting SF versus Θ revealed a strong linear relationship (Fig. 9b).
Figure 9.
Changes in Θ and SF resulting from reduced τh or gNa in different segments of a simulated tissue slab. a. Top: Map of activation times for a representative example (50%τh, 50%gNa); isoline spacing: 2 ms. Middle and Bottom: Θ and SF profiles along axis of vertical symmetry. In the Θ panel, the dark line corresponds to the case shown in a (50%τh, 50%gNa); lighter lines show data for 60–90% cases. In the SF panel, only data corresponding to a are shown. b. Linear relationship between SF and Θ, when the change in Θ results from reduction of either τh (blue dots) or gNa (orange dots). c. Relationships with Θ. Top: The maximum upstroke velocity, , and Qthr as functions of Θ when only GNa was manipulated. Bottom: and σi. as functions of Θ when only gap junction coupling was changed. Regression fits are indicated for the curves along with the regression coefficient.
To obtain further insight on this apparent paradox, we re-plotted data from Figs. 8a-c and 9b with Θ as the dependent variable, as shown in Fig. 9c. For cases in which reduction of INa channel parameters caused more dramatic Θ impairment, we observed a relative decrease in the maximal slope of the action potential upstroke () accompanied by increased Qthr values. In contrast, while there was an obvious quadratic relationship between σi and Θ, was constant across the entire observed range of Θ values.
4. Conclusions
We demonstrate for the first time that our previously-formulated definition of cardiac SF [8] has a linear relationship with, and is normalized by, the actual charge required to elicit a propagating action potential. We applied SF to experimental measurements, showing that it can be used in that context. We then derived a scenario in which the concept of true SF was intuitive and compared values computed using our formulation to expected values in an unambiguous manner. Finally, we looked at several simulated cases relevant to the study of arrhythmogenic mechanisms, highlighting that changes in Θ do not necessarily reflect underlying changes in SF.
4.1. Experimental measurements
An advantage of our SF is that it can be applied to experimentally recorded signals. There are several techniques to calculate Im, including those based on extracellular electrode recordings (as in this study) [16], intracellular microeletrodes [16], optical mapping [16], and loose patch [27]. The single cell threshold must still be known before SF can be computed. In our case, we have extensive experience with the cell line both at the single cell and monolayer layer levels [13] and are confident that coupled cell properties are preserved in single cells. Thus, we knew the threshold current precisely. Experimentally, finding Qthr(tA) may require single cell isolation or involve inverse fitting from tissue measurements to find cellular properties. Nonetheless, the quantities required to calculate SF are standard measurements.
Our experiments with HL-1 cells were dependent on the geometry of cells assumed. We could not reconstruct the shapes in three dimensions from the 2D photographs. Also, we did not try to estimate cell densities around particular electrodes and correct for them. We did show that with justifiable assumptions over a wide range of σe and fvol parameters within accepted physiological bounds, calculated SF values were in a reasonable range (1 ≤ SF ≤ 5). This is in line with expected values as SF ≥ 1 is required for propagation, and the charge is not an order of magnitude higher than required, which would imply a large amount of energy waste. Thus, despite the slow Θ observed experimentally in HL-1 monolayers, propagation was quite robust.
4.2. Validation
We were able to quantitatively validate SF in 1-, 2-, and 3-dimensional tissue simulations, demonstrating a linear relationship between SF and the excess charge delivered. Behavior was the same in all dimensions with a small and inconsequential increase in off diagonal entries for tissue with a higher spatial dimensionality. For the first time, we showed that SF can properly characterize behavior under and near the electrode. The SF spatial profile had no large discontinuities or sharp peaks, and increased in a smooth, monotonic way under the electrode as the stimulus strength was increased. Outside the electrode, there was a jump in the SF profile at SF=1 as expected, since propagation to the ends of the cable suddenly occurred. In all dimensions 1) propagation did not occur for SF < 1, 2) at SF=1 to within at least 4 decimal places, propagating unstable wavelets [26] were initiated, and 3) normal propagation occurred for SF > 1. Thus, SF is dimension-independent, and is especially accurate and sensitive around the propagation threshold.
4.3. Θ and SF.
SF is preserved within regions of different conductivity. This is because the source region driving excitation of the neighboring cells is that covered by the action potential upstroke. Spatially, this spans a length equal to the upstroke duration multiplied by Θ. It is known that . Likewise, the downstream load of the unexcited tissue is proportional to the space constant ( λ ), which is also proportional to . Thus, since the source and sink both increase with the same dependence on σi, SF is preserved. In contrast, at transitions between the regions of differing σi, there is a local SF maximum or minimum as σi decreases or increases, respectively, due to the intrinsic spatial variability in source and sink strength. In the case of extreme fibrosis (70% column of Fig. 7), it was largely not within the fibrotic region itself that propagation failed. On the contrary, propagation within the latter region was robust (SF ≈ 1.5), albeit with a lower Θ, and conduction ultimately failed at the transition back to non-fibrotic tissue. The failure of propagation into regions of increased conductivity has been demonstrated experimentally [28].
For all ionic changes tested, lower Θ was associated with lower SF. This is not unexpected, since greater intake of charge during the action potential upstroke, which results in increased Θ, leads to higher peak potentials and in turn increases the electrical driving force between cells, so long as λ is not affected. Thus, a critical finding of our analysis is that while reduced SF implies reduced Θ, reduced Θ does not necessarily imply reduced SF.
SF profiles often looked like low pass filtered versions of the Θ profile. That is, at points of sharp transitions in Θ, SF displayed wider, lower amplitude (or indistinguishable) peaks. Changes in Θ are more point specific relative to changes in SF, which factor in the spatial extent of source and sink regions, which occur over distances between 2λ and 3λ.
In the Supplemental Material section entitled “Analytical Derivations,” we show that the above results emerge from our SF formulation; here, we discuss final results. Starting with our SF definition (Eq. 1), and assuming a planar wavefront propagating at constant velocity, Θ, we introduce Eqn. 2 and transform the integration variable from time to space. If we vary only the conductivity to affect conduction velocity, that we denote as Θσ, then:
| (6) |
which has no Θ dependence, as observed in our study. See Eqns. A1 to A8 for full derivation. The latter observation is supported experimentally by Rohr et al [26], who remarked that propagation still occurred with a high degree of gap junction uncoupling.
Next, if we manipulate conduction velocity by changing the sodium channel conductance, we note that Qthr(ΘNa) = 1/(A + BΘNa) for positive constants A and B. Making this substitution,
| (7) |
which has a positive, linear dependence as observed. See Eqns. A10 to Al1 for full derivation.
Our conclusion is that qualitative assessment of Θ alone cannot provide an intuitive estimate of SF. In general, pathologies that lead to the development of fibrosis also have some impact on electrophysiology (e.g., through paracrine effects). Reductions in Θ may result from any combination of geometrical transitions, disruption of gap junctions, or modifications to ionic currents, and SF is related to the underlying cause of electrophysiological variability [29]. In acute experiments, where only an agent affecting cell-scale excitability is added, a change in Θ will be associated with an increase or decrease in SF. Experimental results presented in this study are consistent with this prediction, given that an observed spontaneous change in Θ was not associated with a concomitant change in SF (see Fig. 3).
An interesting potential application of SF is to analyze the relationship between microstructural features such as functional heterogeneity of gap junction channels (e.g., due to the formation of macro-molecular complexes involving co-localization of Cx43 with sodium channels and scaffolding proteins at intercalated discs [30]). There is no straightforward way to represent such phenomena using the modeling approach used in the present study, since it is based on a continuum approximation of tissue-scale electrophysiological properties. However, recent work from a different research group has highlighted the fact that our SF formulation can be used to study conduction and excitability at the micro scale [31], suggesting that this could be feasible in future work.
4.4. Arrhythmogenesis
Previously, our group used SF to show that source/sink mismatch at left-right ventricle border might predispose that location for conduction and wavebreak based solely on geometrical reasons [9]. Likewise, SF could be applied around scars and fibrotic regions to identify points of potential wavebreak which could be targets for therapy. Notably, for the section concerning fibrotic tissue, we chose to only look at gross structural remodeling (i.e., tissue replacement), and ignored other factors like electrophysiological changes and diffuse fibrosis. In reality, fibrosis is clearly a multi-factorial process that can be represented in computational models in many different ways, as we have discussed in previous work [32]. The rationale for modeling fibrosis in this way was to illustrate how disruption of local source-sink mismatch affects SF.
Experimentally, SF can be used for analysis to understand reentry initiation and identify mechanisms. For example, one could examine filament centers and sites of wavebreak to determine whether the underlying cause is the impact of substrate characteristics on SF at those points. Using multiple pacing frequencies could also shed light on the substrate as SF may reduce more rapidly in some locations as the pacing rate increases.
4.5. Study limitations
Experimentally, we did not know β at each electrode. This could have been performed by using a different microscope to get the true shape in 3D, and by better estimating the cell density around each electrode. HL-1 cells are a mutant cell line, and the SF range may fall outside of normal myocardium. However, using basic physiological assumptions, the computed SF turned out to be in a reasonable range. The studies with changes to ionic models and conductivity were done in 2D. However, the 1, 2, and 3D simulations all showed the same behavior for the validation portion.
It is relevant to note that that simulations conducted in our study are based on models of rabbit ventricular myocyte kinetics whereas the experimental data analyzed came from HL-1 cells. Our intention with respect to considering experimental data was not to present a one-to-one mapping between experimental and synthetic datasets, but rather to explore the broad question of whether our SF formulation could potentially be applied to any data recorded from cardiomyocytes in culture. Previous analysis suggests that the SF formulation can be applied to arbitrary cell types, as long as proper steps are taken to characterize the cell-specific Qthr(tA) relationship [8], as we did for the HL-1 cells used in this study.
Supplementary Material
Figure S1. Additional data for SF measurements derived from experimentally recorded data. Histograms of SF values calculated at all electrodes over 23 beats for all tested combinations of fvol and σe; axis labels are omitted for ease of readability (see Fig. 2f for details). Red-shaded histogram bars indicate SF values between 1 and 5. Green dashed line indicates specific histogram corresponding to Fig. 2f.
Acknowledgments
PMB was supported by a grant from the American Heart Association (United States) (16-SDG-3044006). EJV was supported by the Agence Nationale de la Recherche (France) (ANR-10-IAHU-04) and acknowledges Partnership for Advanced Computing in Europe (PRACE) support for computing resources. NAT was supported by the National Institutes of Health (United States) (DP1-HL123271,R01-HL116280, and R01-HL126802). This project has received funding from the Fondation Leducq (France) (Research Grant number 16 CVD 02). WHF was supported by the Johns Hopkins University (United States) Whiting School of Engineering's Vredenburg Travel Fund. CH thanks Asociación de Amigos de la Universidad de la Navarra (Spain), Obra Social “la Caixa” (Spain), Fundación Bancaria Caja Navarra (Spain), Ministry of Economy and Competitiveness (Spain) (project fund SAF2014-58286-C2-2-R, and Dr. J. Bragard for fruitful discussions.
A Analytical Derivations
Theoretically, we will derive the dependence of SF on Θ emerging from our SF formulation, and show how our simulation results are consistent with it. We start with our SF definition (Eq. 1) and assume a planar wavefront propagating in x at a constant propagation velocity, Θ, with no stimulus (Qstim = 0). We plug in the expression for Im (Eq. 2), convert to intracellular quantiies [33], and change the integration variable from time to space, t→x/Θ:
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
Now, the temporal derivative is related to the gradient by . The lower limit of integration is the point where Vm has barely started to rise, so the spatial derivative is very small and can be ignored. In Fig. 1, it can be seen that the upper limit is the point where the membrane current is zero and is, thus, the instance of maximal , denoted :
 |
(A7) |
| (A8) |
A.1. Varying tissue conductivity
If we vary only the conductivity to affect the conduction velocity, which we denote as Θσ, then varies little with Θσ ( ≈ 2% over the range 25–100 cm/s, see Fig. 9) [24], and can be considered constant. From theory and verified in our study (see Fig. 9), Θσ varies with the square root of conductivity, so , and it follows:
| (A9) |
where σi(1) is the conductivity producing a conduction velocity of 1 m/s. Qthr(ta) is a single cell property so it is not affected by the tissue conductivity. Therefore, SF is independent of Θσ, consistent with our results (Fig. 8).
A.2. Varying sodium conductance
Next, we start again from Eq. A8 and consider changing the conduction velocity, now denoted ΘNa, by fixing the tissue conductivity while varying membrane excitability through adjusting the sodium channel conductance. Under these conditions, from our simulations (Fig. 9) and supported by experiment [34], it is known that the relationship between the maximum rate of change of the transmembrane voltage and the conduction velocity is given by . With this substitution, we can write
| (A10) |
where (1) is the maximum rate of change of transmembrane voltage with respect to time at a conduction velocity of 1 m/s. Now, Qthr is the charge required to bring the membrane to a voltage such that the inward current is regeneratively greater than the outward current, and is affected by changes in sodium current. As a function of ΘNa, it has the form Qthr(ΘNa) = 1/(A + BΘNa) for positive parameters A and B (see Fig. 9c), so, incorporating this expression,
| (A11) |
which is a linear function with a positive slope as observed (Fig. 9c).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
5 References
- 1.Boukens BJ, Sylva M, de Gier-de Vries C, Remme CA, Bezzina CR, et al. (2013) Reduced sodium channel function unmasks residual embryonic slow conduction in the adult right ventricular outflow tract. Circ Res 113: 137–141. [DOI] [PubMed] [Google Scholar]
- 2.Ciaccio EJ, Ashikaga H, Kaba RA, Cervantes D, Hopenfeld B, et al. (2007) Model of reentrant ventricular tachycardia based on infarct border zone geometry predicts reentrant circuit features as determined by activation mapping. Heart Rhythm 4: 1034–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chang MG, Zhang Y, Chang CY, Xu L, Emokpae R, et al. (2009) Spiral waves and reentry dynamics in an in vitro model of the healed infarct border zone. Circ Res 105: 1062–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fukumoto K, Habibi M, Ipek EG, Zahid S, Khurram IM, et al. (2016) Association of left atrial local conduction velocity with late gadolinium enhancement on cardiac magnetic resonance in patients with atrial fibrillation. Circ Arrhythm Electrophysiol 9: e002897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Leon LJ, Roberge FA (1991) Directional characteristics of action potential propagation in cardiac muscle. A model study. Circ Res 69: 378–395. [DOI] [PubMed] [Google Scholar]
- 6.Delgado C, Steinhaus B, Delmar M, Chialvo DR, Jalife J (1990) Directional differences in excitability and margin of safety for propagation in sheep ventricular epicardial muscle. Circ Res 67: 97–110. [DOI] [PubMed] [Google Scholar]
- 7.Shaw RM, Rudy Y (1997) Ionic mechanisms of propagation in cardiac tissue. Roles of the sodium and L-type calcium currents during reduced excitability and decreased gap junction coupling. Circ Res 81: 727–741. [DOI] [PubMed] [Google Scholar]
- 8.Boyle PM, Vigmond EJ (2010) An intuitive safety factor for cardiac propagation. Biophys J 98: L57–L59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Boyle PM, Park CJ, Arevalo HJ, Vigmond EJ, Trayanova NA (2014) Sodium current reduction unmasks a structure-dependent substrate for arrhythmogenesis in the normal ventricles. PLoS One 9: e86947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kostin S, Klein G, Szalay Z, Hein S, Bauer EP, et al. (2002) Structural correlate of atrial fibrillation in human patients. Cardiovasc Res 54: 361–379. [DOI] [PubMed] [Google Scholar]
- 11.Cabo C, Yao J, Boyden PA, Chen S, Hussain W, et al. (2006) Heterogeneous gap junction remodeling in reentrant circuits in the epicardial border zone of the healing canine infarct. Cardiovasc Res 72: 241–249. [DOI] [PubMed] [Google Scholar]
- 12.Wagner S, Dybkova N, Rasenack ECL, Jacobshagen C, Fabritz L, et al. (2006) Ca2+/calmodulin-dependent protein kinase II regulates cardiac Na+ channels. J Clin Invest 116: 3127–3138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dias P, Desplantez T, El-Harasis MA, Chowdhury RA, Ullrich ND, et al. (2014) Characterisation of connexin expression and electrophysiological properties in stable clones of the HL-1 myocyte cell line. PLoS One 9: e90266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Claycomb WC, Lanson NA, Stallworth BS, Egeland DB, Delcarpio JB, et al. (1998) HL-1 cells: a cardiac muscle cell line that contracts and retains phenotypic characteristics of the adult cardiomyocyte. Proc Natl Acad Sci U S A 95: 2979–2984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Oliphant TE (2007) Python for scientific computing. CiSE 9: 10–20. [Google Scholar]
- 16.Gray RA, Mashburn DN, Sidorov VY, Wikswo JP (2013) Quantification of transmembrane currents during action potential propagation in the heart. Biophys J 104: 268–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Henriquez CS (1993) Simulating the electrical behavior of cardiac tissue using the bidomain model. Crit Rev Biomed Eng 21: 1–77. [PubMed] [Google Scholar]
- 18.Bulai PM, Molchanov PG, Denisov AA, Pitlik TN, Cherenkevich SN (2012) Extracellular electrical signals in a neuron-surface junction: model of heterogeneous membrane conductivity. Eur Biophys J 41: 319–327. [DOI] [PubMed] [Google Scholar]
- 19.Tura A, Sbrignadello S, Cianciavicchia D, Pacini G, Ravazzani P (2010) A low frequency electromagnetic sensor for indirect measurement of glucose concentration: in vitro experiments in different conductive solutions. Sensors 10: 5346–5358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schneider CA, Rasband WS, Eliceiri KW (2012) NIH image to ImageJ: 25 years of image analysis. Nat Methods 9: 671–675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Weiss G (1901) Sur la possibility de rendre comparables entre eux les appareils servant a l'excitation electrique. Arch Ital Biol 35: 413–36. [Google Scholar]
- 22.Vigmond EJ, Hughes M, Plank G, Leon LJ (2003) Computational tools for modeling electrical activity in cardiac tissue. J Electrocardiol 36 Suppl: 69–74. [DOI] [PubMed] [Google Scholar]
- 23.Mahajan A, Shiferaw Y, Sato D, Baher A, Olcese R, et al. (2008) A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys J 94: 392–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fraser JA, Huang CLH, Pedersen TH (2011) Relationships between resting conductances, excitability, and t-system ionic homeostasis in skeletal muscle. J Gen Physiol 138: 95–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wilders R (2012) Arrhythmogenic right ventricular cardiomyopathy: Considerations from in silico experiments. Front Physiol 3: 168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Boyle PM, Madhavan A, Reid MP, Vigmond EJ (2012) Propagating unstable wavelets in cardiac tissue. Phys Rev E Stat Nonlin Soft Matter Phys 85: 011909. [DOI] [PubMed] [Google Scholar]
- 27.Ramos-Franco J, Aguilar-Sanchez Y, Escobar AL (2016) Intact heart loose patch photolysis reveals ionic current kinetics during ventricular action potentials. Circ Res 118: 203–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Daleau P, Délèze J (1998) Conduction block in Purkinje fibers by homogeneous versus localized decrease of the gap junction conductance. Can J Physiol Pharmacol 76: 630–641. [DOI] [PubMed] [Google Scholar]
- 29.Rohr S, Kucera JP, Kléber AG (1998) Slow conduction in cardiac tissue, I. Circ Res 83: 781–794. [DOI] [PubMed] [Google Scholar]
- 30.Agullo-Pascual E, Lin X, Leo-Macias A, Zhang M, Liang FX, et al. (2014) Super-resolution imaging reveals that loss of the C-terminus of Cx43 limits microtubule plus-end capture and NaV1.5 localization at the intercalated disc. Cardiovasc Res 104: 371–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gokhale TA, Asfour H, Verma S, Bursac N, Henriquez CS (2018) Microheterogeneity-induced conduction slowing and wavefront collisions govern macroscopic conduction behavior: A computational and experimental study. PLoS Comp Biol 14: e1006276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Roney CH, Bayer JD, Zahid S, Meo M, Boyle PMJ, et al. (2016) Modelling methodology of atrial fibrosis affects rotor dynamics and electrograms. Europace 18: iv146–iv155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Plonsey R, Barr R (2007) Bioelectricity: A Quantitative Approach. Springer US, 3 edition. [Google Scholar]
- 34.Buchanan JW, Saito T, Gettes LS (1985) The effects of antiarrhythmic drugs, stimulation frequency, and potassium-induced resting membrane potential changes on conduction velocity and dV/dtmax in guinea pig myocardium. Circ Res 56: 696–703. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Additional data for SF measurements derived from experimentally recorded data. Histograms of SF values calculated at all electrodes over 23 beats for all tested combinations of fvol and σe; axis labels are omitted for ease of readability (see Fig. 2f for details). Red-shaded histogram bars indicate SF values between 1 and 5. Green dashed line indicates specific histogram corresponding to Fig. 2f.