Energy renormalization for coarse-graining polymers having different segmental structures

We provide a computational test of the energy renormalization method to coarse-grain polymers with different segmental structures.

Abstract

Multiscale coarse-grained (CG) modeling of soft materials, such as polymers, is currently an art form because CG models normally have significantly altered dynamics and thermodynamic properties compared to their atomistic counterparts. We address this problem by exploiting concepts derived from the generalized entropy theory (GET), emphasizing the central role of configurational entropy s_c in the dynamics of complex fluids. Our energy renormalization (ER) method involves varying the cohesive interaction strength in the CG models in such a way that dynamic properties related to s_c are preserved. We test this ER method by applying it to coarse-graining polymer melts (i.e., polybutadiene, polystyrene, and polycarbonate), representing polymer materials having a relatively low, intermediate, and high degree of glass “fragility”. We find that the ER method allows the dynamics of the atomistic polymer models to be faithfully described to a good approximation by CG models over a wide temperature range.

INTRODUCTION

Polymer glass-forming (GF) materials exhibit complex dynamic and mechanical properties that strongly depend on temperature due to the glass transition (1), and assessing these properties using all-atomistic (AA) molecular dynamics (MD) simulations is inherently challenging because of their limitations of accessing extended time and length scales. Multiscale modeling, such as coarse-grained (CG) modeling techniques, allows for overcoming the spatiotemporal limitations of AA-MD by removing the “unessential” atomistic features and thus reducing the number of degrees of freedom to probe the properties of interest (2). Several CG modeling approaches have been proposed to derive the CG force field from underlying AA models, including the inverse Boltzmann method (IBM) (3), force matching (also called the multiscale coarse-graining) (4, 5), relative entropy (6), inverse Monte Carlo methods (7), and some other approaches based on statistical mechanics (8, 9). While these approaches can preserve key static and structural properties [e.g., radial distribution functions (RDFs)] of the AA systems under coarse-graining, it has been a challenge to capture the dynamic features of those complex polymeric fluids to a good approximation using CG modeling. Several recent studies have shown that by introducing time-scaling factors (10) or nonconservative forces such as frictional and dissipative forces (11, 12), it is possible to develop the CG model to capture the AA dynamics and thermodynamics. However, the “temperature transferability” of CG modeling remains challenging because of a lack of understanding of the temperature effect on molecular friction parameters and relaxation properties of GF materials. This limits the practical usage of CG modeling to identify quantitative rather than qualitative trends in the properties of polymer materials in the temperature range in which they are used.

To address this fundamental problem, we recently proposed a coarse-graining strategy, called the energy renormalization (ER) method, aiming to preserve the dynamics of polymers over a wide temperature range (13) and thereby effectively address the temperature transferability issue in CG modeling. This approach borrows ideas from the Adam-Gibbs (AG) theory (14) and the generalized entropy theory (GET) of glass formation (15), both of which emphasize the critical role of the configurational entropy s_c in the dynamics of cooled liquids. As the system’s s_c decreases because of the reduction of number of degrees of freedom under coarse-graining, the CG models often exhibit an artificial speedup of the dynamics and divergent activation energies relative to the AA counterparts. However, our previous work has shown that this effect on the dynamics of CG models could be compensated by renormalizing the enthalpy of the system (based on the established “entropy-enthalpy compensation” effect) through tuning the cohesive interaction strength of the CG system, often parametrically related to the energetic cohesive interaction parameter ε in the commonly used Lennard-Jones (LJ) potential.

In the present study, we use the ER approach toward developing a CG model of bisphenol-A polycarbonate (BPA-PC) (or simply “PC”) (Fig. 1), which is ubiquitously used in practical applications, such as automotive parts, airplane windows, and high-quality optical lenses, because of its excellent mechanical properties (e.g., high impact strength and ductility and light weight), electrical resistance, and optical transparency. For comparison, we also include our previous simulation data of polystyrene (PS) (13) and polybutadiene (PB) (16) to better understand how the segmental structure influences ER under coarse-graining. In particular, PB is a representative of a wide class of polymers in which large deformability is applied in rubber and tire manufacturing, yet its glassy dynamics is still rather important because the relaxation times are also relatively strongly dependent on the temperature (17). The temperature dependence of relaxation in PS, another important commodity polymer, is intermediate between PB and PC, and these differences in their temperature dependence of structural relaxation can be quantified by the fragility of their glassy dynamics, which measures the sensitivity of the structural relaxation time or viscosity to temperature changes derived from packing “frustration” at a molecular level (18, 19).

Fig. 1. Mapping from AA model to CG model of PC.

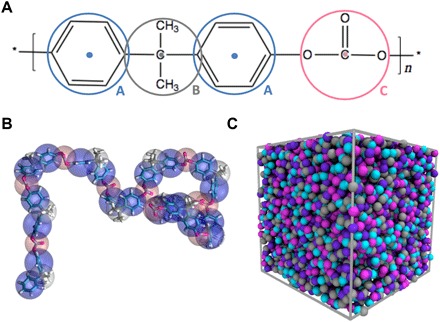
(A) PC chemical structure and the corresponding CG bead types and their force center locations. Each monomer consists of four CG beads with three bead types. The CG bead type “A,” “B,” and “C” represent the phenylene, isopropylidene, and carbonate groups, respectively. (B) The mapping from the AA model to the CG model of a PC chain. (C) Snapshot of the simulated CG model system.

Several previous studies on the development of the CG models of PC (developed via the IBM) have focused more on the static and structural properties, and those models typically exhibit a marked speedup in dynamics compared to its AA counterpart (20–22). In this study, we aim to develop a CG model using the ER method that can capture its temperature-dependent dynamic properties over a wide temperature range. In particular, by comparing three representative polymers having different segmental structures and fragilities (i.e., PB, PS, and PC), we are able to test the general applicability of the ER method of coarse-graining. To coarse-grain our model polymers, we use our recently developed formulation of the ER method by exploiting the localization model (LM) of relaxation that relates the Debye-Waller factor 〈u²〉, a fast-dynamic property defined at a picosecond time scale, to the long-time structural relaxation time τ. Here, we show that preserving 〈u²〉 of the AA model under coarse-graining through ER allows for predictions of dynamics over a wide temperature range. Our study reveals that the derived ER functions for the cohesive interaction of the CG polymer models exhibit a universal sigmoidal temperature dependence, which is strongly associated with their glass formation. Last, the same ER approach is investigated within the framework of the GET for a model flexible polymer, and our theoretical analysis likewise demonstrates a sigmoidal dependence of the cohesive interaction strength parameter of the CG model on temperature.

RESULTS AND DISCUSSION

Application of the ER method to coarse-graining polymer

Previous studies have demonstrated a scaling relationship between a short-time fast dynamics property, the Debye-Waller factor 〈u²〉, and the relaxation time τ via $\mathrm{\tau }~\text{exp}({\mathit{u}}_0^2/\langle {\mathit{u}}^2\rangle )$ with ${\mathit{u}}_0^2$ as an adjustable constant—also called the LM of relaxation—for describing the dynamics of GF liquids (23, 24). 〈u²〉 can be readily obtained from experimental measurements and short-time (on the order of picoseconds) simulations of the materials. In our simulations, the 〈u²〉 is determined from the mean-squared displacement (MSD) 〈r²(t)〉 of the center of mass of monomers of the AA and CG models at around t ≈ 4 ps, corresponding to a caging time scale estimated from our simulations. More recently, Betancourt and co-workers (25) established a more predictive relationship by reducing 〈u²〉 by its value ${\mathit{u}}_{\mathit{A}}^2\equiv \langle {\mathit{u}}^2({\mathit{T}}_{\mathit{A}})\rangle$ at the onset temperature T_A for molecular caging and by fixing the prefactor in the τ − 〈u²〉 relation by the observed value of τ at T_A, leading to the relation

$$\mathrm{\tau }(\mathit{T})={\mathrm{\tau }}_{\mathit{A}}\text{exp}[{({\mathit{u}}_{\mathit{A}}^2/\langle {\mathit{u}}^2(\mathit{T})\rangle )}^{{\mathrm{\alpha }}_0/2}-1]$$ (1)

where the exponent α₀ is related to the shape of the free volume (i.e., regions explored by the center of mass of a rattling particle in the fluid). In our recent work, we have applied this relationship, in conjunction with the ER method, to derive the CG potential for ortho-terphenyl (OTP), a small-molecule GF liquid (26). Here, we take this LM relation as the basis of a strategy for coarse-graining the dynamics of polymer melts. Specifically, we aim to derive the ER factor α(T) [i.e., ε(T) = α(T)ε₀, where ε is the cohesive interaction strength parameter in the commonly used LJ potential and ε₀ is a constant estimated from the radial RDF using the IBM] by preserving 〈u²〉 of the AA system to recover the T-dependent GF dynamics of the AA model over a wide range of T by its CG analog.

Taking PC as a representative polymer model system (Fig. 1), we first examine the influence of cohesive interaction strength by systematically varying α on the Debye-Waller factor 〈u²〉 for the CG model systems. As shown in Fig. 2, for each fixed α value, 〈u²〉 increases with temperature T in a nonlinear fashion for both the AA and the CG systems over a wide T range, which is typical for GF materials. As α increases from 2.5 to 5.0, the 〈u²〉 decreases at any given T, indicating a suppressed mobility when increasing the cohesive interaction strength of the CG system. For each α value, the measured 〈u²〉 of the CG model intersects with the AA 〈u²〉 at a different T. This demonstrates the necessity of renormalizing the cohesive interaction strength at varying T to preserve the value of 〈u²〉 of the AA model under coarse-graining. This observation is largely consistent with our recent work (13, 16, 26) and Chaimovich and Shell’s earlier study (27), emphasizing that the intermolecular potential parameters of CG models describing atomistic systems are generally state dependent. It should be noted that several earlier studies (28–30) have introduced several strategies such as the pressure-matching method to address the temperature transferability issue focusing on preserving the structural and thermodynamic properties of CG models, whereas our focus here is to develop a practical and efficient method for temperature-transferable coarse-graining that preserves the correct AA dynamics to the greatest extent possible.

Fig. 2. Influence of cohesive interaction strength on dynamics of CG model.

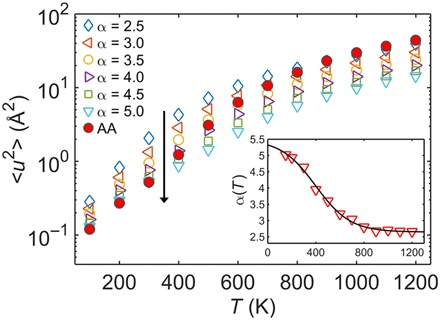
The Debye-Waller factor 〈u²〉 versus temperature T for the AA and CG models of PC with varying ER factor α for cohesive interaction strength. The vertical arrow indicates a dataset with increase in α. Inset: The result of α(T) for the CG model determined by preserving the T-dependent 〈u²〉 of the AA model of PC.

Accordingly, α(T) of the CG model can be phenomenologically determined by preserving T-dependent 〈u²〉 of the AA model, leading to a sigmoidal variation with T (inset in Fig. 2)

$$\mathrm{\alpha }(\mathit{T})=({\mathrm{\alpha }}_{\mathit{A}}-{\mathrm{\alpha }}_{\mathit{g}})\mathrm{\Phi }+{\mathrm{\alpha }}_{\mathit{g}}$$ (2)

where α_g and α_A are the α values in the low-T and high-T limits, respectively; Φ is a two-state crossover function having the form: Φ = 1/[1 + exp(− k(T − T_T))], where k is a parameter related to the temperature breadth of the transition and T_T describes the crossover point of this sigmoidal function. These parameters related to α(T) are summarized in the table S2.

Similarly, we perform the renormalization procedure for the length scale parameter σ through the renormalization factor β(T) for the cohesive interactions. As reported in our previous work (13), this β(T) can be readily determined by demanding the T-dependent density ρ of the CG model to be consistent with that of the AA model, which typically yields a decreasing trend of β(T), with T that can be captured by a polynomial form (table S2). With the implementation of β(T), the CG model can well capture the AA ρ over a wide T range (fig. S4). While β(T) is important to preserve certain static and structural properties of the polymer, such as the density and primary peak location in the RDF, the dynamics of polymer is mainly governed by α(T) as reported in a previous work (13). As a further test of our CG procedure with regard to preserving thermodynamic properties, fig. S4 also shows a good consistency of the T dependence of the isothermal compressibility κ_T between the AA and CG models, where we have reduced κ_T by its value at the onset temperature T_A. This normalization is required for scale-dependent properties whose absolute values cannot be preserved under coarse-graining, as discussed in our previous work for κ_T of the small-molecule model GF liquid, OTP (26).

Implementing the derived α(T) and β(T) for the cohesive interactions into the CG model of PC, we proceed to evaluate the dynamic properties of the CG model. We first look at the MSD 〈r²(t)〉 of the center of mass of monomers for the AA and CG models at various T. Figure 3A shows the comparison of the 〈r²(t)〉 for the AA (lines) and CG (symbols) models. By preserving the atomistic 〈u²〉 (marked by the vertical dashed line) under coarse-graining through ER, the developed CG model can capture the entire 〈r²(t)〉 curves of the AA model to a good approximation over a wide T range spanning from the high-T Arrhenius regime to the low-T glassy regime. We refer the reader to our previous papers for the theoretical motivation of this rescaling, which is described in great detail (13, 26). In the present study, we are more concerned with the general applicability of the method for different types of GF liquids to establish its robust applicability to real materials.

Fig. 3. Comparison of dynamics of AA and CG models over a wide range of temperature.

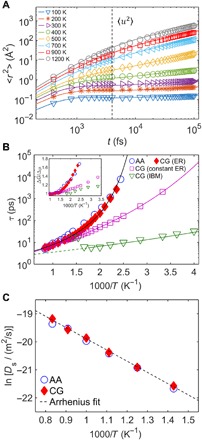
(A) The MSD 〈r²〉 of the center of mass of the monomer versus time for the AA (lines) and CG (symbols) models over a wide T range. The vertical dashed line marks the time scale (around the “caging” time of 4 ps) when 〈u²〉 is obtained from the 〈r²〉 measurement. (B) T-dependent segmental relaxation time τ for the AA and CG models. As a comparison, the τ estimates from the CG models with constant ER (i.e., α = α_A) and derived from the IBM exhibit a growing divergence as lowering T, while the τ estimates from the ER describe the AA τ to a much better approximation. The solid curves show the VFT fits of the τ data. The dashed curve for the CG model from the IBM shows a high T regime where the onset of sample evaporation leads to an increase in τ. Inset shows the activation energies of relaxation ΔG normalized by its value Δμ at high-T Arrhenius regime for the AA and CG models. (C) Self-diffusion coefficient D of chains at elevated T for the AA and CG models, which is well described by an Arrhenius relation (dashed line).

We next evaluate the segmental relaxation time τ by calculating the second Legendre order parameter P₂(t) for both AA and CG models. Figure 3B shows the results of the T-dependent τ for the AA and CG model with ER, which yields a good consistency. As a comparison, we apply a fixed ER factor by setting α = α_A (by matching the high-T AA activation energy) and α = 1 (a first estimate of the activation energy developed from IBM by matching the AA RDF) for the CG model. At temperatures outside the high-T Arrhenius regime (where polymer materials are not thermally stable), it is evident that a constant rescaling of the activation energy provides an inadequate description of the τ data, suggesting that the application of ER in a temperature-dependent fashion correctly captures the slowing down of relaxation dynamics upon approaching the glass-transition temperature (T_g). Formally, we may determine the activation energy of relaxation ΔG(T) through the relationship: ΔG(T) = k_BT ln[τ/τ₀], where τ₀ is the vibrational relaxation time on the order of 10⁻¹² to 10⁻¹³ s. The inset of Fig. 3B shows the results of ΔG normalized by its value Δμ at the high-T Arrhenius regime. The CG model with ER evidently describes ΔG of the AA model rather well, whereas ΔG without ER remains too small at low temperatures. This analysis indicates that CG models without ER simply fail to preserve the AA dynamics in the T range of practical application interest, an effect that we attribute to the loss of the configurational entropy s_c under coarse-graining. This “error” in CG modeling can be largely “corrected” by renormalizing the cohesive interaction strength, i.e., varying α. Later, we show an analytic example of how a change in s_c under coarse-graining might be calculated explicitly from the GET of glass formation and demonstrate that s_c in the non-Arrhenius regime, where s_c is variable with T, can likewise be corrected by making the molecular cohesive interaction variable to be T dependent.

The T dependence of our simulation estimates of structural relaxation time τ (Fig. 3B) can be well described by the well-known Vogel-Fulcher-Tammann (VFT) relation (31)

$$\mathrm{\tau }(\mathit{T})={\mathrm{\tau }}_0\text{exp}\left(\frac{\mathit{D}{\mathit{T}}_0}{\mathit{T}-{\mathit{T}}_0}\right)$$ (3)

where τ₀, D, and T₀ are fitting parameters that characterize the relaxation process of glass formation. Specifically, the VFT temperature T₀, dictates the “end” of glass formation, where τ formally extrapolates to an infinite value; D is inversely related to the fragility parameter K, i.e., $\mathit{K}\equiv 1/\mathit{D}$ (32). Correspondingly, we estimate T₀ to be around 301 K and the fragility K to be about 0.32 for both the AA and the CG model with ER to preserve this property. On the basis of the VFT fit, the T_g can be estimated by extrapolating the relaxation data to the empirical observation time scale τ(T_g) ≈ 100 s, where we find the T_g to be around 330 K for the simulated systems. Using the same method, we also calculated the fragility parameters for the PS (K = 0.29) and PB (K = 0.18) models as reported in our recent work (16), which are smaller compared to the PC model.

At T above the onset temperature T_A (estimated from the τ data) (25), the dynamics of polymer fluids is mainly governed by the large-scale chain motion rather than the segmental mobility. We next examine the self-diffusivity D_s of polymer chains at the high-T melt states (above T_A ≈ 700 K) from around 700 to 1200 K. D_s is obtained from the MSD measurement of the center of mass of chains 〈r_CM²(t)〉 in the diffusive regime, where 〈r_CM²〉 ~ t. At T below this high-T regime, it is challenging to accurately quantify D_s of polymers through MD, as it requires much greater time to fully get into the diffusive regime due to the dramatic slowdown of the chain mobility. Figure 3C shows a good consistency of D_s between the AA and the CG using the ER method, which exhibit a slowdown of diffusion as T decreases. Their T dependence follows an apparent Arrhenius behavior: ${\mathit{D}}_{\mathrm{s}}(\mathit{T})={\mathit{D}}_0\text{exp}(-\frac{\mathrm{\Delta }\mathit{E}}{{\mathit{k}}_{\mathrm{B}}\mathit{T}})$, where D₀ is a prefactor and ΔE is the activation energy of diffusion. From the Arrhenius fit of the data, ΔE is estimated to be around 33.4 kJ/mol∙K for both AA and CG models.

Previous studies (10, 33) have shown that it is possible to capture the dynamics of the AA models under coarse-graining by rescaling the time such that the D_s and the VFT behavior of relaxation can be recovered. This method works mostly at higher temperatures since the system can enter into the diffusive regime in a relatively short time. However, using a single time-rescaling factor fails to reproduce the entire 〈r²(t)〉 curve of the AA model at a lower temperature due to the noticeable existence of the ballistic regime and subdiffusive regime. Here, we have shown that the CG model developed using the ER approach can reproduce the atomistic dynamics and entire 〈r²(t)〉 curves over a wide T range, which is a significant feat in CG modeling of GF polymers, whose relaxation processes are rather complex and involve different relaxation mechanisms occurring at different time scales depending on T. For more complicated polymer systems exhibiting hydrogen bonding network such as polyamide-66, it has been reported that the developed CG model typically exhibits faster dynamics of hydrogen bonds compared to the atomistic model (34). In a future study, it would be interesting to test whether the current ER method is capable of preserving the dynamics of hydrogen bonding fluids under coarse-graining.

Comparison of CG polymers with different segmental structures

Our present results demonstrate the success of the ER method, in conjunction with the generalized LM, to develop a temperature-transferable CG model of PC. We show that by preserving 〈u²〉 of the AA model through renormalizing the cohesive interaction under coarse-graining, the CG model can well capture the dynamics of the underlying AA model over a wide T range from the supercooled glassy regime (below T_g) to the high-T melt regime (well above T_g). The derived ER factor α(T) for the cohesive interactions exhibits a sigmoidal variation with T. Figure 4 shows a comparison of the derived α(T) normalized by α_A for different polymers—PB (i.e., a relatively strong and flexible polymer), PS with a side group (i.e., a semiflexible polymer) and PC (i.e., a relatively fragile polymer). The details of the CG models of PS and PB can be found in our recent work (13, 16). It can be observed that although the chemical structures and GF properties are appreciably different for these three polymers (Fig. 4A), their α(T) universally exhibit sigmoidal variations with T with different magnitudes (Fig. 4B). Specifically, α(T) tends to be plateau values in the high-T Arrhenius and low-T glassy regimes, exhibiting a higher magnitude at a lower T. However, in the non-Arrhenius regime at intermediate T between the glassy and Arrhenius regimes, α(T) is strongly scaled with T. This sigmoidal T dependence of α is also consistent with the predictions from the GET and AG theory that activation energy of relaxation of GF liquids increases upon cooling due to the decrease of the configurational entropy s_c and saturates at both low- and high-T limits (14, 15). This saturation effect of the activation energy and also estimates of the s_c have been experimentally observed (35–37) and predicted by the recent molecular simulations and the GET (38, 39). From Fig. 4B, it also suggests that for the relatively fragile PC, the transition of the crossover of α(T) is broader than that for the PS and PB, which can be attributed to its larger T range of non-Arrhenius relaxation associated with glass formation.

Fig. 4. Energy renormalization for CG polymers having different segmental structures.

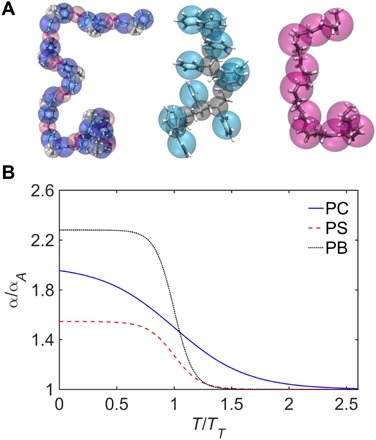
(A) Schematic of the developed CG models of PC, PS, and PB (from left to right) having distinct segmental structures by the ER method. The CG models are overlaid with the underlying AA models. (B) The ER factor α (normalized by its high-T limit α_A) as a function of temperature for the developed CG models of PC, PS, and PB for achieving temperature-transferable coarse-graining of their dynamics.

Another important observation is that α/α_A at lower T is higher for the CG-PB compared to the CG-PS and CG-PC, which indicates that it requires a greater ER for PB to correct the activation energy under coarse-graining. This is not obvious, as PB is a relatively strong glass former, corresponding to a lower fragility. We suggest that this trend can be attributed to the higher degree of coarse-graining λ for the CG-PB model (i.e., “coarser-grained” model) compared with the relatively “fine-grained” CG-PS and CG-PC models. The larger bond length of the CG-PB molecule is consistent with this suggestion. Recent studies have indicated that the bond length greatly influences the fragility of CG models of polymers (40, 41). For the CG models of PC and PS having a similar λ, we find that α/α_A is larger at lower T for PC, which is probably related to its high fragility compared to PS. This observation suggests that the fragility of the polymers should have a large influence on ER factor α, which is natural given evidence that packing efficiency is a significant factor in relation to fragility and that alteration in molecular structure must influence the character of molecular packing (32). We may obtain quantitative insight into these changes of α/α_Aunder coarse-graining from a consideration of the GET of glass formation (15)—a combination of the AG model (14) and the lattice cluster theory (42)—which allows for a direct theoretical calculation of the configurational entropy s_c of polymer melts composed of molecules having different structures, molecular rigidities, and intermolecular interactions.

Analytic investigation of ER method based on the GET

In this section, we summarize illustrative calculations of the effect of coarse-graining on the configurational entropy of model polymer melts based on the GET of glass formation to gain a better theoretical understanding and justification of the ER coarse-graining method. While monomer structures and other molecular factors such as chain stiffness of polymers have been successfully incorporated into the GET (15, 43), here, we consider the simpler model of polymer melts composed of fully flexible linear chains. This restriction is because the GET for semiflexible polymers has its limitations at low T. In particular, this type of lattice model calculations for semiflexible polymers leads to vanishing of s_c at a low finite T that was identified by Gibbs and DiMarzio (44) as an “ideal” T_g. Unfortunately, later analytic and simulation studies have shown that this transition is probably just an artifact of the high-T expansion treatment of chain stiffness (15, 43). However, this mathematical problem no longer exists in the case of flexible polymers (39). All calculations are performed at a constant pressure of P = 0.101 MPa and use a lattice coordination number of z = 6. In line with the simulations, we consider relatively short chains. The reference or “AA” model in the GET is selected to be a polymer melt with M = 24 and ε/k_B = 200 K, where M designates the number of united atom groups in a single chain and ε is the cohesive energy parameter. Specifically, we investigate different degrees of coarse-graining λ on the ER factors by performing calculations for M = 12, 8, and 6 as “CG” models in the GET, corresponding to increasingly coarser-grained models with increasing λ. The cell volume parameter V_cell is adjusted for each M such that the total volume of a single chain is preserved to be a constant of MV_cell, a common requirement in the CG modeling of polymers. More details of the GET calculations are included in the Supplementary Materials.

Figure 5A shows the GET results of the relaxation time τ as a function of T for the CG model with M = 6 at various ε, along with the result for the reference AA model (M = 24). It is evident that T-dependent ER factors for the CG model are required to capture the dynamics of the AA model, as marked by the cross-interaction between the AA (dashed line) and CG (solid lines) with ε. This picture is in line with what we observed in Fig. 2. Figure 5B shows the determined ε as a function of T for various M. Consistent with our simulations, the GET predicts that the ER factors have a sigmoidal variation with T regardless of the degree of coarse-graining, indicating a large cohesive energy required at lower T. Figure 5B reveals that a higher degree of coarse-graining with a smaller M requires ER factors with greater magnitudes to preserve the relaxation dynamics of the AA model, which might explain why the CG-PB model at lower T requires a somewhat larger ER factor in comparison with the CG-PS and CG-PC models (Fig. 4B).

Fig. 5. Analytic calculations of ER factors based on the generalized entropy theory (GET).

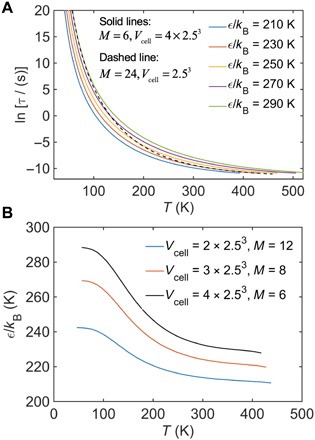
(A) Temperature dependence of structural relaxation time τ for different cohesive interaction parameter ε, as calculated from the GET for a polymer melt composed of fully flexible linear chains with M = 6 and V_cell = 4 × 2.5³ at a constant pressure of P = 0.101 MPa (see main text for details). The dashed line displays the result for M = 24, V_cell = 2.5³, and ε/k_B = 200 K, which is the analog of the AA model in the GET calculation. (B) Temperature-dependent cohesive interaction parameter ε for various M determined by applying the ER method to the GET result. The rescaling of ε is obtained by requiring an identical τ between the reference or AA (M = 24) and “CG” (lower M) models at each T. As in the case of our MD simulations, coarse-graining in the GET leads to an effective ε having a sigmoidal T dependence.

In the previous effort by Foley et al. (45), it has been shown that the resolution of the CG representation has a direct impact on the temperature dependence of the potential of mean force for a CG model through its influence on the loss of configurational entropy under coarse-graining. While their study was mainly focused on the structural and thermodynamic properties of the CG model rather than the dynamics, their observation on the effect of degree of coarse-graining on the configurational entropy is largely in line with our results of MD simulations and GET predictions. The GET not only demonstrates the applicability of the ER method to coarse-graining different polymer models but also provides a feasible route to analytically calculating the loss of configurational entropy under coarse-graining and thus α(T) (with a sigmoidal T dependence) based on the assumption that the activation energy of structural relaxation is proportional to the cohesive interaction strength. Of course, the treatment of this problem requires some further development of the GET calculations of the dynamics and thermodynamics changes accompanying coarse-graining, and we leave this matter to a future investigation.

CONCLUSION

In the present study, we have applied our previous established ER method to develop a temperature transferable CG model of three distinct classes of polymers, i.e., PB, PS, and PC, defined as having low, intermediate, and high fragility, respectively. By exploiting the LM and AG theory of glass formation, we have shown that preserving the AA 〈u²〉, i.e., a fast dynamics physical property at a picosecond time scale, by renormalizing the cohesive interaction parameter ε through α(T) under coarse-graining, the CG model can well capture the GF dynamics of the underlying AA system over a wide T range, from the high-T Arrhenius regime to the intermediate non-Arrhenius regime of glass formation and low-T glassy regime. We show that the ER function α(T) of these different GF polymers universally exhibits sigmoidal variation with T to achieve temperature transferability of their dynamics. Furthermore, the GET of glass formation predicts that coarser-grained models require larger ER factors to preserve the AA dynamics. Our work illustrates the effectiveness and applicability of the ER approach toward building a multiscale temperature-transferable modeling framework for the polymers having different segmental structures, and particularly implies the critical roles of GF properties, such as fragility, and degree of coarse-graining in influencing the CG modeling.

MATERIALS AND METHODS

Description of the CG polymer model

To coarse-grain the AA BPA-PC model, we applied a four-beads-per-monomer mapping scheme, with three different CG bead types A, B, and C, representing phenylene, isopropylidene, and carbonate groups, respectively (Fig. 1A). Figure 1B shows a snapshot of the CG model of one PC chain with a chain length of N = 10 (i.e., number of monomers per chain) overlaid with the atomistic model. A similar mapping scheme for coarse-graining PC has also been adopted in previous works (20–22). The bonded interactions of the CG model, including bonds, angles, and dihedrals, were derived by matching their probability distributions of the AA model using the IBM. The detailed derivation and description of the coarse-graining procedure for the bonded interactions are shown in the Supplementary Materials.

The non-bonded interactions between the CG beads are represented by the standard 12-6 LJ potential: $\mathit{U}(\mathit{r})=4\mathrm{\epsilon }[{\left(\frac{\mathrm{\sigma }}{\mathit{r}}\right)}^{12}-{\left(\frac{\mathrm{\sigma }}{\mathit{r}}\right)}^6]$, where σ governs the effective van der Waals radius and marks the distance where U is 0 and ε is the depth of the potential, a parameter associated with the cohesive interaction strength of the material. The cutoff distance of the LJ potential is 1.5 nm. To achieve the temperature transferability, we introduced temperature-dependent renormalization factors, α(T)and β(T), to rescale ε [i.e., ε(T) = α(T)ε₀] and σ [i.e., σ(T) = β(T)σ₀] for each CG bead type, respectively, where ε₀ and σ₀ are constants that can be taken as initial estimates of ε and σ from the RDF measurement using the IBM. On the basis of our previous work, β(T) was obtainable by preserving the density of the AA system. Here, we focused more on deriving α(T) for the non-bonded cohesive interactions of the CG model since these interactions play a critical role in the dynamic and thermomechanical properties of GF polymers (46).

Calculation of dynamics properties

The CG and AA-MD simulations were carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator software (47). In our simulations, the Debye-Waller factor 〈u²〉 was determined from the MSD 〈r²(t)〉 of the center of mass of monomers of the AA and CG models at around t ≈ 4 ps, corresponding to a caging time scale estimated from our simulations. The segmental relaxation time τ was evaluated by calculating the second Legendre order parameter P₂(t): ${\mathit{P}}_2(\mathit{t})=\frac{3}{2}\langle {\text{cos}}^2\mathrm{\theta }(\mathit{t})\rangle -\frac{1}{2}$, where θ(t) is the angle of a pseudo “bond” vector—defined as CG beads “B-C” between the consecutive isopropylidene group (i.e., labeled as a B-type CG bead) and carbonate group (i.e., labeled as a C-type CG bead)—under consideration at a time t relative to its position at t = 0. For the calculation of self-diffusion D_s, we calculated the MSD of the center of mass of polymer chains via the Einstein relation of the form: ${\mathit{D}}_{\mathrm{s}}={\text{lim}}_{\mathit{t}\to \infty }\frac{1}{6\mathit{t}}\langle {[{\mathit{r}}_{\text{CM}}(\mathit{t})-{\mathit{r}}_{\text{CM}}(0)]}^2\rangle$, where r_CM(t) is the position of the center of mass of each chain at time t.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/4/eaav4683/DC1

Section S1. Overview of MD simulations

Section S2. Bonded potentials for the CG-PC model

Section S3. Analytic calculations of ER based on the GET

Fig. S1. CG bond potentials.

Fig. S2. CG angle potentials.

Fig. S3. CG dihedral potentials.

Fig. S4. Density and isothermal compressibility of AA and CG models.

Table S1. Functional forms of force field and bonded potential parameters for CG model.

Table S2. Functional forms and parameters of the ER function for the CG model.