Accuracy of Left Ventricular Cavity Volume and Ejection Fraction for Conventional Estimation Methods and 3D Surface Fitting

Abstract

Background

While left ventricular cavity volume (LVV) and ejection fraction (LVEF) are used routinely for clinical decision‐making, the errors in LVV and LVEF estimates in the clinic have yet to be rigorously quantified and are perhaps underappreciated.

Methods and Results

The goal of this study was to quantify the accuracy and precision of several common geometric‐model‐based methods for estimating LVV and LVEF using a highly sampled, high‐resolution magnetic resonance imaging data set and an independent ground truth. The effect on LVV and LVEF accuracy of slice number and orientation was also studied. When using the common geometric assumptions and limited short‐ and/or long‐axis views, the expected LVEF measurement uncertainty can be as high as 49%. The composite midpoint rule applied to a stack of short‐axis slices can achieve LVEF error <3% and LVV error of ≈10%, but in the clinic an additional ≈8% uncertainty is expected. An analogous approach applied to a series of radially prescribed long‐axis slices can achieve higher LVEF accuracy, up to 3.9% with 12 slices, and more reliable LVV measurements than methods based solely on short‐axis images. Using a mathematical 3‐dimensional surface model that incorporates anatomic information from multiple views achieves superior accuracy, with LVEF error <4% and LVV error <2.5% when using 6 slices in each short‐ and long‐axis view.

Conclusions

Combining anatomical information from multiple views into a conformal 3‐dimensional surface model greatly reduces errors in LVV and LVEF estimates, with potential clinical benefit via improved early detection of cardiac disease.

Clinical Perspective

What Is New?

• The accuracy and precision of 9 commonly used and 2 recently proposed methods for estimating left ventricular volume and ejection fraction (LVEF) from medical images have been quantified under a variety of slice configurations in a deforming canine heart against an independent ground truth.

• Under nearly ideal imaging conditions, LVEF errors range from 10% to 37% when applying the common geometric models to 3 or fewer measurements, and 3% to 7% when using the composite midpoint method to stacks of 4 to 6 short‐axis slices, but larger errors are expected clinically.

• Methods that incorporate multiple long‐axis views are more accurate and reliable than methods that rely only on short‐axis image slices, in part because they are better able to capture the mitral valve annulus and the apical‐most aspect of the left ventricle throughout the cardiac cycle.

What Are the Clinical Implications?

• Large errors in left ventricular volume and LVEF estimates are present when relying on 3 or fewer measurements and simple geometric models, such as with the Teichholz method (LVEF error >30%); therefore, these methods should be used with caution.

• Left ventricular volume and LVEF errors are expected to increase substantially for imaging modalities and/or slice prescriptions where the endocardial border is less accurately delineated.

• Combining geometric information from multiple views and slices into a conformal 3‐dimensional model of the left ventricular endocardial surface enables the quantification of small (<5%) changes in left ventricular volume or LVEF with statistical certainty, thereby reducing the number of subjects needed for clinical trials and permitting earlier diagnosis of subclinical cardiac dysfunction.

Introduction

Left ventricular cavity volume (LVV) and ejection fraction (LVEF) have well‐established correlations with prognosis and recovery following treatment for a variety of heart conditions.1 However, the accuracy and precision of LVV and LVEF estimates as applied in the clinic have yet to be rigorously quantified, bringing into question the reliance of these metrics for certain applications. For example, San Roman et al2 concluded that LVEF measurement methods need to achieve >5% precision for use in clinical trials of investigative cell therapies, where LVEF changes of only 3% to 5% are expected. Jenkins et al3 asserted that for clinical acceptance, a LVV or LVEF estimation method must match the accuracy of magnetic resonance imaging (MRI)‐based measurements to within 5%, and that 2‐dimensional echocardiography methods do not meet this criterion.

Sources of Error

The primary sources of error in estimation of LVV and LVEF are (1) errors in segmentation of the endocardial border from 2‐dimensional images; (2) inability to sample the entire extent of the left ventricle (LV) from base (at the mitral valve annulus) to the apex; and (3) geometric assumptions used to interpolate in regions where measurements are sparse and/or noisy. Endocardial border segmentation is adversely affected by inadequate contrast or noise at the myocardial edge, and by partial volume effects typically caused by large slice thickness relative to wall curvature. A small error in border segmentation can lead to a relatively large error because of the radius‐cubed dependence of volume on radius. For example, for a 40‐mm‐diameter spherical LV cavity, a 1‐mm underestimation in wall radius will result in a 14% underestimate of LVV. Inadequate sampling of the endocardial surface is typically caused by both lack of time available to acquire a sufficient number of image slices, and inability to acquire images in optimal orientations because of anatomical constraints. Common sampling errors are the inability to delineate accurately the mitral valve annulus and the heart apex from a stack of short‐axis cut‐planes, and to miss undulations of the endocardial wall that occur between radially oriented long‐axis slices. Methods for interpolating between surface measurements are commonly used to overcome the inability to sample over the entire heart volume at all time points, and the inability to accurately delineate the true endocardial border from an image cross‐section. The most common approach is to fit sparse surface data to a simplified geometric model such as an ellipsoid, as championed by Dodge et al4, 5 as early as 1960.

Previous Comparative Work

The quality of LVV and LVEF estimates obtained using a variety of imaging modalities has been addressed previously,3, 6, 7, 8, 9, 10, 11 but the majority of studies merely compared one estimate technique against another without a reliable independent ground truth.7, 12 Thermodilution and angiographic imaging have been used historically as a criterion standard; however, both methods involve simplified geometric assumptions that can severely diminish their accuracy. Magnetic resonance imaging (MRI)–based metrics are also not necessarily viable for ground truth because large discrepancies in LV volume and LV mass estimates occur when using different MRI acquisition and estimation techniques, and with different experts making inferences from the same images.6 In a few notable cases, investigators used as ground truth mechanical cardiac phantoms with simulated ventricular volume changes, for comparison with imaging‐based estimation techniques.6, 10, 13, 14, 15, 16 However, all previous synthetic phantoms had simplistic, often elliptical geometries that too closely matched the simple LV models being tested and had smooth internal walls that did not provide a realistic challenge in delineating the trabeculated and convoluted LV endocardial border.

Previous Validation Work

The most convincing validation studies used actual hearts for geometry and an independent (nonimaging) means for determining the ground truth. Dodge et al5 used excised human hearts and computed correction factors to relate their ellipsoidal model to actual LV volumes. Wyatt et al17 used formalin‐fixed canine left ventricles to validate the use of echocardiography with 6 to 10 short‐axis slices, against several common geometric LVV models. Bloomgarden et al6 imaged animal hearts in vivo using MRI and echocardiography and then excised and weighed the hearts to test the accuracy of LV mass estimates. Creswell et al18 used a fixed canine heart to validate estimates based upon short‐axis MRI slices. Validation of stroke volume and ejection fraction requires a more elaborate experimental design to allow for heart contraction and/or expansion. Mondelli et al19 implanted an electromagnetic flow‐probe around the aorta in dogs to measure stroke volume for comparison with 3D echocardiography in vivo; however, validation of LVV, and thereby LVEF, was not performed. Siu et al20 used an in vivo canine experimental preparation wherein the heart was placed on total bypass, the LV isolated from the remainder of the circulation, and instantaneous LVV was measured by use of an intracavitary balloon connected to an external fluid column. The heart was paced and contracted against the load of the fluid column, with change in volume measured as the time‐varying height of the column. They used this setup to test an early form of 3D echocardiography. Eaton et al21 used a similar experimental setup to test cross‐sectional echocardiography at 16 to 21 short‐axis slices.

Limitations of Previous Work

A limitation of the prior studies involving deformation of real hearts was that they used either ventriculography or echocardiography as their imaging modality.17, 19, 20, 21 While both of these imaging modalities are used commonly in the clinic, they are regarded as having inferior effective resolution and endocardial border delineation in comparison to modern MRI and x‐ray computed tomography. These limitations may contribute to significant errors that can mask differences in accuracy attributable to factors such as the number of imaging planes, imaging plane angles, image resolution, and the choice of geometric model used for estimating LVV.

Aims of this Study

The experimental goal of this study was to quantify errors in LVV and LVEF in a deforming, living heart using an intracavitary balloon for independent ground truth, and high‐resolution, contrast‐enhanced, multiplanar MRI to measure geometric data. With this data set, we sought first to interrogate the errors inherent to the several common geometric models in relation to the number of slices and views. Second, we sought to evaluate a representative conformal 3D surface fitting method to combine information from multiple views and slices, with the hypothesis that this would provide improved accuracy and precision in LVV and LVEF estimates, suitable for many investigational clinical trials.

Methods

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Common Volume Geometric Methods Used in the Clinic

Composite midpoint integration method

The commonly used composite midpoint integration method applies to parallel stacks of short‐axis image planes that, ideally, encompass the entire extent of the LV from the mitral valve annulus to the apex (Figure 1). The LVV is estimated by multiplying the observed cavity area on each slice, A, times the slice thickness, h, to get the volume contribution of each slice, and summing these over all slices (Eqn. 1 in Figure 1). This “stack of disks” approach is also commonly referred to as the Simpson's Rule; however, in mathematics the Simpson's Rule refers specifically to integration using quadric polynomials.22 In this article, the in‐plane cavity area was computed numerically from the user‐selected LV endocardial contour, but in the clinic is often approximated from 1 or 2 user‐defined diameter measurements and a circular or elliptical model for the in‐plane area. A common variant implemented by Wyatt et al17 models the most apical aspect of the LV as a hemisphere that emanates from the bottom half of the most apical slice (Eqn. 2 in Figure 1).

Figure 1.

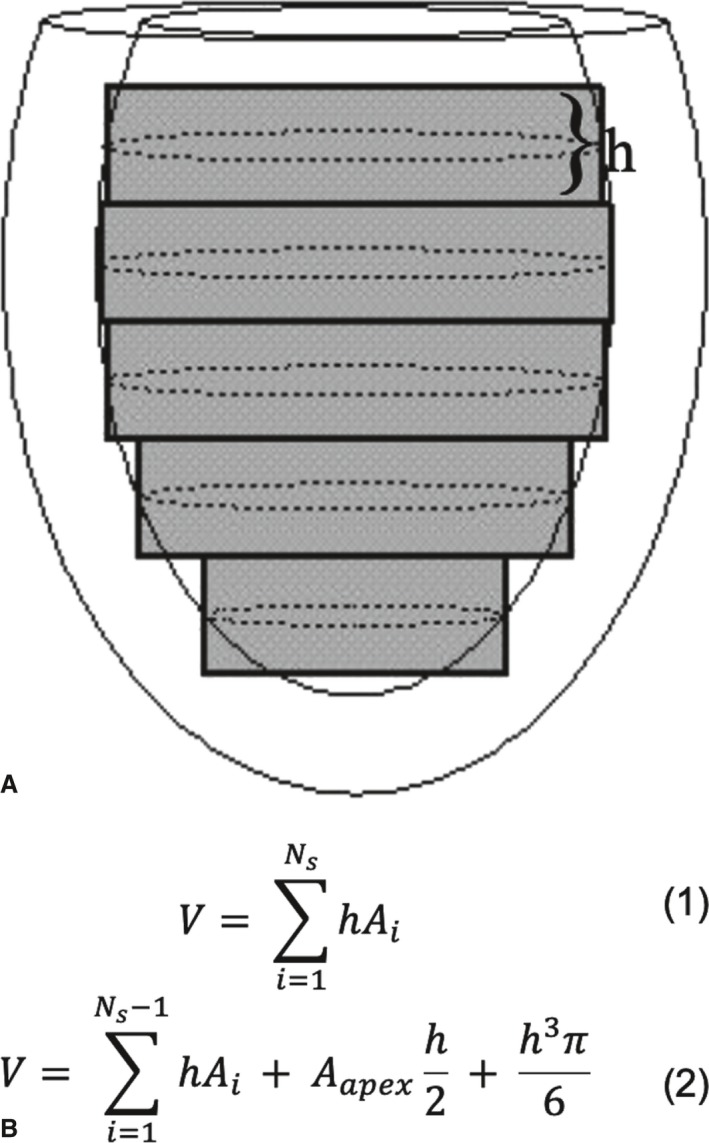
Composite midpoint integration methods for parallel short‐axis image data. A, A diagram of an elliptical virtual left ventricle in a slightly oblique side view with short‐axis cut‐planes of thickness h indicated by gray rectangles. The in‐plane endocardial contours are depicted as dotted‐line ellipses. B (top), Gives the equation for the basic composite midpoint integration method as sum over all (N _s) cross‐sectional slice areas (A _i). B (bottom), Gives a variant from Wyatt et al17 intended to correct for curvature effects at the apex. The sum is over all slices except the apex, then adds half the apex volume plus the volume of a hemisphere of radius equal to half the slice thickness.

Ellipsoidal models

Elliptical and semi‐elliptical models are typically used when only 1 or a few imaging planes are available, and are commonly used with x‐ray ventriculography, single positron emission computed tomography, radionuclide ventriculography, and 2‐dimensional echocardiography.23 Five common methods of computation are depicted in Figure 2 (Eqns. 3–7). The Dodge‐Sandler model4, 5 takes the biplane long‐axis ellipse equation (Eqn. 7) and applies correction factors (in units of cubic centimeters) derived from measurements made on excised human cadaver specimens:

$$V^{\prime }=0.928·V-3.8.$$ (8)

Figure 2.

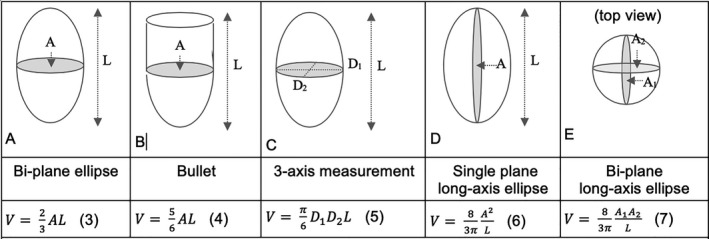
Ellipsoidal and semi‐ellipsoidal geometric models of the left ventricle (LV). The top row depicts the geometric model, the middle row provides the adjectives for each model used in this article, and the bottom row provides the corresponding equation for LV cavity volume. Models (A, C through E) are based on a full‐ellipsoid. The bullet method (B) combines and ellipsoidal bottom with a cylindrical top. Method (E) was championed by Dodge et al4, 5 but used an experimentally determined correction factor based upon human cadaver measurements (Eqn. (8)).

Teichholz's formula

For M‐mode echocardiography, Teichholz's Formula24 (Eqn. (9)) is commonly used. It considers only the largest short‐axis diameter seen on a long‐axis view and estimates the long‐axis cavity diameter based on a model derived from measurements of 100 patients. The LVV (in units of milliliters) is then estimated using a variant of the Dodge‐Sandler model:

$$V=\frac{7D^3}{2.4+D}$$ (9)

Bloomgarden's multiple long‐axis method

When multiple radially oriented long‐axis views are prescribed, the method of Bloomgarden et al6 can be used. The volume contribution for each adjacent contour point pair, [p _i, p _i+1], resembles a pie‐slice and is computed from the average distance from each contour point to the prescription central axis, R _p =(R _i+R _i+1)/2, and the angular separation between the N _s imaging planes, 2π/N _s, via:

$$V=\sum _{s=0}^{N_s}\sum _{p=0}^{N_p-1}\pi R_p^2·\frac{\mathrm{\Delta }{x}_p}{2N_s}$$ (10)

where πR _p ² is the area of the associated disk, Δx _p is the separation between the contour points along the direction of the central axis, N _s is the number of long‐axis slices, and N _P is the number of contour points. This approach was later adopted by Bloomer et al25 to estimate LV mass. This equation, however, relies on the central axis passing exactly through the true apex, which is rarely the case. Figure 3 shows an exaggerated depiction of the effect of this discrepancy. The approach was therefore augmented in this article to account for the volume of myocardial tissue contributed by contour points located between the apex line and the central axis.

Figure 3.

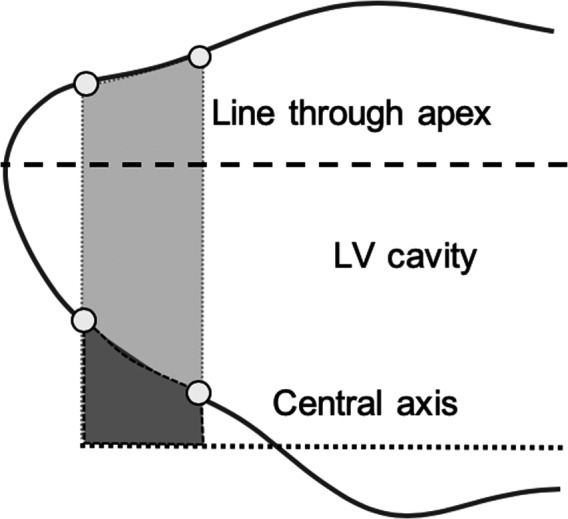
Augmented Bloomgarden method. The volume contribution for contour point pairs above the true apex line (light gray region) contains both left ventricular (LV) cavity and myocardial tissue. Contour point pairs that lie between the true apex line and the prescription central axis contribute only myocardial tissue (dark gray region). The LV cavity volume in the augmented Bloomgarden method is computed by adjusting Equation (10) to subtract the myocardial tissue volume.

Conformal 3D surface fitting

A conformal 3D surface model can be used to combine information from multiple views while interpolating through regions where surface information is sparse. Several methods have been proposed for surface modelling, including finite elements,26, 27 3D active contours,28 and surface B‐splines.18 In this article, the endocardial LV surfaces were represented as an analytical equation for the radial distance, λ, as a function of the longitudinal and circumferential angles, φ and θ, expressed in a prolate‐spheroidal coordinate system, as described previously.29 The series expansion is given by:

$$\begin{array}{cc}\hfill \lambda (\phi ,\theta )& =\sum _{l=0}^L\sum _{m=-l}^l{a}_i{P}_l^{|m|}(cos\phi )·\left\{\begin{array}{cc}sinm\theta \hfill & m>0\hfill \\ cosm\theta \hfill & m\le 0\hfill \end{array}\right.\hfill \\ & =a_0+a_{1}sin(\phi )sin(\theta )+a_{2}cos(\theta )\hfill \\ & +a_{3}sin(\phi )cos(\theta )+a_{4}sin{(\phi )}^{2}cos{(\theta )}^2\hfill \\ & +a_{5}cos(\phi )sin(\phi )cos(\theta )+a_6{(3cos(\mu ))}^2-1)\hfill \\ & +a_{7}cos(\phi )sin(\phi )sin(\theta )\hfill \\ & +a_{8}sin{(\phi )}^{2}sin{(\theta )}^2+\dots \hfill \\ & =\mathit{a}*\mathit{E}\hfill \end{array}$$ (11)

where a=[a₀, a₁, a₂, a₃, …] are the coefficients to be fitted, P _l ^|m|(x) are the Associated Legendre Polynomials, and the vector transpose of E,E ^T are the terms in the series: [1, sin(φ) sin(θ), cos(θ), cos(φ) sin(θ), …]. The 0th‐order term represents the prolate‐spheroidal shell (an ellipsoid) that best fits the contour data. The higher order terms introduce surface modulations onto this elliptical shell. The advantage of using a prolate‐spheroidal coordinate system over Cartesian and cylindrical coordinate systems is that it achieves a close representation of the heart geometry with relatively few terms, thereby giving a higher statistical confidence in the fit. For each sampled surface point, p, and its corresponding set of coordinates, (λ_p, θ_p, φ_p), each term in the vector E is evaluated. From all sampled surface points, a series of simultaneous equations is created and the unknown coefficients, a, are solved using singular value decomposition.30 The best‐fit location of the centroid and apical focal point of the coordinate system are determined by using a 0th‐order fit and adjusting their locations to achieve the least‐squares minimum miss between the ellipsoid and the sampled surface points. Once the coefficients were determined, a grid of 40 circumferential by 40 longitudinal surface mesh points were defined, with the top of the mesh being open and coinciding with the mitral valve ring. This grid density (1600 points in total) was determined to introduce negligible error to the volume estimation (data not shown).

Isolated Canine Heart Preparation

The experimental procedures were conducted according to the American Association for Accreditation of Laboratory Animal Care guidelines for the use of animals in research. A mongrel dog (50–60 lb) was anesthetized with sodium pentobarbital. Heart isolation was achieved using a protocol similar to that detailed by Eaton et al21 and Suga and Sagawa,31 where our objective was to achieve a realistic representation of passive filling of the LV from end‐systole to end‐diastole. Active contraction of the myocardial tissue was not required, so the heart was induced into a passive state, though living and metabolically active, that was stable for several hours without need for perfusion via a separate donor dog or bypass device. In brief, heparin was injected to prevent clotting of the coronary vessels. A cannula was placed into the proximal aorta through the left brachial artery and adenosine (for vasodilation) and a chilled cardioplegic solution (St. Thomas Hospital solution) were back‐perfused into the coronary tree to facilitate cardiac arrest. Extraneous tissue, including fat pads and parts of the atria, and the majority of the right ventricle were removed to ensure that no portion of the heart contacted the bath chamber wall during filling.

After heart isolation, the mitral valve chordae tendonae were cut and a Teflon valve ring collar was sutured to the mitral valve annulus. This collar facilitated the insertion of a balloon into the LV cavity and attachment of the LV to a computer‐controlled pump‐nozzle assembly. An 8‐foot‐long Plexiglas extension tube was inserted between the servo‐pump assembly and the nozzle to maintain the metallic pump at a safe operating distance from the center of the magnet. The relationship between pump head displacement and balloon volume was calibrated using a standing water column. A slit was made through the myocardium at the LV apical dimple to facilitate emptying of any fluids trapped between the balloon and the myocardium. An MR‐compatible catheter‐tip pressure transducer (Millar Instruments Inc., Houston, TX) was positioned through the balloon and mitral valve opening to monitor cavity pressure in real time. The balloon was suitably large when deflated to remain nondistended during the entire filling cycle to enable it to conform fully to the LV endocardial surface and not contribute to elevated cavity pressure. A diagram of the pump assembly is shown in Figure 4. Sinusoidal volume excursions were applied to the passive hearts to achieve physiologic pressures from 0 to 11.5 mm Hg for the diastolic filling phase of the cardiac cycle. Deuterated water (D₂O) produces no MR signal and was introduced into the water that filled the balloon to improve MR signal contrast between the myocardium and the cavity. The volume of the balloon was measured as 4 mL and this value was added to that of the water column to get the total volume inside the LV.

Figure 4.

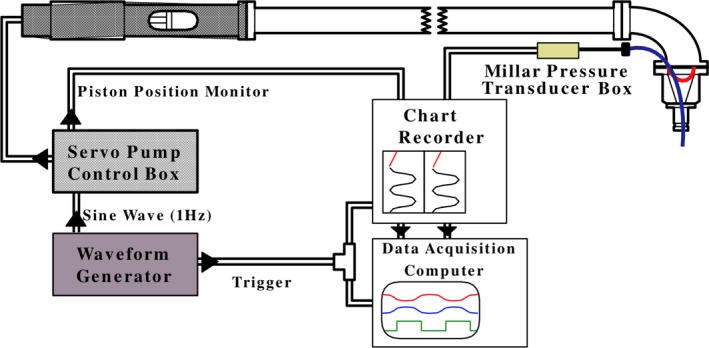
Diagram of the computer‐controlled pump assembly that drove sinusoidally a volume of water into a balloon affixed to the end of the nozzle assembly and inserted into the left ventricular cavity, shown on the top right. The 8‐foot‐long horizontal column was filled with distilled water, while the balloon and nozzle were filled with deuterated water (D₂O). A flexible diaphragm (indicated by the red curve inside the nozzle) separated the distilled water from the D₂O.

MR imaging and heart segmentation

A circa 1993 GE Knee Coil was used in a 1.5 Tesla GE Signa clinical MR scanner (circa 1993) to acquire high‐resolution images with slice thickness 5 mm, image matrix 128×256, and in‐plane pixel dimensions 0.55×1.09 mm in the frequency and phase encoding directions, respectively. Short‐axis images were acquired at 12 contiguous locations spanning the heart. Long‐axis images were obtained at 12 equiangular radial projections (at 15° intervals) about a central axis through the center of the mitral valve annulus. The heart was positioned within the scanner with the midseptum positioned to the left in the short‐axis views. The first long‐axis view (φ=0°) cuts through the middle of the septum thus is similar to the commonly prescribed 4‐chamber view. Images were generated for 14 time frames (at ≈31‐ms intervals) as the ventricle was filled, using an interleaved, partial k‐space image reconstruction.32 DANTE tagging pulses generated parallel sets of tag lines33, 34 in each short‐ and long‐axis view; however, the tag displacement information was not used in this article. Representative MR images are shown in Figure 5. The images were processed with a semi‐automated contour detection program provided by Guttman et al35 to identify and record 64 discrete points along the endocardial surface in each image. For methods that require 1 or 2 in‐plane cavity dimensions, the largest in‐plane diameter(s) was determined directly from a numerical search over the 64 contour points (rather than from a user‐selected line segment). The mitral valve opening was treated as a flat plane. The first and last points of each long‐axis contour were matched to the Teflon collar of the mitral valve ring. Figure 6 shows the collection of 12 short‐axis and 12 long‐axis contour points.

Figure 5.

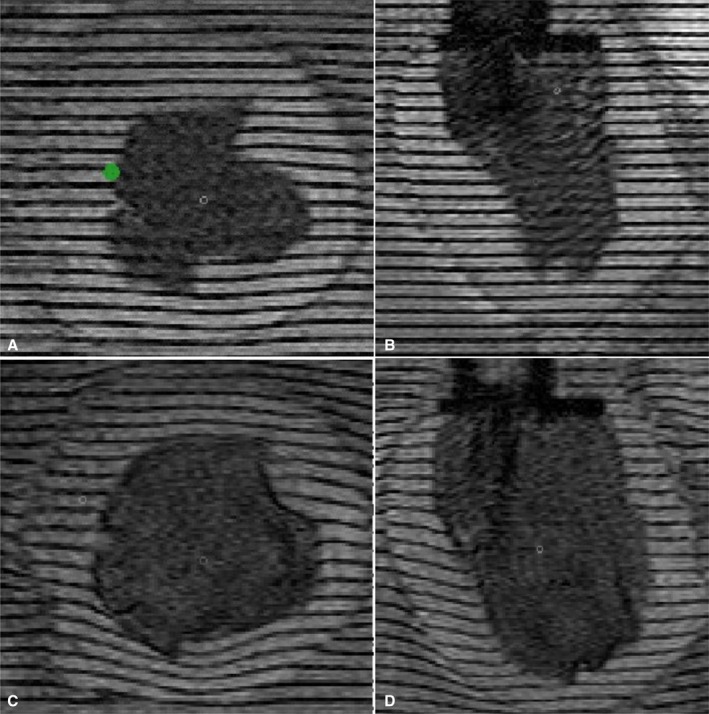
Representative high‐resolution magnetic resonance images of an isolated canine left ventricle (LV) undergoing passive inflation. A and B, Representative short‐axis and long‐axis images in the experimental end‐systolic state. C and D, The same image planes but in the experimental, physiologic end‐diastolic state. The signal decrease in the LV cavity results from deuterium (D₂O) added to the water filling the balloon. The Teflon mitral valve collar and nozzle assembly is apparent as a darker‐appearing slab in the top center of the long‐axis images. The green dot in (A) represents the middle of the septal wall.

Figure 6.

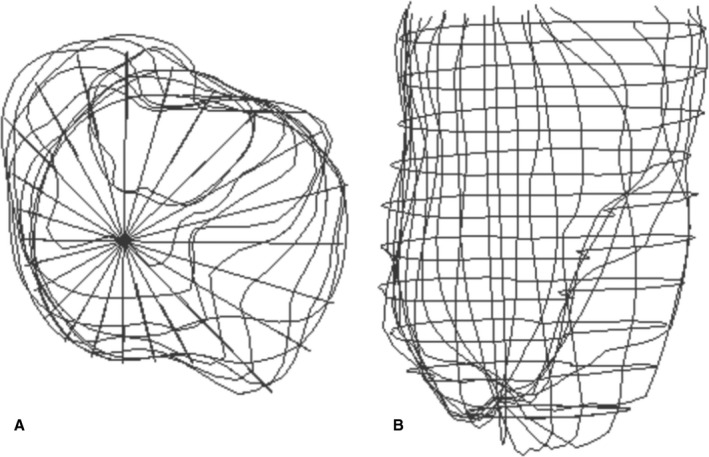
Magnetic resonance imaging–based contour points for the isolated dog heart. A and B, The endocardial contour points from 12 short‐axis and 12 long‐axis views in the isolated dog heart at end‐systole (the first time frame in the filling series). A, The top view where each radial line represents a long‐axis contour seen on end. The septum is positioned on the left in this view. B, The anterior–posterior view from a slightly oblique angle to improve appreciation of the short‐axis points.

The isolated heart was subjected to a sinusoidal volume excursion from 32.8 to 64.3 mL. The MRI acquisition began at 110 ms after the initiation of the trigger pulse that initiates the pump filling cycle, corresponding to a starting LV volume for the imaging of 38.0 mL. The last (14th time frame) image acquisition corresponded to an ending LVV of 64.2 mL. The cavity pressure at time frame 9 (time after trigger of 469 ms) was representative of the normal physiologic filling pressure of 7.5 mm Hg. This time frame, with volume of 60.34 mL, was used as the physiologic end‐diastolic state for this article, with an ejection fraction of 0.403.

Testing robustness to slice number and location

In this experiment, the heart was inflated from a physiologic end‐systolic volume through a physiologic end‐diastolic volume. LVEF was defined conventionally as the change in volume over the end‐diastolic volume. The variability in LVV and LVEF estimates as a function of the number and location of available image slices was tested by systematically omitting slices and views. For the 2 composite midpoint integration methods, the LVV excursion was computed first using all 12 short‐axis slices, then omitting every other slice and starting from either the first or the second slice: this defines 2 variants of 6 slices. The analysis was then repeated by omitting 2 intervening slices and starting at the first, or second, or third slice: defining 3 variants of 4 slices. For the geometric models that utilize a single long‐axis view, each of the 12 available long‐axis views were used, independently, and the mean error, SD of error, and error range were tabulated across the 12 long‐axis views. Where appropriate, the results when using only the first long‐axis slice (similar to the common 4‐chamber view) are presented separately. For Bloomgarden's method using multiple long‐axis views, the analysis was performed using 12, 6, or 4 slices, using the same variants as described above. For the 3D conformal surface fitting approach, the fitting was done first using all 12 short‐ and 12 long‐axis slice locations. The fits were recomputed using only every other short‐axis slice and every other long‐axis slice (12 slices total) in each of the 2 available variants. The surface fitting was then repeated using only 4 short‐ and 4 long‐axis slices (8 slices total), in each of the 3 variants.

Assessment of LVV and LVEF accuracy for each method

In this article, the accuracy of LVV and LVEF estimates is defined in terms of measurement bias and imprecision.36 For each of the estimation methods applied to a single slice variant, the LVV measurement bias was assessed via the mean error (in units of mL) and the root mean square error (RMS; in mL), both with respect to the pump ground‐truth across each of the 9 time‐points. The LVV measurement variability was assessed via the SD in error (in mL) about the mean error. The accuracy of the LVEF calculation was assessed as the absolute miss and the miss as percentage of the ground truth LVEF. For cases where the LVEF was computed for multiple slice variants using the same estimation method, the mean, RMS, and SD in error in LVEF was computed across all variants.

Results

Results Using Commonly Used Geometric Approximations

Composite midpoint integration method (Eqn. 1)

The LV cavity volume excursions over time are presented in Figure 7 for all estimation methods, slice variants, and the ground truth. Table 1 shows the RMS error of the LVV over time (up to the physiologic filling state) as a percentage of the average pump‐determined LVV over this time duration, the LVEF estimate, and the % error in LVEF, for all slice variants when using the composite midpoint integration method. As shown in Figure 7A, the 12‐slice volume estimate consistently overestimated the ground truth, with a mean LVV error of 2.2% and RMS error of 2.4%. The 12‐ and 6‐slice versions had similar overall % LVEF error of 2.2%, while the 4‐slice variant was prone to larger errors, ranging from a 2.7% underestimation to a 7% overestimation of LVEF. The uncertainty in LVV for first 6‐slice variant (computed as mean plus RMS % error) was ≈10%.

Figure 7.

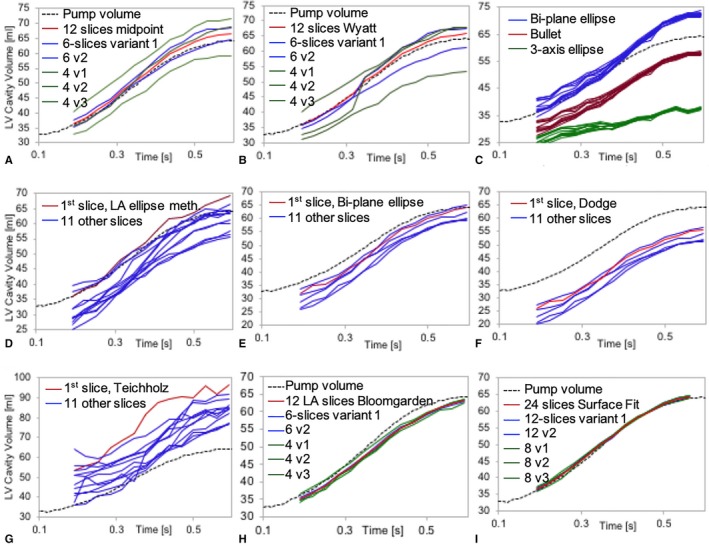
Left ventricular (LV) volume estimates over time for each method and their slice variants. Each plot shows estimated LV volume (mL) on the vertical axis vs over time (seconds) relative to the ground‐truth (dotted black curve). A, Uses the composite midpoint integration method (Eqn. 1) and (B) uses the Wyatt's modified midpoint method (Eqn. 2) when using all 12 short‐axis slices (red), 2 variants of 6 slices (blue), and 3 variants of 4 slices (green). C, The long‐axis bi‐plane ellipse (Eqn. 3—red), bullet (Eqn. 4—blue), and 3‐axis ellipse methods (Eqn. 5—green) where each curve represents running the method independently on each of the 12 long‐axis (LA) slices. D, The long‐axis‐only ellipse method (Eqn. 6), (E) the bi‐plane long‐axis area‐length method (Eqn. 7), (F) shows the Dodge‐Sandler correction (Eqn. (8)), and (G) the Teichholz method (Eqn. (9)), where each curve represents running the method independently on each of the 12 LA slices and red indicates the 4‐chamber view slice. H, The results using the Bloomgarden (Eqn. (10)) method using all 12 LA slices (red), 2 variants of using 6 slices (blue), and 3 variants of using 4 slices (green). I, The surface fitting (Eqn. (11)) results using all 12 short‐ and 12 long‐axis slices (red), 2 variants of 6 slices in each view (blue), and 3 variants of 4 slices each (green).

Table 1.

Results for Mean and RMS Error in LVV Over the Physiologic Volume Range, and EF and % Error in EF Using the Composite Midpoint Integration Method (Eqn. 1) for LVV Estimation Based on 12, 6, and 4 Slices, Compared With the Pump‐Based Ground Truth EF of 0.403

Composite Midpoint Method	12 Slices	6 Slices Var. 1	6 Slices Var. 2	6 Slices Mean	4 Slices Var. 1	4 Slices Var. 2	4 Slices Var. 3	4 Slices Mean
Mean LVV error, mL	1.1	2.4	−0.3	1.0	1.0	6.0	−3.8	1.1
Mean error, %	2.2	5.1	−0.6	3.6	2.1	12.6	−8.0	2.2
RMS error, %	2.4	5.3	1.3	3.3	3.4	12.7	8.1	8.1
EF	0.412	0.414	0.409	0.412	0.431	0.392	0.413	0.412
EF error, %	2.2	2.8	1.6	2.2	7.0	−2.7	2.6	2.3

EF indicates ejection fraction; LVV, left ventricular cavity volume; RMS, root mean square.

Modified midpoint method (Eqn. 2)

The results using the Wyatt modified midpoint method for the same slice variants are shown in Figure 7B and Table 2. In general, the error in LVV and LVEF was larger than those for the standard composite midpoint integration method, especially for the 6‐slice and 4‐slice variants. The LVEF error when using 6 slices ranged from −3.5% to 7.7%. One 4‐slice variant and 1 6‐slice variant underestimated LVV at the lower volumes while overestimating it at high volumes. Presumably this occurred when the heart apex moved downward into the most apical short‐axis slice, which originally did not contribute to LVV, causing a spike in the estimate.

Table 2.

Results for Mean and RMS Error in LVV Over the Physiologic Volume Range, and Left Ventricular EF and % Error in EF Using the Modified Composite Midpoint Integration Method (Eqn. 2) Based on 12, 6, and 4 Slices, Compared With the Ground Truth

Modified Midpoint Integration Method	12 Slices	6 Slices Var. 1	6 Slices Var. 2	6 Slices Mean	4 Slices Var. 1	4 Slices Var. 2	4 Slices Var. 3	4 Slices Mean
Mean LVV error, mL	0.4	0.9	−2.3	−0.7	−1.1	4.0	−7.6	−1.6
Mean error, %	0.8	1.9	−4.8	−1.1	−2.3	8.3	−15.9	−3.3
RMS error, %	2.4	5.3	1.3	3.3	7.2	8.6	16.4	10.7
EF	0.414	0.434	0.399	0.412	0.476	0.357	0.375	0.403
EF error, %	2.8	7.7	−3.5	2.1	18.2	−11.4	−6.9	−0.02

EF indicates ejection fraction; LVV, left ventricular cavity volume; RMS, root mean square.

Variability in long‐axis lengths and areas

The variability of length and area measurements from the 12 available long‐axis views, measured at end‐systole and end‐diastole, are given in Table 3. The extent of the LV cavity in the long‐axis view was constrained by the mitral value Teflon ring at the base, and the observed lowest extent of the LV cavity toward the apex for each slice.

Table 3.

Variability of Long‐Axis Length and Area Measurements Over the 12 Projection Angles at ES and ED

	Length at ES (mm)	Area at ES (mm2)	Length at ED (mm)	Area at ED (mm2)
Mean	49.6	1340.4	54.2	1895.4
StDev	3.0	86.1	0.8	64.8
StDev as %	6.0	6.4	1.4	3.4

Shown are the mean (in mm) and SD error (StDev) in mm, and StDev as a % of the mean. ED indicates end‐diastole; ES, end‐systole

Bi‐plane ellipse (Eqn. 3) and bullet (Eqn. 4) methods

The bi‐plane ellipse and bullet methods differ only by a scaling factor (2/3 versus 5/6). Shown in Figure 7C are the volume versus time plots for these methods. Table 4 provides the accuracy of the volume estimates over the physiologic filling range for these and 3 additional long‐axis‐based methods. The LVEF values and errors are the same for both methods because they differ only by a scaling factor. The LVEF error for the 4‐chamber view was 9.1% (an overestimation). The SD in LVEF error using both methods was 8.4%, with range −12.1% to 16.5%. Using 2 times the LVEF SD as a measure of uncertainty, the measurement uncertainty is 17% when using this approach.

Table 4.

Accuracy of Left Ventricular EF Estimates Relative to Ground Truth EF of 0.403

	3‐Axis Eqn. 5	LA‐Area‐Length Eqn. 6	Bi‐Plane LA Eqn. 7	Dodge Eqn. (8)	Teichholz Eqn. (9)
First slice EF	0.308	4.19			0.407
First slice EF error, %	−23.6	4.0			1.1
Mean EF (n=12 or 6*)	0.271	0.449	0.470*	0.507*	0.361
EF mean error, %	−32.8	11.4	16.7	26.0	10.3
EF SD error, %	10.5	20.0	10.0	11.1	23.0
EF error range, %	−49.9 to −14.6	−20.71 to 42.1	5.5 to 29.0	13.5 to 39.7	−52.5 to 36.3

When using Equations 5, 6, and 9, the mean and SD were computed over 12 independent EF measurements (1 for each long‐axis [LA] slice). The error metrics for Equations 7 and 8 are based on 6 pairs of orthogonal long‐axis slices, as indicated by the asterisks. EF indicates ejection fraction.

Three‐axis measurement based on diameters (Eqn. 5)

For this LVV estimate, the short‐axis slice was identified that had the largest orthogonal in‐plane diameters. These diameters were multiplied by the length from each of the 12 long‐axis slices to get 12 independent estimates of the LVV. The results are shown in Figure 7C and Table 4. The LVEF error for the first long‐axis slice was 23.6% (an underestimation). The mean and SD in LVEF error over all 12 slices was −32.8±10.7%. The LV volume was consistently underestimated and the measurement uncertainty was 21% when using this approach.

Single long‐axis view area‐length method (Eqn. 6)

This method relies on only a single long‐axis image to compute the in‐plane area and longitudinal extent. The results are shown in Figure 7D and Table 4. The LVEF measurement uncertainty is ≈40% when using this approach.

Bi‐plane long‐axis area‐length (Eqn. 7) and the Dodge‐Sandler correction (Eqn. (8))

For these methods, the in‐plane cavity area from each of 2 orthogonal long‐axis slices was combined via the respective equations. Six sets of measures were made, from orthogonal pairs of the 12 available long‐axis slices. The results are shown in Figure 7E and 7F, and Table 4. Using Equation 7, the LVEF % error ranged from 5.5 to 29.0, with mean and SD error of 16.7±10.0%. With the Dodge‐Sandler correction the LVEF % error ranged from 13.5 to 39.7, with mean±SD error of 26.0±11.1%. LVV was consistently underestimated and the LVEF measurement uncertainties were 20% and 22% when using these methods.

Teichholz's formula (Eqn. (9))

The greatest short‐axis diameter seen on a long‐axis slice was used to compute the LV cavity volume via Equation (11). The results are shown in Figure 7G and Table 4. The LVEF % error ranged from −52.4 to 36.3, with mean±SD error of 10.3±23.0%. The LV volume was consistently overestimated and the LVEF measurement uncertainty was ≈46%.

Bloomgarden's multiple long‐axis area method (Eqn. (10))

For this method, the accuracy of the LVV and LVEF estimates were computed for multiple radially oriented long‐axis slices, using all 12 slices, 2 variants of equally spaced 6 slices, and 3 variants of equally spaced 4 slices. The results are presented in Figure 7H and Table 5. LVV was consistently underestimated using this method. When using 6 slices, the mean LVV error was −3.7% and the largest LVEF error was 5.7%.

Table 5.

Results for Mean Error and RMS Error in LVV and EF Over the Physiologic Volume Range Using Bloomgarden's Method25 (Eqn. (10)) That has Been Modified to Account for Central Axis Misalignment

Modified Bloomgarden's Method	12 Slices	6 Slices Var. 1	6 Slices Var. 2	6 Slices Mean	4 Slices Var. 1	4 Slices Var. 2	4 Slices Var. 3	4 Slices Mean
Mean LVV error, mL	−1.9	−1.9	−1.9	−1.9	−0.7	−2.5	−2.6	−1.9
Mean error, %	−3.7	−3.6	−3.7	−3.7	−1.2	−4.7	−5.0	−3.7
RMS error, %	3.9	4.0	3.9	3.96	2.4	4.8	5.3	4.15
EF	0.387	0.380	0.395	0.387	0.370	0.396	0.397	0.387
EF error, %	3.9	5.7	2.1	3.9	8.3	1.7	1.5	3.9

LVV estimates are based on variants of 12, 6, and 4 long‐axis slices. EF indicates ejection fraction; LVV, left ventricular cavity volume; RMS, root mean square.

Surface Fitting Order Optimization

The SD of the fitting error versus order of fitting for the first time‐frame (representing end‐systole) are shown in Figure 8A. A sixth‐order fit was considered to be best for this study because it achieved a SD of the fitting error of 3.1 mm that was near the minimum over all orders, but with fewer terms (49) than when using higher orders. The flattening of the curve suggests that all the real surface feature information contained in the contour point data has been accounted for in the reconstruction, leaving residuals that are predominantly the noise and uncertainty in the data. The sixth‐order endocardial surface at different fitting orders is displayed in Figure 8B and 8C. Fitting at later time frames gave smaller fitting errors (data not shown) because modulations at the endocardial surface (predominantly from the papillary muscles) were less prominent as the heart expanded.

Figure 8.

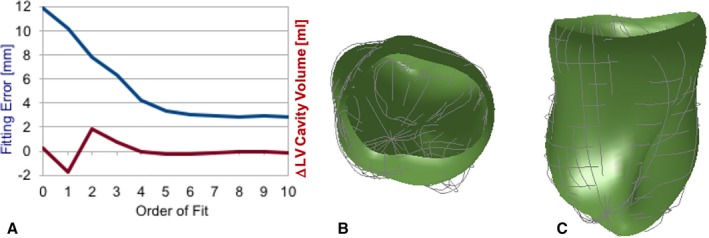
Left ventricular (LV) endocardial surface fitting results at time frame zero (representing end‐systole—the most convoluted state). A, Plots in blue are the SD error between the LV contour point data and surface model estimates vs the order of fitting using Equation (11). Plotted in red is the difference from the mean of the estimated LV cavity volume (in mL). The fitting error levels off around sixth order (with 49 model parameters), with a fitting error of 3.1 mm. B, The top view and (C) the side view of the sixth‐order fitted surfaces (shaded green) where the light gray curves are the contour points.

Conformal 3D surface fitting results

For this method, the accuracy of the LVV and LVEF estimates was computed using all 12 short‐axis and 12 long‐axis slices (labeled as 24 slices), 2 variants of equally spaced 6 slices in each view (labeled as 12 slices), and 3 variants of equally spaced 4 slices in each view (labeled as 8 slices). The results are presented in Figure 7I and Table 6. When using all 24 slices, the mean LVV error was <1%, and LVEF error was 2.1%. For both 12‐slice variants, the mean LVV error was <1% and the largest LVEF error was 3.7%.

Table 6.

Results for Mean and RMS Error in LVV Over the Physiologic Volume Range, and EF and % Error in EF Using 3D Surface Fitting for LV Volume Estimation Based on 12 Short‐Axis Plus 12‐Long‐Axis Slices (24 Slices Total), and Variants Using 6 and 4 Slices in Each View (Labeled 12 and 8 Slice Variants)

3D Surface Fitting	24 Slices	12 Slices Var. 1	12 Slices Var. 2	12 Slices Mean	8 Slices Var. 1	8 Slices Var. 2	8 Slices Var. 3	8 Slices Mean
Mean LVV error, mL	0.36	0.43	0.47	0.45	0.55	−0.03	0.89	0.47
Mean error, %	0.66	0.78	0.86	0.82	0.99	−0.05	1.60	0.85
RMS error, %	1.11	1.27	1.41	1.34	1.39	0.84	2.25	1.49
EF	0.394	0.388	0.394	0.391	0.431	0.404	0.378	0.391
EF error, %	2.1	3.7	2.1	2.9	1.9	−0.3	6.1	2.9

3D indicates 3 dimensional; EF, ejection fraction; LVV, left ventricular cavity volume; RMS, root mean square.

Discussion

The accuracy and precision of several common imaging‐based approaches for estimating LVV and LVEF have been quantified using a highly sampled, high‐resolution MRI data set for determining geometric parameters and validated against an independent ground truth. The effect on LVV and LVEF accuracy of slice number and orientation was also studied. The most accurate results were achieved when incorporating all of the available anatomical data from multiple views to a 3D conformal surface model that achieved <1% mean error in LV volume over the physiologic range, and LVEF error of 2.1% (Table 6). Based on these immediate results, for the goal of achieving <5% error in LVEF for clinical trials, the Bloomgarden's method6 with 12 long‐axis slices, and conformal surface fitting with 12 or more slices (6 in each view) is adequate. Within this experiment, the composite midpoint integration method with 6 or more short‐axis slices also performed adequately (LVEF error <3%); however, in the clinic additional errors on the order of 8% are expected because of the inability to adequately account for the mitral valve plane and the true apical extent of the LV cavity. When using any of the other common geometric models, there was large variability in LVEF accuracy between the competing models, and among the same model when applied individually to each of the 12 available long‐axis views.

Heart Contour Segmentation and Surface Sampling

Error in contour segmentation and the errors in the subsequent volume estimation are dominated by inadequate contrast‐to‐noise ratio of the contour edges, partial volume effects, and inadequate sampling of a convoluted surface. When the slice thickness is large relative to the through‐plane radius of curvature, partial volume effects with black‐blood images will shift the apparent contour location inwardly relative to the true location in the center of the slice. This may partially explain the mismatch between the contours at the intersection of short‐axis and long‐axis slices, as evidenced in Figure 6, and may contribute to the consistent underestimation of LVV when using the Bloomgarden method on long‐axis slices. The magnitude of the mismatch between the short‐axis and long‐axis segmentation results and inherent noise can be quantified via the RMS error of 3D surface fitting where the RMS error converged to ≈3 mm at the highest‐order fits (Figure 8A). LVV and LVEF errors in the clinic are expected to be higher than reported here for multiple reasons. First, an intracavity balloon with deuterated water gave high contrast between the cavity and myocardial tissue. Second, the 5‐mm slice‐thickness reduced partial volume effects relative to the 8‐ to 10‐mm thickness often used clinically with MRI. Third, the experimental setup eliminated motion artifacts caused by breathing and variations in beat‐to‐beat interval that can lead to image blurring and artifact. When extrapolating these results to other imaging modalities, particularly 2‐dimensional and 3D echocardiography, the errors inherent in the geometric assumptions are compounded by larger errors relative to MRI in delineation of the endocardial border and accounting for the full extent of the LV cavity. The effects of these border sampling errors contribute to the observed discrepancies on the order of 4% in estimates of LVEF, and 30% in end‐diastolic LV volume between MRI and 3D echocardiography acquired in the same hearts.6, 12

Mitral valve plane delineation on short‐axis images

Accounting for the location of the mitral valve plane is both a conceptual and technical problem. In the intact heart, the opening is closed during ejection by the thin mitral valves, which although closed during this phase, are pushed upwards into the left atrium as the LV pressure rises. Visualizing and modeling the shape of the leaflets using MRI is not achieved reliably. To objectively define the “top” of the ventricle, it is recommended to define the base of the heart as the plane of the mitral valve annulus. For in vivo heart studies, approximating the top of the heart with a flat surface at the location of the most basal short‐axis slice is problematic for 2 main reasons. First, the plane of mitral valve ring does not necessarily lie parallel to the stack of short‐axis views, and thus is not necessarily contained within a single short‐axis slice at any given cardiac phase. Second, the base of the human heart translates inferiorly to ≈1 to 2 cm and incurs a slight out‐of‐plane rotation during contraction; thus, even if a short‐axis view was carefully prescribed to match the mitral valve ring at end‐diastole, at subsequent time frames this condition would not hold. These limitations are ameliorated in our isolated heart experiment because the mitral valve plane is fixed in space; is well demarcated by the Teflon collar; and the short‐axis slices are prescribed to be exactly parallel to the plane of the mitral valve ring. Because of these effects, in the clinic the errors associated with the composite midpoint integration method are expected to be significantly higher than those reported here, up to the impact of roughly one half of the contribution of the most basal short‐axis slice, or roughly one twelfth (8.5%) of LVV when relying on 6 short‐axis slices. Adding this error to the expected LVV error of 10% found with our experimental setup, and errors in delineating the cavity apex and other factors, one can expect LVV errors on the order of 15% to 18%. Higher errors are likely if the spacing between short‐axis slices is not sufficiently small to capture the convolutions of the endocardial surface, if there are additional errors in delineating the endocardial border, etc.

Capturing the Full Apical Extent of the LV Cavity on Long‐Axis Images

The variability in heart length and long‐axis cavity area over all 12 long‐axis projections at the end‐systolic state was due in part to the apical extent of the LV being captured differently on each image. Prescribing an image plane that passes through the true cavity apex at all phases of the cardiac cycle is nontrivial and not likely to be achieved in the clinical environment. Missing the true apical extent contributes to underestimation in the LVV as evident in the Bloomgarden's method and conformal surface fitting results (Figure 7H and 7I) when using 6 or fewer long‐axis slices. This error will be exacerbated when the viewing angles and/or number of slices are further restricted. When limited to only short‐axis views, delineating the apical tip with >1‐slice thickness accuracy is problematic because of partial volume effect and high curvature of the LV surface at that location.

Limitations in translating these experimental results to the clinic

The motion of the isolated heart in this experiment does not represent true physiologic in vivo motion because the heart was not actively contracting, was suspended in a water bath by a Teflon ring sutured into the mitral valve plane, had the chordae tendonae cut, had the pericardium and right ventricle removed, etc. The experiment mimicked the relaxed filling phase of the cardiac cycle and although the volume excursions are representative of those measured in vivo, differences in the heart geometry during the contraction phase are expected. Moreover, the canine LV endocardial geometry is, on a centimeter scale, more convoluted than the human LV by having 2 prominent papillary muscles rather than 1, but less convoluted on the millimeter scale by having less pronounced trabecular folds on the endocardial surface. All these features likely contribute to differences between these experimental results and what might be obtained in vivo in a human heart. The Dodge‐Sandler method4, 5 (and by extension the Teichholtz method24) is further disadvantaged here because it incorporates correction factors derived from measurements on excised human hearts rather than a living canine heart. However, the 3D conformal surface fitting, composite midpoint integration method, and Bloomgarden's method are independent of geometric assumptions regarding the shape and deformation of the heart and because the canine heart is generally more convoluted, the relative accuracy of each method is expected to hold when applied to human hearts and in instances where the heart is diseased and/or contracting abnormally, whereas methods that rely on simplified geometric models may incur less error in healthy human hearts but additional error in abnormal hearts.

Conclusion

This study quantified the accuracy of several geometry‐based methods for estimating LVV and LVEF, against an independent ground truth. When using the common geometric assumptions and limited short and/or long‐axis views, the expected LVEF measurement uncertainty can be as high as 49%. Using 6 or more short‐axis views, the composite midpoint integration method can achieve LVEF error of <3% and LVV error of ≈10%. Since these measurements were performed in a nearly ideal imaging scenario, the errors in the clinic can be expected to be higher. In particular, the inability to precisely delineate and track the mitral valve annulus and the apical‐most extent of the LV cavity can be expected to contribute an additional ≈8% uncertainty when using only short‐axis images. The augmented Bloomgarden's method uses radially prescribed long‐axis slices and can achieve high LVEF accuracy, up to 3.9% with 12 slices, and more reliable LVV measurements than methods that rely solely on short‐axis images. Using a mathematical 3D conformal surface model that incorporates anatomic information from multiple views can achieve superior accuracy, with LVEF error <3% and LVV error <2% when using 12 short‐axis and 12 long‐axis slices, and LVEF error <4% and LVV error <2.5% when using 6 slices in each view. A disadvantage of using many slices and views is an increased manual effort to segment the heart in each slice. Continued improvements in fully automatic heart segmentation37 and MRI pulse sequences that improve the blood–myocardial contrast promise to alleviate much of this effort. It is hoped that this work makes more evident the limitations of relying on only a few representative slice acquisitions, particularly when they exclude observation of the mitral valve annulus and the apical‐most aspect of the LV. These results should encourage the use of mathematical approaches to combine heart surface information from multiple views, using only existing image acquisition technologies. By reducing the measurement uncertainty, clinical studies can be relied upon to detect more subtle changes in heart function with statistical certainty, thereby reducing the number of subjects needed for some clinical trials and for earlier identification of patients with subclinical cardiac dysfunction.

Sources of Funding

This work was supported by the UF Foundation and the Ocala Royal Dames Foundation for Cancer Research.

Disclosures

None.

(J Am Heart Assoc. 2019;8:e009124 DOI: 10.1161/JAHA.118.009124.)