Post-stimulus fMRI and EEG responses: evidence for a neuronal origin hypothesised to be inhibitory

Abstract

Post-stimulus undershoots, negative responses following cessation of stimulation, are widely observed in functional magnetic resonance (fMRI) blood oxygenation level dependent (BOLD) data. However, the debate surrounding whether the origin of this response phase is neuronal or vascular, and whether it provides functionally relevant information, that is additional to what is contained in primary response, means that undershoots are widely overlooked. We simultaneously recorded electroencephalography (EEG), BOLD and cerebral blood-flow (CBF) [obtained from arterial spin labelled (ASL) fMRI] fMRI responses to hemifield checkerboard stimulation to test the potential neural origin of the fMRI post-stimulus undershoot. The post-stimulus BOLD and CBF signal amplitudes in both contralateral and ipsilateral visual cortex depended on the post-stimulus power of the 8–13 Hz (alpha) EEG neuronal activity, such that trials with highest EEG power showed largest fMRI undershoots in contralateral visual cortex. This correlation in post-stimulus EEG-fMRI responses was not predicted by the primary response amplitude. In the contralateral visual cortex we observed a decrease in both cerebral rate of oxygen metabolism (CMRO₂) and CBF during the post-stimulus phase. In addition, the coupling ratio (n) between CMRO₂ and CBF was significantly lower during the positive contralateral primary response phase compared with the post-stimulus phase and we propose that this reflects an altered balance of excitatory and inhibitory neuronal activity. Together our data provide strong evidence that the post-stimulus phase of the BOLD response has a neural origin which reflects, at least partially, an uncoupling of the neuronal responses driving the primary and post-stimulus responses, explaining the uncoupling of the signals measured in the two response phases. We suggest our results are consistent with inhibitory processes driving the post-stimulus EEG and fMRI responses. We therefore propose that new methods are required to model the post-stimulus and primary responses independently, enabling separate investigation of response phases in cognitive function and neurological disease.

Introduction

The majority of our current understanding of brain function is derived from functional mapping of the neuronal processing that occurs during the delivery of a stimulus. However, it is becoming increasingly clear that a distinct brain response occurs upon stimulus cessation. Magnetoencephalography (MEG) and electroencephalography (EEG) studies observe a post-stimulus event-related synchronisation (PERS) or “rebound” of oscillatory neuronal activity in the alpha (8–13 Hz) and beta (15–30 Hz) frequency bands. PERS activity can be modulated by stimulus duration or intensity [1–3], suggesting that the post-stimulus response is functionally relevant. Further, a significant negative correlation between PERS beta power and symptom severity in schizophrenia patients has recently been shown [4], with patients exhibiting significantly smaller PERS amplitude than healthy controls. This evidence suggests the largely under-studied post-stimulus response phase of neuronal activity is actually integral to brain function, and a potential biomarker of disease.

Evidence of a post-stimulus response phase is also present in blood oxygenation level dependent (BOLD) functional magnetic resonance imaging (fMRI) data, and represents a potential haemodynamic correlate of the EEG/MEG PERS [5]. The post-stimulus undershoot (a reduction of signal below pre-stimulus baseline level) is a well-recognised component of the BOLD response, occurring after stimulation has ceased. However, its relationship with brain function has rarely been investigated as it has traditionally been thought to arise solely from vascular, rather than neuronal, sources [6], and to be intrinsically coupled to the amplitude of the primary response. Recent evidence that the post-stimulus BOLD undershoot is reduced in amplitude and/or prolonged in duration in schizophrenia patients compared with healthy controls, whilst the primary response is unchanged, [7] further suggests a functional significance of the undershoot over and above activity during stimulation and questions the assumed coupling between the two response phases. These response phases are commonly modelled with a fixed relationship in the canonical haemodynamic response function (HRF). This HRF remains the most commonly employed approach to model linear relationships between stimulus presentation and BOLD responses, and is implemented widely in fMRI analysis software such as SPM (http://www.fil.ion.ucl.ac.uk/spm/) and FSL (www.fmrib.ox.ac.uk/fsl/). It is therefore imperative to attain a greater understanding of the origin and the functional importance of the post-stimulus fMRI response.

Whilst the primary positive BOLD response to stimulation is widely accepted to reflect an increase in neuronal activity driving concordant increases in cerebral blood flow (CBF), blood volume (CBV) and metabolic rate of oxygen consumption (CMRO₂) [8–10], the origin and mechanisms underlying the post-stimulus BOLD response are still actively debated [11]. The first hypothesis is that the post-stimulus BOLD response is a passive response which is entirely vascular in origin: driven by a slower return of CBV to baseline levels than CBF or CMRO₂ [6]. However, more recently it has been suggested that the post-stimulus BOLD response is related to neuronal activity [5, 12–16]. Some of these studies have observed CBF and CBV returning to baseline immediately after stimulus cessation whilst calculated CMRO₂ remains elevated [13, 14]. This has been hypothesised to arise due to a rebalancing of ionic gradients across the neuronal membrane required to compensate for the ion displacement during stimulation [14]. Other studies have observed a decrease in CBF with a calculated decrease in CMRO₂, suggesting a post-stimulus decrease in neuronal activity [5, 12, 15, 16]. Putative support for this theory comes from invasive electrophysiological recordings which show a decrease in post-stimulus neuronal activity below baseline levels [17]. Disentangling these last two mechanisms is imperative. If a slow recovery of elevated CMRO₂ back to baseline is the source of the post-stimulus response then a fixed relationship between the primary and post-stimulus BOLD responses would be expected along with an uncoupling of changes in CMRO₂ and CBF. However, if the post-stimulus undershoot is driven by a reduction in post-stimulus neuronal activity then it may not be solely determined by the primary response and hold additional functional information regarding brain activity.

We hypothesize that the primary and post-stimulus phases of the brain’s response are distinct, and at least partly independent neuronal processes. We propose that the negative correlation we previously reported between post-stimulus fMRI responses and EEG PERS alpha power to a sensorimotor task [5] reflects a fundamental neurovascular coupling relationship which will be observed across all sensory regions. Previous work showed that a flicker visual stimulus induced a large undershoot, whereas a static visual stimulus resulted in no undershoot [15]. The authors hypothesized that neuronal inhibition after the flicker stimulus caused the post-stimulus undershoot, whilst sustained neural activity after the static stimulus at least partially cancelled this response and drove the differing responses [15]. Following the hypothesis of Buxton et al [18], we propose that active post-stimulus neuronal inhibition occurring after the flicker visual stimulus may be indexed by an increase in the CMRO₂/CBF coupling ratio (n) during the post-stimulus phase of the fMRI response compared with the primary phase. By this hypothesis, changes in CBF and CMRO₂ are both driven by changes in excitatory and inhibitory neural activity but to different degrees, with inhibitory activity having a proportionally larger effect on CBF than it does on CMRO₂, compared to the effects of excitatory activity. Largely, the change in CMRO₂ (Δ%CMRO₂) is dominated by the change in excitatory neuronal activity (ΔE) arising from the high energy cost of restoring sodium gradients [19, 20], while the change in inhibitory neural activity (ΔI) has a much lower energy cost [21]. The key assumption of our hypothesis is that the effect of increased inhibitory neuronal activity is a positive change in CBF, so that both ΔE and ΔI are strong drivers of changes in CBF (Δ%CBF) [22, 23]. Therefore, for any change in net neural activity, the net n will depend on the balance of overall ΔE and overall ΔI (which in the case of active inhibition will have opposite signs) because Δ%CBF is determined by both ΔE and ΔI while Δ%CMRO₂ is largely determined by ΔE. If proven, our hypotheses of increased n during the post-stimulus phase of the fMRI response compared with the primary phase, would both provide further evidence that the post-stimulus response has a different neuronal origin to the primary response and provide information to illuminate the type of neuronal activity which underlies it.

Here we tested our hypotheses by investigating simultaneously recorded EEG, BOLD and CBF responses to both flicker and static left-hemifield checkerboard visual stimuli. These stimuli were used to modulate the post-stimulus responses in the primary visual cortex (V1) independently of the primary responses [15]. A hemifield checkerboard was used to allow the investigation of the post-stimulus response in both contralateral positive BOLD responses and ipsilateral negative BOLD primary response regions [5]. Specifically we aim to investigate whether: 1) modulations of post-stimulus fMRI and EEG signals occur without comparable changes in the primary responses, evidencing distinct response phases; 2) post-stimulus BOLD undershoots are accompanied by alpha PERS and post-stimulus decreases in both CBF and CMRO₂, evidencing neuronal origin of post-stimulus response; 3) on average, larger BOLD, CBF and CMRO₂ undershoots are seen to flicker than to static stimuli, and whether these are associated with larger EEG PERS; 4) trial-by-trial variations in EEG PERS amplitude are correlated with concurrent fluctuations in fMRI undershoots; which, along with 3), evidences a link with neuronal inhibition [24, 25]; 5) increased n will be observed during the post-stimulus phase of the fMRI response compared with the primary phase, evidencing that the post-stimulus response has a different neuronal origin to the primary response and suggesting that inhibitory activity underlies it.

Materials and Methods

Data were recorded from 17 subjects (age 26 ± 6 yrs (mean ± s.d.), 5 female). This study was conducted with the approval of the local ethics committee and all subjects gave informed consent.

Paradigm

Subjects were instructed to fixate on a centrally displayed white cross on a grey background throughout each experimental run whilst passively viewing left-hemifield radial, black-white checkerboard stimuli. The grey background was isoluminant with both checkerboard stimuli. The checkerboard presented in each trial was either: static with no flicker (0 Hz) and 100% contrast; or had a 3 Hz flicker (6 reversals per second) with 33% contrast. The contrasts for the two stimulus conditions were chosen to induce comparable amplitude primary BOLD responses [15], which were identified through pilot work carried out prior to the main study. An experimental run consisted of a 98.8s baseline period followed by 16 trials, 8 of each stimulus condition, presented in a pseudo-randomised order. Each trial comprised of a 10 s stimulation period and approximately 30 s rest period. This long inter-stimulus interval was chosen to ensure that the EEG and fMRI signals would return to baseline between stimuli, in addition it was jittered by up to 500 ms (30–30.5 s) to prevent stimulation occurring at the same position relative to the MRI acquisition and to reduce the expectation of stimulus onset. Data were recorded in 4 experimental runs for each subject giving a total of 32 trials of each of the static and flicker stimuli.

Data acquisition

EEG data were recorded using an MR-compatible EEG cap (EasyCap, Herrsching, Germany) with 63 scalp electrodes following the extended international 10–20 system and an additional channel for recording the electrocardiogram (ECG). The reference electrode was positioned at FCz. A BrainAmp MR-plus EEG amplifier (Brain Products, Munich) and Vision Recorder (Version 1.10) were used for data acquisition. Data were recorded using a sampling rate of 5 kHz and hardware filtering to the frequency range of 0.016–250 Hz with a roll-off of 30dB/octave at high frequency. The electrode impedances were kept below 20 kΩ. Gradient artefacts were minimised by employing a TR equal to a multiple of the EEG sampling period, isolating EEG amplifiers from the scanner bed and minimising MR room environment noise as previously described [26]. In addition, the subject was positioned such that electrodes Fp1 & Fp2 were at the isocenter of the static magnetic field in the foot/head direction in order to minimise gradient artefacts [27]. Padding was placed around the subject’s head to reduce motion artefacts. The EEG clock was synchronised to the MR scanner clock to ensure consistent sampling of the gradient waveforms [28].

MR data were recorded with a Philips Achieva 3 T MR scanner (Philips Medical Systems, Best, Netherlands), with a body transmit coil and 32-channel receive head coil. Cardiac and respiratory cycles were simultaneously recorded using the scanner’s physiological monitoring system (vector cardiogram (VCG) and respiratory belt). An initial simultaneous EEG-BOLD acquisition was performed to localise the visual cortex and to assess the EEG data quality. A standard axial, multi-slice gradient echo (GE) EPI sequence was employed (TR 2 s, TE 40 ms, 64×64 matrix, 3.25×3.25 mm² in-plane resolution, 5 mm slice thickness, flip angle 85°, SENSE factor 2). Twenty slices were acquired covering the visual cortex. A 100% contrast full-field checkerboard flickering at 8 Hz was used to elicit a strong BOLD response in a paradigm consisting of ten trials of 10 s ON, 20 s OFF (total scan duration of 5 minutes). IViewBOLD (Philips real-time processing of fMRI data) was used to generate statistical maps of the BOLD response to the visual stimulus. The positions of 12 contiguous axial slices to cover visual cortex for the simultaneous EEG-ASL-BOLD experiment were subsequently planned from this localiser. A FAIR Double Acquisition Background Suppression (DABS) sequence [5] was used for simultaneous acquisition of ASL and BOLD data. Importantly, in the DABS scheme, ASL data is collected with a short echo time (TE) following two background suppression pulses, ensuring that the signal from the static tissue in the label and control ASL images is close to suppressed in order to reduce physiological noise and any BOLD contamination in the CBF response. To maximize BOLD contrast, the BOLD data is acquired at the end of each TR period, to allow partial recovery of the static signal, with an echo time approximately matched to the T₂* of grey matter, see Fig S1. Imaging parameters were TR=2.6 s, with background suppression pulses at T_BGS1/T_BGS2=339 ms/ 899 ms, label delay 1400 ms, TE=9 ms (ASL)/ 40 ms (BOLD), 3.25×3.25×5 mm³ voxels, 12 slices, 212 mm FOV, SENSE factor 2.3, 144 volumes [label-control pairs] per run. To facilitate co-registration and normalisation of the functional data, a single volume EPI scan was acquired with the same geometry as the FAIR DABS image volume (TR 8 s, TE 40 ms, flip angle 90°, SENSE factor 2.3), in addition to a whole-head T₁-weighted anatomical image with 1 mm isotropic resolution. After the completion of MRI scanning the locations of the EEG electrodes on the scalp surface, and the shape of the subject’s head were digitally recorded using a Polhemus isotrack 3D system (Polhemus, Vermont, USA). The 3D digitised head shape was subsequently fitted to each subject’s whole-head anatomical MRI scan in order to compute the location of each electrode with respect to the brain anatomy.

Analysis

One subject was excluded from analysis as they fell asleep during the functional runs (self reported and provided no response to questions asked at the end of runs). Data from the remaining 16 subjects were then analysed as follows.

EEG

Off-line EEG signal correction was based on averaging and then subtracting the gradient and pulse artefacts in Brain Vision Analyzer2. For gradient artefact correction, we employed an artefact waveform template of 5.2 s duration (label and control pair) in the form of a sliding window average over 61 artefact repetitions. Cardiac cycles were defined from the VCG trace obtained from the MR scanner’s physiological monitoring [28], temporally aligned to the EEG data and averaged using a sliding window of 21 cardiac cycles to form a template for subsequent pulse artefact correction. Noisy channels and/or stimulation trials were discounted by visual inspection, with an average of 27±5 (27±5) trials of the static (flicker) stimulus, respectively, remaining for further analysis in each subject. Following artefact correction, data were down-sampled to 600 Hz and re-referenced to an average of all non-noisy channels. Inspection of data from electrodes covering the occipital cortex (O1, Oz and O2) showed strong modulation of alpha activity during the stimulus (0–10 s) and post-stimulus (10.5–20 s) period, as hypothesised (Figure S2). Therefore the oscillatory alpha-activity formed the focus of further analysis and the continuous data (prior to epoching into trials) were pass-band filtered between 8–13 Hz (using Butterworth Zero Phase Filters with Slope: 48dB/oct in Brain Vision Analyzer2) to allow in-depth study of this frequency band.

A regularised, scalar beamformer that incorporated a triple-sphere head model was used for spatial localisation of the stimulus-induced changes in alpha power for each subject [29]. This method uses spatial filtering techniques to localise the source of activity whilst reducing sensitivity to residual gradient and pulse artefacts [29]. Pseudo-T-statistic (Ŧ-stat) maps showing significant stimulus-related changes, between a stimulus response (0–9.5 s, relative to stimulus onset) and a control (30–39.5 s) time window, in oscillatory alpha-power were calculated over the whole head. These Ŧ-stat maps were created using both the flicker and static visual stimuli over all experimental runs as no difference in the spatial location of the primary visual response was expected between stimuli. The location of the maximum change in alpha power in the contralateral visual cortex was identified from each subject’s Ŧ-map and chosen as the site of the virtual electrode (VE). Selecting this peak therefore ensures the maximum signal-to-noise ratio of the alpha-time-course and that the signal originates from a visual cortex location comparable to that of the primary fMRI response. Using a single VE location also ensures that the extracted EEG responses originate from the same area of visual cortex for both flickering and static stimuli allowing direct comparisons between stimulus responses to be made. A VE-time-course of the alpha activity during the entire experiment was extracted from this location for each run.

For each single-trial (0–40s relative to stimulus onset), the mean alpha-power during the PERS (10.5–20 s) time window was calculated from the Hilbert envelope of the VE time-course. For each subject, trials were sorted into lower (0–25 %), median (37.5–62.5 %) and upper (75–100 %) quartiles based on the PERS alpha-power, in line with previous methods [5].

fMRI

fMRI data were separated into the BOLD and ASL data for subsequent analysis. The BOLD data were physiologically corrected for cardiac and respiratory effects using RETROICOR [30], whilst background suppression of the ASL static signal prevented the need for this physiological correction for the ASL data [31]. All data were then motion corrected using FLIRT [32] (FSL, http://www.fmrib.ox.ac.uk/fsl/). Using in-house Matlab programmes, separately the ASL data (perfusion (CBF)-weighted images acquired at TE=9ms) and BOLD data (BOLD-weighted images acquired at TE=40ms) were then linearly interpolated (Interp function, Matlab, Mathworks USA) to an effective TR of 2.6 s. Label-control pairs of ASL data (those images acquired at TE=9ms) were subtracted (using simple subtraction) to create perfusion weighted (CBF) images. BOLD-weighted image pairs (those images acquired at TE=40ms, after the ASL label and control), were averaged to produce mean BOLD-weighted data. Further pre-processing was carried out in FSL. Data were spatially smoothed with a Gaussian kernel (5 mm FWHM) and temporally filtered (high pass cut-off >0.01Hz). BOLD data were normalised to the standard MNI template and the same transform was then applied to the CBF data. A mask was created using the BOLD data of the brain voxels present in all subjects and this was used to mask each individual’s BOLD and CBF data.

General linear model (GLM) analysis was carried out separately for the BOLD time-series and CBF (label-control) time-series using FEAT (v6.0, FSL) to identify significant regions of positive or negative fMRI responses to visual stimulation. At the first-level, for each run, the main effects of the static and flicker visual stimuli were each separately modelled using boxcar regressors of the stimulus timings convolved with the canonical double-gamma HRF. As no difference in the spatial location of the visual response was expected between stimuli the response to all visual stimuli, combining both static and flicker regressors, was assessed with a positive and negative contrast. For both contrasts and each subject the average response was calculated across all four runs using second-level fixed-effects analysis. At the third-level, group average statistical maps were calculated using mixed effects (FLAME 1) analysis. All Z-statistic images were thresholded using clusters determined by Z>2.0 and a (FWE corrected) cluster significance threshold of p<0.05. A common mask of BOLD and CBF responses was created to enable direct comparison of BOLD and CBF timecourses from spatially concordant regions of visual cortex. We computed the group-level conjunction of the significant BOLD and CBF voxels, separately for positive and negative responses. These were further masked with a mask of the entire visual cortex defined from the FSL atlas (Harvard Oxford cortical) and then these group-level masks were used to mask subject’s second-level BOLD and CBF Z-stat map to localise individual peak positive and negative fMRI responses within V1.

Regions of interest (ROIs) and fMRI timecourse extraction

Subject-specific, cubic regions-of-interest (ROI) (3×3×3 voxels) were centred on the subject’s peak BOLD Z-stat voxel in both positive (in contralateral V1) and negative (in ipsilateral V1) response regions. For each run, BOLD and CBF single-trial haemodynamic response (HR) time-courses were then extracted from these BOLD ROIs, thereby allowing direct comparison between CBF and BOLD responses from the same spatial location. For each run single-trial HRs (0–40s relative to stimulus onset) were extracted and converted to percentage signal change relative to baseline, where baseline was defined as the 98.8 s prior to the onset of the first trial of each experimental run. HRs were then averaged across all trials and subjects, separately for the flicker and static stimuli, to compare response amplitude and shape. The single-trial BOLD and CBF HRs for each stimulus condition were also sorted into quartiles according to the corresponding single-trial PERS alpha-power values calculated. HRs were then averaged within quartiles and over subjects for each stimulus type.

Time-course statistics for average responses

For the EEG data, the average power during the stimulus response (0–9.5s), PERS (10.5–20 s) and control (30–39.5s) time windows was calculated for static and flicker stimuli in each subject. To test for significant differences in the EEG alpha power between the two stimulus conditions, two-tailed paired t-tests (dof = 15) across subjects were then performed for each time-window. To assess whether the amplitude of post-stimulus responses were significantly different from baseline, two-tailed paired t-tests (dof = 15) were also performed between PERS and control windows.

For the fMRI data, the latency of the peak signal change of the group mean primary (6–15 s) and post-stimulus (15–30 s) BOLD responses to the flicker stimulus were found for both contralateral and ipsilateral V1 ROIs. For both flicker and static stimuli and for each of positive and negative BOLD, positive and negative CBF data the mean response amplitudes at that latency were then found for each subject. Additionally, for each subject and dataset, the mean signal level during the control window (30–39.5s) was also calculated. To test for significant differences in HR amplitude between the flicker and static stimulus conditions, two-tailed paired t-tests (dof = 15) across subjects were then performed separately for the primary response, the post-stimulus response and during the control window. To assess whether the amplitude of post-stimulus responses were significantly different from baseline, two-tailed paired t-tests (dof = 15) were also performed between the post-stimulus and control windows. In all cases, the data passed Kolmogorov–Smirnov tests for normality and Levene’s test of equality of variance.

Time-course statistics for sorted fMRI responses

We investigated whether sorting by PERS alpha power significantly affected the fMRI responses. To allow determination of whether sorting had a differential effect on distinct response phases, the mean sorted (upper, median and lower) HR time-courses were divided into primary (6–15 s), post-stimulus (15–30 s) and control (30–39.5s) windows for each subject. These divided, sorted HR data were then used for subsequent statistical analysis. For each HR time window (primary, post-stimulus and control) separate three-way repeated measures (RM) ANOVA [Factors: trial time points x sorting (upper, median or lower) x stimulus (flicker, static)] were used to test for significant effects of PERS alpha quartile sorting on HR amplitude. Flicker and static responses were included together in the ANOVA since PERS sorting effects were hypothesized to be independent of stimulus type. The three-way RM-ANOVA was performed separately for each of the four HR time-courses (positive and negative BOLD, positive and negative CBF) and each of the HR windows (primary, post-stimulus and control). Data were Greenhouse-Geisser corrected where they failed Mauchly’s test of sphericity. Only when either a significant effect of sorting (by PERS quartile alpha power) or a significant interaction between sorting and time was observed was a further post-hoc test used to identify the significant time-points for flicker and static responses. Specifically, separately for flicker and static stimuli and each of the four HR time-courses, one-way RM ANOVA were then used to test for significant (defined as p<0.05) differences in the HR amplitude between quartiles at each time point.

Estimating CMRO₂ and CMRO₂ –CBF coupling during the post-stimulus undershoot to flicker stimuli

Since we hypothesize that changes in neuronal activity are the origin of both the primary and post-stimulus phases of the BOLD response, the Davis model was applied to estimate the CMRO₂ change during the primary and post-stimulus response phases, as previously carried out in the sensorimotor cortex [5]. The following analysis was focused on the responses to the flicker stimulus only since no clear post-stimulus undershoot was induced by the static stimulus [15] (see Supplementary Information [SI] for similar analysis and results on static stimulus data).

To estimate the change in CMRO₂ during the primary response, as well as the upper and lower quartile post-stimulus responses, the following analyses were performed. From the average contralateral positive and ipsilateral negative BOLD response for each subject the latency of the peak signal change in the primary (6–15 s) and post-stimulus (15–30 s) phases was found. Using these timings, for each subject the peak BOLD and CBF signal change for the primary response as well as the upper and lower PERS quartile post-stimulus responses were found. For each subject the resultant change in CMRO₂ for each ROI, and each response phase was then calculated using Equation [1]:

$$\frac{CMR{O}_2}{{\left(CMR{O}_2\right)}_0}={\left(1-\frac{\left(\frac{\Delta BOLD}{BOL{D}_0}\right)}{M}\right)}^{\frac{1}{\beta }}{\left(\frac{CBF}{CB{F}_0}\right)}^{1-\alpha /\beta }$$ (1)

where α (Grubb constant) was chosen to be 0.2, in line with current MR literature [33], and β, which reflects deoxyhemoglobin concentration, was chosen to be 1.3 [34]. M represents the maximum BOLD signal change, i.e. that due to an increase in CBF, which causes complete oxygen saturation in venous vessels. M is dependent on field strength and TE [35]. Since a hypercapnic challenge was not performed in this study, a range of M-values appropriate for the primary visual cortex were taken from literature, normalised to 3 T and a TE of 40.2 ms, resulting in a value of M between 6% [36] and 40.2% [16]. Paired student t-tests were then performed over the group to ascertain the significance of the differences in BOLD, CBF and CMRO₂ measures between the upper and lower PERS alpha-power quartiles.

An additional analysis was performed to investigate CMRO₂/CBF coupling ratio (n) in the primary and post-stimulus response phases. To allow testing of significant differences in n between the BOLD response phases, coupling ratios were calculated on an individual subject basis, as previously employed [37]. Calculation of an individual’s n for each response phase was performed using multiple within-subject measures. To increase SNR of the post-stimulus measurement, HRs were averaged over small subsets of trials. Averaging HRs over 4 trials was chosen to increase the SNR as much as possible whilst providing sufficient data points to perform the subsequent analysis (between 4 and 8 independent BOLD and CBF measures during the primary and post-stimulus response phases were made per subject, depending on the total number of trials available). The amplitude of the BOLD and CBF signal change at the peak BOLD response latency, was then found for each subset of trials and subject. For each subject, the resultant percentage change in CMRO₂ (Δ%CMRO₂) for each subset of trials was then calculated (Eq. 1). Adapting the methods of [37], the calculated Δ%CMRO₂ values were plotted against the percentage change in CBF (Δ%CBF), and a linear fit was applied to each plot to calculate n for both primary and post-stimulus responses from both positive and negative response regions for each subject. The average and standard error of n over all subjects was then calculated.

Since hypercapnic calibration was not performed to determine the precise values of M for the subjects in this experiment it is useful to eliminate the dependence of M on n where possible. When considering differences in n between responses measured within the same cortical area M is constant and therefore can be eliminated through normalisation [38]. Here, the group mean ratio of post-stimulus BOLD and CBF response amplitudes relative to the primary response amplitudes were calculated, eliminating the effect of M on these data. Theoretical bounds for BOLD and CBF ratios with the same n as the primary response were then calculated using Eq. 1 [39], and physiologically plausible variation in calibration constants: α between −0.2 and 0.2 (a value of α = 0 reflects CBV returns to baseline whilst CBF reduces below baseline, and α < 0 reflects CBV remains elevated whilst CBF reduces below baseline) and β between 0.9 and 1.5 (as previously tested [38]). The CBF ratio for the primary and post-stimulus responses was then plotted against the respective BOLD ratios along with the theoretic iso-n bounds for the primary response. From this plot it was possible to elucidate differences in n between the two phases of the HR independently of M.

To compare between response regions, where M may vary, a range of M-values representing those previously reported for visual cortex were considered: M = 6 [36], 15 (based on the mean of the range in the literature) and 40.2% [16]. n was estimated using the linear fitting process described above for the range of M values (6, 15, 40.2%) for both phases of the response in both contralateral and ipsilateral V1. Akin to the first analysis, α was varied between −0.2 to 0.2 for the post-stimulus phase to investigate the effect of possible variations in CBF/CBV coupling on n. During the primary phase α was kept constant at 0.2, since this is the response phase which has been used to derive α [33]. Paired t-tests were used to evaluate differences in n between response phases and between positive and negative ROIs across the group and explore how variations in M and α affected these relationships. This allowed comparison of coupling ratios between primary and post-stimulus response phases of both the contralateral (positive) and ipsilateral (negative) HRs (coupling comparisons: i) contralateral primary with contralateral post-stimulus; ii) ipsilateral primary with ipsilateral post-stimulus; iii) contralateral primary with ipsilateral primary; iv) contralateral post-stimulus with ipsilateral post-stimulus).

Results

Correspondence between average EEG and fMRI post-stimulus response amplitudes

The static and flicker stimuli elicited a robust primary positive BOLD and CBF response in contralateral V1 and primary negative BOLD and CBF response in ipsilateral V1 (Fig. S3). The corresponding alpha event-related desynchronisation (ERD) during stimulation (0–10 s) also localised to contralateral V1 (Fig. S3). EEG, BOLD and CBF response timecourses were extracted from V1 with average responses showing clear PERS between 10.5–20 s (EEG) and post-stimulus undershoots (contralateral) and overshoots (ipsilateral) (BOLD&CBF) (Fig. 1).

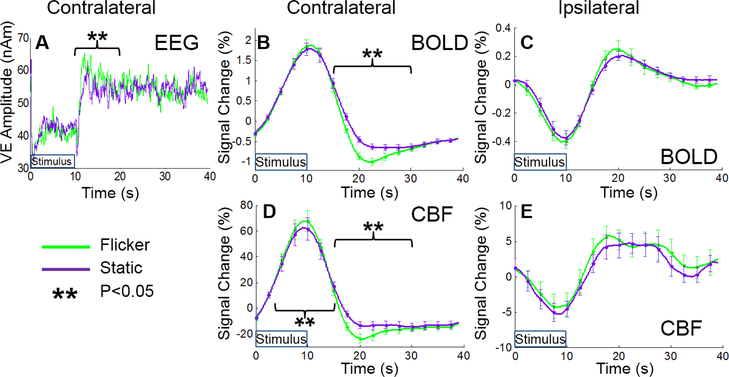
Figure 1.

Average EEG alpha power (A), BOLD (B&C) and CBF (D&E) timecourses for the flicker (green) and static (purple) visual stimuli trials. Contralateral EEG, BOLD and CBF responses (A, B &D) and ipsilateral BOLD and CBF responses (C&E) are shown. EEG measures are taken from the Hilbert envelop of the individual subject virtual electrode (VE) timecourses and averaged over trials and subjects. BOLD and CBF timecourses are taken from the individual subject ROIs (defined from BOLD T-stat maps [see Analysis section]) and averaged over trials and subjects. Error bars (B-E) denote standard error over subjects. ** denotes significant (p<0.05, paired t-test over subjects) differences in average EEG, BOLD and CBF responses between flicker and static stimuli.

We observed a significant difference between the alpha power during the PERS compared to during the control window for the flicker (p=0.006) but not the static (p=0.086) stimuli. Consequently, we observed significantly (p=3×10⁻⁴) larger PERS alpha power in response to the flicker than the static stimuli (Fig. 1A). In the fMRI data, we observed a significant difference in signal amplitude in contralateral V1 (positive primary response region) during the post-stimulus compared to during the control window for the BOLD response to flicker (p=1×10⁻⁴) and static (p=0.047) stimuli, the CBF response to flicker (p=0.007) but not the CBF response to static (p=0.083) stimuli. In ipsilateral V1 (negative primary response region) we observed a significant difference in signal amplitude during the post-stimulus compared to during the control window for the BOLD (p=0.007) and CBF responses to flicker (p=0.022) stimuli, but not the BOLD (p=0.189) or CBF (p=0.615) responses to static stimuli. The flicker stimulus therefore elicited a post-stimulus undershoot in contralateral V1 in both BOLD and CBF data, whilst the static stimulus did not. We observed a significantly larger peak amplitude of the post-stimulus BOLD (p=4×10⁻⁶) and CBF (p=9×10⁻⁵) undershoot responses to flicker compared to static stimuli in contralateral V1 region (Fig. 1 B&D). In ipsilateral V1 regions no significant difference in the post-stimulus BOLD or CBF response was observed between the flicker and static stimuli (Fig. 1 C&E), this may be due to the considerably lower amplitude of the HRs in ipsilateral V1 compared with contralateral V1 (~¼ for the primary responses). Data from a representative subject are displayed in Figure S4.

We further compared the HR amplitude between flicker and static stimuli across subjects for the peak primary response phase (6–15s) and during a passive control phase (30–39.5s). The positive CBF data showed no difference in amplitude during the control phase but a significant (p=0.03) difference in primary response between stimuli, albeit a small difference (3.9%) relative to the CBF response amplitude (60.6%). No difference in HR amplitude was observed between stimuli during either primary or control phases for contralateral BOLD, ipsilateral BOLD or ipsilateral CBF responses. Similarly, no significant difference in average EEG alpha power between flicker and static stimuli during either the stimulus (0–9.5 s) or control window was observed. These results suggest that our two stimuli were well matched in terms of their capacity to elicit similar fMRI and EEG primary responses. As such any differences in the primary response are unlikely to drive the differences in the post-stimulus response that we observe between stimuli.

Modulation of haemodynamic responses by trial-by-trial variations in PERS alpha power

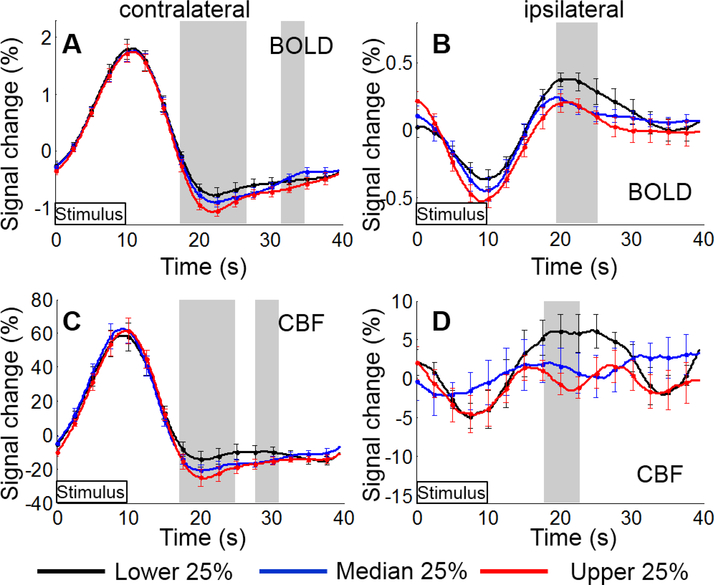
Examining the natural, trial-by-trial variation in responses to a single stimulus type (flicker or static), a negative correlation between post-stimulus EEG alpha power and BOLD and CBF responses was observed (Figs. 2&S5–S6). In contralateral V1, upper quartile PERS alpha power corresponded to a large BOLD and CBF undershoot (panels A&C, red lines) whilst the lower quartile of PERS alpha power exhibited little or no undershoot in either BOLD or CBF (black lines). In ipsilateral V1 the opposite effect was seen: a large overshoot of BOLD and CBF signal corresponded to lower quartile PERS alpha power (panels B&D, black lines). A three-way ANOVA revealed a significant effect of sorting by PERS alpha on post-stimulus fMRI response amplitudes for: contralateral BOLD (F(1.5,23.3)=9.5, p=0.001), contralateral CBF (F(1.7,25.8)=10.5, p=0.0007), ipsilateral BOLD (F(1.4,21.5)=5.4, p=0.01) and ipsilateral CBF responses (F(1.8,27.7)=3.9, p=0.04). Subsequent post-hoc testing for significant differences in HR amplitude between quartiles at individual time-points, revealed a significant (p<0.05, RM ANOVA) effect of PERS alpha power on post-stimulus contralateral BOLD (17.8 – 26.2 s & 17.2 – 25.8 s) and CBF (17.4 – 24.5 s & 18.3 – 25.6 s) responses for flicker and static stimuli respectively (Figs. 2&S5; panels A&C). A significant difference in post-stimulus amplitude between quartiles was also observed for the ipsilateral BOLD (19.7 – 24.8 s) and CBF (18.1 – 22.4 s) responses to the flicker stimulus only (Fig. 2B&D). No significant effect of sorting by PERS alpha was observed on either primary or control response amplitudes for BOLD or CBF data. It is important to note that these post-stimulus sorting effects on the BOLD and CBF HRs were also observed if the ROI was defined based on each individual’s peak CBF Z-stat voxel (still within the region of BOLD-CBF conjunction) rather than the peak BOLD Z-stat voxel (data not shown).

Figure 2.

BOLD (A&B) and CBF (C&D) haemodynamic responses to the visual flicker stimulus; sorted according to quartiles of PERS (10.5–20s) alpha power. Contralateral BOLD and CBF responses (A&C) and ipsilateral BOLD and CBF responses (B&D) are shown. Grey bars show significant (p<0.05, repeated measures ANOVA) differences in haemodynamic response amplitude between lower (black), median (blue) and upper (red) quartiles. Error bars indicate SEM.

Changes in CMRO₂ and the CMRO₂/CBF coupling ratio during the post-stimulus phase

The CMRO₂ and n were estimated during the primary (6–15 s) and post-stimulus (15–30 s) phases of the response to the stimuli, where a correlation was observed between PERS alpha power and all post-stimulus BOLD and CBF responses, thereby enabling us to relate changes in CMRO₂ to EEG-fMRI coupling. We focused our analysis on the flicker stimulus where a clear, well defined, post-stimulus response was observed, with complementary results for the static stimulus (see SI). The higher signal-to-noise ratio (SNR) in the contralateral V1 (positive) than the ipsilateral V1 (negative) response region makes the estimation of CMRO₂ more robust. Therefore we focus our investigation of the metabolic demand of post-stimulus undershoots on contralateral V1, with results for ipsilateral V1 reported in the SI.

Table 1 shows that in contralateral V1 a post-stimulus decrease in CMRO₂ relative to baseline was observed. A significantly larger decrease in CMRO₂ for trials in the upper PERS quartile, that exhibited the largest magnitude BOLD and CBF undershoots, compared to the lower quartile was seen. As expected, during the primary response phase an increase in CMRO₂ relative to baseline was found. CMRO₂ changes in the ipsilateral region were less pronounced (see SI Results and Table S1).

Table 1:

Group mean percentage change (%Δ) in BOLD, CBF and CMRO₂ responses relative to baseline in the contralateral (positive) V1 ROI during the post-stimulus period (15–30s) for the upper and lower PERS alpha power quartiles, and the primary response period (6–15s). CMRO₂ is separately calculated for three M values (6, 15 and 40.2). The associated SE across subjects is also given.

HR (%Δ)	PERS quartile		Primary Response
	Upper	Lower
BOLD	−1.06 ±0.09	−0.8 ±0.1†	1.8 ±0.1
CBF	−24±4	−14±4†	57±6
CMRO2 M=6	−11±4	−4±4*	10±3
M=15	−17±4	−9±4†	32±4
M=40.2	−19±4	−11±4†	41±4

Significance of the difference between upper and lower quartiles (paired t-test):

^†p≤0.05

^*p<0.1.

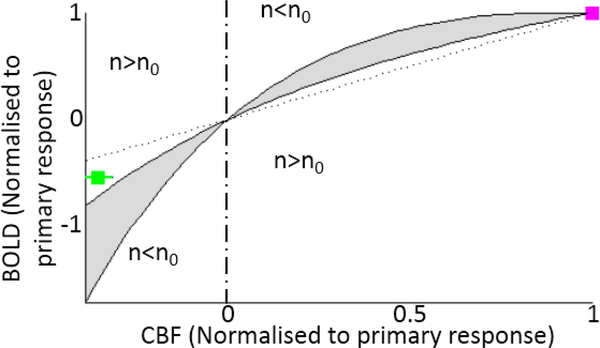
Figure 3 shows group mean ΔBOLD and ΔCBF of the post-stimulus response normalised to the respective ΔBOLD and ΔCBF of the primary response for contralateral V1, as previously carried out [38], to demonstrate differences in n independently of the value of the BOLD scaling parameter M. The grey shaded area indicates all ΔBOLD and ΔCBF response amplitude ratios which could theoretically be achieved with the same n as the primary response, allowing for a range of parameters: α (Grubb constant) = −0.2‒0.2 and β (reflecting deoxyhaemoglobin concentration) = 0.9‒1.5 (Eq 1). The ΔBOLD and ΔCBF for the post-stimulus response fall outside of this iso-n region in an area of the graph representing n larger than that of the primary response. Indeed, using α=0.2, β=1.3 and M (BOLD calibration constant)=15% we found that n=0.86±0.02 in the post-stimulus period, which was significantly larger (p<0.05, paired student t-test) than the value for the primary response (n=0.70 ± 0.02). Figure S7 show individual subject n values for this region, corresponding plots for the ipsilateral V1 are shown in Figure S8. Figure S9 and the SI evaluate possible n values for different response phases in ipsilateral V1 and compare these with contralateral V1.

Figure 3.

BOLD and CBF response ratios. For each subject BOLD and CBF primary and post-stimulus responses from contralateral V1 were normalised to the primary response in that region. Mean values (magenta = primary response phase; green = post-stimulus response phase) over subjects with error bars showing standard error are plotted. The grey shaded region identifies BOLD and CBF response ratios which theoretically have the same coupling ratio as the primary positive response (n₀=0.7). This area was derived using Eq. 1 for a range of model parameters: α= −0.2 – 0.2 & β = 0.9–1.5.

Discussion

Post-stimulus BOLD responses are consistent with inhibitory neuronal activity

Through simultaneous measures of EEG, BOLD and CBF responses to visual stimuli we have provided a body of new evidence that the BOLD post-stimulus response is neuronal in origin, consistent with inhibitory processes which alter the coupling between metabolism and blood flow compared with positive primary responses. We show that whilst static and flicker visual stimuli elicit comparable alpha ERD, primary BOLD and primary CBF responses, flicker stimuli elicit larger magnitude BOLD and CBF post-stimulus undershoots and PERS alpha power than static stimuli (Fig. 1), which complements and extends the work of [15]. This suggests that the driven difference in the post-stimulus response between stimuli is not simply a vascular phenomenon, but instead provides functional information concerning a phase of brain activity that is distinct from initial stimulus processing and occurs following cessation of a stimulus input. Importantly, whilst it is clear that a post-stimulus response requires the presence of an initial stimulus, it is also well known that BOLD, CBF and EEG alpha signals do not provide measures of all aspects of the underlying neural activity. Therefore it is possible that an aspect of the primary neural response exists that could predict the measured post-stimulus response but this is not detected by our current neuroimaging measures. Crucially this work focusses on establishing that the post-stimulus response is neuronal in origin rather than determining its exact relationship with the neural activity occurring during the stimulation. In addition, it is clear that with our measures (fMRI and EEG) the primary and post-stimulus responses appear to represent distinct phases of activity, whose amplitudes are at least partially uncoupled, which must be considered when modelling these responses, for example in a GLM.

We further found that natural trial-by-trial variations in BOLD and CBF post-stimulus responses are reflected in changes in the PERS alpha power, such that trials of high PERS alpha power also exhibited a larger fMRI undershoot in contralateral V1 where a positive primary HR was observed and a smaller fMRI overshoot in ipsilateral V1 regions where a negative primary HR was observed, compared with trials of low PERS alpha power (Figs. 2, S4&S5). This result is consistent with our previous findings in the sensorimotor cortex [5] and provides strong evidence that the links between post-stimulus EEG and fMRI responses are ubiquitous across the brain’s sensory networks and may be bilateral in nature. It is important to note that we do not claim that the post-stimulus EEG-fMRI coupling is entirely driven by alpha frequency activity. In fact, as post-stimulus responses are also well documented within the beta frequency band [1, 3, 40, 41], then the range of post-stimulus neuronal activity which is coupled to the fMRI signal may be task dependent. Therefore, the fMRI post-stimulus response may reflect an amalgamation of neuronal activity over a number of frequency bands, as seen in the primary response [42, 43].

Further evidence for a neuronal origin to the post-stimulus response is provided by the estimated reduction in CMRO₂ from baseline during the post-stimulus response to the flicker stimulus in contralateral V1 (Table 1). Given the strong link between changes in neuronal activity and CMRO₂ [44], this decrease in CMRO₂ reflects an overall reduction in the energy demand of neuronal activity in the contralateral visual cortex during the post-stimulus period relative to baseline. Finally we show a robust, significant difference in n between the contralateral (positive) primary BOLD response and the subsequent post-stimulus response to the flicker stimulus. We suggest this difference in n between the two phases of the response reflects altered neurovascular coupling, which may arise due to a difference in the balance of excitatory and inhibitory neuronal activity [18], due to a difference in the functional roles of the two response phases, see “Functional relevance of post-stimulus responses” section.

Relationship between the duration of stimulation and post-stimulus responses

The post-stimulus BOLD response to our 10 s duration stimulus took ~20 s to return to baseline (Fig. 1B) compared with >60 s in the previous study that used 180 s of visual stimulation [15]. This is in agreement with recent findings that suggest the duration of the beta-frequency MEG rebound is proportional to the duration of the stimulus [1]. The duration of our PERS response (9.5 s window after stimulus cessation) which correlated with the BOLD and CBF responses was longer than the commonly studied rebound, which is reported to last 1–2 s [3]. The difference in the duration of the PERS could be attributed to using a longer duration stimulus in the current study than is typically used in electrophysiology work. We suggest that the cumulative activity and metabolic demand of our visual stimulus could explain the different durations of (EEG and fMRI) post-stimulus responses observed between the present and previous studies.

Methodological considerations in the calculation of CMRO₂ and CMRO₂/CBF coupling

Due to uncertainties in the calibration constants (α, β and M) and the simplicity of the Davis model [45, 46] we explored a physiologically plausible parameter space to validate our findings and conclusions. The M-value is determined specifically for each cortical region and remains constant between HR phases, validating our comparison of Δ%CMRO₂ between high and low PERS quartiles (Tables 1&S1) and primary and post-stimulus fMRI responses (Figs 3&S9). Since hypercapnic calibration was not performed for the current data a range of M-values, reflecting previous literature [16, 36, 47] were tested for comparisons between contralateral and ipsilateral V1. In addition, the precise value of β is also unknown. By exploring possible values of β previously used [38] we eliminate the possibility that β can explain the observed differences in n between the HR phases (Fig. 3).

Our finding of reduced CMRO₂ in the post-stimulus undershoot period relative to baseline is based on applying the Davis model, a steady-state model, to what is traditionally regarded as a dynamic, transient period of the response. It is important to consider whether this could lead to a misinterpretation of the data, either due to the simplicity of the model or to the possible influence of transient uncoupling of CBF, CBV and CMRO₂ during the undershoot period. The Davis model is a simple model of a complex process, and alternative, more detailed compartmental models have been proposed [14]. However, several recent studies have compared the Davis model with a more detailed theoretical model and with simulations on a vascular anatomical network and found that the simple Davis model can provide accurate estimates of CMRO₂ change [45, 48, 49], although the parameter α then takes on more of the role of a fitting parameter capturing several physiological effects rather than a direct reflection of changes in CBV.

Application of the Davis model during a transient period is potentially complicated because two putative physiological explanations have been proposed for the origin of the BOLD undershoot that involve a transient uncoupling of CBF, CBV and CMRO₂. In both these hypotheses CBF returns promptly to the baseline value, but either CMRO₂ [14, 50] or CBV (as in the balloon model [6]) are slow to recover and remain elevated during the undershoot period. This illustrates a primary and longstanding challenge for interpreting the BOLD response: both increased CBV and increased CMRO₂ increase total deoxyhemoglobin and thus decrease the BOLD signal. If a fixed value of α is used in the Davis model analysis we are effectively assuming that there is no balloon effect, and that changes in CBV follow changes in CBF. With this assumption, a transient uncoupling of either CBV or CMRO₂ would be estimated to be a CMRO₂ effect.

If a balloon-type slow recovery of CBV is in fact present but not taken into account in the analysis of the data, the true reduction in CMRO₂ would be even greater than our estimate. That is, the Davis model effectively estimates how much additional deoxyhemoglobin change (due to the combined effects of CBV and CMRO₂ changes) is needed, beyond the deoxyhemoglobin change caused by the measured CBF change, to account for the measured BOLD signal. However, in our analysis the potential altered coupling of CBV and CBF was explored to some extent by considering a range of α within the Davis model. As discussed, uncoupling may result in the post-stimulus CBV signal either: returning to baseline (which may be reflected by α=0) [14]; or remaining elevated, whilst CBF reduces below baseline, due to a balloon effect [6] contribution coupled with a reduction in neuronal activity (reflected by α<0) [12]. Reducing α during the post-stimulus period served to increase the magnitude of calculated Δ%CMRO₂ (i.e. a larger reduction in CMRO₂ is calculated in this scenario to explain the measured BOLD and CBF signals). The larger CMRO₂ reduction results in an increase in n (Fig. S9) when CBV is uncoupled from CBF, exacerbating the difference in n observed between the primary and post-stimulus response phases. The key finding here is that the combined effects of the CBV and CMRO₂ changes is a reduction in deoxyhemoglobin (to explain the measured BOLD and CBF signals), so that if there is an unaccounted post-stimulus elevation of CBV, then the true magnitude of the post-stimulus CMRO₂ decrease would be larger than our estimate.

Importantly, our data differ from the possible scenarios of CBF uncoupling from CBV or CMRO₂ in a critical way: we observe a post-stimulus undershoot of CBF, and a physiological uncoupling is not needed to explain the BOLD undershoot. Applying the Davis model, the estimated Δ%CMRO₂ is negative for our data, not positive, during the undershoot period. This result is in contrast, for example, with the study of Hua et al [51], in which an undershoot of CBF was insufficient to explain the BOLD undershoot, leading them to conclude that the additional contribution to the BOLD undershoot came primarily from a slow CMRO₂ recovery (regardless of whether the Davis or a more complex model was employed) with a smaller contribution from a measured slow CBV recovery. In the current data we see the opposite effect, in that the CBF undershoot is more than sufficient to explain the BOLD undershoot, and a reduction in either CBV or CMRO₂ is needed in addition to fit the BOLD data. An alternative conceivable scenario is that the CBF undershoot is purely a vascular effect uncoupled from neural activity. For example, in the model proposed by Friston et al [52] the CBF responds to a stimulus like a damped harmonic oscillator. Whilst this explanation seems unlikely given the coupling we observed between the EEG with the fMRI responses it is useful to explore what changes in CBV would be required in this scenario. To explain our data as a pure vascular response with no contribution of CMRO₂ during the post-stimulus period (i.e., with n=0), a large CBV reduction in the post-stimulus period would have to occur as shown in Table S2. If there were a large reduction in CBV post-stimulation then our conclusion that n is larger in the post-stimulus period would be invalid, however there currently is no experimental evidence or physiological model to support a large CBV reduction in the undershoot period.

Physiologically plausible, α values can explain the difference in n for the primary response between our contralateral V1 data (n=0.70±0.02, for M = 15%, α = 0.2, β=1.3) compared with previous reports of n = 0.4 – 0.5 for visual cortex [16, 38, 53, 54]. If the traditional value of α=0.38 [16, 55] is used then our calculated coupling ratios reduce to n=0.55±0.02 for the contralateral (positive) primary response and n=0.74±0.02 for the associated undershoot. This brings the primary response n closer to previously reported values whilst still exhibiting a significant difference between our primary and post-stimulus responses. In addition, Liang et al [38] showed that n varies with stimulus contrast; their lowest contrast stimulus evoked a n=0.6, which reduced to n=0.4 for their highest contrast stimulus. Therefore, the larger n we report may also be explained by the 33% contrast flicker visual stimulus used here, compared with the previous studies which used 100% contrast for their stimuli [16, 38, 53, 54].

Therefore, whilst we cannot absolutely quantify Δ%CMRO₂ and n, the pattern of differences between response phases (higher n for the post-stimulus than the primary contralateral response [Figs 3&S9]) and between quartiles (more negative Δ%CMRO₂ during the post-stimulus period for upper than lower PERS [Table 1]), from which our observations and conclusions are drawn, remain valid for the most physiologically plausible parameter space explored. Furthermore, if there is a transient uncoupling of CBV and CBF as in the balloon model our estimate of Δ%CMRO₂ and the CMRO₂/CBF coupling ratio n is an underestimate.

Functional relevance of post-stimulus responses

Our data shed new light on the fMRI post-stimulus response as a haemodynamic correlate of the neuronal response to stimulus cessation. Our data have shown that: i) the post-stimulus EEG alpha power correlated with the fMRI post-stimulus responses; ii) the BOLD undershoot was accompanied by a reduction in both CBF and CMRO₂; iii) n was larger during the post-stimulus than during the primary response in contralateral V1. A body of electrophysiological studies have provided theories that increased alpha power reflects an increase in cortical inhibition e.g. [25]. Therefore our observed correlation between the fMRI and EEG post-stimulus responses leads us to suggest that the fMRI responses may reflect inhibitory processes. Indeed we previously proposed that post-stimulus responses may provide an inhibitory process by which the stimulated network can re-integrate activity after lateralised responses during stimulation [5], consistent with the integrative hypothesis of Donner and Siegel for the role of oscillatory activity in cortical processing [56]. Our current results also support this hypothesis.

In addition, from our fMRI measures in contralateral V1 we report a post-stimulus reduction in both CBF and CMRO₂ relative to baseline, in response to the flicker stimulus (Table 1 & Fig. S7). The reduction in CMRO₂ when a post-stimulus fMRI undershoot is observed shows a reduction in metabolism and tells us that the overall energy cost of post-stimulus neuronal activity is lower than the baseline level. Given the known relative energy demands of inhibitory and excitatory activity [19–21] this result points to a reduction in excitatory synaptic activity as that is the primary energy-consuming aspect of neural activity. Our data cannot preclude the possibility that, alongside the neuronal component, there is an additional vascular component to the post-stimulus fMRI signal [6]. However, if present this vascular mechanism only exacerbates the pattern of differences in Δ%CMRO₂ and n observed between HR phases and therefore does not detract from the functional significance of the post-stimulus response (see also “Methodological considerations in the calculation of CMRO₂ and CMRO₂/CBF coupling” section).

Our finding that n differed significantly between response phases we believe provides additional information on the potential mechanism underlying the post-stimulus BOLD response. Our initial hypothesis of an increase in n during the post-stimulus response phase, relative to the primary phase, reflecting active post-stimulus neuronal inhibitory processes was borne out by our data (Figs. 3&S7–S9). Consequently we suggest a framework into which the current results can be placed which is complementary to previous work. Buxton et al have suggested that n during the primary response phase is not fixed but can be manipulated and may provide an indication of changes in the balance of excitatory and inhibitory neural activity [18]. In a series of studies [37, 38, 47, 57, 58], Buxton et al have observed alterations in n within visual cortex through manipulation of stimulus presentation or baseline states. A simple explanation to encompass previous and current results is to consider a brain volume element consisting of interacting populations of excitatory neurons and inhibitory neurons. The result of these interactions is a net rate of activity for the excitatory (E) and inhibitory (I) neuronal populations. I and E both drive CBF and CMRO₂, but to different degrees. E is a strong positive driver of both CBF and CMRO₂ due to the high energy cost of restoring ion gradients associated with excitatory synaptic activity. The key assumption of our hypothesis is that, compared to excitatory activity, net inhibitory activity is a stronger positive driver of CBF relative to the CMRO₂ cost of that inhibitory activity.

This hypothesis plays out in different ways when the excitatory and inhibitory activity change from a baseline state. For the case of increasing stimulus intensity, as used in [38], an increasing drive to the excitatory population creates an increased ΔE, which in turn drives an increased ΔI locally. Electrophysiological studies suggest that increasing stimulus intensity increases the activity of the inhibitory population faster than the excitatory population, to slow the growth of the excitatory activity [59]. With increasing stimulus intensity the more rapid rise of ΔI relative to ΔE causes Δ%CBF to increase faster than Δ%CMRO₂, causing a decrease in n with stimulus intensity in the primary response phase of the positive BOLD response, in agreement with the finding of Liang et al [38]. For the post-stimulus undershoot in the current study, inhibition may be increased, creating a positive ΔI, in an analogous manner to how inter-hemispheric inhibition involves excitatory input from the contralateral (stimulated) hemisphere activating ipsilateral inhibitory neurons [60]. Following our hypothesis above, the increased inhibitory activity would be associated with a strong CBF increase and a relatively weak CMRO₂ increase in the post-stimulus period. In addition, the increased I leads to a net decrease of the local excitatory activity, causing a negative ΔE. The reduced E would be associated with a decrease of both CBF and CMRO₂. If the net effects on CBF and CMRO₂ are dominated by the reduction in excitatory activity, both should be reduced. However, our hypothesis predicts that each of these reductions is partially offset by the opposite changes driven by the increased inhibitory activity, with the positive CBF offset larger relative to the positive CMRO₂ offset. This corresponds to an increased n in the post-stimulus and primary negative responses compared to the positive primary response phase. The key difference between the case of increasing stimulus intensity in the primary phase compared to changes in inhibition for the post-stimulus undershoot is that ΔE and ΔI have the same sign in the first case but opposite signs in the second case, leading respectively to decreased n and increased n. The source of the difference is that the excitatory population is driven by the stimulus, but the inhibitory population is driven by the active inhibition post-stimulation.

The above interpretation of our results as evidence of increased inhibition is motivated by the idea that the net CBF change results from the interplay of mechanisms driven by both inhibitory and excitatory neural activity, but that these two types of activity contribute in different proportions to the net CMRO₂ change [18]. An alternative way of looking at these data is in terms of the modeling framework recently introduced by Havlicek et al [61, 62] in the context of a forward model for dynamic causal modeling analysis. In this model, the CMRO₂/CBF coupling ratio n is assumed to be a fixed but nonlinear function of CBF, with n increasing as the amplitude of the CBF change reduces, as seen in our data. This model was originally introduced by Buxton and Frank [63] as a fixed relationship between CBF and the oxygen extraction fraction dictated by the assumption that the tissue partial pressure of oxygen (pO₂) is near zero, so that the oxygen gradient from capillaries to tissue needed to support increased CMRO₂ could only come from decreasing the oxygen extraction fraction to increase capillary pO₂. In effect, this model imposed a physical requirement for the mismatch of CBF and CMRO₂ due to a diffusion limitation, that CMRO₂ could not increase more than was allowed by the CBF increase. A number of subsequent experimental studies, however, found that tissue pO₂ in the brain is quite high [64–66]. Incorporating these results, a later hypothesis is that the mismatch of CMRO₂ and CBF serves to maintain tissue pO₂ at near its baseline value, although there is no longer a physical basis for a fixed relationship between CBF and the oxygen extraction fraction because tissue pO₂ can potentially drop [67]. Importantly, though, in the context of the Havlicek model a reduction of CBF is a marker of reduced excitatory activity, consistent with increased inhibitory activity as we propose in interpreting our data.

Even if the biological function of the mismatch of CMRO₂ and CBF changes is to prevent tissue pO₂ from dropping too much, the question of the mechanisms that produce the mismatch remain. Interestingly, there is little evidence that tissue pO₂ itself is the driver of the CBF change. Instead, a number of experimental findings support the idea that CBF is driven in a feed-forward way by neural activity, including both excitatory and inhibitory activity [22, 68, 69]. Our interpretation of the current results is based on this viewpoint. Essentially, taking the CMRO₂ change as an index of the magnitude of the net change in neural activity, the CMRO₂/CBF coupling ratio is an index of net neurovascular coupling, with a lower value indicating stronger neurovascular coupling (a larger CBF change for a given change in neural activity). This view then offers the possibility of interpreting the observed CMRO₂/CBF coupling ratio in terms of mechanisms of neurovascular coupling. At this point any such interpretation must be speculative because of our lack of understanding of how all of the potential mechanisms for altering CBF are coordinated in the awake brain. Ongoing detailed studies in animal models of the CBF changes evoked by the activity of particular neural cell populations, with the associated CMRO₂ changes, will provide a more solid foundation for interpreting observed changes in the coupling ratio in human studies [70].

Cautious interpretation of the responses in ipsilateral V1 is needed until further investigations are carried out (see SI Results and Discussion). However, our observation that the primary negative BOLD response and the bilateral post-stimulus BOLD responses are associated with a larger n than the primary positive BOLD response (Fig. S7–S9), presents the intriguing possibility that post-stimulus and negative responses are driven by a similar underlying neurophysiological mechanism, which is different to the positive primary response. We suggest a similar mechanism to that of the post-stimulus undershoot would explain the negative primary response in ipsilateral V1, where a larger n than the positive contralateral primary response was also observed. In the case of the post-stimulus overshoot the mechanism proposed may be inverted such that there is a reduction in inhibition (negative ΔI) with a concordant increase in excitation (positive ΔE), leading to the overshoot but still the high n observed.

Our interpretations of altered n in terms of mechanisms of neurovascular coupling are consistent with existing data, but the role of inhibitory interneurons in the control of CBF presents a complex picture [22], including both dilation and constriction of blood vessels. Therefore more work is needed in the future to test the key assumption of our basic hypothesis, that the net effect of increased neural inhibition is a positive drive to CBF. For example, a recent study [69], using optogenetic methods in a small animal model, found that a delayed negative CBF response to a brief stimulus was eliminated when the effects of neuropeptide Y (NPY) were blocked. This suggests an alternative hypothesis for how increased inhibitory activity drives a BOLD post-stimulus undershoot, in this case directly due to a CBF undershoot driven by agents related to inhibitory neural activity that constrict blood vessels, such as NPY. The two hypotheses differ in whether the net effect of increased inhibitory activity is a positive or negative contribution to the Δ%CBF. The key test distinguishing these hypotheses is based on the associated Δ%CMRO₂, specifically the direction of change of the coupling ratio n from that of the primary positive response. The first (ours) hypothesis predicts a larger n, while the second (based on [69]) predicts a smaller n. Our current results thus support our initial hypothesis, but this is clearly an important question that requires further investigation, particularly in small animal models in which excitatory and inhibitory activity can be identified and manipulated more directly than is possible in the human brain.

Conclusions

In conclusion, this study of visual cortex shows EEG-fMRI coupling during the post-stimulus period which provides strong evidence that the fMRI post-stimulus response is neuronal in origin, rather than due to a slow recovery of CMRO₂ or blood volume. We show that increased power of the post-stimulus alpha oscillation is associated with an increased post-stimulus fMRI undershoot (contralaterally) and reduced post-stimulus fMRI overshoot (ipsilaterally). Regardless of the parameter values used in the Davis model we observe a pattern of higher CMRO₂/CBF coupling (n) within the post-stimulus response phase, compared with the positive primary response in contralateral V1, which provides further indication that these responses arise from different mechanisms. We suggest that post-stimulus responses are active inhibitory processes needed to return excitatory activity to baseline across the whole sensory network which processed the stimulus input.

Overall, our data suggest that EEG and fMRI post-stimulus responses reflect a functionally relevant phase of neuronal activity which is modulated by the type and duration of stimulation but carries information that is distinct from the primary brain response. Therefore post-stimulus responses require neuroscientific study in their own right. To build more accurate models of their morphology it is imperative to move away from outdated canonical haemodynamic response models, which imply a fixed relationship between the two main temporal phases of the fMRI response to stimulation, as these mask post-stimulus effects of interest. Recent methods such as the P-DCM model recently developed by Havlicek et al [61] provide interesting new modelling approaches which allow for the balance of excitatory and inhibitory activity to alter between response phases, in line with the hypothesis we present here. This method requires further investigation, as discussed above, such as incorporating the dynamic changes in CMRO₂-CBF coupling that we observe between the different phases of the response timecourse, and investigation of how to implement it in such a way to identify brain regions responding to a task which exhibit uncoupled primary and post-stimulus response amplitudes. The development of new analysis methods will enable elucidation of the role of post-stimulus signals in cognitive function as well as neurological disease.

Highlights.

• Simultaneous EEG-BOLD-ASL measures with visual hemifield stimuli

• Post-stimulus EEG-fMRI coupling is a general mechanism across human visual and motor systems

• Post-stimulus EEG and fMRI responses are modulated independently from the primary response

• Altered coupling of CMRO₂ and CBF is found in post-stimulus compared with primary responses

• Hypothesize post-stimulus signals reflect distinct inhibitory neuronal processes