Abstract
The term “policy analysis” describes scientific evaluations of the impacts of past public policies and predictions of the outcomes of potential future policies. A prevalent practice has been to report policy analysis with incredible certitude. That is, exact predictions of policy outcomes are routine, while expressions of uncertainty are rare. However, predictions and estimates often are fragile, resting on unsupported assumptions and limited data. Therefore, the expressed certitude is not credible. This paper summarizes my work documenting incredible certitude and calling for transparent communication of uncertainty. I present a typology of practices that contribute to incredible certitude, give illustrative examples, and offer suggestions on how to communicate uncertainty.
Keywords: incredible certitude, communication of uncertainty, policy analysis
The term “policy analysis” is a shorthand used to describe scientific evaluations of the impacts of past public policies and predictions of the outcomes of potential future policies. For some time, I have criticized the prevalent practice of policy analysis with “incredible certitude,” with particular attention to economic and social policy in the United States (1–3). Exact predictions of policy outcomes and exact estimates of the state of the economy are routine. Expressions of uncertainty are rare. However, predictions and estimates often are fragile, resting on unsupported assumptions and limited data. Therefore, the expressed certitude is not credible.
Leading examples are the Congressional Budget Office (CBO) predictions, called scores, of the federal debt implications of pending legislation. The budgetary impacts of complex changes to federal law are difficult to foresee. However, Congress has required the CBO to make point predictions 10 y into the future, unaccompanied by measures of uncertainty.
Additional leading examples are the official economic statistics published by federal statistical agencies, including the Bureau of Economic Analysis (BEA), the Bureau of Labor Statistics (BLS), and the Census Bureau. These agencies report point estimates of gross domestic product (GDP) growth, unemployment, and household income, respectively. Agency staff know that official statistics suffer from sampling and nonsampling errors. However, the practice has been to report statistics with only occasional measurement of sampling errors and no measurement of nonsampling errors.
CBO scores and official statistics exemplify incredible certitude in the predictions and estimates of the federal government. The phenomenon is also widespread in economic policy analysis performed by researchers at universities and other institutions.
Logic and Practice of Policy Analysis
Policy analysis, like all empirical research, combines assumptions and data to draw conclusions. The logic of inference is summarized by the relationship: assumptions + data ⇒ conclusions. Holding fixed the available data, stronger assumptions may yield stronger conclusions. At the extreme, one may achieve certitude by posing sufficiently strong assumptions. A fundamental difficulty is to decide what assumptions to maintain.
There is a tension between the strength of assumptions and their credibility, which I have called the Law of Decreasing Credibility (ref. 4, p. 1): “The credibility of inference decreases with the strength of the assumptions maintained.” This “Law” implies that analysts face a tension as they decide what assumptions to maintain. Stronger assumptions yield conclusions that are more powerful but less credible.
I use the word credibility regularly, but I must caution that it is a primitive concept that defies deep definition. The Second Edition of the Oxford English Dictionary (OED) defines credibility as “the quality of being credible.” The OED defines credible as “capable of being believed; believable” (5). It defines believable as “able to be believed; credible” (5). Therefore, we come full circle.
Whatever credibility may be, it is a subjective concept. Each person assesses credibility on his or her own terms. Disagreements occur often. Indeed, they may persist without resolution when assumptions are nonrefutable; that is, when alternative assumptions are consistent with the available data.
In principle, policy analysis can illuminate the logic of inference by posing alternative assumptions and determining the conclusions that follow. In practice, analysts tend to sacrifice credibility to obtain strong conclusions. Seeking to explain why incredible certitude has been the norm, I have found it natural as an economist to conjecture that analysts respond to incentives. Many policy makers and members of the public resist facing up to uncertainty, and therefore, analysts are motivated to express certitude.
A story circulates about an economist’s attempt to describe uncertainty about a forecast to President Lyndon B. Johnson. The economist is said to have presented the forecast as a likely range of values for the quantity under discussion. Johnson is said to have replied, “Ranges are for cattle. Give me a number.”
Policy Analysis in a Posttruth World
Although President Johnson may not have wanted the economist to forecast a range of values, I expect that he wanted to hear a number within the range that the economist thought plausible. I expect that the economist interpreted Johnson’s request this way and complied. Likewise, I expect that the analysts who produce CBO scores and official economic statistics generally intend them to be plausible values for the quantities in question.
The 2016 presidential election in the United States initiated a period in which some senior officials of the federal government not only resist expression of uncertainty but seem unconcerned with the plausibility of predictions and estimates. Much has been written about the tenuous relationship between the current president and reality. The situation was summarized well by Ruth Marcus, who opened one of her columns in The Washington Post as follows: “Welcome to ‘brace yourself for’ the post truth presidency. ‘Facts are stubborn things,’ said John Adams in 1770, defending British soldiers accused in the Boston Massacre, ‘and whatever may be our wishes, our inclinations, or the dictates of our passion, they cannot alter the state of facts and evidence.’ Or so we thought, until we elected to the presidency a man consistently heedless of truth and impervious to fact checking” (6).
Also, see the March 23, 2017 cover story of Time that reports an interview with the president (7). The Time cover asks “Is Truth Dead?”
The longstanding failure of policy analysis to communicate uncertainty may seem a minor concern in the current political environment. Nevertheless, I think that it is important that policy analysis communicate uncertainty honestly to enable trustworthy assessment of what we do and do not know.
Having this in mind, I summarize here my work documenting incredible certitude in policy analysis and calling for transparent communication of uncertainty. I first present a typology of practices that contribute to incredible certitude that was laid out in refs. 1 and 2, give illustrative examples, and offer suggestions on how to communicate uncertainty. I then describe incredible certitude in official economic statistics, drawing on ref. 3, and again, offer suggestions on how to communicate uncertainty.
My discussion focuses mainly on economic policy, with attention also to criminal justice, education, and public health. I have been disheartened to find incredible certitude prevalent in each of these domains. However, there are some other areas of policy analysis that make laudable efforts to communicate uncertainty transparently.
A notable case is forecasting by the National Weather Service (NWS). A remarkable example is the tweet issued by the NWS on August 27, 2017 as rainfall from Hurricane Harvey began to inundate southeastern Texas: “This event is unprecedented & all impacts are unknown & beyond anything experienced” (https://twitter.com/nws/status/901832717070983169). Refs. 8–10 have related discussions of communication of scientific uncertainty in multiple policy-relevant domains.
Practices Contributing to Incredible Certitude with Examples
Manski (1, 2) introduced this typology of practices that contribute to incredible certitude.
Conventional certitude: A prediction that is generally accepted as true but is not necessarily true.
Dueling certitudes: Contradictory predictions made with alternative assumptions.
Conflating science and advocacy: Specifying assumptions to generate a predetermined conclusion.
Wishful extrapolation: Using untenable assumptions to extrapolate.
Illogical certitude: Drawing an unfounded conclusion based on logical errors.
Media overreach: Premature or exaggerated public reporting of policy analysis.
I provided illustrative examples and offered suggestions to improve practices. I summarize here and add to my earlier discussion.
Conventional Certitude: CBO Scoring of Legislation
Conventional certitude is exemplified by CBO scoring of federal legislation. The CBO was established in the Congressional Budget Act of 1974. The act has been interpreted as mandating the CBO to provide point predictions (scores) of the budgetary impact of legislation. CBO scores are conveyed in letters that the director writes to leaders of Congress, unaccompanied by measures of uncertainty.
CBO scores exemplify conventional certitude, because they have achieved broad acceptance. They are used by both Democratic and Republican members of Congress. Media reports largely take them at face value.
Well-known examples are the scoring of the Patient Protection and Affordable Care Act of 2010, commonly known as Obamacare or the ACA, and of the American Health Care Act of 2017, which sought to partially repeal the ACA. In March of 2010, the CBO and the Joint Committee on Taxation (JCT) jointly scored the combined consequences of the ACA and the Reconciliation Act of 2010 and reported that “enacting both pieces of legislation...would produce a net reduction of changes in federal deficits of $138 billion over the 2010–2019 period as a result of changes in direct spending and revenue” (ref. 11, p. 2). Media reports largely accepted the CBO score as fact without questioning its validity, the hallmark of conventional certitude.
In March of 2017, the CBO and the JCT scored the American Health Care Act and reported that “enacting the legislation would reduce federal deficits by $337 billion over the 2017–2026 period” (ref. 12, p. 1). The CBO verbally acknowledged uncertainty in the latter prediction, writing that “[t]he ways in which federal agencies, states, insurers, employers, individuals, doctors, hospitals, and other affected parties would respond to the changes made by the legislation are all difficult to predict, so the estimates in this report are uncertain. But CBO and JCT have endeavored to develop estimates that are in the middle of the distribution of potential outcomes” (ref. 12, p. 3–4).
However, the point predictions of reductions in federal deficits of $138 and $337 billion were not accompanied by quantitative measures of uncertainty.
The CBO has established an admirable reputation for impartiality. Perhaps it is best to leave well enough alone and have the CBO express certitude when it scores legislation, even if the certitude is conventional rather than credible. However, I worry that the longstanding social contract to take CBO scores at face value is at risk for breaking down. I think that it is better for the CBO to act to protect its reputation than to have some disgruntled group in the government or the media declare that the emperor has no clothes.
A simple approach would be to provide interval forecasts of the budgetary impacts of legislation. The CBO would produce two scores for a bill, a low score and a high score, and report both. For example, the CBO could report the 0.10 and 0.90 quantiles of the distribution of potential outcomes that it referenced when scoring the American Health Care Act of 2017. Alternately, it could present a full probabilistic forecast in a graphical fan chart, such as the Bank of England uses to predict GDP growth (see the discussion later in this article). If the CBO must provide a point prediction, it can continue to do so, with some convention used to locate the point within the interval forecast.
I have received disparate reactions when I have suggested interval scoring to economists and policy analysts. Academics react positively, but persons who have worked in the federal government tend to be skeptical. Some assert that members of Congress are psychologically or cognitively unable to deal with uncertainty. Some assert that Congressional decision making is a noncooperative game, in which expression of uncertainty may yield inferior legislative outcomes. I am not aware of research that provides foundation for or against either assertion.
Dueling Certitudes: The Deterrent Effect of the Death Penalty
American society has long debated the deterrent effect of the death penalty as a punishment for murder. Disagreement persists, because research has not been able to settle the question. Researchers have used data on homicide rates and sanctions across states and years to examine the deterrent effect of the death penalty. The fundamental difficulty is that the outcomes of counterfactual policies are unobservable. Data alone cannot reveal what the homicide rate in a state without (with) a death penalty would have been had the state (not) adopted a death penalty statute. Data must be combined with assumptions to predict homicides under counterfactual deterrence policies.
A large body of work has addressed deterrence and the death penalty, but the literature has failed to achieve consensus. Researchers studying the question have used much of the same data, but they have maintained different assumptions and have consequently reached different conclusions. Rather than acknowledge uncertainty about the realism of its maintained assumptions, each published article touts its findings as accurate. The result is dueling certitudes across articles.
Two committees of the National Research Council have documented the substantial variation in research findings and have investigated in depth the problem of inference on deterrence (13, 14). The latter committee, reiterating a basic conclusion of the former one, wrote: “The committee concludes that research to date on the effect of capital punishment on homicide is not informative about whether capital punishment decreases, increases, or has no effect on homicide rates” (ref. 14, p. 2).
To illustrate in a simple setting how research that uses the same data but different assumptions can reach very different findings, Manski and Pepper (15) examined data from the critical 1970s period when the Supreme Court decided the constitutionality of the death penalty. The 1972 Supreme Court case Furman v. Georgia resulted in a multiyear moratorium on the application of the death penalty, while the 1976 case Gregg vs. Georgia ruled that the death penalty could be applied subject to certain criteria. We examined the effect of death penalty statutes on homicide rates in 2 y: 1975, the last full year of the moratorium, and 1977, the first full year after the moratorium was lifted. In 1975, the death penalty was illegal throughout the country. In 1977, 32 states had legal death penalty statutes. For each state and year, we observe the homicide rate and whether the death penalty is legal.
Table 1 displays the homicide rate per 100,000 residents in 1975 and 1977 in the states that did and did not legalize the death penalty after the Gregg decision. We call the former the “treated” states and the latter the “untreated” ones. When computing averages across states, we weight each state by its population.
Table 1.
Homicide rates per 100,000 residents by year and treatment status in 1977
| Year | Group | Total | |
| Untreated | Treated | ||
| 1975 | 8.0 | 10.3 | 9.6 |
| 1977 | 6.9 | 9.7 | 8.8 |
| Total | 7.5 | 10.0 | 9.2 |
Reprinted with permission from ref. 15: Springer Nature Journal of Quantitative Criminology, copyright 2012.
The data in the table may be used to compute three simple estimates of the effect of death penalty statutes on homicide. A “before-and-after” analysis compares homicide rates in the treated states in 1975 and 1977. The 1975 homicide rate in these states, when none had the death penalty, was 10.3 per 100,000. The 1977 rate, when all had the death penalty, was 9.7. The before-and-after estimate is the difference between the 1977 and 1975 homicide rates; that is, 9.7 − 10.3 = −0.6. This is interpretable as the average effect of the death penalty on homicide in the treated states if one assumes that nothing germane to homicide occurred in these states between 1975 and 1977 except for legalization of capital punishment.
Alternatively, one might compare the 1977 homicide rates in the treated and untreated states. The 1977 rate in the treated states, which had the death penalty, was 9.7. The 1977 rate in the untreated states, which did not have the death penalty, was 6.9. The estimate is the difference between these homicide rates; that is, 9.7 − 6.9 = 2.8. This is interpretable as the nationwide average effect of the death penalty on homicide in 1977 if one assumes that persons living in the treated and untreated states have the same propensity to commit murder in the absence of the death penalty and respond similarly to enactment of the death penalty. With this assumption, the observed homicide rate in the treated states reveals what the rate would have been in the untreated states if they had enacted the death penalty and vice versa.
However, a third way to use the data is to compare the temporal changes in homicide rates in the treated and untreated states. Between 1975 and 1977, the homicide rate in the treated states fell from 10.3 to 9.7, while the rate in the untreated states fell from 8.0 to 6.9. The so-called difference-in-difference estimate is the difference between these temporal changes; that is, (9.7 − 10.3) − (6.9 − 8.0) = 0.5. This is interpretable as the nationwide effect of the death penalty on homicide if one assumes that all states experience a common time trend in homicide and that enactment of the death penalty has the same effect in all states.
These three estimates yield different empirical findings regarding the effect of the death penalty on homicide. The before-and-after estimate implies that enactment of a death penalty statute reduces the homicide rate by −0.6 per 100,000. The other two estimates imply that having the death penalty raises the homicide rate by 2.8 or 0.5 per 100,000. The idea that capital punishment may increase the homicide rate is contrary to the traditional view of punishment as a deterrent. However, some researchers have argued that the death penalty shows a lack of concern for life that brutalizes society into greater acceptance of commission of murder.
Which estimate is correct? Given certain assumptions, each appropriately measures the effect of the death penalty on homicide. However, the assumptions that justify this interpretation differ across estimates. One may be correct, or none of them may be correct. If three researchers were to each maintain a different one of the assumptions and report one of three estimates, they would exhibit dueling certitudes.
The antidote to dueling certitudes about the deterrent effect of capital punishment is to recognize uncertainty by generating a set of estimates under alternative assumptions. To formalize this idea in a flexible manner, ref. 15 studies the conclusions implied by relatively weak “bounded variation” assumptions that restrict variation in treatment response across places and time. The results are findings that bound the deterrent effect of capital punishment. By successively adding stronger identifying assumptions, we seek to make transparent how assumptions shape inference. We perform empirical analysis using state-level data in the United States in 1975 and 1977. Under the weakest restrictions, there is substantial ambiguity: we cannot rule out the possibility that having a death penalty statute substantially increases or decreases homicide. This ambiguity is reduced when we impose stronger assumptions, but inferences are sensitive to the maintained restrictions. Combining the data with some assumptions implies that the death penalty increases homicide, but other assumptions imply that the death penalty deters it.
Dueling certitudes regarding the deterrent effect of the death penalty exemplify a common phenomenon in analysis of criminal justice policy. Another notable example is dueling certitudes regarding the effect of “right-to-carry” laws on crime rates (16, 17).
Conflating Science and Advocacy: Friedman (18) and Educational Vouchers
I earlier summarized the logic of inference by the relationship: assumptions + data ⇒ conclusions. The scientific method ordinarily supposes that the directionality of inference runs from left to right. One combines assumptions with data to derive conclusions.
One can reverse the directionality, seeking assumptions that imply or negate some predetermined conclusion. Reversing directionality can be scientifically informative if one proceeds neutrally, aiming to learn assumptions that yield or contrariwise, disprove a specified conclusion. However, researchers sometimes do not proceed neutrally. Instead, they seek only to learn assumptions that yield a favored conclusion. This practice characterizes advocacy.
Policy analysts inevitably portray their deliberative processes as scientific. However, some analysis may be advocacy wrapped in the rhetoric of science. Studies published by certain think tanks seem almost inevitably to reach strong liberal or conservative policy conclusions. The conclusions of some academic researchers are similarly predictable. Perhaps these analysts begin without preconceptions and are led by the logic of inference to draw strong conclusions. Alternately, they may begin with conclusions that they find congenial and work backward to support them.
The economist Milton Friedman had a seductive ability to conflate science and advocacy. His advocacy of educational vouchers in the 1950s continues to be influential today. Proponents of vouchers have argued that American school finance policy limits educational options and impedes the development of superior alternatives. Government operation of free public schools, they say, should be replaced by vouchers permitting students to choose any school meeting specified standards. The awakening of modern interest is usually credited to Friedman (18).
Friedman posed a theoretical economic argument for vouchers, in which he entertained several grounds for government operation of schools and then dismissed them. He cited no empirical evidence to justify his conclusions. Instead, he placed the burden of proof on free public schooling, effectively asserting that vouchers are the preferred policy in the absence of evidence to the contrary. This is advocacy, not science. An advocate for public schooling could reverse the burden of proof, arguing that the existing system should be retained in the absence of evidence.
A scientific analysis would have to acknowledge that economic theory per se does not yield conclusions about the optimal design of educational systems. It would have to stress that the merits of alternative designs depend on the magnitudes of the market imperfections and neighborhood effects that Friedman noted as possible justifications for government intervention. Theory alone cannot determine these magnitudes. Also, it would have to observe that information about these matters was almost entirely lacking when Friedman wrote in the mid-1950s. Indeed, much of the needed knowledge remains lacking today.
Wishful Extrapolation: Food and Drug Administration Drug Approval
Extrapolation is essential to policy analysis. A central objective is to inform policy choice by predicting the outcomes that would occur if past policies were to be continued or alternative ones were to be enacted.
Researchers often use untenable assumptions to extrapolate. I have called this manifestation of incredible certitude “wishful extrapolation.” A common form of wishful extrapolation assumes that a future or hypothetical situation would be identical to an observed one in some respect. Analysts regularly make such invariance assumptions, often without basis. Certain invariance assumptions achieve the status of conventional certitudes, giving analysts license to pose them without fear that their validity will be questioned. To illustrate, I will discuss extrapolation from randomized experiments, with attention to the drug approval process of the Food and Drug Administration (FDA).
Randomized experiments are valued for their ability to yield credible certitude about treatment response in a study population, a property called “internal validity.” A common problem is to extrapolate experimental findings credibly, a property called “external validity.” Analysts often assume that the outcomes that would occur under a policy of interest are the same as the outcomes that occur in a treatment group. This invariance assumption may be reasonable but often is wishful extrapolation.
Several forms of extrapolation occur when data from randomized clinical trials (RCTs) are used to approve new drugs. First, the subjects in an RCT are volunteers and often are restricted to persons who lack comorbidities. When trial data are used to approve drugs, clinicians may assume that treatment response in the patient population is similar to that observed in the trial. This invariance assumption may not be accurate.
Second, the drug treatments assigned in RCTs differ from those that would be assigned in practice. Drug trials are generally double blind, with neither the patient nor physician knowing the assigned treatment. A trial reveals response when patients and physicians are uncertain what drug a patient receives. It does not reveal what response would be in a clinical setting, where patients and physicians would have this information and react to it.
Third, we often want to learn long-term outcomes of treatments. However, the longest RCTs for drug approval, called phase 3 trials, typically run only 2–3 y. When trials are not long enough to observe the health outcomes of real interest, the practice is to measure surrogate outcomes and base drug approval decisions on their values. For example, treatments for heart disease may be evaluated using data on patient cholesterol levels and blood pressure rather than data on heart attacks and lifespan. Credible extrapolation from outcomes measured during a trial to long-term outcomes of interest can be challenging.
The FDA collects additional outcome data after drug approval through its postmarket surveillance program, which analyzes outcomes experienced when the drug is used in clinical practice. However, this program only aims to detect adverse side effects of approved drugs, not assess their effectiveness in treating the conditions for which they are intended. The available data are limited by the fact that the FDA cannot compel a firm to perform new trials after a drug has been approved.
The ability of the FDA to cope with uncertainty in drug approval is constrained by the present practice of framing approval as a binary (yes–no) decision between full approval and complete disapproval. Manski (2) argues that it may be beneficial to empower the FDA to institute an adaptive partial approval process, where the extent of the permitted use of a new drug would vary as evidence accumulates. The stronger the evidence on outcomes of interest, the more that use of a new drug would be permitted.
Illogical Certitude: Research on Heritability
Logical errors contribute to incredible certitude. The obvious solution is not to make such errors, but they persist.
A common nonsequitur occurs when a researcher performs a statistical test of a null hypothesis, finds that the hypothesis is not rejected, and interprets nonrejection as proof that the hypothesis is correct. Texts on statistics caution that nonrejection does not prove that a null hypothesis is correct. Nevertheless, researchers often confuse nonrejection with proof.
An exotic nonsequitur has persisted in research on the heritability of human traits. Heritability has been a topic of study and controversy since the latter third of the 19th century. Some social scientists have sought to connect heritability of intelligence quotient (IQ) with social policy, asserting that policy can do little to ameliorate inequality of achievement if IQ is largely heritable.
Lay people often use the word “heritability” in the loose sense of the OED, which defines it as “[t]he quality of being heritable, or capable of being inherited” (5). Much research on heritability has used the word in a specific technical way, defined in terms of an analysis of variance. Large estimates of heritability have been interpreted as implying small potential policy effectiveness. However, Goldberger (19) showed the absurdity of considering heritability estimates to be policy relevant (ref. 2, section 1.7 has additional discussion).
Media Overreach: “The Case for $320,000 Kindergarten Teachers”
The public rarely learns of policy analysis from original sources but rather, learns from the media. The journalists who decide what analysis warrants coverage and how to report it have considerable power to influence societal perspectives. Some media coverage of policy analysis is serious and informative, but overreach is common. The prevailing view seems to be that certitude sells.
A conspicuous instance appeared on the front page of the New York Times on July 28, 2010 (20). The New York Times economics journalist David Leonhardt reported on research investigating how students’ kindergarten experiences affect their income as adults. He began with the question: “How much do your kindergarten teacher and classmates affect the rest of your life?” (20). He then called attention to new work that attempted to answer the question, at least with respect to adult income. Focusing on the impact of good teaching, Leonhardt wrote that the authors “estimate that a standout kindergarten teacher is worth about $320,000 a year. That’s the present value of the additional money that a full class of students can expect to earn over their careers” (20).
The New York Times article exemplifies media overreach. Leonhardt wrote that the new study was “not yet peer-reviewed” (20). In fact, the study did not even exist as a publicly available working paper when he wrote his article. What existed was a set of slides dated July 2010 for a conference presentation made by the authors. A bullet point on the final page of the slides estimated the value of good kindergarten teaching to be $320,000. The slides did not provide sufficient information about the study’s data and assumptions to enable an observer to assess the credibility of this estimate. Thus, the research community had not yet had the opportunity to read or react to the new study, never mind review it for publication.
Premature media reporting on research would lessen to some degree if the media would refrain from covering research that has not yet been vetted within the scientific community through an established peer-review process. However, journalists should not trust peer review per se to certify the logic or credibility of research. Anyone with experience submitting or reviewing articles for publication becomes aware that peer review is an imperfect human enterprise. Weak studies may be accepted for publication, and strong studies may be rejected, even when peer reviewers do their best to evaluate research objectively.
It is unquestionably difficult for journalists and editors, who cannot possibly be sufficiently expert to evaluate personally all policy analysis, to decide what studies to report and how to frame their coverage. However, there are straightforward actions that they can take to mitigate media overreach.
Journalists can scrutinize research reports to assess whether and how the authors express uncertainty about their findings. They should be skeptical of studies that assert certitude. When authors express uncertainty, journalists should pay close attention to what they say.
Moreover, journalists should not rely fully on what authors say about their own work. They should seek perspectives from relevant reputable researchers who are not closely associated with the authors. Careful journalists already do this, but the practice should be standard.
Incredible Certitude in Official Economic Statistics
The above discussion documented incredible certitude in policy analysis. I now do likewise in government communication of the data that support much of the policy analysis. I focus on the official economic statistics produced and released by federal statistical agencies.
Government agencies communicate official economic statistics in news releases that make little if any mention of uncertainty in the reported estimates. Technical publications documenting data and methods acknowledge that official statistics are subject to error. They may use SEs or confidence intervals to measure sampling errors: that is, the statistical imprecision that occurs with finite samples of the population. However, they generally do not attempt to quantify the many forms of nonsampling errors that arise from problems other than small sample size. Neglect of nonsampling errors may reflect the fact that statistical theory has mainly focused on sampling error, making assumptions that imply the absence of nonsampling errors.
Reporting official statistics as point estimates without adequate attention to error manifests conventional certitude. The point estimates may be viewed as true but are not necessarily true. Thus, in the absence of agency guidance, some users of official statistics may naively assume that errors are small and inconsequential. Persons who understand that the statistics are subject to error must fend for themselves and conjecture the error magnitudes. Thus, users of official statistics—macroeconomists, government officials, firm managers, and citizens—may misinterpret the information that the statistics provide.
Considering error from the perspective of users of statistics rather than of statisticians, I think that it is essential to refine the general problem of conventional certitude in point estimation, distinguishing errors in measurement of well-defined concepts from uncertainty about the concepts themselves. I also think that it is useful to distinguish transitory and permanent measurement problems. To highlight these distinctions, Manski (3) separately discussed transitory statistical uncertainty, permanent statistical uncertainty, and conceptual uncertainty. In what follows, I define these ideas, give illustrative examples, and reflect on why government statistical agencies do not adequately communicate uncertainty.
Transitory Uncertainty: Revisions in National Income Accounts
Transitory statistical uncertainty arises, because data collection takes time. Agencies may release a preliminary statistic with incomplete data and revise as new data arrives. Uncertainty diminishes as data accumulates. A leading example is BEA initial measurement of GDP and revision of the estimate as new data arrives. The BEA reports multiple vintages of quarterly GDP estimates. An “advance” estimate combines data available 1 mo after the end of a quarter with trend extrapolations. “Second” and “third” estimates are released after 2 and 3 mo when new data become available. A “first annual” estimate is released in the summer using data collected annually. There are subsequent annual and 5-y revisions. However, the BEA reports GDP estimates without quantitative measures of uncertainty.
A publication by the BEA staff explains the practice of reporting estimates without measures of error as a response to the presumed wishes of the users of GDP statistics. Fixler et al. (21) state: “Given that BEA routinely revises its estimates during the course of a year, one might ask why BEA produces point estimates of GDP instead of interval estimates...Although interval estimates would inform users of the uncertainty surrounding the estimates, most users prefer point estimates, and so they are featured” (ref. 21, p. 2).
BEA analysts have provided an upbeat perspective on the accuracy of GDP statistics (22). In contrast, Croushore (23) offers a more cautionary perspective, writing: “Until recently, macroeconomists assumed that data revisions were small and random and thus had no effect on structural modeling, policy analysis, or forecasting. But realtime research has shown that this assumption is false and that data revisions matter in many unexpected ways” (ref. 23, p. 73).
Communication of the transitory uncertainty of GDP estimates should be relatively easy to accomplish. The historical record of revisions has been made accessible for study in two “realtime” datasets maintained by the Philadelphia and St. Louis Federal Reserve Banks (ref. 23 has a definition of “realtime”). Measurement of transitory uncertainty in GDP estimates is straightforward if one finds it credible to assume that the revision process is time stationary. Then, historical estimates of the magnitudes of revisions can credibly be extrapolated to measure the uncertainty of future revisions.
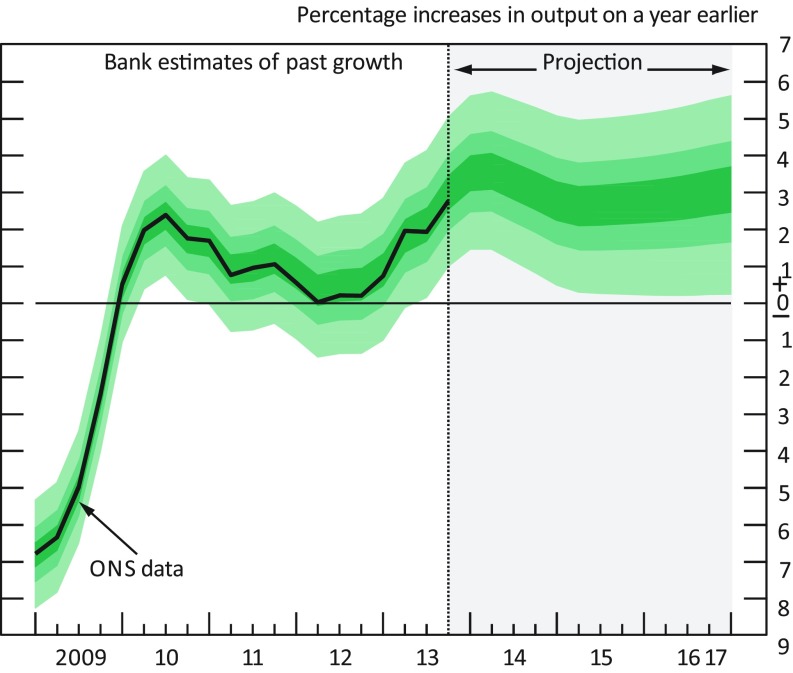
The BEA could communicate uncertainty as a probability distribution via a fan chart, such as the Bank of England does regularly. Fig. 1 gives an example taken from ref. 24. The part of the plot showing growth from late 2013 on is a probabilistic forecast that expresses uncertainty regarding future GDP growth in the United Kingdom. The part of the plot showing growth in the period 2009 through mid-2013 is a probabilistic forecast that expresses uncertainty regarding the revisions that will henceforth be made to estimates of past GDP. The Bank of England explains as follows: “In the GDP fan chart, the distribution to the left of the vertical dashed line reflects the likelihood of revisions to the data over the past” (ref. 24, p. 7). Ref. 25 has commentary on the thinking underlying the Bank of England’s use of fan charts to communicate uncertainty.
Fig. 1.
February 2014 UK GDP fan chart. Reprinted with permission from ref. 24.
Permanent Uncertainty: Nonresponse in Surveys
Permanent statistical uncertainty arises from incompleteness or inadequacy of data collection that is not resolved over time. Sources include sampling error due to finite sample size and nonsampling error due to nonresponse and misreporting. I focus here on nonresponse to employment and income questions in the Current Population Survey (CPS).
Each year, the US Census Bureau reports statistics on the household income distribution based on data collected in a supplement to the CPS. The Census Bureau’s annual Current Population Report provides statistics characterizing the income distribution and measures sampling error by providing 90% confidence intervals for various estimates. The report does not measure nonsampling errors. A supplementary document describes some sources of nonsampling error, but it does not quantify them.
Each month, the BLS issues a news release reporting the unemployment rate for the previous month based on data collected in the monthly CPS. A technical note issued with the release contains a section on reliability of the estimates that acknowledges the possibility of errors (26). The note describes the use of SEs and confidence intervals to measure sampling error. It states that nonsampling errors “can occur for many reasons, including the failure to sample a segment of the population, inability to obtain information for all respondents in the sample, inability or unwillingness of respondents to provide correct information on a timely basis, mistakes made by respondents, and errors made in the collection or processing of the data” (26).
The note does not measure the magnitudes of nonsampling errors.
When the Census Bureau and BLS report point estimates of statistics on household income and employment, they assume that nonresponse is random conditional on specified observed covariates of sample members. This assumption, which implies the absence of nonsampling error, is implemented as weights for unit nonresponse and imputations for item nonresponse. The CPS documentation of its imputation approach offers no evidence that the method yields a distribution for missing data that is close to the actual distribution. Another census document describing the American Housing Survey is revealing. It states that “[t]he Census Bureau does not know how close the imputed values are to the actual values” (27). Indeed, lack of knowledge of the closeness of imputed values to actual ones is common.
Research on partial identification shows how to measure potential nonsampling error due to nonresponse without making assumptions about the nature of the missing data. One contemplates all values that the missing data can take. Then, the data yield interval estimates of official statistics. The literature derives intervals for population means and quantiles. The intervals have simple forms, their lower and upper bounds being the values that the estimate would take if all missing data were to take the smallest or largest logically possible value. The literature shows how to form confidence intervals that jointly measure sampling and nonresponse error. Refs. 4 and 28–31 are original research articles, and ref. 32 is a textbook exposition.
To illustrate, ref. 33 uses CPS data to form interval estimates of median household income and the fraction of families with income below the poverty line in 2001–2011. There is considerable nonresponse to the income questions. During 2002–2012, 7–9% of the sampled households yielded no income data due to unit nonresponse, and 41–47% of the interviewed households yielded incomplete income data due to item nonresponse. One set of estimates recognizes item nonresponse alone, and another recognizes unit response as well. The interval estimate for the family poverty rate in 2011 is 0.14–0.34 if one makes no assumptions about item response but assumes that unit nonresponse is random. The interval is 0.13–0.39 if one drops the assumption that unit nonreponse is random.
Interval estimates of official statistics that place no assumptions on the values of missing data are easy to understand and simple to compute. One might, therefore, think that it would be standard practice for government statistical agencies to report them, but official statistics are not reported this way. It is sometimes said that such interval estimates are “too wide to be informative.” Nevertheless, I recommend that statistical agencies report them.
Wide bounds reflect real data uncertainties that cannot be washed away by assumptions lacking credibility. Even when wide, interval estimates making no assumptions on nonresponse are valuable for three reasons. (i) They are easy to compute and understand. (ii) They are maximally credible in the sense that they express all logically possible values of the statistic of interest. (iii) They make explicit the fundamental role that assumptions play in inferential methods that yield tighter findings.
The above does not imply that statistical agencies should refrain from making assumptions about nonresponse. Interval estimates making no assumptions may be excessively conservative if agency analysts have some understanding of the nature of nonresponse. There is much middle ground between interval estimation with no assumptions and point estimation assuming that nonresponse is conditionally random. The middle ground obtains interval estimates using assumptions that may include random nonresponse as one among various possibilities. Manski (33) poses some alternatives that agencies may want to consider.
Conceptual Uncertainty: Seasonal Adjustment of Official Statistics
Conceptual uncertainty arises from incomplete understanding of the information that official statistics provide about economic concepts or from lack of clarity in the concepts themselves. Conceptual uncertainty concerns the interpretation of statistics rather than their magnitudes.
A leading example is seasonal adjustment of statistics. Viewed from a sufficiently high altitude, the purpose of seasonal adjustment seems straightforward to explain. It is less clear from ground level how one should perform seasonal adjustment.
The prevalent X-12-ARIMA method was developed by Census and is used by the BLS and the BEA. X-12, along with its predecessor X-11 and successor X-13, may be a sophisticated and successful algorithm for seasonal adjustment. Alternately, it may be an unfathomable black box containing a complex set of operations that lack economic foundation. Wright (34) notes the difficulty of understanding X-12, writing: “Most academics treat seasonal adjustment as a very mundane job, rumored to be undertaken by hobbits living in holes in the ground. I believe that this is a terrible mistake, but one in which the statistical agencies share at least a little of the blame” (ref. 34, p. 67).
He states that understanding the practice of seasonal adjustment matters, because “[s]easonal adjustment is extraordinarily consequential” (ref. 34, p. 65).
There presently exists no clearly appropriate way to measure the uncertainty associated with seasonal adjustment. X-12 is a standalone algorithm, not a method based on a well-specified dynamic theory of the economy. It is not obvious how to evaluate the extent to which it accomplishes the objective of removing the influences of predictable seasonal patterns. One might perhaps juxtapose X-12 with other seemingly reasonable algorithms, perform seasonal adjustment with each one, and view the range of resulting estimates as a measure of conceptual uncertainty. More principled ways to evaluate uncertainty may open up if agencies were to use a seasonal adjustment method derived from a well-specified model of the economy. One could then assess the sensitivity of seasonally adjusted estimates to variation in the parameters and the basic structure of the model.
A more radical departure from present practice would be to abandon seasonal adjustment and leave it to the users of statistics to interpret unadjusted statistics. Publication of unadjusted statistics should be particularly valuable to users who want to make year-to-year rather than month-to-month comparison of statistics. Suppose that one wants to compare unemployment in March 2013 and March 2014. It is arguably more reasonable to compare the unadjusted estimates for these months than to compare the seasonally adjusted estimates. Comparison of unadjusted estimates for the same month each year sensibly removes the influences of predictable seasonal patterns, and it compares data collected in the 2 mo of interest.
Why Do Statistical Agencies Practice Incredible Certitude?
The concerns that I have expressed about incredible certitude in official economic statistics are not new. In 1947, Simon Kuznets, the father of national income accounting, called for publication of “margins of error” with these official statistics (35). Soon after, Morgenstern (36, 37) wrote a book that urgently argued for regular measurement of error in all official economic statistics. He was well-placed to influence the status quo, being famous for his contribution to game theory. However, his efforts did not bear fruit. More recently, agencies have not adhered to the National Research Council call for “Openness About Sources and Limitations of the Data Provided” in the document Principles and Practices for a Federal Statistical Agency (38).
Why is it that statistical agencies do so little to communicate uncertainty in official statistics? I am unaware of any valid professional reason that would explain the failure of the BLS and Census to report measures of sampling error in their news releases of employment and income statistics. Agency administrators could task their research staffs to develop measures of nonsampling error. While I cannot conjure a valid professional explanation for the status quo, I do see a possible political explanation. Federal statistical agencies may perceive an incentive to express incredible certitude about the state of the economy when they publish official economic statistics. Morgenstern (37) commented cogently on the political incentives facing statistical agencies when he wrote the following.
Finally, we mention a serious organizational difficulty in discussing and criticizing statistics. These are virtually always produced by large organizations, government or private; and these organizations are frequently mutually dependent upon each other in order to function normally. Often one office cannot publicly raise questions about the work of another, even when it suspects the quality of the work, since this might adversely affect bureaucratic-diplomatic relations between the two and the flow of information from one office to another might be hampered. A marked esprit de corps prevails. All offices must try to impress the public with the quality of their work. Should too many doubts be raised, financial support from Congress or other sources may not be forthcoming. More than once has it happened that Congressional appropriations were endangered when it was suspected that government statistics might not be 100% accurate. It is natural, therefore, that various offices will defend the quality of their work even to an unreasonable degree (ref. 37, p. 11).
Not having the persuasive power of Congressional appropriations, I can only say that federal statistical agencies would better inform policy makers and the public if they were to measure and communicate important uncertainties in official statistics.
Should agencies take the task seriously, I think that it is likely that they will want to develop separate strategies for communication of uncertainty in news releases and in technical documentation of official statistics. News releases are brief and are aimed at a broad audience. Hence, they have only a limited ability to convey nuance. Agencies have more scope for communication of uncertainty in their technical documentation of official statistics.
Communication of Uncertainty and Formation of Public Policy
Policy analysis with incredible certitude can harm formation of public policy in multiple ways. If policy makers incorrectly believe that existing analysis provides an errorless description of the current state of society and accurate predictions of policy outcomes, they will not recognize the potential value of new research aiming to improve knowledge. Also, they will not appreciate the potential usefulness of decision strategies that may help society cope with uncertainty and learn.
One such strategy, called “adaptive diversification,” was proposed and studied in the works of Manski (2, 39). Financial diversification is a familiar recommendation for portfolio allocation. Diversification enables an investor facing uncertain asset returns to limit the potential negative consequences of placing “all eggs in one basket.” Analogously, policy is diversified if a social planner facing uncertainty randomly assigns observationally similar persons to different policies. At any point in time, diversification enables the planner to avoid gross errors in policy making. Over time, it yields new evidence about treatment response, as one observes the outcomes of the persons randomly assigned to different policies. As evidence accumulates, a planner can revise the fraction of persons assigned to each policy in accord with the available knowledge. This idea is adaptive diversification.
I have remarked on the tendency of policy makers to resist measurement of uncertainty in policy analysis. President Johnson wanted to receive a point forecast rather than a range. Congress requires the CBO to provide point predictions of the fiscal implications of legislation. The BEA staff has commented that users of GDP statistics want to receive point estimates. Kuznets (35) and Morgenstern (36, 37) were unsuccessful in persuading federal statistical agencies to quantify error in official economic statistics. Some economists with experience in the federal government have suggested to me that concealment of uncertainty is an immutable characteristic of the American policy environment. Hence, they argue that the prevailing practice of policy analysis with incredible certitude will have to continue as is.
A more optimistic possibility is that concealment of uncertainty is a modifiable social norm. Then, salutary change may occur if awareness grows that incredible certitude is both prevalent and harmful.
Footnotes
The author declares no conflict of interest.
This paper results from the Arthur M. Sackler Colloquium of the National Academy of Sciences, “The Science of Science Communication III” held November 16–17, 2017, at the National Academy of Sciences in Washington, DC. The complete program and audio files of most presentations are available on the NAS Web site at www.nasonline.org/Science_Communication_III.
This article is a PNAS Direct Submission.
References
- 1.Manski C. Policy analysis with incredible certitude. Econ J. 2011;121:F261–F289. [Google Scholar]
- 2.Manski C. Public Policy in an Uncertain World. Harvard Univ Press; Cambridge, MA: 2013. [Google Scholar]
- 3.Manski C. Communicating uncertainty in official economic statistics: An appraisal fifty years after Morgenstern. J Econ Lit. 2015;53:631–653. [Google Scholar]
- 4.Manski C. Partial Identification of Probability Distributions. Springer; New York: 2003. [Google Scholar]
- 5. Oxford English Dictionary (1989), eds Simpson j, Weiner E (Clarendon Press, Oxford, United Kingdom), 2nd Ed.
- 6.Marcus R. December 2, 2016 Welcome to the post-truth presidency. The Washington Post. Available at https://www.washingtonpost.com/opinions/welcome-to-the-post-truth-presidency/2016/12/02/baaf630a-b8cd-11e6-b994-f45a208f7a73_story.html?utm_term=.650f5713beb9. Accessed September 13, 2018.
- 7.Scherer M. March 23, 2017 Can President Trump handle the truth? Time. Available at time.com/4710614/donald-trump-fbi-surveillance-house-intelligence-committee/. Accessed March 27, 2017.
- 8.Morgan M, Henrion M. Uncertainty: A Guide to Dealing with Uncertainty in Quantitative Risk and Policy Analysis. Cambridge Univ Press; Cambridge, UK: 1990. [Google Scholar]
- 9.Fischhoff B. Communicating uncertainty: Fulfilling the duty to inform. Issues Sci Technol. 2012;28:63–70. [Google Scholar]
- 10.Fischhoff B, Davis AL. Communicating scientific uncertainty. Proc Natl Acad Sci USA. 2014;111:13664–13671. doi: 10.1073/pnas.1317504111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Elmendorf D. 2010 Letter to Honorable Nancy Pelosi, Speaker, US House of Representatives. Congressional Budget Office. Available at housedocs.house.gov/energycommerce/hr4872_CBO.pdf. Accessed April 5, 2017.
- 12.Congressional Budget Office 2017 Cost estimate. American Health Care Act. Available at https://www.cbo.gov/system/files/115th-congress-2017-2018/costestimate/americanhealthcareact.pdf. Accessed April 5, 2017.
- 13.Blumstein A, Cohen J, Nagin D, editors. Deterrence and Incapacitation: Estimating the Effects of Criminal Sanctions on Crime Rates. National Academy Press; Washington, DC: 1978. [Google Scholar]
- 14.National Research Council . Deterrence and the Death Penalty. National Academies Press; Washington, DC: 2012. [Google Scholar]
- 15.Manski C, Pepper J. Deterrence and the death penalty: Partial identification analysis using repeated cross sections. J Quant Criminol. 2013;29:123–141. [Google Scholar]
- 16.National Research Council . In: Firearms and Violence: A Critical Review. Wellford C, Pepper J, Petrie C, editors. National Academy Press; Washington, DC: 2005. [Google Scholar]
- 17.Manski C, Pepper J. How do right-to-carry laws affect crime rates? Coping with ambiguity using bounded-variation assumptions. Rev Econ Stat. 2018;100:232–244. [Google Scholar]
- 18.Friedman M. The role of government in education. In: Solo R, editor. Economics and the Public Interest. Rutgers Univ Press; New Brunswick, NJ: 1955. [Google Scholar]
- 19.Goldberger A. Heritability. Economica. 1979;46:327–347. [Google Scholar]
- 20.Leonhardt D. July 28, 2010. The case for $320,000 kindergarten teachers. NY Times, A1.
- 21.Fixler D, Greenaway-McGrevy R, Grimm B. Revisions to GDP, GDI, and their major components. Surv Curr Bus. 2014;94:1–23. [Google Scholar]
- 22.Fixler D, Greenaway-McGrevy R, Grimm B. Revisions to GDP, GDI, and their major components. Surv Curr Bus. 2011;91:9–31. [Google Scholar]
- 23.Croushore D. Frontiers of real-time data analysis. J Econ Lit. 2011;49:72–100. [Google Scholar]
- 24.Bank of England 2014 Inflation report fan charts February 2014. Available at https://www.bankofengland.co.uk/news?NewsTypes=ce90163e489841e0b66d06243d35d5cb&Taxonomies=5f979b00da74476cb74a7237ae20ae70&Direction=Latest. Accessed September 13, 2018.
- 25.Aikman D, et al. Uncertainty in macroeconomic policy-making: Art or science? Philos Trans A Math Phys Eng Sci. 2011;369:4798–4817. doi: 10.1098/rsta.2011.0299. [DOI] [PubMed] [Google Scholar]
- 26.Bureau of Labor Statistics 2017 Employment situation technical note. Available at https://www.bls.gov/news.release/empsit.tn.htm. Accessed April 6, 2017.
- 27.US Census Bureau 2011. American Housing Survey for the United States: 2009 (US Government Printing Office, Washington, DC), Current Housing Reports, Series H150/09.
- 28.Manski C. Anatomy of the selection problem. J Hum Resour. 1989;24:343–360. [Google Scholar]
- 29.Manski C. The selection problem. In: Sims C, editor. Advances in Econometrics, Sixth World Congress. Cambridge Univ Press; Cambridge, UK: 1994. pp. 143–170. [Google Scholar]
- 30.Horowitz J, Manski C. Censoring of outcomes and regressors due to survey nonresponse: Identification and estimation using weights and imputations. J Econom. 1998;84:37–58. [Google Scholar]
- 31.Imbens G, Manski C. Confidence intervals for partially identified parameters. Econometrica. 2004;72:1845–1857. [Google Scholar]
- 32.Manski C. Identification for Prediction and Decision. Harvard Univ Press; Cambridge, MA: 2007. [Google Scholar]
- 33.Manski C. Credible interval estimates for official statistics with survey nonresponse. J Econom. 2016;191:293–301. [Google Scholar]
- 34.Wright J. Unseasonal seasonals? Brookings Pap Econ Act. 2013;2013:65–126. [Google Scholar]
- 35.Kuznets S. Discussion of the new department of commerce income series. Rev Econ Stat. 1948;30:151–179. [Google Scholar]
- 36.Morgenstern O. On the Accuracy of Economic Observations. Princeton Univ Press; Princeton: 1950. [Google Scholar]
- 37.Morgenstern O. On the Accuracy of Economic Observations. 2nd Ed Princeton Univ Press; Princeton: 1963. [Google Scholar]
- 38.National Research Council . Principles and Practices for a Federal Statistical Agency. 5th Ed National Academies Press; Washington, DC: 2013. [Google Scholar]
- 39.Manski C. Diversified treatment under ambiguity. Int Econ Rev. 2009;50:1013–1041. [Google Scholar]