Cone photoreceptor classification in the living human eye from photostimulation-induced phase dynamics

Significance

The three spectral types of cone photoreceptors underlie color perception and are largely responsible for inherited and acquired color vision anomalies. In vivo mapping of the trichromatic cone mosaic by imaging provides the most direct and quantitative means to assess the role of photoreceptors in color vision, but remains challenging because cone reflections only weakly differentiate cone types. Here, we show a noninvasive light microscopy modality that reveals the cell’s spectral type, using the optical phase change that arises within the cell when stimulated with light. Our procedure is orders of magnitude faster and more accurate than prior approaches and makes in vivo cone classification promising for a much wider range of color vision applications.

Abstract

Human color vision is achieved by mixing neural signals from cone photoreceptors sensitive to different wavelengths of light. The spatial arrangement and proportion of these spectral types in the retina set fundamental limits on color perception, and abnormal or missing types are responsible for color vision loss. Imaging provides the most direct and quantitative means to study these photoreceptor properties at the cellular scale in the living human retina, but remains challenging. Current methods rely on retinal densitometry to distinguish cone types, a prohibitively slow process. Here, we show that photostimulation-induced optical phase changes occur in cone cells and carry substantial information about spectral type, enabling cones to be differentiated with unprecedented accuracy and efficiency. Moreover, these phase dynamics arise from physiological activity occurring on dramatically different timescales (from milliseconds to seconds) inside the cone outer segment, thus exposing the phototransduction cascade and subsequent downstream effects. We captured these dynamics in cones of subjects with normal color vision and a deuteranope, and at different macular locations by: (i) marrying adaptive optics to phase-sensitive optical coherence tomography to avoid optical blurring of the eye, (ii) acquiring images at high speed that samples phase dynamics at up to 3 KHz, and (iii) localizing phase changes to the cone outer segment, where photoactivation occurs. Our method should have broad appeal for color vision applications in which the underlying neural processing of photoreceptors is sought and for investigations of retinal diseases that affect cone function.

Vision begins when photoreceptors capture photons and hyperpolarize. All photoreceptors respond to light, but response magnitude to a specific light depends on the photopigments contained in their outer segments (OSs). In most humans, each cone contains and is classified by one of three photopigments with different spectral sensitivities. The spatial arrangement and spectral sensitivities of these cone types fundamentally limit color vision (1). Most color vision anomalies are caused by absence or dysfunction of one or more cone types; these deficits can either be genetically inherited or acquired from disease or aging (2–4).

Human color vision has been extensively studied for centuries, but the placement of photoreceptors at the back of the eye has impeded direct physiological investigation. The proportions of cone types have been inferred using indirect and noninvasive methods such as psychophysics (5–11) and electroretinography (11–17), but these methods lack the resolution to assess spatial arrangement of cone types and its variation across the retina. Direct ophthalmic imaging methods have recently been enhanced by the use of adaptive optics (AO) to correct ocular aberrations (18), permitting imaging of individual photoreceptors and bringing the study of color vision to the cellular scale. The trichromatic cone mosaic has been successfully mapped using AO-enhanced retinal densitometry to selectively bleach particular photopigments (19–22). However, a variety of factors necessitate high bleach levels by multiple light sources and repeated measurements to attain an adequate signal. These include low [≤0.4 log unit (22–24)] and varied (25) optical densities of cones, interference noise within cones (25, 26), background noise from other reflective retinal tissue, and the similarity of M and L cone spectral sensitivity functions. These factors result in long experiments [5 d (19), 1–3 d (21), 3–9 h (22)] and uncertainties of 3.6 ± 1.6% in classification [average ± SD of uncertainty of 20 eyes reported in four AO retinal densitometry studies (19–22)]. These shortcomings have limited the use of AO-enhanced retinal densitometry in color vision studies.

In contrast, our approach uses nanometer-scale optical path length changes (ΔOPL) occurring inside photoreceptors during photoactivation (photoreceptor response to light) to identify cone spectral types with unprecedented sensitivity, accuracy, and efficiency. We achieved dramatically smaller uncertainties (<0.02%) compared with AO retinal densitometry and with notably shorter data acquisition times. We achieved repeatability errors of 0.2–0.37%, which may capture classification performance better than uncertainty does, but has not been reported in the classification literature (19–22). We measured the ΔOPL signature of cones in terms of an equivalent phase change by combining AO and phase-sensitive optical coherence tomography (AO-OCT) (27–30). This combination yielded sufficient resolution to reveal individual cone reflections in 3D and sufficient phase sensitivity to detect optical path length changes as small as 5 nm. Our rapid image acquisition sampled phase at 3 KHz, permitting assessment and quantification of extremely transient phototransduction-related dynamics.

In AO-OCT, cone OSs are characterized by a bright reflection at each tip (Fig. 1A). The resolution of our apparatus was 2.4 × 2.4 × 4.7 μm³ (width × length × depth), sufficient to resolve these reflections in all three dimensions. We acquired most AO-OCT volume images 3.7° temporal to the fovea. Our three subjects were free of ocular disease; one of the three was a deuteranope. Brief flashes of visible light (2–10 ms) of different intensities and spectra (Fig. 1B) were delivered to the retina during image acquisition. Fast and slow dynamics of the cones’ phase response were subsequently extracted from the images (Fig. 1A), using B-scan (0.33 ms) and volume (0.1 s) sampling, respectively (SI Appendix, Materials and Methods). We first characterized the phase responses of cones under different illuminant intensities and spectra, then established the relationship between these phase changes and the three cone spectral types, and finally used this relationship to classify and map cones in our three subjects.

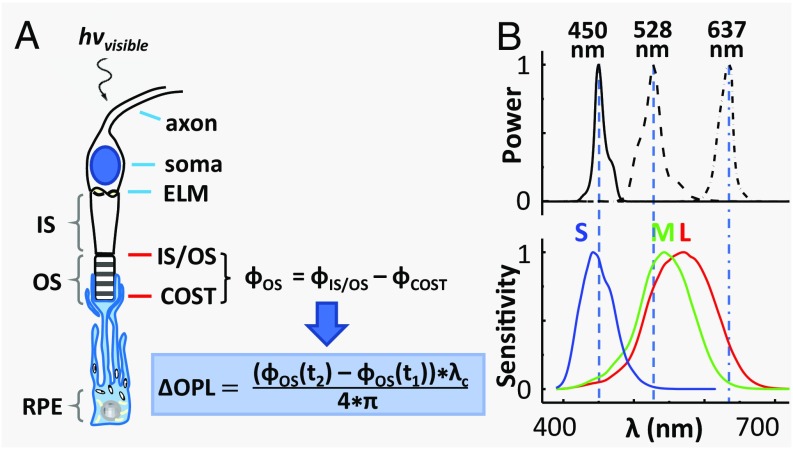
Fig. 1.

The physiological response of a cone cell to light produces nanometer OPL changes in its OS, which we detect with AO-OCT. (A) Schematic shows the axon, soma, inner segment (IS), and OS of a cone cell, and the underlying retinal pigment epithelium (RPE) cell that ensheathes it. The cone cell is stimulated with a visible flash during AO-OCT imaging, and the resulting phase and OPL changes are defined mathematically, as shown. The phase difference, ϕ_OS, is between the two bright reflections at opposing ends of the cone OS, which are labeled as IS/OS and COST (cone OS tip). (B) Normalized spectra of the three light sources that stimulate the cones are shown with the normalized sensitivity functions of the three cone types that are sensitive to short- (S), medium- (M), and long- (L) wavelength light (31).

Results and Discussion

Experiment 1—Characterizing the Phase Response of Cones to Light Stimulation: Temporal Properties and Energy Dependence.

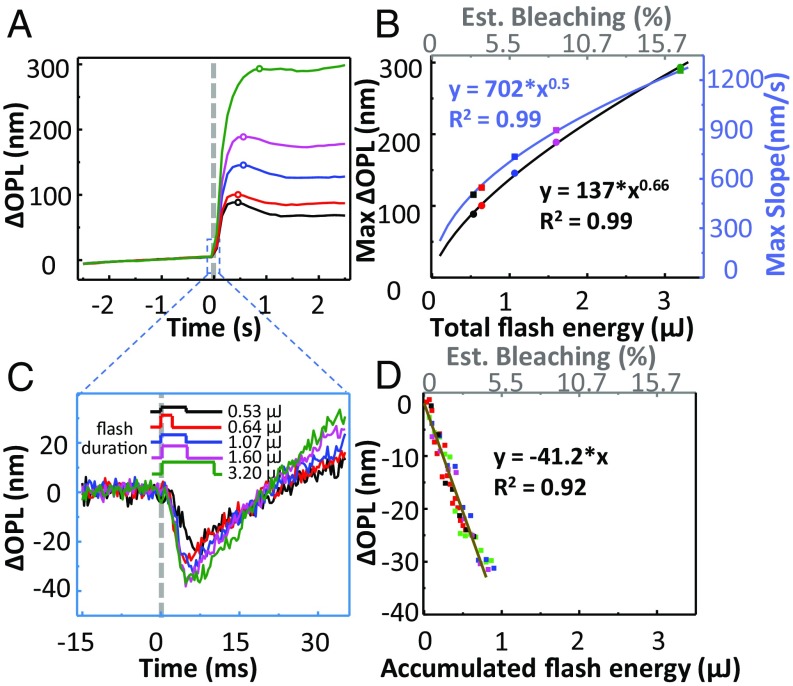
We assessed the phase response of cones to brief flashes of 637-nm light over a sixfold energy range. We first quantified the slow dynamics of the cones’ response (0.1–2.5 s) by averaging ΔOPL across all cones within each volume (∼1,100 cones), yielding the mean cone response at the 10-Hz volume acquisition rate. Fig. 2A and SI Appendix, Fig. S1A show the averaged traces for the two normal subjects. Regardless of flash energy, ΔOPL rapidly increased immediately after stimulation, reached a peak after 0.3–0.5 s, and then slightly dipped and plateaued for the remainder of the measurement period. We quantified the energy effects using the height of the plateau (peak value) and rate of the rapid increase (maximum slope) of ΔOPL, which are plotted against energy and estimated bleach level in Fig. 2B and SI Appendix, Fig. S1B. These data are well fit by power functions of flash energy (E): E^0.66 (peak) and E^0.5 (max slope) (Fig. 2B) and E^0.63 (peak) and E^0.5 (max slope) (SI Appendix, Fig. S1B). These plots illustrate two important points: First, the asymptotic behavior of ΔOPL (peak and plateau) is strongly energy dependent and consistent with an earlier report (32). We take advantage of this association in our cone-classification method, as most of the power for differentiating responses to different lights is contained in the peak and plateau. Second, contrary to the same earlier report (32), we find that the rate of rapid increase of ΔOPL is also energy dependent, indicating that increased stimulus accelerates the underlying physiology.

Fig. 2.

Phase response of cones is biphasic with amplitude increasing with flash energy in subject 1. The dashed gray lines at 0 s in A and C represent the 637-nm stimulus onset. (A) Average responses of 1,094 cone cells sampled at the 10-Hz volume rate for flash energies over a sixfold range and averaged over 10 videos to improve signal to noise. Phase response was referenced to the average of the prestimulus volumes. (B) Maximum ΔOPL and maximum slope of ΔOPL in A are plotted against the total flash energy and the predicted percentage of photopigment bleaching (top secondary axis). Solid curves represent best power fits. (C) Average fast response of cone cells as analyzed on a per B-scan basis over the single volume during which flash stimulation occurred. SD of the prestimulus signal was measured at 2.4 nm, which corresponds to the noise floor. (D) ΔOPL during the downward portion of the traces in C is plotted against accumulated flash energy and corresponding predicted percentage of photopigment bleaching. Solid line represents best linear fit. Key specifies energy level at eye and flash duration of stimulation. Note that the 0.64 μJ, 1.60 μJ, and 3.20 μJ flashes were of the same 320 μW intensity; the 0.53 μJ and 1.07 μJ flashes were 107 μW and 213 μW, respectively.

To assess the fast dynamics of ΔOPL that occurred within milliseconds of flash onset, we examined individual B-scans from the volume containing the light flash (SI Appendix, Materials and Methods). This yielded a sampling interval of 0.33 ms instead of the 100-ms volume-sampling interval, trading signal-to-noise ratio for a 300-fold increase in temporal resolution. Results are shown in Fig. 2C and SI Appendix, Fig. S1C for the two subjects. At this scale and resolution, an initial rapid decrease in ΔOPL was followed by a gradual larger increase corresponding to the start of the slow dynamics observed in Fig. 2A and SI Appendix, Fig. S1A. To characterize the fast dynamics before onset of the slow dynamics (which begin near the response minimum), Fig. 2D and SI Appendix, Fig. S1D plot only the downward portion of the response versus accumulated flash energy. The accumulated flash energy is the portion of the total flash energy that illuminates the retina before the AO-OCT measurement. Both downward portions exhibit a linear relation with 7.7-nm (subject 1) and 5.5-nm (subject 2) decreases in ΔOPL per 1% bleach.

Collectively, our AO-OCT results reveal two distinct dynamics in the cone ΔOPL caused by brief flashes of light: an initial decrease that is brief, small, and varies linearly with bleach level, followed by an increase that is much longer and larger and varies nonlinearly with bleach level.

We know of only a few studies that report fast dynamics in the cone phase response to flash stimuli in the living human eye. Using AO flood imaging systems, Jonnal et al. (26) and Bedggood and Metha (25) inferred physiological dynamics of cones as early as a few milliseconds after flash onset, although neither was able to discern the direction and magnitude of the change as we have here. More recently, Hillmann et al. (32) used full-field SS-OCT to measure a similar biphasic response with initial reduction in ΔOPL. However, they did not analyze the fast dynamics, likely because their relatively coarse measurement sampling (6 ms) and long flash duration (50 ms) would have masked the fast dynamic properties.

The timescale and linear behavior of the fast response are consistent with the photoactivation of photopigment molecules, which is the first step of the phototransduction cascade, occurs within ∼0.5 ms of photon absorption, and is linearly proportional to bleach level (1). The time of minimum ΔOPL (averaged over our two subjects) never lagged the flash offset by more than 1.2 ms. This maximum lag time falls within our measurement error (SD = 0.6 ms), implying that the fast dynamics of the response are confined to the flash interval. This, in turn, suggests that these fast changes in ΔOPL originate from changes in refractive index and/or physical length that are specifically associated with activation onset, as cone photopigments are believed to remain active for several tens of milliseconds (33, 34). We can rule out potential causes for the fast response that are influenced by sustained photopigment activation, such as amplification stages involving transducin and phosphodiesterase.

The slow phase of the response is easier to detect but harder to attribute. Maximum ΔOPL occurred 0.3–0.5 s after the flash, a duration longer than activation and deactivation of phototransduction combined (35). This maximum phase change is therefore probably dominated by indirect effects of transduction. Osmotic swelling of the OS is one possibility and was hypothesized by Jonnal et al. (26) to explain dynamics on a similar timescale to ours. A model of osmotic swelling was recently used to explain ΔOPL changes in mouse rods exposed to light flashes (36), albeit over much longer time and larger magnitude scales. The slow dynamics we measured appear consistent with those reported by Hillmann et al. (32); however, they found no effect of flash energy on maximum slope, whereas we found it to increase with flash energy (E^0.5). This energy dependence and our finding that the maximum increase rate of ΔOPL occurs very early in the slow dynamic process (∼20 ms; SI Appendix, Results and Discussion 1) are both consistent with the energy dependence and temporal scale of transducin and phosphodiesterase activation (1), so both are possible contributors.

In general, our results demonstrate a strong association of cone ΔOPL with flash energy, both in the rate of the initial transient and in the sustained response. This implies that the absorption efficiencies of cones influence ΔOPL. We therefore hypothesized that cones with different absorption efficiencies, arising, for example, from differences in spectral sensitivity (S, M, and L cones), would have different ΔOPL responses to the same light.

Experiment 2—Phase Response of Cones Reveals Cone Spectral Type.

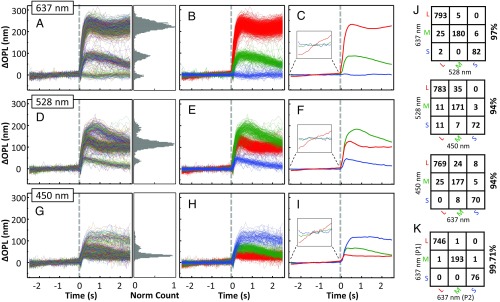
We tested our hypothesis by measuring the slow dynamics of individual cones in two normal subjects after stimulating them with light flashes of three different spectra (Fig. 1B), thereby manipulating the absorption efficiencies of the three cone types. To classify cones, we grouped the traces into three classes with a k-mean cluster algorithm (37) that made use of all available information in each trace, and subsequently assigned cone groups to spectral classes on the basis of expected spectral sensitivities to each stimulus wavelength. Fig. 3 summarizes the phase responses of cones to the three different stimuli. The left column and associated histograms show the individual responses of the entire cell population, the left-middle column shows the individual responses grouped by color based on the results of the k-mean classification algorithm, and the right-middle column depicts the mean responses within each of the three color groups. As evident in Fig. 3A (637-nm stimulus), ΔOPL for the vast majority of cones increased after the flash, reaching a peak ∼0.5 s after stimulus onset. Critically, the phase traces appear to form a trimodal distribution. As the spectral sensitivities of the three standard cone types to a 637-nm stimulus obey the ordinal relation L > M > S (Fig. 1B), we assumed (our hypothesis) that the three response groups of large, intermediate, and small ΔOPL changes correspond to L, M, and S cones, respectively. We therefore assigned the three groups to cone spectral classes accordingly. This classification resulted in the color-coded traces (red, green, and blue for L, M, and S cones) shown in Fig. 3B. Fig. 3C is the group average of these three cone classes. We also observed three distinct groups of responses to the 528-nm stimulus (Fig. 3D), albeit less separated. At this wavelength (528 nm), the spectral sensitivity relation of the three cone types obeys M > L > S. We again classified the cone responses into three groups and color coded them accordingly, as shown in Fig. 3E for individual cones and Fig. 3F for group averages. Results from the 450-nm stimulus are shown in Fig. 3 G–I. The similar responses of M and L cones to this last stimulus was expected, given their close spectral sensitivities at short wavelengths (Fig. 1B). Nevertheless, some M and L separation is still evident in the figure histogram, and we were able to classify the cone responses into three groups. A distinct advantage of the 450-nm and 528-nm stimuli over 637 nm is that both generate positive responses from all cone types, allowing functional cones to be distinguished from potential nonabsorbing or nonfunctioning ones (SI Appendix, Results and Discussion 2).

Fig. 3.

Phase response of cones varies with cone type (S, M, and L) and wavelength of the stimulus in subject 1. The dashed gray line at 0 s represents the 5-ms stimulus flash. Response traces of individual cones are shown for stimulation at (Upper) 637 nm and 1.6 μJ, (Middle) 528 nm and 0.5 μJ, and (Bottom) 450 nm and 1.0 μJ. (A, D, and G) Individual traces of 1,094 cone cells are randomly colored. Histogram of normalized cone count is shown for 0.6–1.0 s after flash. Average SD of individual S and M cone traces before stimulation was measured at 5 nm, which corresponds to the system noise floor. L cones were excluded from the analysis because their slight sensitivity to the imaging wavelength would have biased the measurement. Phase response was referenced to the average of the prestimulus volumes. (B, E, and H) Cone responses in A, D, and G are colored red (L), green (M), or blue (S) based on the k-mean classification and expected spectral sensitivity of each cone type to the stimulus wavelength. (C, F, and I) Average responses of the grouped traces in B, E, and H. (J) To quantify the agreement of our method to classify cones, three confusion matrices were constructed that show the number of cones that were classified as S, M, or L by one stimulus (450, 528, or 637 nm) and as S, M, or L by another stimulus (450, 528, or 637 nm). Percentage agreement is shown to the right of each matrix. (K) Repeatability error was quantified by comparing classification results of two independent subsets of videos (P1 and P2) obtained with the 637-nm stimulus. Each subset contains seven videos.

To further test our hypothesis that the three response groups of cones correspond to the three spectral types of cones, we performed a cross-comparison analysis of our classification results of Fig. 3. Fig. 3J summarizes the comparison using confusion matrices and shows that individual cones were consistently classified as S, M, or L cones, regardless of stimulus wavelength. Agreement between stimuli at 637 nm and 528 nm, 637 nm and 450 nm, and 528 nm and 450 nm are 97%, 94%, and 94%, respectively. The small fraction of cones that were classified differently when stimulated with different wavelengths (i.e., nondiagonal components of the agreement matrices) were typically those cones that had lower signal-to-noise ratios in the AO-OCT images. Similar results were obtained from the other normal subject (SI Appendix, Fig. S4J). In general, the strong agreement in classification between the different stimuli supports our hypothesis and demonstrates that our results are highly repeatable, even when different spectral stimuli are used.

We also observed a distinct change in OPL before the stimulus (Fig. 3 C, F, and I and SI Appendix, Fig. S4 C, F, and I). The ΔOPL baseline traces of L cones show a slow (∼5.9 nm/s) but significant increase. This is likely a result of excitation by the 790-nm AO-OCT imaging source, as L cones are more sensitive at 790 nm than M and S cones. Although unintended, our classification likely benefited from this increase, as it further distinguished L cones from the other two types. A similar benefit also occurs with flashes of higher energy. This trend is shown in SI Appendix, Fig. S5 (SI Appendix, Results and Discussion 3), using the Experiment 1 data (Fig. 2), and demonstrates that even better classification would be obtained than that reported here by simply increasing stimulus energy.

Finally, we mapped cone types. We used the 637-nm classification results, which gave the best separation of cone responses, to identify the spectral type of each cone in the en face intensity maps for the two normal subjects (Fig. 4 A, B, D, and E) and to compute the relative proportions of the three cone types. The proportion of S cones was 7.7% for both subjects, which is consistent with the 7% estimated histologically (38) at 3.7° temporal retina. The L:M ratios of the two subjects were 3.8 and 1.7, differing by more than a factor of two, but falling within the normal range (5, 6, 8–11, 14–17, 19–22). It is poorly understood how the proportion of these cone populations varies across the retina. Although our study focused on the classification of cones at a single retinal location near the fovea, our method can be readily applied elsewhere. SI Appendix, Results and Discussion 4 demonstrates this application and the notable variation in cone proportions observed across the macula.

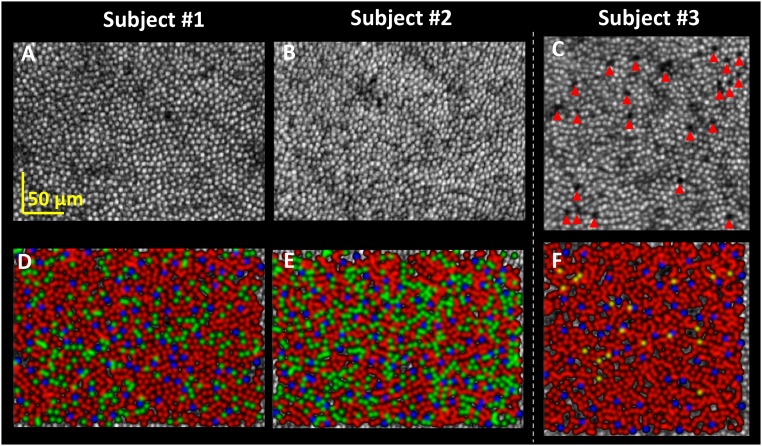
Fig. 4.

Mapping the trichromatic cone mosaic of the three subjects. (A–C) En face intensity images show the cone mosaics at 3.7° retinal eccentricity, as projected through their OSs (Movies S1–S3). Images are shown on a log scale (C) The dark holes in the mosaic of the deuteranope are marked by red arrows and are suggestive of missing cone OSs. The holes reflect little light (the 22 marked holes are 35 ± 10 times dimmer than their brightest neighboring cone) and show no evidence of waveguiding (no punctated reflection at hole center). Cone density of the deuteranope is 17,587 cones/mm², and falls in the normal range for this retinal eccentricity (39). (D–F) The cone mosaics from A–C are color coded on the basis of cone classification using the 637-nm stimulus results in Fig. 3A and SI Appendix, Figs. S4A and S10A (S = blue; M = green; L = red; Unidentified = yellow). Spatial coordinates and class type of cones of the three subjects are listed in Dataset S1.

Experiment 2—Cone Classification Error.

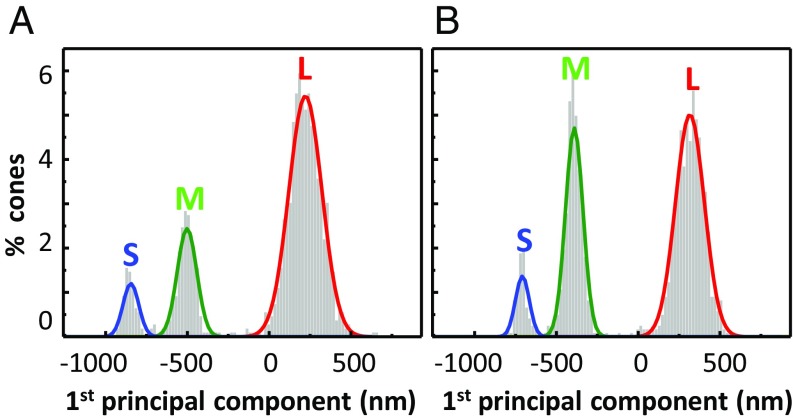
Roorda and Williams (19) estimated the uncertainty of their retinal densitometric method by fitting Gaussian models to the two response groups of cones (M and L) that they observed, and defining the measurement uncertainty as the area of overlap of the two Gaussians. We could not directly apply their method (based on fitting 1D Gaussians to two cone types) to our datasets because we included all three cone types (S, M, and L) and our measurements extended across 50 dimensions (50 measurements per cone per AO-OCT video), all of which were used by the k-mean classification algorithm. We reduced the 50 dimensions, using principal component analysis, and then applied their uncertainty analysis to the first principal component of our 637-nm responses. This analysis overestimates the classification uncertainty of our method relative to theirs because (i) less information was used to analyze than to classify and (ii) S cone assignment error contributed to our uncertainty. Fig. 5 shows the distribution of the first principal component of the traces in Fig. 3A and SI Appendix, Fig. S4A, with Gaussian fits for the three clusters included. The overlap between the three Gaussians is <0.02% for both subjects, indicating cone classification uncertainty <0.02% by the criterion of Roorda and Williams (19). In addition, 95% confidence intervals are 0.002–0.100% (subject 1) and 0.003–0.076% (subject 2), which reflect the reliability of our uncertainty estimates. Our uncertainty (0.02%) is 180-fold better than the 3.6 ± 1.6% for AO retinal densitometry (19–22). This exceedingly small uncertainty supports our contention that we have found a highly sensitive method for classifying cones, provided the stimulus wavelength (e.g., 637 nm) effectively separates cone responses.

Fig. 5.

Cone classification uncertainty is less than 0.02%. (A and B) Distribution of the first principal component of ΔOPL traces for the two color-normal subjects as obtained from Fig. 3A and SI Appendix, Fig. S4A, using the 637-nm stimulus. Gaussian fits to the three clusters are color coded and identified by spectral type (S, M, L). Total cones in both plots equal 100%.

The error fitting method of Roorda and Williams (19) allowed us to compare our method’s performance with others, but a disadvantage is its insensitivity to cone outliers. To better capture this effect, we performed three different repeatability studies, as described in SI Appendix, Results and Discussion 6. We found repeatability errors to be consistent across the studies, ranging from 0.2% to 0.37% when using 7–10 videos to classify cones. This error is an order of magnitude larger than our uncertainty error from Gaussian fitting (0.02%), indicating cone outliers are likely present in our data, although the number must be exceedingly small as only 1 of every 270–500 cones was identified differently.

Experiment 2—Cone Classification in a Deuteranope.

To test for classification differences in color blindness, we analyzed the cones of a deuteranope. Signal traces of individual cones for the 637-nm stimuli are shown in SI Appendix, Figs. S9A and S10A and separate mainly into two groups. Their responses are consistent with those of S and L cones from the two color-normal subjects, and the lack of a third group is expected, given the absence of M cones in deuteranopia. Visualizing in principal component space (the first three components), two distinct clusters are indeed present and overlap with those of S and L cones of the two color-normal subjects. However, a third nondistinct cluster (not observed in either of the two normal subjects) is also apparent, being sparsely populated, diffuse, and extending into the other two clusters. Surprisingly, the response of cones in this third cluster increased little compared with the other two clusters when the stimulus energy was doubled, as shown in SI Appendix, Fig. S9. Cones in this third cluster also did not respond as expected of S, M, or L cones at 450 and 528 nm (SI Appendix, Fig. S10); in particular, this third cluster responded more strongly than the others at both of these wavelengths. We labeled cones of this third cluster as unidentified (U) because their responses do not resemble those of typical S, M, or L cones as we understand them. Some of these U cones might be misclassified S or L cones. However, their enhanced responses to short-wavelength light suggest that many of them are of a distinct cone type, albeit undetermined. In terms of proportions, the S cone proportion (6.5%) is lower than that of our two normal subjects, but falls within the normal range (38). The L cone proportion is large (91.4%), consistent with deuteranopia. Only 2.1% of cones are classified as unidentified. Note that this proportion falls below the uncertainty of retinal densitometry methods (∼3.6%) and would probably not have been detected. Although questions remain about these unidentified cones, the preponderance of cones in this patch respond as expected. We found strong agreement (≥98%) between classifications made using the three wavelengths (SI Appendix, Fig. S10J).

We mapped the trichromatic cone mosaic of the deuteranope, using the 637-nm classification results of SI Appendix, Fig. S10. L cones clearly dominate the mosaic with a sparse intermingling of S and unidentified cones (Fig. 4F color map). Unlike the two color normal subjects, whose cone mosaics are essentially contiguous (Fig. 4 A and B), the deuteranope’s mosaic is distinctly mottled with dark holes indicative of missing cone OSs (red arrows in Fig. 4C). We noticed that these holes often coincide with a bright punctate reflection near the expected location of the ellipsoid and myoid interface of the cone’s inner segment (Movie S4). We recently discovered the same reflectance oddity in subjects with retinitis pigmentosa and hypothesized that cones with this pattern are undergoing cell death.

Carroll et al. (40) have reported an interesting correlation between cone genotype and phenotype in red–green color blindness with two dichromatic subjects. Their proposed model suggests that the cone mosaic of a dichromat with a single L/M gene should be complete. Genetic analysis of our deuteranope performed in the Neitz laboratories at the University of Washington detected only L-opsin genes (no M-opsin genes), and sequencing showed no heterozygosity at any of the spectral tuning sites. MassARRAY analysis (41) confirmed that the subject is a single L gene deuteranope. Thus, our deuteranope does not support the model of Carroll et al. (40) given the observed (sporadic) gaps in his cone mosaic. This disagreement illustrates the power of our imaging method to elucidate phenotype information pertinent for testing these models.

Future.

We have developed a highly efficient and accurate method for classifying cones in the living human eye by taking advantage of their phase response to light. Cones were classified on the basis of their slow response, but we expect their fast response to also carry useful information, as it also covaries with stimulus energy and is initiated by photoactivation of photopigment. These responses straddle the phototransduction cascade; thus, their combined use should provide even more power for distinguishing cones. This study was also limited to the reflections of the cone OS. As evident from our flythrough movies, we can now observe reflections from all major cone components (IS, OS, soma, and axon). Use of these additional reflections opens up the exciting possibility of spatially resolving dynamics across the entire cone cell, enabling a more detailed view of how photoreceptors respond in vivo.

Methods

Subjects.

Two color-normal subjects aged 22 (subject 2) and 52 (subject 1) years and one deuteranope aged 26 years (subject 3) participated in the study. All subjects were male and had best corrected visual acuity of 20/20 or better and a spherical equivalent refraction between 0 and −2.5 diopters. Subjects were free of ocular disease. Eye lengths ranged from 23.27 to 25.40 mm, as measured with the IOLMaster (Zeiss), and were used to scale the retinal images from degrees to millimeters (42). Color vision phenotype of the subjects was assessed using the Rayleigh match (HMC Anomaloskop), the Farnsworth-Munsell D-15, and pseudoisochromatic plates (Ishihara and Hardy-Rand-Rittler). Subjects 1 and 2 met the accepted criteria for normal color vision; subject 3 met that for deuteranopia. All procedures on the subjects adhered to the tenets of the Declaration of Helsinki and were approved by the Institutional Review Board of Indiana University. Written consent was obtained after the nature and possible risks of the study were explained.

Experiment Design.

The subject’s eye was cyclopleged and dilated with tropicamide 0.5% and aligned to the Indiana AO-OCT system (28, 29). System focus was placed at the photoreceptor layer to maximize sharpness of the cone mosaic. AO-OCT volumes were acquired in all of the subjects at ∼3.7° temporal to the fovea, and at six additional locations (2°, 4°, 6°, 8°, 10°, and 12° temporal to the fovea) in one of the subjects.

Each AO-OCT video consisted of 25 or 50 volumes [0.8° × 1° or 1.3° × 1.5° field of view (FOV)] that were acquired in 5 s (at either 4.7 or 10.2 volumes/s). Halfway through the video acquisition, a 2° FOV brief flash (2–10 ms; 0.53–3.20 μJ) of visible stimulus was applied to the retina being imaged, thus providing 2.5 s baseline and 2.5 s response of each cone in the volume. Three fiber-based LED light sources provided the stimulation with central wavelengths of 450, 527, and 638 nm. Video acquisition with light stimulation was repeated 5, 10, or 15 times for the same retinal patch. Between video acquisitions, the subject remained in darkness to allow cone photopigment to regenerate. We empirically found 90 s was sufficient to prevent influence from preceding video acquisitions.

Two experiments were conducted. Experiment 1 characterized the cone phase response to 637-nm light flashes of increasing energy 0.53, 0.64, 1.07, 1.60, and 3.20 μJ, which were estimated to bleach 3%, 3.6%, 5.7%, 8.7%, and 16.7% of the L:M cone photopigment, respectively (43). Ten 0.8° × 1° volume videos of the ∼3.7° retinal location were acquired at 10.2 volumes/s for each energy level. Experiment 2 characterized the cone phase response to light flashes of three different spectra that were estimated to bleach 1.1% (450 nm), 9.9% (528 nm), and 8.7% (637 nm) of the L:M photopigment (43). Fifteen 0.8° × 1° volume videos of the ∼3.7° retinal location were acquired at 10.2 volumes/s.

Postprocessing of AO-OCT Volumes.

Volumes were reconstructed, dewarped to correct nonlinearities in the fast-axis scan pattern, and registered in three dimensions to correct eye motion artifacts using a custom 3D strip-wise registration algorithm (44). Registration entailed selecting one volume as a reference based on good image quality and minimum eye motion artifact. All volumes collected at the same retinal location were registered to this reference, regardless of stimulus protocol. Using a common reference allowed us to compare changes in the same cones under different stimulus conditions. Temporal changes in the OPL of the cone OSs were extracted from the registered AO-OCT volumes using the complex form of the signal (SI Appendix, Materials and Methods).