Digital logic for soft devices

Significance

Soft devices offer many useful characteristics, including safe operation in close proximity to humans, the ability to adapt to their surroundings, ease of sterilization, simplicity, low cost, and light weight. Current soft devices, however, are still actuated by hard valves and electronic controls, and reliance on these components limits the use of soft devices in applications where hard structures or electronics are not compatible. This work demonstrates completely soft digital logic gates that can be integrated into soft devices and that allow computation and control within these devices, without hard valves or electronics. We demonstrate data storage, signal processing, digital-to-analog conversion, environmental sensing, and collaborative interaction between humans and soft devices.

Abstract

Although soft devices (grippers, actuators, and elementary robots) are rapidly becoming an integral part of the broad field of robotics, autonomy for completely soft devices has only begun to be developed. Adaptation of conventional systems of control to soft devices requires hard valves and electronic controls. This paper describes completely soft pneumatic digital logic gates having a physical scale appropriate for use with current (macroscopic) soft actuators. Each digital logic gate utilizes a single bistable valve—the pneumatic equivalent of a Schmitt trigger—which relies on the snap-through instability of a hemispherical membrane to kink internal tubes and operates with binary high/low input and output pressures. Soft, pneumatic NOT, AND, and OR digital logic gates—which generate known pneumatic outputs as a function of one, or multiple, pneumatic inputs—allow fabrication of digital logic circuits for a set–reset latch, two-bit shift register, leading-edge detector, digital-to-analog converter (DAC), and toggle switch. The DAC and toggle switch, in turn, can control and power a soft actuator (demonstrated using a pneu-net gripper). These macroscale soft digital logic gates are scalable to high volumes of airflow, do not consume power at steady state, and can be reconfigured to achieve multiple functionalities from a single design (including configurations that receive inputs from the environment and from human users). This work represents a step toward a strategy to develop autonomous control—one not involving an electronic interface or hard components—for soft devices.

Pneumatic soft actuators perform certain functions (for example, handling delicate objects with irregular shapes) using much simpler controls than their hard counterparts, because many control functions—functions that require sensors and feedback control in hard actuators—can be provided by the materials and structures of soft actuators (1). (We describe this capability with the phrase “the material is the controller.”) An elastomeric gripper can, for example, handle fruit, raw eggs, and live animals without computer control because its compliance automatically limits the pressure that it exerts, and because this compliance allows the gripper to conform to the shape of the object (2, 3). This so-called embodied intelligence (3–5) has led to the design of actuators driven by simple control systems (often no more than on–off control of a single pressure source, albeit using hard switches). In addition to the embodied intelligence of soft actuators, advantages they exhibit—compared with designs incorporating hard materials—include (i) safety and compatibility with humans and animals (3, 6), (ii) relatively low cost (3), (iii) light weight and resistance to impact that would damage hard structures of equal weight (1, 7, 8), (iv) resistance to corrosive chemicals and harsh conditions (e.g., for medical and food applications) (9), and (v) high cycle lifetime (millions of cycles, without degradation in performance, have been demonstrated) (7, 10, 11).

Because there are no practical soft controllers for soft pneumatic or electrical actuators, they are controlled almost entirely by hard components [for pneumatic systems, solenoid valves that open and close in response to electronic or pneumatic signals (3, 4, 12); for electrical systems, conventional electrical circuits and components (13, 14)]. Although the compliance of soft systems allows them to accomplish many functions using only on–off control, complex functions for soft actuators may require more complicated, hard, electronic control systems (15–17).

Recent work on soft valves has begun to increase the scope of soft actuators by eliminating the need for hard control systems, to reduce the complexity of the inputs required for specific behaviors [e.g., oscillation (7, 18)]. Examples of soft valves that have been incorporated into soft devices include unidirectional check valves in a soft device powered by combustion (19) and a soft microfluidic oscillator that caused the arms of a soft octopus-shaped device to flail (although not to function purposefully) (18). We previously developed a soft, bistable valve, and we used this valve for autonomous gripping when the valve (integrated into a gripper) contacted an object. We also demonstrated locomotion driven with a single, constant-pressure supply of air by leveraging an instability made possible with the bistable valve (7). Integration of soft, pneumatic control and actuation directly into the structure of soft systems is, however, still at an early stage, and demonstrations have been limited to check valves, simple oscillators, and on–off switches (7, 18, 19).

More “intelligent” control—for example, control based on digital logic and computation—has been demonstrated broadly (20, 21), typically in microfluidic devices (22–24)—including pneumatic devices (23, 25)—as a method to achieve complex operations. Microfluidic control systems are typically based on the monolithic polydimethylsiloxane-based valve proposed by Quake and coworkers (24) (the “Quake valve”) or a similar valve introduced one week later by Hosokawa and Maeda (26). Thousands of these valves can be integrated onto a microfluidic chip (27), and combinations of these valves can emulate the digital logic circuits found in computers (28–32). Investigations by Mathies and coworkers (33, 34) and, more recently, by Hui and coworkers (25, 35) convincingly demonstrate the capabilities of the pneumatically operated versions of these microfluidic digital logic circuits. Other recent work has shown frequency- and flow-dependent valves (36, 37), as well as oscillators incorporating valves described by Takayama and coworkers (38, 39).

Five issues, however, have precluded the use of microfluidic control with macroscale soft devices. (i) Actuation of the only (currently) useful soft devices—devices that are “large” relative to commonly used microfluidic systems—is now prohibitively slow because of the low rates of airflow (0.01 to 10 mL/min) in the small channels that the microfluidic devices use (23, 40). (ii) The choice of materials is a common hurdle in fabrication of soft logic gates on microfluidic platforms, in that microfluidic logic circuits often rely on hard materials, like glass or hard plastics (23, 25, 35, 41), although it is possible to fabricate microfluidic logic circuits entirely from soft materials (18, 28). (iii) The working principle of the valves used in microfluidic logic circuits requires consumption of power at steady state—a vacuum or pressure source is connected, via a pneumatic resistor, to atmospheric pressure (25, 28, 35)—and this built-in inefficiency is undesirable, especially for mobile applications where power (or pressurized air) is limited (42, 43). (iv) The requirement for separate designs for each type of logic gate functionality (e.g., NOT, AND, OR, etc.) increases the complexity required of these systems (28). (v) These microfluidic logic circuits are permanent once fabricated and cannot be reconfigured (23, 28, 41).

Here we demonstrate—using only soft components—pneumatic digital logic gates on the same scale as commonly used soft actuators that enable complex behaviors in soft devices. We demonstrated three logic elements—NOT, AND, and OR logic gates—using a single soft, pneumatic valve as a reconfigurable platform. This set of logic gates exhibits functional completeness and can therefore act as the basis for any logic circuit (44). We demonstrated several features of modern electronic computers: memory of multiple past states or events (in a completely soft two-bit shift register), decision making based on the current state (shown by toggling between two states triggered by a single input signal), and conversion between digital and analog data (by converting a pneumatic digital input to a “continuous” analog output). We also implemented a logic circuit that, together with a soft pushbutton, enables tactile interaction between humans and soft devices and thus introduces a different strategy in haptic design.

This work represents a step toward embodying control functions into the structure of soft devices that enable autonomy and “intelligent” behavior without requiring an electronic interface or hard components. It has potential for uses where hard or (many) electrical components may be unsuitable (e.g., in vivo, in high-radiation environments, or near high magnetic fields), and it provides controllers that withstand deformations due to shear, bending, and tensile or compressive stress (3, 4, 7). The approach demonstrated here is modular, because a single valve can be configured as multiple logic gates, and because a logic circuit can be rearranged after fabrication to perform other functions (45). These logic circuits do not consume power at steady state, in contrast with designs using soft microfluidic “transistors.” They are scalable to high rates of airflow (2 to 4 L per minute; detailed in SI Appendix, Fig. S11) and are thus compatible with the scale of most soft devices now being used practically (1, 3, 4).

Results

The Soft Valve.

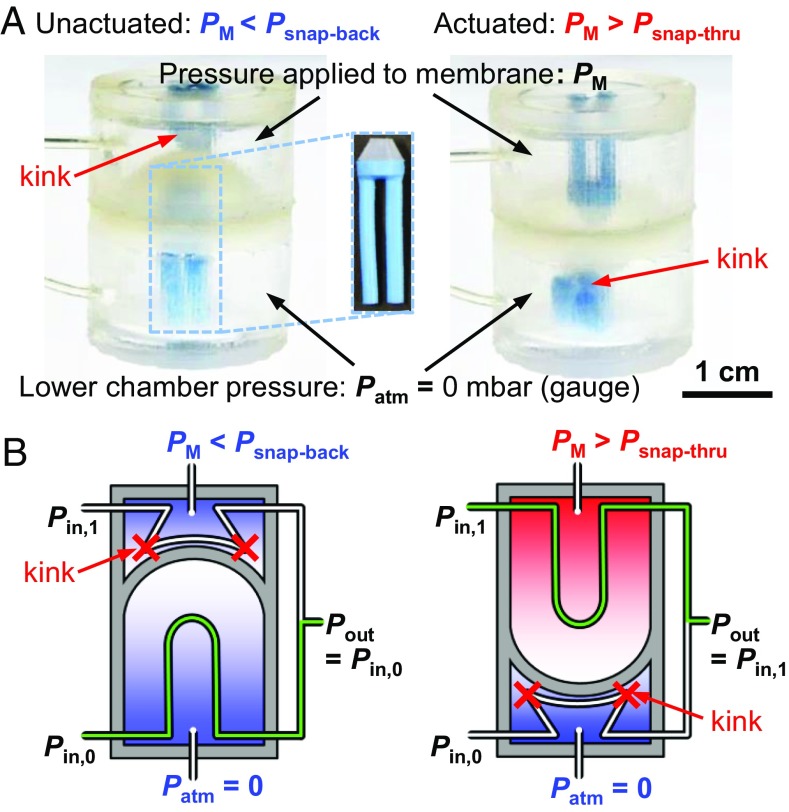
The soft logic gates demonstrated here build on the soft, bistable valve described previously (7). The valve consists of two cylindrical chambers, which are separated by a bistable hemispherical membrane (Fig. 1A). This membrane has two stable, steady states: unactuated or actuated. Elastomeric tubing leads through each chamber to a common output, with output pressure P_out (Fig. 1B). The bottom tubing is connected to an input pressure P_in,0 and the top tubing to an input pressure P_in,1. When the upper internal chamber is unpressurized [P_M = 0 mbar (gauge pressure, equal to 1 atm absolute pressure)], the membrane remains in its unactuated state, deflected upward, and blocks flow through the tubing above the membrane by forming a kink in this tubing [a type of buckling instability (46, 47)], such that the input P_in,1 is isolated from the other connections; the bottom tubing, however, is unkinked, and P_out is directly connected to the input pressure of the bottom tubing, P_in,0 (Fig. 1B, connection path indicated by shaded tubing). Pressurization of the upper chamber to pressures smaller than the critical pressure for membrane snap-through (P_snap-thru) deflects the membrane only slightly toward the bottom chamber and does not change the pattern of airflow through the tubing (the bottom chamber is always connected to atmospheric pressure, so the pressure difference across the membrane is always equal to P_M). We denote this state the “unactuated” state.

Fig. 1.

The soft valve shown in A consists of two pathways for airflow, one on either side of an internal membrane with pressure P_M applied above the membrane and atmospheric pressure P_atm maintained below the membrane. The membrane blocks one of the two pathways at any given time by kinking tubing along that pathway. In the unactuated state, when P_M is less than the membrane snap-back pressure, P_snap-back, the upper pathway is kinked and the output pressure, P_out, is connected to the lower input pressure, P_in,0; conversely, in the actuated state, when P_M is greater than the membrane snap-through pressure, P_snap-thru, the lower pathway is kinked and the output pressure, P_out, is connected to the upper input pressure, P_in,1, shown schematically in B. The internal tube, shown as an inset in A, is detailed in SI Appendix, Figs. S1, S2, and S4.

Only when the pressure difference across the membrane exceeds the critical pressure required for snap-through (P_M > P_snap-thru) (7, 48) does the membrane “snap” toward the bottom chamber, open the top tube, and simultaneously kink the bottom tube. In this “actuated” state, P_out is connected to the input pressure P_in,1, while P_in,0 becomes isolated (Fig. 1B). Because the snap-through instability is hysteretic, the valve switches back to the unactuated state only when P_M decreases below the critical pressure for snap-back, P_snap-back. This behavior restricts the output pressure to two values (corresponding to the two inputs P_in,0 and P_in,1) over a continuous range of input pressure, P_M, applied to the membrane. For all of the soft, bistable valves used in this work, P_snap-thru = 110 mbar, and P_snap-back = 25 mbar. Therefore, for any value of P_M > 110 mbar, a valve is in the actuated state; for any value of P_M < 25 mbar it is in the unactuated state; and for values 25 mbar < P_M < 110 mbar the valve remains in the state from which it came.

Digital Logic Gates.

To establish a context with which to understand digital logic, we assigned pressure P = 150 mbar the binary value “1” and pressure P = 0 mbar (gauge pressure, equal to 1 atm absolute pressure) the binary value “0.” Since these pressures are above the membrane snap-through pressure, P_snap-thru, and below the membrane snap-back pressure, P_snap-back, respectively, the value of P_out is not hysteretic or path-dependent and instead depends only on the instantaneous values of P_in,0, P_in,1, and P_M when these inputs are either 1 or 0.

A NOT gate inverts its input signal; an input of 1 generates an output of 0, and vice versa. The truth table for a NOT gate illustrates this behavior by summarizing the inputs and corresponding outputs (Fig. 2A). We fabricated a completely soft NOT logic gate by setting P_in,1 = 0 mbar (binary 0) and P_in,0 = 150 mbar (binary 1) by connecting these inputs to sources of constant pressure (Fig. 2B); in this configuration, P_out varied only with P_M. Over the full range of input pressure P_M (including states between 0 and 1), the output pressure switches (decreases) from a high to low value when the input pressure rises above a given threshold, and the output pressure switches (increases) from a low to high value only when the input pressure falls below a different, smaller threshold; this difference in pressure to cause switching results in hysteretic behavior (Fig. 2C).

Fig. 2.

A NOT gate inverts its input, such that an input of binary 0 results in an output of 1, and an input of 1 results in an output of 0, shown in the truth table in A. In this work, binary 0 is defined as 0 mbar, and binary 1 is defined as 150 mbar (both are gauge pressures). The NOT gate is constructed by connecting the input P_in,1 (Fig. 1B) to a source of pressure of value 0, and connecting the input P_in,0 to a source of pressure of value 1 (B). Over a continuous range of input pressures, P_M, the output pressure, P_out, is hysteretic due to the difference between P_snap-thru and P_snap-back for the membrane, shown in C. When operated only at pressures below P_snap-back and above P_snap-thru, however, the valve exhibits binary switching (C). Specifically, when the value of P_M is constrained to the binary set of inputs A = [0, 1], the valve inverts the input signal and functions as a NOT gate, with output Q taking the opposite value of input A (D).

This functionality is analogous to that of the Schmitt trigger, a type of operational amplifier used in electronics for analog-to-digital conversion, level detection, and line reception (49–52); the hysteresis of the Schmitt trigger makes it a basis for oscillators and noise filters for digital signals (7, 52). Transistor-based electronic switches and logic gates—including electronic Schmitt triggers built from combinations of transistors, as well as the pneumatic transistors and logic gates demonstrated in prior work—differ importantly from the pneumatic Schmitt trigger we demonstrate, in that they consume power at steady state due to a continuous current (or pressurized air) leakage through a pull-up or pull-down resistor, which is required to set one of the two output states (28, 35, 52). The pneumatic Schmitt inverter, however, does not require power at steady state. The properties of the material used to fabricate it (an elastomer), and the snap-through instability of the membrane and buckling of internal tubes in two unique, functional states with no leaks or pneumatic pathways directly to the surroundings, preclude a constant drain in power for this system by eliminating both the need for a pull-up/down resistor and the corresponding power loss associated with this component. This construction is analogous to complementary metal-oxide-semiconductor (CMOS) technology, in which a single electronic input simultaneously opens one pathway for current and closes another, separate pathway (SI Appendix, Fig. S7 shows a comparison between traditional transistor circuits, CMOS, and our soft valve).

We attached a variable binary input “A” to P_M (when A = 0, P_M = 0 mbar, and when A = 1, P_M = 150 mbar; input A was generated by a computer and an electronic pressure regulator, detailed in SI Appendix). We measured the binary output value “Q” (Q = 0 for P_out = 0 mbar, Q = 1 for P_out = 150 mbar) as a function of input A, and established, from the behavior shown in Fig. 2D, that, when A = 0, Q = 1, and, conversely, when A = 1, Q = 0. The deviation in the shapes of the rising and falling edges of A and Q resulted from the physical response of the soft logic gate; a step change in pressure A at the electronic regulator, from 0 to 1, did not instantaneously switch the pressure within the upper chamber of the logic gate from 0 or 1 but instead required ∼0.5 s to equilibrate due to the delay associated with inflation (i.e., pneumatic capacitance) and resistance to airflow within the tubing leading to the logic gate. We characterize this delay in detail in SI Appendix, Fig. S10, as a function of both number of cascaded logic elements and the logic circuit supply pressure. The delay could be minimized by either increasing the connector tubing inner diameter or reducing the connector tubing length (to reduce friction loss due to flow), or by reducing the internal volume of the logic elements themselves to reach snap-through (or snap-back) pressures more quickly. The “kinks” in the rising and falling edges of A in Fig. 2D correspond to snap-through of the internal membrane.

The same soft valve can be reconfigured as both OR and AND logic gates by modifying the input pressure connections. OR and AND gates each require two inputs, in contrast with the NOT gate, which required only one input. An OR gate has two binary inputs, A and B. When at least one of these inputs is 1, the binary output Q of the OR gate is 1; otherwise, it is 0 (Fig. 3A). This functionality can be achieved with the soft valve by configuring it with P_in,0 = A, P_M = B, and the top tubing, P_in,1, connected to a constant source of pressure of value 1 (= 150 mbar) (Fig. 3B). When input B = 0, the input A connects directly, through the internal tubing, to the output Q of the logic gate, so that output Q = 0 when input A = 0, and output Q = 1 when input A = 1 (Fig. 3B, left two schematics). When input B = 1, the membrane snaps through (48) and connects the output Q to the constant source of pressure P_in,1 = 1, independent of the value of input A (Fig. 3B, right two schematics). We demonstrated experimentally the functionality of the OR gate in every possible input configuration (Fig. 3C).

Fig. 3.

OR and AND logic gates are depicted symbolically, along with truth tables summarizing their two binary inputs and resulting binary output values (A and D); because the two inputs are binary, four distinct states exist for each gate. The pneumatic connections for the OR and AND gates are shown in B and E, respectively, with schematic representations of the valves in each of their four possible states (direct connections from either of the inputs to the output are shaded). We experimentally characterized these logic gates over each of their four possible states by varying the two inputs independently (C and F).

In contrast to the OR gate, the output Q of an AND gate is 1 only when inputs A and B are both 1; otherwise, it is 0 (Fig. 3D). The valve is configured as an AND gate when P_in,1 = A, P_M = B, and the bottom tubing, P_in,0, is connected to a constant source of pressure of value 0 (= 0 mbar) (Fig. 3E). In this configuration, when input B = 0, output Q = 0 independent of the value of input A (Fig. 3E, left two schematics). Only when input A = 1, pressurizing the upper tube inlet, and input B = 1 (thus causing the membrane to snap through) does the output of the logic gate become Q = 1. We demonstrated experimentally the functionality of the AND gate in all input configurations (Fig. 3F).

Combining Logic Gates: Digital Logic Circuits.

Implementation of these completely soft logic gates enables simple decision making that can be directly embedded in soft devices. For example, a soft device may be programmed to respond to a certain pressure-based physical stimulus only if another criterion—physical force, orientation with respect to gravity, or ambient temperature—is simultaneously met (as achieved with one AND gate). Alternatively, a single stimulus at any number of an array of many soft pressure-based sensors could trigger a response (multiple OR gates). With AND, OR, and NOT gates, any logical function can be implemented; that is, this pneumatic valve provides the basis for a functionally complete set of logical connectives (44). In other words, these soft, pneumatic logic gates could, in principle, replicate the functionality of an electronic computer (although it is not practical for them to do so because of size and not useful because of speed). Multiple soft logic gates can be arranged synergistically for many applications: certain combinations of gates can store data and “remember” multiple past events, respond to their current state or environment, or convert between digital and analog pressure signals.

Set–Reset Latch.

A simple logic circuit consisting of three logic gates, the set–reset (SR) latch, exhibits “memory,” in that it can be programmed to retain one bit of data (0 or 1); that bit of data is stored, without any further external control or stimulus, and can be read (input) into other logic elements as a source of pressure. The SR latch can also be reprogrammed at a later time. The fundamental concept underlying the functionality of the SR latch is a feedback loop, where a stored output value of 1 can “hold” itself at a pressurized state by controlling at least one of its own inputs, directly or indirectly.

An SR latch has two inputs, a “set” input, S, and a “reset” input, R (Fig. 4). When the SR latch receives signal 1 at the set input, it switches the output, Q, to 1. When it receives signal 1 at the reset input, it switches the output back to 0 (52). Fig. 4 shows a design for an SR latch that incorporates each of the three pneumatic logic gates—NOT, OR, and AND—and experimental demonstration of the SR latch. The SR latch allows storage of one bit of data using a single feedback loop: when the “set” input signal S is 1, the output signal, Q, becomes 1 and remains 1, even if S returns to 0, by holding its state via the feedback loop (shown in Fig. 4C after S is cycled on and off at 5 s on the independent axis, but before R is cycled at 15 s). Similarly, when the “reset” input signal R is 1, Q becomes 0 and remains at 0, even if R returns to 0 (shown in Fig. 4C after R is cycled at 15 s, but before S is cycled at 25 s). Therefore, the SR latch enables the embodiment of memory in a soft device. It “remembers” which input (set or reset) was pressurized (to state 1) most recently.

Fig. 4.

The SR latch, an example of soft pneumatic memory, outputs a binary value of pressure depending on the most recent nonzero input signal of pressure. We incorporated memory by feeding the output back into the logic circuit (A, top-most line in schematic) with valves configured as shown (B). When the set input, S, is activated (S = 1), the output becomes 1, even after S returns to 0, exhibiting the ability for data storage within a completely soft device. The output remains 1 until the reset input, R, is activated, at which time the output returns to 0 indefinitely (or until switched intentionally, shown experimentally in C).

Shift Register.

A serial-in/parallel-out shift register—another example of a device with memory—can reduce the number of inputs used in a device to two, while retaining the ability to control many actuators via multiple parallel outputs. For instance, a five-bit, serial-in/parallel-out shift register could control five soft actuators with its five parallel outputs while only requiring two inputs: one input for a channel of data to provide the bits to be stored at (and dictate the state of) the five outputs and another input to trigger when a bit from the channel of data will be recorded [this input is typically called the “clock” (53)]. This implementation of soft logic can enable a significant reduction in the complexity of inputs required for soft devices and eliminate the need for many valves and separate controllers.

A serial-in/parallel-out shift register records data sequentially from a single input channel of data (which may be either 0 or 1 at a given time) and stores these data in an array of parallel memory locations that each have their own output channel. Data are recorded one bit at a time, and instances of data recording are triggered by the “clock”: each time the clock pulses (i.e., temporarily takes the value 1), the shift register records the current value of the channel of data into its memory on a first-in, last-out basis (bits exiting the memory are discarded). A pneumatic clock signal could come from a computer-controlled electronic pressure regulator, a soft pneumatic oscillator (7), or even a human user pressing a soft button whenever they would like to record a bit; the clock signal’s pulses do not need to be evenly spaced in time. Fig. 5 demonstrates a two-bit, serial-in/parallel-out shift register. In this work, we generate the clock signal with a computer-controlled electronic pressure regulator, which proves useful because we demonstrate, through our experiments, that the soft shift register functions as a “black box” with interchangeable inputs and outputs; a soft, pneumatic oscillator (7), or a soft button (with a human user; see Fig. 8) could be used in place of the electronic regulator to generate the clock signal.

Fig. 5.

Experimental demonstration of a shift register. Soft pneumatic logic gates were arranged into a D-type latch (A), which has inputs D (incoming data) and CLK (clock) and output Q (stored data). When the clock is 1, Q takes the value of the incoming data stream, D; when the clock is 0, Q remains the same regardless of the incoming data. Two D-type latches and a pressure follower (an inverted NOT gate) were arranged into a two-bit shift register (B), which has the capability to convert between serial and parallel data. We demonstrated the functionality of the shift register experimentally in the serial-in/parallel-out mode (C), where, when the clock is pulsed, the bit stored in Q₀ is transferred to Q_1, and the incoming bit value of the stream of data, D, is stored in Q₀ (the bit previously stored in Q₁ is discarded).

Fig. 8.

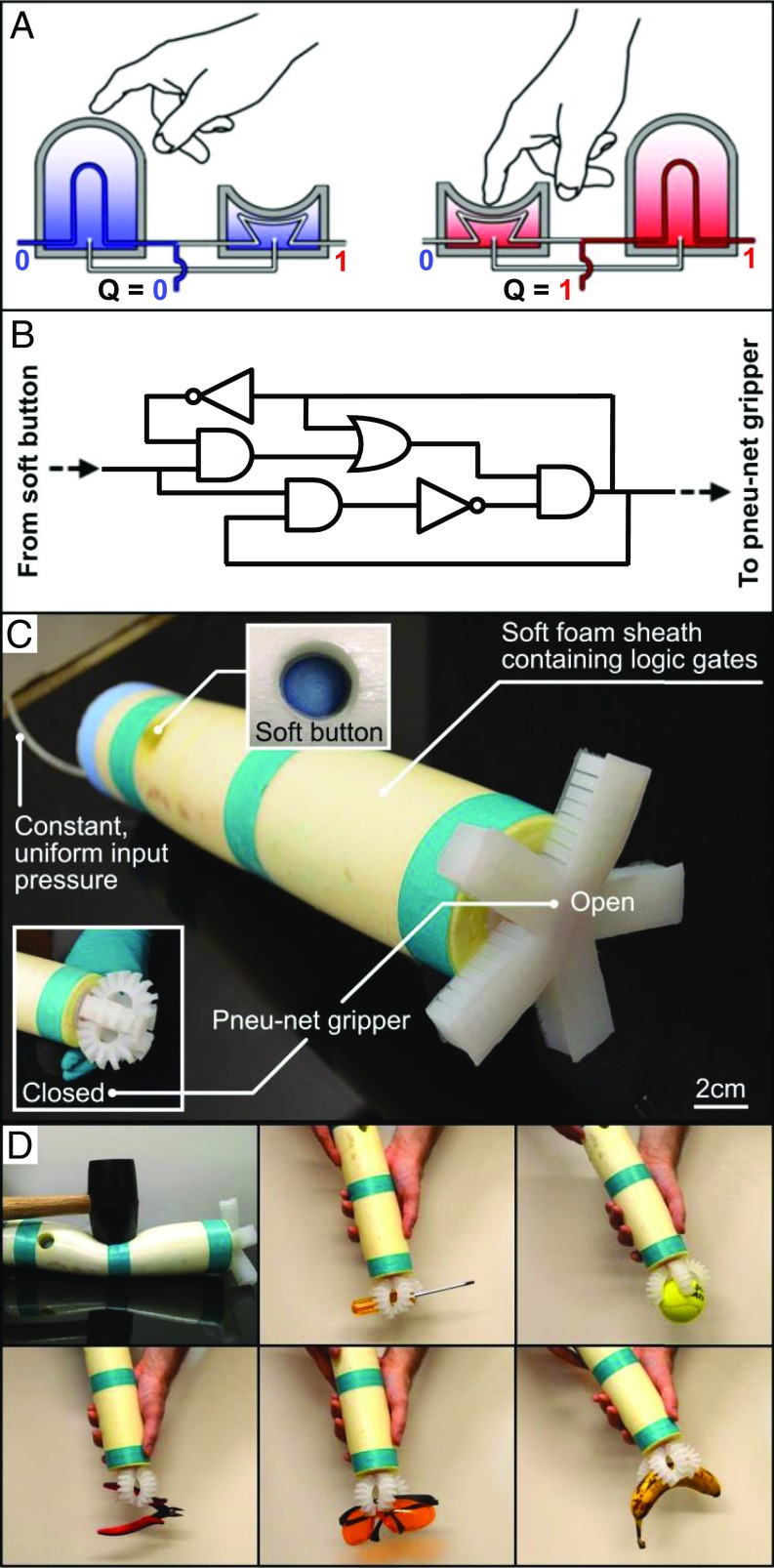
Human-operated, completely soft gripper with toggle button. We modified the soft, bistable valve to create a button that converts human input to a binary pneumatic signal (A). When the button is unperturbed, its output is 0. When it is depressed, the left membrane is manually snapped-through, and the built up pressure also snaps the right membrane through, simultaneously kinking the left tube and unkinking the right tube, and changing the button’s output to 1. We attached the button to a toggle logic circuit (B) composed of soft logic gates, where a temporary input of 1 (from the button) toggles the output to 0 if it was 1 at the time the button was pressed, and vice versa. The output of the toggle circuit actuates a pneu-net gripper. We integrated the soft button and the toggle logic circuit into a soft foam sheath with the pneu-net gripper mounted on one end and a single, constant input pressure of 150 mbar attached, via a rubber tube, to the other end (C). This soft gripper could pick up a variety of oddly shaped or fragile objects, even after being struck by a mallet (D).

The two-bit shift register contains two D-type latches (Fig. 5A) and a single pressure follower to create a short delay ahead of the first D-type latch. In brief, the D-type latch and pressure follower operate as follows (see SI Appendix for details). The D-type latch has two binary inputs: the channel of data, D, and the clock, CLK (Fig. 5A). When the clock input CLK becomes 1, the output, Q, of the D-type latch is equal to the current value of the data channel, D. When CLK becomes 0, Q retains whatever value D had when CLK was most recently 1. In principle, a D-type latch could be simplified by construction from combinations of NOR or NAND logic gates, but, in our case, these logic gates would require multiple soft valves (detailed in SI Appendix, Fig. S8); we instead used only NOT, OR, and AND logic gates, each of which requires a single soft valve. Meanwhile, the pressure follower has one input and one output, and the output always takes the same value as the input. The pressure follower is useful as a delay because, when the input changes state, the corresponding change in the output is delayed by the response time of the valve (∼0.5 s when operated at 150 mbar). The shift register uses the pressure follower as a delay to allow data to transfer from the first bit of memory (Q₀ in Fig. 5B) to the second bit of memory (Q₁) before the first bit of memory is overwritten by the current value of the data channel; the pressure follower is illustrated schematically by a triangle (upstream of the left D-type latch in Fig. 5B).

In the two-bit shift register, the incoming data stream is denoted as “D,” the clock signal is denoted as “CLK,” and the two stored bits are “Q₀” and “Q₁.” When the clock pulses (i.e., temporarily takes the value 1) the bit of data stored in the first data storage location, Q₀, is passed to the second data storage location, Q₁; then, the value of the incoming data channel, D (either 0 or 1), is stored in Q₀. The bit (0, 1) that was contained in Q₁ before the clock pulse is discarded. Fig. 5C shows this behavior experimentally; three other demonstrations are included in SI Appendix.

Leading-Edge Detector.

We generated the clock signal for the shift register in this work with an electronic pressure regulator, but it could also be produced by a soft pneumatic oscillator (7, 18, 23) that cycles between high- and low-pressure states; the soft, pneumatic shift register would then have the potential to control many outputs with only one input (the data channel, D). If the clock signal lasts too long (e.g., remains in state 1), however, data can be overwritten. To address this issue, the leading edge of an extended clock signal can be extracted as a pulse, which can also precisely control when a datum is recorded from the incoming stream of data.

We achieved this functionality with a leading-edge detector, comprising one AND gate and three NOT gates (Fig. 6). Initially, when the input to the leading-edge detector, IN, is 0, the upper input to the AND gate is also 0, but the lower input is 1 (because it has been inverted an odd number of times). When IN transitions from 0 to 1, the upper input to the AND gate immediately becomes 1; the lower input, however, does not become 0 until the bistable membranes within all three NOT gates snap through, and, during this process, both inputs to the AND gate are 1, and its output, OUT, is temporarily 1. (The duration of this output pulse is equal to the response time of one logic gate, ∼0.5 s, multiplied by the three inverters in the lower leg of the circuit, yielding a pulse width of 1.5 s). Later, when IN switches from 1 to 0, the upper input to the AND gate immediately becomes 0, and OUT is therefore also 0, regardless of the value of the lower input to the AND gate. To achieve different pulse widths of the output signal, the number of logic gates on the lower leg can be changed to incorporate any number of pressure followers, and any odd number of inverters, resulting in a pulse width of the logic gate response time (∼0.5 s) multiplied by the number of logic gates in the lower leg. We demonstrate a leading-edge detector experimentally in Fig. 6; this logic circuit exemplifies time-dependent manipulation of an input signal to produce a desired output.

Fig. 6.

The leading-edge detector captures the leading edge of a signal that has transitioned from 0 to 1. It can reduce the duration of a CLK input controlling complex logic circuits if CLK lasts too long (to avoid setting both Q₀ and Q₁ to the current value of D in the two-bit shift register, for example). We demonstrated reduction of a 15-s input to a 1.5-s pulse at the leading edge; if a longer (or shorter) pulse is desired, followers or inverters can be added (or removed) from the lower leg of the circuit, as long as the total number of inverters is odd.

Digital-to-Analog Converter.

We demonstrated conversion of digital signals—for example, the pneumatic 0 and 1 used with the logic gates in this work—to an analog, or continuous, output with a digital-to-analog converter (DAC). A DAC accepts a digital (binary) input over several channels (e.g., a two-bit DAC accepts the four unique, ordered digital inputs of 00, 01, 10, and 11). Meanwhile, the DAC can also produce a number of—usually evenly spaced—levels of “analog” output; the number of analog levels is equal to the number of ordered digital inputs, and the analog levels are typically mapped, in increasing order, directly to the ordered list of digital inputs (e.g., in an electronic DAC, the set of digital inputs [00, 01, 10, 11] may map to analog voltage output levels of [0, 1, 2, 3] V). The output is not purely analog but rather an approximation of an analog signal with resolution determined by the number of bits in the input digital signal. In this work, we demonstrated a completely soft, two-bit DAC (Fig. 7). Binary inputs from two channels control an analog output pressure ranging from 0 to 150 mbar in four discrete steps. For this demonstration, we configured four logic gates as simple single-pole single-throw relays, shown schematically in Fig. 7A, to regulate the discretized pressure supplies. The entire DAC logic diagram is shown in Fig. 7B, with experimental pressure measurements in Fig. 7C. We used the two-bit DAC to pressurize a pneu-net gripper in four steps of analog pressures, during which it closed to different extents (Fig. 7D). This demonstration illustrates that the binary signals generated by the soft logic gates in this work can be converted to quasi-analog outputs for generation of patterns of actuation more complex than on/off, open/closed, and so on.

Fig. 7.

DAC. Four valves were configured as single-pole single-throw relays (A) and connected, along with the previously described logic elements, to form a two-bit DAC (B). Binary inputs over two input channels, ranging from AB = 00 to 11, produced a variable pressure output ranging from 0 to 150 mbar in increments of 50 mbar (C), which we used to control the degree of closure of a pneu-net gripper (D).

Human–Soft Device Interaction.

Soft button.

These digital logic circuits are capable of interacting with their environment. We demonstrated closure of a gripper to different extents controlled by the DAC, exhibiting a useful physical output obtained from a digital logic circuit. Input to a digital logic circuit (e.g., signals from sensors or from human users) can also be obtained from the environment. We developed a soft button with a binary pneumatic output to allow human users to interface with and control soft logic circuits and devices (Fig. 8A). The soft button is composed of two cylinders, each cylinder having its own bistable membrane; the left bistable membrane curves upward at rest, while the right bistable membrane curves downward. The two cylinders are connected to each other pneumatically, and each cylinder also has internal tubing for flow of air. In the left cylinder the internal tubing is initially open to airflow, while in the right cylinder the tubing is initially kinked by the downward-facing bistable membrane. Therefore, in its rest state, the output of the button, Q, is directly connected, via the internal tubing in the left cylinder, to a constant input pressure of value 0, so when the button is not depressed, Q = 0. When depressed by a user, however, the pressure within the left cylinder of the button increases due to the force applied by the user’s finger until the bistable membrane snaps through, at which time the membrane of the right cylinder also snaps through because, as the cylinders are connected pneumatically, the right cylinder has also become pressurized. As a result, the internal tubing inside the left cylinder becomes kinked, while the internal tubing inside the right cylinder unkinks, and the output of the button, Q, is directly connected to a constant input pressure of 1, so, when the button is depressed by a user, Q = 1.

Toggle switch.

The soft button was connected to a toggle logic circuit (Fig. 8B), where, if the current output of the toggle circuit is 0, depressing the button changes the output to 1, and vice versa. This logic circuit is another form of memory, similar to, but with function distinct from, the SR latch described previously. The output from the toggle circuit was attached to a soft pneu-net gripper, where an output of 1 from the toggle circuit would cause the gripper to actuate (grasp), while an output of 0 from the toggle circuit would allow the gripper to relax. The entire device was then incorporated into a soft foam sheath powered only by a single, constant source of pressure (provided here by an external supply, but pressure may be provided by an onboard source of compressed gas, or a gas-forming chemical reaction, for an untethered device) to create a completely soft, human-controlled gripper that toggles between actuated (gripping) and unactuated (open gripper) states whenever the single soft button is depressed (Fig. 8C). The human input received by the soft button, in combination with the onboard logic, enables effective human–soft device interaction, demonstrated in SI Appendix, Fig. S8 and Movie S1 where a human performs a pick-and-place task with the assistance of the completely soft logic-enabled gripper.

This soft logic-enabled gripper has two potential impacts. (i) The device represents, by itself, a promising solution for human–soft device collaboration in grasping or handling of materials dangerous to humans (e.g., radioactive devices or sick mice in laboratory studies), or in environments where hard devices and electronic-based logic and computation are undesirable (underwater, in the presence of high magnetic fields, or where the device may undergo extreme compressive strain). (ii) As a proof of concept, this demonstration paves the way for future, more intricate, completely soft devices that will work in collaboration with humans.

Submersible Logic-Enabled Soft Robot.

Soft pressure sensor.

We reconfigured a NOT gate as an environmental pressure sensor (Fig. 9A), enabling, in addition to the human input provided via the soft button, inputs from environmental stimuli. The input of the sensor (which is connected to the internal chamber toward which the hemispherical membrane is deflected with no applied pressure differential) is exposed to the environment at pressure P_env. The other internal chamber of the sensor is maintained at atmospheric pressure (0 mbar). When P_env is less than the snap-back pressure (P_env < P_snap-back ≈ 25 mbar), the pressure sensor outputs 1, and, conversely, when the environmental pressure is greater than the snap-through pressure (P_env > P_snap-thru ≈ 110 mbar), the sensor outputs 0.

Fig. 9.

Semiautonomous submersible robot. Hydrostatic pressure is measured by a NOT gate reconfigured as an environmental pressure sensor, with its input opened to the environment at pressure P_env (A). When the environmental pressure is less than the snap-back pressure (∼25 mbar), the pressure sensor outputs binary 1, and, conversely, when the environmental pressure is greater than the snap-through pressure (∼110 mbar), the sensor outputs 0. The outputs from the environmental pressure sensor and a soft button are received by a soft digital logic circuit (B) designed to control a semiautonomous submersible robot (C). The robot dives when it senses low pressure (near the surface of the water) and surfaces when it senses high pressure (at depth), resulting in a cyclic diving–surfacing behavior. Diving and surfacing are driven by the buoyant force of a balloon, constrained by an inextensible mesh, attached to the robot; this balloon is either inflated or deflated by the logic circuit. The snap-through hysteresis of the membrane in the pressure sensor results in oscillating surfacing–diving behavior between two known heights (25 cm and 110 cm) that correspond, approximately, to the hydrostatic pressures equal to P_snap-back and P_snap-thru (D). The robot can also surface on command at the touch of the soft button, by a human user, regardless of the state of the pressure sensor (E).

Underwater operation.

The outputs from the environmental pressure sensor and a soft button (Fig. 8A) are received by a soft digital logic circuit (Fig. 9B) designed to control a semiautonomous submersible robot (Fig. 9C) which dives when it senses low pressure and surfaces when it senses high pressure or a signal from the soft button. Diving and surfacing depend on the buoyant force of a balloon, constrained by an inextensible mesh, attached to the robot; this balloon is either inflated or deflated by the logic circuit.

The snap-through hysteresis of the membrane in the pressure sensor results in oscillating surfacing–diving behavior between two heights (25 cm and 110 cm) that correspond, approximately, to the hydrostatic pressures equal to P_snap-back and P_snap-thru. The robot can also surface on command at the touch of the soft button by a human user. We demonstrated operation of the submersible soft robot in a water tank, in which it oscillated between two heights (Fig. 9D) and also surfaced on command when a human user pressed a soft button (outside of the water tank; design shown in Fig. 8A) attached to the robot (Fig. 9E and Movie S2). This semiautonomous robot incorporated inputs from both the environment, and from a human user. Soft underwater robots are attractive because, by index-matching to the surrounding water they may be fabricated to be completely transparent—both optically and to sonar (14, 54)—which remains a limitation of current hard robots. The semiautonomous soft robot presented here represents a step toward practically undetectable, intelligent, and autonomous underwater robots for applications in biology and ecology (nonintrusive sample collection), and the military.

Discussion

Soft devices have several attractive features, including collaboration with humans, use with fragile objects, and mechanical and environmental robustness (1). Despite their remarkable “material intelligence,” however, autonomy for soft devices has remained a challenge; embedded soft control is elusive (even for simple functions), and, typically, control requires hard valves and electronics. This work demonstrates macroscale pneumatic NOT, AND, and OR digital logic gates, compatible with soft devices, and made entirely from soft material (silicone rubber, although other elastomers would also work). Each logic gate utilizes a single soft, pneumatic bistable valve; the valves differ only in their configuration of pneumatic inputs. Each bistable valve, in turn, relies on the interplay of two instabilities—snap-through of an internal, hemispherical membrane and buckling (kinking) of internal tubes that allow (or block) the flow of air—and, by utilizing these two instabilities to open and close two pathways for flow simultaneously, sets itself apart from devices previously used for digital logic (including electronic transistors and microfluidic Quake valves) that only control one pathway for flow and, consequently, must draw power even in the steady state.

We combined logic gates to form digital logic circuits with the basic functionalities required of computers, including the ability to remember past states (the SR latch and two-bit shift register), decision making based on the current state (shown by toggling between two states triggered by a single input signal), processing and manipulation of signals (the leading-edge detector), and conversion between digital and analog data (by converting a pneumatic digital input to a “continuous” analog output). The DAC and toggle switch could control a soft actuator [a pneu-net (11)] with a response time on the order of seconds, enabled by the high rates of airflow through the macroscale bistable valve (thousands of milliliters per minute). The results also demonstrate interactions of humans and soft devices using soft logic and thus highlight a path to enhanced interactions and collaborations between humans and soft devices. Finally, environmental sensing was demonstrated on a semiautonomous submersible soft robot, which responded to either the local hydrostatic pressure or to input from a human user; completely soft underwater robots can incorporate both optical and sonic camouflage (14, 54).

Fabrication of the bistable valves used here as logic gates remains too complicated for high-throughput, advanced manufacturing techniques like 3D printing, injection molding, or roll-to-roll processing; this challenge in fabrication must be overcome—either with this or an equivalent soft device—before we can achieve large-scale implementation of soft, pneumatic digital logic (e.g., soft computers) or wide use with soft devices. The macroscale design of logic gates presented here is, however, scalable to high airflow volumes and does not consume power at steady state. A single, simple design can be reconfigured to perform multiple functions as digital logic gates. The strategy for autonomy and control in soft devices shown here does not involve an electronic interface or hard components and therefore enables application of functional and intelligent, yet completely soft, devices for practical use.