A Practical Approach to Adjusting for Population Stratification in Genome-wide Association Studies: Principal Components And Propensity Scores (PCAPS)

Abstract

Genome-wide association studies (GWAS) are susceptible to bias due to population stratification (PS). The most widely used method to correct bias due to PS is principal components (PCs) analysis (PCA), but there is no objective method to guide which PCs to include as covariates. Often, the ten PCs with the highest eigenvalues are included to adjust for PS. This selection is arbitrary, and patterns of local linkage disequilibrium may affect PCA corrections. To address these limitations, we estimate genomic propensity scores based on all statistically significant PCs selected by the Tracy-Widom (TW) statistic. We compare a principal components and propensity scores (PCAPS) approach to PCA and EMMAX using simulated GWAS data under no, moderate, and severe PS. PCAPS reduced spurious genetic associations regardless of the degree of PS, resulting in odds ratio (OR) estimates closer to the true OR. We illustrate our PCAPS method using GWAS data from a study of testicular germ cell tumors. PCAPS provided a more conservative adjustment than PCA. Advantages of the PCAPS approach include reduction of bias compared to PCA, consistent selection of propensity scores to adjust for PS, the potential ability to handle outliers, and ease of implementation using existing software packages.

Introduction

Genome-wide association studies (GWAS) are an effective approach for identifying common genetic variants associated with disease risk. GWAS have increasingly been used with very large sample sizes that combine participants from many (potentially ancestrally heterogeneous) centers, and there is an increasing trend to undertake GWAS in population admixture (i.e. stratification). Thus, GWAS associations may be biased due to population stratification (PS). The most widely used method to address PS is principal components analysis (PCA) (Price et al., 2006). PCA is a method of correction for population structure in genetic association studies on unrelated individuals. The original PCA approach was proposed by Price et al. (2006) with subsequent extension by Patterson et al. (2006). This method uses genome-wide genotype data to estimate principal components axes that can be used as covariates in subsequent association analyses. The implication of this approach is that these axes represent features of genomic ancestry that capture PS. Since the adjustment of each single nucleotide polymorphism (SNP) varies along each axis of ancestry, PCA corrects not only for false positives but also for false negatives.

Despite its utility and ease of application, there are limitations to the PCA approach. The PCA method usually recommends using the top 10 principal components (PCs) to adjust for population stratification (Price et al. 2010; Feng et al. 2009; Kang et al. 2009). However, the recommendation to use 10 PCs is arbitrary. Adjusting for more PCs than needed to sufficiently adjust for PS can harm efficiency. Using fewer PCs than needed may results in residual bias. Most importantly, patterns of local linkage disequilibrium (LD) may cause PCA to create “nuisance axes”, which may be interpreted as the existence of subpopulations that reflect localized LD phenomena rather than plausible PS (Zou et al. 2010). These axes are not related to ancestry overall, but instead end up separating individuals according to their genotype in local genomic regions. Such PCs are dominated by relatively few SNPs that map to a few small chromosomal regions with extended LD (Feng et al.; Wang et al. 2009). These SNPs with local LD are referred to as outlier SNPs, and PCA is sensitive to such outliers. Specifically, due to individual outliers (a handful of individuals with very different ancestry origin from the rest of the cohort), numerous dimensions of ancestry may appear to model a statistically significant amount of variation in the data, but in actuality they function to separate a single observation from the bulk of the data (Lee et al. 2010).

Price et al. (2006) and Bouaziz et al. (2011) provide reviews of several methods that correct for population stratification in GWAS including genomic control (Devlin and Roeder 1999), adjusted regressions and meta-analyses. Several PCA-based approaches (Zhang et al. 2013a; Zhang et al. 2013b; Liu et al. 2013; Pritchard et al. 2000) have been proposed to correct PS in GWAS. A number of other methods such as structural association (Pritchard et al.) multidimensional scaling (Li and Yu 2008), linear mixed modeling (Zhang et al. 2010), variance component models (Kang et al. 2010), matching (Lee et al.; Luca et al. 2008; Epstein et al. 2012) and logistic mixed models (Cheng et al. 2016) have also been used to correct PS. However, these methods can be computationally intensive in GWAS (Lee et al.; Liu et al.; Pritchard et al.; Luca et al.; Epstein et al. 2012) or have similar limitations that PCA suffers from (Zhang et al. 2013a; Zhang et al. 2013b; Li and Yu; Chen et al.). Kang et al. (2010) developed the EMMAX program, taking to an expedited mixed linear model approach to correct for sample structure within human GWASs.

Recently, we developed the genomic propensity score (GPS) approach (Zhao et al. 2009; Zhao et al. 2012), which is a propensity score (Rosenbaum and Rubin 1983) based approach to correct for bias due to population stratification that allows estimation of the effect of a genotype under a wide range of genetic models (dominant, recessive, additive) while simultaneously adjusting for genetic markers along with patient and disease characteristics. The GPS reduced bias in estimated genetic effects and performed the same as or better than other existing approaches including PCA. Lin and Zeng (2011) further presented a theoretical justification for the GPS. However, one shortcoming of the GPS method is that it was developed in the context of candidate gene studies, and thus is not readily applicable to GWAS as currently formulated. To overcome the limitations of PCA and to extend the GPS for GWAS data, we propose a new approach that combines principal components and propensity scores (PCAPS) that is based on the Tracy Widom (TW) statistic (Tracy and Widom 1993; Trach and Widom 1994; Tracy and Widom 1996). This approach allows us to correct for confounding due to population stratification at each locus by adjusting for a summary covariate (the propensity score) which captures and balances differences in allele frequencies between the two comparison groups. Our goal is to obtain an unbiased estimate of the SNP association after adjusting for this confounder. The propensity score captures population stratification by summarizing the differences in all of the allele frequencies between the comparison groups. Using GWAS simulation studies under varying scenarios, we directly compare PCAPS to using PCA adjustment alone and EMMAX. We illustrate our approach in a GWAS of testicular germ cell tumors (TCGT) (Kanetsky et al. 2009).

Materials and Methods

Theoretical Framework

Selection of the number of significant PC’s requires testing the significance of the k^th largest eigenvalues. Tracy and Widom (1993, 1994, 1996) laid the foundation for this approach by proposing an analytical expression of the largest eigenvalue. Johnstone (2001) later proposed using the TW statistic to select significant components. Patterson et al. demonstrated the potential of using the TW statistic with PCA to uncover population structure. Zhao et al. (2009, 2012) first developed propensity score-based approaches to correct for population stratification and Lin and Zeng provided theoretical justification for using the propensity score in a logistic regression model. PCs are bounded from 0 to 1, and so they can be used to down weight the effect of outliers (Imbens 2004). Attributed to these theoretical justifications, we propose a new approach to adjust for population stratification based on propensity scores. First, we select the number of statistically significant genotype principal components based on the TW test. We then calculate the propensity score as the likelihood of an individual having a particular genotype given the individual’s significant PCs. Finally, the propensity scores are incorporated into the association model to adjust for population stratification.

The TW distribution is the probability distribution of the normalized largest eigenvalue of a random Hermitian matrix (Dominici and Maier 2008). The TW distribution (Tracy and Widom 1993) is defined as

$${\text{F}}_1\left(\text{s}\right)=\exp (-\frac{1}{2}{\int }_s^{\infty }q\left(x\right)dx){\left({\text{F}}_2\left(\text{s}\right)\right)}^{1/2}$$

where ${\text{F}}_2\left(\text{s}\right)=\exp (-{\int }_s^{\infty }\left(x-s\right)q^2\left(\text{x}\right)\text{dx})$. The function q(x) is the Hastings-McLeod solution (Hastings and McLeod 1980) of a Painlevé equation of type II where $q″\left(\text{s}\right)=\text{sq}\left(\text{s}\right)+2\text{q}{\left(\text{s}\right)}^3$, satisfying the boundary condition q(s) → Ai(s), s → ∞; where Ai(s) is the Airy function (Airy 1838).

Johnstone showed that F₁(s) is the limiting distribution of the largest eigenvalue of a real sample covariance matrix. Let C = MM^T where M is m x n matrix with each entry be independently and identically distributed as ~N (0, 1), and let λ₁ be the largest eigenvalue of C. Define

$$\text{μ}\left(\text{m, n}\right)={\left(\sqrt{m-1}+\sqrt{n}\right)}^2\text{and }\mathrm{\sigma }\left(\text{m, n}\right)=\left(\sqrt{m-1}+\sqrt{n}\right)\left(\frac{1}{\sqrt{m-1}}+\frac{1}{\sqrt{n}}\right)$$

If ${\lim }_{n\to \infty }\frac{n}{m}=\mathrm{\gamma }$ where γ ∈ (0, 1], then ${\text{L}}_1=\frac{\text{λ1}-\mathrm{\mu }\left(\text{m,n}\right)}{\mathrm{\sigma }\left(\text{m,n}\right)}~{\text{TW}}_1$

where TW₁ is the TW probability density function, i.e., ${\text{TW}}_1=\frac{d}{ds}{\text{F}}_1\left(\text{s}\right)$.

We denote G as one of the top hit SNPs from a GWAS analysis without PS correction (0, 1, 2 genotypes), D denotes disease status (0,1 affected vs. unaffected), and X denotes a vector of statistically significant PC axes based on the TW statistic. We define the principal component and propensity score (PCAPS) to be the likelihood of an individual having a particular genotype based on that individual’s covariate makeup. This can be stated explicitly as PCAPS_i(g_i, x_i) = P(G_i| x_i), where PCAPS_i(g_i, x_i) is the genomic propensity score for individual i calculated from that individual’s x_i, which represents that individual’s vector of statistically significant PCs based on TW statistic, and where G_i is that individual’s test-locus genotype. For example, for an additive disease risk allele a and reference allele A, G = 2 may represent the high-risk genotype aa, G = 1 may represent the heterozygote risk genotype Aa, and G = 0 may represent the homozygote reference genotype AA. In the current situation, the proportional odds model can be used to model the cumulative probabilities P(G=0|X) and P(G=0|X) + P(G=1|X) jointly as follows:

$$\log \left[\text{P}\left(\text{G=0|X}\right)/\left(1-\text{P}\left(\text{G=0|X}\right)\right)\right]={\mathrm{\alpha }}_1+{{\mathrm{\beta }}_1}^{\text{t}}\text{X}$$

$$\text{log }\left[\left(\text{P}\left(\text{G}=0|\text{X}\right)+\text{P}\left(\text{G}=1|\text{X}\right)\right)/\text{P}\left(\text{G}=2|\text{X}\right)\right]={\mathrm{\alpha }}_2+{{\mathrm{\beta }}_1}^{\text{t}}\text{X}$$

where α₁ and α₂ are intercepts and β₁ is a vector of coefficients. Since $\text{P}\left(\text{G}=0|\text{X}\right)+\text{P}\left(\text{G}=1|\text{X}\right)+\text{P}\left(\text{G}=2|\text{X}\right)=1$, then we have,

$$\text{P}\left(\text{G}=0|\text{X}\right)=\exp ({\mathrm{\alpha }}_1+{{\mathrm{\beta }}_1}^{\text{t}}\text{X})/[1+\exp ({\mathrm{\alpha }}_1+{{\mathrm{\beta }}_1}^{\text{t}}\text{X})]$$

$$\text{P}\left(\text{G}=2|\text{X}\right)=1/[1+\exp ({\mathrm{\alpha }}_2+{{\mathrm{\beta }}_1}^{\text{t}}\text{X})]$$

$$\text{P}\left(\text{G}=1|\text{X}\right)=1–\text{ P}\left(\text{G}=0|\text{X}\right)–\text{P}\left(\text{G}=2|\text{X}\right)$$

In the subsequent text, we suppress the index i corresponding to the i^th individual. Assuming strong ignorability (Rosenbaum and Rubin), we can assume that given PCAPS (g, x), X and G are conditionally independent, thus

$$\text{P}\left(X,G|PCAPS\left(g,x\right)\right)=\text{P}\left(X|PCAPS\left(g,x\right)\right)\text{P}\left(G|PCAPS\left(g,x\right)\right)$$

which balances measured PCs based on TW statistic across genotypes.

We define a general class of models that specify the potential relationship among disease D, test-locus genotype G, and genetic covariates X as f (E(D | G, X)) = η, where f (.) is a link function, such as the logit function, that determines the relationship among D, G and X; E (D | G, X) denotes the conditional mean of D given G and X; and η is a function of covariates, usually a linear function such that

$$\mathrm{\text{η}}=\alpha +\beta \text{G }+{\text{ γ}}_{1}PCAPS\left(\text{G}=1|\text{X}\right)+{\text{γ}}_{2}PCAPS\left(\text{G}=2|\text{X}\right)$$

where α and β are log odds ratios and γ₁ and γ₂ are nuisance parameters. We fit the disease prevalence model assuming a logit link to estimate the effect of risk genotype(s) β as

$$\text{logit}\left(\text{D}|\text{G},PCAPS\left(\text{G, X}\right)\right)=\alpha +\beta G+{\text{ γ}}_{1}PCAPS\left(\text{G}=1|\text{X}\right)+{\text{ γ}}_{2}PCAPS\left(\text{G}=2|\text{X}\right)$$

The PCAPS Procedure

Using GWAS data, EIGENSOFT (http://www.hsph.harvard.edu/alkes-price/software/) (Price et al. 2006; Patterson et al.) was used to identify a number of statistically significant PC axes based on the TW method (Johnstone) described in Patterson et al. (2006). PLINK (http://pngu.mgh.harvard.edu/~purcell/plink) (Purcell et al. 2007) was then used to obtain uncorrected SNP effect estimates based on various association models. For all SNPs without PS correction, PCAPS scores were calculated for each SNP using the previously identified number of significant PCs by TW test. The resulting PCAPS scores were then used as covariates in subsequent association analyses to identify potential disease associated SNPs (i.e., SNPs remaining significant after correction by PCAPS scores).

Simulation Study

We used GWAsimulator (http://biostat.mc.vanderbilt.edu/GWAsimulator) (Li and Li 2008) to simulate GWAS data. GWAsimulator simulates whole genome case-control samples according to user-specified multi-locus disease models. GWAsimulator can use HapMap phased genotype data as input, and the simulated data have similar linkage disequilibrium (LD) patterns as the HapMap data.

We used HapMap 3 genotypes data to generate two populations (http://hapmap.ncbi.nlm.nih.gov/downloads/genotypes/2010–05_phaseIII/). HapMap 3 data include 165 samples from the CEU (Utah residents with Northern and Western European ancestry from the CEPH collection) dataset and 203 from the YRI (Yoruba in Ibadan, Nigeria) dataset. Of 165 CEU samples, 112 founders were used as input phased data for simulating population 1 by GWAsimulator. Of 203 YRI samples, 147 founders were used as input phased data for simulating population 2.

The simulation study involved the following steps. First, two populations were generated using HapMap 3 data as phased input data. The first population used Caucasian (CEU) data, and the second population used Yoruba (YRI) data as described above. To reduce the computing time, 9 chromosomes (1, 2, 3, 6, 7, 8, 17, 18, and 19) were arbitrarily selected without loss of generality. For each chromosome, one disease locus was specified with a single SNP with OR 2, 1.5, 1, 1.5, 1, 2, 2, 1, and 1.5 for the 9 chromosomes, respectively. A population of 1000 cases and 1000 controls was simulated. After generation of the two populations separately, the populations were combined to induce population stratification by varying the case:control ratio 400:600, 450:550, 500:500, 550:450 and 600:400 within each subpopulation. Common SNPs from both subpopulations were kept in the combined sample dataset. SNPs with minor allele frequency (MAF) < 0.05 were excluded. Three study samples were created to reflect different levels of population structure (Table S1).

For each sample dataset (Table S1), GWAS association analyses were conducted using PLINK. To address multiple testing issues in GWAS under a model with no PS, only SNPs with Benjamini and Hochberg false positive rate less than 0.05 were selected. The top 9 SNPs without PS correction were identified along with the pre-defined 9 SNPs. The LD pattern between the 9 SNPs and top hit SNPs were examined using pairwise r². The combined top 9 hits and/or pre-defined 9 SNPs were identified for further association analyses. For each sample dataset, we then analyzed the genetic effect for each SNP identified above by obtaining p-values with 1) No adjustment; 2) PCA adjustment; 3) EMMAX; and 4) PCAPS adjustment (Table S2). The latest release of EMMAX can be downloaded at EMMAX Download Page (http://csg.sph.umich.edu//kang/emmax/download/index.html). The performance of the four methods were evaluated by true (false) positive (negative) rates based on identified disease SNPs vs. true disease SNPs (Table 1). We further analyzed all SNPs for the GWAS sample dataset under moderate PS (Figure 2 and Table 2). For the PCA adjustment used to compare against PCAPS, the first 10 PCs were used. We added the simulation results when all statistically significant PCs (based on the TW statistic) were adjusted (PCA-TW) and the first 10 PCs were used to calculate PCAPS (PCAPS-10) (Tables S3). Finally, we compared estimated ORs with the pre-defined “true” ORs using no adjustment, PCA and PCAPS adjustment methods (Tables 3 and S4).

Table 1.

Performance of no adjustment, PCA, EMMAX and PCAPS evaluated using the nine most significantly associated peak SNPs in GWAS simulation under each scenario

PS	Method	Nine Peak SNPs*				False Positive	False Negative	Positive Predict	Accuracy
		TP	FP	FN	TN	Rate (95%CI)	Rate (95% CI)	Value (95%CI)	Rate (95%CI)
						FP / (FP+TN)	FN / (TP+FN)	TP / (TP+FP)	(TP+TN) / (TP+FP+FN+TN)
No
	No Adjustment	7	2	0	0	100% (16 – 100%)	0% (0 – 41%)	78% (40 – 97%)	78% (40 – 97%)
	PCA	7	2	0	0	100% (16 – 100%)	0% (0 – 41%)	78% (40 – 97%)	78% (40 – 97%)
	EMMAX	7	2	0	0	100% (16 – 100%)	0% (0 – 41%)	78% (40 – 97%)	78% (40 – 97%)
	PCAPS	7	0	0	2	0% (0 – 84%)	0% (0 – 41%)	100% (59 – 100%)	100% (66 – 100%)
Moderate
	No Adjustment	7	2	0	0	100% (16 – 100%)	0% (0 – 41%)	78% (40 – 97%)	78% (40 – 97%)
	PCA	6	1	1	1	50% (1 – 99%)	14% (1 – 58%)	84% (42 – 100%)	78% (40 – 97%)
	EMMAX	7	1	0	1	50% (1 – 99%)	0% (0 – 41%)	88% (47 – 100%)	89% (52 – 100%)
	PCAPS	6	0	1	2	0% (0 – 84%)	14% (1 – 58%)	100% (54 – 100%)	89% (52 – 100%)
Severe
	No Adjustment	3	6	0	0	100% (54 – 100%)	0% (0 – 71%)	33% (7 – 70%)	33% (7 – 70%)
	PCA	2	1	1	5	17% (1 – 64%)	33% (1 – 91%)	67% (9 – 99%)	78% (40 – 97%)
	EMMAX	2	1	1	5	17% (1 – 64%)	33% (1 – 91%)	67% (9 – 99%)	78% (40 – 97%)
	PCAPS	2	0	1	6	0% (0 – 46%)	33% (1 – 91%)	100% (16 – 100%)	89% (52 – 100%)
Overall
	No Adjustment	17	10	0	0	100% (69 – 100%)	0% (0 – 20%)	63% (42 – 81%)	63% (42 – 81%)
	PCA	15	4	2	6	40% (12 – 74%)	12% (1 – 36%)	79% (54 – 94%)	78% (58 – 91%)
	EMMAX	16	4	1	6	40% (12 – 74%)	6% (1 – 29%)	80% (56 – 94%)	81% (62 – 94%)
	PCAPS	15	1	2	10	0% (0 – 31%)	12% (1 – 36%)	100% (78 – 100%)	93% (76 – 99%)

PCA, principal components analysis correcting for the first 10 principal components; EMMAX, efficient mixed-model association expedited; PCAPS, principal components and propensity score correcting for Tracy-Wisdom significant principal components; SNP, single nucleotide polymorphism; PS, population stratification; CI, confidence interval. The 95% confidence intervals were calculated using the Binomial distribution.

^*Positive disease SNP is the pre-defined SNP with odds ratio 1.5 or 2, or linkage disequilibrium (r² ≥ 0.3) with pre-defined disease SNP. If p-value is less than 7.5X10⁻⁶ for a peak SNP using a given method, then the peak SNP is identified as disease SNP by that method. Otherwise, the peak SNP is identified as non-disease SNP. TP – true positive, i.e. identified disease SNP is disease SNP; FP – false positive, i.e. identified disease SNP is non-disease SNP; FN – false negative, i.e. identified non-disease SNP is disease SNP; TN – true negative, i.e. identified non-disease SNP is non-disease SNP.

Figure 2. Q-Q plot of GWAS simulation data under moderate population stratification.

X-axis: expected –log10 (p-value); Y-axis: observed −log10 (p-value). The genomic lambda values are 0.99984, 1.06462, 0.99787 and 0.98565 for PCA-10, PCA-TW, PCAPS-10 and PCAPS-TW, respectively.

Table 2.

Performance of no adjustment, PCA, EMMAX and PCAPS evaluated using the significantly associated SNPs from each method under moderate population stratification in GWAS simulation

Method	Number of SNPs*				False Positive	False Negative	Positive Predict	Accuracy
	TP	FP	FN	TN	Rate (95%CI)	Rate (95% CI)	Value (95%CI)	Rate (95%CI)
					FP / (FP+TN)	FN / (TP+FN)	TP / (TP+FP)	(TP+TN) / (TP+FP+FN+TN)
No Adjustment	9	1628	0	6	99.6% (99.2 – 99.9%)	0% (0 – 34%)	0.5% (0.3 – 1%)	0.9% (0.5 – 1.5%)
PCA-10	8	6	1	6	50% (21 – 79%)	11% (0.3 – 48%)	57% (29 – 82%)	67% (43 – 85%)
PCA-TW	8	4	1	6	40% (12 – 74%)	11% (0.3 – 48%)	67% (35 – 90%)	74% (49 – 91%)
EMMAX	9	7	0	6	54% (25 – 81%)	0% (0 – 34%)	56% (30 – 80%)	68% (45 – 86%)
PCAPS-10	8	6	1	6	50% (21 – 79%)	11% (0.3 – 48%)	57% (29 – 82%)	67% (43 – 85%)
PCAPS-TW	8	0	1	6	0% (0 – 46%)	11% (0.3 – 48%)	100% (63 – 100%)	93% (68 – 99.8%)

PCA-10, principal components analysis correcting for the first 10 principal components; PCA-TW, principal components analysis correcting for Tracy-Wisdom significant principal components; EMMAX, efficient mixed-model association expedited; PCAPS-10, principal components and propensity score correcting for the first 10 principal components; PCAPS-TW, principal components and propensity score correcting for Tracy-Wisdom significant principal components; SNP, single nucleotide polymorphism; CI, confidence interval. The 95% confidence intervals were calculated using the Binomial distribution.

^*Positive disease SNP is the pre-defined SNP with odds ratio 1.5 or 2, or linkage disequilibrium (r² ≥ 0.3) with pre-defined disease SNP. If p-value is less than 7.5X10⁻⁶ for a SNP using a given method, then the SNP is identified as disease SNP by that method. Otherwise, the SNP is identified as non-disease SNP. Negative disease SNP is defined as pre-defined SNP with odds ratio 1 or linkage disequilibrium (r² ≥ 0.3) with pre-defined non-disease SNP. TP – true positive, i.e. identified disease SNP is disease SNP; FP – false positive, i.e. identified disease SNP is non-disease SNP; FN – false negative, i.e. identified non-disease SNP is disease SNP; TN – true negative, i.e. identified non-disease SNP is non-disease SNP.

Table 3.

Comparison of estimated odds ratio (OR) for pre-defined disease SNPs under moderate population stratification in GWAS simulation

PS	Chr	rsID	True OR	Estimated Odds Ratio (95% CI)		Absolute % Change from True OR
				PCA	PCAPS	PCA	PCAPS	Less-biased Method
Moderate
	2	rs13027563	1.5	1.419 (1.244 – 1.619)	1.430 (1.246 – 1.641)	5.4%	4.7%	PCAPS
	6	rs214445	1.5	1.517 (1.338 – 1.719)	1.495 (1.311 – 1.704)	1.1%	0.3%	PCAPS
	19	rs919276	1.5	1.466 (1.239 – 1.736)	1.486 (1.239 – 1.783)	2.3%	0.9%	PCAPS
	1	rs1334997	2	2.070 (1.757 – 2.445)	1.965 (1.653 – 2.331)	3.5%	1.8%	PCAPS
	8	rs12680139	2	1.965 (1.689 – 2.283)	1.908 (1.634 – 2.227)	1.8%	4.6%	PCA
	17	rs2598435	2	2.119 (1.842 – 2.439)	2.066 (1.776 – 2.410)	6.0%	3.3%	PCAPS

PS, population stratification; Chr, chromosome; rsID, dbSNP rs number; OR, odds ratio; PCA, principal components analysis; PCAPS, principal components and propensity score.

TCGT Data

We used a genome-wide association study of 292 cases with testicular germ cell tumors (TGCT) and 919 controls (Kanetsky et al.). The strongest signal was observed on chromosome 12. Of the 11 top SNPs, six were on chromosome 12. These six SNPs were all from KITLG. We used the top six GWAS SNPs, and treated the corresponding gene KITLG as a candidate gene. We then calculated PCA scores using EIGENSOFT software (Price et al. 2006; Patterson et al.), and calculated TW statistics and their associated p-values for each PC axis (Patterson et al.). Only PCs with p ≤ 0.05 by the TW test were retained for subsequent analysis. We then estimated PCAPS for each individual using the PCs as predictors in a logistic model. We compared the results of the associations at KITLG with PCA using the top 10 PCs and PCAPS adjustment.

Results

Simulation Results

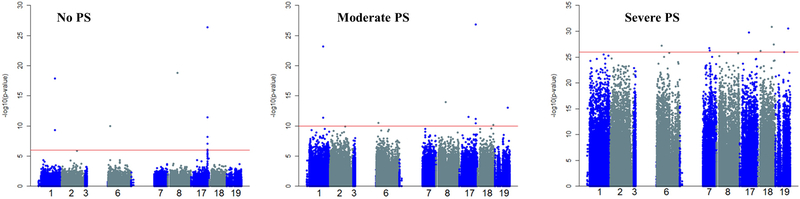
Figure 1 shows Manhattan plots under no, moderate, and severe PS. The top ranking nine SNPs (above red line) were identified under no, moderate, and severe PS. As expected, Figure 1 indicates that there were more significant associations than one would expect by chance under moderate or severe PS. Figure S1 shows Q-Q plots for the visualization of population stratification. Under no PS, p-values fit the expected distribution well. Under moderate PS, many markers have p-values that exhibit modest inflation. Finally, under severe PS, a large number of markers exhibit small p-values demonstrating severe inflation. Significant deviation from the line under moderate and severe PS in Figure S1 confirms that there were more significant associations than one would expect by chance.

Figure 1. Manhattan plot of GWAS simulation results by population stratification (PS).

X-axis: Chromosomes 1–3, 6–8, and 17–19; Y-axis: −log (p-value). Red line shows the threshold to identify top 9 SNPs in each sub-figure.

Tables S2 and S3 show the p-values for the nine most significantly associated SNPs under each scenario by PS status and different adjustment methods. Among the nine top-associated SNPS under no or moderate PS, seven are either a pre-defined disease SNP or in LD with a pre-defined disease SNP (true positive); the remaining two SNPs (true negative) are potential false positive findings. Under severe PS, only three pre-defined disease SNPs are among the nine top hits SNPs. The remaining six true negative SNPs are potential false positive SNPs for all three PS-correction methods. PCAPS consistently yielded larger p-values compared to PCA for almost all of these potential false positive SNPs. This suggests that some false positive findings might be correctly identified by PCAPS, but not by PCA. If a peak SNP is a disease SNP or in LD with a disease SNP, and its p-value is less than 7.5×10⁻⁶ (1/133750 total SNPs) using a specific method, then the peak SNP is correctly identified as disease SNP by that method. Similarly, if a peak SNP is neither a disease SNP nor in LD with a disease SNP, and if its p-value is greater than 7.5×10⁻⁶ using a specific method, then the peak SNP is correctly identified as non-disease SNP by that method. For example, rs2305347 and rs2250054 under no PS, rs8071679 under moderate PS, and rs880295 under severe PS were correctly identified as true negatives by PCAPS, but as false positives by PCA in Table S2. As expected, Tables S2 and S3 indicate that PCA-TW outperforms PCA-10 as more PCs are adjusted in the association models for PCA-TW.

Table 1 shows the performance of no adjustment, PCA, EMMAX and PCAPS methods by using the nine peak associated SNPs in GWAS simulation by PS status. Without adjustment, all non-disease SNPs were incorrectly identified as disease SNPs. Under no, moderate and severe PS, 100%, 50% and 17% non-disease SNPs, respectively, were incorrectly identified as disease SNPs by PCA. No non-disease SNPs were incorrectly identified as disease SNPs by PCAPS. As expected, the false negative rates tend to be inflated from no to moderate, and moderate to severe PS for both PCA and PCAPS. Regarding positive predictive value, 100% of PCAPS identified disease SNPs were true disease SNPs, while only 67% – 84% PCA identified disease SNPs were true disease SNPs. The accuracy rate is 78% by PCA, while PCAPS accuracies are in the range of 89% – 100%. PCAPS demonstrates advantages over PCA by consistently yielding overall low false positive rates (0% vs. 40%), high positive predictive values (100% vs. 79%) and high accuracy rates (93% vs. 78%) regardless of the level of PS. The performance of EMMAX is somewhat between the PCA and PCAPS.

Figure 2 shows Q-Q plots for the visualization of PCA and PCAPS under moderate population stratification. For PCA-TW, many markers have p-values that exhibit modest inflation. PCA-10 and PCAPS-10 p-values fit the expected distribution well. Figure 2 demonstrates that PCAPS-TW performs better than PCA-10 and PCAPS-10 with less significant associations than one would expect by chance. The performance of EMMAX was intermediate to the PCA and PCAPS results (data not shown).

Table 2 shows the performance of no adjustment, PCA, EMMAX and PCAPS methods by using all SNPs in GWAS simulation under moderate PS. Without adjustment, all non-disease SNPs were incorrectly identified as disease SNPs. Without adjustment, 99.6% non-disease SNPS were incorrectly identified as disease SNPs. With PCA-10, PCA-TW, EMMAX, and PCAPS-10 adjustment methods, approximately 40 – 50% non-disease SNPs were incorrectly identified as disease SNPs. No non-disease SNPs were incorrectly identified as disease SNPs by PCAPS-TW. The false negative rates were 0% for no adjustment and EMMAX, and approximately 10% for all other methods. Regarding positive predictive value, 100% of PCAPS identified disease SNPs were true disease SNPs, while only 57% – 67% PCA-10, PCA-TW, EMMAX or PCAPS-10 identified disease SNPs were true disease SNPs. The accuracy rate is 93% by PCAPS-TW, while PCA-10, PCA-TW, EMMAX and PCAPS-10 accuracies are in the range of 67% – 74%. PCAPS demonstrates advantages over PCA and EMMAX by consistently yielding overall low false positive rates (0% vs. >40%), high positive predictive values (100% vs. <67%) and high accuracy rates (93% vs. <74%). The performance of EMMAX is somewhat between the PCA and PCAPS.

Table 3 gives the comparison of estimated odds ratio for the six pre-defined SNPs between PCA and PCAPS under moderate PS in GWAS simulation. For all three pre-defined disease SNPs with OR=1.5 (rs1302756, rs214445, rs919276), PCAPS yielded consistently less-biased estimates. For two out of three pre-defined disease SNPs with OR=2 (rs1334997, rs12680139, rs2598435), PCAPS yielded less-biased estimates. Table S4 gives the comparison of estimated odds ratio for the six pre-defined SNPs between PCA-TW and PCAPS-TW under moderate PS in GWAS simulation. For two out of three pre-defined disease SNPs with OR=1.5 (rs1302756, rs214445, rs919276) or with OR=2 (rs1334997, rs12680139, rs2598435), PCAPS-TW yielded less-biased estimates. When comparing width of confidence interval for odds ratio between PCA-TW and PCAPS-TW, PCAPS-TW had consistently narrower CIs and thus yielded less-biased estimates (Table S4).

Results of TCGT Data Analysis

GWAS analysis results for TGCT data were published by Kanetsky et al. (2009). The estimated genomic control inflation factor was 1.013 indicating mild PS. We conducted association analysis between TGCT and the six markers from KITLG gene using PCA and PCAPS. Table 4 shows the risk allele frequency and per allele odds ratio of the association between TGCT and six selected SNP markers. All estimated ORs are similar for all six SNPs regardless of the method used. The similarity of results is due to the very low-level population stratification in this study population and very high LD correlations among these SNPs. Table 4 also shows 95% confidence intervals for the estimated OR under PCA and PCAPS adjustments. Our PCAPS method resulted in more precise confidence intervals compared to the PCA method, even under conditions of low PS. This gain in efficiency may be attributed to over-adjustment for PS in the PCA approach which included 10 PCs as opposed to only 2 additional covariates that were included in the PCAPS approach.

Table 4.

Summary of association between six selected SNP markers and testicular germ cell tumor

Gene	Marker	Nonrisk/risk	RAF		Per Allele OR (95% CI)		Width of CI
		Allele	Controls	Cases	PCA	PCAPS	PCA	PCAPS
KITLG	rs4474514	A/G	0.802	0.899	2.33 (1.68–3.24)	2.03 (1.48–2.79)	1.56	1.31
	rs3782181	T/G	0.798	0.894	2.21 (1.61–3.05)	1.95 (1.43–2.66)	1.44	1.23
	rs1472899	T/C	0.801	0.897	2.18 (1.58–3.00)	1.92 (1.41–2.62)	1.43	1.21
	rs3782179	A/G	0.802	0.896	2.22 (1.61–3.07)	1.95 (1.43–2.67)	1.46	1.24
	rs11104952	C/A	0.802	0.896	2.22 (1.60–3.05)	1.95 (1.43–2.65)	1.45	1.23

Marker, dbSNP rs number; RAF, risk allele frequency; OR, odds ratio; CI, confidence interval; PCA, principal components analysis; PCAPS, principal components and propensity score.

Discussion

Propensity scores are widely used to correct for confounding effects in general observational studies. Population stratification (PS) in GWAs occurs when cases and controls have different population genetic backgrounds, which is a special case of confounding. PCA has been used to correct for PS in population based genetic association studies. Here, we use a combined approach that uses propensity scores and PCA to improve on the correction for confounding. The PCAPS values are propensity scores, which are calculated using significant PCA values by TW test. Intuitively, using propensity scores to summarize PCA values rather than using the PCAs themselves has the advantage of summarizing and capturing the variability across PCAs and capitalizes on the propensity score’s balancing properties. PCAPS efficiently extends our previously developed GPS approach (Zhao et al. 2009; Zhao et al. 2012) to GWAS data to correct for bias due to population stratification. Unlike PCA, PCAPS values are calculated for each specific SNP and for each individual using TW significant PCs. Hence, this method is able to correct for PS bias and downweight the influence of outliers at both the SNP and individual levels. In contrast, PCA values are calculated based on the profile of all SNPs for a given individual and the same values are adjusted for each SNP using an arbitrarily selected identical set of 10 PCs. It may appear that using PCs to construct the stratification score is equivalent to including PCs as covariates in a model as is done in Eigenstrat (Epstein et al. 2007). However, this is not the case, as the variance estimators are different. Extensive experience with propensity scores for prospective data (Lunceford and Davidian 2004), as well as simulations performed by Epstein et al. (2007) attest to the validity of the stratification variance estimators (Allen et al. 2010). In contrast, McPeek and Abney (2008) have shown a variety of situations in which Eigenstrat gives inflated type I error or has diminished power.

Ray and Basu (2017) proposed POM-PS approach based on Allen et al. stratification score, which estimates the probability of case status (disease) conditional on covariates whereas we estimate the probability of the exposure (genetic variant) conditional on covariates. The POM-PS would result in a reduction of power if this score is used for adjustment in the disease model since the score itself is based on disease. Our PCAPs approach, on the other hand, is not estimated based on disease status and thus intuitively should have more power to detect the exposure-disease association. We show in our simulations that PCAPS tends to reduce the number of false-positive findings after removing bias due to confounding even though this may reduce the power to detect a true association under certain conditions. However, consistent with the goal of GWAS to maximize true positive associations, it is preferable to avoid false-positive associations, which may lead to unnecessary follow-up or expensive validation studies.

Price et al. (2010) reviewed methods that correct for stratification while accounting for population structure as well as data that contain family structure or cryptic relatedness. A limitation of PCAPS is that it may not be able to directly account for family structure or cryptic relatedness (Voight and Pritchard 2005; Weir et al. 2006). A possible solution is to calculate principal components using SNP loadings (Patterson et al.), which measure the correlation of each SNP to a given PC in PCA. Further studies are warranted to explore how PCAPS might be able to correct for family structure and cryptic relatedness by using SNP loadings from a set of unrelated samples, either by using a different set of samples from those in the disease study or by using an unrelated subset of samples from the disease study (Zhu et al. 2008). Another approach to the study of admixed populations in family data is to calculate PCAPS based on PCs that take into account the family structure (de Andrade et al. 2015). Zhang and Pan (2015) proposed a hybrid approach that combines the advantages of PCA and LMM. The hybrid approach combines the advantages of PCA and LMM by separating out the genetic confounders and environmental confounders. Currently, the PCAPS is only proposed to capture the genetic confounders. However, PCAPS can be readily extended to the hybrid approach by using the top q PCs and random effect to calculate PCAPS. If there are known environmental confounders, these confounders can be used directly to define and calculate PCAPS.

For choosing the PCs, Li et al. (2009) proposed a PC-Finder procedure using a distance-based regression model to identify a minimal set of PCs while permitting an effective correction for PS. This procedure could be useful for removing PCs that do not appear to have “a significant effect” in reducing the level of PS. This is important when selected PCs are directly adjusted for to correct for PS, such as in the PCA approach. However, when applying PCAPS, only the propensity score is directly adjusted for to correct for PS which is calculated using many PCs. Including a few less influential PCs in the calculation of the propensity score is of less concern and has less impact (Drake 1993).

There are several advantages to using PCAPS over PCA in adjusting for population stratification. The direct consequence of using PCAPS is dramatically reduced data dimensionality. PCAPS offers distinct advantages because it can control for numerous PCs and environmental confounders simultaneously by reducing to a single scalar variable; this greatly simplifies model building and estimation. Furthermore, it has been shown that adjusting for the estimated propensity score is better at removing bias than adjusting for the true propensity score (Cepeda et al. 2003). This is because adjusting for the estimated propensity score can remove both systematic and chance imbalances, while adjusting for the true propensity score removes only systematic imbalances. In addition, it has been shown that misspecification of an outcome model is more serious that misspecification of a propensity score model; hence, the PCAPs approach is more robust to model misspecification (Drake). Finally, it may seem at first glance that using PCs to construct the propensity scores is equivalent to including PCs as covariates in a model such as PCA. However, this is not the case, as the estimated PCAPS values are different for different loci, whereas PCA values are always the same at each locus. This provides a unique opportunity for using PCAPS for SNP-specific correction of population stratification in GWAS studies. One advantage of our approach is that “nuisance axes” values can actually be incorporated into the estimation of the SNP-specific PCAPS to capture any additional variation even if it is small since the goal of the propensity score estimation is not inference but to obtain the best probability estimates. This distinguishes PCAPS from the limitations of using PCA alone. Regarding outliers, the propensity scores are bounded between 0 and 1; hence, PCAPs will down weight the effect of outlier SNPs unlike PCAs which are not bounded.

Our proposed PCAPS method provides an innovative and practical way of correcting population stratification in GWAS. For full GWAS data, all SNPs with p-value less than the genome-wide threshold of 5e-8 could be used to define PCAPS. If this number is still very large, then only most biologically relevant-SNPs may be considered to define PCAPS. For each selected SNP (or all SNPs), all PCs that have significantly large genetic variation according to the TW test should be used to calculate SNP-specific PCAPS. The SNP-specific PCAPS is then added in the association model for adjustment. Our simulation studies demonstrate that PCAPS outperforms PCA and EMMAX when used to correct for bias due to population stratification in GWAS. We show that PCAPS is able to correctly identify additional false positives (i.e. true negatives) compared with PCA and EMMAX regardless of the level of PS in the study population. PCAPS also consistently yields narrower confidence intervals of OR than PCA as shown in simulations and our TGCT analysis. The advantages of our approach are the uniform selection of PCAPS scores, the ability to automatically account for the effect of outliers, and its easy implementation in standard statistical packages such as SAS, R or Stata. Since we define a general class of models that specify the potential relation among disease, genotype, and genetic covariates as f(E(D|G, X)) = ƞ, where f(.) is a link function, the PCAPS approach is readily generalizable to other traits, such as continuous traits by using a generalized linear model approach. In fact, for binary traits (or other non-collapsible models such as Cox proportional hazards mode) it is recommended that the PCAPs be included as an inverse-probability weight rather than a covariate adjustment. For continuous traits or collapsible models, PCAPS adjustment in the model is fine Wan and Mitra 2016). Further studies are needed to compare the PCAPS and other methods for a continuous trait and to assess the performance of PCAPS in adjusting for PS bias in next-generation sequencing studies.