RF-induced heating in tissue near bilateral DBS implants during MRI at 1.5 T and 3T: The role of surgical lead management

Abstract

Access to MRI is limited for patients with deep brain stimulation (DBS) implants due to safety hazards, including radiofrequency (RF) heating of tissue surrounding the leads. Computational models provide an exquisite tool to explore the multi-variate problem of RF heating and help better understand the interaction of electromagnetic fields and biological tissues. This paper presents a computational approach to assess RF-induced heating, in terms of specific absorption rate (SAR) in the tissue, around the tip of bilateral DBS leads during MRI at 64MHz/1.5 T and 127MHz/3T. Patient-specific realistic lead models were constructed from post-operative CT images of nine patients operated for subthalamic nucleus DBS. Finite element method was applied to calculate the SAR at the tip of left and right DBS contact electrodes. Both transmit head coils and transmit body coils were analyzed. We found a substantial difference between the SAR and temperature rise at the tip of right and left DBS leads, with the lead contralateral to the implanted pulse generator (IPG) exhibiting up to 7 times higher SAR in simulations, and up to 10 times higher temperature rise during measurements. The orientation of incident electric field with respect to lead trajectories was explored and a metric to predict local SAR amplification was introduced. Modification of the lead trajectory was shown to substantially reduce the heating in phantom experiments using both conductive wires and commercially available DBS leads. Finally, the surgical feasibility of implementing the modified trajectories was demonstrated in a patient operated for bilateral DBS.

I). Introduction

Deep brain stimulation (DBS) of the thalamus or basal ganglia represents an effective technique to treat several major debilitating movement disorders including Parkinson’s disease, essential tremor, and dystonia [1–9]. While decades have passed since the inception of DBS and its clinical utility has grown exponentially, its underlying therapeutic mechanisms of action remain controversial. Uncertainties remain about which circuits are affected, which exact fiber bundles need to be targeted, and the most efficient stimulation protocol [10, 11]. The meticulous use of neuroimaging, both for target verification and for post-operative monitoring of treatment-induced changes in the functional connectivity of affected brain networks is essential to interpret clinical outcomes, test new hypotheses, and design enhanced therapeutic protocols. Due to its superb soft tissue contrast and high-resolution visualization of the brain anatomy, magnetic resonance imaging (MRI) is excellently poised as a non-invasive imaging tool to address open questions regarding DBS targeting and mechanism. Unfortunately, the interaction between the MRI scanners and implanted DBS devices can result in restricting safety hazards that limit the accessibility of MRI for this patient population [12].

Since first reports of harmful interaction between MRI environment and implantable electronic devices in 1989 [13] significant improvement has been made in design and manufacturing of medical implants. Such improvements include for example, reduction of ferromagnetic material to reduce the risk of device dislodgement due to static magnetic fields [14], and enhanced programming to reduce the risk of device malfunction due to MRI gradient effects [15]. The major restriction of present MRI technology for DBS imaging is the interaction of radiofrequency (RF) fields and implanted electrodes. The coupling of RF fields with long conductive leads induces electric currents on lead wires, which increase energy absorption in the tissue surrounding the lead electrodes. Such high energy may in turn generate excessive temperature rise and possible tissue damage [16, 17]. To limit such risks, the conditions under which patients with DBS are indicated for MRI are restrictive. For example, only static magnetic field of 1.5 T is recommended, and applied pulse sequences need to have limited RF power (in terms of either reduced SAR or B₁ rms). Such limitations exclude for example, patients in centers that have only 3T MRI systems and current state-of-the-art MRI multi-transmit technology is absolutely contraindicated as well [18]. Although recent developments in introducing patient-adjustable MRI technology [19, 20] and parallel transmit techniques [21–23] have shown promising results for DBS imaging, such advancements are still far from clinical application. Practical and easy-to-implement lead management strategies that mitigate the risk of RF heating are thus, highly desirable.

RF heating is a complex phenomenon with several interplaying factors including the anatomy of the patient, imaging landmark, frequency, geometry, and type of the RF transmitter, as well as the topology of the implant [24–27]. Phantom experiments have established that the lead trajectory has a substantial effect on the SAR in the tissue [28–30], yet almost nothing is known about the variation of RF heating as a function of lead implantation path in real patient populations. In this study, a computational approach is applied to assess the SAR in the tissue around the tip of DBS leads in patient-specific computational models. CT-data from 9 patients were used to generate computational models of realistic lead trajectories and RF heating was studied using finite-element simulations. Results were used to optimize the routing of DBS leads to reduce the heating.

In what follows, the conventional DBS implantation procedure and typical features of ipsilateral and contralateral leads are discussed; details of finite element modeling and SAR calculation at the tip of realistic lead trajectories inside an RF head coil and an RF body coil at two frequencies and different feed positions are presented; a new metric to predict the SAR from relative orientation of the lead with respect to the incident electric field is introduced; results of phantom experiments with implanted wires and commercially available leads are presented; modified implantation paths that reduce the risk of RF heating are examined, and finally, surgical feasibility of implementing MRI-friendly DBS trajectories is demonstrated. The paper concludes with a discussion of safety considerations and a brief description of future work to devise surgical DBS guidelines that reduce the risk of post-operative MRI examinations.

SAR in contralateral vs. ipsilateral DBS leads: patient-derived simulations at 1.5 T and 3 T

When it comes to the RF safety of elongated implants, the position and configuration of the lead are shown to have a substantial effect on the SAR distribution [24–27]. Commercial DBS leads come with a prefixed length which is usually longer than needed. In conventional DBS surgery, surgeons tend to keep the extra portion of lead extension at the level of cranium to avoid positioning against the soft tissue in the neck. As a result, leads are looped several times in a random pattern, leading to a substantial patient-to-patient variation in their routing (see Figure1). In most cases where bilateral leads are implanted, a two-channel implanted pulse generator (IPG) is positioned unilaterally in the chest to stimulate both leads. In such cases, ipsilateral and contralateral leads follow different geometrical paths. Figure 1 shows postoperative CT images of nine patients with bilateral leads. As shown, contralateral leads which exit the surgical burr-hole at a further point from the IPG are first tunneled to the IPG side along a medio-lateral straight path. The ipsilateral leads in contrast, are first looped right at the burr-hole (complete or half-loop) before being routed toward the neck. Antenna theory indicates that the source of induced currents along conductive leads is the tangential – rather than perpendicular - component of the incident electric field along the lead trajectory (E_tan) [27, 31]. Specifically, the integral of E_tan along the lead generates a virtual distributed voltage source across the entire lead length, inducing RF currents on the wires that in turn give rise to scattered electric fields in the tissue at the vicinity of the exposed tip. These scattered secondary fields are responsible for amplifying the energy absorption in the tissue; if the energy increase is not counterbalanced by the tissue thermoregulatory system, temperature increase, and possible thermal damage can occur. Because ipsilateral and contralateral leads have different orientations with respect to the incident electric field E_tan, we hypothesize that the SAR at the tip of these lead groups will be significantly different. Specifically, we hypothesize that contralateral leads exhibit a higher SAR due to the strong coupling of the initial extracranial segment of the lead with the incident electric field. Section II outlines the details of numerical modeling and results of SAR amplification around tips of ipsilateral and contralateral DBS leads in nine patient-specific models. Analysis was performed at both 64MHz/1.5T and 127 MHz/3T and with both transmit head coils and body coils. Section III describes phantom experiments with wire implants as well as Medtronic lead models 3389 and 3387 and demonstrates modified lead trajectories that substantially reduce the heating at the tip. Finally, section IV describes an example of the clinical application of modifying lead trajectory as suggested by simulation results. It is important to note however, that the present study is limited to the assessment of DBS leads in isolation, i.e., prior to their attachment to the lead extensions and/or the IPG. Further investigation is required to establish whether the data presented here applies to the fully implanted systems.

Figure 1:

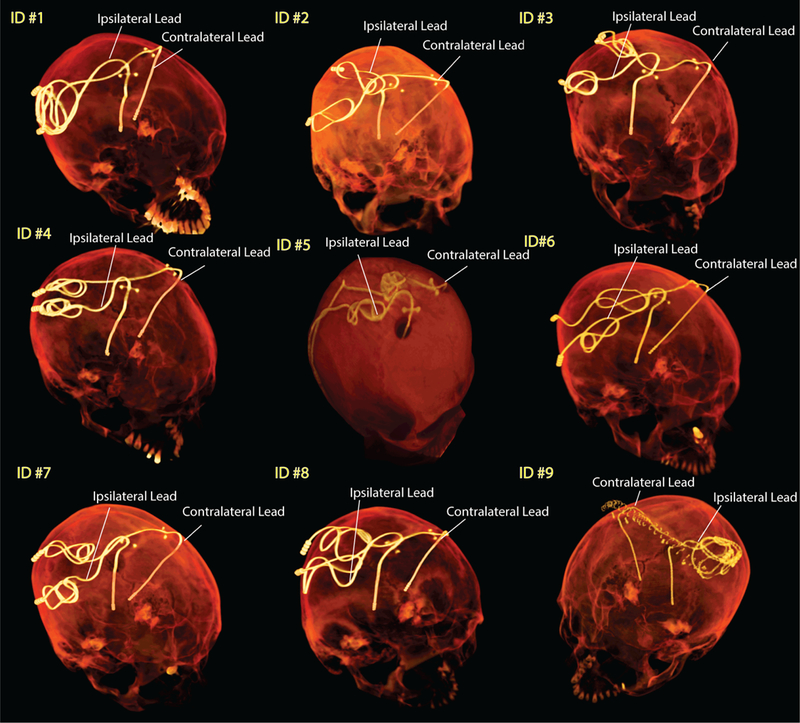
Post-operative CT images of patients with bilateral DBS leads. The ipsilateral and contralateral labels are with respect to the system IPG.

II). Numerical Modeling

Realistic lead models

Intraoperative CT images of nine patients who had undergone bilateral DBS implantation at Massachusetts General Hospital and Albany Medical Center were used for modeling (Figure 1). CT images of patients 1–4 and 6–8 had 0.4 mm×0.4 mm×0.6 mm voxel resolution whereas those of patients 5 and 9 had 0.6 mm×0.6 mm×1.2 mm voxel resolution. Amira 5.3 (Thermo Fisher Scientific, Waltham MA) was used for image segmentation and construction of the preliminary 3D surface of the leads. First, a thresholding mask was applied to select the hyper dense DBS lead from CT images using Amira’s segmentation module (Figure 2B). Threshold values were selected manually on a case-by-case basis such that the resulting mask covered the center of the artifact but not the surrounding tissue such as bone. Labels were smoothed with a Gaussian filter (3×3 pixel size) and the resulting mask was used to generate preliminary 3D surfaces of the lead trajectories (Figure 2C). 3D lead surfaces were exported to a CAD tool (Rhino3D^®, Robert McNeal and Associates, Seattle, WA) in which lead trajectory lines were manually reconstructed. Adjustments were made as necessary to ensure there is more than 1.27 mm gap between overlapping segments, so that reconstructed lead do not intersect itself after addition of the insulation layer (Figure 2D). The reconstructed trajectory lines were exported to ANSYS HFSS where models of electrode contacts, core, and insulation were constructed around them (Figure 2F). A total of 18 leads were modelled. Models were composed of four cylindrical contacts (outer diameter = 1.27 mm, wall thickness = 150 µm), connected through a solid straight central core (diameter = 260 µm) and embedded in polyurethane insulation (diameter = 1.27 mm, σ = 10⁻¹⁰s/m, ε_r = 3.5 [32]). Electrode contacts were made of 90%:10% platinum-iridium (Pt:Ir, σ = 4 × 10⁶ S/m) positioned 0.5- mm apart [33]. The reconstructed lead models were incorporated either into a homogeneous version of the anatomically-precise head model “MIDA” [34] (for simulations with transmit head coil) or a homogeneous head and torso model (for simulations with a transmit body coil). Anatomical models were assigned electrical properties equal to the average brain tissue (σ = 0.49 S/m, ε_r = 66[35, 36]). A triangulated surface of the patient’s head was generated from CT images and used for rigid alignment of the lead inside the body.

Figure 2:

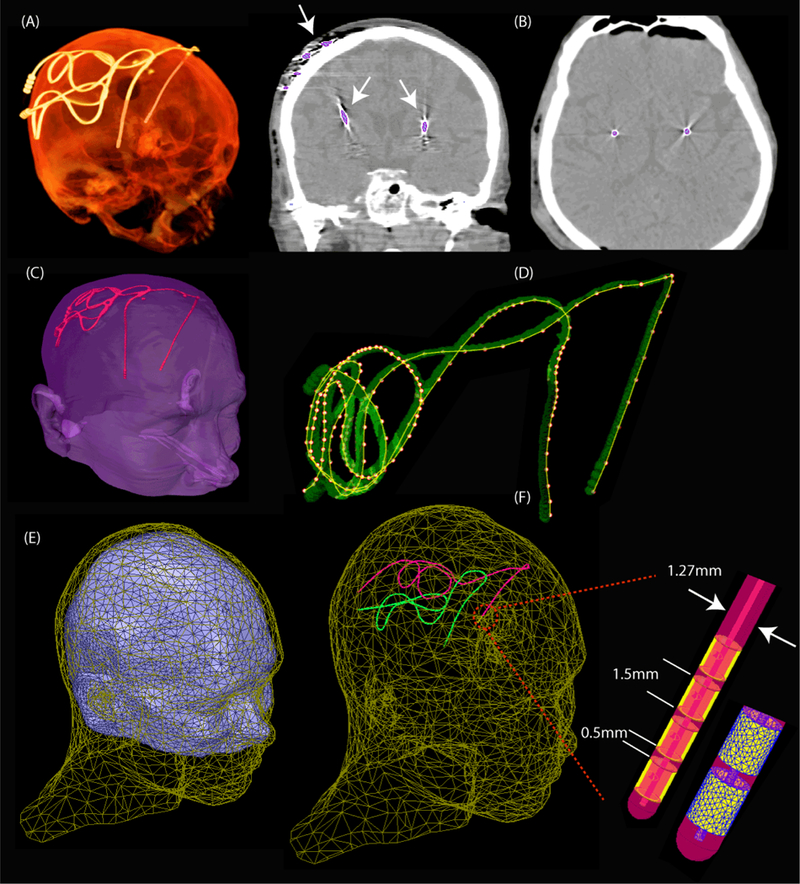
Steps of image segmentation and lead model construction. (A) 3D view of the CT image of a patient (B) Threshold mask covering the center of hyper dense lead artifact (C) Preliminary 3D surfaces of patient’s head and lad trajectories constructed in Amira. (D) Lead trajectories reconstructed in Rhino3D. Adjustments were made to assure there was at lead 1.27 mm gap between overlapping segments. (E) Patient’s head aligned with the homogeneous MIDA model. (F) Details of lead structure and mesh in HFSS.

MRI RF coil models and electromagnetic simulations

Electromagnetic simulations were implemented in ANSYS Electronics Desktop (HFSS 16.2, Designer, ANSYS Inc., Canonsburg, PA). Numerical models of two high-pass birdcage body coils (620mm length, 607mm diameter) and two low-pass transmit head-only coils (292mm length, 356mm diameter) were implemented and tuned to their respective Larmor frequencies - 64 MHz (1.5 T proton imaging) and 127 MHz (3 T). A quadrature excitation was implemented by feeding the coils at two ports on the bottom end-ring that were 90° apart in position and phase (Figure 3A).

Figure 3:

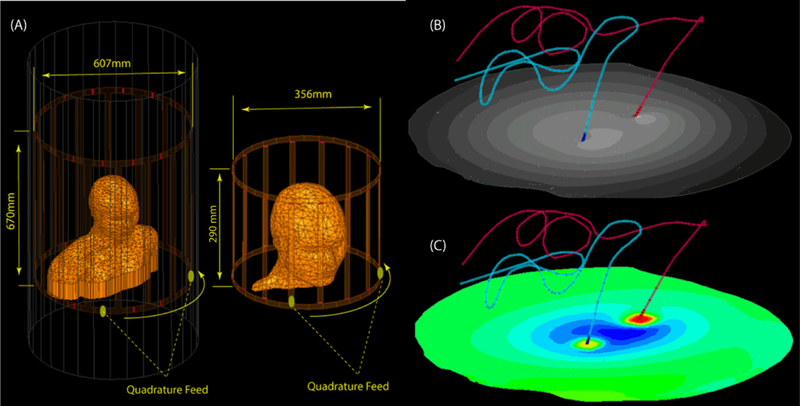
(A) position of paitent body in head and body coils. (B) the B₁+ and (C) 1gSAR calculated on an axial plane passing through electrode contacts.

The effect of the phase distribution of the transmit field on the RF heating of conductive wires has been established in earlier studies [37]. Recently, it was demonstrated that the position of the feed of quadrature birdcage coils with respect to the body has a non-negligible effect on the heating of elongated implants [38]. Therefore, for each patient model coils were rotated around the head with 45º increments to account for the variability of incident electric field orientation with respect to the leads.

A total of 288 simulations were performed (nine patient models × four RF transmit coils × eight different feed positions). For each simulation, the input power of the coil was adjusted to produce a spatial mean of B₁⁺=2µT on a transverse plane passing through the center of the coil (Figure 3B). This is in line with the current DBS MRI guideline which states the maximum B₁⁺rms should not exceed 2µT for safe use of the device at 1.5 T [18]. Hence, reporting the associated local SAR values for this RF level are relevant. 1g-averaged SAR was calculated according to IEEE STD P1528.4 recommendation [39], using the built-in SAR calculation module in ANSYS HFSS. The maximum of 1g-averaged SAR in a 2cm×2cm×2cm cubic area around the tip of each lead was calculated and reported as MaxSAR1g (Figure 3C).

Numerical convergence

At the start of each simulation, ANSYS HFSS was set to follow an adaptive mesh scheme. The algorithm started with a user-controlled initial tetrahedral mesh which forced a fine resolution on the DBS lead (maximum tetrahedron edge < 0.5 mm). The adaptive algorithm then refined the mesh by 30% between each two iterative simulations. At each step, the maximum change in the magnitude of S-parameters, ΔS, was defined as ΔS=Max_ij|S_Nij-S_N-1ij|, where i and j cover all matrix entries and N represents the iteration number. The adaptive simulation continued until the threshold of ΔS<0.01 was reached. All simulations converged after N=4 adaptive passes. Details of mesh statistics for a typical simulation are given in Table 1.

Table 1:

Mesh statistics for a typical simulation. The total number of tetrahedral element including the coil and the region surrounding the model was 2006158.

	Mesh elements	Min edge length	Max edge length
Left lead core	50052	0.008mm	0.5mm
Right lead core	49150	0.008mm	0.5mm
Left lead insulation	140149	0.005mm	2.5mm
Right lead insulation	136927	0.02mm	2.5mm
Body	783910	0.06mm	12mm

The incident electric field

To better understand how the orientation of the incident electric field with respect to lead trajectory affects SAR at the tip, we calculated the incident E_tan along the length of lead trajectories. To do this, simulations were performed without lead being present for both head coils and body coils and at both 64 MHz and 127 MHz. Polylines representing lead trajectories were imported to HFSS, and their unit tangent vectors were extracted using HFSS Field Calculator module. E_tan(t) at each point along the length of the lead was calculated as:

$$E_{tan}\left(t\right)=\overrightarrow{E}\left(t\right)\cdot \widehat{a}$$ [1]

Here $\overrightarrow{E}$ is the incident electric field and $\widehat{a}$ is a unit vector tangential to the lead path. Figure 4A shows all 18 lead trajectories superimposed in the head model with blue lines representing ipsilateral leads and red lines representing contralateral leads. Green arrows in Figure 4B show the incident electric field $\overrightarrow{E}$ at a certain time point along ipsilateral and contralateral leads of a representative patient (Patient 2). Figure 4B also shows the calculated E_tan(t) along the length of the leads overlaid as a color field on top of lead trajectories for a specific time point. As it can be observed, E_tan has a distinct value at any point along the length of the lead. Also note that the magnitude of E_tan as calculated in [1] is a function of time as the orientation of the electric field changes as the field rotates. The evolution of the E_tan(t) along the length of ipsilateral and contralateral leads of Figure 4 at five different time points through the cycle are given in the Supplementary Figure S1.

Figure 4:

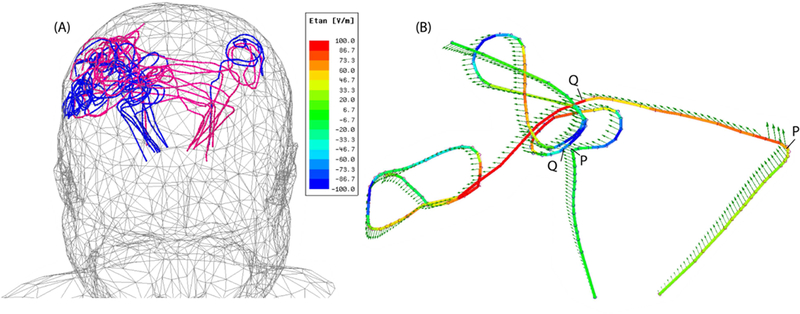
(A) Trajectories of ipsilateral and contralateral leads superimposed in one head model. (B) Incident electric field (green arrows) and E_tan (color field) along the trajectory of ipsilateral and contralateral leads in Patient 2. Points P and Q show the limits of the initial segment over which the induced voltage V_8cm in equation [2] was calculated. The evolution of E_tan at different time points through the cycle is given in Supplementary Figure S1.

To have a metric that allows comparison of different trajectories, we calculated the peak-to-peak value of the induced voltage along the first 8 cm of the extracranial portion of each lead as:

$$V_{8cm}pp={\displaystyle {\int }_P^Q{E}_{tan}}\left(t\right)dl{|}_{peak-to-peak}$$ [2]

The integration in [2] is taken between the point P (i.e., lead exit point from the skull), and point Q 8cm further along the extracranial portion of the lead. This is the portion of the lead where ipsilateral and contralateral trajectories follow substantially different paths, with contralateral leads following a straight path to be tunneled toward the IPG side, and ipsilateral leads being looped at their exit point on the skull (see Figure 4A and Figure S1 in the Supplementary Material). Figure 5 shows the time evolution of ${\displaystyle {\int }_P^Q{E}_{tan}}dl$ for contralateral and ipsilateral leads of patient 2.

Figure 5:

Time evolution of the induced voltage over the first 8cm segment of contralateral and ipsilateral leads in Patient 2.

Simulation results

Figure 6 gives the result of the single patient analysis, reporting the mean values of MaxSAR1g (averaged over feed positions) at each resonant frequency (64 MHz, 127 MHz) and for both head and body coils. As expected, there was a substantial difference between MaxSAR1g at the tip of contralateral vs. ipsilateral leads, with the latter being substantially lower. The effect was persistent in all patients and was consistent over different coil types and resonant frequencies. Specifically, the change of feed position did not alter the balance between contralateral and ipsilateral SAR (not apparent in Figure 6). This means that in all patient models when the coil was rotated around the head, ipsilateral SAR remained lower than the contralateral SAR.

Figure 6:

MaxSAR1g for contralateral and ipsilateral leads in patients 1–9 for RF exposure at 64 MHz and 127 MHz with transmit head coil and transmit body coil.

Table 2 summarizes the results of group analysis on patients 1–9, reporting the mean of MaxSAR1g for each coil type and resonant frequency. At 64 MHz, the mean MaxSAR1g of contralateral leads was approximately 7 times higher than that of ipsilateral leads. At 127 MHz, the mean MaxSAR1g of contralateral leads was approximately 3 times higher than that of ipsilateral leads.

Table 2:

Mean of MaxSAR1g± standard deviation for head and body coils at 64 MHz and 127 MHz

	MaxSAR1g Contralateral	MaxSAR1g Ipsilateral
Body Coil 127 MHz	28.4±5.3	10.7±5.7
Body Coil 64 MHz	28.1±9.5	3.7±2.2
Head Coil 127 MHz	28.6±8.9	9.5±4.7
Head Coil 64 MHz	25.4±7.4	3.1±1.6

Interpretation of the results in the light of lead trajectory features

The SAR results presented here can be explained in the light of the specific features of lead trajectories, considering topological differences in the routing of ipsilateral vs contralateral leads. In all our patients, a single IPG was used to stimulate both left and right DBS leads. In eight patients (1–8), the IPG was implanted in the right pectoral region. In these patients, the right DBS lead was labeled as ipsilateral and the left lead as contralateral. One patient (Patient 9) had the IPG implanted in the left pectoral region for which the right DBS lead was labeled as contralateral and the left DBS leas as ipsilateral. A close examination of the tangential component of incident E field shows that E_tan adds up constructively over the initial extracranial straight segment of contralateral leads whereas its effect is mostly canceled out along the initial loop in ipsilateral leads. This effect is particularly pronounced in cases that demonstrated the larger difference between contralateral and ipsilateral SAR. An example is given for Patient 2 in Figure 5.

Figure 7 gives the scattering plots and correlation coefficients of MaxSAR1g vs V_8cm for all 18 leads. As it can be observed, there is a strong correlation between the induced voltage along the initial segment of the lead and the SAR amplification at the tip. This suggests that modifying the routing of contralateral leads in a way that reduces the induced voltage may also reduce the SAR amplification at the tip. Specifically, we hypothesize that introducing a looped section in the initial extracranial segment of the lead (right out of burr-hole) reduces the heating at the tip, as this part of the lead is exposed to the maximum tangential E field. The next Section outlines the phantom experiments to verify this hypothesis.

Figure 7:

Scattering plots and correlation coeffecients of V_8cm and MaxSAR1g for different body coils and at different resonant frequencies

III). Reducing the SAR through modification of the lead trajectory: phantom experiments at 1.5 T and 3 T

Phantom and lead construction

We tested the hypothesis that modification of the initial extracranial segment of the contralateral lead helps to reduce the SAR at its tip, by performing phantom experiments on lead models of Patient 2 which showed the largest difference between ipsilateral and contralateral MaxSAR1g. Digital models of the leads were 3D printed out of polycarbonate plastic (4mm diameter) and were used as a guide. Two pieces of insulated wire (Ga 14, 40 cm long, 1cm exposed tip) were shaped around 3D printed guides to follow the ipsilateral and contralateral trajectories (Figure 8A). Semi-solid anthropomorphic head phantoms were constructed from agar-doped saline solutions with electrical and thermal properties mimicking biological tissues (ε_r ≅ 70, σ ≅ 1 S/m, C_p = 4150 J/kg℃). Phantom recipe and construction method is given in previous studies [20]. Leads were implanted into the gel phantom following the entrance point, angle, and trajectories as observed from CT images of the patient (Figure 8B). To investigate the effect of trajectory, a modified contralateral lead trajectory was prepared where a single loop was introduced at the initial segment of the wire (Figure 8F). Experiments were also repeated with commercially available DBS leads (Models 3387 and 3389, Medtronic, Minneapolis MN) (Figure 8D).

Figure 8:

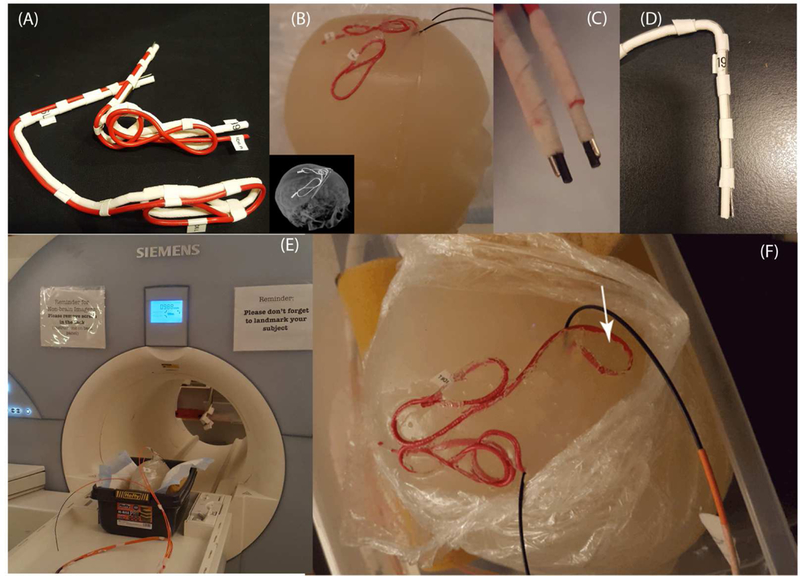
(A) 3D printed DBS lead phantoms used as a guide to shape wires in the form of patient-derived trajectories. (B-E) Generic metallic wires and commercially available leads (Models 3387 and 3389, Medtronic Inc., Minneapolis) implanted into semi-solid anthropomorphic head phantoms for MRI at 1.5 T and 3T. (F) Modified contralateral trajectory of Patient 2 with an extracranial loop added at the surgical burr-hole.

RF exposure and temperature measurements

The temperature was recorded using fluoroptic temperature probes (OSENSA, BC, Canada) secured at the exposed tip of the leads (Figure 8C). Experiments were performed at a 1.5T Magnetom Avanto system and a 3T TIM Trio system (Siemens Healthineers, Germany). Gradient coils were disabled and a train of 1ms rectangular RF pulses was transmitted using the scanner transmit body coil to achieve a better control over the characteristics of the RF exposure. To do this, the “rf_pulse” sequence from Siemens Service Sequence directory was used in the first level operating mode. Pulse sequence parameters are summarized in Table 3 for each experiment.

Table 3:

Characteristics of the RF pulses

Frequency	Flip Angle	Duration	TR	Patient weight entered	Whole-body SAR
64 MHz	200°	166 s	6.5 ms	68 kg	3.7 W/kg
127 MHz	250°	148 s	28.9 ms	68 kg	4 W/kg

Table 4 gives the temperature rise in the gel at the tip of ipsilateral and contralateral leads during ~2.5 minute RF exposure at 64 MHz and 127 MHz. As predicted by simulations, ipsilateral leads generated substantially less heating than contralateral leads. Our measurements also showed that Medtronic Lead 3389 consistently produced more heating than Lead 3387, an observation reported by other groups [33].

Table 4:

Temperature rise in the gel at the tip of ipsilateral and contralateral leads for RF exposures of Table 3.

Temperature rise [℃]	1.5 T (64 MHz)		3 T (127 MHz)
	Ipsilateral	Contralateral	Ipsilateral	Contralateral
Wire	1.4	3.6	2.3	3.3
Medtronic Lead 3389	0.8	2.3	0.2	2.0
Medtronic Lead 3387	0.3	1.2	0.2	1.0
Wire, modified trajectory	1.4	0.6	2.3	0.5

Interestingly, the modified contralateral lead trajectory with a loop at the burr-hole produced less heating than the ipsilateral lead. This confirms our hypothesis that modification of the lead trajectory to reduce the induced voltage along the critical portion of the lead that is exposed to the maximum tangential incident electric field also reduces the heating at the tip.

IV). Modified lead trajectories: surgical feasibility and application

To explore the surgical feasibility of implementing the modifications previously described, we attempted to introduce loops in the trajectory of both ipsilateral and contralateral leads at the surgical burr-hole. To attempt to control the lead trajectory, we used curved mayo scissors passed posterior and to the left of the incision. These scissors were inserted into the opening of the blades and opened to their widest to create a pathway for a coiled lead to be inserted. We then coiled the lead upon itself in 2–3 concentric circles at the burr-hole before passing the rest of the lead toward the temporal lobe where it would be later connected to the extension. Figure 9A shows postoperative CT images of a representative patient (Patient 10) with modified routing. Image segmentation, lead model construction and simulations were performed on Patient 10 similar to those described in previous sections patients 1–9.

Figure 9:

(A) Postoperative CT images of a patient (Patient 10) operated using the modified lead trajectories. (B-E) Calculated MaxSAR1g at the tip of ipsilateral and contralateral leads of a computational model derived from Patient-10 data compared to mean MaxSAR1g values calculated with models derived from patients 1–9.

Figure 9B-E gives the simulated results of MaxSAR1g for Patient 10 in comparison with group analysis results of patients 1–9. At 127 MHz, the modified trajectory reduced the MaxSAR1g of contralateral lead by 18-folds for transmit body coil and by 10-folds for transmit head coil. At 64 MHz the modified trajectory reduced the MaxSAR1g of contralateral lead by 80% for both head and body coils.

V). Discussion and Conclusion

Numerical modeling has been long used to understand the phenomenology of wave-tissue interaction in a wide variety of medical and diagnostic applications. Examples include use of electrostatic finite element modeling to predict the volume of activated tissue in electrical brain stimulation [40–42], analyzing performance of neurostimulators [43–45], eddy current modeling to assess the distribution of cortical currents and safety of magnetic brain stimulation [46–49], analysis of body exposure to low frequency magnetic fields, and safety hazards due to motion of medical implants in magnetic fields [50–52]. The role of numerical modeling has been also emphasized in RF safety assessment of MRI in patients with DBS implants [53–57].

The problem of RF heating of implants in MRI environment is a complex multi-variate problem with several interplaying factors. These includes the position and configuration of the implant in the body [25, 26, 58], the anatomy of the patient and the position in the MRI coil [27, 59, 60], and the phase of the incident RF field [20, 37, 38, 61]. Traditionally, safety assessment of active implanted medical devices (such as DBS, as well as pacemakers, and spinal cord stimulators) has been evaluated through phantom experiments employing simplified lead trajectories [62]. In more recent years, as the large scope of parameters and complex incident field conditions has led to a significant effort in determining the incident field conditions, a four-tier approach combining numerical simulations and phantom experiments has been introduced by a joint working group of MR manufacturers, medical device manufacturers and subject matter experts. This approach is described in the ISO TS 10974 [63]. An example illustrating the application of such approach to DBS implants has been carried on by Cabot et al. in [56].

This work is the first attempt to apply computer modeling to cast light on the phenomenology of interaction of MRI RF fields and DBS implants in patient-specific computational models. Our results revealed a significant difference between the SAR at the tip of ipsilateral vs contralateral DBS leads in cases where both leads were routed toward the same side of the head to be later connected to one implanted IPG. Specifically, we demonstrated that the distinct routing features of ipsilateral and contralateral leads and their orientation with respect to the incident electric field are factors responsible for the difference observed in SAR and RF heating. Placement of loops right at the surgical burr-hole was shown to significantly reduce the SAR due to cancelation of the induced voltage along the initial segment of the lead, which is the part that is exposed to the maximum tangential electric field. Placement of extracranial loops has been previously suggested as a method to reduce the SAR of DBS leads [28, 64], but to our knowledge this work is the first to give a detailed explanation of its mechanism of action. We also observed that placement of extracranial loops had a substantially larger effect in reducing SAR during MRI at 3 T compared to 1.5 T, which in agreement with results of previous studies [64]. Finally, we demonstrated the surgical feasibility of modifying the routing of the leads without requiring external guides and in such a way that does not add to the complexity and time of the surgery.

It is important to note however, that the current study is limited to the assessment of heating at the tips of DBS leads in isolation, i.e., prior their connection to the extension cables and the IPG, thus the results presented here should not be the extended to other configurations. Further investigation is necessary to establish the efficacy of the technique in a fully implanted system.

Another limitation of this work is that it is focused only on the RF heating of the leads due to transmit coils. Recent studies have drawn attention to the overlooked role of gradients in heating of bulk metallic implants [65–67]. Simulation studies of the temperature rise induced around metallic hip prostheses by traditional, split and nunipolar gradient coils predicted a temperature rise of up to 14℃ in the tissue depending on body’s position within the gradient coil, coil’s geometry, and composition of the implant [65]. Experiments with an acetabular cup exposed to continues trapezoidal z gradients showed up to 26℃ temperature rise in the implant itself for the case of thermally insulated implant, and up to 3.8 ℃ when the implant was immersed in gel. Although in these cases the tissue does not directly heat up from low-frequency induced currents of the gradient coils, its temperature could potentially rise up by conduction through the heated implant. This effect however, has been observed in bulk metallic objects, and whether or not thin wires of the leads are prone to the same effect remains to be investigated. Also in this work we used homogenous models and phantoms for simulations and experiments. The effect of tissue heterogeneity needs to be further investigated.

Future work will focus on the quantification of the SAR-reduction performance of the lead management in a cohort of patients operated using the introduced surgical technique.