Population pharmacokinetics of lenalidomide in patients with B‐cell malignancies

Abstract

Aims

Lenalidomide is an immunomodulatory imide drug used broadly in the treatment of multiple myeloma and lymphoma. It continues to be evaluated in chronic lymphocytic leukaemia (CLL) at lower doses due to dose‐related toxicities including tumour flare and tumour lysis syndrome. This study aimed to develop a population pharmacokinetic model for lenalidomide in multiple cancers, including CLL, to identify any disease‐related differences in disposition.

Methods

Lenalidomide concentrations from 4 clinical trials were collated (1999 samples, 125 subjects), covering 4 cancers (multiple myeloma, CLL, acute myeloid leukaemia and acute lymphoblastic leukaemia) and a large dose range (2.5–75 mg). A population pharmacokinetic model was developed with NONMEM and patient demographics were tested as covariates.

Results

The data were best fitted by a 1‐compartment kinetic model with absorption described by 7 transit compartments. Clearance and volume of distribution were allometrically scaled for fat‐free mass. The population parameter estimates for apparent clearance, apparent volume of distribution and transit rate constant were 12 L/h (10.8–13.6), 68.8 L (61.8–76.3), and 13.5 h⁻¹ (11.9–36.8) respectively. Patients with impaired renal function (creatinine clearance <30 mL/min) exhibited a 22% reduction in lenalidomide clearance compared to patients with creatinine clearance of 90 mL/min. Cancer type had no discernible effect on lenalidomide disposition.

Conclusions

This is the first report of a lenalidomide population pharmacokinetic model to evaluate lenalidomide pharmacokinetics in patients with CLL and compare its pharmacokinetics with other B‐cell malignancies. As no differences in pharmacokinetics were found between the observed cancer‐types, the unique toxicities observed in CLL may be due to disease‐specific pharmacodynamics.

What is already known about this subject

• Lenalidomide is approved for use in multiple myeloma, but not chronic lymphocytic leukaemia

• Using multiple myeloma doses of lenalidomide in chronic lymphocytic leukaemia patients results in increased toxicity

What this study adds

• This is the first report on the population pharmacokinetics of lenalidomide in chronic lymphocytic leukaemia

• No difference in pharmacokinetics was found between chronic lymphocytic leukaemia, multiple myeloma and acute myeloid leukaemia

• Differences in total plasma pharmacokinetics are unlikely to contribute to the different toxicity profile in chronic lymphocytic leukaemia

• The nonlinear relationship between creatinine clearance and total clearance suggests that secretion is an important clearance pathway for lenalidomide and that impairment of glomerular filtration may not result in impaired secretion

1. INTRODUCTION

Lenalidomide is a structural analogue of thalidomide belonging to a class of medications known as immunomodulatory drugs. It works by binding to cereblon, causing downstream signalling1, 2 that results in antiproliferative and antiangiogenic effects, along with an improvement in immune effector cell functions.3, 4 The action of lenalidomide is well suited for many haematological malignancies and has been evaluated in numerous clinical trials assessing its safety and efficacy in multiple cancers as both a single agent and in combination. Based on clinical data demonstrating superior efficacy over standard of care at the time, lenalidomide gained approval in multiple myeloma (MM)5 and myelodysplastic disorders6 in the USA, Europe and Australia among other countries.

Additional clinical trials have investigated the use of lenalidomide in chronic lymphocytic leukaemia (CLL), mantle‐cell lymphomas and acute myeloid leukaemia.7 These trials unveiled unique problems in CLL that were not present when studying other diseases. Initial trials revealed that doses suited for MM patients were associated with high toxicity in CLL patients, with many patients experiencing tumour flare.8 The tumour flare reaction observed in this study was not seen in other haematological cancers and presents with swelling of lymph nodes, spleen and/or liver. This prompted a change in dosing starting at 5 mg (25 mg in MM) and has shown that the risk of toxicity can be reduced without substantial loss of therapeutic benefit.9, 10, 11

Lenalidomide has high oral bioavailability, with 90% of the dose absorbed into the blood when taken under fasting conditions.12 It also shows a rapid absorption when fasting, with maximum concentrations (C_max) occurring at 1 hour after the dose. In the fed state a reduction in both the C_max and area under the plasma concentration–time curve (AUC) of lenalidomide were observed, with the values being 50% and 80%, respectively, when compared to fasted values.13 The time to C_max was also delayed by 1.63 hours. This implies that food slowed the rate of absorption of lenalidomide, with a relative decrease in bioavailability of 20%. The magnitude of the food effect was deemed clinically insignificant and, as a result, lenalidomide can be taken with or without food according to the product information.14

As lenalidomide has linear pharmacokinetics, plasma concentrations scale linearly with the quantity of absorbed drug. The apparent volume of distribution as determined in young healthy volunteers ranged from 75–125 L, indicating that it is moderately distributed into tissues. Protein binding was low, with mean protein binding ranging from 22.7–29.2%.14 The predominant excretion pathway of lenalidomide is the kidneys, accounting for 80% of total clearance.15 The remainder of the drug is either not absorbed or forms inactive metabolites via hydroxylation.12 Lenalidomide is not a substrate, inhibitor or inducer of cytochrome P450 enzymes.16 The apparent clearance of lenalidomide is higher than its glomerular filtration, with clearances of >200 mL/min seen in healthy volunteers.13 The magnitude of the clearance also suggests that both active and passive renal elimination is involved, with secretion playing a significant part. Lenalidomide is a weak substrate of P‐glycoprotein,17 but it is unclear if this transporter is responsible for all of the secretion of lenalidomide as experimental studies have found no activity with numerous common secretory transporters. The dependence of lenalidomide on renal excretion makes renal function an important factor to consider when dosing and is used at reduced doses in patients with creatinine clearance <60 mL/min.14

Population pharmacokinetic modelling enables parameter estimation or concentration time‐course prediction for both the study population and individual subjects simultaneously.18 Population pharmacokinetic models already exist for lenalidomide in the literature. The first published model utilised data from 15 MM patients, where a 1‐compartment kinetic model with 3 transit absorption was found to best fit the data.19 Additionally, the investigators found that creatinine clearance and body surface area had a significant covariate effect on clearance (CL) and volume of distribution (Vd), respectively.

An earlier model can be found in abstracts and government assessment reports for lenalidomide.20, 21 It was developed using data from 147 patients with MM (68 patients), myelodysplastic syndromes (25 patients) and mantle cell lymphoma (24 patients) and found that a 2‐compartment kinetic model with 2 transit absorption and a lag‐time best fit the data. Creatinine clearance was found to be a covariate for CL, while body weight, instead of body surface area, was used as a covariate on Vd. While this early model cannot be recreated from the literature, a model using some of the same patient data has been published.22 It was made using 305 healthy individuals and 83 patients; 60 with MM and 23 with myelodysplastic syndromes. It shares the same covariates with the early model, but also found that the healthy study population had higher CL and Vd than the patient population. No differences were found between cancer types in either model.

There are currently no reported population pharmacokinetic models for lenalidomide that examine pharmacokinetic differences in CLL. It was hypothesised that the different dosage required in CLL may be a result of different exposure to lenalidomide in these patients. The variation in exposure between cancer types may be a result of certain cancers changing lenalidomide pharmacokinetics, emphasising a need for direct comparison and evaluation of potential pharmacokinetic differences in CLL relative to other diseases. As a result, the aims of this study were to: (i) develop a population pharmacokinetic model for lenalidomide covering multiple cancers (including CLL); (ii) determine the influence of patient characteristics and cancer type on lenalidomide's pharmacokinetics; and (iii) compare this model to current models in the literature.

2. METHODS

2.1. Clinical dataset

The data discussed in this manuscript was collated from 4 phase I clinical studies conducted at The Ohio State University.23, 24, 25, 26 The studies administered Revlimid lenalidomide capsules daily for 21–28 days of a 28‐day cycle. The studies did not control for food effect and included a range of doses and diseases, which are summarised in the Electronic Supplementary Material. The studies also had varying inclusion/exclusion criteria depending on the disease and combination drugs given. Patients across all studies were required to be 18 years or older, have an Eastern Cooperative Oncology Group performance status of 2 or less, have normal organ and marrow function, have a serum creatinine of <177 μmol/L and have no active infections or uncontrolled intercurrent illnesses. All studies collected blood samples in EDTA tubes at predose and various nominal times up to 24 hours postdose. Differences between actual sample times and nominal times were recorded and were used during model development. Plasma samples were analysed using published liquid chromatography/tandem mass spectrometry assay for lenalidomide.27

2.2. Compliance with ethical standards

Ethics approval was attained for all study protocols by The Ohio State University Institutional Review Board and the National Cancer Institute Cancer Therapy Evaluation Program, and written informed consent was provided by all trial participants. All procedures performed in studies involving human participants were in accordance with both the ethical standards of the institutional research committee and the 1964 Helsinki declaration and its later amendments.

2.3. Model development

Population pharmacokinetic modelling was conducted using NONMEM (version 7.3; ICON Development Solutions, Ellicott City, MD, USA) software and an Intel Composer XE 2013 Fortran compiler. Pre‐ and postprocessing of data were conducted using Wings for NONMEM v73328 and R v3.3.029 with the ggplot2, plyr, reshape2, stringr, readxl, MASS and MBESS packages.30, 31, 32, 33, 34, 35, 36 First order conditional estimation with interactions (FOCE‐I) was used to fit models. The modelling procedure was completed in 3 stages: (i) development of the base structural model describing the data best without covariates; (ii) development of the covariate model using statistically significant patient characteristics; and (iii) evaluation and validation of the model.

The models were evaluated for both 1‐ and 2‐compartment kinetics based on previous models in the literature and visual inspection of the data. Varying alterations of these candidate models were used to try to best describe absorption of lenalidomide, including lag and transit models. For transit models, the methods outlined by Savic et al.37 were used to determine the appropriate number of transit compartments.38 The final number of transit models found by this method was rounded to the closest whole value, then used directly to improve both minimisation and simulation of the model.

The pharmacokinetic model estimated the following parameters (as appropriate): apparent clearance (CL/F), apparent volume of distribution (Vd/F), absorption rate constant (k_a), transit compartment absorption rate (k_TR) and absorption lag time. Population parameter variability was added to structural model parameters to model differences in these parameters between patients. This between‐subject variability was assumed to be log‐normally distributed (Equation 1).

$${\theta }_i={\theta }_{\mathit{pop}}·e^{{\eta }_i}{\eta }_i~N\left(0,{\omega }_{\theta }^2\right)$$ (1)

where θ _i is the individual parameter value for the i ^th individual, θ _pop is the population parameter value, η _i is an independent random variable with a mean of zero and variance ω ². Between‐occasion variability was also trialled.

Random unexplained variability was tested as proportional residual error models with and without additive residual error. CL/F and Vd/F were scaled according to allometric theory,39 with total body weight and fat free mass (FFM) being tested. FFM was calculated with the method proposed by Janmahasatian et al.40

During initial model development, outliers were flagged using visual inspection of the data and the conditional weighted residuals of the base model (conditional weighted residuals ≥±6). The model was fitted again without the outliers, to determine if they had a significant effect on the model parameters. The outliers were considered influential if parameter estimates differed by 15% or more. If the outliers were found to have an insignificant effect on the model, they would remain in the clinical dataset. In the case where they were influential, all subsequent models would be designed without these observations.

Tested covariates were chosen based on prior lenalidomide models19, 22 and plausibility. Continuous covariates were normalised using population median values (Equation 2).

$${\theta }_i={\theta }_{\mathit{pop}}·{\left(\frac{{\mathit{COV}}_i}{{\mathit{COV}}_{\mathit{med}}}\right)}^{{\theta }_{\mathit{cov}}}·e^{{\eta }_i}$$ (2)

where COV_i is the covariate value for the i ^th individual, COV_med is the covariate median and θ _cov is a parameter determining the covariate effect. Categorical covariates were modelled to determine the difference between patient groups (Equation 3).

$${\theta }_i={\theta }_{\mathit{pop}}·\left(1+{\theta }_{\mathit{cov}}\right)·e^{{\eta }_i}$$ (3)

where mathematical terms are the same as the equation for continuous covariates however θ _cov is dependent on the category of the individual. One category was used as a baseline (θ _cov = 0), while the others either increased (θ _cov > 0) or decreased (θ _cov < 0) the individual parameter value. Covariates that were considered included creatinine clearance, cancer type (CLL, acute myeloid leukaemia, acute lymphoblastic leukaemia, MM), age, sex, clinical study and interactions between these covariates. Creatinine clearance was calculated using the Cockcroft–Gault formula.41

While there were no data on fasted or fed status, it is known that that food can affect the pharmacokinetics of lenalidomide.13 This lack of data had the potential to result in a bimodal distribution for parameters describing absorption. Therefore, a mixture model was trialled to determine if 2 distinct fed and fasted populations could be observed in the data. Food effect was tested on both relative bioavailability and transit rate constant; alone and in combination.

Model selection was guided by: (i) the Akaike information criterion42; (ii) standard goodness‐of‐fit plots; (iii) the parameter estimate plausibility; (iv) the standard error of estimated values (obtained by parametric methods); (v) prediction‐corrected visual predictive checks (pcVPC)43; and (vi) noncompartmental analysis visual predictive checks (NCA VPCs). Goodness‐of‐fit plots included plots of observed concentrations vs. either population‐ or individual‐predicted concentrations, plots assessing weighted residuals over ranges in time and concentration and distribution plots of random effects in the model. pcVPCs were used due to the large range of dosages used in the study (2.5–75 mg). pcVPCs were made using the original data and 1000 simulations of the final model and were plotted using time after last dose due to the short half‐life of lenalidomide and low likelihood of accumulation. NCA VPCs were used to assess the model's ability to estimate AUC, C_max and t_max by determining these metrics for the 1000 simulations of the final model and comparing them to the NCA results from the observed data.

2.4. Model evaluation and comparison

The model was evaluated using bootstrapping and simulation–estimation methods. Bootstrap resampling was performed 1000 times sampling with replacement using the original data. Population parameters were obtained by fitting to each of these datasets. The median and 95% confidence intervals of the model parameters were then calculated. Stochastic simulation and estimation were used as a retrospective power analysis to confirm negative conclusions during covariate analysis. When no covariate relationship was found, the final model was simulated including the proposed covariate relationship creating a dataset that would result in a positive finding. This model was simulated 1000 times, which each of those simulations fitted using the final model with and without the supposedly absent covariate relationship. Each set of estimated model pairs were compared to determine whether the inclusion of the covariate resulted in a statistical improvement over its exclusion, thus demonstrating that, if the covariate effect existed in the original dataset, it would have been found during covariate analysis.

The model was compared to the 2 pharmacokinetic models currently in the literature; the Guglieri‐López model and the Connarn model.19, 22 These models were initially externally evaluated with the clinical dataset used for model development. pcVPCs and NCA VPCs were created using the process utilised in model evaluation. Additional comparison was performed using a simulated dataset of 15 000 MM patients. The patient demographics from the Guglieri‐López model were used as patient characteristics for the simulation. The patients were split into groups of 15 to create 1000 study datasets. The patient's weight and height were sampled from a multivariate log‐normal distribution and were strongly correlated (correlation coefficient 0.7). Patient age and serum creatinine were sampled from a normal and log‐normal distribution respectively. Patient sex and dose were weighted according to study proportions and then randomly sampled with replacement. The creatinine clearance was calculated from these patient characteristics using the Cockcroft–Gault equation. Final patient values outside of the ranges described by Guglieri‐López et al.19 were resampled. Using these covariates, simulations were conducted for each model and compared by overlaying the VPCs.

2.5. Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY,44 and are permanently archived in the Concise Guide to PHARMACOLOGY 2017/18.45

3. RESULTS

3.1. Study population

The pharmacokinetic data were obtained from 125 subjects across 4 phase I clinical trials, with participants contributing 1999 lenalidomide plasma concentrations. The number of observations per patient ranged from 9 to 26, with a median of 17 observations. There were no data for 10.8% of observations. As these samples had no differentiation between missing and below limit of quantification, they were all assumed to be missing. Missing samples were located predominantly near trough concentrations. Plasma lenalidomide concentrations of individuals receiving the same dose were variable, as seen in Figure 1. Demographic and clinical information for the patients are summarised in Table 1. No data on fed or fasted status were available for the study population. Other than this, there were no missing covariate data for the phase I clinical trials. Where dose time data were missing, they was imputed assuming each dose was taken 24 hours after the first dose time.

Figure 1.

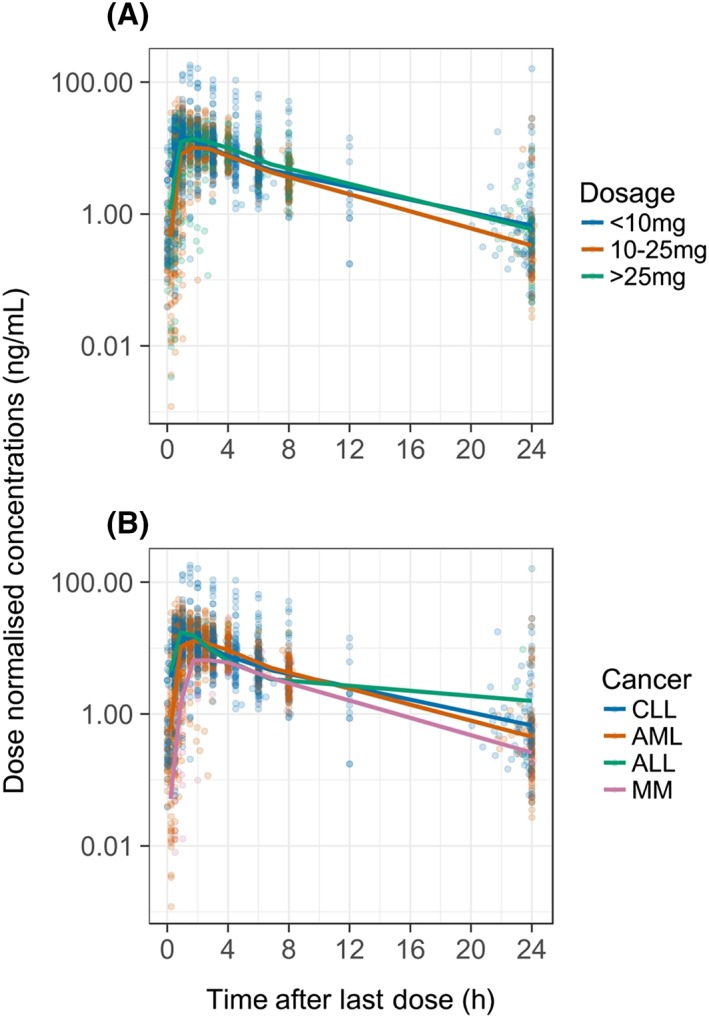
Plasma lenalidomide concentration–time profiles normalised for dose. The coloured dots represent each data point, with the colours corresponding to the dose ranges A, or cancer type B, according to the legend. ALL, acute lymphoblastic leukaemia; AML, acute myeloid leukaemia; CLL, chronic lymphocytic leukaemia; MM, multiple myeloma

Table 1.

Demographic and clinical information for clinical trials

	Mean	SD	Median	Range
Age (years)	58.2	12.8	61	22–79
TBW (kg)	88.8	22.7	86	48–152
Height (cm)	171	22.7	171	150–196
FFM (kg)	57.7	12.8	58.4	32–84
Creatinine (μmol/L)	82.8	21.4	80.4	42–147
CrCl (ml/min)	80.1	29.5	75.5	36–211

	Count		Percentage (%)
Dose (mg)
2.5	38		30.4
5	5		4
7.5	3		2.4
15	1		0.8
20	6		4.8
25	39		31.2
30	11		8.8
35	9		.2
50	10		8
75	3		2.4
Type of cancer
ALL	3		2.4
AML	53		42.4
CLL	49		39.2
MM	20		16
Sex (n)
Female	49		39
Male	76		61

SD, standard deviation; TBW, total body weight; FFM, fat free mass; CrCl, creatinine clearance; ALL, acute lymphoblastic leukaemia; AML, acute myeloid leukaemia; CLL, chronic lymphocytic leukaemia; MM, multiple myeloma.

3.2. Model development

The best model that fit the lenalidomide concentrations was a 1‐compartment kinetic model with a 7‐transit compartment absorption model (Electronic Supplementary Material). The population parameter estimates for apparent clearance, apparent volume of distribution and transit rate constant were 12 L/h (10.8–13.6), 68.8 L (61.8–76.3) and 13.5 h⁻¹ (11.9–36.8) respectively. Population parameters were found to be best allometrically scaled using FFM as opposed to total body weight (comparative reduction in objective function value of 5.9). Between‐subject variability was implemented on apparent clearance (CL/F), apparent volume of distribution (Vd/F) and the transit compartment rate constant k_TR, using a correlation matrix for CL/F and Vd/F. Due to the high percentage of lenalidomide excreted unchanged in the urine,15, 46 clearance was assumed to be entirely renal. A proportional error model best fit the data when compared to a combined additive and proportional error model. Despite data being available from multiple doses, between‐occasion variability did not improve the overall fit of the model and was not included in further model development.

Upon visual inspection and consideration of conditional weighted residuals, 24 concentrations were considered outliers. These outliers were associated with imputed dose times, resulting in concentrations resembling maximum concentrations occurring before a dose and troughs occurring after a dose. The removal of these data resulted in CL/F increasing by 20%, meeting the criteria for removal of the outliers. Additionally, between‐subject variability and residual unexplained variability were reduced by up to 15.7%. As a final check, a pcVPC was produced with this reduced dataset and showed obvious visual improvement. This dataset and model were used for subsequent analysis of covariates.

The examination of covariate effects on pharmacokinetic parameters identified no significant difference between different cancer types. The use of a mixture model failed to determine fed or fasted status from their respective absorption rate constants. Creatinine clearance was found to have a nonlinear covariate effect on CL/F and was the only significant covariate in the final model. The final equation used was:

$$\mathit{CL}=12·{\left(\frac{\mathit{\text{CRCL}}}{90}\right)}^{0.224}·e^{{\eta }_i}$$ (4)

where CL is the predicted clearance for an individual, CRCL is the creatinine clearance for an individual and η _i is an independent random variable with a mean of zero and coefficient of variance of 54.4%. The relative standard error of the final population parameters, parameter variability and covariates were satisfactory, indicating good estimation of the final parameter estimates (Table 2).

Table 2.

Population parameter estimates for base, final and bootstrap models

Parameter	Base model [%RSE]	Final model [%RSE]	Bootstrap [95% CI]
CL/F (L/h) [θ*(FFM/55)0.75]	12.4 [5.2]	12.0 [5.0]	12.0 [10.8–13.6]
CrCl covariate effect [*(CrCl/90)θ]		0.224 [31.6]	0.226 [0.046–0.396]
Vd/F (L) [θ*(FFM/55)1.0]	75.4 [5.1]	68.8 [5.0]	68.8 [61.8–76.3]
KTR (h−1)	13.5 [5.8]	13.5 [5.8]	13.4 [11.9–36.8]
Correlation between CL/F and Vd/F	0.856	0.862	0.870 [0.686–0.933]
BSV CL/F (%CV)	55.3 [9.9]	54.4 [10.7]	54.2 [42.8–66.7]
BSV Vd/F (%CV)	52.8 [9.9]	53.3 [10.3]	53.1 [43.0–64.6]
BSV KTR (%CV)	60.7 [6.4]	60.6 [6.4]	60.8 [52.3–120]
Proportional RUV (%CV)	43 [4.2]	43 [4.2]	43.1 [39.5–47.5]

BSV, between‐subject variability; CI, confidence intervals; CL/F, apparent clearance; CrCl, creatinine clearance; FFM, fat free mass; K_TR, transit rate constant; RUV, residual unexplained variability; Vd/F, apparent volume of distribution; θ, estimated parameter; %CV, percentage coefficient of variation; %RSE, percentage relative standard error.

The goodness‐of‐fit plots for the final model showed that the data was well represented by the predicted concentrations (Figure 2). Slight misspecifications in the model can be seen at low concentrations and early time points. It is likely that these are due to erroneous dosage times, resulting from availability of dosage times being limited to the initial dose. The pcVPC from the final model showed concordance between the observed and simulated data, with the median and 90% confidence intervals of the observed data sufficiently matching the 95% confidence intervals of the simulated data (Figure 3). The NCA VPC also showed adequacy in estimating the distributions of AUC, C_max and t_max (Figure 4).

Figure 2.

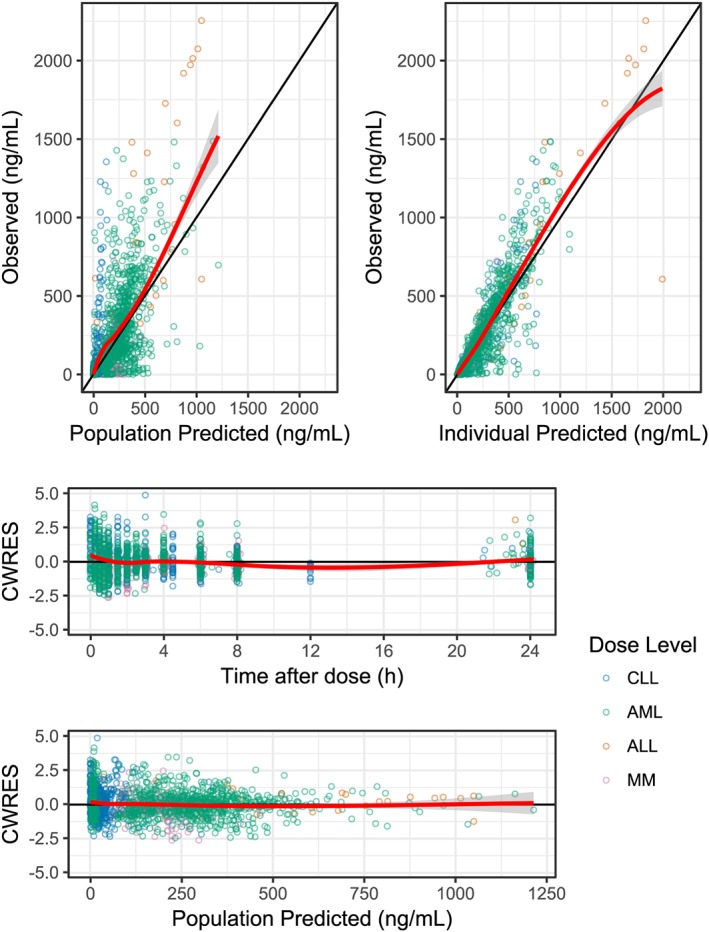
Goodness‐of‐fit plots both comparing observed concentrations with population and individual predicted concentrations and observing conditional weighted residuals (CWRES) over time and across population predicted concentrations. The data points are coloured according to the cancer type as shown in the legend. The red line represents the loess smoothed mean, with the grey ribbon representing the 95% confidence intervals of the smooth. ALL, acute lymphoblastic leukaemia; AML, acute myeloid leukaemia; CLL, chronic lymphocytic leukaemia; MM, multiple myeloma

Figure 3.

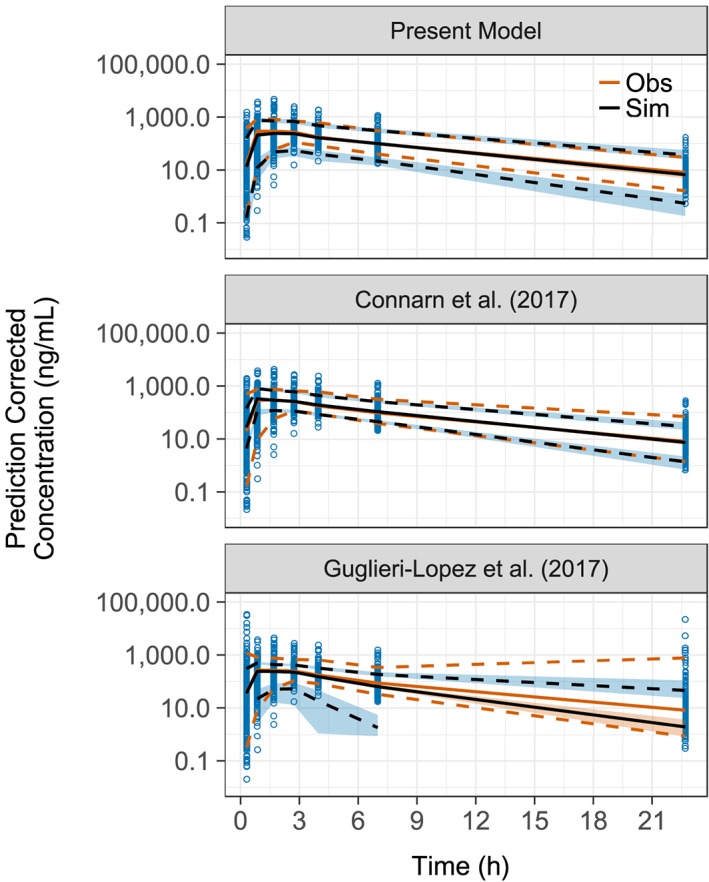
Prediction corrected visual predictive check. The visual predictive check was done for each of the 3 models being compared. Each visual predictive check compares the mean of the observed data (Obs) with the median of the simulated data (Sim) represented by solid lines. The dashed lines represent the upper and lower 90% confidence intervals of the data. The blue points show the binned data concentrations. The ribbons represent the 95% confidence intervals around the median and 90% confidence intervals of the simulation data

Figure 4.

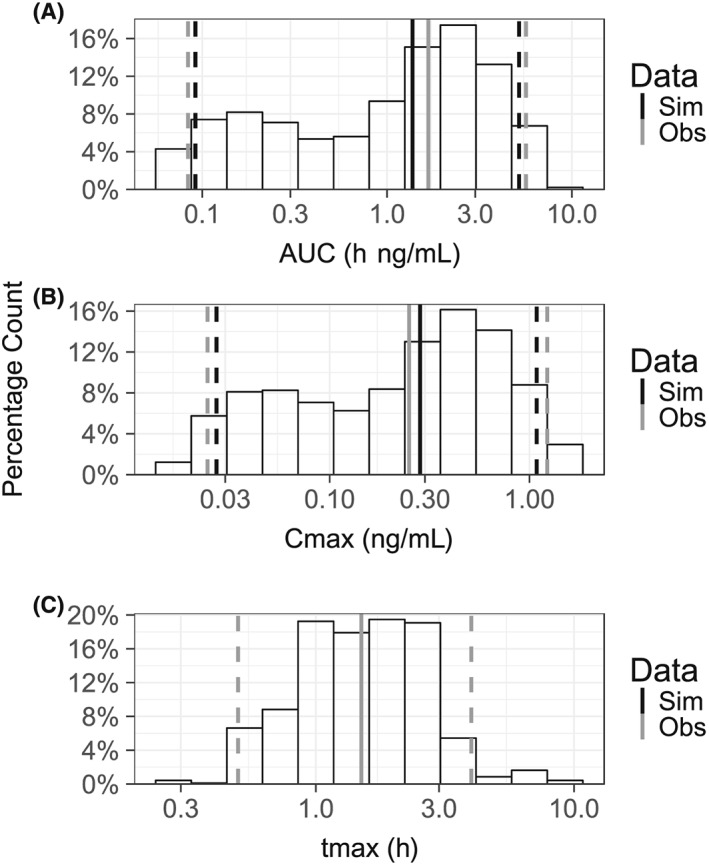
Noncompartmental analysis (NCA) visual predictive check. The visual predictive check consists of a histogram for the NCA metrics estimated from the data simulated from the model (Sim). The solid black and grey lines represent the median value of each metric for the data simulated from the model and from data used to develop the model (Obs). The dashed black and grey lines represent the 5^th and 95^th percentiles of each of the datasets outlined in the legend. NCA metrics compared were: A, area under the concentration curve (AUC); B, maximum concentration (C_max); and C, time of maximum concentration (t_max). In C, the median, 5^th and 95^th percentiles for the present model (black lines) do not appear as they are overlapped by the same values for the observed data (grey lines)

Several study effects were found during covariate analysis. A study containing 20 MM patients (the only patients in the dataset to be from this disease category) were found to have absorption rate constants on average 47% lower than other studies. Another study containing 14 CLL patients had a distinctly larger amount of variability in CL/F and Vd/F parameters. While the study effects were statistically significant, their addition caused no improvement in diagnostic plots or pcVPCs. As no clinically significant disease effects could be elucidated from them, they were not included in the final model.

3.3. Model evaluation and comparison

The results of the 1000 bootstraps showed adequate confidence intervals for the majority of parameters, with 993 of the bootstraps successfully minimising (Table 2). Given the negative result finding cancer type, the power of the analysis to detect such a finding was prospectively determined. The stochastic simulation and estimation method simulated the final model with the inclusion of a 20% reduction in total clearance for CLL patients. This relationship was found to be statistically significant in 829 of the 1000 covariate analysis model pairs, demonstrating that the original covariate analysis had an 82.9% power to determine whether different cancers had different pharmacokinetics.

The pcVPCs produced from external evaluation of existing models in the literature show that the Guglieri‐López model was unable to adequately predict patient concentrations for the clinical dataset (Figure 3). The Connarn model was able to predict terminal concentrations better than the present model; however, this model had predicted higher concentrations in the absorption phase than were seen in our data. The NCA VPCs of each model presented similar results, with the median and 95% confidence intervals for AUC, C_max and t_max being superior for the present model (Electronic Supplementary Material).

The MM datasets that resulted from simulating the patient demographics in Guglieri‐López et al.19 had similar covariate summary statistics as the patient population from which they were simulated. The resulting VPCs (Figure 5) showed that the model developed in this paper simulated similar terminal concentrations to the Connarn model, although the current model had differing absorption profiles. The Guglieri‐López model simulation shows a similar absorption curve to that of the Connarn model. However, the terminal concentrations of the Guglieri‐López model deviate greatly from the other 2 models.

Figure 5.

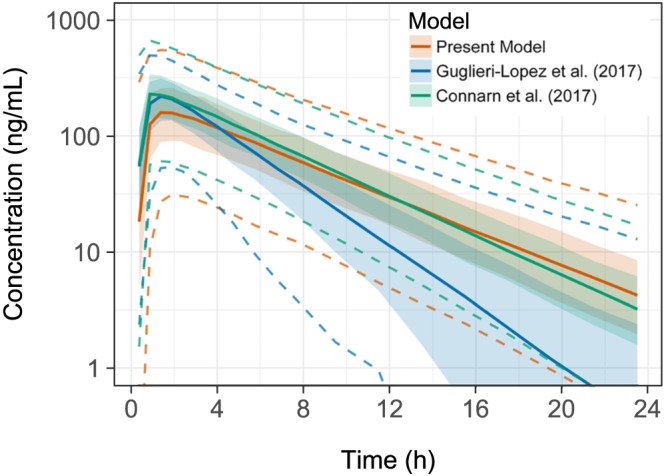
Visual predictive check of simulated multiple myeloma data. The coloured solid line shows the median of the data simulated from each of the models, while the dashed coloured lines represent the 90% confidence intervals of that data. The ribbons represent the 95% confidence intervals around the median of the simulation data

4. DISCUSSION

A population pharmacokinetic model has been developed to describe plasma concentrations for lenalidomide using data from 4 different pharmacokinetic phase I clinical studies. This model is the first lenalidomide population pharmacokinetic model to include data from CLL patients to be presented in the literature. The final model was found to have 1‐compartment kinetics like other models in the literature. However, the structure for the absorption models differed with the Guglieri‐López model using a transit model with 3 compartments instead of 7 and the Connarn model opting for 1st order absorption with a lag‐time.

Comparisons between the models show that the present model and the Connarn model described similar concentration–time profiles and adequately predict patient concentrations. The Guglieri‐López model showed large differences compared to the other 2 models and performed poorly in visual predictive checks. These large differences are expected, given that the model was developed using 15 patients taking lenalidomide outside of a clinical trial, where conditions are often different due to no strict inclusion criteria. The data used to develop this model had no time points beyond 6 hours, while the data in both the present model and the Connarn model had time points up to 24 hours and beyond. Additionally, the lower limit of quantification for the assay used in obtaining the data for the Guglieri‐López model was higher than the other models (100 ng/mL vs 0.3–5 ng/mL). As a result, the Guglieri‐López model was able to represent the absorption phase of the drug with reasonable accuracy but, with a lack of extended data in the elimination phase, it was unable to predict beyond 6 hours.

The use of cancer type as a covariate is not present in any of the current models. The comparison between models seen in Figure 3 and 4 showed that the Connarn model could adequately predict concentrations in CLL patients, despite being developed with MM and MDS patients. This suggests that the pharmacokinetics of lenalidomide in CLL patients is not different to other haematological cancers. This outcome may be a result of using empirical pharmacokinetic models, and a different modelling method (physiologically based pharmacokinetic modelling) would help provide more certainty in this conclusion. A lack of difference in the pharmacokinetics between different cancer types may also suggest disease‐specific pharmacodynamics in lenalidomide. Differences in receptor expression due to cancer cell types or changes in organ physiology, such as spleen composition changes in CLL patients,47 could be potential vectors for exploring this idea.

The absorption rate constant had the largest between‐subject variability out of any parameter for all models, indicating a large range of absorption constants to adequately represent their respective populations. The model presented in this paper and the Guglieri‐López model both had lower between‐subject variability for the absorption rate constant than the Connarn model (60 and 62% compared to 146% coefficient of variation). This may be due to the use of transit compartments to model the delay in absorption caused by the food effect, instead of a lag‐time. The large range of absorption constants is expected for lenalidomide patients as drug administration was not controlled for food intake, with the product information stating that lenalidomide can be taken with or without food.14

The Connarn model was found to over predict concentrations during the absorption phase for some patients in our dataset. This could be in part a result of the dataset used to create their model. The original population of the Connarn model had a large cohort of healthy individuals that took part in early clinical trials. It is possible that these clinical trials controlled for food intake (purposefully or inadvertently), resulting in a model that is better suited for predicting concentrations in fasted patients. No such controls were in place for trials producing the data used in the present model, which might then reflect a mixture of fasted and fed states.

A mixture model was unsuccessful in determining whether a patient was fed or fasted from their respective absorption rate constants. Theoretically, this could have explained some of the variability in lenalidomide absorption; however, the nutritional content of the meal can differ greatly between fed patients making the prediction of discrete groups difficult. Having data on patient meals from a lenalidomide study would greatly help in reducing the unexplained variability in absorption between patients and provide more accurate predictions. No correlation was found between clearance and the absorption rate constant while developing the present model. Therefore, it is unlikely that the variability in absorption has a significant impact on the ability to predict lenalidomide exposure using the present model and the Connarn model.

The final estimate for CL/F in the developed model was substantially higher than the median creatinine clearance for each patient. When taking this into consideration along with lenalidomide's fraction bound to plasma protein and that renal clearance makes up 80% of total clearance, approximately 60% of renal clearance may be due to secretion. Creatinine clearance was found as a nonlinear covariate for CL/F in all models but differed in the magnitude of its effect. This finding is reflected in the label approved by the FDA, where dose adjustment is required in patients with moderate or severe renal impairment. The low effect of creatinine clearance may be a result of the secretion pathway of lenalidomide's clearance.13, 24, 46

A recent investigation into glomerular filtration and tubular secretion found that the proportional impairment of the 2 renal processes correlated poorly.48 The creatinine clearance covariate value suggested by this investigation was not substantially different from that presented in this study (0.28 vs 0.224). The nonlinear covariate relationship presented in this study further supports the conclusion by Wright et al., suggesting that tubular secretion may be partly independent of impairment to glomerular filtration.49

A population pharmacokinetic model was developed for lenalidomide. This model demonstrates the nonlinear effect of creatinine clearance on renal elimination and the wide range of absorption rates present in lenalidomide patients. It is the first model to represent patients with CLL and has shown that there are no major differences in lenalidomide pharmacokinetics between cancer types. While this suggests that the increased lenalidomide toxicity in CLL patients is not due to unique lenalidomide plasma pharmacokinetics, but instead is due to either disease‐specific pharmacodynamics or altered pharmacokinetics in CLL cells.

CONTRIBUTORS

J.H.H. wrote the manuscript; M.A.P., R.N.U., S.E.R., J.C.B. and D.J.R.F. revised the manuscript; J.H.H., M.A.P., Y.G., J.C.B., M.R.G., C.C.H., G.M., W.B. and K.A.B. designed the research; J.H.H. performed the research and analysed the data; J.H.H., M.A.P., Y.G., R.N.U., S.E.R. and D.J.R.F. contributed analytical tools.

Supporting information

Supplementary Material 1.

Summary of study designs used for modelling and external validation

Supplementary Material 2: NONMEM control stream

Supplementary Material 3: NONMEM control stream used for determining ideal number of transit compartments.

Supplementary Material 4: Additional plots

Hughes JH, Phelps MA, Upton RN, et al. Population pharmacokinetics of lenalidomide in patients with B‐cell malignancies. Br J Clin Pharmacol. 2019;85:924–934. 10.1111/bcp.13873