Importance of the Force Field Choice in Capturing Functionally Relevant Dynamics in the von Willebrand Factor

Abstract

Whether recent updates and new releases of atomistic force fields can model the structural and dynamical properties of proteins containing both folded and partially disordered domains is still unclear. To address this fundamental question, we tested eight recently released force fields against our set of nuclear magnetic resonance (NMR) observables for a complex and medically relevant system, the major factor VIII binding region on the von Willebrand factor. This biomedically important region comprises both a folded and a partially structured domain. By using an enhanced sampling technique (temperature replica-exchange molecular dynamics simulations), we find that some force fields indeed rise to the challenge and capture the structural and dynamical features of the NMR ensemble and, therefore, are the appropriate choice for simulations of proteins with partially structured domains. What is more, we show that only such force fields can qualitatively capture the effects of a pathogenic mutation on the structural ensemble.

Recent advancements in computer architectures¹ and the parallelization of computer codes have increased the usefulness of atomistic molecular dynamics (MD) simulations in modeling complex biological systems and enabled them to reach unprecedented time scales and system sizes. However, one of the main questions that keeps arising is whether the commonly used Lifson-type force fields can describe the structural and dynamical properties of macromolecules with sufficient accuracy.^2,3 In an extensive force field comparison study, Lindorff-Larsen et al. showed that many recent force fields performed reasonably well when it came to folded, globular proteins. However, their performance faltered with intrinsically disordered peptides (IDPs).⁴ To tackle this issue, atomistic protein and water force fields have been subjected to multiple rounds of refinement.

In the AMBER family of force fields, the torsional parameters of the a99 force field were progressively modified to improve side-chain rotamer and backbone secondary structure preferences of folded proteins.⁵⁻⁹ These efforts were followed by a recent rewrite of a99SB by Robustelli et al. (a99SB-disp), which tried to improve the modeling of IDPs while retaining an accurate description of folded protein properties.¹⁰ The a99SB-disp force field came with its own four-point water model—a modified version of TIP4P-D.¹¹ Another notable adaptation of a99SB is the residue-specific force field (RSFF2),¹² which was optimized through additional nonbonded potential functions to reproduce the conformational distributions of amino acids from a protein coil library. Its improved version, RSFF2+,¹³ further stabilized α-helical hydrogen bonds and was combined with the TIP4P-D water model to address the previously observed overstabilization of IDPs.

The CHARMM family of force fields also went through several updates since C27¹⁴⁻¹⁶ to improve its representation of protein folding and IDPs.⁴ First, C36 was released to address incorrect equilibrium sampling of helical and extended conformations in folding simulations.¹⁷ However, Rauscher et al. showed that C36 tends to produce a high population of left-handed helices, inconsistent with experimental data.¹⁸ C36m was released to rectify this issue and further improve modeling of IDPs.¹⁹ Despite the corrections, C36m still keeps some IDPs overly compact, unless the Lennard-Jones parameters of the water hydrogens are also adjusted.¹⁰

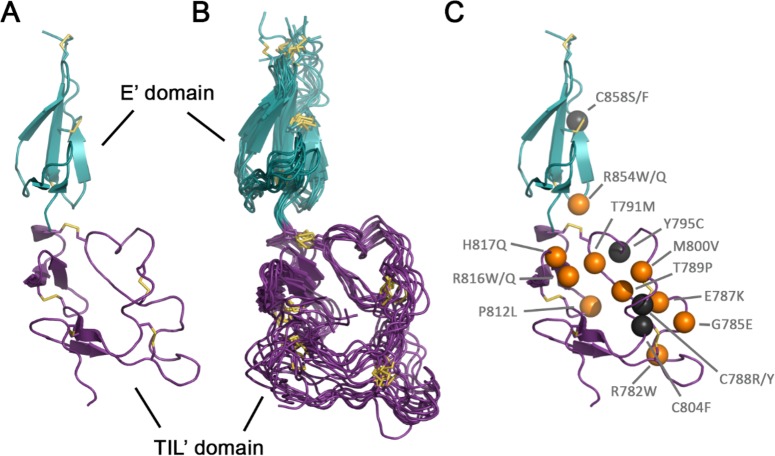
To understand how these force fields perform when it comes to a more demanding target than a typical folded protein and whether there are fundamental qualitative differences in their predictions, we used our recently solved solution NMR structure of the TIL′E′ (D′) region of the von Willebrand factor (VWF).²⁰ Previously, we solved the NMR structure of TIL′E′ using experimentally derived distance and backbone dihedral restraints, as well as vector orientation restraints and backbone chemical shifts. The NMR structure in combination with dynamics data allowed us to characterize VWF in unprecedented details. VWF plays a prominent role in the arrest of bleeding, and its malfunction leads to the common human inherited bleeding disorder von Willebrand disease (VWD).²¹ Type 2N VWD arises due to destabilization of the VWF complex with coagulation factor VIII (FVIII) mainly as a result of mutations in the TIL′E′ region that forms the major binding interface.²¹ The region itself comprises two domains: the E′ domain that is predominantly composed of β-sheets and the trypsin-inhibitor-like (TIL′) domain that is folded but has almost no secondary structure (Figure 1A,B). Eight disulfide bridges (3 in the E′ domain, 5 in the TIL′ domain) give additional stability to the region. Relaxation experiments have shown that the loop region of the TIL′ domain is dynamic.²⁰ The dual structural nature of VWF provides an excellent opportunity to test how well force fields handle a protein with a partially structured region and whether they can reproduce the experimental observables and probe the effects of pathogenic mutations associated with VWD (Figure 1C).²⁰

Figure 1.

Structural models of the TIL′E′ region of VWF obtained through NMR.²⁰ (A) Lowest-energy solution structure (PDB ID: 2MHP, model 1). (B) Structural ensemble calculated to include motions over the ps−μs time scale (PDB ID: 2MHQ). (C) Pathogenic mutations associated with type 2N von Willebrand disease with the original residue numbers. The N-terminal TIL′ domain is shown in purple, the C-terminal E′ domain is shown in teal, while the disulfide bridges are shown as yellow sticks. Type 2N mutations are shown as black spheres if they include cysteine residues and as orange spheres otherwise.

We simulated the TIL′E′ region of VWF with eight different force fields using replica-exchange molecular dynamics (REMD),²² an enhanced sampling technique where independent simulations (replicas) span a range of temperatures and regularly exchange conformations among themselves to increase the conformational sampling of the system. We used 30 replicas spanning a 298–345 K temperature range and compared the ensemble obtained at 300 K with the experimental observables. Each replica was sampled for 500 ns with a total of 15 μs of sampling per force field. For the modeling of our system, we settled on three force fields commonly used for folded proteins, a99SB*-ILDN,⁷ C27¹⁴⁻¹⁶ and a14SB,⁹ as well as five recently released force fields that are expected to handle modeling of the partially structured region better, a99SB-disp,¹⁰ C36m¹⁹ and its slightly modified version for IDPs (C36m IDP),¹⁹ RSFF2,¹² and RSFF2+¹³ (see the Methods section in the SI for details). We checked the convergence of the observables by performing a block analysis (Figure S1, Table S1).

In general, we observe that the E′ domain (Figure 1) is more rigid across all of the simulations with the different force fields. The average structures are also similar and reproduce fairly well the structure obtained from NMR. All of the force fields keep the β-sheets of the rigid E′ domain in place (with only small instabilities in the last β-sheet in the case of RSFF2, RSFF2+, and a14SB). The main differences in the structural ensembles are observed for the partially structured TIL′ domain. To better understand the differences, we compared the secondary structure propensity arising from the various force fields and the NMR ensemble (Figure S2; see the Methods section in the SI for details). According to the experimental data, the TIL′ domain is structured but mostly devoid of specific secondary structural motifs, except for a short β-sheet motif occasionally identified between residues 772–775 and 807–810, a longer, stable β-sheet within residues 814–823, and a 3₁₀-helical turn formed by residues 792–796. C36m, a99SB-disp, and RSFF2+ are the only force fields that were able to maintain the shorter TIL′ β-sheet motif similarly to the deposited NMR ensemble, while a99SB*-ILDN, C27, a14SB, and a99SB-disp seem to overstabilize the very short 3₁₀-helical turn. Furthermore, almost all of the force fields (except for C36m) also explore a short α-helical turn formed by residues 776–782.

In the comparison of average contact maps (see the Methods section for details), the folded E′ domain predominantly shows a slight gain of contact, and overall, all force fields agree well with the NMR ensemble. With respect to the flexible TIL′ domain, the analyses indicate that all force fields show a loss of contact compared to the NMR ensemble (Figure S3). RSFF2+ and a99SB-disp ensembles came the closest to the NMR ensemble (Figure S1, Table S1), with a14SB and C36m following right behind. Considering the secondary structure comparison, it is not surprising that the regions with loss of contacts primarily comprise the shorter β-sheet motif, as well as the 3₁₀- and α-helical turns described above.

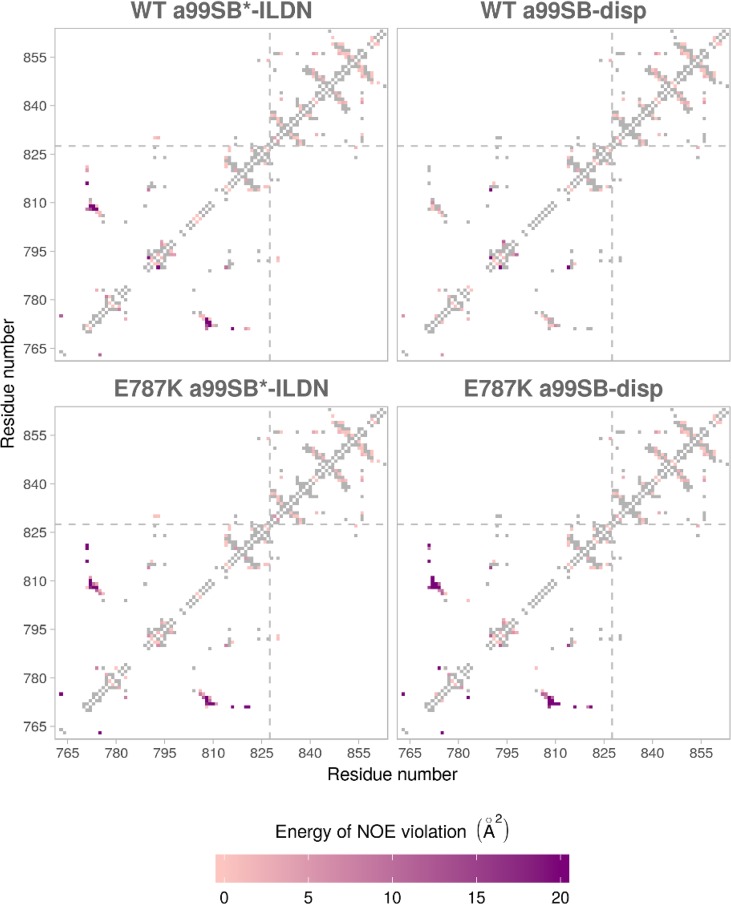
The performance of the selected force fields was assessed further by comparing how well they agreed with the experimental NMR data across several categories: (1) nuclear Overhauser effect (NOE) data, (2) chemical shifts, and (3) backbone dihedral angles sampling. We first tested the force fields based on how much their generated ensembles violated the experimentally determined NOE distance restraints (see the Methods section). a99SB-disp, both variants of C36m, and RSFF2+ show the best agreement with the experimental values (Table 1). We also looked at NOE violations calculated for each residue pair to see the agreement for each domain, with 42.5% of NOEs belonging to the TIL′ domain and 55.2% to the E′ domain (Figure 2). The worst NOE violations typically occurred between the residues that form the shorter β-sheet motif and the 3₁₀-helical turn in the TIL′ domain. Curiously, residues 776–782, forming the short α-helical turn observed in the majority of force field simulations but not in the NMR ensemble, are not involved in any major NOE violation. Force fields that showed small instabilities in maintaining the C-terminal β-sheet motif of the E′ domain also show minor NOE violations in the same region (RSFF2, RSFF2+, and a14SB).

Table 1. Energy Scores Given for the Wild-Type VWF Protein Across Five Comparison Categories^a.

	NOEs (Å2)	CamShift (ppm2)	backbone dihedrals	secondary structure	contacts (Å2)
a99SB*-ILDN	383.57	385.75	1959.85	5.99	182.57
C27	952.62	343.81	1508.67	4.17	217.62
C36m	126.84	381.02	1976.79	2.12	160.64
C36m IDP	120.44	388.51	2149.86	2.11	164.71
a14SB TIP4P-D	224.30	360.53	1673.64	4.02	145.29
a99SB-disp	123.56	367.02	1454.51	3.74	135.39
RSFF2	192.44	380.12	2048.52	4.84	174.82
RSFF2+	101.16	345.89	1699.71	3.35	129.28

^aSee the Methods section for details.

Figure 2.

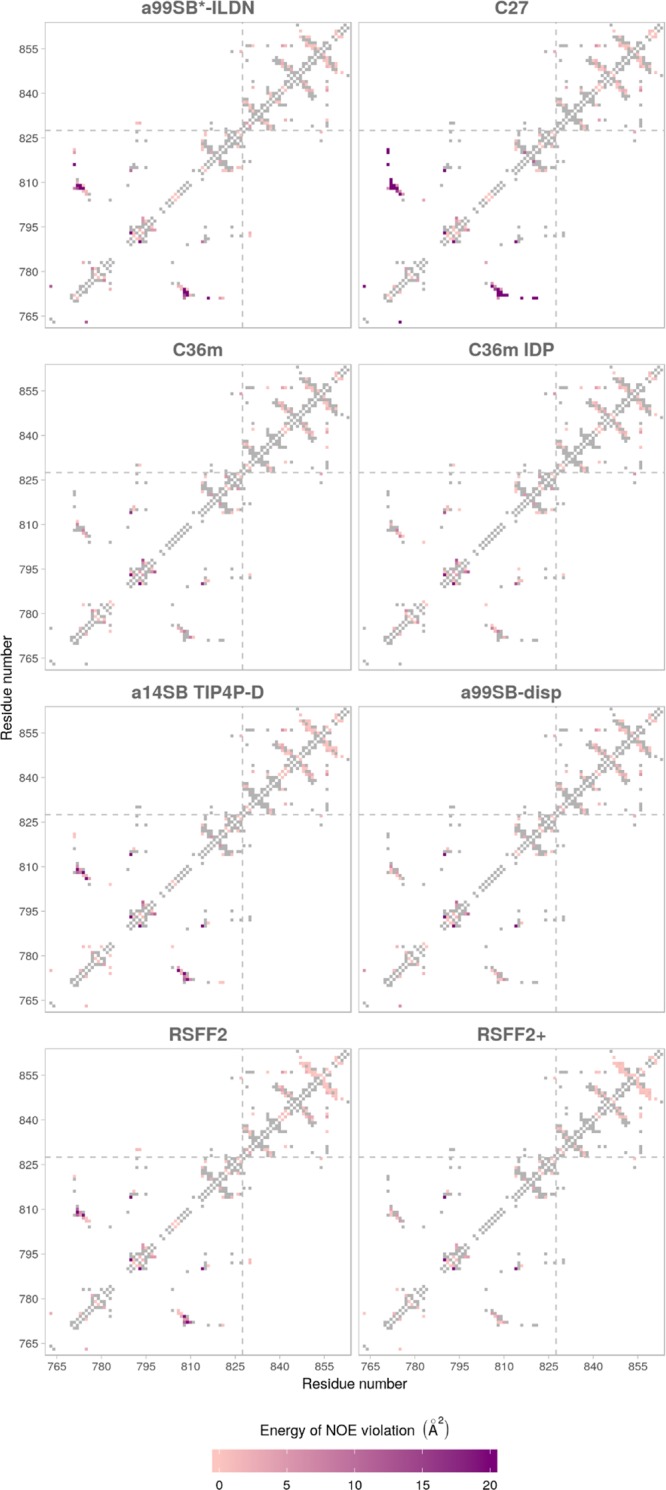
NOE violations shown for each of the tested force fields and given as energy terms for each residue pair (see the Methods section for details). Gray rectangles indicate no NOE violation. TIL′ and E′ domains are separated by a gray dashed line.

We also compared the chemical shifts computed from the simulation trajectories (see the Methods section in the SI) with the experimentally obtained values (Tables 1 and S1). When we considered the chemical shifts for C_α, C_β, H_α, H, and N atoms, then the force field whose shifts were the closest to the experimental ones was C27, followed closely by RSFF2+ and then a14SB and a99SB-disp. However, when we considered only C_α, C_β, and H_α atoms (essentially comparing secondary structure), the best agreement again came for C27, followed closely by RSFF2+ and then a14SB, RSFF2, a99SB-disp, and a99SB*-ILDN. Unlike for NOEs, there were no major differences observed for the TIL′ and E′ domains (Figure S4), although large disagreements were present for residues composing the short β-sheet motif in the TIL′ domain, reflecting the secondary structure observations.

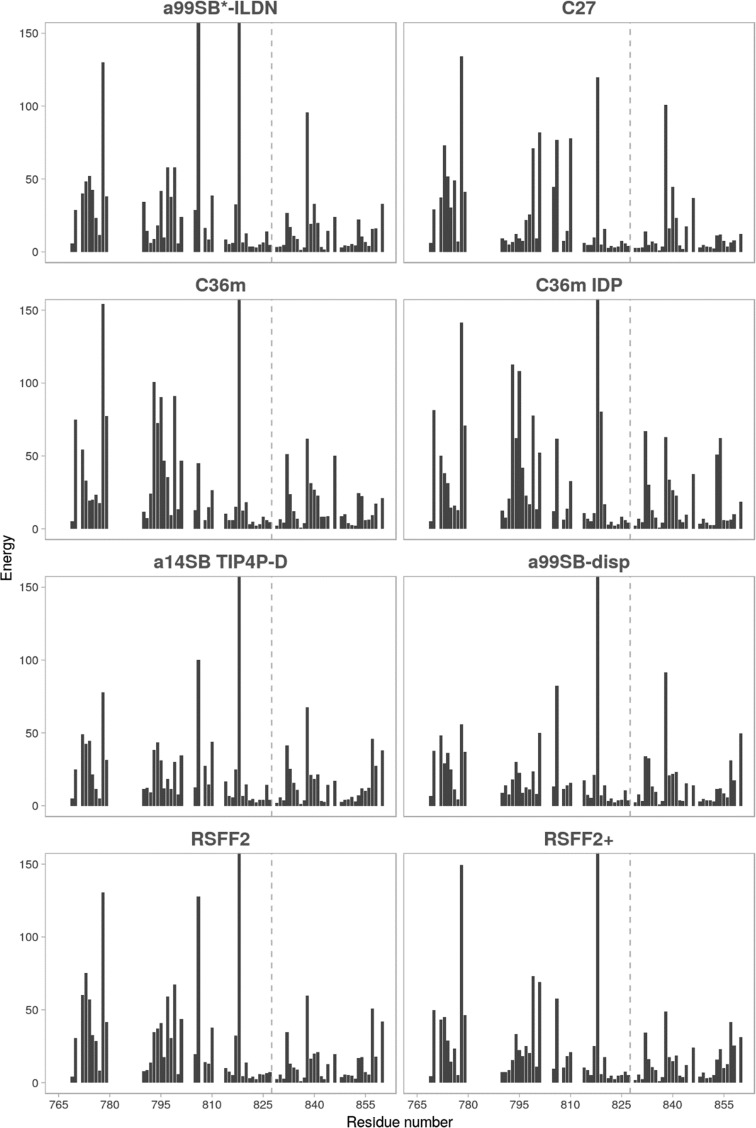
Lastly, we compared the force fields using the agreement of backbone dihedral angle sampling in the simulations with that predicted by TALOS-N from backbone chemical shifts²³ (Table 1). The best-performing force field in this case was a99SB-disp, followed closely by C27 and then a14SB and RSFF2+. A closer look at individual energy scores per residue (Figure 3) reveals an already familiar situation in which the substantial differences between simulated and predicted angles are generally contained in the TIL′ domain with several angles that seem to be problematic for most of the force fields. Namely, residues 778, 806, 818, and 838 show the largest disagreement. While residues 778 and 806 are not part of the shorter β-sheet motif, they are in its vicinity, which might explain their high score. On the other hand, residues 818 and 838 are located in turns (connecting two β-strands or β-sheets) whose backbone dihedral angles are typically more difficult to predict.²³

Figure 3.

Energy score for the difference between backbone dihedral angles obtained in MD simulations and those predicted with TALOS-N for each residue. The y-scale is cut off at 150 for clarity. TIL′ and E′ domains are separated by a gray dashed line.

Effects of the pathogenic mutation on the structural ensemble. Comparison of the ¹H–¹⁵N heteronuclear single-quantum coherence (HSQC) spectra of the wild-type (WT) and the pathogenic E787K mutant of the TIL′E′ region of VWF shows that the mutation causes significant changes in the underlying structural ensemble (Figure 4). We used REMD simulations to probe these changes on the molecular level. We chose two force fields from those tested on the WT protein to describe the mutant: a99SB-disp that performed consistently well across all comparison categories for the WT and a99SB*-ILDN that belongs to the same force field family but has failed to accurately capture features of the partially structured domain. In both cases, multiple replica 500 ns long simulations were produced and evaluated against experimental data in an identical manner to the WT variants (Figure 5). The convergence of the simulations was again confirmed using block analysis (Figure S5, Table S3).

Figure 4.

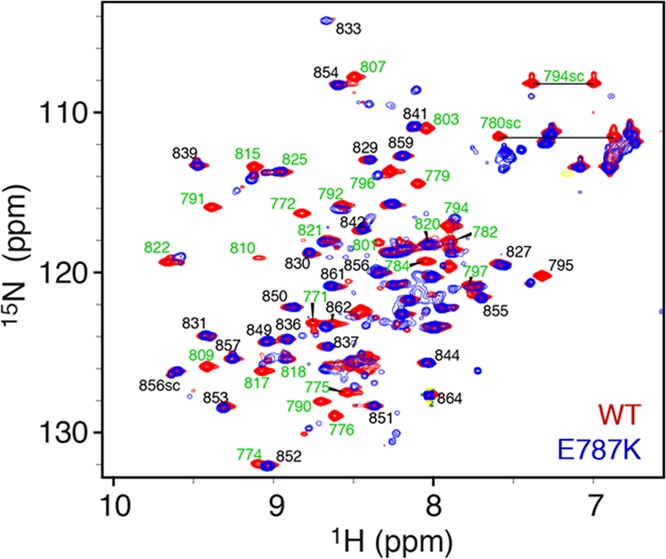
Assigned ¹H–¹⁵N HSQC spectrum of VWF TIL′E′ WT (blue) and E787K mutant (red). Each peak in the spectrum represents a backbone amide group or a Trp/Asn/Gln side-chain amide. The chemical shift assignments of TIL′E′ WT are shown²⁰ with the residue number of the full-length VWF protein. Large differences are observed between the WT and E787K spectrum for residues in the TIL′ domain (green labels), whereas only minor changes are observed in the E′ domain (black labels).

Figure 5.

NOE violations shown for each of the tested force fields for WT and E787K mutants and given as energy terms for each residue pair (see the Methods section for details). Gray rectangles indicate no NOE violation. TIL′ and E′ domains are separated by a gray dashed line.

The differences in the energy scores for the mutant and WT simulations showed that the E787K mutant explored different conformations (Tables 2 and S3, Figure S5). This difference is particularly pronounced when comparing NOE distances, and the mutant simulation performed using a99SB-disp correctly produced an ensemble that agrees significantly worse (10 times) with the experimental WT data than the WT simulation itself. While a99SB*-ILDN force field also produced different ensembles for the mutant and the WT, these differences are not as pronounced, and both WT and mutant systems deviate notably from the experimental WT data. Most of the changes introduced by the E787K mutation were contained in the region of the short β-sheet motif in the TIL′ domain loop (Figure 5), which was no longer formed in the mutant (Figure S6), as evident from the analysis of the a99SB-disp force field. These changes were also reflected in the contacts comparison, which showed a re-formation of interactions in the shorter β-sheet motif and its surrounding residues (Figure S7). Generally, there was very little change in sampling of the backbone dihedral angles (Figure S8). Considering that the mutation introduced a change in charge, we also looked at the differences in the formation of salt bridges for the WT and E787K mutant constructs (Table 3). We found a number of changes involving residues whose mutations are implicated in type 2N VWD (Figure 1C), such as R854, R782, R816, and H817, and that likely also affect the formation of the shorter β-sheet motif.

Table 2. Energy scores Given for the E787K Mutant VWF across Four Comparison Categories with the WT Data^a.

	NOEs (Å2)	backbone dihedrals	secondary structure	contacts (Å2)
E787K a99SB*-ILDN	560.66	1923.33	4.69	170.20
E787K a99SB-disp	1320.39	1434.07	4.59	155.58

^aSee the Methods section for details.

Table 3. Percentage of Charged Residue Pairs Whose Minimal Side-Chain Distance Was below the 5 Å Cutoff.

salt bridge in a99SB-disp	WT (%)	E787K (%)
D796-R854	18.04	9.77
E798-K790	3.96	12.56
E787-R782	6.44
D779-R782	5.91	11.44
E784-R782	12.37	6.93
E798-K787		4.99
E784-K787		3.58
E784-K790	3.39	0.18
E835-H817	54.85	51.98
E787-K790	2.97
E787-R816	2.55
E787-K773	1.86

Here, we assessed the performance of eight MD force fields, two which are often the first choice when it comes to investigating folded proteins and six that have been recently developed to improve the modeling of intrinsically disordered proteins. To the best of our knowledge, this is the first time that these force fields were tested on a complex target exhibiting a very diverse structural behavior—the TIL′E′ region of VWF comprising the folded E′ domain and the partially structured TIL′ domain. The chosen protein is not only of pharmaceutical interest but poses a real challenge for force fields due to its structural heterogeneity, which is typically difficult to model accurately. Accurate models of heterogeneous and dynamic systems are of great importance as recent studies have estimated that over 40% of any eukaryotic proteome contains disordered regions.²⁴⁻²⁶

In our enhanced sampling simulations of VWF, the force fields that overall agree best with the NMR data are a99SB-disp¹⁰ and RSFF2+, followed by C36m. Robustelli et al. developed a99SB-disp to perform universally well across systems ranging from folded proteins to IDPs. However, their extensive benchmark only included calmodulin as an example of a protein with two folded domains connected through a flexible linker; it contained no test systems akin to the TIL′E′ where one of the domains is partially structured. Therefore, our study confirms that the a99SB-disp force field performs well in such systems. Out of the three top-performing force fields, it is worth noting that C36m uses the TIP3P-Charmm water model, which is computationally less expensive than TIP4P-D used otherwise. However, C36m does not necessarily perform well when it comes to modeling IDPs.^10,19 Because RSFF2+ has not been benchmarked as extensively as other force fields, it is less clear how well it would perform with IDPs and flexible systems outside of the original parametrization study.¹³ On the basis of our results, it appears to describe proteins containing partially structured domains very well.

Once we identified force fields that can reproduce the experimental NMR data well, we were able to extend our study to the type 2N VWD E787K mutant. NMR shows that the mutant causes considerable structural changes, and the simulations predict that they are due to the rearrangement of salt bridge interactions in the TIL′ domain involving some of the other residues whose mutation also results in the type 2N VWD, pointing to a similar mechanism of action in such cases. These results also provide a possible molecular explanation to the observations that high ionic strength and low pH result in a much lower affinity of the VWF·FVIII complex.^27,28

We would like to stress that from all of the analyses performed above we find the comparison of NOE data to be the most relevant as it most directly compares simulated data to experimental observables. For folded regions, chemical shifts and TALOS-N provide a similarly robust experimental metric, but they are targeted toward well-folded proteins. The other analyses (contact maps, secondary structure; see the SI) make use of derived data and should therefore be used with caution.²⁹

In conclusion, our study provides a much-needed benchmark for MD simulations of proteins with both folded and partially structured domains, which will undoubtedly aid the community in simulation setup as well as force field development. It also provides insight into the effects of a mutation linked to a severe form of VWD, which is bound to guide future drug design studies. Finally, it shows the crucial importance of force field choice to correctly capture the effect of subtle structural changes; the effect of a severe pathogenic mutation in VWF was only correctly captured by using a force field that reproduces both the properties of folded and partially disordered protein domains.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00517.

• Detailed description of the computational and NMR methods and tables and figures showing the block analysis, secondary structure assignment, and distance difference between the simulated and the NMR ensembles (PDF)

Author Contributions

^§ A.K. and R.B.P. contributed equally.

The authors declare no competing financial interest.