Radiobiological parameters for breast cancer: a Monte Carlo analysis of START trial published results

Abstract

Objective:

Trial results are usually given in terms of end point confidence intervals, the data concerning the participating patients being not available. Sometimes, it would be useful or necessary to obtain derived quantities, such as dose–response relationships, from the known information. In this work, we describe a methodology that allows to do that and illustrate it by analyzing the UK standardization of breast radiotherapy (START) trials.

Methods:

Using Monte Carlo techniques, virtual data sets were generated by sampling trial outcome distributions in terms of the tumor control probability (described by means of a logistic dose response and the equations of isoeffect in the linear-quadratic model). After fitting the available experimental data, the radiobiological parameters of interest and their confidence intervals were obtained from the TCP vs 'EQD2 curve in which the surgery effect is also taken into account.

Results:

The value of $\alpha /\beta$ obtained for breast cancer was 3.6 Gy, with a 95% confidence interval of (1.5,15.5) Gy, in agreement with the one estimated by the START group. The time factor, referred to a scheme of 2 Gy per fraction, was 0.74 (0.41,2.67) Gy day^–1, of the same order than that estimated for head and neck cancers.

Conclusion:

A methodology permitting an analysis of trial results was developed and tested with the results of the START trials. The procedure does not require detailed knowledge of the distributions actually found in the trials. The values obtained for the parameters are similar to those of the START estimations and this can be considered an independent confirmation of their validity, thus showing the model usefulness. The methodology presented here relies on basic statistical methods that are general enough to permit it to be applied to any kind of trial. This may be particularly interesting when the original data are no longer available.

Advances in knowledge:

The main novelty of this paper is to provide with a Monte Carlo based tool that permits an independent analysis of published trial results in order to obtain radiobiological parameters without a detailed knowledge of the data corresponding to the participating patients.

Introduction

Usually, detailed data about all patients participating in trial tests are not available, and the corresponding results are provided by the researchers conducting them in terms of confidence intervals (CIs) for the end points studied. However, it seems appropriate to have the possibility of performing an independent analysis of these results. In this work, we have analyzed the UK standardization of breast radiotherapy (START) trials,^{1, 2} by means of a methodology based on a Monte Carlo procedure that permits to extract details about the subjects of the trial using the reduced information available.

In the START trials, the results obtained in a conventional fractionation schedule for treatment of early breast cancer, with 50 Gy imparted in 25 fractions of 2 Gy each during 5 weeks, are compared to those found for other schedules with lower total doses, imparted with doses per fraction larger than 2 Gy during 3 or 5 weeks.

The results of these trials have permitted to obtain the radiobiological parameters of both tumor and healthy tissues involved, whose values are very important for the application of the isoeffect model in the clinical practice. The START Trialists’ Group^{3, 4} has quoted the values of the $\alpha /\beta$ ratio of the parameters of the linear-quadratic (LQ) isoeffect model⁵ and the time factor, respectively, for breast cancer. This last parameter is crucial to evaluate the effect of prolonging the overall treatment time in fractionated radiotherapy.

In the present work, we have carried out an independent determination of the tumor control probability (TCP) model that reproduces the published outcomes of the START trials. This has permitted to obtain the radiobiological quantities of interest such as the $\alpha /\beta$ ratio and the time factor for tumor response. To do that, only the information about START trials shown in Table 1 has been considered, the (unavailable) whole data set of the trials being not required.

Table 1.

Local-regional and local relapse values obtained in the different treatment schedules of the START trials³. Each schedule is characterized by the total dose imparted to patients, D, the dose per fraction, d, and the overall treatment time of the fractionated schedule, T. The relapses, R, found after 5 and 10 years follow ups are given in terms of the average and the 95% confidence interval (between brackets)

					R (%)
Local-regional relapse		Local relapse
Trial		D (Gy)	d (Gy)	T (week)	5 year	10 year	5 year	10 year
START A	A1	50.0	2.00	5	4.0 [2.8,5.7]	7.4 [5.5,10.0]	3.4 [2.3,5.1]	6.7 [4.9,9.2]
A2	41.6	3.20	5	3.8 [2.6,5.5]	6.3 [4.7,8.5]	3.1 [2.0,4.7]	5.6 [4.1,7.8]
A3	39.0	3.00	5	5.1 [3.7,7.1]	8.8 [6.7,11.4]	4.4 [3.1,6.2]	8.1 [6.1,10.7]
START B	B1	50.0	2.00	5	3.5 [2.5,4.8]	5.5 [4.2,7.2]	3.3 [2.4,4.6]	5.2 [3.9,6.9]
B2	40.0	2.67	3	2.3 [1.5,3.4]	4.3 [3.2,5.9]	1.9 [1.2,3.0]	3.8 [2.7,5.2]

START, UK standardization of breast radiotherapy.

Methods and materials

Data analyzed

Table 1 summarizes the information corresponding to the START trials that have been analyzed. The important data are the local-regional and local relapse values, $R$, after follow ups of 5 and 10 years. They are given in terms of the average and the 95% CI.³

In Table 1, the relapses found for different treatment schedules are shown. They are characterized by the total dose imparted to patients, $D$, the dose per fraction, $d$, and the overall treatment time of the fractionated schedule, $T$. In particular, the conventional fractionation schedule for treatment of early breast cancer, with 50 Gy imparted in 25 fractions of 2 Gy each during 5 weeks (configurations A1 and B1), is compared to other treatment configurations with lower total doses, imparted with doses per fraction larger than 2 Gy during 5 weeks (schedules A2 and A3) or 3 weeks (schedule B2).

Dose response and isoeffect models

In what follows, we refer to a radiotherapy treatment schedule by giving its characteristics as a triad ${\displaystyle \left(D,d,T\right)}$. As the schedules whose results are shown in Table 1 are different, the relapse values quoted cannot be directly compared. To do this, the biologically effective dose of a given schedule is required. Assuming the LQ isoeffect approach with a time factor included, it can be written as:⁵

$${\displaystyle BED\left(D,d,T\right)=D\left(1+\frac{d}{\alpha /\beta }\right)-k\underset{}{max}\left[T-T_{\text{K}},0\right]}$$

where $\alpha /\beta$ is the parameter related to the effect considered (the tumor response in our case), $k$ represents the time factor, which takes into account the cell repopulation, and $T_{\text{K}}$ is the onset time, which indicates the minimum time required, since the beginning of the treatment, for the time effect to appear.

Given a treatment schedule $(D,d,T)$, the equivalent dose, ${\displaystyle EQ{D}_{d\prime ,T\prime }}$, is defined as the total dose imparted in a schedule ${\displaystyle \left(EQ{D}_{d\prime ,T\prime },d\prime ,T\prime \right)}$ that produces the same biological effect than the former one; that is:

$${\displaystyle BED\left(EQ{D}_{d\prime ,T\prime },d\prime ,T\prime \right)=BED\left(D,d,T\right)}$$

According to Equation (1), and assuming that $T_{\text{K}}$ is smaller than the usual overall treatment times, we have that

$${\displaystyle EQ{D}_{d\prime ,T\prime }\equiv EQ{D}_{d\prime ,T\prime }\left(D,d,T\right)=D\frac{d+\alpha /\beta }{d\prime +\alpha /\beta }-k_{d\prime }\left(T-T\prime \right)}$$

where

$${\displaystyle k_{d\prime }=k\frac{\alpha /\beta }{d\prime +\alpha /\beta }}$$

In what follows, and to simplify the writing, the dependence of ${\displaystyle EQ{D}_{d\prime ,T\prime }}$ on $D$, $d$, and $T$ will not be explicitly indicated.

The equivalent dose in Equation (3) allows comparing the results obtained in different treatment schedules. In this work we have considered the $TCP$ as the magnitude to do that comparison. This quantity is related to the relapse value $R$, which is the output quantity provided in the START trials, as

$${\displaystyle TCP=1-R}$$

and to model it we assumed a logistic dose-response approach⁶

$${\displaystyle TCP\left(D\right)=TC{P}_{\text{surgery}}+\left(1-TC{P}_{\text{surgery}}\right){\left[1+{\left(\frac{D_{50}}{D}\right)}^{4\gamma }\right]}^{-1}}$$

Here, ${TCP}_{\text{surgery}}$ is the fraction of cures due to surgery, $D_{50}$ is the total dose needed to achieve 50% of the cures due to radiation and $\gamma$ is the normalized dose-response gradient at $D_{50}$.

In what respect to ${TCP}_{\text{surgery}}$, a reasonable value is the one found by Clarke et al⁷ and Yarnold et al⁸ who estimated it as ~0.7. In any case, and to have an idea of the influence of this quantity, the extreme case of ${TCP}_{\text{surgery}}=0$ was also analyzed. The other two parameters, $D_{50}$ and $\gamma$, have a well-known clinical relevance and may be obtained by fitting the model function of Equation (6) to the data provided by the trials, as it is described below.

The procedure we followed involved two steps. In the first one, we considered the data of A1, A2, A3 and B1 schedules. As seen in Table 1, all these schedules were imparted in the same time, 5 weeks, that corresponds to $T=33\text{day}$, if one assumes that all treatments begin on Monday. The results of these four schedules were compared by considering the equivalent doses corresponding to a reference schedule with ${\displaystyle d\prime =2\text{Gy}}$ and ${\displaystyle T\prime =33\text{day}}$ According to Equation (3), they are given by:

$${\displaystyle EQ{D}_{2\text{Gy},33\text{day}}=D\frac{d+\alpha /\beta }{2\text{Gy}+\alpha /\beta }}$$

Taking into account Equations (6) and (7) we can write:

$$\begin{gathered} {\displaystyle TCP\left(EQ{D}_{2\text{Gy},33\text{day}}\right)= \\ =TC{P}_{\text{surgery}}+\left(1-TC{P}_{\text{surgery}}\right){\left[1+{\left(\frac{D_{50}}{EQ{D}_{2\text{Gy},33\text{day}}}\right)}^{4\gamma }\right]}^{-1} \\ =TC{P}_{\text{surgery}}+\left(1-TC{P}_{\text{surgery}}\right){\left[1+{\left(\frac{D_{50}}{D}\frac{2\text{Gy}+\alpha /\beta }{d+\alpha /\beta }\right)}^{4\gamma }\right]}^{-1}} \end{gathered}$$

It is obvious that for A1 and B1 schedules, for which ${\displaystyle d=2\text{Gy}}$, ${\displaystyle EQ{D}_{2\text{Gy},33\text{day}}=D}$.

The first step of the procedure consisted in fitting this function to the data mentioned. As a result, the values of $D_{50}$ and $\gamma$ as well as that of $\alpha /\beta$ were obtained.

The second step allowed estimating the only parameter that remained unknown: the time factor $k$. To determine it, Equation (2) was applied to the treatment schedule B2 and then we had:

$${\displaystyle BED\left(EQ{D}_{2\text{Gy},33\text{day}},2\text{Gy},33\text{day}\right)=BED\left(40\text{Gy},2.67\text{Gy},19\text{day}\right)}$$

Here we considered that, if treatments begin on Monday, the 3 week schedule B2 took 19 days. Taking now into account Equation (1), we can write for the time factor:

$${\displaystyle k=\frac{1}{14\text{day}}\left[EQ{D}_{2\text{Gy},33\text{day}}\left(1+\frac{2\text{Gy}}{\alpha /\beta }\right)-40\text{Gy}\left(1+\frac{2.67\text{Gy}}{\alpha /\beta }\right)\right]}$$

The value ${EQD}_{2\text{Gy},33\text{day}}$ was determined directly from the $TCP$ curve obtained in the first step of the procedure here proposed.

Statistical methods

The key information that must be determined is the one linked to the distributions of the four parameters involved in the problem, these are $D_{50}$, $\gamma$, $\alpha /\beta$ and $k$. In our case, we adopted a Monte Carlo approach for this purpose. In what follows, we describe the steps of the procedure.

(1) As it can be seen in Table 1, the CI $\left[R_{\text{low}},R_{\text{high}}\right]$ provided by the START trials for the local-regional relapse are asymmetric with respect to the average value, $R_{\text{ave}}$. On the other hand, the corresponding distributions are not known. However, we found that the transformation

$${\displaystyle g(R)=1\mathrm{n}\frac{R}{1-R}}$$

defined symmetric intervals in all cases quoted in Table 1. At this point, we assumed that the transformed values $g\left(R_{\text{ave}}\right)$ and $\left[{g(R}_{\text{low}}),g(R_{\text{high}})\right]$ represented the average and the 95% CI corresponding to the Gaussian distribution ${\displaystyle N\left[g\left(R_{\text{ave}}\right),\sigma \right]}$, with

$${\displaystyle \sigma =\frac{1}{3.92}\left[g\left(R_{\text{high}}\right)-g\left(R_{\text{low}}\right)\right]}$$

The value $3.92=$ 2 $\times 1.96$ in the previous equation is due to the fact that the CI is at 95% probability.

(2) The previous Gaussian distribution was sampled and, from each $g$ generated in this sampling, an $R$ value was calculated using

$${\displaystyle R=\frac{\exp \left(g\right)}{1+\exp \left(g\right)}}$$

which is the inverse transformation of the one in Equation (11).

In this way, we generated five $R$ values, one for each of the START treatment schedules that were being analyzed and, using Equation (5), the corresponding $TCP$ values were calculated.

In order to check the robustness of our procedure, we have considered two additional distributions generating the $R$ values. Specifically, we have used a normal distribution ${N[\mu }_{\text{N}},{\sigma }_{\text{N}}]$ characterized by

$${\displaystyle {\mu }_{\text{N}}={\displaystyle \frac{R_{\text{high}}+R_{\text{low}}}{2}},{\sigma }_{\text{N}}={\displaystyle \frac{R_{\text{high}}-R_{\text{low}}}{3.92}}}$$

and an uniform distribution ${\displaystyle U\left[R_{\text{low}},R_{\text{high}}\right].}$

(3) The model $TCP$ function in Equation (8) was fitted to the ${TCP}_{\text{A1}}$, ${TCP}_{\text{A2}}$, ${TCP}_{\text{A3}}$ and ${TCP}_{\text{B1}}$ values using the Levenberg-Marquardt method.⁹ As a result, the parameters $D_{50}$, $\gamma$, and $\alpha /\beta$ were obtained

(4) Using the specific values of $D_{50}$ and $\gamma$, the corresponding $TCP$ vs $EQD$ curve was built and, from the ${TCP}_{\text{B2}}$ value obtained in the sampling, the equivalent dose for the B2 schedule was calculated as:

$${\displaystyle EQ{D}_{2\text{Gy},33\text{day}}=D_{50}{\left(\frac{1-TC{P}_{\text{surgery}}}{TCP{}_{\text{B2}}-TC{P}_{\text{surgery}}}-1\right)}^{-\frac{1}{4\gamma }}}$$

Using this value in Equation (10), the time factor $k$ was determined and, according to Equation (4), we obtained:

$${\displaystyle k_{2\text{Gy}}=k\frac{\alpha /\beta }{2\text{Gy}+\alpha /\beta }}$$

(5) By repeating these steps a number of times (in our case $2.5\times {10}^4$), we generated the distributions of the various radiobiological parameters of interest with enough statistics. As these distributions are usually asymmetric, the results were given in terms of the median and the 95% CI corresponding to the interval between the 2.5 and 97.5 percentiles.

Results

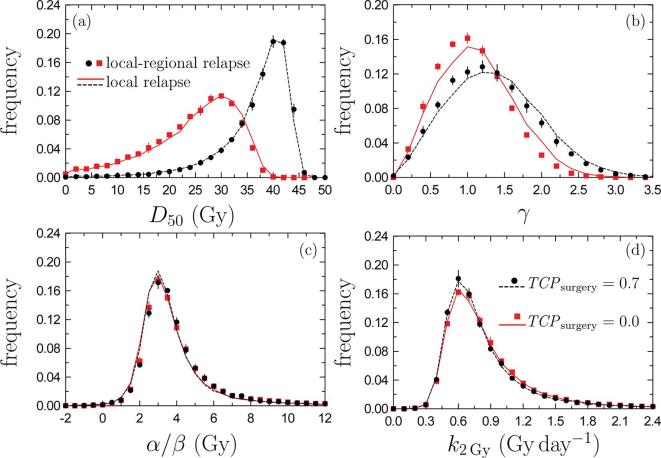
Figure 1 shows the distributions of the radiobiological parameters calculated in our Monte Carlo analysis of the START trial output information for a follow up of 10 years. Black solid circles correspond with local-regional relapses while black dashed curves were obtained for the local ones, in both cases assuming ${TCP}_{\text{surgery}}=0.7$. Table 2 summarizes the results obtained in terms of the corresponding medians and 95% CIs of each parameter.

Figure 1.

Parameter distributions found in our Monte Carlo procedure. Symbols correspond to local-regional relapses while curves stand for local relapses. Black circles and black dotted curves have been obtained for ${\displaystyle TC{P}_{\text{surgery}}=0.7}$; red squares and red solid curves are for ${\displaystyle TC{P}_{\text{surgery}}=0}$. Uncertainties are shown with a coverage factor 2 only for local-regional relapse results; those of local relapses are of the same order. All values plotted are for 10 year follow-ups. TCP, tumor control probability.

Table 2.

Parameter values obtained by using the Monte Carlo procedure developed Results for the local-regional and local relapse data of the START trials and for 5 and 10 year follow-ups are shown. The median and 95% CI (as the 2.5 and 97.5% percentiles) are given.

		START A/B (this work)
Local-regional relapse		Local relapse
${\displaystyle TC{P}_{\text{surgery}}}$	Parameters	5 year	10 year	5 year	10 year
0.7	${\displaystyle D_{50}(\text{Gy)}}$	32.45 [7.60,41.13]	38.75 [17.90,44.30]	32.68 [6.59,41.32]	38.52 [16.92,44.06]
${\displaystyle \gamma }$	1.12 [0.25,2.46]	1.26 [0.30,2.58]	1.21 [0.25,2.66]	1.34 [0.31,2.68]
${\displaystyle \alpha /\beta (\text{Gy)}}$	3.60 [1.09,19.59]	3.57 [1.50,15.52]	3.02 [0.71,13.98]	3.33 [1.37,13.07]
${\displaystyle k\text{(Gy}{\text{day}}^{-1})}$	1.28 [0.60,6.95]	1.15 [0.64,4.44]	1.33 [0.58,8.95]	1.17 [0.64,4.77]
${\displaystyle k_{2\text{Gy}}\text{(Gy}{\text{day}}^{-1})}$	0.83 [0.40,3.93]	0.74 [0.41,2.67]	0.81 [0.38,4.28]	0.73 [0.41,2.88]
0.0	${\displaystyle D_{50}(\text{Gy)}}$	22.39 [2.12,34.60]	26.07 [4.35,36.17]	23.41 [2.13,35.28]	26.71 [4.38,36.63]
$\gamma$	1.01 [0.25,2.19]	1.03 [0.27,2.06]	1.11 [0.26,2.41]	1.10 [0.28,2.20]
${\displaystyle \alpha /\beta (\text{Gy)}}$	3.59 [1.26,18.68]	3.54 [1.57,15.73]	3.01 [0.86,13.94]	3.32 [1.38,12.95]
${\displaystyle k\text{(Gy}{\text{day}}^{-1})}$	1.31 [0.62,6.21]	1.19 [0.65,4.32]	1.37 [0.61,7.73]	1.21 [0.64,4.67]
${\displaystyle k_{2\text{Gy}}\text{(Gy}{\text{day}}^{-1})}$	0.84 [0.40,3.46]	0.76 [0.42,2.63]	0.83 [0.38,3.75]	0.76 [0.41,2.77]

START, UK standardization of breast radiotherapy.

The first point to be noted is that the parameter distributions obtained for the two types of relapses considered are very similar and, with the exception of $\gamma$ (Figure 1b), where a slight difference can be observed, the corresponding distributions are almost overlapping. This is corroborated by the results shown in Table 2. The values obtained for the median of $\gamma$ in the cases studied are relatively small, between 1.01 and 1.34. For example, those estimated for head and neck cancers are higher.¹⁰ This may indicate a large dosimetric and biological heterogeneity in the patient sample of START trials.

In Figure 2, the TCP values obtained from the START data, for local-regional relapses and ${TCP}_{\text{surgery}}=0.7$, are shown: black squares and triangles are for START A and B data, respectively. The curves represent the corresponding fitted $TCP\text{s}$, as given by Equation (8): the black dotted curve corresponds to the 5 year follow-up and the black solid line stands for the 10 year follow-up. The insets show, for the two follow-up periods considered, the detail of the dose range where START data occur. Similar results are obtained if the local relapse data are considered instead of local-regional ones.

Figure 2.

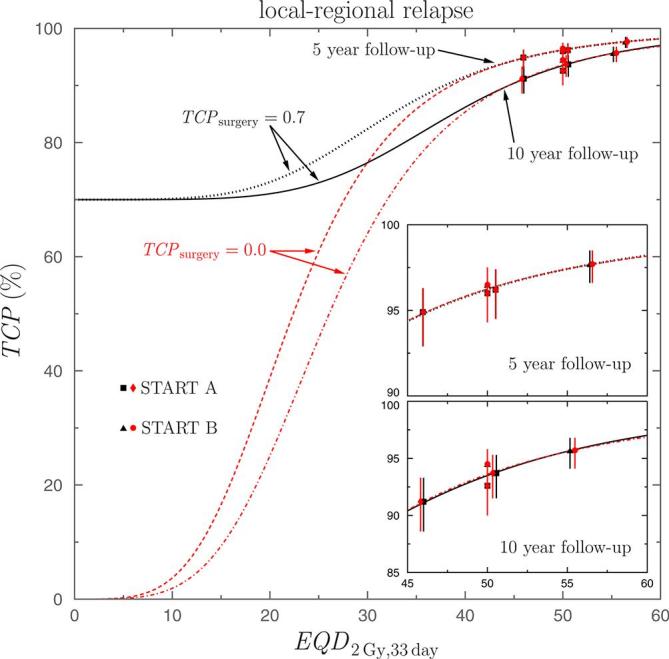
${\displaystyle TCP}$ values found for the local-regional relapses, as a function of the equivalent dose ${\displaystyle EQ{D}_{2\text{Gy},33\text{day}}}$. Results from START A (black squares and red diamonds) and START B (black triangles and red circles) schedules are shown. The curves represent the results obtained by fitting Equation (8) to data. Black dotted and solid curves correspond to ${\displaystyle TC{P}_{\text{surgery}}=0.7,}$ while those found for ${\displaystyle TC{P}_{\text{surgery}}=0}$ are shown with the red dashed and dashed-dotted ones. The upper and lower insets show the dose region where data occur for the 5 and 10 year follow-ups, respectively. START, UK standardization of breast radiotherapy; TCP, tumor control probability.

As it can be seen, the data of the START schedules correspond to a region of the $TCP$ curve showing a rather smooth dependence on the equivalent dose ${EQD}_{2\text{Gy},33\text{day}}$. As the slope of $TCP$ therein is small and the data uncertainties are relatively large, the sampling procedure may generate spurious situations in which the fits to the virtual data sets produce negative values of $D_{50}$ and $\gamma$ that have no sense within the model we have considered. We have determined that the amount of cases in which this occurs is ~ 20% and ~10% for 5 and 10 year follow-ups, respectively. In our analysis, these cases have not been considered, and to avoid artifacts produced in the fitting procedure, we imposed the following restrictions to the fitting parameters: ${\displaystyle D_{50}>0}$, ${\displaystyle \gamma >0}$, ${\displaystyle \alpha /\beta >-4\text{Gy}}$ and ${\displaystyle k<50\text{Gy}{\text{day}}^{-1}}$. In any case, it is worth noting that using the medians as the parameters characterizing the central values of the corresponding distributions makes the final results to be rather independent of the specific values considered for these restrictions.

In Table 3, the results obtained are compared to those found for the other two distributions considered for sampling $R$. The comparison has been done for local relapses and a 10 year follow-up. Similar results are obtained in the other situations. As it can be seen, the average values of the different radiobiological parameters are very similar in the three cases while, as expected, the CIs are slightly larger in the case of the uniform distribution.

Table 3.

Parameter values obtained by using the Monte Carlo procedure for the local relapse data of the START trials, for 10 year follow-up and for ${\displaystyle TC{P}_{\text{surgery}}=0.7}$. Here, the results obtained with the three distributions considered for the sampling of R within the CI are compared.

		START A/B (this work)
Local relapse (10 year follow up)
${TCP}_{\text{surgery}}$	Parameters	${\displaystyle g\left(R\right)}$	${\displaystyle N\left[{\mu }_{\text{N}},{\sigma }_{\text{N}}\right]}$	${\displaystyle U\left[R_{\text{low}},R_{\text{high}}\right]}$
0.7	${\displaystyle D_{50}(\text{Gy)}}$	38.52 [16.92,44.06]	38.48 [16.05,44.15]	38.96 [13.21,44.48]
${\displaystyle \gamma }$	1.34 [0.31,2.68]	1.28 [0.28,2.64]	1.35 [0.24,2.78]
${\displaystyle \alpha /\beta (\text{Gy)}}$	3.33 [1.37,13.07]	3.42 [1.35,13.74]	3.32 [1.04,15.48]
${\displaystyle k\text{(Gy}{\text{day}}^{-1})}$	1.17 [0.64,4.77]	1.21 [0.68,5.51]	1.18 [0.64,7.14]
${\displaystyle k_{2\text{Gy}}\text{(Gy}{\text{day}}^{-1})}$	0.73 [0.41,2.88]	0.77 [0.43,3.08]	0.74 [0.41,4.09]

START, UK standardization of breast radiotherapy; TCP, tumor control probability.

Discussion

As our procedure has permitted us to obtain the dependence of $TCP$ as a function of ${EQD}_{2\text{Gy},33\text{day}}$ (Figure 2), it could be used to analyze any breast cancer treatment schedule whose configuration is within the limits of applicability of the LQ model. This is so because ${EQD}_{2\text{Gy},33\text{day}}$ can be evaluated from the parameters characteristic of the specific schedule: the total dose, the dose per fraction and the overall treatment time. It should be highlighted the particular importance of the later in the calculation of the equivalent dose, crucial in the case of the hypofractionated schedules that are commonly prescribed nowadays.

Once the $TCP$ vs ${EQD}_{2\text{Gy},33\text{day}}$ model has been established, the radiobiological parameters defining it can be obtained and analyzed. So the time factor values, both $k$ and $k_{2\text{Gy}}$, and the corresponding CIs obtained for the local-regional relapses are very similar to those found for the local ones. However, the quantities $D_{50}$ and $\gamma$ are slightly smaller and larger, respectively, for local relapses. Nevertheless, this has almost no influence on the $TCP$ curves. In fact, the fitted $TCP\text{s}$ agree within $\pm 1\%$.

The $\alpha /\beta$ ratio found for the local-regional relapses is larger than that obtained for the local ones. However, while in the former case the values found for 5 and 10 year follow-ups are very close, in the latter the $\alpha /\beta$ value found for 5 year follow-up is 10% smaller than that corresponding to the 10 year one.

The parameters obtained for the local-regional relapses may be compared to those quoted as results of the START schedules. For $\alpha /\beta$ START A found $4.0\left[\mathrm{0.0,8.9}\right]\text{Gy}$, and the START pilot trial $3.5\left[\mathrm{1.2,5.7}\right]\text{Gy}$.³ The medians we have found for the two follow-up periods considered are in good agreement with these START results, though our CIs show a larger queue toward high values of the parameter.

On the other hand, the combined analysis of START A, B and pilot trials has produced, for local-regional relapse, a time factor ${\displaystyle k_{2\text{Gy}}=0.65\left[0.12,1.66\right]\text{Gy}{\text{day}}^{-1}}$.⁴ Despite the overlap between the CI of this value and ours, the time factor we have estimated with our procedure is noticeably larger, being of the order of those usually found for head and neck tumors.

As expected, when the follow-up time goes from 5 to 10 year, $D_{50}$ increases and $TCP$ reduces. On the contrary, the $\gamma$ distribution remains practically the same. Independently of the tumor control that can be ascribed to surgery, the normalized slope of the $TCP$ curve at ${EQD}_{2\text{Gy},33\text{day}}=50\text{Gy}$ is 0.15 and 0.25 for the follow ups of 5 and 10 years, respectively. These values are important in what respect to the clinical improvement that can be expected from a given enhancement of ${\displaystyle EQ{D}_{2\text{Gy},33\text{day}}.}$ However, that improvement is small and shows a drawback of the START data that had been pointed out by the START Trial Management Group.⁴ This is due to the fact that only a single scheme in which the treatment duration changes with a significant increase of ${EQD}_{2\text{Gy},33\text{day}}$ is available in START trials.

The results just discussed were obtained by assuming ${TCP}_{\text{surgery}}=0.7$.^{7, 8} As the important point would be to evaluate the impact of surgery in the final tumor control and, as a consequence, in the estimated radiobiological parameters, we considered the extreme value ${TCP}_{\text{surgery}}=0$. In this way, we quantified the maximum effect that may be attributable to uncertainties in the ratio of cures due to surgery. The results obtained are included in Table 2 and the distributions of the parameters of interest are shown in Figure 1 with red solid squares for the local-regional relapses and with red solid curves for the local ones. In Figure 2 the corresponding $TCP$ data obtained in this case are shown with red diamonds and circles (for START A and B, respectively) and the red dashed and dashed-dotted curves correspond to the fits found for 5 and 10 year follow-ups, respectively.

In what refers to the parameter distributions we see in Figure 1 that significant changes occur for those corresponding to $D_{50}$ and $\gamma$, while those of $\alpha /\beta$ and $k_{2\text{Gy}}$ remain almost unaltered. This is due to the fact that the START data analyzed are all of them at relatively large doses, for ${EQD}_{2\text{Gy},33\text{day}}$ above 45 Gy, and therein the $TCP$ curves fitted are practically unaffected by the value of ${TCP}_{\text{surgery}}$. As it can be seen in Figure 2 the curves corresponding to ${TCP}_{\text{surgery}}=0$ overlap those found to ${TCP}_{\text{surgery}}=0.7$ at these high doses. The differences between the $TCP$ curves corresponding to the two values of ${TCP}_{\text{surgery}}$ appear at lower doses.

The fact that the three different distributions considered for the relapse values produce very similar mean radiobiological parameters (as seen in Table 3) indicates that the method is robust. Even if the CI are unknown, adequate central values of the parameters of interest can be obtained. On the other hand, and as it is obvious, the uncertainties of these parameters depend on the specific distributions considered, being larger for the distributions with less information (the uniform one in our case). It is worth pointing out that by taking directly the normal distribution (instead of the transformation that symmetrizes the CI) shows up a minimal influence in these uncertainties.

We have applied our method to a specific case (START) in which the authors have published their outcomes and have calculated the derived radiobiological parameters. Starting from the outcomes of the START trials, we have been able to obtain several derived radiobiological quantities whose values compare rather well with those provided by the trial conductors. Then, our method permits to analyze the coherence between these derived quantities and the published outcomes.

In the case the raw data of a trial are not available and derived quantities have not been calculated, our tool allows obtaining such derived quantities producing an useful information.

Part of the uncertainties of the results of a method like the one we are proposing are related to the method itself. But, a non-negligible component of them is linked to the size of the CIs ( i.e. to the quality) of the trial outcome data used as inputs. Our method produces larger uncertainties in the derived quantities than those expected from the direct analysis of the raw data; this may be seen as a limitation of the approach, but does not invalidate the overall results.

An important point is that the use of this Monte Carlo procedure permits to include additional information such as the variations in treatment courses (e.g. patients receiving a tumor bed boost), or the variability of the various quantities entering into the problem (absorbed dose, dose per fraction, actual week day when treatments begin, and other).¹¹ The knowledge of these data would permit to obtain better and feasible results, at least a priori.

Conclusions

In this work we have performed an independent analysis of the results of the START trials using a method based on a Monte Carlo approach that does not require the detailed knowledge of participating patients.

The relation $TCP$ vs ${EQD}_{2\text{Gy},33\text{day}}$ reproducing the trial outcomes has been obtained, including the surgery contribution, and the radiobiological parameters of clinical interest have been determined using it.

The values obtained for the $\alpha /\beta$ parameter are similar to those of the START estimations and this can be considered as an independent confirmation of their validity. Our results show large time factors for breast cancer, of the same order as those estimated for head and neck cancers.

The basic statistical methods used make the methodology presented here general enough to be applied to other trials.